Features of Metalorganic Chemical Vapor Deposition Selective Area Epitaxy of AlzGa1−zAs (0 ≤ z ≤ 0.3) Layers in Arrays of Ultrawide Windows
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabrication of Experimental Samples
2.2. SAE Simulation Model
3. Results and Discussion
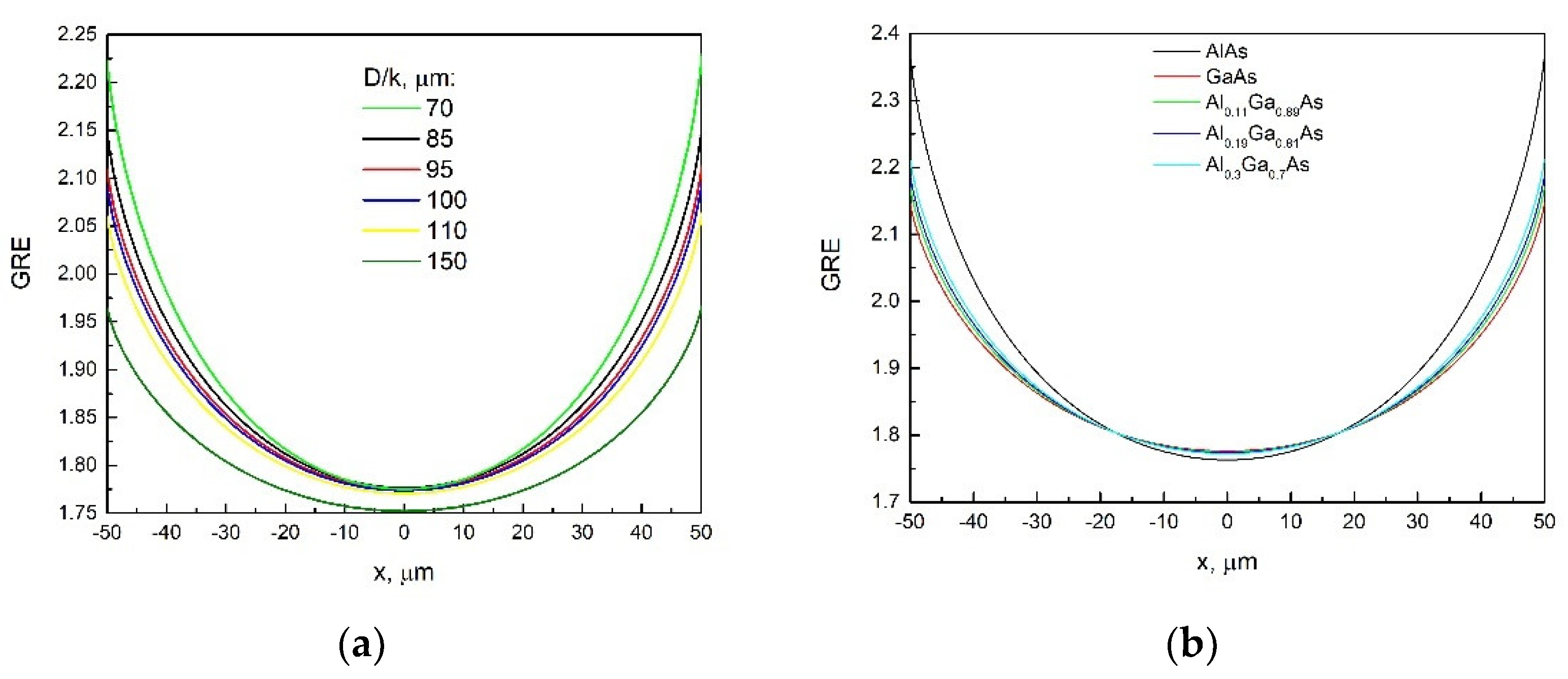
3.1. Studies of the SAE-Grown AlGaAs Layers’ Thickness Profiles across the Window
3.2. Studies of the SAE-Grown AlGaAs Layers’ Composition Profiles across the Window
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Williams, K.A.; Bente, E.A.J.M.; Heiss, D.; Jiao, Y.; Ławniczuk, K.; Leijtens, X.J.M.; van der Tol, J.J.G.M.; Smit, M.K. InP photonic circuits using generic integration [Invited]. Photon. Res. 2015, 3, B60–B68. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Li, X. III–V Nanowire Transistors for Low-Power Logic Applications: A Review and Outlook. IEEE Trans. Electron. Devices 2016, 63, 223–234. [Google Scholar] [CrossRef]
- Dietrich, C.P.; Fiore, A.; Thompson, M.G.; Kamp, M.; Höfling, S. GaAs integrated quantum photonics: Towards compact and multi: Functional quantum photonic integrated circuits. Laser Photonics Rev. 2016, 10, 870–894. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Miao, X.; Chabak, K.D.; Li, X. A review of III–V planar nanowire arrays: Selective lateral VLS epitaxy and 3D transistors. J. Phys. D Appl. Phys. 2017, 50, 393001. [Google Scholar] [CrossRef] [Green Version]
- Bogdanov, S.; Shalaginov, M.Y.; Boltasseva, A.; Shalaev, V.M. Material platforms for integrated quantum photonics. Opt. Mater. Express. 2017, 7, 111–132. [Google Scholar] [CrossRef] [Green Version]
- Smit, M.; Williams, K.; van der Tol, J. Past, present, and future of InP-based photonic integration. APL Photonics 2019, 4, 050901. [Google Scholar] [CrossRef] [Green Version]
- Heinecke, H.; Milde, A.; Baur, B.; Matz, R. Selective-area growth of III/V semiconductors in chemical beam epitaxy. Semicond. Sci. Technol. 1993, 8, 1023–1031. [Google Scholar] [CrossRef]
- Coleman, J.J. Metalorganic chemical vapor deposition for optoelectronic devices. Proc. IEEE 1997, 85, 1715–1729. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.D.; Chen, X.; Coleman, J.J. 10 Selective Area Masked Growth (Nano to Micro). In Handbook of Crystal Growth, 2nd ed.; Kuech, T.F., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 3A, pp. 441–481. [Google Scholar] [CrossRef]
- Wang, B.; Zeng, Y.; Song, Y.; Wang, Y.; Liang, L.; Qin, L.; Zhang, J.; Jia, P.; Lei, Y.; Qiu, C.; et al. Principles of Selective Area Epitaxy and Applications in III–V Semiconductor Lasers Using MOCVD: A Review. Crystals 2022, 12, 1011. [Google Scholar] [CrossRef]
- Delprat, D.; Ramdane, A.; Silvestre, L.; Ougazzaden, A.; Delorme, F.; Slempkes, S. 20-Gb/s integrated DBR laser-EA modulator by selective area growth for 1.55-μm WDM applications. IEEE Photon. Technol. Lett. 1997, 9, 898–900. [Google Scholar] [CrossRef]
- Osowski, M.L.; Lammert, R.M.; Coleman, J.J. A dual-wavelength source with monolithically integrated electroabsorption modulators and Y-junction coupler by selective-area MOCVD. IEEE Photon. Technol. Lett. 1997, 9, 158–160. [Google Scholar] [CrossRef]
- Fujii, T.; Takeda, K.; Nishi, H.; Diamantopoulos, N.-P.; Sato, T.; Kakitsuka, T.; Tsuchizawa, T.; Matsuoand, S. Multiwavelength membrane laser array using selective area growth on directly bonded InP on SiO2/Si. Optica 2020, 7, 838–846. [Google Scholar] [CrossRef]
- Xu, J.; Liang, S.; Liu, S.; Qiao, L.; Sun, S.; Deng, Q.; Zhu, H. Passively mode-locked quantum-well laser with a saturable absorber having gradually varied bandgap. IEEE Photon. Technol. Lett. 2017, 29, 889–892. [Google Scholar] [CrossRef]
- Lemaıtre, F.; Latkowski, S.; Fortin, C.; Lagay, N.; Pajkovic, R.; Smalbrugge, E.; Decobert, J.; Ambrosius, H.; Williams, K. Selective area growth in generic integration for extended range tunable laser source. In Proceedings of the 2018 IEEE Photonics Conference (IPC), Reston, VA, USA, 30 September–4 October 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Kim, H.; Wei, W.; Kuech, T.F.; Gopalan, P.; Mawst, L.J. Room temperature operation of InAs quantum dot lasers formed by diblock-copolymer lithography and selective area MOCVD growth. In Proceedings of the 2017 IEEE Photonics Conference (IPC), Orlando, FL, USA, 1–5 October 2017; pp. 405–406. [Google Scholar] [CrossRef]
- Barrigón, E.; Heurlin, M.; Bi, Z.; Monemar, B.; Samuelson, L. Synthesis and applications of III–V nanowires. Chem. Rev. 2019, 119, 9170–9220. [Google Scholar] [CrossRef]
- Nishinaga, T.; Bacchin, G. Selective area MBE of GaAs, AlAs and their alloys by periodic supply epitaxy. Thin Solid Films 2000, 367, 6–12. [Google Scholar] [CrossRef]
- Zannier, V.; Li, A.; Rossi, F.; Yadav, S.; Petersson, K.; Sorba, L. Selective-Area Epitaxy of InGaAsP Buffer Multilayer for In-Plane InAs Nanowire Integration. Materials 2022, 15, 2543. [Google Scholar] [CrossRef]
- Gibbon, M.; Stagg, J.P.; Cureton, C.G.; Thrush, E.J.; Jones, C.J.; Mallard, R.E.; Pritchard, R.E.; Collis, N.; Chew, A. Selective-area low-pressure MOCVD of GaInAsP and related materials on planar InP substrates. Semicond. Sci. Technol. 1993, 8, 998–1010. [Google Scholar] [CrossRef]
- Decobert, J.; Dupuis, N.; Lagreeb, P.Y.; Lagay, N.; Ramdane, A.; Ougazzaden, A.; Poingt, F.; Cuisin, C.; Kazmierski, C. Modeling and characterization of AlGaInAs and related materials using selective area growth by metal-organic vapor-phase epitaxy. J. Cryst. Growth 2007, 298, 28–31. [Google Scholar] [CrossRef]
- Colas, E.; Shahar, A.; Soole, B.D.; Tomlinson, W.J.; Hayes, J.R.; Caneau, C.; Bhat, R. Lateral and longitudinal patterning of semiconductor structures by crystal growth on nonplanar and dielectric-masked GaAs substrates: Application to thickness-modulated waveguide structures. J. Cryst. Growth 1991, 107, 226–230. [Google Scholar] [CrossRef]
- Kayser, O. Selective growth of InP/GaInAs in LP-MOVPE and MOMBE/CBE. J. Cryst. Growth 1991, 107, 989–998. [Google Scholar] [CrossRef]
- Yamaguchi, K.-I.; Okamoto, K. Lateral Supply Mechanisms in Selective Metalorganic Chemical Vapor Deposition. Jpn. J. Appl. Phys. 1993, 32, 1523–1527. [Google Scholar] [CrossRef]
- Sugiyama, M. Selective area growth of III-V semiconductors: From fundamental aspects to device structures. In Proceedings of the 22nd International Conference on Indium Phosphide and Related Materials (IPRM), Kagawa, Japan, 31 May–4 June 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Shamakhov, V.; Nikolaev, D.; Slipchenko, S.; Fomin, E.; Smirnov, A.; Eliseyev, I.; Pikhtin, N.; Kop’ev, P. Surface Nanostructuring during Selective Area Epitaxy of Heterostructures with InGaAs QWs in the Ultra-Wide Window. Nanomaterials 2021, 11, 11. [Google Scholar] [CrossRef] [PubMed]
- Slipchenko, S.; Shamakhov, V.; Nikolaev, D.; Fomin, E.; Soshnikov, I.; Bondarev, A.; Mitrofanov, M.; Pikhtin, N.; Kop’ev, P. Basics of surface reconstruction during selective area metalorganic chemical vapour-phase epitaxy of GaAs films in the stripe-type ultra-wide window. Appl. Surf. Sci. 2022, 588, 152991. [Google Scholar] [CrossRef]
- Yamaguchi, K.-I.; Okamoto, K. Analysis of Deposition Selectivity in Selective Epitaxy of GaAs by Metalorganic Chemical Vapor Deposition. Jpn. J. Appl. Phys. 1990, 29, 2351–2357. [Google Scholar] [CrossRef]
- Eraky, M.S.; Sanad, M.M.S.; El-Sayed, E.M.; Shenouda, A.Y.; El-Sherefy, E.-S. Phase transformation and photoelectrochemical characterization of Cu/Bi and Cu/Sb based selenide alloys as promising photoactive electrodes. AIP Adv. 2019, 9, 115115. [Google Scholar] [CrossRef] [Green Version]
- Eraky, M.S.; Sanad, M.M.S.; El-Sayed, E.M.; Shenouda, A.Y.; El-Sherefy, E.-S. Influence of the electrochemical processing parameters on the photocurrent–voltage conversion characteristics of copper bismuth selenide photoactive films. Eur. Phys. J. Plus 2022, 137, 907. [Google Scholar] [CrossRef]
- Casey, H.C.; Panish, M.B. Heterostructure Lasers Part B: Materials and Operating Characteristics; Academic Press: San Francisco, CA, USA; London, UK, 1978; 344p. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamakhov, V.; Slipchenko, S.; Nikolaev, D.; Soshnikov, I.; Smirnov, A.; Eliseyev, I.; Grishin, A.; Kondratov, M.; Rizaev, A.; Pikhtin, N.; et al. Features of Metalorganic Chemical Vapor Deposition Selective Area Epitaxy of AlzGa1−zAs (0 ≤ z ≤ 0.3) Layers in Arrays of Ultrawide Windows. Technologies 2023, 11, 89. https://doi.org/10.3390/technologies11040089
Shamakhov V, Slipchenko S, Nikolaev D, Soshnikov I, Smirnov A, Eliseyev I, Grishin A, Kondratov M, Rizaev A, Pikhtin N, et al. Features of Metalorganic Chemical Vapor Deposition Selective Area Epitaxy of AlzGa1−zAs (0 ≤ z ≤ 0.3) Layers in Arrays of Ultrawide Windows. Technologies. 2023; 11(4):89. https://doi.org/10.3390/technologies11040089
Chicago/Turabian StyleShamakhov, Viktor, Sergey Slipchenko, Dmitriy Nikolaev, Ilya Soshnikov, Alexander Smirnov, Ilya Eliseyev, Artyom Grishin, Matvei Kondratov, Artem Rizaev, Nikita Pikhtin, and et al. 2023. "Features of Metalorganic Chemical Vapor Deposition Selective Area Epitaxy of AlzGa1−zAs (0 ≤ z ≤ 0.3) Layers in Arrays of Ultrawide Windows" Technologies 11, no. 4: 89. https://doi.org/10.3390/technologies11040089







