Bank Credit Risk Management and Rating Migration Analysis on the Business Cycle
Abstract
:1. Introduction
2. Literature Review
 , they are assumed to be stationary and the Markov chain is also stationary or time-homogeneous [24]. Finally, key macroeconomic factors are argued to be critical inputs to be incorporated in the modeling process, in order to proxy business cycles and states of the economy.
, they are assumed to be stationary and the Markov chain is also stationary or time-homogeneous [24]. Finally, key macroeconomic factors are argued to be critical inputs to be incorporated in the modeling process, in order to proxy business cycles and states of the economy.2.1. First-Order Markov Process
2.2. Time-Homogeneity
2.3. Macroeconomic Factors
3. The Discrete-Time Maximum Likelihood Framework
3.1. Time-Homogeneity in Transition Probabilities
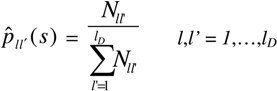
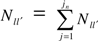 is the total number of verified transitions from l to l’.
is the total number of verified transitions from l to l’.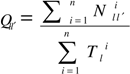
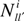 denotes the number of l → l’ transitions made by an obligor i and
denotes the number of l → l’ transitions made by an obligor i and 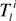 is the overall time that obligor i has spent in class l [26]. This is the duration estimator which counts every rating drift in a given period divided by the total time spent in each rating class. With no information available about the timing of events between observation times or about the exact transition time, neither the numerator nor the denominator of Equation (3) can be calculated [30]. Assuming discrete data (observations corresponding to a sequence of discrete time points), the duration intensities cannot be used to evaluate the transition intensities; moreover, the observation times must be identical and equally spaced, in order for the cohort estimator (Equation (1)) to provide ML estimations.
is the overall time that obligor i has spent in class l [26]. This is the duration estimator which counts every rating drift in a given period divided by the total time spent in each rating class. With no information available about the timing of events between observation times or about the exact transition time, neither the numerator nor the denominator of Equation (3) can be calculated [30]. Assuming discrete data (observations corresponding to a sequence of discrete time points), the duration intensities cannot be used to evaluate the transition intensities; moreover, the observation times must be identical and equally spaced, in order for the cohort estimator (Equation (1)) to provide ML estimations. , Equation (2) develops into Equation (4):
, Equation (2) develops into Equation (4):
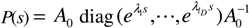
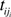 with the rating of firm i as xi0,xi1,…,
with the rating of firm i as xi0,xi1,…, 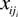 respectively [x ∊{l,…,lD}] and those that are censored at the end of the observation time period.
respectively [x ∊{l,…,lD}] and those that are censored at the end of the observation time period.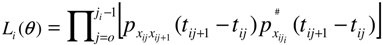
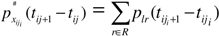
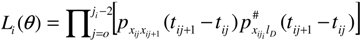
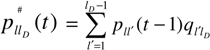
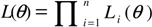
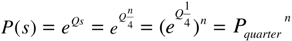
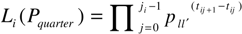
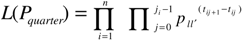
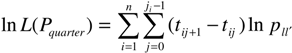
3.2. Business Cycles in Transition Probabilities
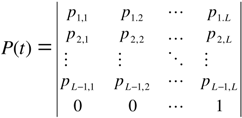
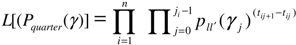
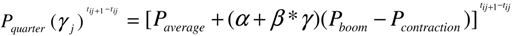
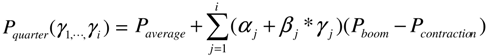
3.3. Statistical Measurements
3.3.1. Singular Value Decomposition Metric

3.3.2. Bootstrap Method
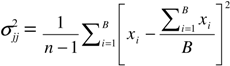
4. Empirical Application
4.1. Macroeconomics and States of the Economy
4.2. Transition Probabilities in Time-Homogeneity
| From → To | 1 | 2 | 3 | 4 | 5 | Default |
|---|---|---|---|---|---|---|
| Panel A: The one-year cohort transition matrix | ||||||
| 1 | 0.96911 | 0.01821 | 0.00553 | 0.00712 | 0.00003 | 0.00000 |
| (0.00173) | (0.00152) | (0.00052) | (0.00023) | (0.00006) | (0.00000) | |
| 2 | 0.01272 | 0.93790 | 0.03723 | 0.01022 | 0.00157 | 0.00036 |
| (0.00093) | (0.00218) | (0.00192) | (0.00081) | (0.00035) | (0.00012) | |
| 3 | 0.00024 | 0.00411 | 0.95197 | 0.03925 | 0.00392 | 0.00051 |
| (0.00004) | (0.00021) | (0.00083) | (0.00073) | (0.00027) | (0.00005) | |
| 4 | 0.00024 | 0.00071 | 0.02382 | 0.95481 | 0.01661 | 0.00381 |
| (0.00003) | (0.00011) | (0.00055) | (0.00076) | (0.00040) | (0.00029) | |
| 5 | 0.00020 | 0.00006 | 0.00482 | 0.05120 | 0.92452 | 0.01920 |
| (0.00012) | (0.00004) | (0.00052) | (0.00240) | (0.00280) | (0.00156) | |
| Default | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 1.00000 |
| Panel B: The one-year discrete-time ML transition matrix | ||||||
| 1 | 0.94045 | 0.04672 | 0.00833 | 0.00388 |  | 0.00039 |
| (0.00283) | (0.00273) | (0.00081) | (0.00052) | (0.00019) | (0.00029) | |
| 2 | 0.03066 | 0.85443 | 0.08177 | 0.02993 | 0.00283 | 0.00038 |
| (0.00188) | (0.00293) | (0.00239) | (0.00193) | (0.00039) | (0.00133) | |
| 3 | 0.00122 | 0.01982 | 0.87608 | 0.09555 | 0.00611 | 0.00122 |
| (0.00017) | (0.00044) | (0.00152) | (0.00121) | (0.00025) | (0.00015) | |
| 4 | 0.00067 | 0.00261 | 0.07211 | 0.87706 | 0.04122 | 0.00633 |
| (0.00007) | (0.00002) | (0.00084) | (0.00249) | (0.00082) | (0.00018) | |
| 5 | 0.00052 | 0.00054 | 0.01883 | 0.13331 | 0.78439 | 0.06241 |
| (0.00026) | (0.00027) | (0.00073) | (0.00422) | (0.00467) | (0.00390) | |
| Default | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 1.00000 |
4.3. Transition Probabilities in Time-Dependence
| From → To | 1 | 2 | 3 | 4 | 5 | Default |
|---|---|---|---|---|---|---|
| Panel A: The one-year cohort transition matrix | ||||||
| 1 | 0.92706 | 0.03771 | 0.03112 | 0.00411 | 0.00000 | 0.00000 |
| (0.019662) | (0.01233) | (0.01781) | (0.00406) | (0.00000) | (0.00000) | |
| 2 | 0.00281 | 0.93668 | 0.04612 | 0.01273 | 0.00166 | 0.00000 |
| (0.00199) | (0.00590) | (0.00441) | (0.00231) | (0.00088) | (0.00000) | |
| 3 | 0.00044 | 0.00551 | 0.94806 | 0.04113 | 0.00482 | 0.00004 |
| (0.00021) | (0.00084) | (0.00272) | (0.00233) | (0.00071) | (0.00022) | |
| 4 | 0.00000 | 0.00022 | 0.02572 | 0.95981 | 0.01322 | 0.00103 |
| (0.00000) | (0.00021) | (0.00162) | (0.00217) | (0.00188) | (0.00044) | |
| 5 | 0.00000 | 0.00000 | 0.00492 | 0.07111 | 0.91564 | 0.00833 |
| (0.00000) | (0.00000) | 0.00182 | 0.00729 | 0.00833 | 0.00281 | |
| Default | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 1.00000 |
| Panel B: The one-year discrete-time ML transition matrix | ||||||
| 1 | 0.83581 | 0.12773 | 0.01222 | 0.02378 | 0.00042 | 0.00004 |
| (0.02773) | (0.02114) | (0.00722) | (0.00872) | (0.00019) | (0.00001) | |
| 2 | 0.00668 | 0.84458 | 0.11729 | 0.02871 | 0.00255 | 0.00019 |
| (0.00198) | (0.00626) | (0.00551) | (0.00277) | (0.00715) | (0.00002) | |
| 3 | 0.00154 | 0.01622 | 0.84838 | 0.12521 | 0.00810 | 0.00055 |
| (0.00048) | (0.00152) | (0.00303) | (0.00322) | (0.00082) | (0.00027) | |
| 4 | 0.00051 | 0.00177 | 0.08221 | 0.87883 | 0.03198 | 0.00470 |
| (0.00021) | (0.00031) | (0.00372) | (0.00333) | (0.00278) | (0.00069) | |
| 5 | 0.00005 | 0.00062 | 0.00923 | 0.13302 | 0.80487 | 0.05221 |
| (0.00002) | (0.00061) | (0.00140) | (0.01662) | (0.01442) | (0.00523) | |
| Default | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 1.00000 |
| From → To | 1 | 2 | 3 | 4 | 5 | Default |
|---|---|---|---|---|---|---|
| Panel A: The one-year ML boom transition matrix | ||||||
| 1 | 0.84978 | 0.11443 | 0.00634 | 0.02877 | 0.00066 |  |
| (0.02555) | (0.02288) | (0.00421) | (0.01729) | (0.00027) | (0.0000) | |
| 2 | 0.00524 | 0.83984 | 0.11960 | 0.03175 | 0.00351 |  |
| (0.00143) | (0.00911) | (0.00832) | (0.00420) | (0.00165) | (0.00002) | |
| 3 | 0.00087 | 0.01332 | 0.85209 | 0.12778 | 0.00582 |  |
| (0.00038) | (0.00144) | (0.00525) | (0.00425) | (0.00096) | (0.00004) | |
| 4 | 0.00053 | 0.00177 | 0.08465 | 0.86928 | 0.04230 | 0.00147 |
| (0.00024) | (0.00048) | (0.00363) | (0.00488) | (0.00264) | (0.00049) | |
| 5 |  | 0.00133 | 0.00843 | 0.27555 | 0.67904 | 0.03559 |
| (0.00002) | (0.00096) | (0.00061) | (0.01664) | (0.01773) | (0.00521) | |
| Default | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 1.00000 |
| Panel B: The one-year ML contraction transition matrix | ||||||
| 1 | 0.79315 | 0.18223 | 0.01223 | 0.01188 | 0.00048 |  |
| (0.03882) | (0.03216) | (0.008150) | (0.01929) | (0.00028) | (0.00001) | |
| 2 | 0.00799 | 0.83415 | 0.12833 | 0.02811 | 0.00126 |  |
| (0.00221) | (0.00836) | (0.00825) | (0.00372) | (0.00182) | (0.00003) | |
| 3 | 0.00187 | 0.01722 | 0.86320 | 0.10277 | 0.01322 | 0.00172 |
| (0.00056) | (0.00177) | (0.00523) | (0.00449) | (0.00142) | (0.00033) | |
| 4 | 0.00032 | 0.00066 | 0.08280 | 0.86913 | 0.04221 | 0.00488 |
| (0.00028) | (0.00015) | (0.00427) | (0.00522) | (0.00303) | (0.00161) | |
| 5 |  |  | 0.01722 | 0.27731 | 0.65329 | 0.05208 |
| (0.00002) | (0.00003) | (0.00466) | (0.01662) | (0.01734) | (0.00911) | |
| Default | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 1.00000 |
| From → To | 1 | 2 | 3 | 4 | 5 | Default |
|---|---|---|---|---|---|---|
| Panel A: The one-year ML boom transition matrix | ||||||
| 1 | 0.83987 | 0.11701 | 0.01752 | 0.02505 | 0.00051 | 0.00004 |
| 2 | 0.00611 | 0.84785 | 0.11761 | 0.02551 | 0.00276 | 0.00016 |
| 3 | 0.00177 | 0.01882 | 0.85582 | 0.11662 | 0.00623 | 0.00074 |
| 4 | 0.00063 | 0.00152 | 0.08339 | 0.87966 | 0.03119 | 0.00361 |
| 5 | 0.00005 | 0.00094 | 0.00735 | 0.29901 | 0.64047 | 0.05218 |
| Default | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 1.00000 |
| γi = 89.81 (i = 1, 2, 3, 4) | ||||||
| Panel B: The one-year ML contraction transition matrix | ||||||
| 1 | 0.7785 | 0.17772 | 0.02881 | 0.01455 | 0.00038 | 0.00004 |
| 2 | 0.00731 | 0.84295 | 0.12673 | 0.02117 | 0.00166 | 0.00018 |
| 3 | 0.00155 | 0.01773 | 0.84886 | 0.11732 | 0.01282 | 0.00172 |
| 4 | 0.00038 | 0.00722 | 0.08221 | 0.86740 | 0.03661 | 0.00618 |
| 5 | 0.00003 | 0.00009 | 0.01662 | 0.17629 | 0.73488 | 0.07209 |
| Default | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 1.00000 |
| γi = 69.23 (i = 1, 2, 3, 4) | ||||||
| Panel C: The one-year ML average transition matrix | ||||||
| 1 | 0.81204 | 0.14422 | 0.01442 | 0.02884 | 0.00044 | 0.00004 |
| 2 | 0.00644 | 0.82010 | 0.14802 | 0.02319 | 0.00211 | 0.00014 |
| 3 | 0.00141 | 0.01622 | 0.83144 | 0.14290 | 0.00711 | 0.00092 |
| 4 | 0.00052 | 0.00162 | 0.08518 | 0.86802 | 0.03981 | 0.00485 |
| 5 | 0.00005 | 0.00070 | 0.00852 | 0.16619 | 0.77172 | 0.05282 |
| Default | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 1.00000 |
| γi = 74.33 (i = 1, 2, 3, 4) | ||||||
| Panel D: The one-year ML mixed transition matrix | ||||||
| 1 | 0.82524 | 0.12773 | 0.01883 | 0.02771 | 0.00044 | 0.00005 |
| 2 | 0.00641 | 0.85217 | 0.11662 | 0.02188 | 0.00275 | 0.00017 |
| 3 | 0.00177 | 0.01622 | 0.87185 | 0.10031 | 0.00851 | 0.00134 |
| 4 | 0.00057 | 0.00166 | 0.08510 | 0.87538 | 0.03287 | 0.00442 |
| 5 | 0.00004 | 0.00056 | 0.00955 | 0.17739 | 0.75950 | 0.05296 |
| Default | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 1.00000 |
| γ1 = 89.81; γ2 = 74.33; γ3 = 74.33; γ4 = 69.23 | ||||||
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Basel Committee on Banking Supervision (BCBS). Principles for the Management of Credit Risk. Basel, Switzerland: Bank for International Settlements, 2000. [Google Scholar]
- Basel Committee on Banking Supervision (BCBS). International Convergence of Capital Measurement and Capital Standards: A Revised Framework. Basel, Switzerland: Bank for International Settlements and Basel Committee on Banking Supervision Publications, 2004. [Google Scholar]
- Basel Committee on Banking Supervision (BCBS). Guidelines for Computing Capital for Incremental Risk in the Trading Book. Basel, Switzerland: Bank for International Settlements, 2009. [Google Scholar]
- J. Hull. Risk Management and Financial Institutions, 3rd ed. Hoboken, NJ, USA: Wiley Finance, 2012. [Google Scholar]
- M.B. Gordy. “A risk-factor model foundation for ratings-based bank capital rules.” J. Financ. Intermed. 12 (2003): 199–232. [Google Scholar] [CrossRef]
- T. Van Gestel, and B. Baesens. Credit Risk Management: Basic Concepts: Financial Risk Components, Rating Analysis, Models, Economic and Regulatory Capital. Oxford, UK: Oxford University Press, 2009. [Google Scholar]
- A. Saunders, and L. Allen. Credit Risk Measurement In and Out of the Financial Crisis: New Approaches to Value at Risk and Other Paradigms, 3rd ed. Hoboken, NJ, USA: Wiley Finance, 2010. [Google Scholar]
- A Andersson, and P. Vanini. “Credit Migration Risk Modelling. National Centre of Competence in Research Financial Valuation and Risk Management.” Working Paper No. 539. 9 June 2009. [Google Scholar]
- A. De Servigny, and O. Renault. Measuring and Managing Credit Risk. Columbus, OH, USA: McGraw Hill, 2004. [Google Scholar]
- F. Rikkers, and A.E. Thibeault. “The optimal rating philosophy for the rating of SMEs.” Vlerick Leuven Gent Management School. 2007. [Google Scholar] [CrossRef]
- E.I. Altman, and A. Saunders. “Credit risk measurement: Developments over the last 20 years.” J. Bank. Financ. 21 (1998): 1721–1742. [Google Scholar] [CrossRef]
- Y. Tsaig, A. Levy, and Y. Wang. “Analysing the impact of credit migration in a portfolio setting.” J. Bank. Financ. 35 (2011): 3145–3157. [Google Scholar] [CrossRef]
- B. Belkin, S. Suchover, and L. Forest. “A one-parameter representation of credit risk and transition matrices.” Credit Metr. Monit. 1 (1998): 46–56. [Google Scholar]
- J. Kim. “Conditioning the transition matrix.” Credit Risk, 1999, October. 37–40. [Google Scholar]
- A. Bangia, F.X. Diebold, A. Kronimus, C. Schagen, and T. Schuermann. “Ratings migration and the business cycle, with application to credit portfolio stress testing.” J. Bank. Financ. 26 (2002): 445–474. [Google Scholar] [CrossRef]
- J. Wei. “A multi-factor, credit migration model for sovereign and corporate debts.” J. Int. Money Financ. 22 (2003): 709–735. [Google Scholar] [CrossRef]
- F. Fei, A.M. Fuertes, and E. Kalotychou. “Credit rating migration risk and business cycles.” J. Bus. Financ. Account. 39 (2012): 229–263. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia. “Maximum likelihood estimation of discretely sampled diffusions: A closed-form approximation approach.” Econometrica 70 (2002): 223–262. [Google Scholar] [CrossRef]
- S. Rabe-Hesketh, A. Skrondalb, and A. Pickles. “Maximum likelihood estimation of limited and discrete dependent variable models with nested random effects.” J. Econom. 128 (2005): 301–323. [Google Scholar] [CrossRef]
- R.L. Chambers, D.G. Steel, S. Wang, and A.H. Welsh. Maximum Likelihood Estimation for Sample Surveys. Boca Raton, FL, USA: Taylor and Francis Group, 2012. [Google Scholar]
- Basel Committee on Banking Supervision (BCBS). International Convergence of Capital Measurement and Capital Standards: A Revised Framework. Basel, Switzerland: Bank for International Settlements, 2006. [Google Scholar]
- S. Truck. “Forecasting credit migration matrices with business cycle effects: A model comparison.” Eur. J. Financ. 14 (2008): 359–379. [Google Scholar] [CrossRef]
- S. Truck, and T. Rachev. Rating Based Modelling. of Credit Risk: Theory and Application of Migration Matrices. Amsterdam, The Netherlands: Elsevier Academic Press, 2009. [Google Scholar]
- E. Regina, J. Rodrigues, and A. Achcar. Applications of Discrete-Time Markov Chains and Poisson Processes to Air Pollution Modelling and Studies. New York, NY, USA: Springer, 2013. [Google Scholar]
- E.I. Altman, and D.L. Kao. “The implications of corporate bond ratings drift.” J. Financ. Anal. 48 (1992): 64–67. [Google Scholar] [CrossRef]
- D. Lando, and T.M. Skodeberg. “Analysing rating transitions and rating drift with continuous observations.” J. Bank. Financ. 26 (2002): 423–444. [Google Scholar] [CrossRef]
- J. Christensen, E. Hansen, and D. Lando. “Confidence sets for continuous-time rating transition probabilities.” J. Bank. Financ. 28 (2004): 2575–2602. [Google Scholar] [CrossRef]
- A. Guttler, and P. Raupach. “The impact of downward rating momentum.” J. Financ. Serv. Res. 37 (2010): 1–23. [Google Scholar] [CrossRef]
- A. Arvanitis, J. Gregory, and J.P. Laurent. “Building models for credit spreads.” J. Deriv. 6 (1999): 27–43. [Google Scholar] [CrossRef]
- T. Mahlmann. “Estimation of rating class transition probabilities with incomplete data.” J. Bank. Financ. 30 (2006): 3235–3256. [Google Scholar] [CrossRef]
- D.T. Hamilton, and R. Cantor. “Rating Transition and Default Rates Conditioned on Outlooks.” J. Fixed Income. 14 (2004): 54–70. [Google Scholar] [CrossRef]
- N.M. Kiefer, and C.E. Larson. “A simulation estimator for testing the time-homogeneity of credit rating transitions.” J. Empir. Financ. 14 (2007): 818–835. [Google Scholar] [CrossRef]
- H. Frydman, and T. Schuermann. “Credit rating dynamics and Markov mixture models.” J. Bank. Financ. 32 (2008): 1062–1075. [Google Scholar] [CrossRef]
- S. Hanson, H. Pesaran, and T. Schuermann. Firm Heterogeneity and Credit Risk Diversification. Working Paper; Philadelphia, PA, USA: Wharton Financial Institutions Centre, 2007. [Google Scholar]
- D. Parnes. “Time series patterns in credit ratings.” Financ. Res. Lett. 4 (2007): 217–226. [Google Scholar] [CrossRef]
- A. McNeil, and J. Wendin. “Bayesian inference for generalized linear mixed models of portfolio credit risk.” J. Empir. Financ. 14 (2007): 131–149. [Google Scholar] [CrossRef]
- C. Czado, and C. Pfluger. “Modelling dependencies between rating categories and their effects on prediction in a credit risk portfolio.” Appl. Stoch. Models Bus. Ind. 24 (2008): 237–259. [Google Scholar] [CrossRef]
- P. Nickell, W. Perraudin, and S. Varotto. “Stability of rating transitions.” J. Bank. Financ. 24 (2000): 203–227. [Google Scholar] [CrossRef]
- Y. Jafry, and T. Schuermann. “Measurement, estimation and comparison of credit migration matrices.” J. Bank. Financ. 28 (2004): 2603–2639. [Google Scholar] [CrossRef]
- S. Truck, and T. Rachev. “Credit portfolio risk and probability of default confidence sets through the business cycle.” J. Credit Risk 1 (2005a): 61–88. [Google Scholar]
- R. Weissbach, and H. Dette. “Kolmogorov–Smirnov-type testing for the partial homogeneity of Markov processes with application to credit risk.” Appl. Stoch. Models Bus. Ind. 23 (2007): 223–234. [Google Scholar] [CrossRef]
- S. Hanson, and T. Schuermann. “Confidence intervals for probabilities of default.” J. Bank. Financ. 30 (2006): 2281–2301. [Google Scholar] [CrossRef]
- K. Kadam, and P. Lenk. “Bayesian inference for issuer heterogeneity in credit ratings migration.” J. Bank. Financ. 32 (2008): 2267–2274. [Google Scholar] [CrossRef]
- T. Wilson. “Portfolio credit risk.” Econ. Policy Rev. 4 (1998): 71–82. [Google Scholar]
- F.X. Diebold, and R.S. Mariano. “Comparing predictive accuracy.” J. Bus. Econ. Stat. 20 (2002): 134–144. [Google Scholar] [CrossRef]
- D. Kavvathas. Estimating Credit Rating Transition Probabilities for Corporate Bonds. Working Paper; Chicago, IL, USA: AFA New Orleans Meeting, 2001. [Google Scholar]
- K. Carling, T. Jacobson, J. Linde, and K. Roszbach. Capital Charges under Basel II: Corporate Credit Risk Modelling and the Macroeconomy. Working Paper, No. 142; Stockholm, Sweden: Sveriges Riksbank, 2002. [Google Scholar]
- F. Couderc, and O. Renault. Time-to-Default: Life Cycle, Global and Industry Cycle Impacts. Working Paper, No. 142; Geneva, Switzerland: International Center for Financial Asset Management and Engineering, University of Geneva, 2005. [Google Scholar]
- D. Duffie, L. Saita, and K. Wang. “Multi-period corporate default prediction with stochastic covariates.” J. Financ. Econ. 83 (2007): 635–665. [Google Scholar] [CrossRef]
- P. Fledelius, D. Lando, and J.P. Nielsen. “Non-parametric analysis of rating transition and default data.” J. Invest. Manag. 2 (2004): 71–85. [Google Scholar]
- S.J. Koopman, and A. Lucas. “Business and default cycles for credit risk.” J. Appl. Econom. 20 (2005): 311–323. [Google Scholar] [CrossRef]
- S.J. Koopman, A. Lucas, and P. Klaassen. “Empirical credit cycles and capital buffer formation.” J. Bank. Financ. 29 (2005): 3159–3179. [Google Scholar] [CrossRef]
- S. Truck, and T. Rachev. Changes in Migration Matrices and Credit VAR. A New Class. of Difference Indices. Working Paper; Karlsruhe, Germany: University of Karlsruhe. p. 2005b.
- P. Gagliardini, and C. Gourieroux. “Migration correlation: Definition and efficient estimation.” J. Bank. Financ. 29 (2005): 865–894. [Google Scholar] [CrossRef]
- S.J. Koopman, and A. Lucas. “A non-Gaussian panel time series model for estimating and decomposing default risk.” J. Bus. Econ. Stat. 26 (2007): 510–525. [Google Scholar] [CrossRef]
- S.J. Koopman, A. Lucas, and A. Monteiro. “The multi-state latent factor intensity model for credit rating transitions.” J. Econom. 142 (2008): 399–424. [Google Scholar] [CrossRef]
- D. Feng, C. Gourieroux, and J. Jasiak. “The ordered qualitative model for rating transitions.” J. Empir. Financ. 15 (2008): 111–130. [Google Scholar] [CrossRef]
- K. Banachewicz, A. Lucas, and A. van der Vaart. “Modelling portfolio defaults using hidden Markov models with covariates.” Econom. J. 11 (2008): 155–171. [Google Scholar] [CrossRef]
- T. Rolski, H. Schmidli, V. Schmidt, and J. Teugels. Stochastic Processes for Insurance and Finance. Chichester, UK: John Wiley & Sons, 1999. [Google Scholar]
- D.R. Cox, and H.D. Miller. The Theory of Stochastic Processes. London, UK: Chapman & Hall, 1965. [Google Scholar]
- J.D. Kalbfleisch, and J.F. Lawless. “The analysis of panel data under a Markov assumption.” J. Am. Stat. Assoc. 80 (1985): 863–871. [Google Scholar] [CrossRef]
- J.D. Kalbfleisch, J.F. Lawless, and W.M. Vollmer. “Estimation in Markov models from aggregate data.” Biometrics 39 (1983): 907–919. [Google Scholar] [CrossRef]
- Q. Dai, K.G. Singleton, and W. Yang. “Regime shifts in a dynamic term structure.” Rev. Financ. Stud. 20 (2007): 1669–1706. [Google Scholar] [CrossRef]
- A. Blochlinger. Linking the TTC and PIT Default Probabilities. Working Paper; Zürcher, Switzerland: Kantonalbank, 2008. [Google Scholar]
- J.A. Bennell, D. Crabbe, S. Thomas, and O. Gwilym. “Modelling sovereign credit ratings: Neural networks versus ordered probit.” Expert Syst. Appl. 30 (2006): 415–425. [Google Scholar] [CrossRef]
- H. Xing, N. Sun, and Y. Chen. “Credit rating dynamics in the presence of unknown structural breaks.” J. Bank. Financ. 36 (2012): 78–89. [Google Scholar] [CrossRef]
- H. Abdi. “The Singular Value Decomposition.” In Encyclopedia of Measurement and Statistics. Edited by N. Salkind. Thousand Oaks, CA, USA: Sage, 2007, pp. 907–912. [Google Scholar]
- B. Efron, and R.J. Tibshirani. An. Introduction to the Bootstrap. New York, NY, USA: Chapman & Hall, 1993. [Google Scholar]
- D.W.K. Andrews, and M. Buchinsky. “On the number of bootstrap repetitions for BCa confidence intervals.” Econom. Theory 18 (2002): 962–984. [Google Scholar]
- Moody’s. Ratings Symbols and Definitions. New York, NY, USA: Moody’s Investors Service. p. 2009.
- Fitch Ratings. Definitions of Ratings and Other Forms of Opinion. New York, NY, USA: Ratings Definitions, Ratings Research, Fitch Ratings, 2012. [Google Scholar]
- Standard & Poor’s. What Are Credit Ratings and How Do They Work? Guide to Credit Rating Essentials, Version 1.4. New York, NY, USA: Standard & Poor’s, 2011. [Google Scholar]
- W.F. Treacy, and M. Carey. “Credit risk rating systems at large US banks.” J. Bank. Finance. 24 (2000): 167–201. [Google Scholar] [CrossRef]
- S. Figlewski, H. Frydman, and W. Liang. “Modelling the effect of macroeconomic factors on corporate default and credit rating transitions.” Int. Rev. Econ. Financ. 21 (2012): 87–105. [Google Scholar] [CrossRef]
- C. Stefanescu, R. Tunaru, and S. Turnbull. “The credit rating process and estimation of transition probabilities: A Bayesian approach.” J. Empir. Financ. 16 (2009): 216–234. [Google Scholar] [CrossRef]
- C. Corrado, and J. Mattey. “Capacity utilization.” J. Econ. Perspect. 11 (1997): 151–167. [Google Scholar] [CrossRef]
- B. Baumohl. The Secrets of Economic Indicators: Hidden Clues to Future Economic Trends and Investment Opportunities, 3rd ed. Upper Saddle River, NJ, USA: Wharton School Publishing, 2012. [Google Scholar]
- G. Delianedis, and R. Geske. Credit Risk and Risk Neutral Default Probabilities: Information about Rating Migrations and Defaults. Working Paper; Los Angeles, CA, USA: The Anderson School, UCLA, 1998. [Google Scholar]
- M. Livingston, A. Naranjo, and L. Zhou. “Split bond ratings and rating migration.” J. Bank. Financ. 32 (2008): 1613–1624. [Google Scholar] [CrossRef]
- D. Van Deventer, and K. Imai. Credit Risk Models and the Basel Accords. New York, NY, USA: Wiley Finance, 2003. [Google Scholar]
- 1Whereas “credit rating migration probabilities” characterize the probability of a credit rating being upgraded, downgraded or remaining unchanged within a specific time period, “credit migration matrices” characterize the evolution of credit quality for issuers with the same approximate likelihood of default; they are constructed by mapping the rating history of the entities into transition probabilities.
- 2Similar to a probability transition matrix, an intensity matrix, Q, can be constructed, containing all possible intensities between various states. An outcome containing K states, for instance, would have the following intensity matrix, Q:Q(t) =
. The following constraints apply on the row entries, qij(t), of intensity matrices: (a) the off-diagonals must be non-negative, i.e., qij(t)≥0 for i ≠ j; (b) the rows must sum to zero i.e.,
= 0 [59].
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gavalas, D.; Syriopoulos, T. Bank Credit Risk Management and Rating Migration Analysis on the Business Cycle. Int. J. Financial Stud. 2014, 2, 122-143. https://doi.org/10.3390/ijfs2010122
Gavalas D, Syriopoulos T. Bank Credit Risk Management and Rating Migration Analysis on the Business Cycle. International Journal of Financial Studies. 2014; 2(1):122-143. https://doi.org/10.3390/ijfs2010122
Chicago/Turabian StyleGavalas, Dimitris, and Theodore Syriopoulos. 2014. "Bank Credit Risk Management and Rating Migration Analysis on the Business Cycle" International Journal of Financial Studies 2, no. 1: 122-143. https://doi.org/10.3390/ijfs2010122






