Multi-Decadal Trend and Decadal Variability of the Regional Sea Level over the Indian Ocean since the 1960s: Roles of Climate Modes and External Forcing
Abstract
:1. Introduction
1.1. Background
1.2. Present Research
2. Materials and Methods
2.1. Datasets: Sea Level and Surface Wind
2.2. Large Ensemble (LE) Experiment Results from Two Climate Models
2.3. Datasets for Climate Modes and Other Climate Indices
2.4. The Bayesian DLM and Partial DLM
2.5. Choice of Analysis Region
3. Results
3.1. Multi-Decadal Trends
3.2. Decadal Variations
3.2.1. Natural Internal Variability Versus External Forcing
3.2.2. Effects of Climate Modes
3.3. Influences of Winds Associated with Climate Modes
4. Summary and Discussions
- (1)
- For the 48-yr trend pattern of the sea level (with global SLR removed) from 1958–2005, natural internal variability dominates the external forcing in causing the spatially uneven sea level change patterns over the IO, with natural variability (external forcing) accounting for ~81% (19 ± 2.4%) of the observed falling trend over the Seychelles Islands where both the observed and externally forced trends obtain their maxima (Figure 2). These percentage values are obtained using the average of ORAS4 and SODA to represent the observation and the 100-member mean of the external forcing ensemble, with each member being the ensemble average of 98 members (70% of 140) randomly chosen from the 140 members of the two climate models (100 from MPI and 40 from CESM1), to represent external forcing (Table 1; see Section 3.1 for detailed descriptions on the Monte Carlo method of assessing external forcing and uncertainty). This is because large quantitative or even qualitative differences exist in some regions between ORAS4 and SODA data and between the MPI and CESM1 results (Figure 2, Figure 3 and Figure 4), even though both reanalysis data produce similar basin-wide patterns. The ORAS4 product agrees the best with the AVISO sea level since 1993 (pattern correlation r = 0.84) compared to SODA (r = 0.48) and the thermosteric sea level (Figure 3), likely due to the ORAS4 assimilated satellite-observed sea level data. The 100-member ensemble mean agrees well with the subsamples of the 40-member ensemble means of the MPI model, even though some quantitative differences remain in some regions. This suggests that 40-member ensemble averages can reasonably damp internal variability in the multi-decadal trend, and the large differences between the MPI and CESM1 simulations result from the model dependence of the sea level response to the same external forcing.
- (2)
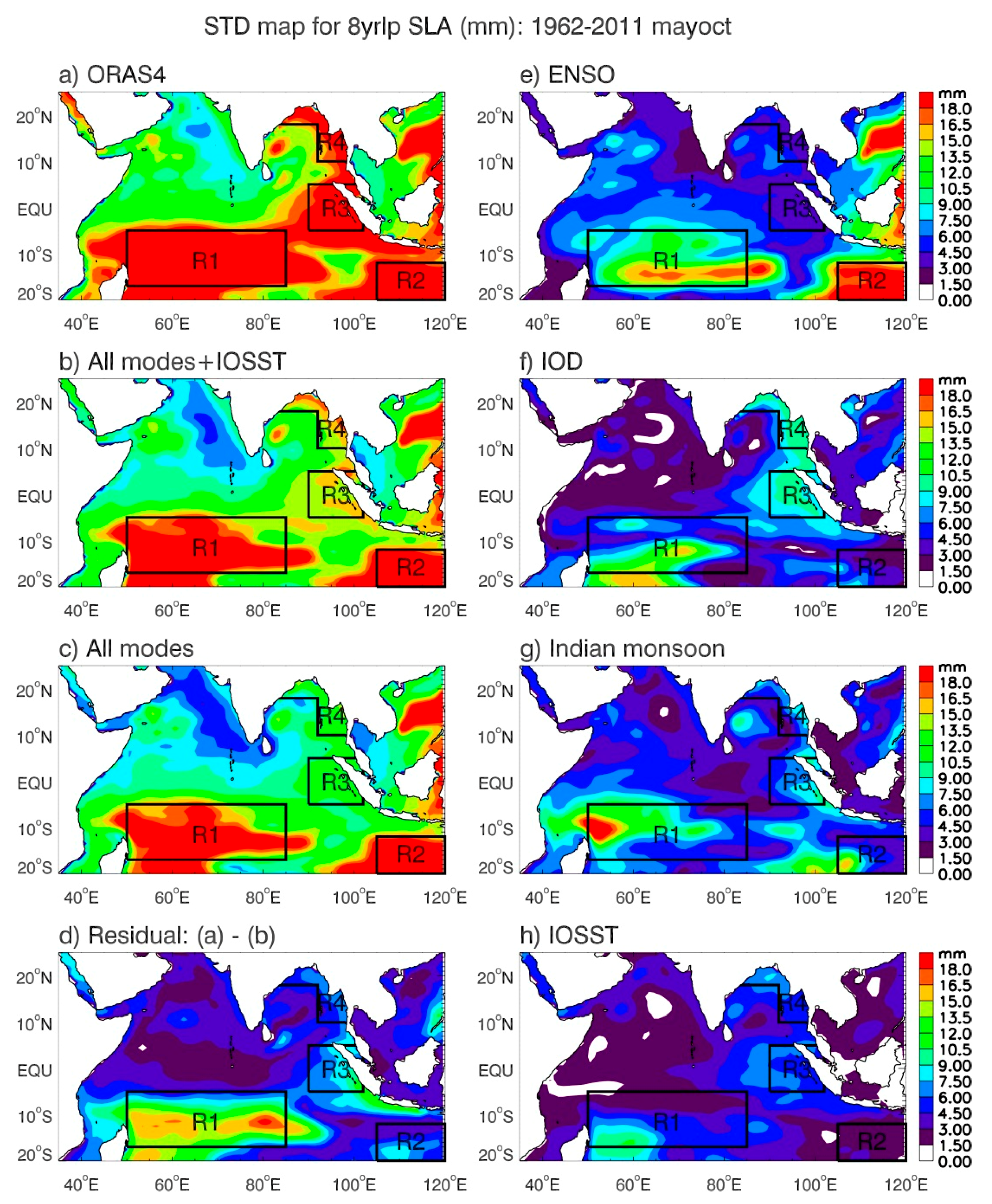
- For decadal variability, represented by 8 year low-passed SLA from 1962–2011 (both global SLR and regional trend removed), the largest contribution of external forcing (measured by the 1.65STD of the 100-member mean of the external forcing ensemble) is 18 ± 17% of the observed SLA STD (ORAS4 and SODA average) in the Seychelles region and 17 ± 11% in the southeastern basin near the ITF (Figure 4 and Figure 5). Consequently, the observed decadal SLA results predominantly from natural internal variability. While the variances of the decadal SLA from the MPI and CESM1 reach large magnitudes in similar areas, the time series of their LE averaged decadal SLAs for the same areas differ considerably in amplitude and phase, showing weak or negative correlations. These results suggest that the decadal predictions and future projections of the regional sea level can be strongly model-dependent because they can respond very differently to the same external forcing on regional scales. Efforts should be made to understand the causes for the strong model-dependence and identify their biases, with a hope to improve the physical representations of processes in climate models, and ultimately improve their simulations, predictions, and future projections.
- (3)
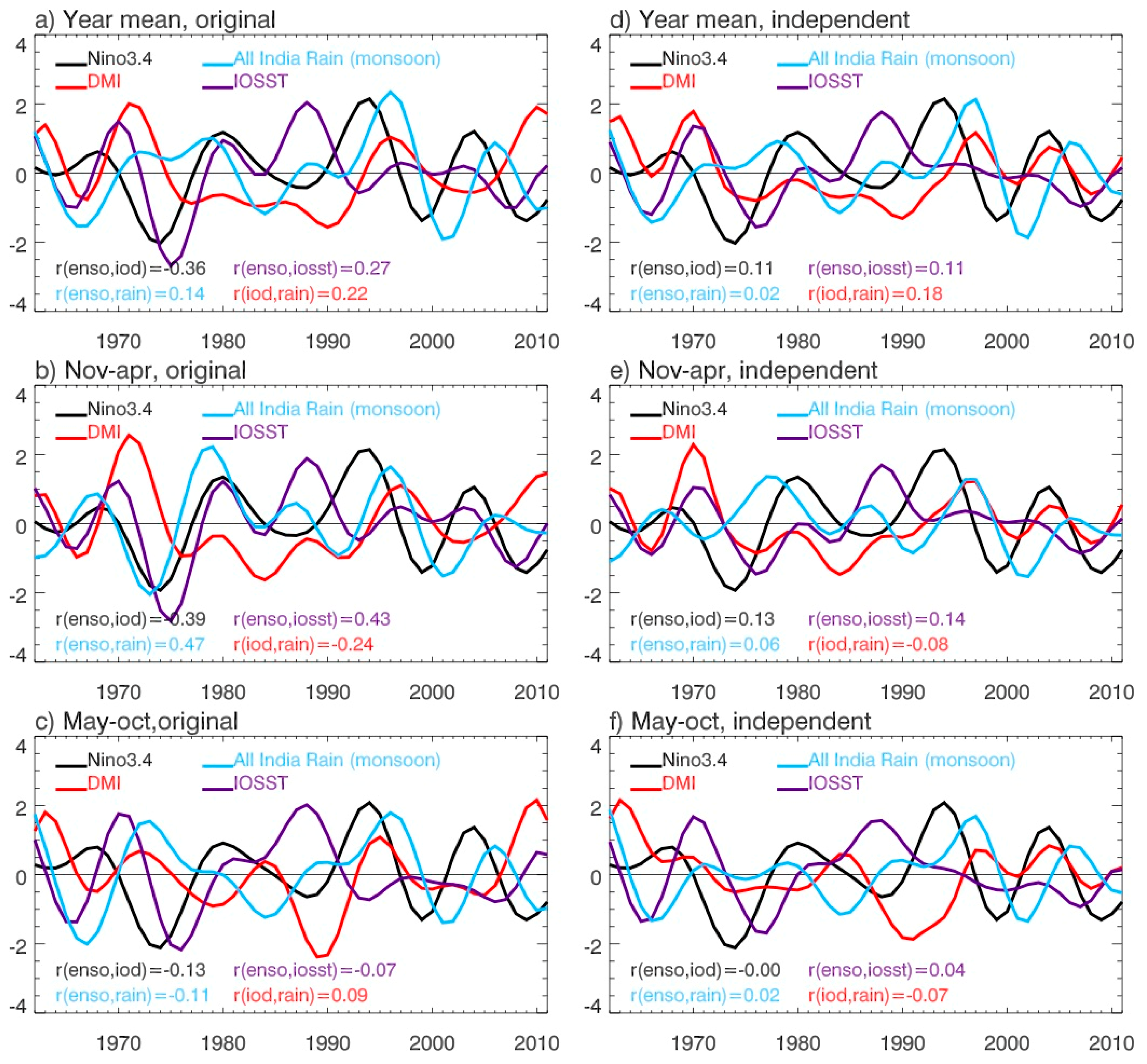
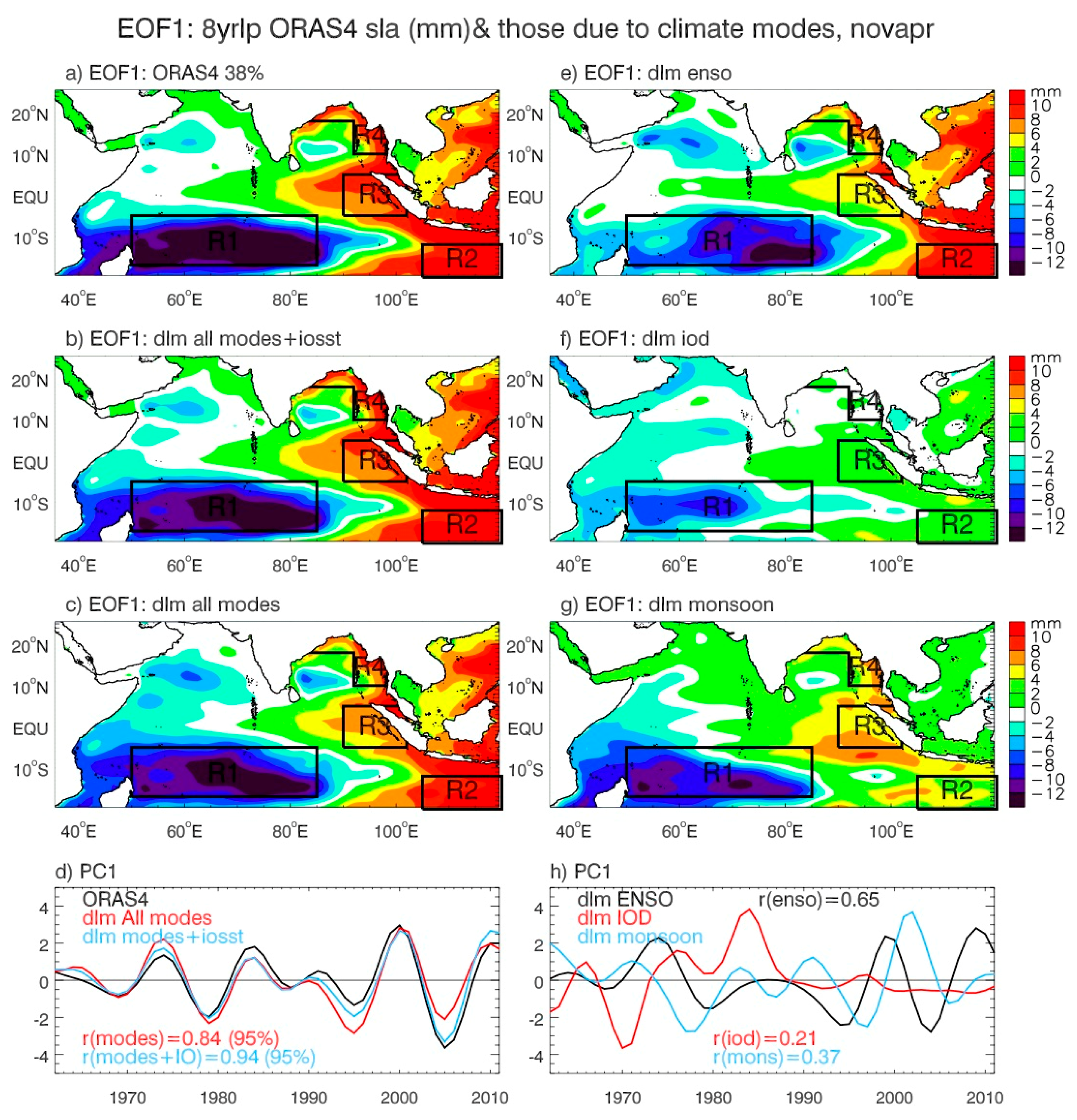
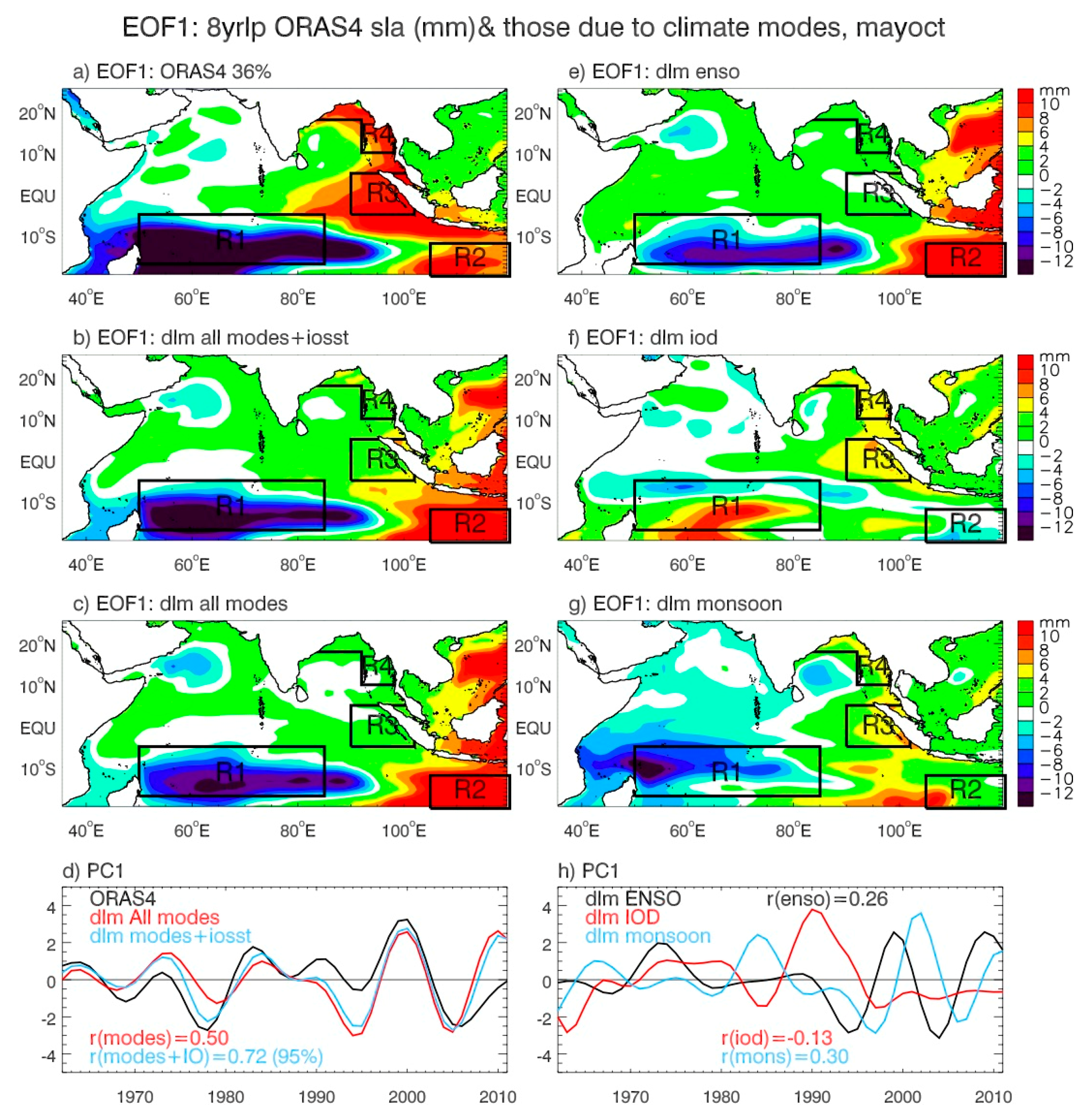
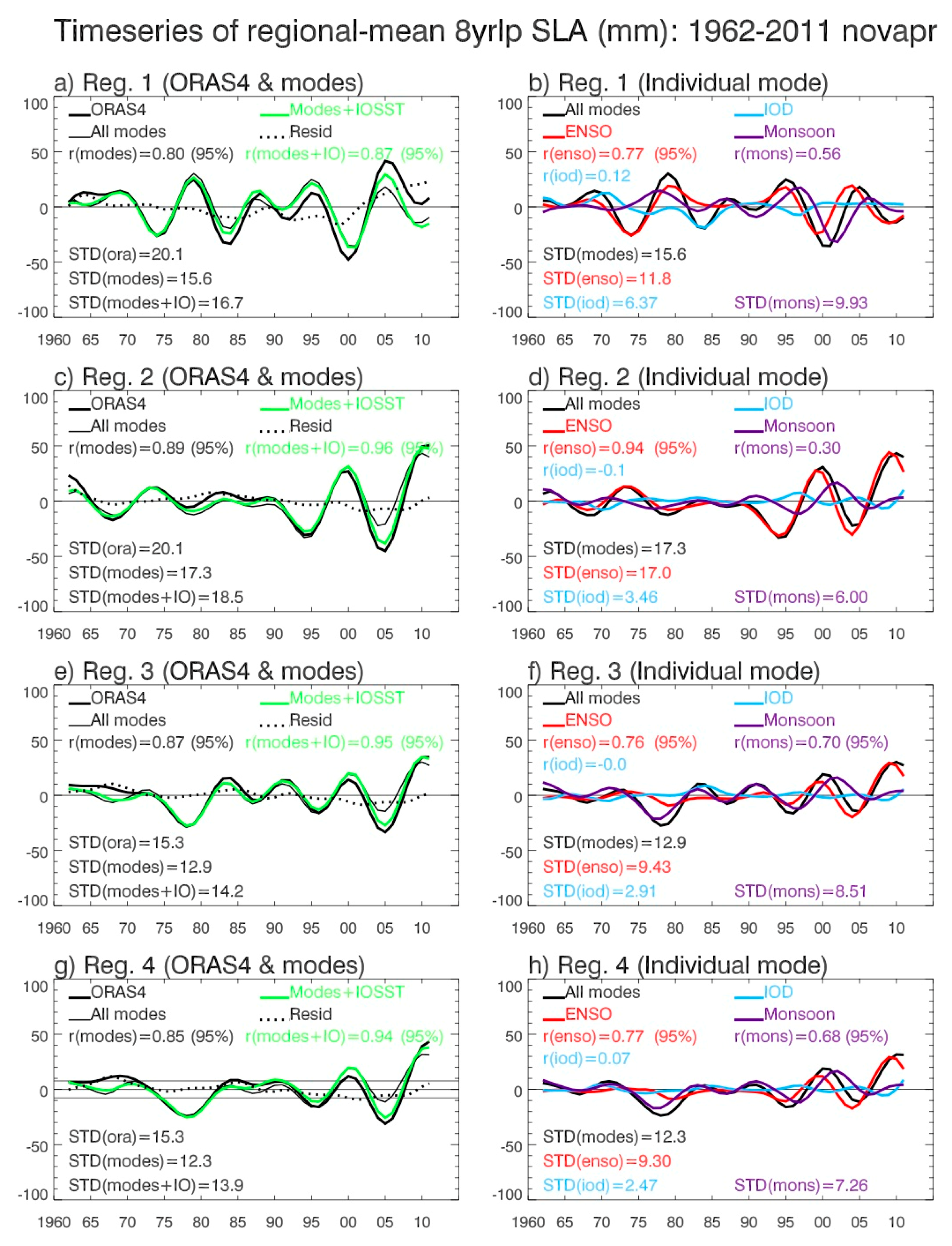
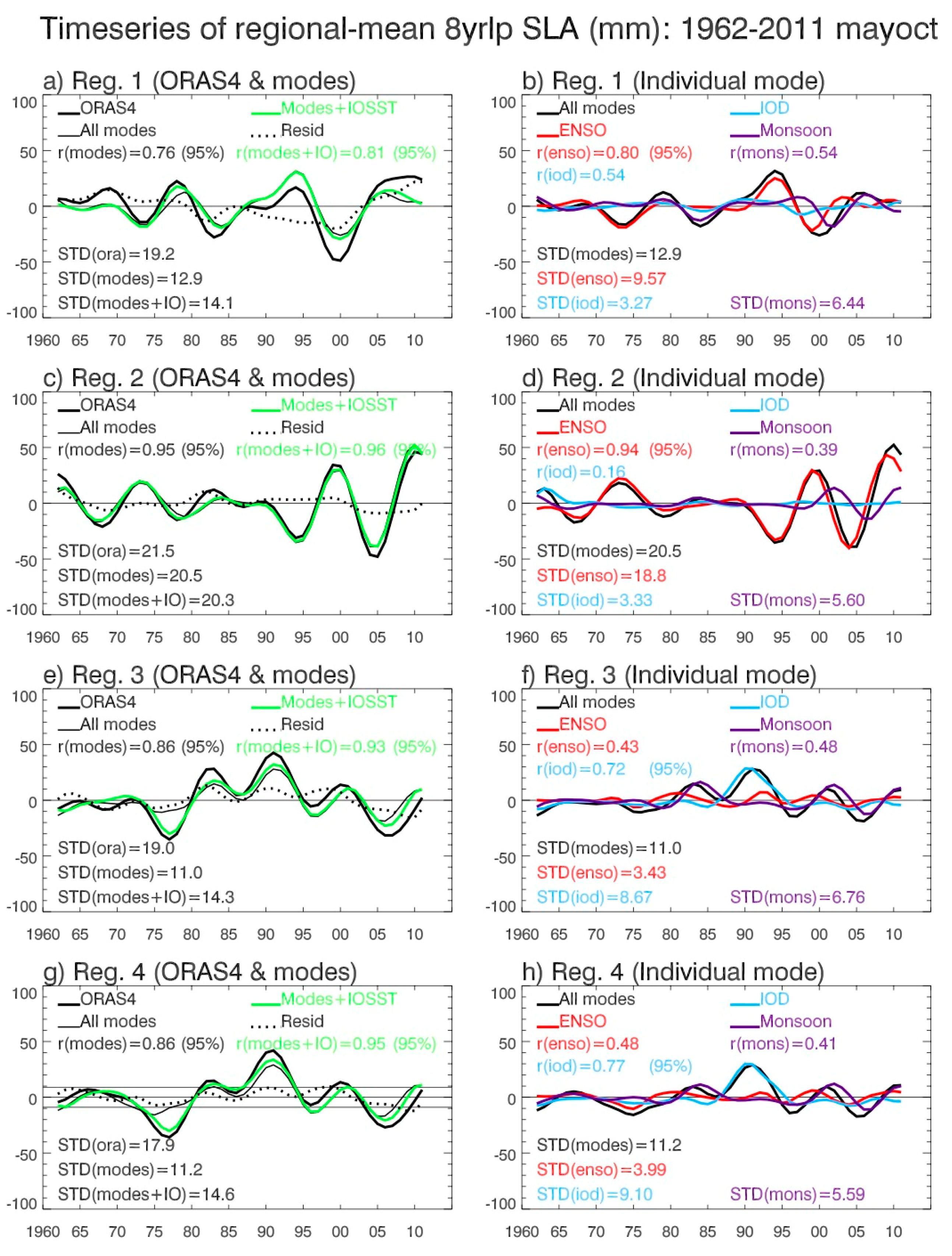
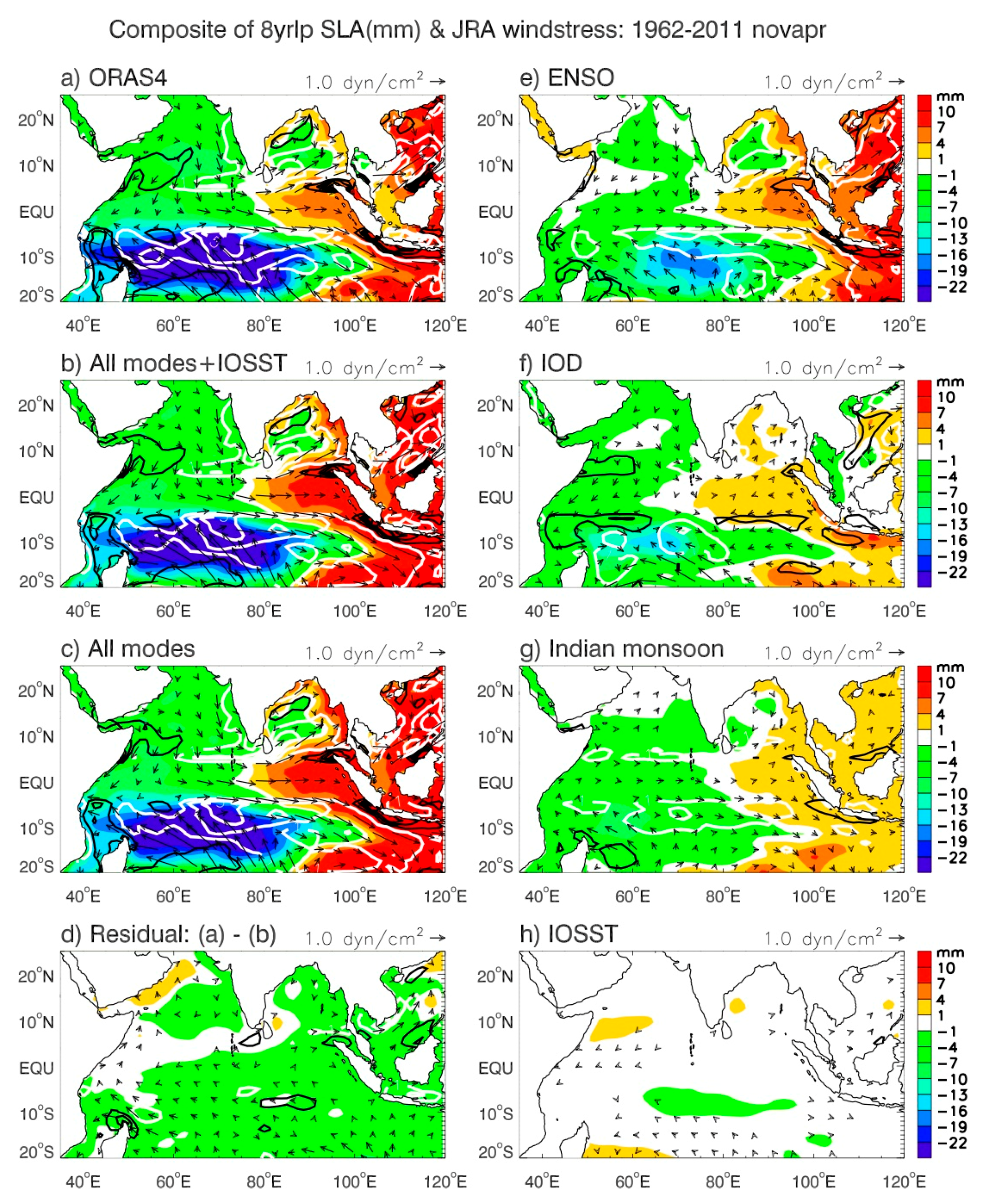
- Decadal SLAs exhibit distinct basin-wide patterns, with the sea level fall in the southwest tropical IO accompanying the sea level rise in the eastern basin (Figure 9 and Figure 10). The strong decadal variability overlies on the multi-decadal falling trend in the western basin, but on the rising trend in the eastern basin, particularly in the coastal regions of Sumatra and the Bay of Bengal. This can increase the stress of SLR for coastal countries such as Bangladesh, whose elevation is near the sea level. Climate modes (the sum of decadal ENSO, IOD, and monsoon) explain a large fraction of the observed decadal sea level variability, regardless of whether the decadal SLAs are based on the annual (12-month) mean winter (November–April) or summer (May–October) seasons, and the impacts of the individual modes exhibit apparent seasonality (Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12).During November–April (Figure 11), the STD ratios between the climate-modes-associated and observed decadal SLAs are ~80–86% and their correlation coefficients are r = 0.80–0.89 (>95% significance) in the four key regions where the decadal SLAs are large, that is, the Seychelles Islands (Reg. 1), the ITF area (Reg. 2), west coasts of Sumatra (Reg. 3), and the east and north coasts of the Bay of Bengal (Reg. 4). The smallest impact occurs over Seychelles (78% and r = 0.80) and the largest impact occurs near the ITF (86% and r = 0.89). Adding the IOSST, which represents part of the external forcing, increases the STD ratios to >90% and r to ≥0.94 in all areas but the Seychelles, where the ratio increases to 83% and r to 0.87 (Figure 11). The decadal ENSO is the largest contributor to the basin-wide pattern and individual areas in both the basin interior and along the coasts (Figure 7 and Figure 9) and it controls the SLA near the ITF area. Decadal variability of the monsoon also has evident effects in all regions except for the ITF, and the influence of the decadal IOD is relatively weak, with its strongest effect occurring over Seychelles. The caveat for the weak IOD influence in the eastern IO coast during boreal winter is that part of the IOD impact is embedded in the effect of ENSO because we removed the ENSO signals from the DMI to ensure the independence of predictors in the DLM equations (Section 2.4). The removal of ENSO from the DMI implies that the ENSO affects IOD but IOD does not affect ENSO. Yet existing studies have suggested the active impact of IOD on ENSO. This procedure may, to some degree, overestimate the ENSO effect and underestimate the IOD effect (Section 3.2.2).During May–October, the climate modes explain a lower percentage of the observed SLA variance compared to winter, both for the basin-wide EOF patterns and for the individual regions over Seychelles, Sumatra coasts, and Bay of Bengal coasts where the STD ratios between climate-modes-associated and observed SLAs are 67%, 58%, and 63% and correlations are r = 0.76, 0.86, and 0.86, respectively (Figure 8, Figure 10 and Figure 12). Adding IOSST increases the STD ratios to 73%, 75%, and 82% and the correlation to 0.81, 0.93, and 0.95. An exception is for the ITF area where the total effects of the climate modes, which are higher than their corresponding winter values, explain 95% of the observed STD with r = 0.95. Decadal ENSO is the determining factor for the ITF area, with the decadal monsoon having a comparable contribution in the past decade or so (1997–2011). Over the Seychelles area, decadal ENSO is the largest contributor, with decadal monsoon also having considerable contributions particularly in the past decade. The effect of decadal IOD is also non-negligible. Along the coasts of Sumatra and the Bay, decadal IOD is the largest contributor overall from 1962–2011 and is the controlling factor from the end of the 1980s to early 1990s, while decadal monsoon is the largest contributor in the past decade.
- (4)
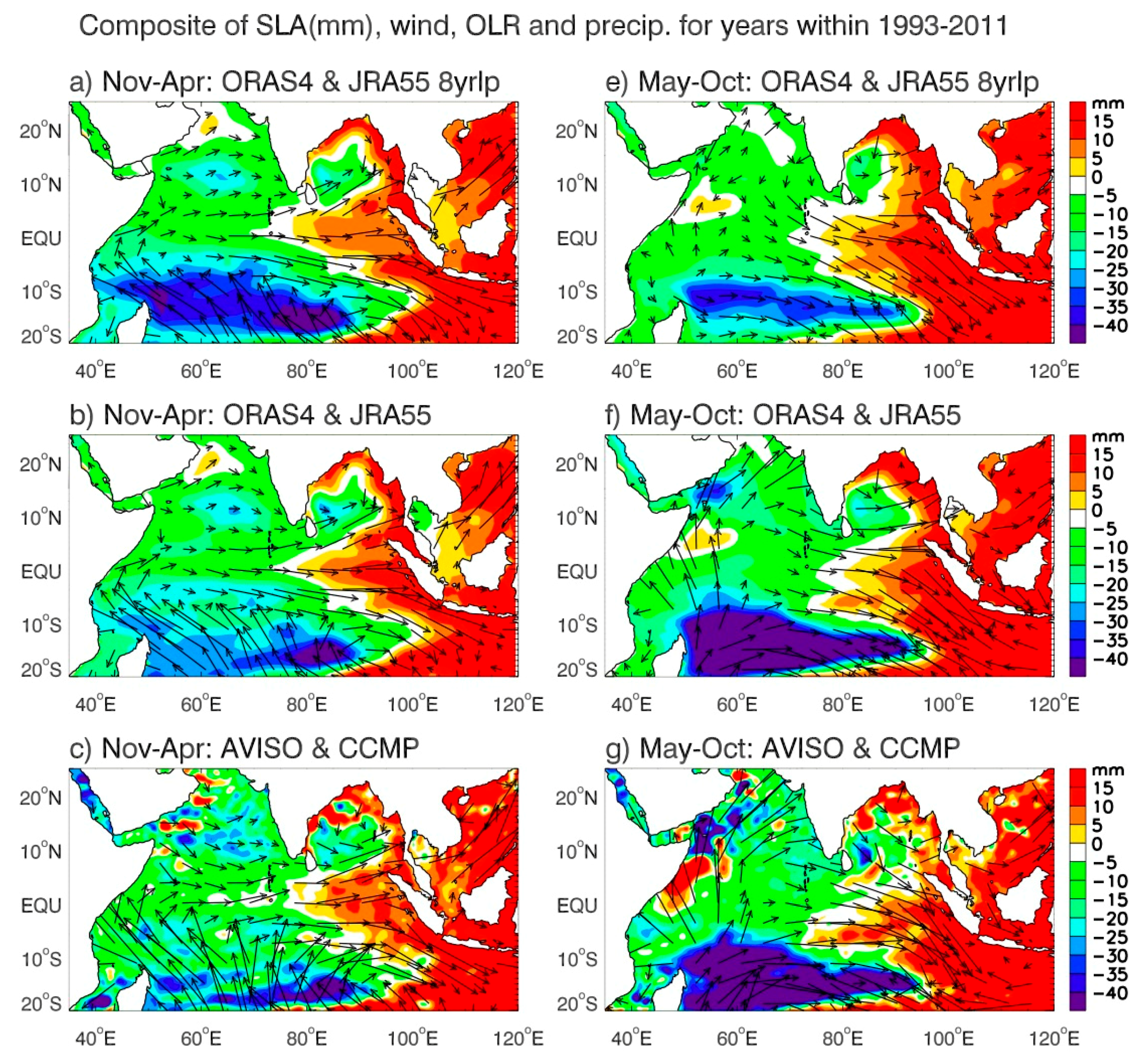
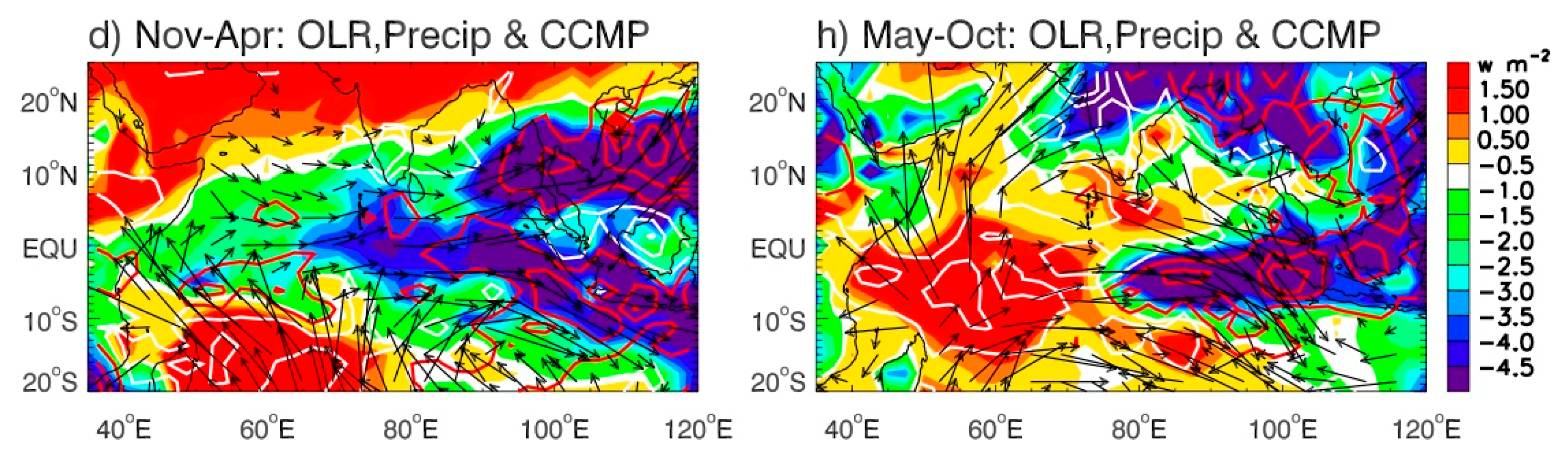
- Decadal variability of the surface winds over the IO plays a vital role in causing decadal SLAs over most regions of the IO, except for the ITF area where the remote forcing from the Pacific via the ITF is also important. While the Ekman pumping velocity is the major cause for the large SLAs over the Seychelles Islands, the zonal equatorial wind anomalies associated with the Walker Circulation primarily determines the SLAs along the coasts of Sumatra, Java, and the Bay of Bengal for both the winter and summer seasons. The local Ekman pumping velocity near the Sumatra and Java coasts, together with the alongshore winds and Ekman pumping velocity in the eastern Bay during summer, enhance the SLA amplitudes in the coastal regions. These results, which are based on reanalysis data, are supported by the AVISO satellite sea level and CCMP winds for their overlapping periods during recent decades. In addition, satellite-observed convection (that is, OLR) and GPCP precipitation further confirm the wind variations, and they also suggest a compensating effect of thermosteric and halosteric sea level. This is because in regions of increased convection and precipitation, such as the western equatorial IO associated with +IOD, the reduction in the shortwave flux and upper ocean temperature act to decrease thermosteric sea level; meanwhile, the increased precipitation increases the halosteric sea level. This compensation weakens the total effect of buoyancy forcing on regional, decadal SLA. Topographic trapping of the Rossby wave energy by the continental shelf along the west Australian coast [98], together with frictional damping of coastal Kelvin and Rossby waves will also affect coastal SLA. These coastal effects will be investigated in our future research using high-resolution numerical models.
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Nicholls, R.J.; Cazenave, A. Sea-Level Rise and Its Impact on Coastal Zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef] [PubMed]
- Neumann, B.; Vafeidis, A.T.; Zimmermann, J.; Nicholls, R.J. Future Coastal Population Growth and Exposure to Sea-Level Rise and Coastal Flooding—A Global Assessment. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Milne, G.A.; Gehrels, W.R.; Hughes, C.W.; Tamisiea, M.E. Identifying the causes of sea-level change. Nat. Geosci. 2009, 2, 471–478. [Google Scholar] [CrossRef] [Green Version]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; et al. Sea Level Change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2014; pp. 1137–1216. [Google Scholar] [CrossRef]
- Stammer, D.; Cazenave, A.; Ponte, R.M.; Tamisiea, M.E. Causes for Contemporary Regional Sea Level Changes. Annu. Rev. Mar. Sci. 2013, 5, 21–46. [Google Scholar] [CrossRef] [PubMed]
- Kopp, R.E.; Horton, B.P.; Kemp, A.C.; Tebaldi, C. Past and future sea-level rise along the coast of North Carolina, USA. Clim. Chang. 2015, 132, 693–707. [Google Scholar] [CrossRef] [Green Version]
- Mccreary, J.P.; Kundu, P.K.; Molinari, R.L. A Numerical Investigation of Dynamics, Thermodynamics and Mixed-Layer Processes in the Indian-Ocean. Prog. Oceanogr. 1993, 31, 181–244. [Google Scholar] [CrossRef]
- Murtugudde, R.; Busalacchi, A.J. Interannual variability of the dynamics and thermodynamics of the tropical Indian Ocean. J. Clim. 1999, 12, 2300–2326. [Google Scholar] [CrossRef]
- Hermes, J.C.; Reason, C.J.C. Annual cycle of the South Indian Ocean (Seychelles-Chagos) thermocline ridge in a regional ocean model. J. Geophys. Res. Ocean. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Yokoi, T.; Tozuka, T.; Yamagata, T. Seasonal variation of the Seychelles Dome. J. Clim. 2008, 21, 3740–3754. [Google Scholar] [CrossRef]
- Han, W.Q.; Meehl, G.A.; Rajagopalan, B.; Fasullo, J.T.; Hu, A.X.; Lin, J.L.; Large, W.G.; Wang, J.W.; Quan, X.W.; Trenary, L.L.; et al. Patterns of Indian Ocean sea-level change in a warming climate. Nat. Geosci. 2010, 3, 546–550. [Google Scholar] [CrossRef]
- Timmermann, A.; McGregor, S.; Jin, F.F. Wind Effects on Past and Future Regional Sea Level Trends in the Southern Indo-Pacific. J. Clim. 2010, 23, 4429–4437. [Google Scholar] [CrossRef]
- Dunne, R.P.; Barbosa, S.M.; Woodworth, P.L. Contemporary sea level in the Chagos Archipelago, central Indian Ocean. Glob. Planet. Chang. 2012, 82–83, 25–37. [Google Scholar] [CrossRef]
- Schwarzkopf, F.U.; Boning, C.W. Contribution of Pacific wind stress to multi-decadal variations in upper-ocean heat content and sea level in the tropical south Indian Ocean. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Han, W.Q.; Vialard, J.; McPhaden, M.J.; Lee, T.; Masumoto, Y.; Feng, M.; De Ruijter, W.P.M. Indian Ocean Decadal Variability A Review. Bull. Am. Meteorol. Soc. 2014, 95, 1679–1703. [Google Scholar] [CrossRef]
- Du, Y.; Xie, S.P. Role of atmospheric adjustments in the tropical Indian Ocean warming during the 20th century in climate models. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Zhou, T.J.; Wu, B. Indian Ocean warming during 1958-2004 simulated by a climate system model and its mechanism. Clim. Dyn. 2014, 42, 203–217. [Google Scholar] [CrossRef]
- Lee, T.; McPhaden, M.J. Decadal phase change in large-scale sea level and winds in the Indo-Pacific region at the end of the 20th century. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Thompson, P.R.; Piecuch, C.G.; Merrifield, M.A.; McCreary, J.P.; Firing, E. Forcing of recent decadal variability in the Equatorial and North Indian Ocean. J. Geophys. Res. Ocean. 2016, 121, 6762–6778. [Google Scholar] [CrossRef]
- Srinivasu, U.; Ravichandran, M.; Han, W.Q.; Sivareddy, S.; Rahman, H.; Li, Y.L.; Nayak, S. Causes for the reversal of North Indian Ocean decadal sea level trend in recent two decades. Clim. Dyn. 2017, 49, 3887–3904. [Google Scholar] [CrossRef]
- Trenary, L.L.; Han, W.Q. Local and remote forcing of decadal sea level and thermocline depth variability in the South Indian Ocean. J. Geophys. Res. Ocean. 2013, 118, 381–398. [Google Scholar] [CrossRef] [Green Version]
- Nidheesh, A.G.; Lengaigne, M.; Vialard, J.; Unnikrishnan, A.S.; Dayan, H. Decadal and long-term sea level variability in the tropical Indo-Pacific Ocean. Clim. Dyn. 2013, 41, 381–402. [Google Scholar] [CrossRef]
- Feng, M.; McPhaden, M.J.; Xie, S.P.; Hafner, J. La Nina forces unprecedented Leeuwin Current warming in 2011. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef] [PubMed]
- Llovel, W.; Fukumori, I.; Meyssignac, B. Depth-dependent temperature change contributions to global mean thermosteric sea level rise from 1960 to 2010. Glob. Planet. Chang. 2013, 101, 113–118. [Google Scholar] [CrossRef]
- Wu, Q.R.; Zhang, X.B.; Church, J.A.; Hu, J.Y. Variability and change of sea level and its components in the Indo-Pacific region during the altimetry era. J. Geophys. Res. Ocean. 2017, 122, 1862–1881. [Google Scholar] [CrossRef]
- Llovel, W.; Lee, T. Importance and origin of halosteric contribution to sea level change in the southeast Indian Ocean during 2005–2013. Geophys. Res. Lett. 2015, 42, 1148–1157. [Google Scholar] [CrossRef]
- Han, W.Q.; Meehl, G.A.; Stammer, D.; Hu, A.X.; Hamlington, B.; Kenigson, J.; Palanisamy, H.; Thompson, P. Spatial Patterns of Sea Level Variability Associated with Natural Internal Climate Modes. Surv. Geophys. 2017, 38, 217–250. [Google Scholar] [CrossRef]
- Li, Y.L.; Han, W.Q. Decadal Sea Level Variations in the Indian Ocean Investigated with HYCOM: Roles of Climate Modes, Ocean Internal Variability, and Stochastic Wind Forcing. J. Clim. 2015, 28, 9143–9165. [Google Scholar] [CrossRef]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef] [PubMed]
- Webster, P.J.; Moore, A.M.; Loschnigg, J.P.; Leben, R.R. Coupled ocean-atmosphere dynamics in the Indian Ocean during 1997–98. Nature 1999, 401, 356–360. [Google Scholar] [CrossRef] [PubMed]
- Frankcombe, L.M.; McGregor, S.; England, M.H. Robustness of the modes of Indo-Pacific sea level variability. Clim. Dyn. 2015, 45, 1281–1298. [Google Scholar] [CrossRef]
- Xie, S.P.; Du, Y.; Huang, G.; Zheng, X.T.; Tokinaga, H.; Hu, K.M.; Liu, Q.Y. Decadal Shift in El Nino Influences on Indo-Western Pacific and East Asian Climate in the 1970s. J. Clim. 2010, 23, 3352–3368. [Google Scholar] [CrossRef]
- Han, W.Q.; Meehl, G.A.; Hu, A.X.; Zheng, J.; Kenigson, J.; Vialard, J.; Rajagopalan, B.; Yanto. Decadal Variability of the Indian and Pacific Walker Cells since the 1960s: Do They Covary on Decadal Time Scales? J. Clim. 2017, 30, 8447–8468. [Google Scholar] [CrossRef]
- Kumar, K.K.; Rajagopalan, B.; Hoerling, M.; Bates, G.; Cane, M. Unraveling the mystery of Indian monsoon failure during El Nino. Science 2006, 314, 115–119. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.-J.; Sasaki, W.; Masumoto, Y. Indian Ocean warming modulates Pacific climate change. Proc. Natl. Acad. Sci. USA 2012, 109, 18701–18706. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Xie, S.P.; Wu, L.X.; Kosaka, Y.; Lau, N.C.; Vecchi, G.A. Seasonality and Predictability of the Indian Ocean Dipole Mode: ENSO Forcing and Internal Variability. J. Clim. 2015, 28, 8021–8036. [Google Scholar] [CrossRef]
- Wittenberg, A.T.; Rosati, A.; Delworth, T.L.; Vecchi, G.A.; Zeng, F.R. ENSO Modulation: Is It Decadally Predictable? J. Clim. 2014, 27, 2667–2681. [Google Scholar] [CrossRef]
- Petris, G.; Petrone, S.; Campagnoli, P. Dynamic linear models. In Dynamic Linear Models with R; Springer: Berlin/Heidelberg, Germany, 2009; pp. 31–84. [Google Scholar]
- Goddard, L.; Baethgen, W.; Kirtman, B.; Meehl, G. The urgent need for improved climate models and predictions. Eos Trans. Am. Geophys. Union 2009, 90, 343. [Google Scholar] [CrossRef]
- Hurrell, J.; Meehl, G.A.; Bader, D.; Delworth, T.L.; Kirtman, B.; Wielicki, B. A Unified Modeling Approach to Climate System Prediction. Bull. Am. Meteorol. Soc. 2009, 90, 1819–1832. [Google Scholar] [CrossRef] [Green Version]
- Meehl, G.A.; Goddard, L.; Murphy, J.; Stouffer, R.J.; Boer, G.; Danabasoglu, G.; Dixon, K.; Giorgetta, M.A.; Greene, A.M.; Hawkins, E.; et al. DECADAL PREDICTION Can It Be Skillful? Bull. Am. Meteorol. Soc. 2009, 90, 1467–1485. [Google Scholar] [CrossRef]
- Meehl, G.A.; Goddard, L.; Boer, G.; Burgman, R.; Branstator, G.; Cassou, C.; Corti, S.; Danabasoglu, G.; Doblas-Reyes, F.; Hawkins, E.; et al. DECADAL CLIMATE PREDICTION An Update from the Trenches. Bull. Am. Meteorol. Soc. 2014, 95, 243–267. [Google Scholar] [CrossRef]
- Pohlmann, H.; Jungclaus, J.H.; Kohl, A.; Stammer, D.; Marotzke, J. Initializing Decadal Climate Predictions with the GECCO Oceanic Synthesis: Effects on the North Atlantic. J. Clim. 2009, 22, 3926–3938. [Google Scholar] [CrossRef]
- Doblas-Reyes, F.J.; Balmaseda, M.A.; Weisheimer, A.; Palmer, T.N. Decadal climate prediction with the European Centre for Medium-Range Weather Forecasts coupled forecast system: Impact of ocean observations. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Polkova, I.; Kohl, A.; Stammer, D. Predictive Skill for Regional Interannual Steric Sea Level and Mechanisms for Predictability*. J. Clim. 2015, 28, 7407–7419. [Google Scholar] [CrossRef]
- Balmaseda, M.A.; Mogensen, K.; Weaver, A.T. Evaluation of the ECMWF ocean reanalysis system ORAS4. Q. J. Roy Meteor. Soc. 2013, 139, 1132–1161. [Google Scholar] [CrossRef]
- Carton, J.A.; Giese, B.S. A reanalysis of ocean climate using Simple Ocean Data Assimilation (SODA). Mon. Weather Rev. 2008, 136, 2999–3017. [Google Scholar] [CrossRef]
- Vidard, A.; Balmaseda, M.; Anderson, D. Assimilation of Altimeter Data in the ECMWF Ocean Analysis System 3. Mon. Weather Rev. 2009, 137, 1393–1408. [Google Scholar] [CrossRef]
- Nidheesh, A.G.; Lengaigne, M.; Vialard, J.; Izumo, T.; Unnikrishnan, A.S.; Meyssignac, B.; Hamlington, B.; Montegut, C.D. Robustness of observation-based decadal sea level variability in the Indo-Pacific Ocean. Geophys. Res. Lett. 2017, 44, 7391–7400. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.I.; Boyer, T.P.; Baranova, O.K.; Garcia, H.E.; Locarnini, R.A.; Mishonov, A.V.; Reagan, J.R.; Seidov, D.; Yarosh, E.S.; et al. World ocean heat content and thermosteric sea level change (0–2000 m), 1955–2010. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Ishii, M.; Kimoto, M.; Sakamoto, K.; Iwasaki, S.I. Steric sea level changes estimated from historical ocean subsurface temperature and salinity analyses. J. Oceanogr. 2006, 62, 155–170. [Google Scholar] [CrossRef]
- Ducet, N.; Le Traon, P.Y.; Reverdin, G. Global high-resolution mapping of ocean circulation from TOPEX/Poseidon and ERS-1 and-2. J. Geophys. Res. Ocean. 2000, 105, 19477–19498. [Google Scholar] [CrossRef]
- Rio, M.H.; Guinehut, S.; Larnicol, G. New CNES-CLS09 global mean dynamic topography computed from the combination of GRACE data, altimetry, and in situ measurements. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Jpn. 2015, 93, 5–48. [Google Scholar] [CrossRef] [Green Version]
- Atlas, R.; Hoffman, R.N.; Ardizzone, J.; Leidner, S.M.; Jusem, J.C.; Smith, D.K.; Gombos, D. A Cross-Calibrated Multiplatform Ocean Surface Wind Velocity Product for Meteorological and Oceanographic Applications. Bull. Am. Meteorol. Soc. 2011, 92, 157. [Google Scholar] [CrossRef]
- Liebmann, B.; Smith, C.A. Description of a complete (interpolated) outgoing longwave radiation dataset. Bull. Am. Meteorol. Soc. 1996, 77, 1275–1277. [Google Scholar]
- Adler, R.F.; Gu, G.J.; Sapiano, M.; Wang, J.J.; Huffman, G.J. Global Precipitation: Means, Variations and Trends During the Satellite Era (1979–2014). Surv. Geophys. 2017, 38, 679–699. [Google Scholar] [CrossRef] [Green Version]
- Duchon, C.E. Lanczos Filtering in One and 2 Dimensions. J. Appl. Meteorol. 1979, 18, 1016–1022. [Google Scholar] [CrossRef]
- Deser, C.; Phillips, A.S.; Tomas, R.A.; Okumura, Y.M.; Alexander, M.A.; Capotondi, A.; Scott, J.D.; Kwon, Y.O.; Ohba, M. ENSO and Pacific Decadal Variability in the Community Climate System Model Version 4. J. Clim. 2012, 25, 2622–2651. [Google Scholar] [CrossRef] [Green Version]
- Meyssignac, B.; Becker, M.; Llovel, W.; Cazenave, A. An Assessment of Two-Dimensional Past Sea Level Reconstructions Over 1950-2009 Based on Tide-Gauge Data and Different Input Sea Level Grids. Surv. Geophys. 2012, 33, 945–972. [Google Scholar] [CrossRef]
- Han, W.Q.; Meehl, G.A.; Hu, A.X.; Alexander, M.A.; Yamagata, T.; Yuan, D.L.; Ishii, M.; Pegion, P.; Zheng, J.; Hamlington, B.D.; et al. Intensification of decadal and multi-decadal sea level variability in the western tropical Pacific during recent decades. Clim. Dyn. 2014, 43, 1357–1379. [Google Scholar] [CrossRef]
- Kay, J.E.; Deser, C.; Phillips, A.; Mai, A.; Hannay, C.; Strand, G.; Arblaster, J.M.; Bates, S.C.; Danabasoglu, G.; Edwards, J.; et al. The Community Earth System Model (Cesm) Large Ensemble Project A Community Resource for Studying Climate Change in the Presence of Internal Climate Variability. Bull. Am. Meteorol. Soc. 2015, 96, 1333–1349. [Google Scholar] [CrossRef]
- Bittner, M.; Schmidt, H.; Timmreck, C.; Sienz, F. Using a large ensemble of simulations to assess the Northern Hemisphere stratospheric dynamical response to tropical volcanic eruptions and its uncertainty. Geophys. Res. Lett. 2016, 43, 9324–9332. [Google Scholar] [CrossRef] [Green Version]
- Song, Q.; Vecchi, G.A.; Rosati, A.J. Indian Ocean variability in the GFDL coupled climate model. J. Clim. 2007, 20, 2895–2916. [Google Scholar] [CrossRef]
- Tozuka, T.; Luo, J.J.; Masson, S.; Yamagata, T. Decadal modulations of the Indian Ocean dipole in the SINTEX-F1 coupled GCM. J. Clim. 2007, 20, 2881–2894. [Google Scholar] [CrossRef]
- Zhang, X.B.; Church, J.A. Sea level trends, interannual and decadal variability in the Pacific Ocean. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Rayner, N.A.; Brohan, P.; Parker, D.E.; Folland, C.K.; Kennedy, J.J.; Vanicek, M.; Ansell, T.J.; Tett, S.F.B. Improved analyses of changes and uncertainties in sea surface temperature measured in situ since the mid-nineteenth century: The HadSST2 dataset. J. Clim. 2006, 19, 446–469. [Google Scholar] [CrossRef]
- Parthasarathy, B.; Munot, A.A.; Kothawale, D.R. All-India Monthly and Seasonal Rainfall Series—1871–1993. Theor. Appl. Climatol. 1994, 49, 217–224. [Google Scholar] [CrossRef]
- Klein, S.A.; Soden, B.J.; Lau, N.C. Remote sea surface temperature variations during ENSO: Evidence for a tropical atmospheric bridge. J. Clim. 1999, 12, 917–932. [Google Scholar] [CrossRef]
- Dong, L.; Mcphaden, M.J. Why Has the Relationship between Indian and Pacific Ocean Decadal Variability Changed in Recent Decades? J. Clim. 2017, 30, 1971–1983. [Google Scholar] [CrossRef]
- Zhang, L.; Han, W.Q.; Sienz, F. Unraveling Causes for the Changing Behavior of the Tropical Indian Ocean in the Past Few Decades. J. Clim. 2018, 31, 2377–2388. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Strassburg, M.W.; Leben, R.R.; Han, W.; Nerem, R.S.; Kim, K.Y. Uncovering an anthropogenic sea-level rise signal in the Pacific Ocean. Nat. Clim. Chang. 2014, 4, 782–785. [Google Scholar] [CrossRef]
- Loschnigg, J.; Meehl, G.A.; Webster, P.J.; Arblaster, J.M.; Compo, G.P. The Asian monsoon, the tropospheric biennial oscillation, and the Indian Ocean zonal mode in the NCAR CSM. J. Clim. 2003, 16, 1617–1642. [Google Scholar] [CrossRef]
- Meehl, G.A.; Arblaster, J.M.; Loschnigg, J. Coupled ocean-atmosphere dynamical processes in the tropical Indian and Pacific Oceans and the TBO. J. Clim. 2003, 16, 2138–2158. [Google Scholar] [CrossRef]
- Izumo, T.; Vialard, J.; Lengaigne, M.; Montegut, C.D.; Behera, S.K.; Luo, J.J.; Cravatte, S.; Masson, S.; Yamagata, T. Influence of the state of the Indian Ocean Dipole on the following year’s El Nino. Nat. Geosci. 2010, 3, 168–172. [Google Scholar] [CrossRef]
- Krishnaswamy, J.; Vaidyanathan, S.; Rajagopalan, B.; Bonell, M.; Sankaran, M.; Bhalla, R.S.; Badiger, S. Non-stationary and non-linear influence of ENSO and Indian Ocean Dipole on the variability of Indian monsoon rainfall and extreme rain events. Clim. Dyn. 2015, 45, 175–184. [Google Scholar] [CrossRef]
- Yanto; Rajagopalan, B.; Zagona, E. Space-time variability of Indonesian rainfall at inter-annual and multi-decadal time scales. Clim. Dyn. 2016, 47, 2975–2989. [Google Scholar] [CrossRef]
- Han, W.Q.; McCreary, J.P.; Anderson, D.L.T.; Mariano, A.J. Dynamics of the eastern surface jets in the equatorial Indian Ocean. J. Phys. Oceanogr. 1999, 29, 2191–2209. [Google Scholar] [CrossRef]
- Han, W.Q.; McCreary, J.P.; Masumoto, Y.; Vialard, J.; Duncan, B. Basin Resonances in the Equatorial Indian Ocean. J. Phys. Oceanogr. 2011, 41, 1252–1270. [Google Scholar] [CrossRef]
- Shankar, D.; Aparna, S.G.; McCreary, J.P.; Suresh, I.; Neetu, S.; Durand, F.; Shenoi, S.S.C.; Al Saafani, M.A. Minima of interannual sea-level variability in the Indian Ocean. Prog. Oceanogr. 2010, 84, 225–241. [Google Scholar] [CrossRef]
- Han, W.Q.; McCreary, J.P. Modeling salinity distributions in the Indian Ocean. J. Geophys. Res. Ocean. 2001, 106, 859–877. [Google Scholar] [CrossRef] [Green Version]
- Hamlington, B.D.; Leben, R.R.; Nerem, R.S.; Han, W.; Kim, K.Y. Reconstructing sea level using cyclostationary empirical orthogonal functions. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Pfeffer, J.; Allemand, P. The key role of vertical land motions in coastal sea level variations: A global synthesis of multisatellite altimetry, tide gauge data and GPS measurements. Earth Planet. Sci. Lett. 2016, 439, 39–47. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J. The 2004-2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the Argo Program. Prog. Oceanogr. 2009, 82, 81–100. [Google Scholar] [CrossRef]
- Von Schuckmann, K.; Gaillard, F.; Le Traon, P.Y. Global hydrographic variability patterns during 2003–2008. J. Geophys. Res. Ocean. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Hosoda, S.; Suga, T.; Shikama, N.; Mizuno, K. Global Surface Layer Salinity Change Detected by Argo and Its Implication for Hydrological Cycle Intensification. J. Oceanogr. 2009, 65, 579–586. [Google Scholar] [CrossRef]
- Durack, P.J.; Wijffels, S.E. Fifty-Year Trends in Global Ocean Salinities and Their Relationship to Broad-Scale Warming. J. Clim. 2010, 23, 4342–4362. [Google Scholar] [CrossRef] [Green Version]
- Helm, K.P.; Bindoff, N.L.; Church, J.A. Changes in the global hydrological-cycle inferred from ocean salinity. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef] [Green Version]
- Church, J.A.; White, N.J. Sea-Level Rise from the Late 19th to the Early 21st Century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef] [Green Version]
- Bradshaw, E.; Richards, L.; Thorkild, A. Sea level data archaeology and the Global Sea Level Observing System (GLOSS). GeoResJ 2015, 6, 9–16. [Google Scholar] [CrossRef]
- Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M.; et al. The Community Climate System Model Version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef] [Green Version]
- Cai, W.J.; Cowan, T. Why is the amplitude of the Indian Ocean Dipole overly large in CMIP3 and CMIP5 climate models? Geophys. Res. Lett. 2013, 40, 1200–1205. [Google Scholar] [CrossRef] [Green Version]
- Weller, E.; Cai, W.J. Realism of the Indian Ocean Dipole in CMIP5 Models: The Implications for Climate Projections. J. Clim. 2013, 26, 6649–6659. [Google Scholar] [CrossRef]
- Storto, A.; Masina, S.; Balmaseda, M.; Guinehut, S.; Xue, Y.; Szekely, T.; Fukumori, I.; Forget, G.; Chang, Y.S.; Good, S.A.; et al. Steric sea level variability (1993–2010) in an ensemble of ocean reanalyses and objective analyses. Clim. Dyn. 2017, 49, 709–729. [Google Scholar] [CrossRef]
- Slangen, A.B.A.; Meyssignac, B.; Agosta, C.; Champollion, N.; Church, J.A.; Fettweis, X.; Ligtenberg, S.R.M.; Marzeion, B.; Melet, A.; Palmer, M.D.; et al. Evaluating Model Simulations of Twentieth-Century Sea Level Rise. Part I: Global Mean Sea Level Change. J. Clim. 2017, 30, 8539–8563. [Google Scholar] [CrossRef] [Green Version]
- Meyssignac, B.; Slangen, A.B.A.; Melet, A.; Church, J.A.; Fettweis, X.; Marzeion, B.; Agosta, C.; Ligtenberg, S.R.M.; Spada, G.; Richter, K.; et al. Evaluating Model Simulations of Twentieth-Century Sea-Level Rise. Part II: Regional Sea-Level Changes. J. Clim. 2017, 30, 8565–8593. [Google Scholar] [CrossRef] [Green Version]
- Han, W.Q.; Webster, P.J. Forcing mechanisms of sea level interannual variability in the Bay of Bengal. J. Phys. Oceanogr. 2002, 32, 216–239. [Google Scholar] [CrossRef]
- Furue, R.; McCreary, J.P.; Benthuysen, J.; Phillips, H.E.; Bindoff, N.L. Dynamics of the Leeuwin Current: Part 1. Coastal flows in an inviscid, variable-density, layer model. Dyn. Atmos. Ocean. 2013, 63, 24–59. [Google Scholar] [CrossRef]







| West: Tropical South IO (Seychelles) (50° E–85° E, 17° S–5° S) | East: EQ Indian Ocean (90° E–103° E, 7° S–7° N) | |
|---|---|---|
| Obs-ORAS4 | −1.74 ± 0.12 | 0.55 ± 0.13 |
| Obs-SODA | −0.73 ± 0.12 | 0.33 ± 0.12 |
| Obs-mean | −1.23 ± 0.12 | 0.44 ± 0.12 |
| MPI 100 | −0.29 ± 0.04 | −0.22 ± 0.03 |
| CESM1 40 | −0.08 ± 0.07 | −0.21 ± 0.06 |
| Model-mean | −0.23 ± 0.03 | −0.22 ± 0.03 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, W.; Stammer, D.; Meehl, G.A.; Hu, A.; Sienz, F.; Zhang, L. Multi-Decadal Trend and Decadal Variability of the Regional Sea Level over the Indian Ocean since the 1960s: Roles of Climate Modes and External Forcing. Climate 2018, 6, 51. https://doi.org/10.3390/cli6020051
Han W, Stammer D, Meehl GA, Hu A, Sienz F, Zhang L. Multi-Decadal Trend and Decadal Variability of the Regional Sea Level over the Indian Ocean since the 1960s: Roles of Climate Modes and External Forcing. Climate. 2018; 6(2):51. https://doi.org/10.3390/cli6020051
Chicago/Turabian StyleHan, Weiqing, Detlef Stammer, Gerald A. Meehl, Aixue Hu, Frank Sienz, and Lei Zhang. 2018. "Multi-Decadal Trend and Decadal Variability of the Regional Sea Level over the Indian Ocean since the 1960s: Roles of Climate Modes and External Forcing" Climate 6, no. 2: 51. https://doi.org/10.3390/cli6020051






