1. Introduction
Speaking about the Israeli-Palestinian conflict,
Atran et al. (
2007) concluded their article devoted to exploring sacred values and conflict resolution by the following words: “
We urgently need more scientific research to inform better policy choices”. The aim of the present paper is to shed some light on the economic consequences in terms of poverty dynamics on the Palestinian population of what is called by the Israeli government
a separation wall, a
security fence. The building of this wall was decided in 2002, after many political discussions, in order to prevent terrorist attacks starting from the West Bank. It was presented by the Israeli Government as being temporary, meant to be destroyed after peace negotiations. However, as underlined in
Leuenberger (
2016), “
other factors were equally, if not more, influential, such as: demography, location of water aquifers, as well as the inclusion of (what under international law are considered illegal) Jewish settlements within the Occupied Palestinian Territories, inside Israeli-controlled territory. Assessments of the Barrier’s function can thus quickly become mired in controversy.” As a matter of fact, this
security fence is called
a wall of apartheid by the Palestinians while the simple term
wall is used by the International Court of Justice.
1 Where does the controversy comes from? In fact, the wall does not follow the
Green Line, the international separation between the State of Israel and the occupied West Bank. With a total length of 708 kilometers, the Wall is more than double the length of the Green Line and at times runs 18 kilometers deep inside the West Bank. As described in
Cohen (
2006), “
many of the portions of the wall that comprise imposing concrete slabs are located in the heart of Palestinian communities, splitting towns, villages, streets, and even extended families (Usher 2006). In other places the fence portions separate Palestinian farmers from their fields, jobs, or schools, cresting visible and acute disruption of normal life.” A detailed map produced by the
Applied Research Institute Jerusalem is reproduced in
Leuenberger (
2016, Figure 3), showing that about 85% of the route followed by the wall runs inside the West Bank, well away from the internationally recognised Green Line.
This wall was built not only to separate Palestinians from Israelis, but also to separate them from Israeli settlements inside the West Bank. As a result, around 943 square kilometres of land located between the wall and the Green Line 1967 border (16.8% of the total West Bank area) has been declared by the Israeli army as a military zone known as the
Seam Zone. This area has become inaccessible to Palestinians living on the eastern side of the wall and having no special or seasonal permits. The permits allow accessing the
Seam Zone only through a few gates in the wall and during short time periods, usually 15 min in the morning and 15 min in the evening (
Hareuveni 2012).
In the post-Oslo peace agreements period (1993–1995) and prior to the wall construction (2002), the occupied West Bank and the Gaza Strip have been subject to a closure policy imposed by the Israeli army. Total closure made movements between the West Bank and the Gaza Strip almost impossible; then internal closure in the West Bank prevented Palestinians from accessing Jerusalem. The checkpoints system installed between West Bank localities made movements and access to land more and more difficult.
2Many academic studies were led to measure the consequences of the wall. However, those were mainly concerned about law and politics.
Hassan (
2005) discusses the implications of the advice of the International Court of Justice on the relationships between Israel and the US Government.
Kattan (
2007) discusses the examination by the Supreme Court of Israel of the Advisory Opinion rendered by the International Court of Justice concerning the legality of the Wall.
Malone (
2004) examines how the route followed by the Wall affects water access for Palestinian villages of the West Bank when
Reynolds (
2015) details environmental damages and reduction of bio-diversity.
We focus here on the economic consequences of the Wall on the Palestinian society. As underlined in
Roy (
2000),
“Given the extreme dependence of the Palestinian economy on Israel, the impact of closure- restricting the jobs and income of Palestinians working in Israel, reducing Palestinian trade levels, lowering production levels, and so on, has been to heighten poverty”. Palestinians in West Bank found themselves separated from lands behind the wall and from the economic resources they represent. Land behind the wall is known to be more fertile for agriculture and to contain rich natural resources. This zone used to offer scope for future economic development of the occupied Palestinian territory, as well as urban expansion (
World Bank 2008)).
In addition to the segregation of Palestinians from agricultural land, the wall deprives Palestinians from employment opportunities in Israel. Employment in Israel, that concerns mostly unskilled workers and which is paid higher than in the local Palestinian market, represented an unstable but important income source for low-income and low-asset households. According to the Palestinian Central Bureau of Statistics labour force surveys (
PCBS 2000,
2005), around 26% of total Palestinian employment in the West Bank was located in Israel in 1999, but this share declined to around 12% in 2003 and 2004 due to the decline in the number of permits issued by Israel and also due to the wall and checkpoints in the West Bank.
Adnan (
2015) finds, using the Palestinian Labour Force Survey, that closures and living on the West Bank side of the wall deter out-migration to Israel and increase the probability of being unemployed. In an anthropological paper,
Bornstein (
2001) argues that the wall does not make it impossible for Palestinian workers to illegally enter Israel, but it makes it impractical on a daily basis. The segregation policy forces Palestinian workers without permits to stay hidden for weeks on construction sites and in factories, due to the risk of being arrested. This increased risk either discourages Palestinians from working in Israel or may imply long term life deterioration, including reduction in income and consumption, for those subject to this risk. In both cases, households are pushed into chronic poverty traps.
Evidence for eastern and southern African countries (
Jayne et al. 2003) shows that land distribution among smallholders is related to income poverty. In the occupied Palestinian territory, land access restrictions and land confiscations render land prices excessively steep (
World Bank 2008). This resulted in higher asset-value inequality and income inequality between Palestinians who own or work in lands behind the wall and Palestinians who own highly demanded lands on the eastern side of the wall.
Negative consumption and income shocks in conflict areas may have long-term effects on school drop-out, displacement, nutrition and health status deterioration, which may imply a chronic poverty status (
Carter and Barrett 2006;
Ibañez and Moya 2010). Moreover, if shocks persistently result in asset losses or in inaccessibility to their location, income can fall below the critical threshold for several periods and households will be more likely to fall into chronic poverty (
Dercon 1998). Households subject to shocks usually refer to credit markets or sell part of their non-productive assets as a strategy of adjustment to shocks, but credit markets exclude low-income and low-asset households. Thus, the initial condition of a low consumption level with insufficient asset-base pushes households into poverty traps (
Zimmermann and Carter 2003;
Carter and Barrett 2006;
Reynolds 2015).
Evidence is found in the literature for a downward spiral of poverty and resource degradation. Poor people over-use existing accessible resources due to high population growth, limited access to resources and inequality in resource allocation. Overuse leads again to resource degradation and increasing poverty (
Cleaver and Schreiber 1994;
Forsyth and Scoones 1998;
Scherr 2000).
A similar case under colonisation and resource access restrictions in recent history is South Africa, where black South Africans had no access to certain resources including land and water. Five years after the fall of the apartheid regime, poverty prevalence was still increasing among black South Africans with a high probability of chronic poverty (
Carter and May 2001). Candidates for chronic poverty in South Africa are mostly black, female, rural, people with health problems, elderly and farm workers (
Aliber 2003). Moreover, education is found to be an important factor in poverty dynamics determination (
Jalan and Ravallion 2000;
Fuwa 2007).
The objective of this paper is to measure poverty dynamics and income mobility in the occupied Palestinian territory and its determinants. We focus on the West Bank region, excluding the Gaza Strip, but including the Jerusalem area behind the wall. The focus on Palestinians in the West Bank only is for two reasons. First, the wall exists neither in the Gaza Strip nor in Jerusalem. The wall does not prevent Palestinians living in Jerusalem from working in Israel. Second, poverty dynamics and patterns are different in the Gaza Strip and in Jerusalem from what they are in the West Bank. In the Gaza Strip, poverty is due to closure and wars. In Jerusalem, Palestinians are more likely to work in Israel, but they are constrained by Israeli fiscal policies and they are consuming at Israeli prices.
To quantify the impact of the wall on poverty dynamics, we use the model of
Cappellari and Jenkins (
2004) which provides a convincing approach to modelling poverty entry and poverty persistence. However, the only data we have are provided by the
Palestinian Expenditure and Consumption Survey (PECS) collected for the years 1998, 2004 and 2011, which are repeated cross-sections. For the years 2004 and 2011, the PECS contains a geographical variable indicating if a household is located or not in a zone impacted by the wall. We introduce a new Bayesian method of generating pseudo panels, treating the question as an incomplete data problem. Inside the loop of a Gibbs sampler, we explain the income-to-needs ratio using time invariant data for 2004 and 2011 to generate the missing values. Then we use both observed and latent variables to explain the income-to-needs ratio for 2011, this time conditionally on being poor in 2004 and being affected or not by the wall. We have thus two ways of measuring poverty dynamics and the final effect of the wall on poverty dynamics is determined by a difference between a marginal probability and a conditional probability taking into account the effect of the wall.
The paper is organised as follows. After this introduction,
Section 2 describes the
Palestinian Expenditure and Consumption Survey, and discusses the definition of the poverty line.
Section 3 proposes a first measure of the impact of the wall on poverty and shows how a naive strategy would provide wrong results.
Section 4 presents a new model for poverty dynamics and shows how this model can be adapted for a repeated cross-section in a Bayesian framework and how the impact of the wall can be measured. Then,
Section 5 presents our empirical results. Conclusions and recommendations are presented in the last section.
4. A Model of Poverty Dynamics in Repeated Cross-Sections
We propose a model for inference on poverty dynamics when the data are only in the form of repeated cross-sections, using a Bayesian approach. The Bayesian approach is particularly suited here because repeated cross-sections can be seen as an incomplete data problem. We first review the classical literature on poverty dynamics and on repeated cross-sections in order to formulate a model in terms of latent variables. We then present inference procedures to measure the impact of the wall on poverty dynamics.
4.1. Literature
The literature on poverty dynamics has much more recent roots than that of income dynamics. The founding papers were
Lillard and Willis (
1978) and
Bane and Ellwood (
1986). The former proposes a Markov chain model of income transitions. The latter is attached to the modelling of the length of poverty spells and the probability of exiting poverty. However, it is concerned only with head-count poverty and requires rather long panels.
Rodgers and Rodgers (
1993) still rely on long panels, but can distinguish between the three aspects of poverty (incidence, intensity and inequality) and propose a decomposition between chronic and transitory poverty.
Cappellari and Jenkins (
2004) tackle the question of attrition when measuring poverty dynamics, building a three equation model. The first equation explains the probability that an individual observed at time
can still be observed at time
t. The second equation explains the marginal probability of being in poverty at time
. The last equation explains the conditional probability of being in poverty at time
t when in poverty at time
. A key parameter is the correlation
of the error terms between
t and
. This model is essentially a dynamic probit model with selection bias. It serves to explain poverty persistence and exit from poverty.
Dang et al. (
2014) have the same concern, but using a rather different strategy based on linear regressions (and not on probit models) explaining consumption or income. Their main originality is that they deal with repeated cross-sections instead of true panels, using time invariant explanatory variables to link two periods. However,
Dang et al. (
2014) could only provide bounds for poverty persistence and poverty exit probabilities as
is not identified in their model.
4.2. Modelling Poverty Dynamics Using Panel Data
We first develop a model inspired by
Cappellari and Jenkins (
2004), estimating poverty persistence and exit from poverty, assuming provisionally that we have a balanced panel over two periods, 1 and 2 (2004 and 2011 in our case). In a next sub-section, we shall adapt this model to repeated cross-sections. The main variable that we have to explain is the log of the income-to-needs ratio
where
is the income of individual
i in period 1 and
is the poverty line applicable in time period 1. The following regression provides information on the initial state:
Individual
i is in a state of poverty if
. If the error term is Gaussian with zero mean and variance
, the marginal probability of being poor in the initial period for individual
i is equal to
. As we are interested in a transition probability between periods 1 and 2, given the observed state in period 1, we define the dummy variable
:
where
is the indicator function equal to 1 if
a is true and 0 otherwise. The income-to-needs ratio for the second period can now be explained by the observed past state of poverty
and by some other exogenous variables
related to the initial state and influencing the next state. The effect of
should be allowed to be different, depending on the nature of the previous state. So the equation explaining the income-to-needs ratio in period 2 is:
where
is a set of exogenous variables observed in period 1, containing
and at least another variable. The error term
is assumed to be Gaussian with zero mean and variance
. The two error terms are correlated over time with
for the same individual
i and independent between two different individuals. In the model of
Cappellari and Jenkins (
2004),
is identified only if
has an element which is not in
.
Let us define a second dummy variable for period 2:
Following
Cappellari and Jenkins (
2004), poverty persistence is defined as the state of being poor in period 2 while having being poor in period 1. Its probability is given by:
which corresponds to the ratio between a joint probability and a marginal probability,
being the bivariate Gaussian cumulative distribution. Poverty entry is defined in a similar way as:
Estimating model (
1)–(
3) is quite simple if we observe the same individual over the two periods. Poverty persistence and poverty exit are just simple transformations of the estimated parameters. However, of course we need a true panel, which of course is not the case here. We have only repeated cross-sections, which makes the problem more complex.
4.3. Poverty Dynamics and Repeated Cross-Sections
Feasible panel data sets are not so common, especially in developing countries and so techniques have been found in order to retrieve information from repeated cross-sections.
Deaton (
1985) first proposed to take means inside cohort clusters defined by time invariant instrumental variables (following the terminology used in
Verbeek 2008). However, this approach can lead to a substantial loss of information. An alternative approach was taken in a series of papers, mainly
Dang et al. (
2011);
Dang and Lanjouw (
2013) and
Dang et al. (
2014), following an initial idea of out-of-sample imputation of
Elbers et al. (
2003). Let us consider again two periods, and two samples coming from the same population. The starting point is a two-equation model explaining the log of the income-to-needs ratio as before, denoted
y here for simplicity of notation, for period 1 and period 2:
There are
individuals with
and
, so that there is no overlapping between the two periods or if there is, we do not know which individuals are present in the two periods. So initially it would seem there is no clear link between these two equations, apart from the fact that the two samples are drawn from the same population, while
i and
j do not concern the same observed individuals or households. The first link that is introduced between the two samples is that
and
are time invariant exogenous variables and so it is clear that
and
. The idea used in
Dang et al. (
2014) is to simulate values for the missing individuals in one of the two periods. Because both
and
are drawn from the same population and are functions of the same time invariant exogenous variables, we can simulate for instance the unobserved
, using
. So having estimated separately the two equations in (
7) and (
8),
Dang et al. (
2014) define the event of entering a state of poverty as the joint event of not being poor at time 1 and being poor at time 2. This joint probability is given by:
This probability is a function of the joint distribution of
with a coefficient of association
. If
, then mobility attains its upper bound. If
, then mobility reaches its lower bound. A positivity assumption for
is justified on the basis of household fixed effect and the persistence of shocks. However, apart from this prior restriction,
is not identified because the two equations in (
8) are totally symmetric. Without further assumptions,
Dang et al. (
2014) can propose only bounds for poverty transition probabilities. Assuming a Gaussian distribution for the error terms, the probability of entering poverty becomes:
where the four quantities
,
,
and
have been estimated directly from the two equations of the initial model. A set of values for
has to be picked in the interval [0, 1] in order to compute (
10).
We should point out the main differences between the model of
Dang et al. (
2014) and our first model (
1)–(
3) based on
Cappellari and Jenkins (
2004). Our first model is fundamentally asymmetric whereas the model of
Dang et al. (
2014) assumes a perfect symmetry. Entering poverty in (
6) is normalised by the probability of the initial state. The probability of entering poverty in (
10) depends essentially on the differences between
and
and the differences between
and
. There is no way of including the effect of the wall, except in a symmetric way in
. In addition, in
Section 3.2, we have seen that to do so was not a reasonable solution.
4.4. Repeated Cross-Section as an Incomplete Data Problem
We want of course to treat the problem in a different way and show that a repeated cross-section is fundamentally an incomplete data problem. In a full data model, unobserved individuals in period 1,
and the unobserved individuals in period 2,
are treated as latent variables so that we have
individuals (observed and unobserved) for each period. Formally, this means:
For instance
represents the observed group in period 2 while
represents the same group being unobserved in period 1. The assumption that
x does not vary over time (variables such as age, sex, religion, localisation,…) implies that
and that
. This is an identification assumption that will allow us to make inference in this model. The second identification assumption is that the parameters are constant over all the individuals within the same period.
Let us now discuss the joint distribution of the four error terms which are
. We assume that it is Gaussian with zero mean and variance-covariance matrix
. This matrix has a particular structure which results from the following very simple assumptions. We have assumed that within each period, the two error terms (corresponding to observed and to latent variables) have the same variance for identification reasons. We assume now that the individuals are not correlated, which means that there is no spatial correlation, simply because our data are not informative on that dimension. The important parameter to specify is the correlation
between two income observations for the same individual over the two periods. If we translate these assumptions into mathematical terms, we have:
which leads to the following variance-covariance matrix:
So even if (
13) has a block diagonal structure, this does not mean that we have imposed restrictions that could be testable.
Dang et al. (
2014) have chosen to simulate only one of the two latent variables, considering one of the two distributions,
or
, treating thus the two periods independently. For instance, for the first period, they are using:
By doing so, they loose a part of the available information. We prefer first to simulate both
and
, and second to condition on all the other variables, so as to take into account the between periods correlation. Due to the particular structure of matrix (
13), we have however the simplification
:
which means that it is necessary to condition only on the observed variables when simulating the latent variables. Conversely, for simulating
, we have:
Equations (
15) and (
16) will be our basic tools to simulate the missing observations and thus build a completed panel. So despite the apparent restrictive structure of (
13), the simulation of the latent variables takes into account as much information as possible.
A model written as an incomplete data problem leads logically to a Gibbs sampler. Missing observations are generated conditionally on values of the parameters which are then reevaluated conditionally on the simulated missing variables. However in our case, things are not as simple as that. The identifying assumptions
and
provide information for both the regression coefficients
and the latent variables. For the present we have no specific source of information for the correlation coefficient
while it is needed for simulating the latent variables. We need to provide an extra source of information and this will be the object of
Section 4.6. It is important to remember that
Dang et al. (
2014) provide only bounds for
.
4.5. Inference on the Regression Parameters
Conditional on simulated values for the latent variables, our two period regression model with variance-covariance matrix (
13) corresponds to a simple SURE (Seemingly Unrelated Regression) model. In
Bauwens et al. (
1999, Chap. 9), it is shown how Bayesian inference in a SURE model can be done using a Gibbs sampler for estimating jointly the regression parameters and the correlation structure. We can also decompose inference into two stages: the regression parameters on one hand and the correlation structure on the other hand. For that purpose, we decompose
as given in (
13) into the product of two diagonal matrices
S containing
and
, sandwiching a correlation matrix
R, so that
, following a suggestion made in
Barnard et al. (
2000). In our case, these matrices are:
Let us now factorise the product
using a Choleski decomposition. We then form the matrix
which is equal to:
If we pre-multiply our system of four equations by
L, the matrix of variance covariance of the error terms will be transformed into a diagonal matrix:
meaning that we can make inference on the two blocks separately. Let us pre-multiply our model (
11) and (
12) by
L. Due to the particular structure of
L, the model for the first period is left unchanged:
with
,
. The model for the second period is modified into a conditional model with:
with
and
Let us now define the following matrices with
rows so as to write our model in a matrix form:
where
,
are respectively two vectors of dimension
and
(
,
are of dimension
and
) and
,
are two matrices with corresponding number of rows
and
. Our model for the first period can be written as:
and Bayesian inference on its regression parameters can be done separately from inference on the other parameters. Because the model is symmetric between the two periods, we can adopt the reverse ordering for the Choleski decomposition, obtain another matrix
L and consider for period two the symmetric model:
So conditional on the simulated values for the latent variables, the two regression models (
19) and (
20) can be analysed separately. Under a non-informative prior, the posterior densities of
and
are two conditional normal densities while those of
and
are two inverse gamma2 densities with:
5
where
,
and:
We have the needed formulae for conducting Bayesian inference on the regression parameters, conditional on the simulated values for the latent variables. We must now detail how to make inference on the correlation parameter .
4.6. Inference on Correlation
Returning to the remaining equations in the system (
17) and (
18) where
appears explicitly, let us multiply them both by
, rearrange the terms and adopt a similar matrix notation as before. We get:
where
is defined in (
20) with zero mean and variance-covariance matrix
. From the previous step, we have knowledge of
,
,
and
. So in theory we could recover information on
using this regression which is nothing but a regression of the residuals from the period 2 model on the residuals from period 1 model. However, things are not as simple as that, because in fact no new information is brought in by this autoregressive model which only compares observations to their simulated counterpart (
to
and
to
). We have to find a source of extra information.
Verbeek and Vella (
2005) and
Verbeek (
2008) have proposed to use the grouping technique of
Deaton (
1985) for making inference in autoregressive pseudo panel models, using the fact that taking group averages is equivalent to IV estimation with the group dummies as instruments. We shall use time invariant information such as birth date and gender as instruments to determine
cohorts and then compute the cell means of each vector or matrix of observations. We collect these
C cell means into new vectors noted
,
having each
C rows and two new matrices
,
with also
C rows. They correspond respectively to the
C cell means of
,
and of
,
. Let us now define the following vectors and matrices:
which all have
rows. Let us rearrange (
25) into:
We then replace in (
27)
by
,
by
and
X by
so as to get:
When comparing (
28) to (
27), we see that we have replaced
by
, but also
by the same
. A similar replacement was done for the endogeneous variable of the first period. This means that we have replaced latent variables by observed cell means.
6 This model can be simplified if we consider the deviation matrix
. Let us pre-multiply (
28) by
to get:
We shall use (
29) to get information on
, assuming that
was determined in the previous step.
7 With (
29), we have an autoregressive regression model where inference can be conducted in a simple way, conditionally on
. We assume that the error term
is of zero mean and variance-covariance matrix
. It is interesting to introduce the possibility of an informative natural conjugate prior for
. We consider the following prior information:
The conditional posterior density of
is a normal density and that of
is an inverse gamma2 density with:
where:
The parameter
has to be constrained to a specific range. It has to be strictly less than 1 for stability reasons and
Dang et al. (
2014) have shown that it has to be positive. So we have to constraint
. Consequently, we shall not draw
directly from its conditional posterior density
, but from this posterior density truncated between 0 and 1.
4.7. A Separate Dynamic Equation for Implementing a Diff-In-Diff Strategy
The last equation we have to discuss corresponds to (
3) where we introduce the effect of the wall in the second period. We have to suppose that the households impacted by the wall do not change over the two periods, which means that the wall is a time invariant variable (even if its effect is diluted over time) and that the households do not migrate (we shall document that point later). Let us call
W the vector containing the index of the impacted households by the wall in period 1 and in period 2. Let us define a random dummy variable
which indicates for period 1 if a household was in a state of poverty or not:
This variable is a function of all the parameters because
contains simulated values of a latent variable. We can then specify our last equation to estimate as being:
with
u being Gaussian with zero mean and variance-covariance matrix
. It can be put in a matrix form if we define:
The posterior density of
in the regression
has the usual form under a non-informative prior:
with
and
We propose to measure the effect of the wall on poverty dynamics by a diff-in-diff strategy. Poverty follows its own trend which can be measured by a transition matrix, as we were able to simulate the income-to-needs ratios,
and
, for the two periods, using (
15) and (
16). The corresponding matrix of marginal poverty transition is defined as:
with rows summing to one and generic element
.
is the probability of staying in a state of poverty between periods 1 and 2 while
is the probability of entering poverty in period 2. For each draw
l of the parameters, this matrix can be evaluated as:
where
is defined in (
32) with
being replaced by
and
is defined accordingly for period 2. These dummy variables indicate for the two periods and for each draw if an household is in a state of poverty or not. As they are computed for each MCMC draw of the parameters,
and
are estimated by averaging over the MCMC output.
These marginal probabilities are modified when we take into account the wall effect by means of the dynamic conditional model (
33). With the Gibbs output for
and
, we can evaluate the vectors of poverty persistence
and poverty entry
. More precisely, for poverty persistence, we have:
which corresponds to the ratio between a joint probability and a marginal probability,
being the bivariate Gaussian cumulative distribution. While for poverty entry, we get:
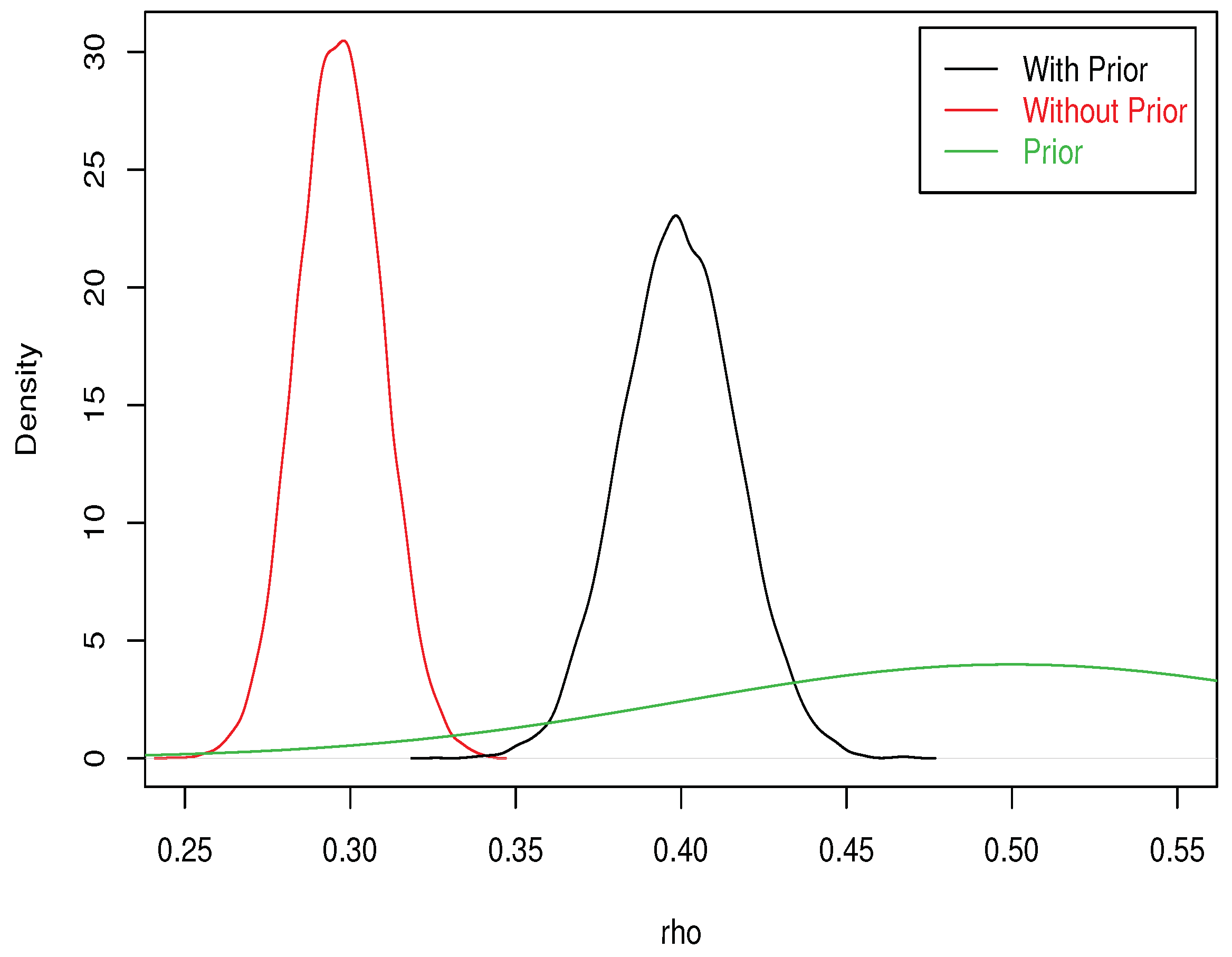
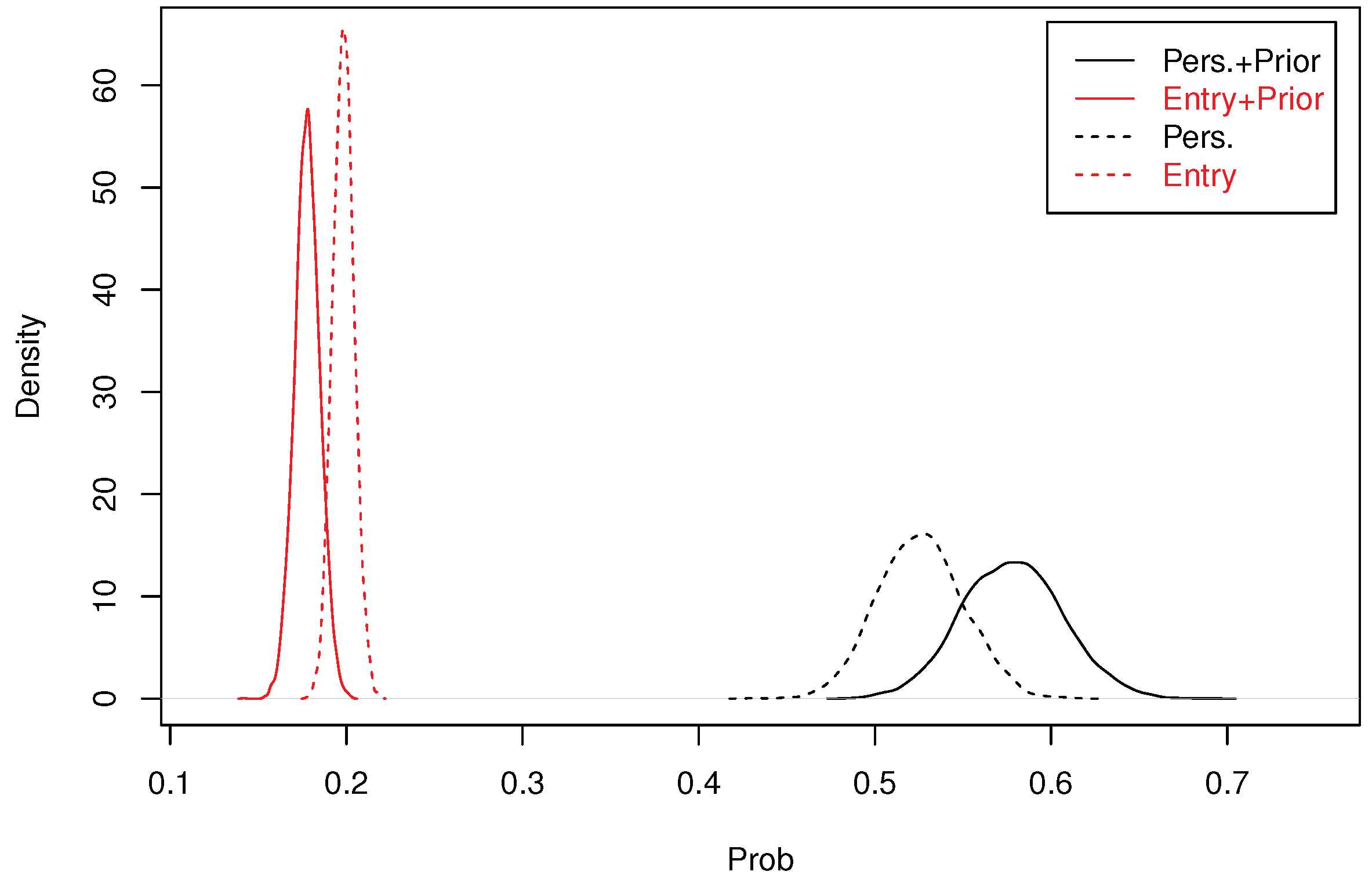
If we impose the restriction , then , while the restriction would imply . Consequently the net effect of the wall is measured by the influence of and and is obtained by computing the posterior density of the two differences: for the effect of the wall on poverty persistence; for the effect of the wall on poverty entry.
4.8. Summarised Gibbs Sampler Algorithm
Inference on , , , , and is provided by a Gibbs sampler for which we have found all the conditional posterior densities. We summarise the whole process in the following Gibbs sampler algorithm:
Define starting values for:
, obtained using OLS on .
, obtained using OLS on .
compute .
determine cohort cells means for , and , .
compute , , and .
obtained using OLS on .
Start iterations for the Gibbs sampler over :
From this MCMC output, we can produce graphs of the posterior density of poverty entry and poverty persistence. All computations were done in R, using the packages truncnorm for drawing from a truncated normal and pbivnorm for the bivariate Gaussian cumulative.
6. Conclusions
Governments have always been tempted to build walls to solve problems confronting them. The first historical example is the Great Wall of China, the building of which started three centuries B.C., soon followed by the Hadrian Wall in Scotland built by the Roman Emperor Hadrian. These walls were designed to keep others out of the frontiers. In the Twentieth century, the meaning of the Wall in Berlin was different, the aim being to keep people in. The destruction of this wall was synonymous of freedom regained. Following
Cohen (
2006), the aim of the wall built by the Israeli government is to keep people both in and out. We can note that this wall is by no mean an exception in the world, witness the long list detailed in
Vallet and David (
2012a,
2012b) showing their exponential increase since the fall of Berlin wall. However, no other wall has been subject of so many emotional reactions as underlined by
Cohen (
2006). It is certainly because its route “
harms Palestinians to a disproportionate degree.” However, the same author concludes his paper by the following sentence: “
Perhaps then, in the context of a negotiated settlement between Israelis and Palestinians, it can join other famous walls in becoming obsolete.” This statement finds some grounds in the results of
Longo et al. (
2014) who exploited a natural experiment based on a 2009 policy toward the “easement” of checkpoints in the West Bank. They found, using a diff-in-diff approach that “easement” made the treated populations less likely to support violence.
We have shown empirically that the wall had a large impact on poverty dynamics in the West Bank. This result was obtained using pseudo panels and a Bayesian approach. The method we propose provides a coherent way of simulating unobserved values, stating the question in the framework of incomplete data problems. It resulted in a Gibbs sampler from which we could provide inference for two different types of probabilities concerning poverty entry and poverty persistence. These different types come from the distinction between a marginal model and a conditional model taking into account state dependence, or phrased differently taking or not into account the previous state of poverty. In our model, we allow the wall to have a different effect, depending if the household was poor or not during the previous period. We identified a clear different effect which allows us to evaluate how the dynamics of poverty was impacted by the wall. We have documented a rather weak effect of 1.50% using a simple diff-in-diff approach when examining stylised facts and no panel structure. With a much more elaborated model using pseudo panels, we could extract more precise information from our sample which led to measuring an increase of 18 percentage points for poverty entry and of 58 percentage points for poverty persistence. In addition, these results were quite robust to the specification of the prior used for . However, we must note that these results are dependent of important identification assumptions which are not testable. It would be interesting to have a true panel in order to be less constrained in the specification of the model in order to check the accuracy of our evaluation of the impact of the wall on poverty dynamics.