Jump Variation Estimation with Noisy High Frequency Financial Data via Wavelets
Abstract
:1. Introduction
1.1. Motivation
1.2. Integrated Volatility, Realized Volatility and Jump Variation
1.3. Market Microstructure Noises
1.4. Wavelet Basics
2. Statistical Analysis
2.1. Choosing a Frequency Level to Differentiate Jumps
2.1.1. Starting from X and [X, X]
2.1.2. Moving on to Y and [Y, Y]
2.1.3. Subsampling and Averaging on [Y, Y]
2.2. Threshold Selection and Jump Location Estimation
2.3. Estimation of Jump Variation
2.3.1. Without Microstructure Noise Assumption
2.3.2. With the Microstructure Noise Assumption
3. Simulations
- A sample path of is from the geometric OU volatility model
- A sample path of is fromwith .
- Jump locations are randomly selected, and three jumps are added to with size from i.i.d. .
- Noises ϵ’s are from i.i.d. with η at four different levels: 0.01, 0.02, 0.03, 0.04. Then, a sample path of is from .
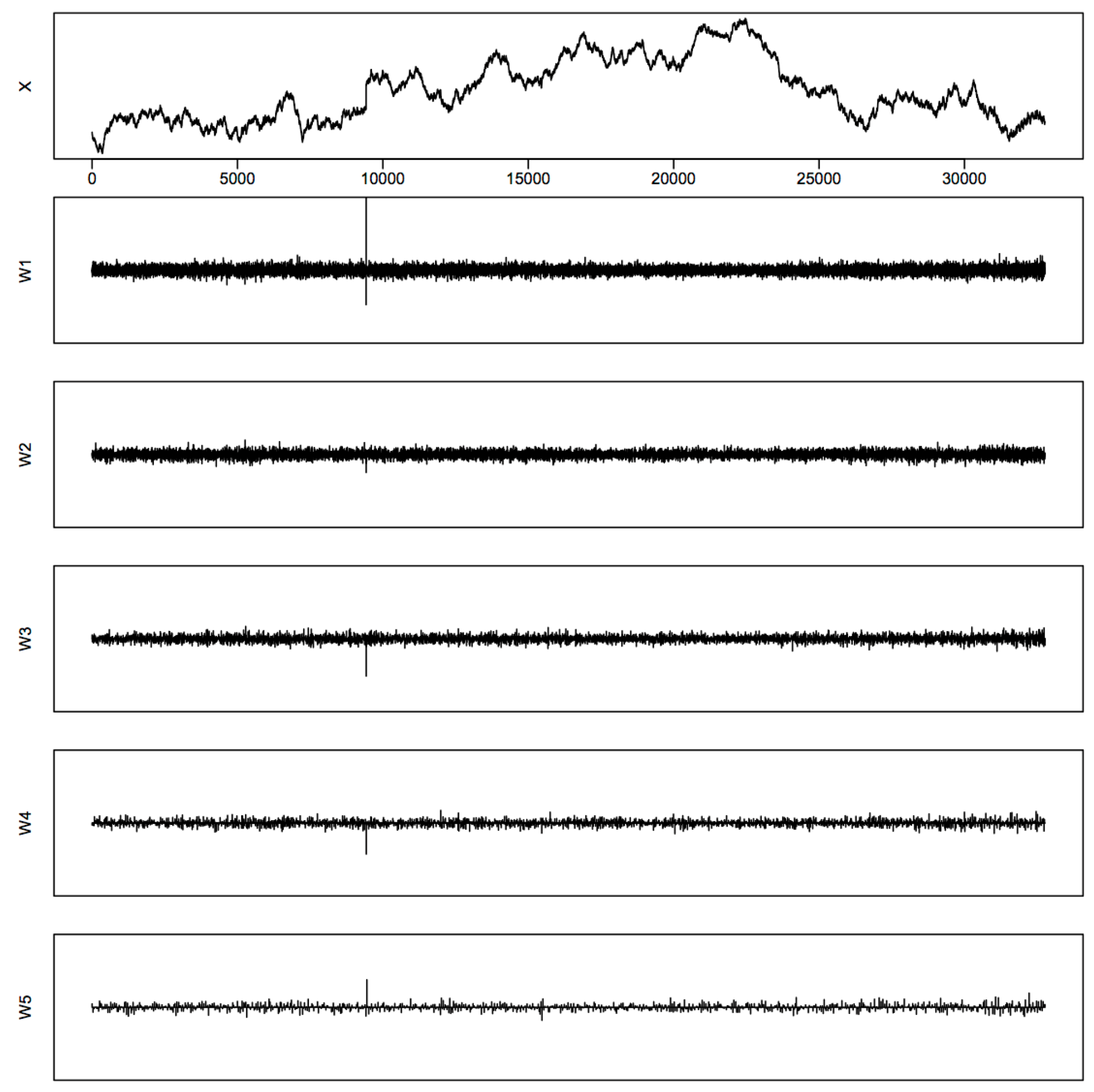
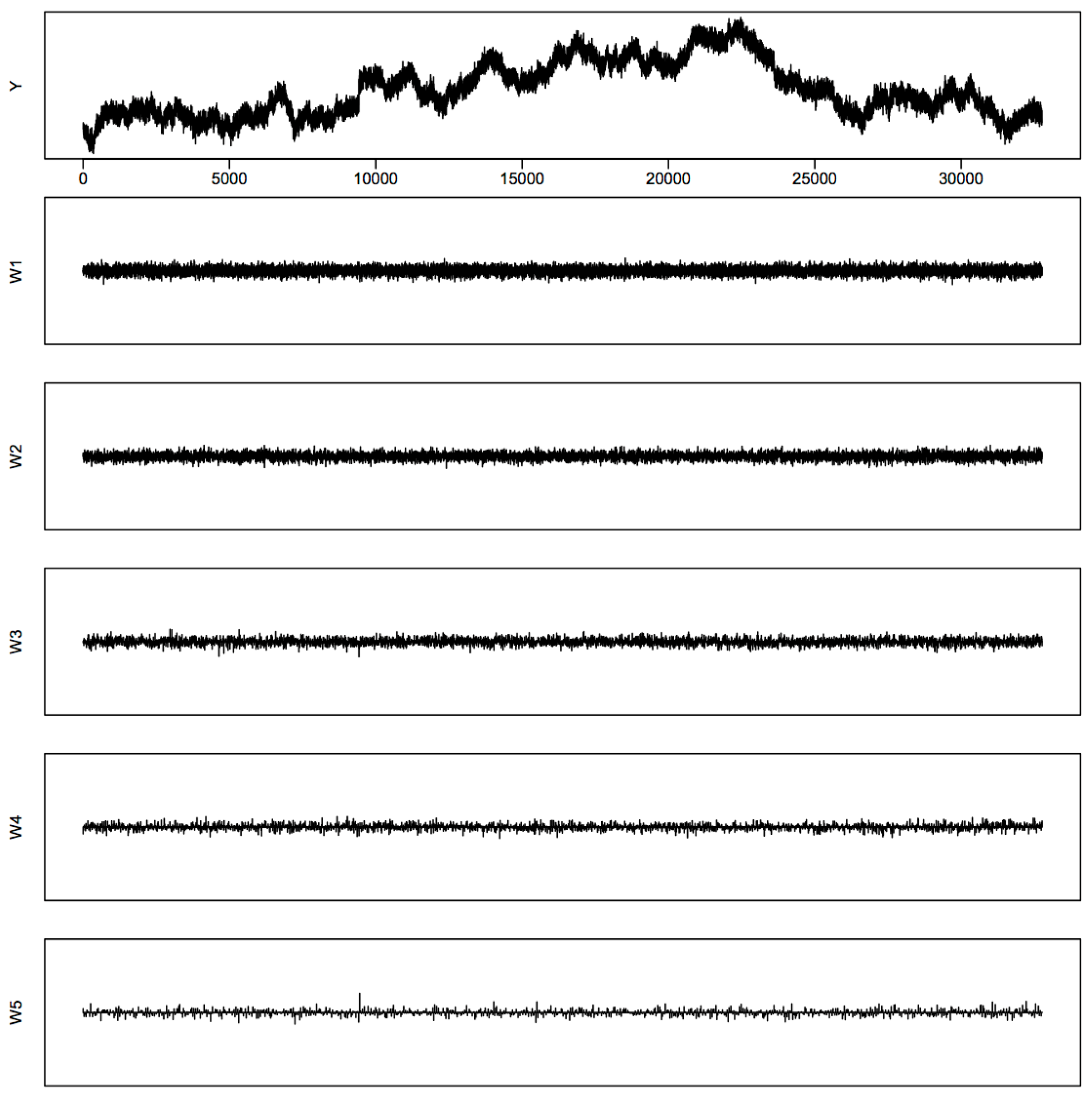
- Realized volatility processes are calculated using a moving window of 32,768 observations. We actually simulate 65,536 of records, so that we have 32,768 complete observations of all processes for calculating these realized volatility processes. There are eight of such processes: X, , Y, , , , , . Figure 1 displays their sample paths as an example to show how those processes look under our scheme.
- Discrete wavelet transformations are performed using Daubechies wavelet D20 on those realized volatility processes. We illustrate the behaviors of the wavelet coefficients at different frequency levels in Figure B1 and Figure B2 in Appendix B using those of the X process and the Y process as an example. We use the notations in Percival and Walden (2000) [42]: W1 represents the highest frequency level, W2 the second highest, and so on and so forth. At each frequency level from W1 to W5, if any standardized wavelet coefficient exceeds the threshold in (20), we declare the location associated with that coefficient as an estimated jump location. Here, we use , since the results in Section 2 and the simulation study show that the method based on is better than others.
- For each estimated jump location, we estimate the jump size and jump variation as described in Section 2. For X and Y, we use intervals of length 64. For , , , , , , we use intervals of length 128.
- The whole simulation procedure is repeated 1000 times.
4. Empirical Study
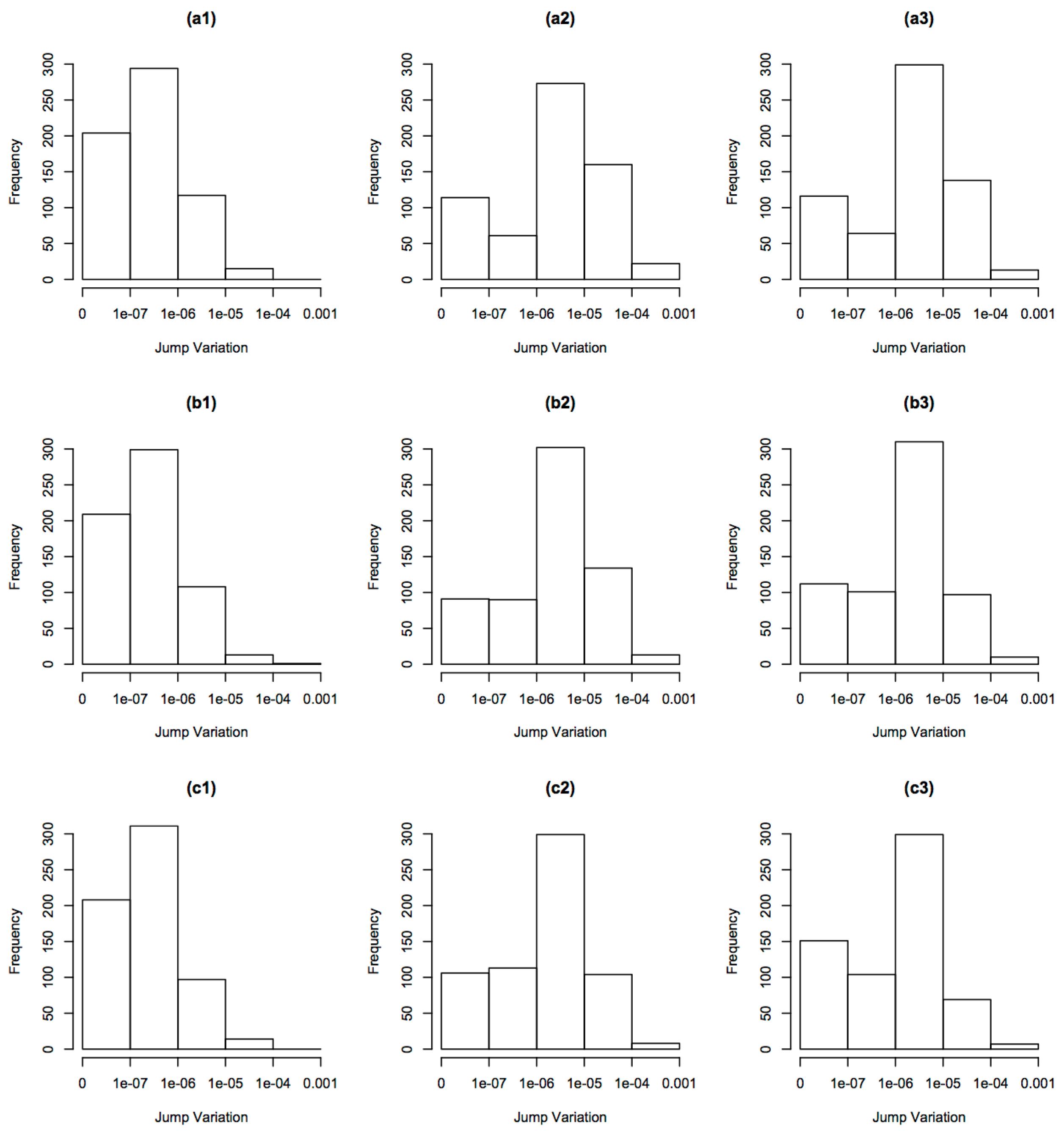
4.1. Distribution of Jump Variation
4.2. Evidence of Microstructure Noises
5. Discussion
6. Proof of Theorems
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Lemmas
- Case 1:
- . Since all other , we have .
- Case 2:
- . Then, we have , so
- Case 3:
- . Then, we have , so
Appendix B. Tables and Figures
| Component | X | Y | |||
|---|---|---|---|---|---|
| cont. drift (≤) | |||||
| cont. diffusion (≤) | |||||
| jump (≥) | |||||
| noise () | 0 |
| X | Y | |||
|---|---|---|---|---|
| NA |
| X | Y | |||
|---|---|---|---|---|
| NA |
References
- O.E. Barndorff-Nielsen, and N. Shephard. “Econometric Analysis of Realized Volatility and Its Use in Estimating Stochastic Volatility Models.” J. R. Stat. Soc. Ser. B 64 (2002): 253–280. [Google Scholar] [CrossRef]
- L. Zhang, P.A. Mykland, and Y. Aït-Sahalia. “A Tale of Two Time Scales: Determining Integrated Volatility with Noisy High-Frequency Data.” J. Am. Stat. Assoc. 100 (2005): 1394–1411. [Google Scholar] [CrossRef]
- L. Zhang. “Efficient Estimation of Stochastic Volatility Using Noisy Observations: A Multi-Scale Approach.” Bernoulli 12 (2006): 1019–1043. [Google Scholar] [CrossRef]
- F.M. Bandi, and J.R. Russell. “Microstructure Noise, Realized Variance, and Optimal Sampling.” Rev. Econ. Stud. 75 (2008): 339–369. [Google Scholar] [CrossRef]
- O.E. Barndorff-Nielsen, P.R. Hansen, A. Lunde, and N. Shephard. “Designing Realized Kernels to Measure Ex-post Variation of Equity Prices in the Presence of Noise.” Econometrica 76 (2008): 1481–1536. [Google Scholar]
- J. Jacod, Y. Li, P.A. Mykland, M. Podolskij, and M. Vetter. “Microstructure Noise in the Continuous Case: The Pre-averaging Approach.” Stoch. Process. Their Appl. 119 (2009): 2249–2276. [Google Scholar] [CrossRef]
- J. Jacod, M. Podolskij, and M. Vetter. “Limit Theorems for Moving Averages of Discretized Processes Plus Noise.” Ann. Stat. 38 (2010): 1478–1545. [Google Scholar] [CrossRef]
- D. Xiu. “Quasi-maximum Likelihood Estimation of Volatility with High Frequency Data.” J. Econ. 159 (2010): 235–250. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia. “Telling from Discrete Data Whether the Underlying Continuous-Time Model Is a Diffusion.” J. Finance 57 (2002): 2075–2121. [Google Scholar] [CrossRef]
- O.E. Barndorff-Nielsen, and N. Shephard. “Power and Bipower Variation with Stochastic Volatility and Jumps (with discussion).” J. Financ. Econ. 2 (2004): 1–48. [Google Scholar]
- R.C. Merton. “Option Pricing When Underlying Stock Returns Are Discontinuous.” J. Financ. Econ. 3 (1976): 125–144. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia. “Disentangling Volatility from Jumps.” J. Financ. Econ. 74 (2004): 487–528. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia, and J. Jacod. “Testing for Jumps in a Discretely Observed Process.” Ann. Stat. 37 (2009): 184–222. [Google Scholar] [CrossRef]
- T.G. Andersen, D. Dobrev, and E. Schaumburg. “Jump-robust Volatility Estimation Using Nearest Neighbor Truncation.” J. Econ. 169 (2012): 75–93. [Google Scholar] [CrossRef]
- O.E. Barndorff-Nielsen, and N. Shephard. “Econometrics of Testing for Jumps in Financial Economics using Bipower Variation.” J. Financ. Econ. 4 (2006): 1–30. [Google Scholar] [CrossRef]
- P. Carr, and L. Wu. “What Type of Process Underlies Options? A Simple Robust Test.” J. Finance 58 (2003): 2581–2610. [Google Scholar] [CrossRef]
- B. Eraker, M. Johannes, and N. Polson. “The Impact of Jumps in Returns and Volatility.” J. Finance 58 (2003): 1269–1300. [Google Scholar] [CrossRef]
- B. Eraker. “Do Stock Prices and Volatility Jump? Reconciling Evidence From Spot and Option Prices.” J. Finance 59 (2004): 1367–1404. [Google Scholar] [CrossRef]
- Y. Fan, and J. Fan. “Testing and Detecting Jumps Based on a Discretely Observed Process.” J. Econom. 164 (2011): 331–344. [Google Scholar] [CrossRef]
- X. Huang, and G.T. Tauchen. “The Relative Contribution of Jumps to Total Price Variance.” J. Financ. Econ. 4 (2005): 456–499. [Google Scholar]
- G.J. Jiang, and R.C. Oomen. “Testing for Jumps When Asset Prices Are Observed with Noise—A “Swap Variance” Approach.” J. Econ. 144 (2008): 352–370. [Google Scholar] [CrossRef]
- S.S. Lee, and J. Hannig. “Detecting Jumps From Lévy Jump Diffusion Processes.” J. Financ. Econ. 96 (2010): 271–290. [Google Scholar] [CrossRef]
- S.S. Lee, and P.A. Mykland. “Jumps in Financial Markets: A New Nonparametric Test and Jump Dynamics.” Rev. Financ. Stud. 21 (2008): 2535–2563. [Google Scholar] [CrossRef]
- T. Bollerslev, U. Kretschmer, C. Pigorsch, and G. Tauchen. “A Discrete-time Model for daily S & P500 Returns and Realized Variations: Jumps and Leverage Effects.” J. Econ. 150 (2009): 151–166. [Google Scholar]
- V. Todorov. “Estimation of Continuous-Time Stochastic Volatility Models with Jumps Using High-Frequency Data.” J. Econ. 148 (2009): 131–148. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia, J. Jacod, and J. Li. “Testing for Jumps in Noisy High Frequency Data.” J. Econ. 168 (2012): 207–222. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia, and J. Jacod. “Estimating the Degree of Activity of Jumps in High Frequency Data.” Ann. Stat. 37 (2009): 2202–2244. [Google Scholar] [CrossRef]
- B.Y. Jing, X.B. Kong, and Z. Liu. “Estimating the Jump Activity Index of Lévy Processes Under Noisy Observations Using High Frequency Data.” J. Am. Stat. Assoc. 106 (2011): 558–568. [Google Scholar] [CrossRef]
- B.Y. Jing, X.B. Kong, Z. Liu, and P.A. Mykland. “On the Jump Activity Index for Semimartingales.” J. Econ. 166 (2012): 213–223. [Google Scholar] [CrossRef]
- V. Todorov, and G. Tauchen. “Limit Theorems for Power Variations of Pure-Jump Processes with Application to Activity Estimation.” Ann. Appl. Probabil. 21 (2011): 546–588. [Google Scholar] [CrossRef]
- B.Y. Jing, X.B. Kong, and Z. Liu. “Modeling High Frequency Data by Pure Jump Processes.” Ann. Stat. 40 (2012): 759–784. [Google Scholar] [CrossRef]
- X.B. Kong, Z. Liu, and B.Y. Jing. “Testing For Pure-jump Processes For High-Frequency Data.” Ann. Stat. 43 (2015): 847–877. [Google Scholar] [CrossRef]
- V. Todorov, and G. Tauchen. “Volatility Jumps.” J. Bus. Econ. Stat. 29 (2011): 356–371. [Google Scholar] [CrossRef]
- T.G. Andersen, T. Bollerslev, and F.X. Diebold. “Roughing it Up: Including Jump Components in the Measurement, Modeling, and Forecasting of Return Volatility.” Rev. Econ. Stat. 89 (2007): 701–720. [Google Scholar] [CrossRef]
- T.G. Andersen, T. Bollerslev, and X. Huang. “A Reduced Form Framework for Modeling and Forecasting Jumps and Volatility in Speculative Prices.” J. Econ. 160 (2011): 176–189. [Google Scholar] [CrossRef]
- T.G. Andersen, T. Bollerslev, and N. Meddahi. “Realized Volatility Forecasting and Market Microstructure Noise.” J. Econ. 160 (2011): 220–234. [Google Scholar] [CrossRef]
- Y. Wang. “Selected Review on Wavelets.” In Frontier Statistics, a Festschrift for Peter Bickel. Edited by H. Koul and J. Fan. London, UK: Imperial College Press, 2006, pp. 163–179. [Google Scholar]
- Y. Wang. “Jump and Sharp Cusp Detection by Wavelets.” Biometrika 82 (1995): 385–397. [Google Scholar] [CrossRef]
- J. Fan, and Y. Wang. “Multi-scale Jump and Volatility Analysis for High-Frequency Financial Data.” J. Am. Stat. Assoc. 102 (2007): 1349–1362. [Google Scholar] [CrossRef]
- I. Daubechies. Ten Lectures on Wavelets. Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, 1992. [Google Scholar]
- M. Raimondo. “Minimax Estimation of Sharp Change Points.” Ann. Stat. 26 (1998): 1379–1397. [Google Scholar] [CrossRef]
- D.B. Percival, and A.T. Walden. Wavelet Methods for Time Series Analysis. Cambridge, UK: Cambridge University Press, 2000. [Google Scholar]
- A. Rényi. “On Stable Sequences of Events.” Sankhyā Ser. A 25 (1963): 293–302. [Google Scholar]
- D.J. Aldous, and G.K. Eagleson. “On Mixing and Stability of Limit Theorems.” Ann. Probab. 6 (1978): 325–331. [Google Scholar] [CrossRef]
- P. Hall, and C.C. Heyde. Martingale Limit Theory and Its Application. Boston, MA, USA: Academic Press, 1980. [Google Scholar]
- J. Jacod, and P. Protter. “Asymptotic Error Distributions for the Euler Method for Stochastic Differential Equations.” Ann. Probab. 26 (1998): 267–307. [Google Scholar] [CrossRef]



| level | X | |
|---|---|---|
| W1 | ||
| W2 | ||
| W3 | ||
| W4 | ||
| W5 |
| level | X | |
|---|---|---|
| W1 | 3.0 × 10 | 1.4 × 10 |
| W2 | 3.7 × 10 | 3.0 × 10 |
| W3 | 1.7 × 10 | 8.6 × 10 |
| W4 | 6.0 × 10 | 2.4 × 10 |
| W5 | 2.2 × 10 | 8.4 × 10 |
| level | η | Y | |||||
|---|---|---|---|---|---|---|---|
| W1 | 0.01 | 2.3 (0.9) | 2.5 (0.7) | 2.5 (0.8) | 2.5 (0.8) | 2.6 (0.9) | 2.7 (0.9) |
| W2 | 0.01 | 2.4 (0.9) | 2.7 (0.9) | 2.6 (0.8) | 2.7 (0.9) | 3.6 (1.3) | 5.1 (1.8) |
| W3 | 0.01 | 2.3 (0.9) | 2.9 (1.1) | 3.3 (1.0) | 3.6 (1.2) | 5.3 (1.8) | 7.6 (2.6) |
| W4 | 0.01 | 2.6 (0.8) | 3.3 (1.3) | 4.2 (1.3) | 6.6 (2.1) | 7.8 (2.4) | 9.9 (3.0) |
| W5 | 0.01 | 2.7 (0.8) | 2.7 (1.0) | 3.2 (0.9) | 5.1 (1.8) | 6.6 (2.1) | 7.0 (2.4) |
| W1 | 0.02 | 1.5 (1.0) | 2.0 (0.9) | 2.0 (0.9) | 2.1 (0.9) | 2.2 (0.9) | 2.2 (0.9) |
| W2 | 0.02 | 1.7 (0.9) | 2.1 (1.0) | 2.1 (0.9) | 2.1 (0.9) | 2.3 (0.9) | 2.8 (1.1) |
| W3 | 0.02 | 1.7 (1.0) | 2.3 (1.2) | 2.7 (0.9) | 2.6 (0.9) | 3.0 (1.1) | 4.1 (1.5) |
| W4 | 0.02 | 2.3 (0.9) | 2.7 (1.4) | 3.2 (1.0) | 3.7 (1.3) | 4.0 (1.4) | 5.9 (2.1) |
| W5 | 0.02 | 2.6 (0.9) | 2.0 (1.1) | 2.8 (0.9) | 3.3 (1.2) | 4.0 (1.4) | 4.7 (1.7) |
| W1 | 0.03 | 1.0 (0.9) | 1.5 (0.9) | 1.6 (0.9) | 1.7 (0.9) | 1.8 (0.9) | 1.9 (0.9) |
| W2 | 0.03 | 1.1 (0.9) | 1.7 (1.1) | 1.7 (0.9) | 1.8 (0.9) | 1.9 (0.9) | 2.1 (0.9) |
| W3 | 0.03 | 1.2 (0.9) | 1.8 (1.2) | 2.5 (1.0) | 2.3 (0.9) | 2.4 (1.0) | 2.8 (1.1) |
| W4 | 0.03 | 1.9 (0.9) | 2.2 (1.4) | 2.9 (1.1) | 3.2 (1.2) | 3.1 (1.2) | 3.7 (1.5) |
| W5 | 0.03 | 2.4 (0.9) | 2.5 (1.1) | 2.6 (1.0) | 2.9 (1.1) | 2.9 (1.1) | 3.2 (1.4) |
| W1 | 0.04 | 0.6 (0.8) | 1.2 (0.9) | 1.2 (0.9) | 1.4 (0.9) | 1.5 (0.9) | 1.6 (0.9) |
| W2 | 0.04 | 0.8 (0.8) | 1.3 (1.0) | 1.3 (0.9) | 1.4 (0.9) | 1.6 (0.9) | 1.8 (0.9) |
| W3 | 0.04 | 0.8 (0.8) | 1.4 (1.2) | 2.3 (1.0) | 2.0 (2.0) | 2.1 (1.0) | 2.2 (1.0) |
| W4 | 0.04 | 1.5 (0.9) | 1.8 (1.4) | 2.6 (1.1) | 3.0 (1.2) | 2.7 (1.2) | 3.0 (1.3) |
| W5 | 0.04 | 2.2 (0.9) | 1.2 (1.0) | 2.3 (1.1) | 2.7 (1.2) | 2.5 (1.0) | 2.6 (1.1) |
| level | η | Y | |||||
|---|---|---|---|---|---|---|---|
| W1 | 0.01 | 4.3 × 10 | 3.0 × 10 | 8.9 × 10 | 1.2 × 10 | 2.1 ×10 | 5.8 × 10 |
| W2 | 0.01 | 4.6 × 10 | 1.4 × 10 | 8.9 × 10 | 1.5 × 10 | 2.4 × 10 | 6.3 × 10 |
| W3 | 0.01 | 1.9 × 10 | 1.8 × 10 | 1.8 × 10 | 1.6 × 10 | 2.7 × 10 | 6.1 × 10 |
| W4 | 0.01 | 7.2 × 10 | 2.5 × 10 | 2.1 × 10 | 2.7 × 10 | 3.9 × 10 | 5.0 × 10 |
| W5 | 0.01 | 1.2 × 10 | 8.0 × 10 | 1.2 × 10 | 2.8 × 10 | 4.2 × 10 | 5.1 × 10 |
| W1 | 0.02 | 2.4 × 10 | 1.8 × 10 | 3.5 × 10 | 2.9 × 10 | 3.3 × 10 | 6.7 × 10 |
| W2 | 0.02 | 2.0 × 10 | 3.5 × 10 | 3.5 × 10 | 2.8 × 10 | 3.2 × 10 | 6.9 × 10 |
| W3 | 0.02 | 3.7 × 10 | 4.2 × 10 | 5.2 × 10 | 2.0 × 10 | 3.0 × 10 | 6.2 × 10 |
| W4 | 0.02 | 7.5 × 10 | 9.9 × 10 | 5.1 × 10 | 3.6 × 10 | 4.6 × 10 | 5.3 × 10 |
| W5 | 0.02 | 1.4 × 10 | 2.8 × 10 | 4.1 × 10 | 7.3 × 10 | 5.6 × 10 | 5.2 × 10 |
| W1 | 0.03 | 1.2 × 10 | 6.1 × 10 | 1.6 × 10 | 9.6 × 10 | 7.0 × 10 | 7.8 × 10 |
| W2 | 0.03 | 1.2 × 10 | 9.2 × 10 | 1.6 × 10 | 5.1 × 10 | 6.8 × 10 | 6.9 × 10 |
| W3 | 0.03 | 1.3 × 10 | 1.3 × 10 | 1.0 × 10 | 4.9 × 10 | 3.5 × 10 | 7.2 × 10 |
| W4 | 0.03 | 8.7 × 10 | 2.2 × 10 | 6.4 × 10 | 5.9 × 10 | 5.4 × 10 | 5.8 × 10 |
| W5 | 0.03 | 1.5 × 10 | 4.9 × 10 | 5.1 × 10 | 1.8 × 10 | 6.9 × 10 | 6.6 × 10 |
| W1 | 0.04 | 3.5 × 10 | 1.5 × 10 | 4.4 × 10 | 2.7 × 10 | 1.8 × 10 | 1.5 × 10 |
| W2 | 0.04 | 2.6 × 10 | 2.1 × 10 | 4.7 × 10 | 3.2 × 10 | 1.6 × 10 | 1.2 × 10 |
| W3 | 0.04 | 3.0 × 10 | 3.1 × 10 | 1.9 × 10 | 1.2 × 10 | 7.2 × 10 | 7.4 × 10 |
| W4 | 0.04 | 1.1 × 10 | 4.3 × 10 | 1.4 × 10 | 1.2 × 10 | 5.6 × 10 | 6.6 × 10 |
| W5 | 0.04 | 1.5 × 10 | 7.1 × 10 | 5.3 × 10 | 3.0 × 10 | 1.5 × 10 | 7.7 × 10 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Kim, D.; Wang, Y. Jump Variation Estimation with Noisy High Frequency Financial Data via Wavelets. Econometrics 2016, 4, 34. https://doi.org/10.3390/econometrics4030034
Zhang X, Kim D, Wang Y. Jump Variation Estimation with Noisy High Frequency Financial Data via Wavelets. Econometrics. 2016; 4(3):34. https://doi.org/10.3390/econometrics4030034
Chicago/Turabian StyleZhang, Xin, Donggyu Kim, and Yazhen Wang. 2016. "Jump Variation Estimation with Noisy High Frequency Financial Data via Wavelets" Econometrics 4, no. 3: 34. https://doi.org/10.3390/econometrics4030034
APA StyleZhang, X., Kim, D., & Wang, Y. (2016). Jump Variation Estimation with Noisy High Frequency Financial Data via Wavelets. Econometrics, 4(3), 34. https://doi.org/10.3390/econometrics4030034





