On the Validity of Granger Causality for Ecological Count Time Series
Abstract
:1. Introduction
2. Materials and Methods
2.1. Vector Autoregressive Models and Granger Causality
2.2. Simulations
2.3. Applications
3. Results
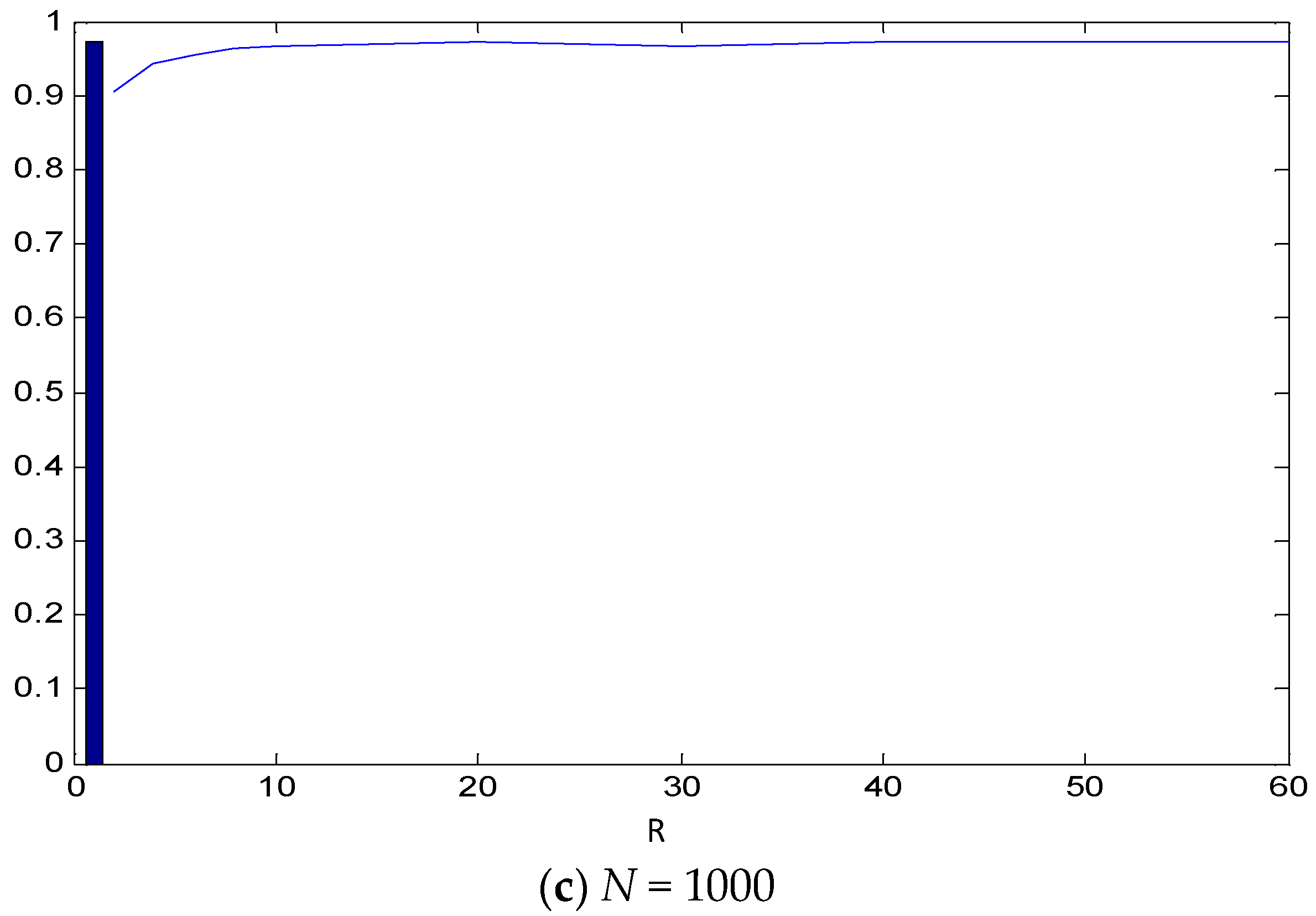
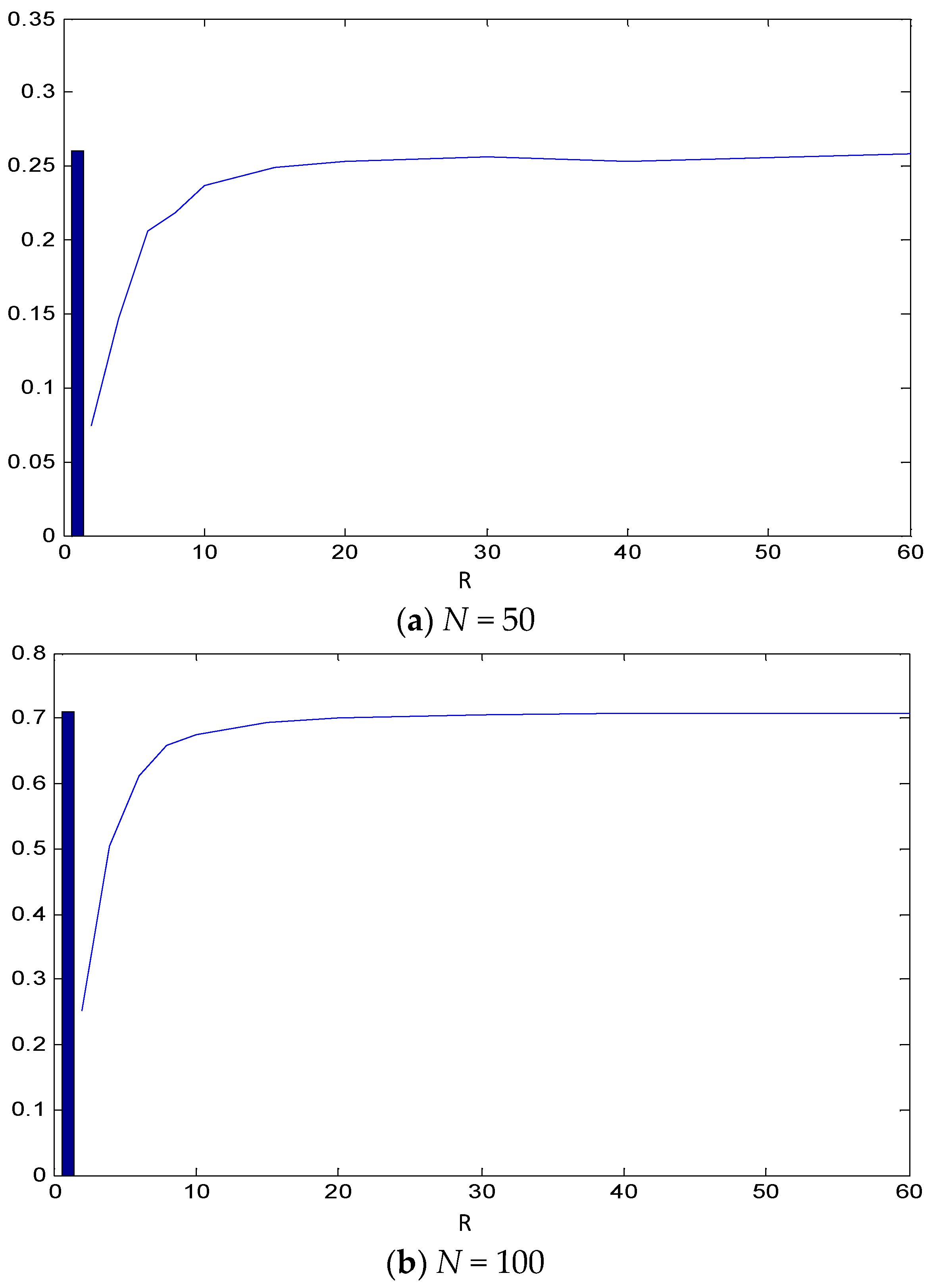
3.1. Simulations
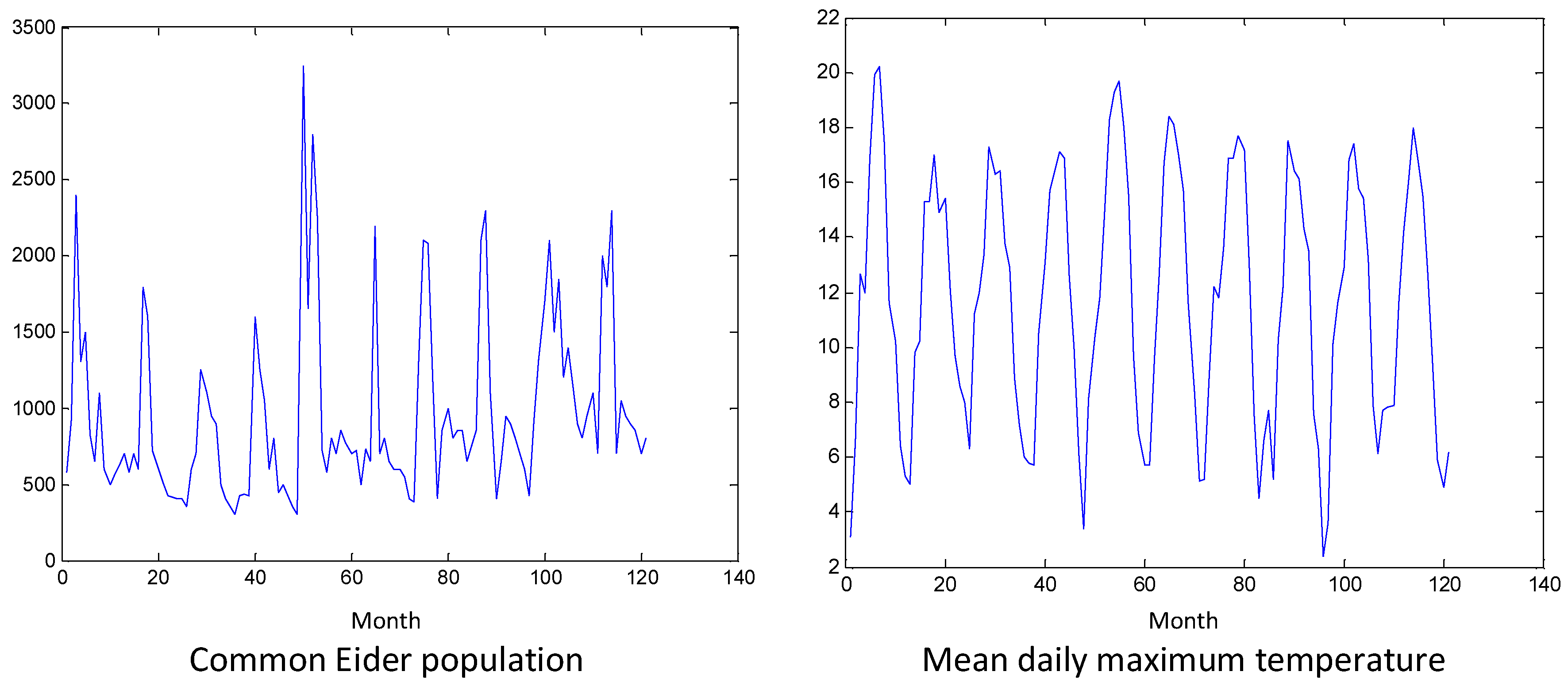
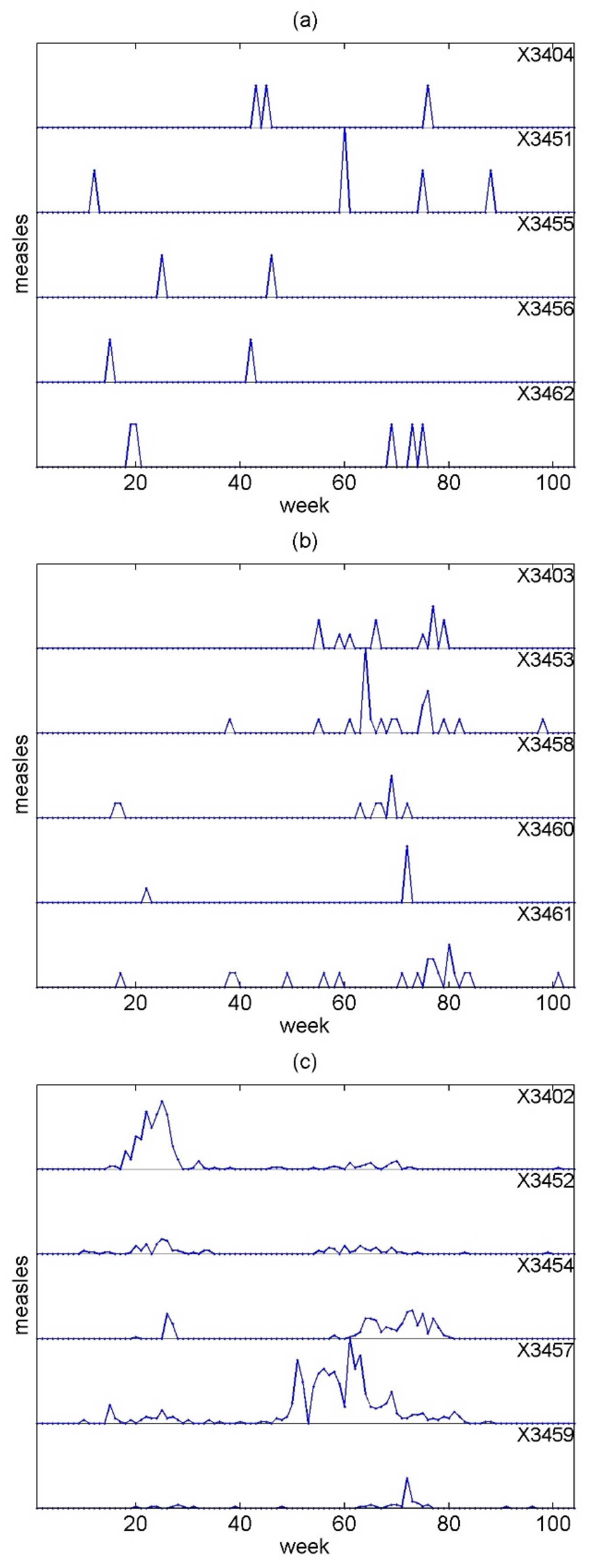
3.2. Applications
4. Discussion
4.1. Practical Implications
- Tools of quantitative (numerical) analysis can indeed be applied to variables that take only a minimum of count values, for example 0, 1. For Granger causality, the shortcoming of having time series of few counts can be balanced by having long time series.
- Based on the latter result, it is suggested to rather use a small sampling time in the observation of ecological populations than aggregating the data in longer sampling times to produce bigger counts, and then use tools developed for continuous-valued data. Data aggregation, which is often the common practice, reduces the length of the time series and may have considerable effects (estimation accuracy, undetected seasonality or periodicity, occurrence of instantaneous causality). Indeed, it was shown in the simulation study that Granger causality is less accurately estimated with short time series.
- The present study suggests that the data precision can be relaxed at the cost of accuracy in the estimation of Granger causality. However, this cost can be compensated for by increasing the time series length, so that in the cases where high-quality data collection is difficult or costly, low-resolution observations may be adequate if the time series is long enough. For example, the abundance of the Common Eider species was rounded to hundreds of Eiders, and the same Granger causality relationships were estimated by counting the abundance in 10 classes of Eiders from 0 to 9 (0 for no Eiders). Some abiotic factors could easily be collected directly from the observers of Eiders, during their work, in similar classes. For instance, the temperature could have been classified in a scale from 0 to 9 (0 for temperatures close to the area’s minimum temperature for the season of observations).
4.2. Theoretical Implications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmad, Ali, and Christian Francq. 2016. Poisson QMLE of Count Time Series Models. Journal of Time Series Analysis 37: 291–314. [Google Scholar] [CrossRef]
- Al-Osh, Mohamed A., and Aus A. Alzaid. 1987. First-Order Integer-Valued Autoregressive (INAR(1)) Process. Journal of Time Series Analysis 8: 261–75. [Google Scholar] [CrossRef]
- Andersson, Jonas, and Dimitris Karlis. 2014. A Parametric Time Series Model with Covariates for Integers in Z. Statistical Modelling 14: 135–56. [Google Scholar] [CrossRef]
- Angers, Jean-François, Atanu Biswas, and Raju Maiti. 2017. Bayesian Forecasting for Time Series of Categorical Data. Journal of Forecasting 36: 217–29. [Google Scholar] [CrossRef]
- Auger-Méthé, Marie, Ken Newman, Diana Cole, Fanny Empacher, Rowenna Gryba, Aaron A. King, Vianey Leos-Barajas, Joanna Mills Flemming, Anders Nielsen, Giovanni Petris, and et al. 2021. A Guide to State–Space Modeling of Ecological Time Series. Ecological Monographs 91: e01470. [Google Scholar] [CrossRef]
- Barraquand, Frédéric, Coralie Picoche, Matteo Detto, and Florian Hartig. 2020. Inferring Species Interactions Using Granger Causality and Convergent Cross Mapping. Theoretical Ecology 14: 87–105. [Google Scholar] [CrossRef]
- Barry, Simon C., and Alan H. Welsh. 2002. Generalized Additive Modelling and Zero Inflated Count Data. Ecological Modelling 157: 179–88. [Google Scholar] [CrossRef]
- Benjamini, Yoav, and Yosef Hochberg. 1995. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society: Series B (Methodological) 57: 289–300. [Google Scholar] [CrossRef]
- Bonan, Gordon B., and Herman H. Shugart. 1989. Environmental Factors and Ecological Processes in Boreal Forests. Annual Review of Ecology and Systematics 20: 1–28. [Google Scholar] [CrossRef]
- Boudreault, Mathieu, and Arthur Charpentier. 2011. Multivariate Integer-Valued Autoregressive Models Applied to Earthquake Counts. arXiv arXiv:1112.0929. [Google Scholar]
- Bourguignon, Marcelo, Josemar Rodrigues, and Manoel Santos-Neto. 2019. Extended Poisson INAR(1) Processes with Equidispersion, Underdispersion and Overdispersion. Journal of Applied Statistics 46: 101–18. [Google Scholar] [CrossRef]
- Brandt, Patrick, and John Williams. 2007. Multiple Time Series Models. Thousand Oaks: Sage. [Google Scholar]
- Catania, Leopoldo, and Roberto Di Mari. 2021. Hierarchical Markov-Switching Models for Multivariate Integer-Valued Time-Series. Journal of Econometrics 221: 118–37. [Google Scholar] [CrossRef]
- Chan, Jennifer So Kuen, and Wai Yin Wan. 2014. Multivariate Generalized Poisson Geometric Process Model with Scale Mixtures of Normal Distributions. Journal of Multivariate Analysis 127: 72–87. [Google Scholar] [CrossRef]
- Christou, Vasiliki, and Konstantinos Fokianos. 2015. On Count Time Series Prediction. Journal of Statistical Computation and Simulation 85: 357–73. [Google Scholar] [CrossRef]
- Cunningham, Ross B., and David B. Lindenmayer. 2005. Modeling Count Data of Rare Species: Some Statistical Issues. Ecology 86: 1135–42. [Google Scholar] [CrossRef]
- Davis, Richard A., and Rongning Wu. 2009. A Negative Binomial Model for Time Series of Counts. Biometrika 96: 735–49. [Google Scholar] [CrossRef]
- Davis, Richard A., Konstantinos Fokianos, Scott H. Holan, Harry Joe, James Livsey, Robert Lund, Vladas Pipiras, and Nalini Ravishanker. 2021. Count Time Series: A Methodological Review. Journal of the American Statistical Association 116: 1533–47. [Google Scholar] [CrossRef]
- Detto, Matteo, Annalisa Molini, Gabriel Katul, Paul Stoy, Sari Palmroth, and Dennis Baldocchi. 2012. Causality and Persistence in Ecological Systems: A Nonparametric Spectral Granger Causality Approach. American Naturalist 179: 524–35. [Google Scholar] [CrossRef]
- Fokianos, Konstantinos. 2012. Count Time Series Models. In Handbook of Statistics. Amsterdam: Elsevier, vol. 30, pp. 315–47. [Google Scholar]
- Fokianos, Konstantinos. 2021. Multivariate Count Time Series Modelling. Econometrics and Statistics, in press. [Google Scholar] [CrossRef]
- Fokianos, Konstantinos, Anders Rahbek, and Dag Tjøstheim. 2009. Poisson Autoregression. Journal of the American Statistical Association 104: 1430–39. [Google Scholar] [CrossRef]
- Fokianos, Konstantinos, and Roland Fried. 2010. Interventions in INGARCH Processes. Journal of Time Series Analysis 31: 210–25. [Google Scholar] [CrossRef]
- Fokianos, Konstantinos, Roland Fried, Yuriy Kharin, and Valeriy Voloshko. 2022. Statistical Analysis of Multivariate Discrete-Valued Time Series. Journal of Multivariate Analysis 188: 104805. [Google Scholar] [CrossRef]
- Franke, Jürgen, and T. Subba Rao. 1993. Multivariate First Order Integer Valued Autoregressions. Berichte Der Arbeitsgruppe Technomathematik. Kaiserslaute: Universitgt Kaiserslautern, Fachbereich Mathematik. [Google Scholar]
- Gan, Jianbang. 2006. Causasilty among Wildfire, ENSO, Timber Harvest, and Urban Sprawl: The Vector Autoregression Approach. Ecological Modelling 191: 304–14. [Google Scholar] [CrossRef]
- Gerber, Brian D., and William L. Kendall. 2017. Evaluating and Improving Count-Based Population Inference: A Case Study from 31 Years of Monitoring Sandhill Cranes. The Condor 119: 191–206. [Google Scholar] [CrossRef]
- Geweke, John. 1982. Measurement of Linear Dependence and Feedback Between Multiple Time Series. Journal of the American Statistical Association 77: 304–13. [Google Scholar] [CrossRef]
- Granger, Clive W. J. 1969. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica 37: 424–38. [Google Scholar] [CrossRef]
- Hampton, Stephanie E., Elizabeth E. Holmes, Lindsay P. Scheef, Mark D. Scheuerell, Stephen L. Katz, Daniel E. Pendleton, and Eric J. Ward. 2013. Quantifying Effects of Abiotic and Biotic Drivers on Community Dynamics with Multivariate Autoregressive (MAR) Models. Ecology 94: 2663–69. [Google Scholar] [CrossRef] [PubMed]
- Heinen, Andreas, and Erick Rengifo. 2007. Multivariate Autoregressive Modeling of Time Series Count Data Using Copulas. Journal of Empirical Finance 14: 564–83. [Google Scholar] [CrossRef]
- Held, Leonhard, Michael Höhle, and Mathias Hofmann. 2005. A Statistical Framework for the Analysis of Multivariate Infectious Disease Surveillance Counts. Statistical Modelling 5: 187–99. [Google Scholar] [CrossRef]
- Hostetler, Jeffrey A., and Richard B. Chandler. 2015. Improved State-Space Models for Inference about Spatial and Temporal Variation in Abundance from Count Data. Ecology 96: 1713–23. [Google Scholar] [CrossRef]
- Jassby, Alan D., and Thomas M. Powell. 1990. Detecting Changes in Ecological Time Series. Ecology 71: 2044–52. [Google Scholar] [CrossRef]
- Jung, Robert C., Roman Liesenfeld, and Jean-François Richard. 2011. Dynamic Factor Models for Multivariate Count Data: An Application to Stock-Market Trading Activity. Journal of Business & Economic Statistics 29: 73–85. [Google Scholar]
- Kong, Jiajie, and Robert Lund. 2023. Seasonal Count Time Series. Journal of Time Series Analysis 44: 93–124. [Google Scholar] [CrossRef]
- Lam, Weng Siew, Weng Hoe Lam, Saiful Hafizah Jaaman, and Pei Fun Lee. 2023. Bibliometric Analysis of Granger Causality Studies. Entropy 25: 632. [Google Scholar] [CrossRef]
- Lindén, Andreas, and Samu Mäntyniemi. 2011. Using the Negative Binomial Distribution to Model Overdispersion in Ecological Count Data. Ecology 92: 1414–21. [Google Scholar] [CrossRef]
- Lütkepohl, Helmut. 2005. New Introduction to Multiple Time Series Analysis. Berlin and Heidelberg: Springer. [Google Scholar]
- Matthews, Brian W. 1975. Comparison of the Predicted and Observed Secondary Structure of T4 Phage Lysozyme. Biochimica et Biophysica Acta (BBA)-Protein Structure 405: 442–51. [Google Scholar] [CrossRef]
- McKenzie, Ed. 1985. Some Simple Models for Discrete Variate Time Series. JAWRA Journal of the American Water Resources Association 21: 645–50. [Google Scholar] [CrossRef]
- Met Office, UK. 2014. Historic Station Data: Nairn. Available online: http://www.metoffice.gov.uk/pub/data/weather/uk/climate/stationdata/nairndata.txt (accessed on 16 July 2014).
- Meyer, Sebastian, Leonhard Held, and Michael Höhle. 2017. Spatio-Temporal Analysis of Epidemic Phenomena Using the R Package Surveillance. Journal of Statistical Software 77: 1–55. [Google Scholar] [CrossRef]
- Milne, H. 1965. Seasonal Movements and Distribution of Eiders in Northeast Scotland. Bird Study 12: 170–80. [Google Scholar] [CrossRef]
- Mountford, Andrew, and Harald Uhlig. 2009. What Are the Effects of Fiscal Policy Shocks? Journal of Applied Econometrics 24: 960–92. [Google Scholar] [CrossRef]
- NERC Centre for Population Biology, Imperial College. 2010. The Global Population Dynamics Database Version 2. Available online: http://www.sw.ic.ac.uk/cpb/cpb/gpdd.html (accessed on 16 July 2014).
- Neumann, Michael H. 2011. Absolute Regularity and Ergodicity of Poisson Count Processes. Bernoulli 17: 1268–84. [Google Scholar] [CrossRef]
- Newman, Ken, Stephen Terrence Buckland, Byron Morgan, Ruth King, David Louis Borchers, Diana Cole, Panagiotis Besbeas, Olivier Gimenez, and Len Thomas. 2014. Modelling Population Dynamics: Model Formulation, Fitting and Assessment Using State-Space Methods. Methods in Statistical Ecology. New York: Springer. [Google Scholar]
- O’Hara, Robert, and Johan Kotze. 2010. Do Not Log-transform Count Data. Methods in Ecology and Evolution 1: 118–22. [Google Scholar] [CrossRef]
- Papapetrou, Maria, Elsa Siggiridou, and Dimitris Kugiumtzis. 2022. Adaptation of Partial Mutual Information from Mixed Embedding to Discrete-Valued Time Series. Entropy 24: 1505. [Google Scholar] [CrossRef] [PubMed]
- Park, YouSung, and Chan Wook Oh. 1997. Some Asymptotic Properties in INAR(1) Processes with Poisson Marginals. Statistical Papers 38: 287–302. [Google Scholar] [CrossRef]
- Paul, Michaela, and Leonhard Held. 2011. Predictive Assessment of a Non-Linear Random Effects Model for Multivariate Time Series of Infectious Disease Counts. Statistics in Medicine 30: 1118–36. [Google Scholar] [CrossRef]
- Paul, Michaela, Leonhard Held, and André M. Toschke. 2008. Multivariate Modelling of Infectious Disease Surveillance Data. Statistics in Medicine 27: 6250–67. [Google Scholar] [CrossRef] [PubMed]
- Pedeli, Xanthi, and Dimitris Karlis. 2011. A Bivariate INAR(1) Process with Application. Statistical Modelling 11: 325–49. [Google Scholar] [CrossRef]
- Pedeli, Xanthi, and Dimitris Karlis. 2013a. On Composite Likelihood Estimation of a Multivariate INAR(1) Model. Journal of Time Series Analysis 34: 206–20. [Google Scholar] [CrossRef]
- Pedeli, Xanthi, and Dimitris Karlis. 2013b. Some Properties of Multivariate INAR(1) Processes. Computational Statistics & Data Analysis 67: 213–25. [Google Scholar]
- Piancastelli, Luiza S. C., Wagner Barreto-Souza, and Hernando Ombao. 2023. Flexible Bivariate INGARCH Process with a Broad Range of Contemporaneous Correlation. Journal of Time Series Analysis 44: 206–22. [Google Scholar] [CrossRef]
- Richards, Shane A. 2008. Dealing with Overdispersed Count Data in Applied Ecology. Journal of Applied Ecology 45: 218–27. [Google Scholar] [CrossRef]
- Salmon, Maëlle, Dirk Schumacher, and Michael Höhle. 2016. Monitoring Count Time Series in R: Aberration Detection in Public Health Surveillance. Journal of Statistical Software 70: 1–35. [Google Scholar] [CrossRef]
- Santos, Cláudia, Isabel Pereira, and Manuel Scotto. 2021. On the Theory of Periodic Multivariate INAR Processes. Statistical Papers 62: 1291–348. [Google Scholar] [CrossRef]
- Schelter, Björn, Matthias Winterhalder, Bernhard Hellwig, Brigitte Guschlbauer, Carl Hermann Lücking, and Jens Timmer. 2006. Direct or indirect? Graphical models for neural oscillators. Journal of Physiology-Paris 99: 37–46. [Google Scholar] [CrossRef]
- Scotto, Manuel G., Christian H. Weiß, and Sónia Gouveia. 2015. Thinning-Based Models in the Analysis of Integer-Valued Time Series: A Review. Statistical Modelling 15: 590–618. [Google Scholar] [CrossRef]
- Scotto, Manuel G., Christian H. Weiß, Maria Eduarda Silva, and Isabel Pereira. 2014. Bivariate Binomial Autoregressive Models. Journal of Multivariate Analysis 125: 233–51. [Google Scholar] [CrossRef]
- Shojaie, Ali, and Emily B. Fox. 2022. Granger Causality: A Review and Recent Advances. Annual Review of Statistics and Its Application 9: 289–319. [Google Scholar] [CrossRef] [PubMed]
- Siggiridou, Elsa, Christos Koutlis, Alkiviadis Tsimpiris, and Dimitris Kugiumtzis. 2019. Evaluation of Granger Causality Measures for Constructing Networks from Multivariate Time Series. Entropy 21: 1080. [Google Scholar] [CrossRef]
- Sims, Christopher A. 1980. Macroeconomics and Reality. Econometrica 48: 1–48. [Google Scholar] [CrossRef]
- Song, Peter X.-K., R. Keith Freeland, Atanu Biswas, and Shulin Zhang. 2013. Statistical Analysis of Discrete-Valued Time Series Using Categorical ARMA Models. Computational Statistics & Data Analysis 57: 112–24. [Google Scholar]
- Sugihara, George, Robert May, Hao Ye, Chih-hao Hsieh, Ethan Deyle, Michael Fogarty, and Stephan Munch. 2012. Detecting Causality in Complex Ecosystems. Science 338: 496–500. [Google Scholar] [CrossRef]
- Tjøstheim, Dag. 2012. Some Recent Theory for Autoregressive Count Time Series. TEST: An Official Journal of the Spanish Society of Statistics and Operations Research 21: 413–38. [Google Scholar] [CrossRef]
- Tong, Howell. 1977. Some Comments on the Canadian Lynx Data. Journal of the Royal Statistical Society: Series A (General) 140: 432–36. [Google Scholar] [CrossRef]
- Tong, Howell, and Keng S. Lim. 1980. Threshold Autoregression, Limit Cycles and Cyclical Data. Journal of the Royal Statistical Society: Series B (Methodological) 42: 245–68. [Google Scholar] [CrossRef]
- Turchin, Peter, and Andrew D. Taylor. 1992. Complex Dynamics in Ecological Time Series. Ecology 73: 289–305. [Google Scholar] [CrossRef]
- Ver Hoef, Jay M., and Peter L. Boveng. 2007. Quasi-Poisson vs. Negative Binomial Regression: How Should We Model Overdispersed Count Data? Ecology 88: 2766–72. [Google Scholar] [CrossRef] [PubMed]
- Weiß, Christian H. 2008. Serial Dependence and Regression of Poisson INARMA Models. Journal of Statistical Planning and Inference 138: 2975–90. [Google Scholar] [CrossRef]
- Weiß, Christian H. 2021. Stationary Count Time Series Models. WIREs Computational Statistics 13: e1502. [Google Scholar] [CrossRef]
- Winterhalder, Matthias, Björn Schelter, Wolfram Hesse, Karin Schwab, Lutz Leistritz, Daniel Klan, Reinhard Bauer, Jens Timmer, and Herbert Witte. 2005. Comparison of Linear Signal Processing Techniques to Infer Directed Interactions in Multivariate Neural Systems. Signal Processing 85: 2137–60. [Google Scholar] [CrossRef]
- Yip, Paul S. F., Simon Sai Man Kwok, Feng Chen, Xiaochen Xu, and Ying-Yeh Chen. 2013. A Study on the Mutual Causation of Suicide Reporting and Suicide Incidences. Journal of Affective Disorders 148: 98–103. [Google Scholar] [CrossRef]
- Zeger, Scott L. 1988. A Regression Model for Time Series of Counts. Biometrika 75: 621–29. [Google Scholar] [CrossRef]




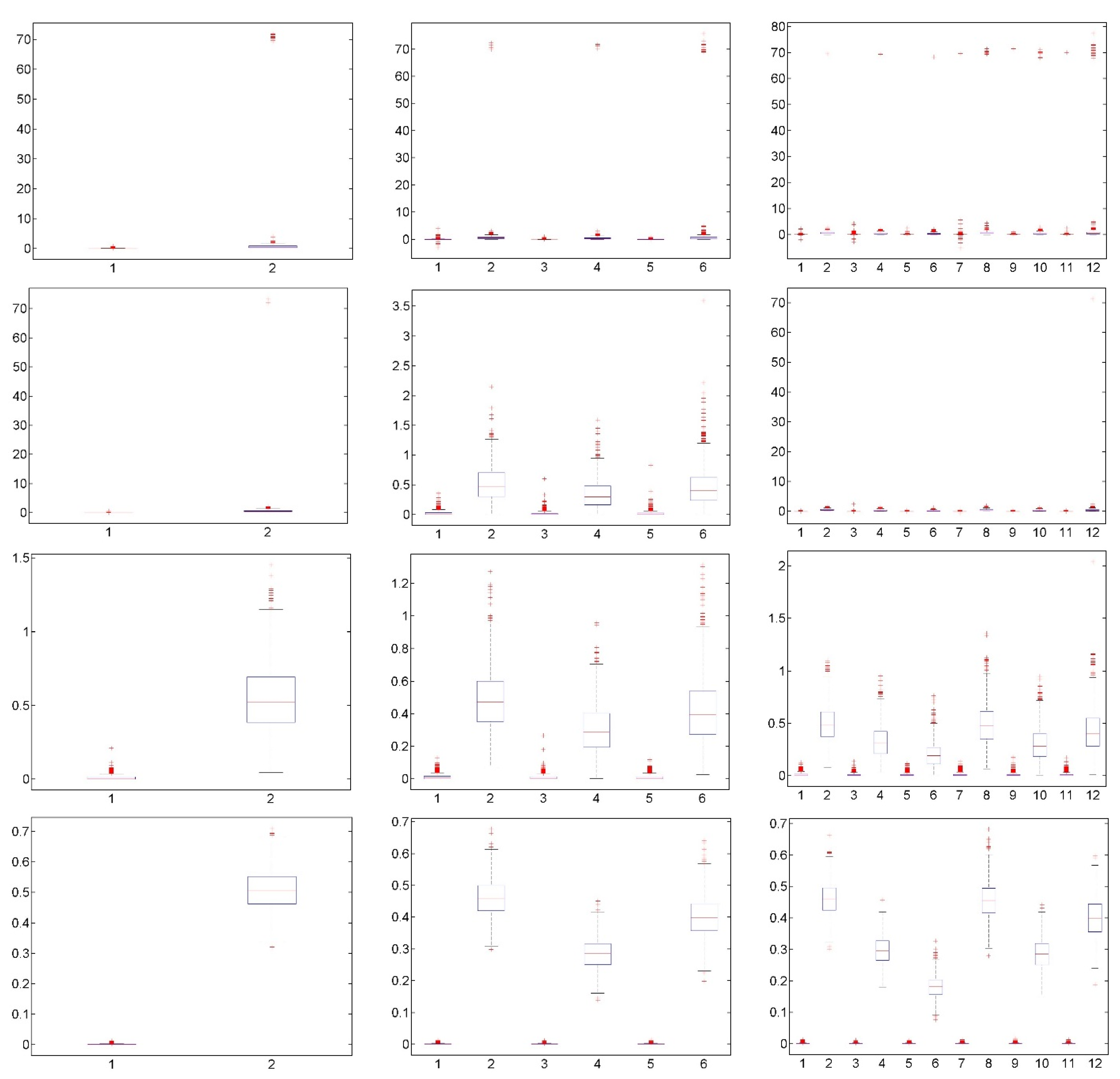

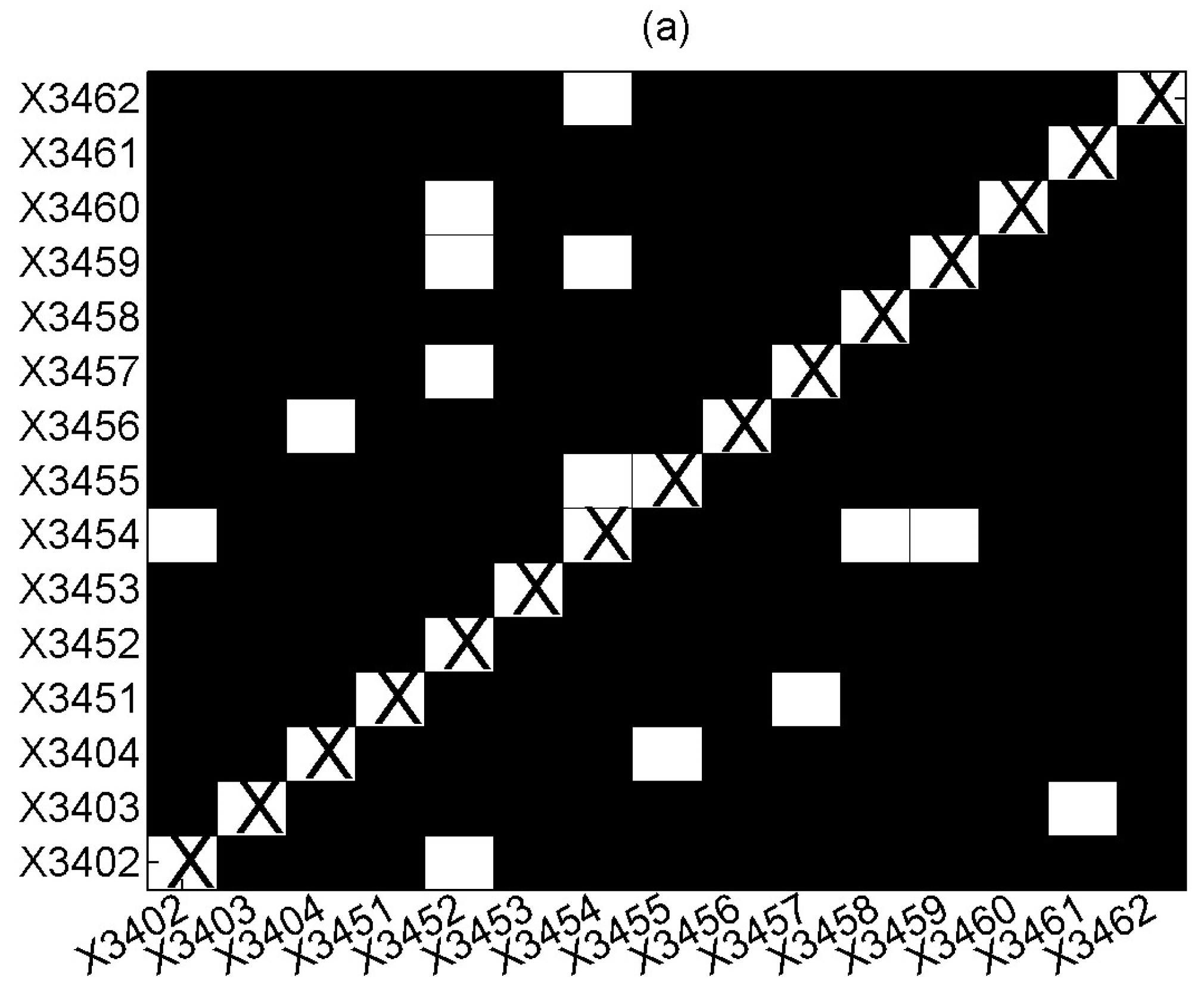
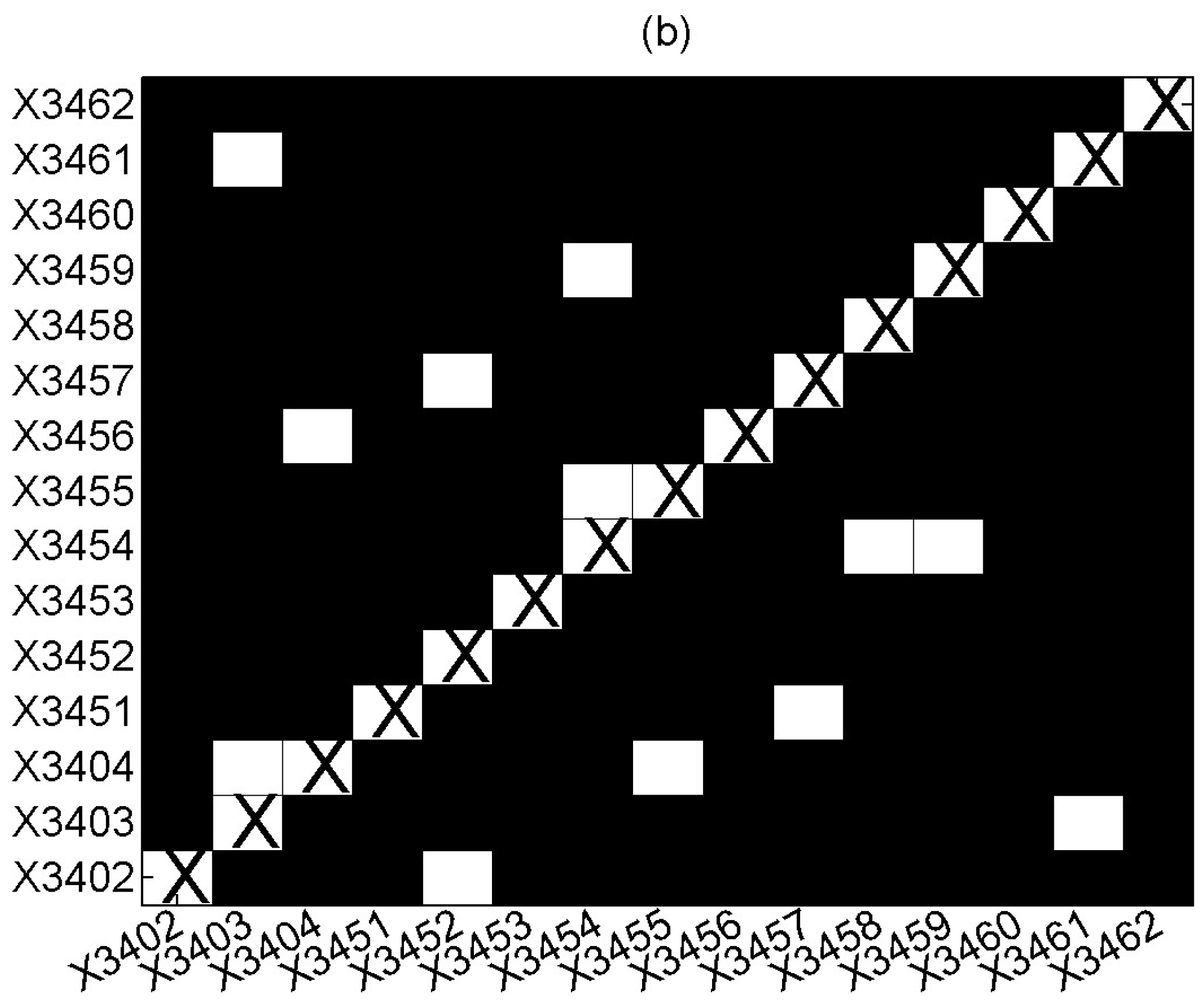
| Pair | CGCI (VAR) | FDR (VAR) | CGCI (DVAR) | FDR (DVAR) |
|---|---|---|---|---|
| X1 → X2 | 0.1906 | 18 | 0.1848 | 19 |
| X2 → X1 | 0.8900 | 890 | 0.3924 | 118 |
| X1 → X3 | 0.7560 | 781 | 1.0750 | 320 |
| X3 → X1 | 0.1922 | 16 | 0.1762 | 11 |
| X1 → X4 | 0.1847 | 19 | 0.1859 | 10 |
| X4 → X1 | 0.1868 | 17 | 0.1988 | 9 |
| X2 → X3 | 0.5097 | 419 | 0.1974 | 15 |
| X3 → X2 | 0.1885 | 20 | 0.1964 | 12 |
| X2 → X4 | 0.1925 | 18 | 0.1927 | 8 |
| X4 → X2 | 0.7879 | 830 | 0.3985 | 140 |
| X3 → X4 | 0.1864 | 25 | 0.1932 | 13 |
| X4 → X3 | 0.1905 | 18 | 0.1916 | 14 |
| K = 2 | N = 25 | N = 50 | N = 100 | N = 1000 | ||||
| Relation | GCI | FDR | GCI | FDR | GCI | FDR | GCI | FDR |
| X1 → X2 | 0.051 | 55 | 0.024 | 49 | 0.012 | 65 | 0.001 | 80 |
| X2→ X1 | 2.580 | 850 | 0.740 | 973 | 0.552 | 998 | 0.508 | 1000 |
| K = 3 | N = 25 | N = 50 | N = 100 | N = 1000 | ||||
| Relation | CGCI | FDR | CGCI | FDR | CGCI | FDR | CGCI | FDR |
| X1 → X2 | 0.059 | 54 | 0.026 | 46 | 0.012 | 46 | 0.001 | 55 |
| X2→ X1 | 1.008 | 749 | 0.521 | 961 | 0.488 | 1000 | 0.461 | 1000 |
| X1 → X3 | 0.047 | 23 | 0.021 | 31 | 0.011 | 37 | 0.001 | 26 |
| X3→ X1 | 0.758 | 602 | 0.342 | 844 | 0.311 | 985 | 0.286 | 1000 |
| X2 → X3 | 0.048 | 31 | 0.024 | 35 | 0.011 | 30 | 0.001 | 45 |
| X3→ X2 | 1.687 | 689 | 0.469 | 907 | 0.424 | 994 | 0.403 | 1000 |
| X1 → X2 | 0.059 | 54 | 0.026 | 46 | 0.012 | 46 | 0.001 | 55 |
| K = 4 | N = 25 | N = 50 | N = 100 | N = 1000 | ||||
| Relation | CGCI | FDR | CGCI | FDR | CGCI | FDR | CGCI | FDR |
| X1 → X2 | 0.066 | 42 | 0.027 | 53 | 0.013 | 37 | 0.001 | 49 |
| X2→ X1 | 0.714 | 770 | 0.547 | 976 | 0.497 | 1000 | 0.462 | 1000 |
| X1 → X3 | 0.068 | 42 | 0.026 | 41 | 0.011 | 38 | 0.001 | 37 |
| X3→ X1 | 0.493 | 550 | 0.357 | 864 | 0.326 | 992 | 0.299 | 1000 |
| X1 → X4 | 0.052 | 23 | 0.022 | 36 | 0.010 | 32 | 0.001 | 34 |
| X4→ X1 | 0.382 | 416 | 0.232 | 686 | 0.206 | 931 | 0.183 | 1000 |
| X2 → X3 | 0.136 | 46 | 0.025 | 47 | 0.012 | 39 | 0.001 | 47 |
| X3→ X2 | 1.239 | 732 | 0.526 | 945 | 0.493 | 1000 | 0.457 | 1000 |
| X2 → X4 | 0.132 | 37 | 0.023 | 36 | 0.010 | 30 | 0.001 | 50 |
| X4→ X2 | 1.056 | 563 | 0.342 | 828 | 0.307 | 982 | 0.286 | 1000 |
| X3 → X4 | 0.132 | 28 | 0.026 | 44 | 0.012 | 36 | 0.001 | 38 |
| X4→ X3 | 1.905 | 643 | 0.537 | 886 | 0.429 | 994 | 0.402 | 1000 |
| X1 → X2 | 0.066 | 42 | 0.027 | 53 | 0.013 | 37 | 0.001 | 49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papaspyropoulos, K.G.; Kugiumtzis, D. On the Validity of Granger Causality for Ecological Count Time Series. Econometrics 2024, 12, 13. https://doi.org/10.3390/econometrics12020013
Papaspyropoulos KG, Kugiumtzis D. On the Validity of Granger Causality for Ecological Count Time Series. Econometrics. 2024; 12(2):13. https://doi.org/10.3390/econometrics12020013
Chicago/Turabian StylePapaspyropoulos, Konstantinos G., and Dimitris Kugiumtzis. 2024. "On the Validity of Granger Causality for Ecological Count Time Series" Econometrics 12, no. 2: 13. https://doi.org/10.3390/econometrics12020013






