Cooperative Control for Multiple Autonomous Vehicles Using Descriptor Functions
Abstract
:1. Introduction
2. Literature Review
2.1. Behavioral Approaches
2.2. Consensus Protocols
2.3. Coverage and Connectivity
2.4. Abstractions and Models
3. The Descriptor Function Framework
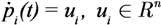
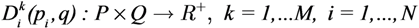
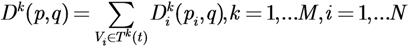
4. The Swarm Control Law
4.1. Gradient-Based Control
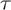 ) ≥ 0, ∀
) ≥ 0, ∀ 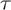 ∈ R+ and f(t) = 0, “t < 0”; σ(q) ≥ 0, ∀q ∈ Q, is an appropriate weighting function. The assumptions on f(.) are necessary in order to penalize only the lack of resources. In fact, the excess of resources does not foreclose task completion. The control problem is then formulated as an optimization and the resulting control law for each agent i derives directly from the gradient of the cost function, via steepest descent:
∈ R+ and f(t) = 0, “t < 0”; σ(q) ≥ 0, ∀q ∈ Q, is an appropriate weighting function. The assumptions on f(.) are necessary in order to penalize only the lack of resources. In fact, the excess of resources does not foreclose task completion. The control problem is then formulated as an optimization and the resulting control law for each agent i derives directly from the gradient of the cost function, via steepest descent:
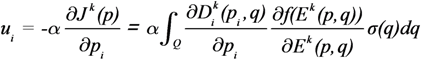
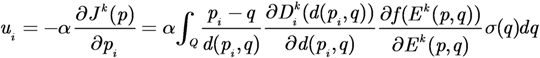
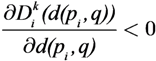
4.2. Potential Field-Based Control
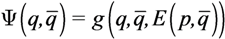
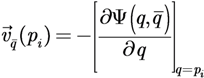
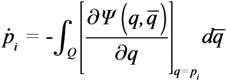
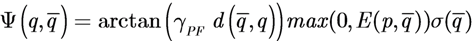
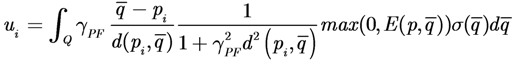
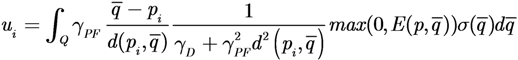
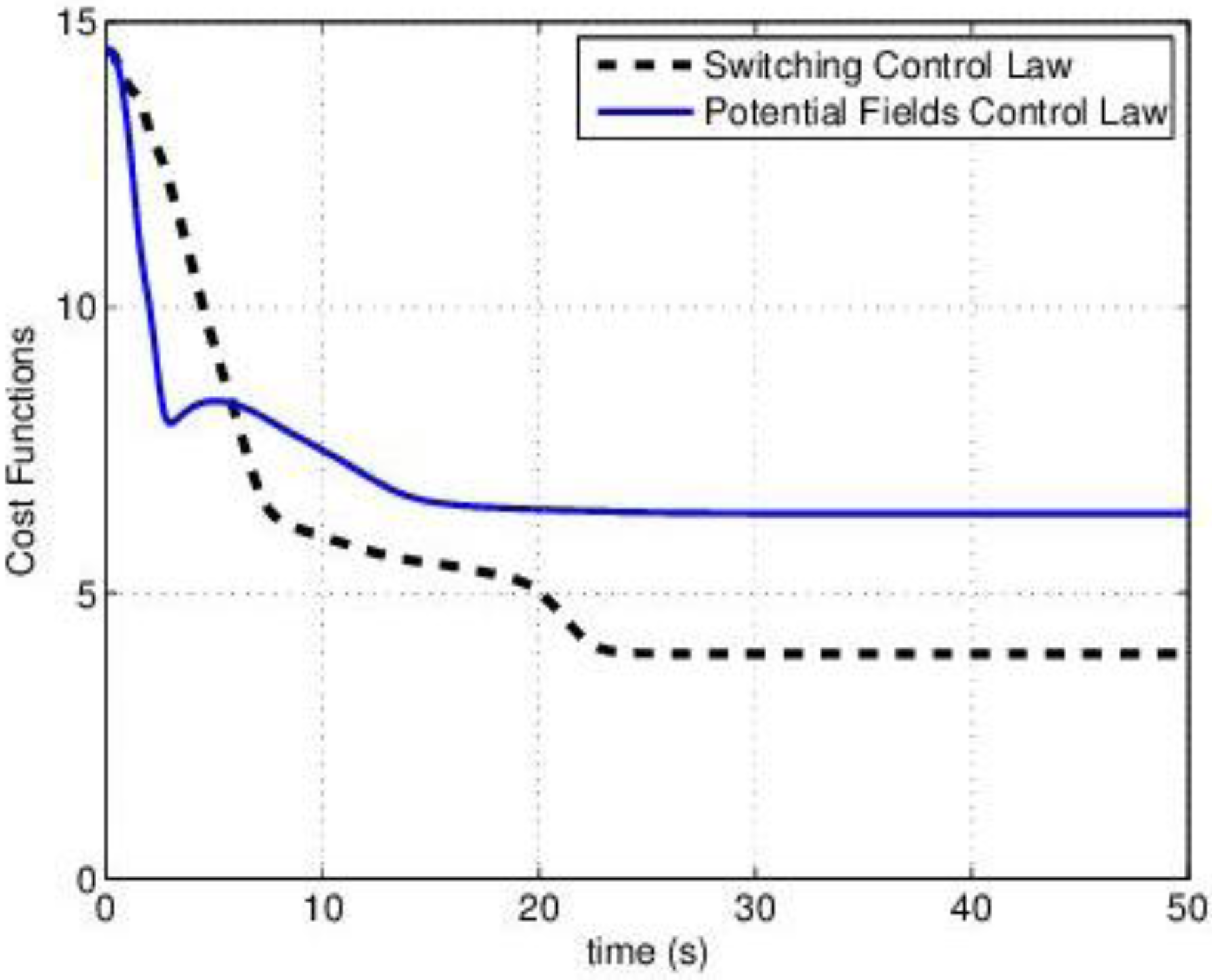
4.3. Combined (Switching) Control Law
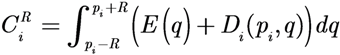
 with a function of the total contribution that the agent could provide. If
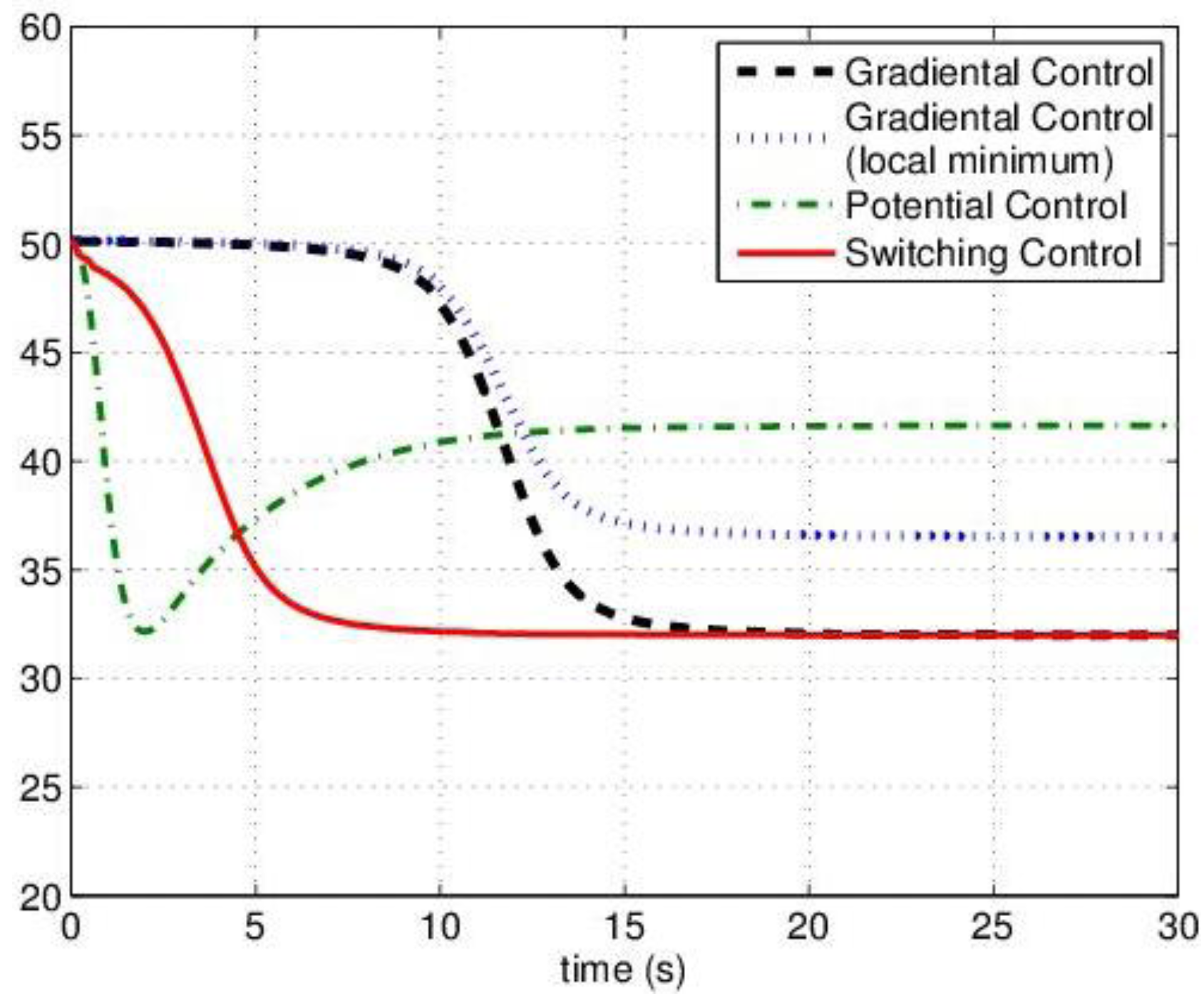
with a function of the total contribution that the agent could provide. If  then the Potential Field control law is used, otherwise the Gradient based controller law is used. Roughly speaking, an agent switches to the Potential Field control law if in its neighborhood it is not contributing to a sufficient reduction of the TEF. We must note that, at this point, the above conjecture has no formal proof of the stability of the overall dynamic behavior. To illustrate the behavior of the agents under the three control laws, let us consider four agents that must cover a circular region centered in [0, 0] and radius 4. The results are shown in Figure 2, where in red the footprint of the desired DF is shown. The cost function was built using: f(t) = max(0, t)2, and σ was set equal to 1.
then the Potential Field control law is used, otherwise the Gradient based controller law is used. Roughly speaking, an agent switches to the Potential Field control law if in its neighborhood it is not contributing to a sufficient reduction of the TEF. We must note that, at this point, the above conjecture has no formal proof of the stability of the overall dynamic behavior. To illustrate the behavior of the agents under the three control laws, let us consider four agents that must cover a circular region centered in [0, 0] and radius 4. The results are shown in Figure 2, where in red the footprint of the desired DF is shown. The cost function was built using: f(t) = max(0, t)2, and σ was set equal to 1. 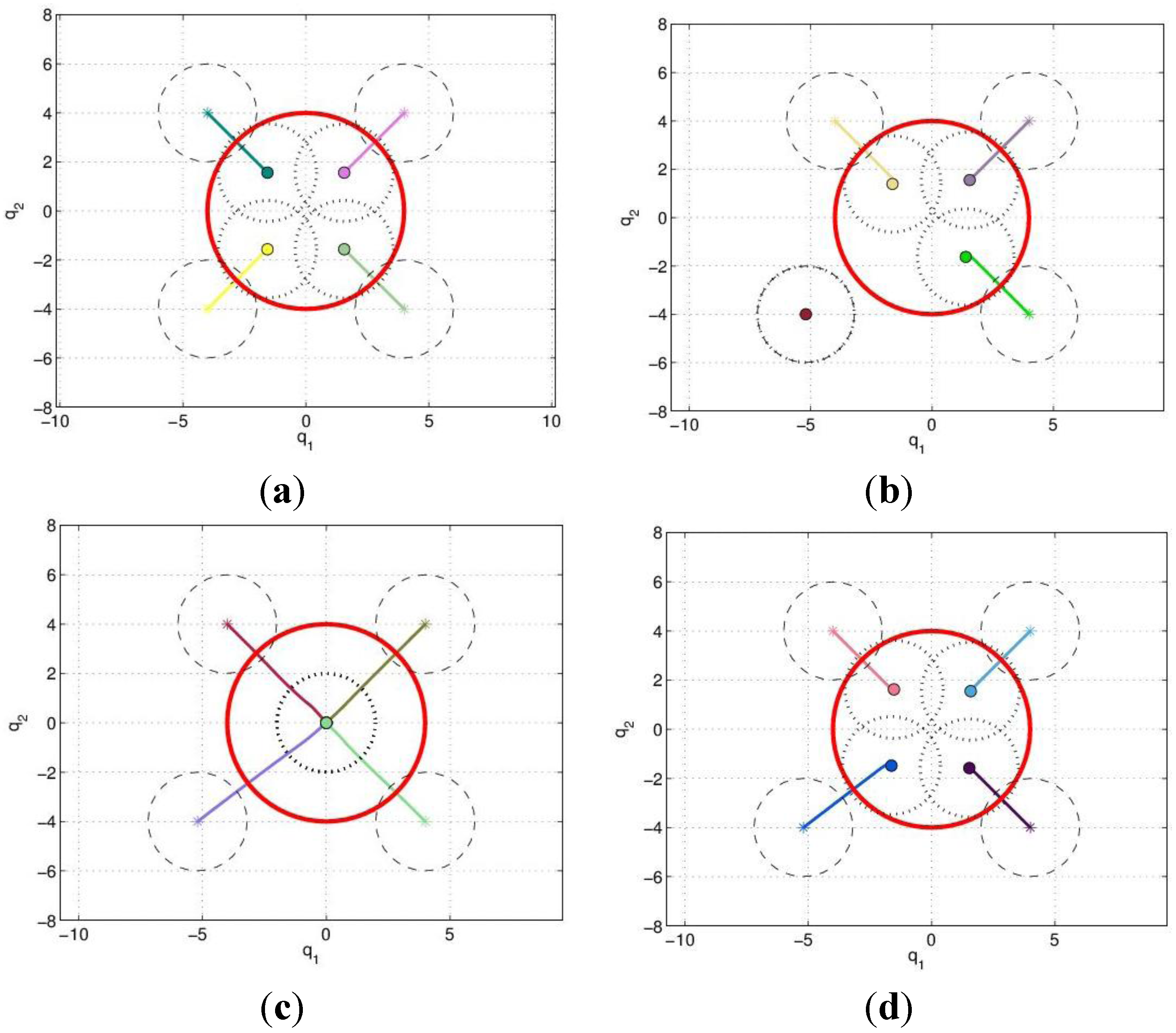
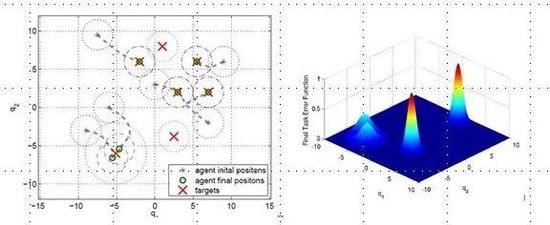
5. Case Study: Target Assignment
 (pi,q). Given the position of the targets wi ∈ Q, the desired TDF is constructed as:
(pi,q). Given the position of the targets wi ∈ Q, the desired TDF is constructed as:
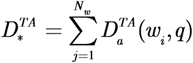
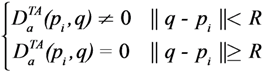
 is zero. Each agent moves using the switching control law presented in Section 4.3. In particular, it uses the gradient control law when it is far from the targets and the Potential Field controller when its DF intersects the DF of at least one target of a given amount, selected by design.
is zero. Each agent moves using the switching control law presented in Section 4.3. In particular, it uses the gradient control law when it is far from the targets and the Potential Field controller when its DF intersects the DF of at least one target of a given amount, selected by design.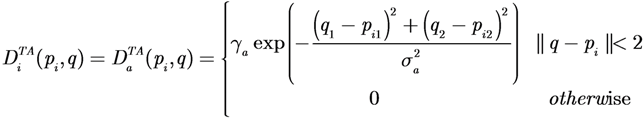
5.1. Example 1
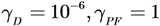
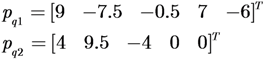

5.2. Example 2
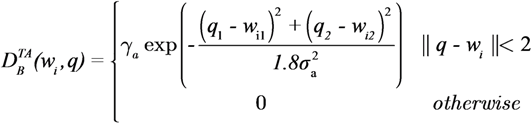

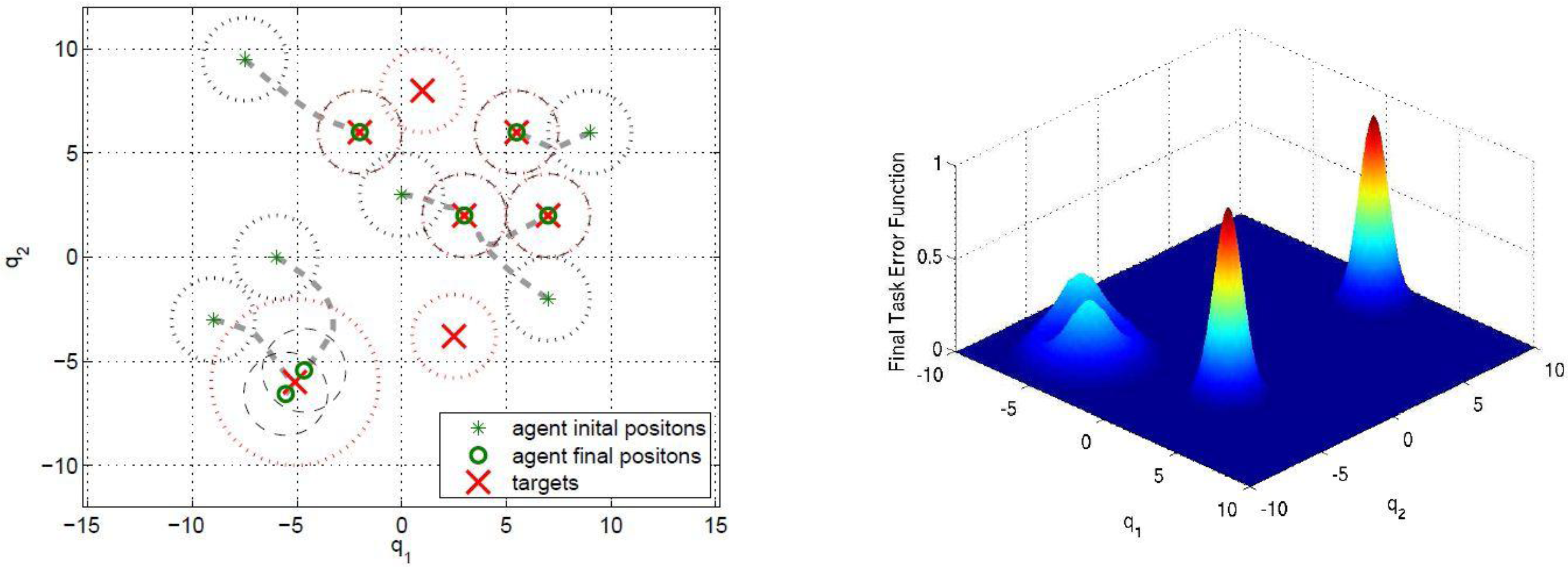
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Kennedy, J.; Eberhart, R.C. Swarm Intelligence; Academic Press: London, UK, 2001. [Google Scholar]
- Bonabeau, E.; Dorigo, M.; Theraulaz, G. Swarm Intelligence: From Natural to Artificial Systems; Oxford University Press: Oxford, NY, USA, 1999. [Google Scholar]
- Giulietti, F.; Pollini, L.; Innocenti, M. Autonomous formation flight. IEEE Control Syst. 2000, 20, 34–44. [Google Scholar] [CrossRef]
- Giulietti, F.; Innocenti, M.; Napolitano, M.; Pollini, L. Dynamic and control issues of formation flight. Aerosp. Sci. Technol. 2005, 9, 65–71. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Bracci, A.; Innocenti, M.; Pollini, L. Cooperative Task Assignment Using Dynamic Ranking. In Proceedings of the 17th IFAC World Congress, Seoul, Korea, 6–11 July 2008.
- Clerc, M. Particle Swarm Optimization; ISTE Ltd.: London, UK, 2005. [Google Scholar]
- Bullo, F.; Cortés, J.; Martínez, S. Distributed Control of Robotic Net-Works; Applied Mathematics Series; Princeton University Press: Princeton, NJ, 2008. [Google Scholar]
- Beard, R.L.; Ren, W. Distributed Consensus in Multi Vehicle Cooperative Control; Springer-Verlag: London, UK, 2008. [Google Scholar]
- Freeman, R.A.; Yang, P.; Lynch, K.M. Distributed Estimation and Control of Swarm Formation Statistics. In Proceedings of the American Control Conference, Minneapolis, MN, USA, June 2006. [CrossRef]
- Munkres, J. Algorithms for the assignment and transportation problems. SIAM J. 1957, 5, 32–38. [Google Scholar]
- Schouwenaars, T.; DeMoor, B.; Feron, E.; How, J. Mixed Integer Linear Programming for Multi-Vehicle Path Planning. In Proceedings of the European Control Conference 2001, Porto, Portugal, 4–7 September 2001; pp. 2603–2608.
- Reynolds, C. Flocks, herds, and schools: A distributed behavioral model. Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Giulietti, F.; Pollini, L.; Innocenti, M. Formation Flight: A Behavioral Approach. In Proceedings of the AIAA Guidance, Navigation, and Control, Montreal, QC, Canada, 6–9 August 2001. [CrossRef]
- Passino, K.M. Biomimicry for Optimization, Control, and Automation; Springer-Verlag: London, UK, 2005. [Google Scholar]
- Passino, K.M. Stability analysis of swarms. IEEE Trans. Autom. Control 2003, 48, 692–697. [Google Scholar]
- Tanner, H.G.; Jadbabaie, A.; Pappas, G.J. Stable Flocking of mobile Agents, Part I: Fixed Topology. In Proceedings of the IEEE Control and Decision Conference, Maui, HI, USA, 9–12 December 2003. [CrossRef]
- Tanner, H.G.; Jadbabaie, A.; Pappas, G.J. Stable Flocking of mobile Agents, Part II: Dynamic Topology. In Proceedings of the IEEE Control and Decision Conference, Maui, HI, USA, 9–12 December 2003. [CrossRef]
- Ronchieri, E.; Innocenti, M.; Pollini, L. Decentralized Control of a Swarm of Unmanned Air Vehicles. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Hilton Head, SC, USA, 20–23 August 2007. [CrossRef]
- Hague, M.H.; Egerstedt, M.; Martin, C.F. First-Order Networked Control Models of Swarming Silkworm Moths. In Proceedings of the American Control Conference, Seattle, WA, USA, 11–13 June 2008. [CrossRef]
- De Groot, M.H. Reaching a consensus. J. Am. Stat. Soc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Cortes, J.; Bullo, F. Coordination and geometric optimization via distributed dynamical systems. SIAM J. Control Optim. 2005, 44, 1543–1574. [Google Scholar] [CrossRef]
- Muhammad, A.; Egerstedt, M. Connectivity graphs as models of local interactions. Appl. Math. Comput. 2005, 168, 243–269. [Google Scholar] [CrossRef]
- Ji, M.; Egerstedt, M. Distributed coordination control of multi-agent systems while preserving connectedness. IEEE Trans. Robot. 2007, 23, 693–703. [Google Scholar] [CrossRef]
- Belta, C.; Kumar, V. Abstractions and control for groups of robots. IEEE Trans. Robot. 2004, 20, 865–875. [Google Scholar] [CrossRef]
- Pimenta, L.C.; Nathan, M.; Mesquita, R.C. Control of Swarms Based on Hydrodynamic Models. In Proceedings of the IEEE Inter-national Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008.
- Jung, B.; Sukhatme, S.G. A Generalized Region-Based Approach for Multi-Target Tracking in Outdoor Environments. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 2189–2195.
- Rimon, E.; Koditschek, D. Exact robot navigation using artificial potential functions. IEEE Trans. Robot. Autom. 1992, 8, 501–518. [Google Scholar] [CrossRef]
- Leonard, N.; Lekien, F. Non-uniform coverage and cartograms. SIAM J. Control Optim. 2009, 48. [Google Scholar] [CrossRef]
- Niccolini, M.; Innocenti, M.; Pollini, L. Near Optimal Swarm Deployment Using Descriptor Functions. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; Volume 1, pp. 4952–4957.
- Ferrari-Braga, A.; Innocenti, M.; Pollini, L. Multi-Agent Coordination with Arbitrarily Shaped Descriptor Functions. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Boston, MA, USA, 19–22 August 2013.
- Pollini, L.; Innocenti, M. A synthetic environment for dynamic systems control and distributed simulation. IEEE Control Syst. 2000, 20, 49–61. [Google Scholar] [CrossRef]
- Niccolini, M. Swarm Abstractions for Distributed Estimation and Control. Ph.D. Dissertation, Department of Electrical Systems and Automation, University of Pisa, Pisa, Italy, July 2011. [Google Scholar]
- Brooks, R.A. Cambrian Intelligence: The Early History of the New AI; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Murphy, R.R. Introduction to AI Robotics; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Pollini, L.; Niccolini, M.; Rosellini, M.; Innocenti, M. Human-Swarm Interface for Abstraction Based Control. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Niccolini, M.; Pollini, L.; Innocenti, M. Cooperative Control for Multiple Autonomous Vehicles Using Descriptor Functions. J. Sens. Actuator Netw. 2014, 3, 26-43. https://doi.org/10.3390/jsan3010026
Niccolini M, Pollini L, Innocenti M. Cooperative Control for Multiple Autonomous Vehicles Using Descriptor Functions. Journal of Sensor and Actuator Networks. 2014; 3(1):26-43. https://doi.org/10.3390/jsan3010026
Chicago/Turabian StyleNiccolini, Marta, Lorenzo Pollini, and Mario Innocenti. 2014. "Cooperative Control for Multiple Autonomous Vehicles Using Descriptor Functions" Journal of Sensor and Actuator Networks 3, no. 1: 26-43. https://doi.org/10.3390/jsan3010026