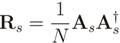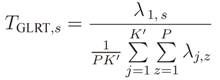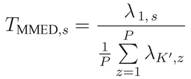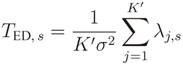1. Introduction
Due to the increased demand for wireless communication services and the adoption of a fixed spectral allocation policy that designates a specific band for primary systems in a given geographical region and on a long-term basis, spectral scarcity has become of main concern. The spectral scarcity is one of the greatest obstacles to the deployment of existing and new wireless communication systems and services. With the advent of the concept of cognitive radio (CR) [
1], cognition-based dynamic access techniques to spectral bands have arisen to contribute to solving the problem of spectrum congestion and scarcity. This is done by allowing for the opportunistic occupation of an underutilized portion of the spectrum by secondary CR networks.
Spectrum sensing is the fundamental task performed by a CR in order to gain access to a band of interest. As the name suggests, it is the task of monitoring a given band of interest in order to find spectral holes for subsequent opportunistic occupation. CRs with spectrum sensing capability have to identify spectrum holes efficiently and avoid harmful interference to primary users by either switching to an unoccupied band or keeping the interference below a maximum acceptable level [
2].
Third-generation (3G) broadband systems are mostly based on direct-sequence spread spectrum (DSSS), such as Evolution-Data Optimized (EV-DO) or High-Speed Packet Access (HSPA). Fourth-generation (4G) systems, however, predominately use multicarrier systems, like orthogonal frequency division multiplexing (OFDM), combined with or without its access counterpart, the orthogonal frequency division multiple access (OFDMA) [
3,
4]. A reason for the adoption of OFDM is that it has some advantages in delivering high speed data, especially in a multipath, frequency selective fading channel [
3]. As OFDM/OFDMA is being adopted as the scheme of choice in broadband communication systems, it is important for CR networks to sense this kind of signal.
Due to the high importance of OFDMA signals in wireless communication systems and the high importance of spectral sensing in the context of cognitive radio networks, ongoing researches are proposing new methods of wideband spectral sensing and existing ones are being combined to improve the performance of cognitive radio networks. This paper aims at contributing to this research effort by proposing a new approach to the spectrum sensing of OFDMA and other wideband signals.
1.1. Related Works
Several spectrum sensing techniques have been proposed so far, which can be classified as narrowband and wideband according to the bandwidth of the spectrum sensed. Narrowband sensing techniques are limited to detect the presence of primary signals in a single band, while wideband techniques aim at jointly or sequentially monitoring multiple bands.
In what concerns narrowband sensing, energy detection (ED) [
5,
6], matched filter detection (MFD) [
7] and cyclostationary feature detection (CFD) [
8] are widely discussed in the literature. For wideband sensing, recent studies point to three major techniques: energy detection [
9,
10], wavelet-based detection (WD) [
11] and compressed (or compressive) sensing detection (CSD) [
12,
13]. Eigenvalue-based detection [
14,
15,
16,
17] are one of the most recent and promising techniques for spectrum sensing. Likewise ED, eigenvalue detection can be applied to narrowband and to wideband signals.
In wideband ED, the presence of the primary signal is detected from the energy of the received signal in each pre-defined band. The spectral partition can be done by using a filter bank approach [
18] or by splitting the wideband signal into parallel narrowband signals via fast Fourier transform (FFT) [
9,
10]. In this case, the FFT is applied to the time domain samples of the received signal and the presence or absence of primary signals in each band is jointly determined by the energy level of the corresponding frequency-domain signal samples.
Wavelet detection uses the wavelet transform to detect discontinuities in the power spectrum density (PSD) of the signal received by a CR, thus defining the frequency boundaries in the primary signal [
11]. The frequency boundaries are in local maxima of the first derivative of the wavelet transform. Having established the boundaries, the level of the PSD is estimated by the average of the signal’s PSDs in each frequency band estimated via wavelet transform.
Compressed sensing uses a procedure of parameter estimation from a sampling with rate below the Nyquist rate (sub-Nyquist sampling) [
12,
13]. Through the solution of an optimization problem, which is typically convex, the signal’s PSD is estimated and the signal presence in each band is determined using a procedure analogous to the one adopted in the wavelet transform approach.
In eigenvalue-based spectrum sensing, the test statistic is computed from the eigenvalues of the received signal covariance matrix [
14,
15], as for instance the eigenvalue-based generalized likelihood ratio test (GLRT), the maximum-minimum eigenvalue detection (MMED), also known as eigenvalue ratio detection (ERD), and the maximum eigenvalue detection (MED), also known as Roy’s largest root test (RLRT). The advantage of eigenvalue-based spectrum sensing is that no
a priori knowledge about the primary transmitted signal is needed for computing the test statistic. In schemes like the GLRT and MMED, the knowledge of the thermal noise variance is not needed either.
Although spectrum sensing can be performed by each CR individually and independently from others CRs, cooperative spectrum sensing is being considered as a possible solution for problems experienced by cognitive networks with a non-cooperative spectrum sensing, such as receiver uncertainty, multipath fading and correlated shadowing [
2].
Cooperative spectrum sensing can be centralized, distributed or relay-assisted [
2]. In centralized cooperative sensing, data collected by each cooperating CR (e.g., samples from the received signal) is sent to a fusion center (FC) through a dedicated control channel. This process is called data fusion. After the data is processed, the FC decides upon the occupation state of the channel. Centralized cooperative spectrum sensing can be executed as well from the decisions about the channel occupancy state made by each cooperating CR individually. This operation is called decision fusion, where the final decision about the channel state is accomplished through binary operations on the CR decisions. In both centralized schemes, the final decision is informed back to the CRs through the control channel. The access algorithm adopted by the secondary network then takes place.
It is worth mentioning that the role of an FC in a centralized cooperative spectrum sensing can be assigned to a cluster-head in the context of clustered network topologies [
19], which is the case of most wireless sensor networks (WSN). This clustering approach can be of particular value in large area networks, where the adoption of a single FC could prohibitively increase the control channel traffic and lead to inefficient spectrum utilization. This inefficiency can be caused by the distinctive spectrum occupancy in different regions of the network, which could be misled by large-area-based centralized decisions.
1.2. Contributions and Structure of the Paper
This paper proposes a new eigenvalue-based centralized cooperative spectrum sensing approach for OFDMA and other wideband signals. In this approach, the energy detection in [
9,
10] is replaced by a technique based on the eigenvalues of the received signal covariance matrix. For general wideband signals (This eigenvalue fusion scheme was briefly discussed in a shorter paper, in Portuguese, which was presented in the 30th Brazilian Telecommunications Symposium (SBrT’12), under the title “Sensoriamento Espectral Cooperativo Baseado em Autovalores para Sinais de Banda Larga” (Eigenvalue-Based Cooperative Spectrum Sensing for Wideband Signals) [
20]), the technique aims at locating spectral holes to the level of sub-bands. An adapted version of the technique that addresses the problem of sensing OFDMA signals to the level of subchannels is also proposed. In this case, the interest is to jointly sense all carriers of a subchannel, allowing for the opportunist occupancy of a vacant subchannel by one CR or allowing for the division of a vacant subchannel to multiple CRs.
Three forms of data fusion were addressed: (i) the fusion of samples from each CR, but in the frequency domain; (ii) the fusion of binary decisions made by all cooperating CRs and (iii) the new fusion approach in which the eigenvalues estimated by each CR are combined at the FC.
Simulation results show that the new eigenvalue fusion scheme can overcome the performance of the sample and decision fusion for detection of unoccupied sub-bands in a general wideband signal and for detection of unoccupied subchannels in an OFDMA signal.
The eigenvalue fusion scheme demands less transmitted data to the FC when compared with sample fusion schemes with similar performances. However, the amount of data transmitted to the FC in eigenvalue fusion and sample fusion can be, by far, greater than those in decision fusion schemes with similar system parameters.
The remaining of the paper is organized as follows.
Section 2 briefly reviews the cooperative centralized eigenvalue-based spectrum sensing technique. In
Section 3, the proposed eigenvalue fusion and other fusion schemes are considered for the detection of general wideband signals. In
Section 4, the eigenvalue fusion and other fusion schemes are considered for the detection of OFDMA signals. Numerical results and their interpretations are presented in
Section 5.
Section 6 deals with the tradeoff between the complexity of the radios and the volume of data sent to the fusion center. Conclusions and suggestions for new research are in
Section 7.
2. Traditional Eigenvalue-based Cooperative Spectrum Sensing
Consider a discrete-time memoryless multiple input multiple output (MIMO) model, where each of the m sensors (antennas) in a CR or each single-sensor CR collects n samples of the received signal from
p primary transmitters during the sensing period. Those samples are arranged in a matrix Y ∈ ℂ
m×n. Analogously, consider that the signals transmitted by the
p transmitters are organized in a matrix X ∈ ℂ
p×n. Let H ∈ ℂ
m×p be the channel matrix with elements
![Jsan 02 00001 i001]()
= 1, 2, . . . ,
p, representing the channel gain between the
![Jsan 02 00001 i002]()
-th primary transmitter and the
i-th sensor (antenna or CR). It is assumed that these gains do not vary during the sensing period. Finally, let V ∈ ℂ
m×n be the matrix with thermal noise samples corrupting the signal received by the
m sensors. Therefore, the matrix with received samples under this MIMO channel model is given by
In eigenvalue-based cooperative spectrum sensing, a spectral hole is detected by applying a binary hypothesis test where the test statistic is built from the eigenvalues of the received signal ensemble covariance matrix
![Jsan 02 00001 i004]()
, where
![Jsan 02 00001 i005]()
is the expected value operator. Since the ensemble covariance matrix is normally unknown, it is replaced by its maximum-likelihood estimate, the sample covariance matrix
where (·)
† denotes the conjugate and transpose operations. The eigenvalues {λ
1 ≥ λ
2 ≥ · · · λ
m } of
R are computed and then, the test statistics for the GLRT, MMED, MED and ED are formed. In [
21,
22,
23], binary hypothesis tests for multiple sources are deduced. Here, for simplicity reasons, we consider just a single primary transmitter, and in this case the following test statistics apply [
14]:
where σ
2 is thermal noise variance at the input of each sensor, and tr(·) and ║·║
F correspond to the trace and the Frobenius norm of the matrix, respectively. The sensing process is then concluded by comparing the test statistic with a threshold pre-defined according to the desired performance of the sensing process. If the test statistic is greater than the threshold, the channel is deemed occupied; otherwise the channel is declared vacant.
The performance of a sensing technique is usually measured in terms of the probability of false alarm (
Pfa ) and the probability of detection (
Pd ).
Pfa is the probability of inferring that a sensed band is occupied when it is in fact vacant,
i.e.,
![Jsan 02 00001 i011]()
. Pd is the probability of inferring that a sensed band is occupied when it is indeed occupied,
i.e.,
![Jsan 02 00001 i012]()
. Here
![Jsan 02 00001 i013]()
is the decision threshold, and
![Jsan 02 00001 i014]()
are the hypotheses that the primary transmitted signal is absent and present, respectively. It is thus desirable that
Pfa is minimized and
Pd is maximized. However, these objectives are conflicting ones: increasing the threshold decreases
Pfa , but also decreases
Pd. As a consequence, a tradeoff must be adopted so that the correct threshold is established. The tradeoff is usually determined with the aid of receiver operating characteristic (ROC) curves that show the variation of
Pfa versus
Pd with changes in the threshold value.
5. Numerical Results
In this section, we compare the proposed eigenvalue fusion scheme with schemes using sample and decision fusions. Two types of primary signal were considered: a general wideband signal and an OFDMA signal. In the case of a general wideband signal, the performance is relative to sensing at the level of sub-bands. In the case of OFDMA, the performance is relative to sensing at the subchannel level. In all cases, the ROC curves were built from the average of Pfa and Pd in all frequency sub-bands of general wideband signals, or in all subchannels of OFDMA signals. The curves were obtained via Monte Carlo simulations, counting a minimum of 100 false alarm or detection events (which occurs first) or a maximum of 5000 runs. The code was implemented in MATLAB according to the models and test statistics described throughout the paper. The primary radio signal activity in each sub-band and subchannel was modeled as a Bernoulli random variable with 50% of the time in the ON state (for Pd computations) and 50% in the OFF state (for Pfa computations).
5.1. Results for a General Wideband Signal Detection
To simulate the detection of a general wideband signal, we have considered a single primary transmitter whose total bandwidth was partitioned into K = 8 sub-bands. We have also considered: m = 6 single sensor (single antenna) cooperating CRs, signal-to-noise ratio SNR = −10 dB, and Gaussian-distributed primary signal with unitary transmitted power. The channel between the primary transmitter and each CR was a multipath fading channel with L = 8 uncorrelated propagation paths having Rayleigh-distributed magnitudes, unitary second moment and uniformly-distributed phase in (0, 2π]. The channel was considered static during a sensing period, changing independently and identically distributed from one period to another.
It is known that the number of collected samples and the order of the sample matrix used in the computation of the covariance matrix influence the sensing performance of eigenvalue-based spectrum sensing. Then, for a fair comparison, both should be the same in all fusion schemes analyzed here. However, this is only possible in the case of the eigenvalue and decision fusion, as can be verified in
Section 4; see Equations (10) and (11). For comparisons considering general wideband signals, we have chosen to make the order of the sample matrices the same. The consequence of this is that the number of collected samples in each CR had to be larger for the eigenvalue and decision fusion schemes, when compared with the decision fusion. In practice, this will not be an issue, since a larger amount of samples in a given sensing interval can be obtained by increasing the sampling rate. Nevertheless, as a counterexample, we have also carried out simulations assuming an equal number of collected samples per carrier in all fusion schemes.
For the eigenvalue and decision fusion schemes, the total number of samples collected by each CR was n = K N = 8 × 300 = 2, 400 (N = 300 samples in each frequency sub-band). To simulate the sample fusion scheme, n = K N = 8 × 50 = 400 samples (N = 50 in each frequency sub-band) were utilized to form the covariance matrix at the FC. In order to consider the same number of samples for all fusion schemes, we have also simulated the sample fusion with N = 300 samples per carrier. The order of the covariance matrix for sample fusion was m × m = 6 × 6 and J × J = 6 × 6 for eigenvalue and decision fusions.
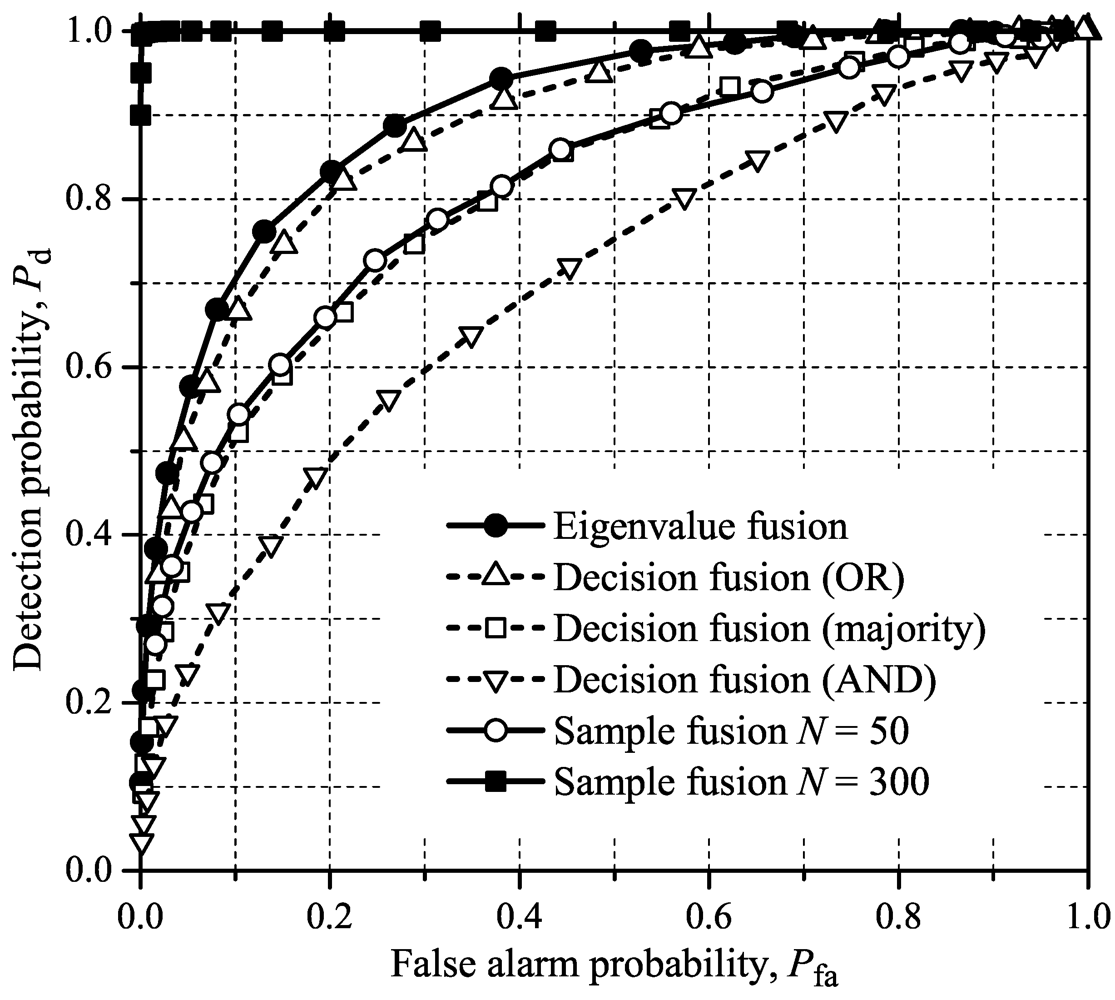
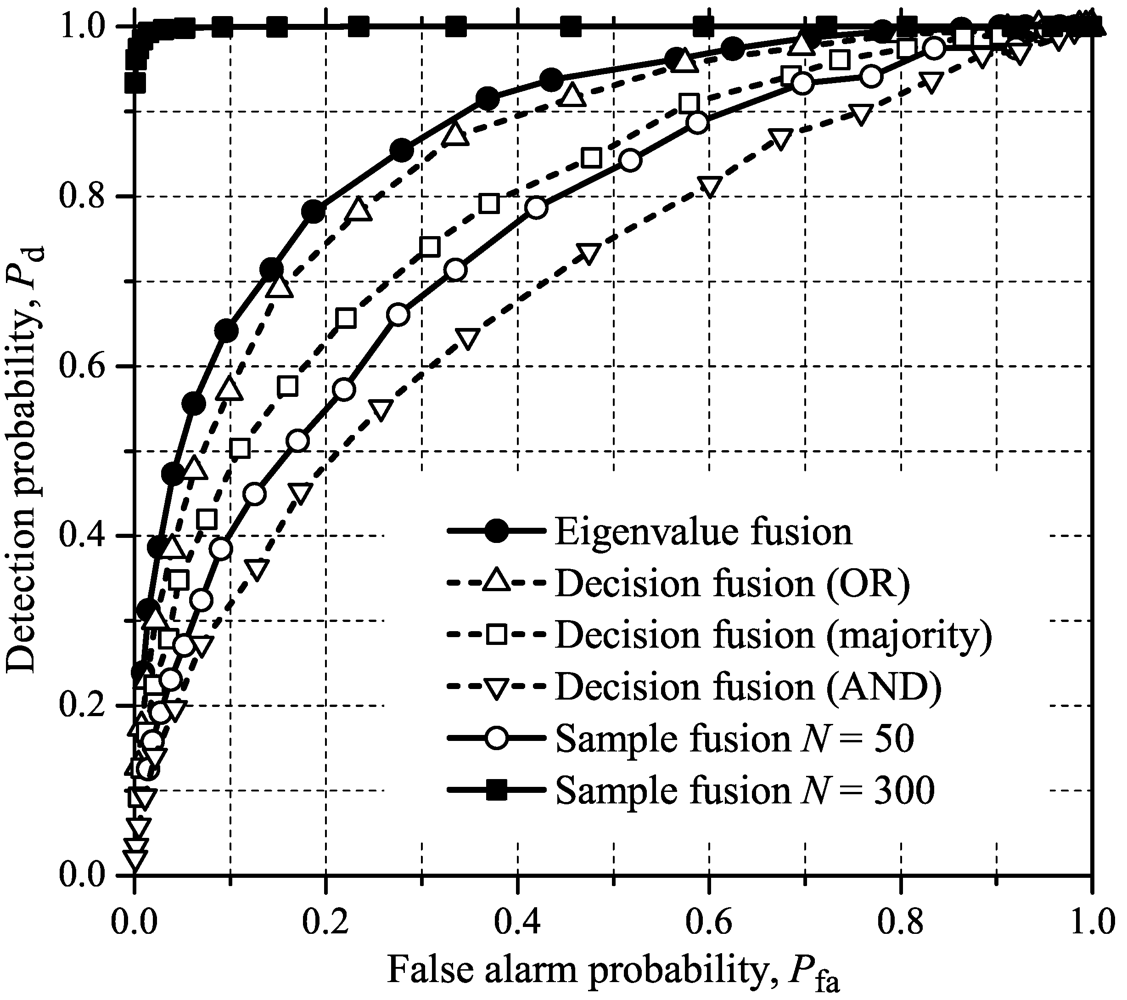
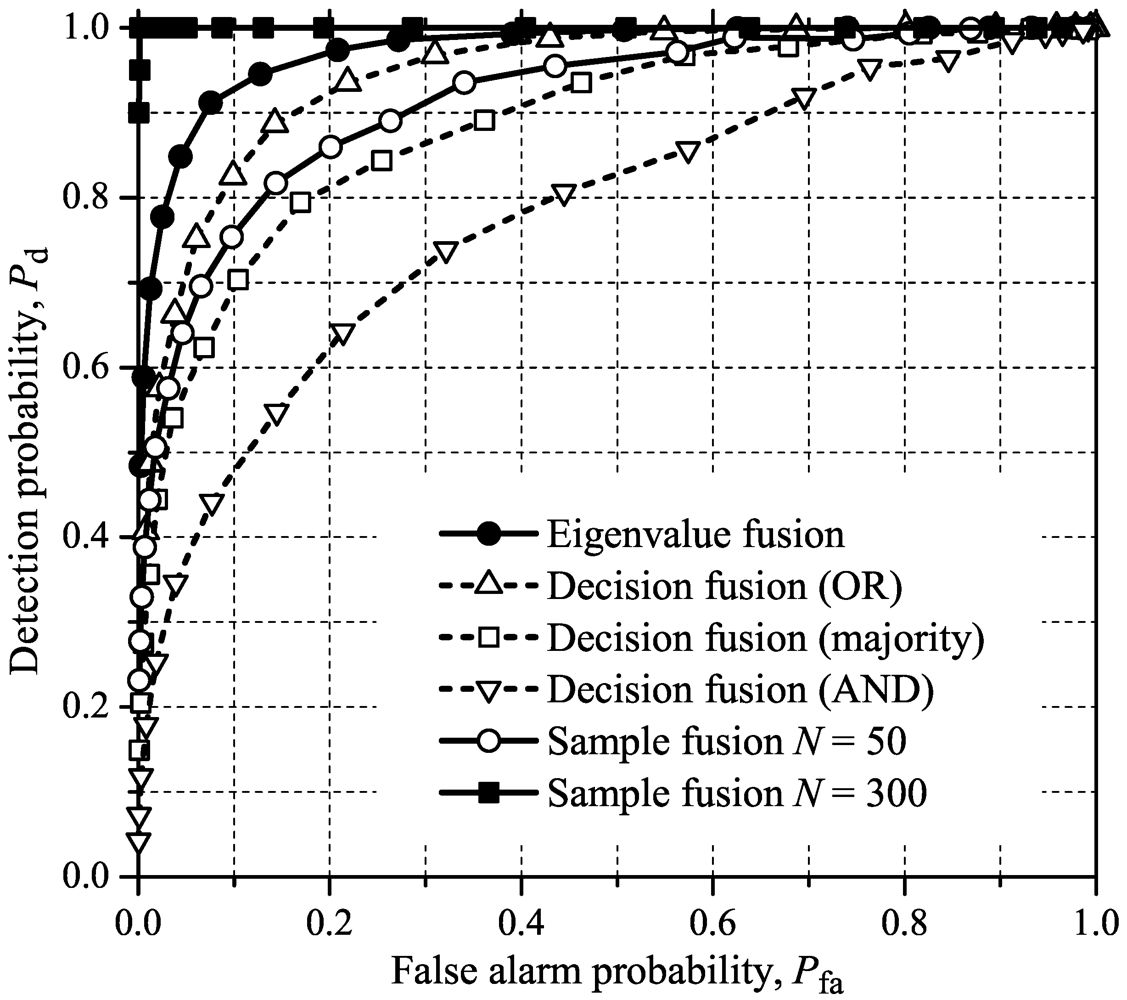
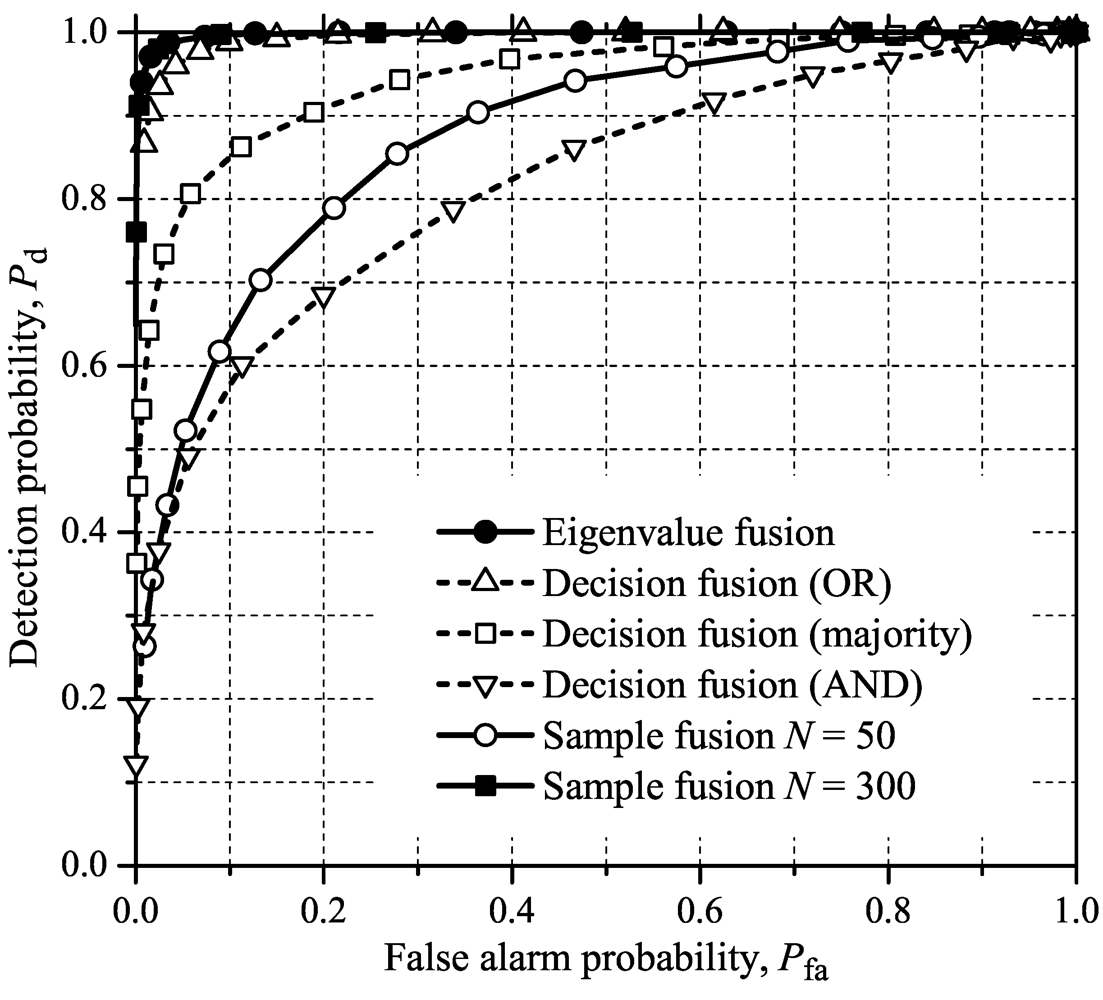
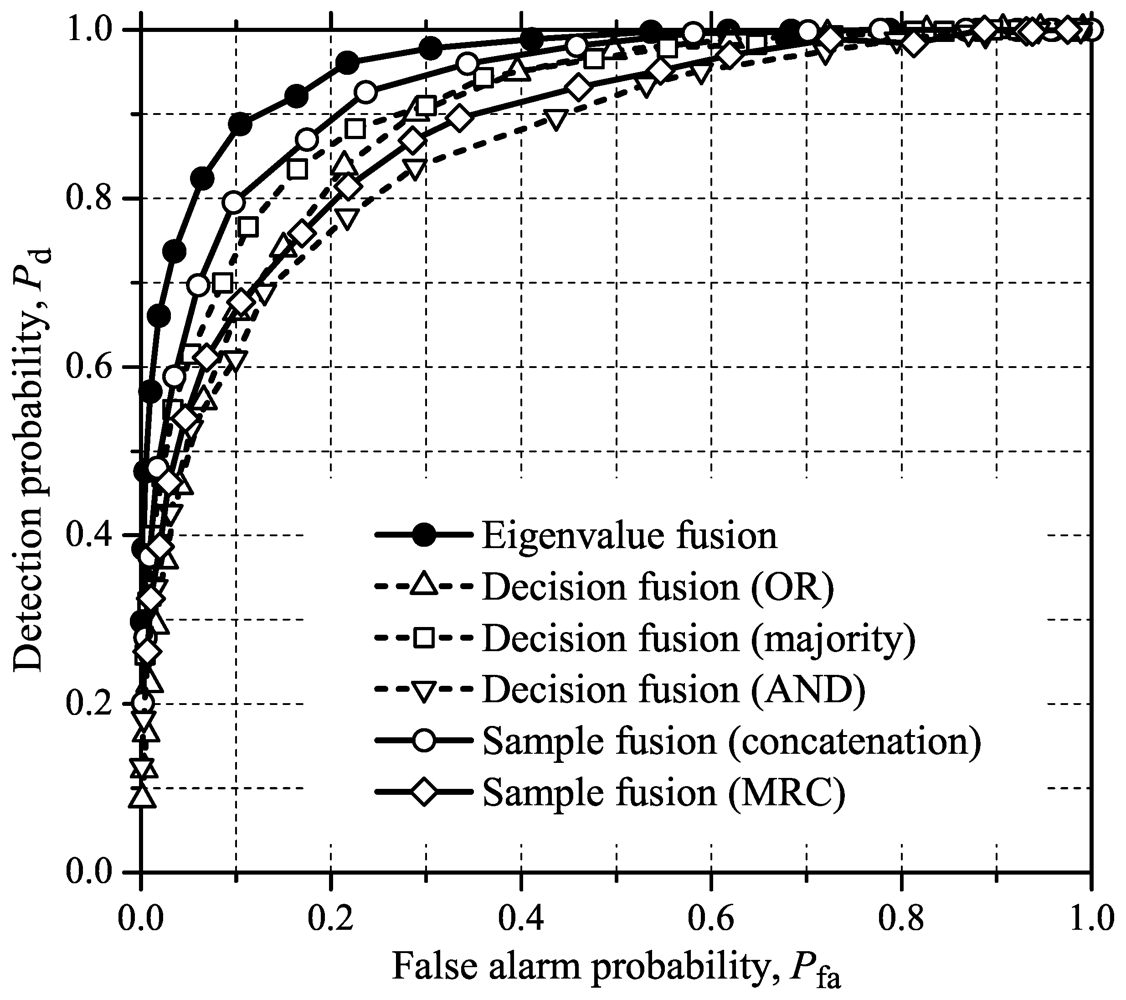
Figure 1,
Figure 2,
Figure 3 and
Figure 4 show ROC curves for the proposed eigenvalue fusion scheme parallel to sample and decision fusion curves. The test statistics Equations (3)–(6) were used for the sample fusion, and the tests Equations (18)–(21) were used for individual CR decisions. The test statistics Equations (14)–(17) were considered for the eigenvalue fusion. The performances with sample fusion are in close agreement with those reported in [
14], which were obtained under the same system parameters adopted here. As expected, this indicates that processing the samples in the frequency domain leads to the same results as in the case of processing them in the time domain.
From
Figure 1,
Figure 2,
Figure 3 and
Figure 4, one can notice that the proposed eigenvalue fusion scheme outperforms all other fusion and combining methods for all test statistics considered in this paper, except in the case of
N = 300 samples per carrier for the sample fusion. The performance of the eingenvalue fusion is closely followed by the OR decision fusion, except for MED where the performance gap is larger. For MMED and ED, the sample fusion is worse than the decision fusion with OR and majority-voting combining, overcoming only AND. For GLRT and MED, the sample fusion overcomes the AND rule significantly, showing a slightly better performance than majority-voting. The AND is the worst among all fusion rules and test statistics under analysis. These results are not meant to state that the relative performances of the decision combining rules will always be kept the same. As mentioned in [
2], the performance ranking of AND, OR and majority-voting can vary with different system parameters or scenarios.
Figure 1.
ROCs for sample fusion, decision fusion and eigenvalue fusion using GLRT for sensing a general wideband signal.
Figure 1.
ROCs for sample fusion, decision fusion and eigenvalue fusion using GLRT for sensing a general wideband signal.
Figure 2.
ROCs for sample fusion, decision fusion and eigenvalue fusion using MMED for sensing a general wideband signal.
Figure 2.
ROCs for sample fusion, decision fusion and eigenvalue fusion using MMED for sensing a general wideband signal.
Figure 3.
ROCs for sample fusion, decision fusion and eigenvalue fusion using MED for sensing a general wideband signal.
Figure 3.
ROCs for sample fusion, decision fusion and eigenvalue fusion using MED for sensing a general wideband signal.
Figure 4.
ROCs for sample fusion, decision fusion and eigenvalue fusion using ED for sensing a general wideband signal.
Figure 4.
ROCs for sample fusion, decision fusion and eigenvalue fusion using ED for sensing a general wideband signal.
When N = 300 samples per carrier in the sample fusion scenario, the performance is better than the performance of the other fusion schemes, except in the case of ED (for the same number of samples per carrier, computing the signal energy using sample values is equivalent to computing the energy using the average of the eigenvalues). However, when N = 300, the number of samples sent to the FC is six times the number of samples when N = 50. Moreover, the sample matrices used for covariance matrices computations have order 6 × 300 for N = 300 and 6 × 50 for N = 50. Although the resulting covariance matrices have the same order (6 × 6), it was expected that more samples led to better performances. This scenario is clearly favoring the sample fusion, resulting in unfair comparisons.
Still referring to the results in
Figure 1,
Figure 2,
Figure 3 and
Figure 4, surprisingly the ED tests overcome the MED tests for eigenvalue combining and for the decision fusion schemes with majority-voting, AND and OR rules, inverting the behavior obtained with the use of sample fusion. In other words, the test statistics proposed in Equations (17) and (21) unveiled more statistical power than the test Equations (16) and (20), respectively, indicating that the latter ones have margin for further improvements in their expressions.
5.2. Results for an OFDMA Signal Detection
To simulate the application of the eigenvalue fusion technique for detecting subchannels of a single OFDMA signal, we have considered a primary network with P = 4 subchannels. The number of cooperating CRs was m = 6. An OFDMA channel with K = 20 subcarriers was adopted. The subchannels were created by forming P = 4 sets with K ′ = K/P = 5 subcarriers randomly selected. We also considered unitary primary signal power and SNR = −10 dB. The wireless channel was modeled as a 20-path slow frequency-selective fading channel whose frequency response was kept constant during a sensing period, being varied from one sensing period to another. As in the case of general wideband signals, the second moment of the channel gains were normalized so as to keep the average received signal power equal to the average transmitted signal power. The number of samples collected in each subcarrier frequency was N = 60 for all fusion schemes.
The test statistics Equations (31)–(34) were used for the sample fusion (using concatenation and MRC) and for individual CR decisions. The test statistics Equations (24)–(27) were considered for the eigenvalue fusion.
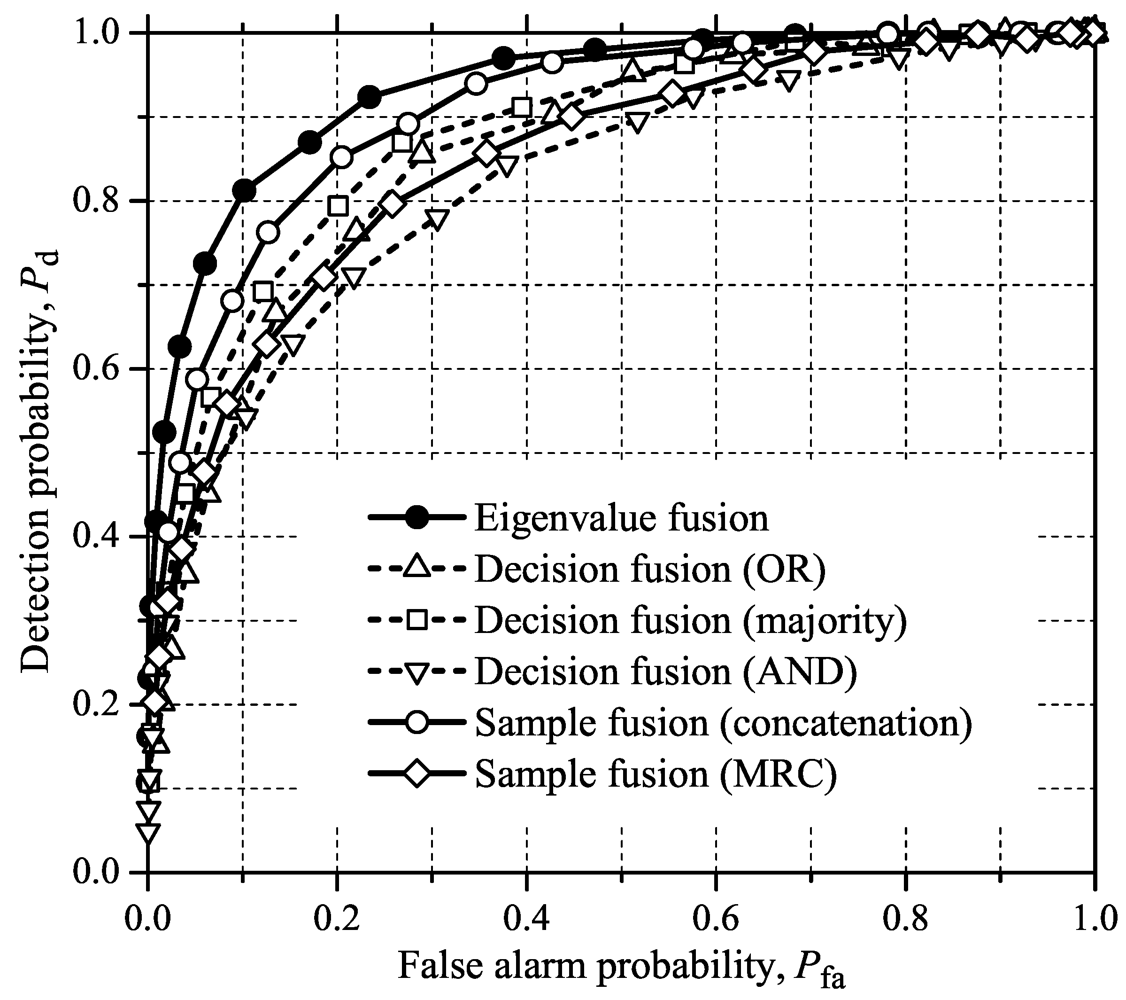
Figure 5,
Figure 6,
Figure 7 and
Figure 8 show the ROCs for the eigenvalue fusion, the sample fusion and the decision fusion schemes for the detection of the OFDMA signal previously considered, for all test statistics considered in this paper. It is in order to remember that the aim of the spectrum sensing in this case is to determine the status of an entire subchannel occupation, differing from the sub-band occupation in the case of a general wideband signal.
As in the case of a general wideband signal, the eigenvalue fusion scheme delivered the best performance among all fusion methods under analysis, for all test statistics, closely followed by the sample fusion using the concatenation approach for constructing the sample matrices. The performance of the sample fusion using the MRC approach produced a worse performance than the concatenation approach, also having the drawback of needing to know the channel gains. The better performance of the concatenation approach can be accredited to the large number of columns in the matrices used to compute the sample covariance matrices, as shown by Equation (28). We conjecture that the poor performance of the sample fusion for sensing OFDMA signals can be accredited to the different channel gains affecting each row of the sample matrices used for covariance matrices computations: notice in Equation (28) that the concatenated matrices come from different CRs and, thus, result from different channel gains. This is in contrast with the model presented in
Section 2, which assumes that the channel gain present in the elements of each row of the sample matrix is the same. The test statistics Equations (3)–(6) considered as references for all test statistics proposed in this paper subsumes this invariant gain. Then, when the gains vary within a given row, performance degradation is expected.
Figure 5.
ROCs for sample fusion, decision fusion and eigenvalue fusion using GLRT for sensing OFDMA subchannels.
Figure 5.
ROCs for sample fusion, decision fusion and eigenvalue fusion using GLRT for sensing OFDMA subchannels.
Figure 6.
ROCs for sample fusion, decision fusion and eigenvalue fusion using MMED for sensing OFDMA subchannels.
Figure 6.
ROCs for sample fusion, decision fusion and eigenvalue fusion using MMED for sensing OFDMA subchannels.
Figure 7.
ROCs for sample fusion, decision fusion and eigenvalue fusion using MED for sensing OFDMA subchannels.
Figure 7.
ROCs for sample fusion, decision fusion and eigenvalue fusion using MED for sensing OFDMA subchannels.
Figure 8.
ROCs for sample fusion, decision fusion and eigenvalue fusion using ED for sensing OFDMA subchannels.
Figure 8.
ROCs for sample fusion, decision fusion and eigenvalue fusion using ED for sensing OFDMA subchannels.
The ranking of the performances considering different test statistics still has ED in the first position, followed by MED, GLRT and MMED. Again it is observed the inversion of the behaviors of ED and MED when comparing with traditional eigenvalue detection of narrowband signals via Equations (3)–(6). This indicates that the empirical test statistics Equations (27) and (34) have more statistical power than Equations (26) and (33), which means that Equations (26) and (33) have margin for improvements in their definitions.
Still referring to
Figure 5,
Figure 6,
Figure 7 and
Figure 8, the AND decision combining scheme has shown to be the worst among all fusion rules, as happened with the detection of subcarriers or sub-bands of general wideband signals. However, the performance gap from the best result was reduced when comparing with the results in
Figure 1,
Figure 2,
Figure 3 and
Figure 4. Also notice that the majority-voting has gained the best results among the decision combining rules, whereas it was the second better result in the case of detecting general wideband signals. This reinforces the statement that the AND, OR and majority-voting rules can alternate their performance ranking in different system parameters or scenarios.
The major difference between the sample fusion and the eigenvalue fusion strategies is the amount of data sent to the FC. For the parameters used in the numerical results for the OFDMA signal, we had the following situation: The primary signal was made up with n = K N = 20 0 = 1, 200 samples in the time domain. Therefore, the number of samples sent to the FC in the sample fusion scheme was mK N = 6 × 1, 200 = 7, 200. With K ′ = 5 subcarriers in each subchannel, the order of the covariance matrices was K ′ ×K ′ = 5×5 . Thus, the total number of eigenvalues sent to the FC was mK ′ P = 6×5× 4 = 120. Considering that sample values and eigenvalues are digitized with the same number of bits, the required amount of data in the case of the eigenvalue fusion is mKN/mK ′ P = mK N/m(K/P )P = N = 60 times less than in the case of sample fusion. Obviously, this reduction in the volume of data sent to the FC must be traded with the increased complexity of the CRs due to the need of local estimation of the eigenvalues.
A general analysis of the volume of data sent to the FC and the complexity tradeoff is made in the next section, also considering the sensing of general wideband signals.
6. Complexity and Volume of Data Sent to the FC
In this section, we generalize the exemplifying analysis given in the previous subsection, concerning the tradeoff between the volume of data sent to the FC and the complexity related to the number of samples handled and to the computations of eigenvalues for all fusion methods under analysis. We consider a WiMAX system as a case study for providing numerical results as well.
Assume that the WiMAX channel has 2048 subcarriers. For spectral roll-off reasons, only 1, 680 subcarriers are utilized, leaving unused the subcarriers at the edge of the channel. The OFDMA subchannels are created by partitioning the K = 1, 680 useful subcarriers in groups of K ′ = 24 subcarriers, resulting in P = 70 subchannels.
Let us consider first that detecting the
unused subcarriers of the OFDM signal is the objective of the spectrum sensing. For a sample fusion scheme, the number of samples must be much greater (say, 10 times or more) than the number of cooperating CRs, so that a good estimate of the sample covariance matrix is achieved. Considering a secondary network with
m = 10 cooperating CRs and assuming that each CR collects
N = 100 samples per subcarrier, a total of
n =
K N = 1, 680 × 100 = 168, 000 samples are collected per CR. Therefore,
mK N = 10 × 1, 680 × 100 = 1, 680, 000 samples are sent to the FC. Assuming that each sample undergoes a 3-bit quantization [
25], then the total amount of data sent to the FC is 5, 040, 000 bits.
Consider now an eigenvalue fusion scheme. For a fair comparison, assume again that received sample matrices of order J × N/J = 10 × 100 are formed at each CR per subcarrier, also leading to covariance matrices of order J × J = 10 × 10. The total number of samples taken by each CR is then n = K J (N/J ) = K N = 1680 × 1000 = 1, 680, 000, ten times more than in the case of sample fusion (notice that this increased number of samples can be obtained during the same sensing period by increasing the sampling rate J times compared with the sample fusion case). Each CR computes J = 10 eigenvalues per subcarrier to be transmitted to the FC. Also assuming that each eigenvalue undergoes a 3-bit quantization, the total amount of data sent to the FC is 3mK J = 3×10×1, 680×10 = 504, 000 bits.
The above analysis shows that the volume of data sent to the FC in the case of sample fusion (∝ mK N bits) is much greater than in the case of eigenvalue fusion (∝ mK J bits), since N≫ J . In the scenario of decision fusion, only the individual CR decisions are sent to the FC. Therefore, the FC receives mK binary decisions, which represents a volume of data much smaller than in the case of other fusion schemes.
In terms of complexity, in the case of eigenvalue and decision fusions, each CR must be capable of processing n = K J (N/J ) = K N samples and estimate K J eigenvalues. In the case of sample fusion, the complexity of the CR is reduced, since the eigenvalues are computed at the FC. However, the FC must be capable of processing m times more samples, i.e., mn = mK N samples and estimate mK eigenvalues (notice that m = J in the above fair scenario).
Now, let us consider that detecting the unused subchannels of the OFDMA signal is the goal. Consider first the eigenvalue fusion scheme. The number of lines in the received sample matrix Equation (22) is equal to the number of subcarriers in a subchannel, which is K ′ = 24 in the WiMAX example under analysis. Again, for a good estimation of the sample covariance matrix, the number of samples must be much greater (say, 10 times or more) than the number of subcarriers in a subchannel, which is the order of the covariance matrices. Then, let us consider that the number of samples per subcarrier is N = 240. Thus, the total number of samples collected by the each CR is n = K N = 1, 680 × 240 = 403, 200. Each CR generates P = 70 sample matrices (one per subchannel) of order K ′ × N = 24 × 240, resulting in 70 covariance matrices of order K ′ × K ′ = 24 × 24 and K ′ = 24 eigenvalues per subchannel. Also assuming that each eigenvalue undergoes a 3-bit quantization, then the total amount of data sent to the FC is 3mK ′ P = 3mK = 3 × 10 × 1, 680 = 50, 400 bits in the case of eigenvalue fusion. The scenario of decision fusion is similar, but only the individual CR decisions about a subchannel occupation are sent to the FC. Therefore, only mP = 10 × 70 = 700 binary decisions are sent to the FC, which represents a much smaller volume than in the case of the other fusion schemes.
Let us now consider a sample fusion process, using the concatenation approach to form the received sample matrices, as determined from Equation (28). The choice for the concatenation approach is based on the fact that it produces better performance than MRC, also avoiding the need of knowing the channel gains used in the MRC. A number of K ′ N = 24 × 240 = 5, 760 samples are collected by each CR for each of the P = 70 subchannels. These samples are then sent to the FC, where a number of mP = 10 × 70 = 700 sample matrices of order K ′ × N = 24 × 240, as in Equation (22), are formed. The matrices corresponding to the subchannels from all CRs are concatenated according to Equation (28), leading to P = 70 sample matrices of order K ′ ×mN = 24 ×2400. A number of P K ′ = 70 ×24 = 1, 680 eigenvalues are subsequently estimated to form the test statistics for the P = 70 subchannels.
The analysis considering the detection of unused OFDMA subchannels shows that the volume of data sent to the FC in the case of decision fusion is mP bits. For the eigenvalue fusion this volume is bmK = bK ′ mP bits, where b is the number of bits per eigenvalue. For the sample fusion, this volume grows to bmK N bits. Then, the volume of data sent to the FC in the case of eigenvalue fusion is bK ′ times the volume of data in the case of decision fusion, and N times smaller than in the case of sample fusion.
In terms of complexity, in the case of eigenvalue and decision fusions, each CR must be capable of processing n = K N samples and estimate K ′ P = (K/P )P = K eigenvalues. In the case of sample fusion the complexity of the CR is reduced, since the eigenvalues are computed at the FC. However, the FC must be capable of processing mK N samples, which is m times greater than the number of samples processed by each CR. Nevertheless, the FC must estimate P K ′ eigenvalues, the same number of eigenvalues estimated by each CR in the decision fusion and eigenvalue fusion cases.
Let us make a last comparison between the eigenvalue fusion and the samples fusion by fixing the number of samples. Assume that each CR will take N samples per subcarrier. Therefore each CR will collect n = N K samples in the time domain. If the purpose is to sense each subcarrier or sub-band of a general wideband signal, in a sample fusion scenario the amount of samples sent to the FC will be mN K = m2K N/m. In the eigenvalue fusion scheme, if each CR forms covariance matrices of order J = m (as before) and computes J = m eigenvalues, the total amount of samples sent to the FC is m2 K . Notice that the sample fusion scheme sends N/m times more data than the proposed eigenvalue scheme. Since the expected number of cooperating CRs is by far smaller than the number of collected samples in a real system, one can conclude that the eigenvalue fusion is capable of reducing considerably the amount of data in the control channel when compared with the sample fusion.
7. Conclusions and Suggestions for New Research
In this paper, a new eigenvalue-based fusion scheme has been proposed for sensing subcarriers or sub-bands of general wideband signals and for sensing subchannels of OFDMA signals, in the context of cognitive radio systems.
Simulations were performed, comparing our scheme with the fusion of samples collected by the cooperating CRs and with the fusion of CR decisions, considering the test statistics GLRT, MMED, MED, ED and their empirically-modified versions proposed here.
If the system parameters are chosen to build a fair comparison scenario, the eigenvalue strategy can provide better performance than all fusion schemes, for any test statistic and for any wideband signal. Moreover, the eigenvalue fusion can drastically reduce the amount of data sent to the fusion center when compared with the sample fusion method, reducing the volume of data in the corresponding control channel. If local decisions at the CRs are made from the eigenvalues computed, a decision fusion strategy can be adopted, which can further reduce the amount of data sent do the fusion center. The reduction in the volume of data produced by the eingenvalue and decision fusion, however, must be traded with the increased complexity of the cognitive radios, since they must be able to compute the eigenvalues of the received signal covariance matrices before forwarding them (or the decisions) to the fusion center. An analysis of this tradeoff was also presented in this paper.
Comparing the spectrum sensing of general wideband signals with that of OFDMA signals, one can notice that two major differences arise: the general wideband channel is partitioned according to the channelization chosen for sensing purposes, while the OFDMA channel is partitioned according to the sub-channel definition. As a consequence, the strategies for constructing the sample matrices are different from each other. Nevertheless, the approach for detecting OFDMA signals can be adapted to the detection of a general wideband signal by partitioning each sub-band or channel of the general wideband signal as follows: the number of sub-bands or channels of the wideband signal becomes the number
P of sub-channels of the OFDMA approach; the number of partitions of each sub-band or channel of the wideband signal becomes the number K ′ of subcarriers of each OFDMA sub-channel. All OFDMA sensing procedures apply unchanged in the sequel, as described in
Section 4. The definition of the partition of each sub-band or channel of the wideband signal in the OFDMA-like approach, as well as the influence of the remaining system parameters in this partition and in the overall sensing performance, remains an open problem.
One can notice that if the sensing of subchannels in OFDMA systems can be coordinated under the information of unused subchannels in a given area, the data traffic in the control channel for the eigenvalue fusion can be further reduced, since some subchannels would not need to be sensed at all.
The performances of the decision fusion with OR logic and with majority-voting have shown to be close to the performances obtained with the eigenvalue fusion, for sensing subcarriers or sub-bands of general wideband signals, and for sensing subchannels of OFDMA signals, respectively. Since the volume of data sent to the FC is smaller than in other fusion schemes, our immediate conclusion is that these decision fusion strategies are preferred over the eigenvalue fusion. However, we conjecture that bit errors in the control channel can be more disastrous to the data representing CR decisions than to the data representing eigenvalues. This in turn would demand increased protection of the decisions data, reducing the difference in the volume of data in the cases of eigenvalue and decision fusion. This conjecture represents a good opportunity for further contributions. Nevertheless, this investigation could be complemented with an analysis of the influence of different system parameters in the spectrum sensing performance, which could help in constructing the conclusions concerning the influence of these differences on the ranking of the decision fusion combining rules.
It was verified that the wideband spectrum sensing approach proposed here can be applied to any wideband signal. Combined with the subcarrier nulling flexibility of OFDM signals, OFDM-based cognitive radios [
26] can opportunistically reuse underutilized spectrum bands. This is particularly favorable to the recently-proposed generalized frequency division multiplexing (GFDM), which is arising as a candidate to be used in the next generation of wireless communications [
27,
28]. GFDM signals are more flexible than OFDM in terms of spectral shaping capability and are able to produce much lower out-of-band radiation when compared with OFDM. Thus, for future research, it will be interesting to investigate the performance of the eigenvalue fusion scheme to detect GFDM signals, as well as to analyze a GFDM-based opportunistic access strategy in this scenario.
In [
14], the authors showed that the GLRT can be viewed as a modified version of the MED, where the actual noise variance is replaced by its maximum-likelihood estimate. It would be interesting to analyze the influence of replacing the actual noise variance with its estimate in the MED-like and ED-like tests empirically proposed in this paper. The objective is to verify if this replacement would produce attractive performance results, thus giving a more practical appeal to these tests that do not demand the use of the actual noise variance, which is not accurately known in real systems.
 = 1, 2, . . . , p, representing the channel gain between the
= 1, 2, . . . , p, representing the channel gain between the  -th primary transmitter and the i-th sensor (antenna or CR). It is assumed that these gains do not vary during the sensing period. Finally, let V ∈ ℂm×n be the matrix with thermal noise samples corrupting the signal received by the m sensors. Therefore, the matrix with received samples under this MIMO channel model is given by
-th primary transmitter and the i-th sensor (antenna or CR). It is assumed that these gains do not vary during the sensing period. Finally, let V ∈ ℂm×n be the matrix with thermal noise samples corrupting the signal received by the m sensors. Therefore, the matrix with received samples under this MIMO channel model is given by
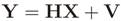
 , where
, where  is the expected value operator. Since the ensemble covariance matrix is normally unknown, it is replaced by its maximum-likelihood estimate, the sample covariance matrix
is the expected value operator. Since the ensemble covariance matrix is normally unknown, it is replaced by its maximum-likelihood estimate, the sample covariance matrix

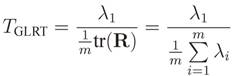
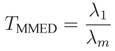
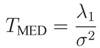

 . Pd is the probability of inferring that a sensed band is occupied when it is indeed occupied, i.e.,
. Pd is the probability of inferring that a sensed band is occupied when it is indeed occupied, i.e.,  . Here
. Here  is the decision threshold, and
is the decision threshold, and  are the hypotheses that the primary transmitted signal is absent and present, respectively. It is thus desirable that Pfa is minimized and Pd is maximized. However, these objectives are conflicting ones: increasing the threshold decreases Pfa , but also decreases Pd. As a consequence, a tradeoff must be adopted so that the correct threshold is established. The tradeoff is usually determined with the aid of receiver operating characteristic (ROC) curves that show the variation of Pfa versus Pd with changes in the threshold value.
are the hypotheses that the primary transmitted signal is absent and present, respectively. It is thus desirable that Pfa is minimized and Pd is maximized. However, these objectives are conflicting ones: increasing the threshold decreases Pfa , but also decreases Pd. As a consequence, a tradeoff must be adopted so that the correct threshold is established. The tradeoff is usually determined with the aid of receiver operating characteristic (ROC) curves that show the variation of Pfa versus Pd with changes in the threshold value. represents the absence of the primary signal and
represents the absence of the primary signal and  represents the presence of the primary signal in the k-th band with k = 1, . . . , K .
represents the presence of the primary signal in the k-th band with k = 1, . . . , K .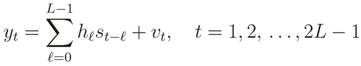
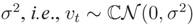 . We assume that noise samples are independent of signal samples.
. We assume that noise samples are independent of signal samples.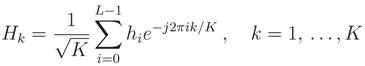
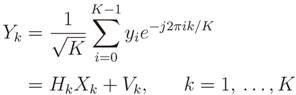

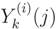 is the j-th sample collected by the i-th CR in the k-th sub-band. The total number of samples received by the FC is then mK N . The sample covariance matrix in this case is computed at the FC and is given by
is the j-th sample collected by the i-th CR in the k-th sub-band. The total number of samples received by the FC is then mK N . The sample covariance matrix in this case is computed at the FC and is given by
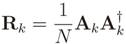
 with samples from the k-th sub-band or subcarrier can be formed by arranging the N samples taken by the i-th CR in J rows and N/J columns, preferably with N/J≫ J (which implies N≫ J ) for more accuracy of the subsequent sample covariance matrix computation. Matrix
with samples from the k-th sub-band or subcarrier can be formed by arranging the N samples taken by the i-th CR in J rows and N/J columns, preferably with N/J≫ J (which implies N≫ J ) for more accuracy of the subsequent sample covariance matrix computation. Matrix  is then
is then
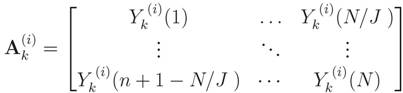
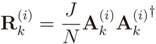

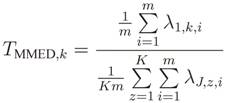
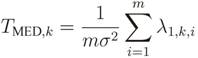
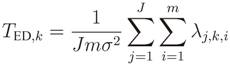
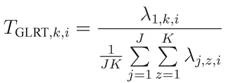
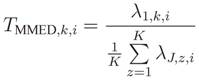

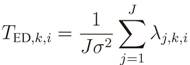
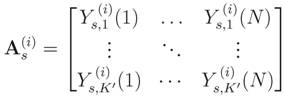
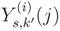 is the j-th sample collected by the i-th CR in the k′ -th subcarrier pertaining to the s-th subchannel. From Equation (22), the next step is to compute the corresponding sample covariance matrices, according to
is the j-th sample collected by the i-th CR in the k′ -th subcarrier pertaining to the s-th subchannel. From Equation (22), the next step is to compute the corresponding sample covariance matrices, according to
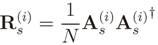
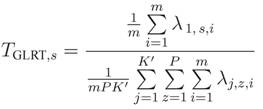
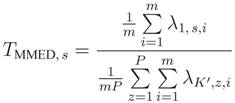
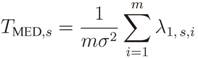
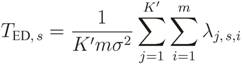
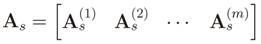
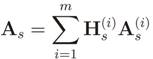
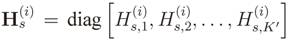 is the diagonal gain matrix whose diagonal entries
is the diagonal gain matrix whose diagonal entries 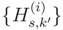 are the channel gains in the frequency domain between the primary transmitter and i-th CR in the k′ -th subcarrier of the s-th OFDMA subchannel, i = 1, 2, . . . m; s = 1, 2, . . . P ; k′ = 1, 2, . . . K ′. From the matrices in Equation (28) or Equation (29), the corresponding sample covariance matrices
are the channel gains in the frequency domain between the primary transmitter and i-th CR in the k′ -th subcarrier of the s-th OFDMA subchannel, i = 1, 2, . . . m; s = 1, 2, . . . P ; k′ = 1, 2, . . . K ′. From the matrices in Equation (28) or Equation (29), the corresponding sample covariance matrices