1. Introduction
Cities are becoming increasingly vulnerable to all kinds of hazards or events, such as floods and earthquakes, because of the unpredictable impacts of global climate changes. As a critical aspect of disaster relief operations, the development of comprehensive and efficient rescue plans for urban spaces is urgent. The timely and effective mobilization of resources is essential in aiding people who are vulnerable to natural disasters. However, variations in road travel times under disaster conditions may render emergency responses ineffective and result in increased uncertainties. Therefore, it is important to develop strategies for creating reliable emergency rescue plans.
The problem to be addressed in this research is rescue vehicle routing with stochastic link travel times. Many models and algorithms have been proposed to solve the vehicle routing problem (VRP) from different perspectives, such as the VRP related to pickup and delivery [
1], the multidepot VRP [
2], and the VRP with a time window [
3,
4,
5]. However, most of them consider the transportation network to be deterministic. The complex nature of emergencies, as well as the lack of knowledge of data (e.g., demand, supply, or cost) in such situations, imply uncertainties in rescue vehicle route optimization. Although some models have been developed for emergency logistics with demand or supply uncertainty [
6], for instance, one study [
7] proposed a decision support framework for addressing emergency routing problems by taking into account both travel time and deadline uncertainty, the research on travel time/cost uncertainty is relatively insufficient [
8]. The lack of research in this direction may be attributed to the lack of real disaster-related travel time data.
In view of the above, this study aims to propose a multiobjective rescue routing (MORR) model, which considers travel time uncertainty for scenarios in which multiple rescue vehicles are dispatched to multiple destinations. Travel time uncertainty will be estimated based on real data. The reliability of travel time is defined as the frequency of successful trips made within a desired time interval [
9,
10,
11]. Determining the α-reliable path requires finding a reliable path with the minimum travel time budget, such that the probability that the path travel time is less than or equal to the travel time budget, which is greater than or equal to α [
9]. The α-reliable path is used to guarantee reliability, with a confidence level α, in a stochastic transportation environment.
The objectives of the proposed model are to minimize the sum of the travel time budgets of all rescue vehicles and the maximum travel time budget of an individual rescue vehicle with a certain reliable arrival probability, α. A hybrid metaheuristic integrating ant colony algorithm (ACO) and tabu search (TS) is proposed to solve this routing model. An experiment on optimizing rescue routing plans for an urban storm flooding disaster will be carried out to validate the proposed model.
The rest of this paper is organized as follows. The next section presents a brief literature review.
Section 3 defines travel time reliability, the bi-level rescue network, and the rescue vehicle routing problem. A multiobjective optimization model and a hybrid metaheuristic are presented in
Section 4.
Section 5 introduces the study area and data used.
Section 6 analyzes the results of the computational experiments and discusses the sensitivities of the travel time budget of routing plans for different on-time arrival probabilities. The final section provides concluding remarks and future research directions.
2. Literature Review
In recent years, there have been many studies on disaster relief logistics. These studies mainly fall into one of four categories: facility location, inventory management, relief supply collaboration, and network flow problems [
8,
12]. For network flow problems, many studies have been conducted to achieve rescue path optimization during an emergency response [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23]. In general, these studies have focused on how to develop suitable mathematical models and algorithms to derive optimal solutions regarding minimum travel time or cost. Transportation networks are considered to be deterministic in most studies. For instance, in the research of [
20], a robust methodology for the dispatching and routing of emergency vehicles in a post-disaster environment was proposed, and the traversal speed of each road segment was estimated using a linear function of the expected level of damage of this road. According to Wang et al. [
21], route-traveling time is dependent on the length of the route and the normal or maximum velocity associated with a vehicle. These studies considered time-dependent or damage-level-related travel time, but the uncertainties related to disasters were neglected.
Research on the uncertainties of emergency logistics is mainly related to demand or supply uncertainty [
6]. Different models have been developed for emergency logistics preparation planning under demand uncertainty [
16,
24,
25]. For instance, Mete and Zabinsky [
25] presented a two-stage stochastic programming model for the warehouse selection and storage of medical supplies in the case of demand uncertainty. All sources of uncertainty (demand/supply/cost) can also be integrated into a multiobjective stochastic programming model to determine the location of relief distribution centers, the required inventory quantities for each type of relief item in storage, and the amount of transportation from relief distribution centers to affected areas [
18]. However, research on travel time/cost uncertainty is relatively insufficient [
8]. Although the study in [
7] proposed a decision support framework for addressing emergency routing problems, taking into account both travel time and deadline uncertainty, the travel time uncertainty was assigned with different levels according to the author’s experience.
Some studies have focused on the shortest path calculation between an origin–destination pair, while considering travel time uncertainty [
26,
27,
28]. Miao et al. [
26] proposed a reliable route searching method in an uncertain network, with the uncertainty of the road network travel time being depicted by means of a disaster scenario union. Zhang and Kong [
27] built a route choice model by considering travel time reliability, road disruption risk, and complexity. Lu and Sheu [
28] proposed a model for minimizing the worst-case deviation in the maximum travel time between urgent relief distribution centers and relief stations. Due to random link capacity degradations, travel times are highly stochastic [
29]. Travel times were thus viewed as random variables, and followed a probability distribution, for example an exponential, normal, or lognormal distribution [
30]. Algorithms have been proposed to find reliable shortest paths or most reliable paths between an origin–destination pair by assuming travel times following a normal or lognormal distribution [
9,
31]. However, these cannot be easily applied to rescue vehicle routing in the case of multiple destinations (affected areas).
The problem in this research is the rescue vehicle routing problem with stochastic link travel times, which is a variant of the VRP. As a non-deterministic polynomial-time hard (NP-hard) problem, the VRP has been studied for decades, and many algorithms have been proposed to solve it [
32,
33,
34,
35,
36,
37,
38]. Among the approaches proposed in the literature, metaheuristics are considered to be efficient and effective state-of-the-art methods. One of the most studied metaheuristic algorithms for vehicle routing problems is ACO [
33]. ACO has some advantages, including its ability to explore a solution space [
34,
35], while it is prone to fall into local optima. TS is another widely used metaheuristic. There are some examples of TS for vehicle routing problems [
36,
37]. TS starts from a certain initial solution and applies short- or long-term memory to escape from local optima [
30]. The quality of the initial solution is of vital importance for the efficiency of TS. Therefore, ACO and TS will be integrated to improve the quality of solutions and the convergence speed [
38].
5. Study Area and Data Description
With the acceleration of global change and urbanization, urban storm flooding disasters caused by continuous heavy rain have become more and more frequent in some metropolises [
44,
45,
46]. Water on road surfaces will greatly affect traffic along these roads. In severe circumstances, vehicles can become stranded on some roads because the water depth exceeds the safety threshold of vehicles. Traffic along these roads is cut off by water, causing serious traffic congestion on adjacent roads. Hence, it is important to develop reliable route plans for rescuing stranded vehicles.
The study area of this research is the central urban district of Guangzhou city. It is located in southern China and has abundant rainfall during the summer, which can easily lead to serious urban storm flooding disasters. Once this kind of disaster occurs, people and vehicles stranded in flooded areas should be rescued as quickly as possible. According to the
Guangzhou Water Affair Annual White Paper released in 2013 [
47], three flood rescue teams were set up in Guangzhou, and one warehouse containing specialized rescue equipment was established. The transportation network comprised 791 road segments and 690 road nodes.
We used the urban flooding disaster that occurred on 14–15 August 2013, as an example to verify the effectiveness and applicability of the proposed MORR model and algorithms. The urban rainstorms caused by Typhoon Utor resulted in dozens of flooded areas. The exact locations of the 10 most severely submerged flooded areas and the warehouse are shown in
Figure 5, where flooded areas are denoted by their IDs.
The stochastic travel times of the roads in this study were derived from the GPS-enabled tracking data of taxis. With the rapid development of information technology, city-wide data from global positioning system (GPS) receivers equipped on taxis have been collected and made available. This data has been widely applied in traffic status analyses [
47,
48]. Travel time variations can be measured using taxi-enabled GPS tracking data for travel time estimation. On the other hand, large-scale GPS tracking data can cover a city-wide traffic network, which can support research on emergency logistics by providing real data related to real road networks. The GPS data used in this study came from the Guangzhou Commission of Transport, a municipal administration governing the operation of taxis, buses, and other types of road transportation. The data covered all the taxi companies in Guangzhou. The GPS-enabled taxi data included records of the license plate number, latitude, longitude, speed, and status of the taxis, taken every 20 s. This research used GPS-enabled taxi data from 14–15 August 2013, for the analysis.
To measure the travel time along road segments of varying lengths, minute/km was adopted as the unit. The average travel time was calculated at intervals of 10 min. Before computing the mean and variance values of each road segment, we fitted the distribution of the samples extracted using a simple random sampling method with both a lognormal distribution and a normal distribution. The fitting results are shown in
Figure 6. From the comparison of the
R-squared and reduced chi-square values, it can be inferred that the lognormal distribution model was superior to the normal distribution model, in this study.
6. Experiment and Results
To evaluate the rescue performance of the proposed model under uncertain traffic conditions, three problems were defined for comparison (
Table 2).
Problem S1: The objective was to minimize the average travel time (ATT) of rescue paths under a deterministic network (DN), with the road travel time as the weight.
Problem S2: The objective was to minimize the travel time budget (TTB) of rescue paths with an on-time arrival probability, α, under a stochastic network (SN).
Problem S3: The objective was to minimize the TTB of all rescue paths, as well as the maximum TTB of an individual rescue vehicle (Max-TTB) with an on-time arrival probability, α. This is a multiobjective optimization, performed to balance the time costs of different rescue paths.
As defined above, Problem S1 represents the traditional approach, which ignores travel time uncertainty. Problem S2 represents the optimal rescue routing plan under a stochastic network. Problem S3 aims to balance the time budgets of different rescue routes.
The upper-level VRP network was first built, before rescue route planning. The average travel times between the warehouse and the 10 flooded areas are shown in
Table 3. The ID of the warehouse is 0, and the IDs of the flooded areas range from 1 to 10. In addition, the travel time budgets between the warehouse and flooded areas are presented in
Table 4. The budgets were calculated by using the multicriteria label-setting algorithm mentioned in
Section 4.2, with an on-time probability of α = 0.9, which is a high probability used to guarantee that rescue vehicles will arrive at the flooding points on time. As shown in
Table 3 and
Table 4, the average travel times were less than the travel time budgets for each VRP node pair, which implies that the fastest paths are not always reliable if the stochastic characteristics of the transportation network are considered.
There are several main parameters in the proposed ACO-TS: δ, β, ρ for ACO, and
L (the length of the tabu list) for the TS algorithm. These can affect the algorithm’s ability to find optimization solutions and its convergence speed. Previous literature suggests some empirical values or value ranges for these parameters [
35,
38]. We looped through the ACO-TS with different parameter combinations to find the optimal value. In these iterations, the values of δ and β were increased from 0 to 2 by increments of 0.2. The value of ρ was increased from 0.6 to 0.9 by increments of 0.1. The value of L was increased from 1 to 10 by increments of 1.
Table 5 lists the parameters used in the proposed ACO-TS. The capacity of each rescue vehicle, that is,
C in Formula (20), was set to 4, which meant that, in this study, a maximum of 4 sets of rescue equipment were loaded onto each vehicle.
We first compared the routing results of the proposed ACO-TS with those of the VRP tool in the ArcGIS Network Analyst module to verify the efficiency of our proposed method. The VRP tool is based on tabu search metaheuristics. As a classical indicator, the total length of the routes was used for comparison. As shown in
Table 6, the total length of the routes of the ACO-TS was 52.62 km, which was less than that of the classical VRP tool in the ArcGIS Network Analyst module. This comparison demonstrates the technical strength of the proposed ACO-TS.
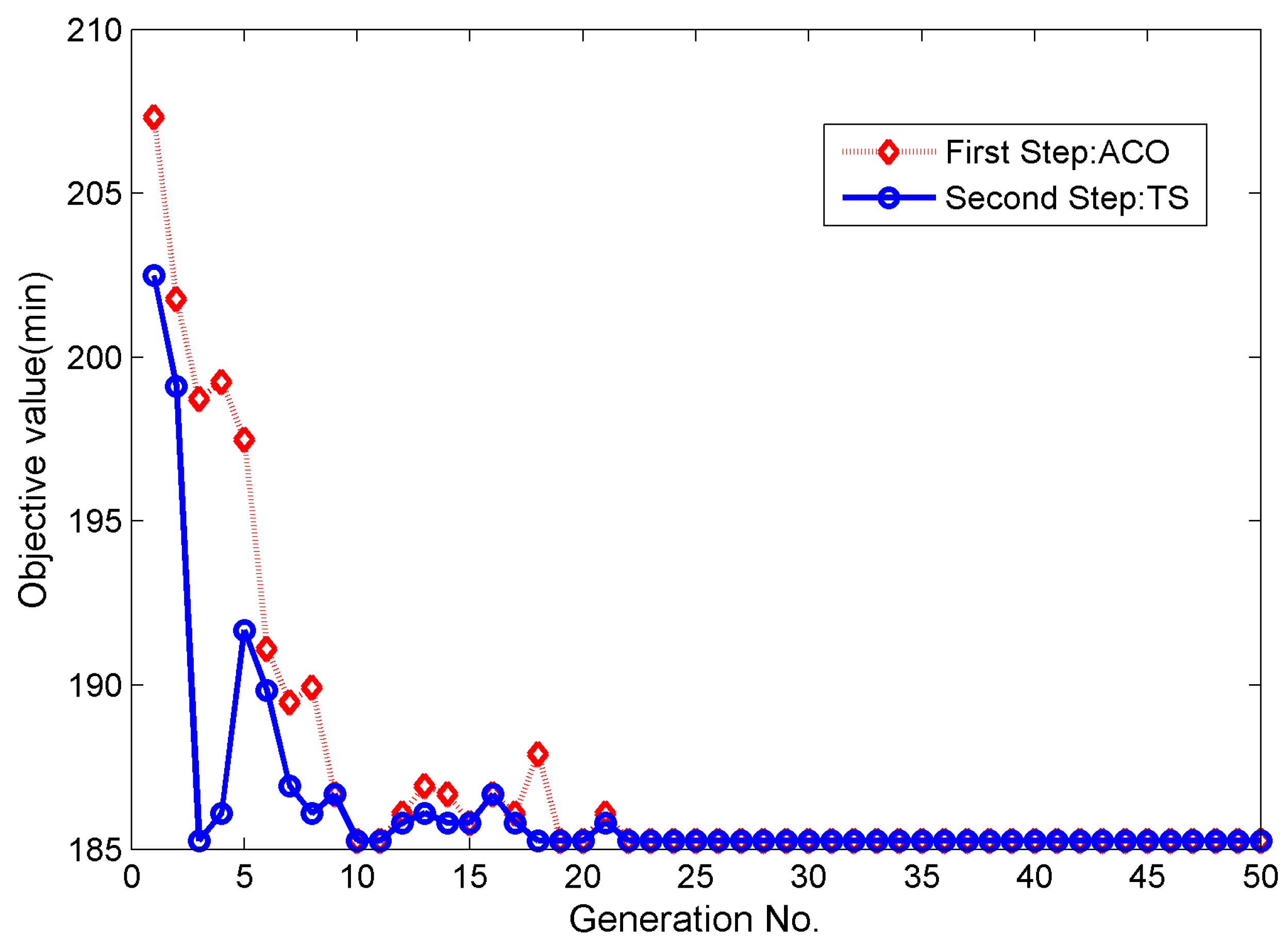
Figure 7 illustrates the optimization of
R via the iteration process in problem S3. In each iteration, the objective value was optimized via ACO first, then the candidate solutions were optimized again using the tabu search strategy with neighbor search operators. The differences between the objective values obtained via ACO and TS indicated that the integration of ACO and TS improved the efficiency and capability of optimization.
The routing plans (and their performances) of the three problems (S1, S2, and S3) are compared in
Table 7 to show the significance of considering travel time reliability when planning rescue routes. The details of the open routes, the length, the
ATT, the
TTB, and the mean and variance values of the open routes of S1, S2, and S3 are listed and compared. There were three open routes in each problem, and each open route was for a rescue team. We numbered the open route covering four flooded areas as 0 and the other two open routes covering three flooded areas as 1 and 2.
In
Table 7, the
ATTs of the three open routes of S1 are 64.84 min, 18.58 min, and 19.56 min. According to the mean, μ, and variance, δ, values of each open route, the actual on-time arrival probability of each open route can be calculated as 0.47, 0.13 and 0.14, respectively. On the other hand, the sum of the
TTBs of these three open routes reached 137.36 min when the on-time arrival probability was 0.9, a value that was 34.38 min greater than the
ATT value. The results quantitatively indicated that the planned routes in S1 were uncertain.
Regarding the values of the open route length, ATT and TTB, we found that the differences in sums of the open route length and ATT between S2 and S1 were very small, while the sum of the TTBs of S2 were reduced by 14.8% when compared to that of S1. This result shows that the proposed model can find rescue routes with a high on-time arrival probability that have the almost shortest route length and average travel time. Note that the differences in the TTBs among the open routes of S2 were still very large. In S2, the TTB of open route 1 was 71.28 min, while the TTBs of open routes 2 and 3 were only 21.80 min and 23.99 min, respectively. This result implies that flooded area 7 will wait at least 71.28 min before being visited. In S3, since the maximum TTB of the open routes was also minimized, the TTB of each open route was more balanced. The TTBs of open routes 0, 1, and 2 in S3 were 49.27 min, 56.41 min, and 23.99 min, respectively. The flooded area with the longest waiting time was also area 7, but its waiting time was reduced to 56.41 min.
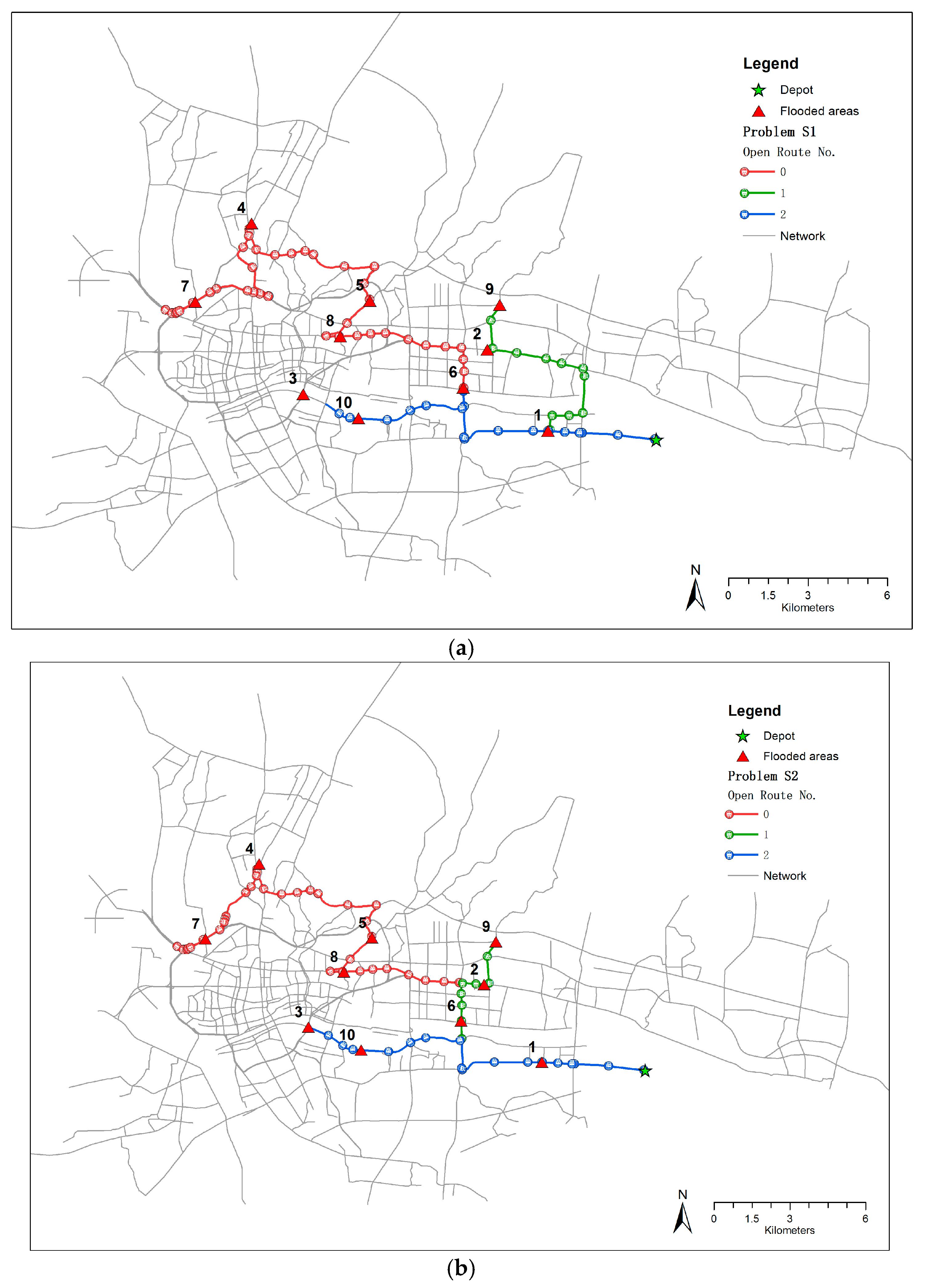
The rescue routes of S1 and S2 are displayed on the road networks in
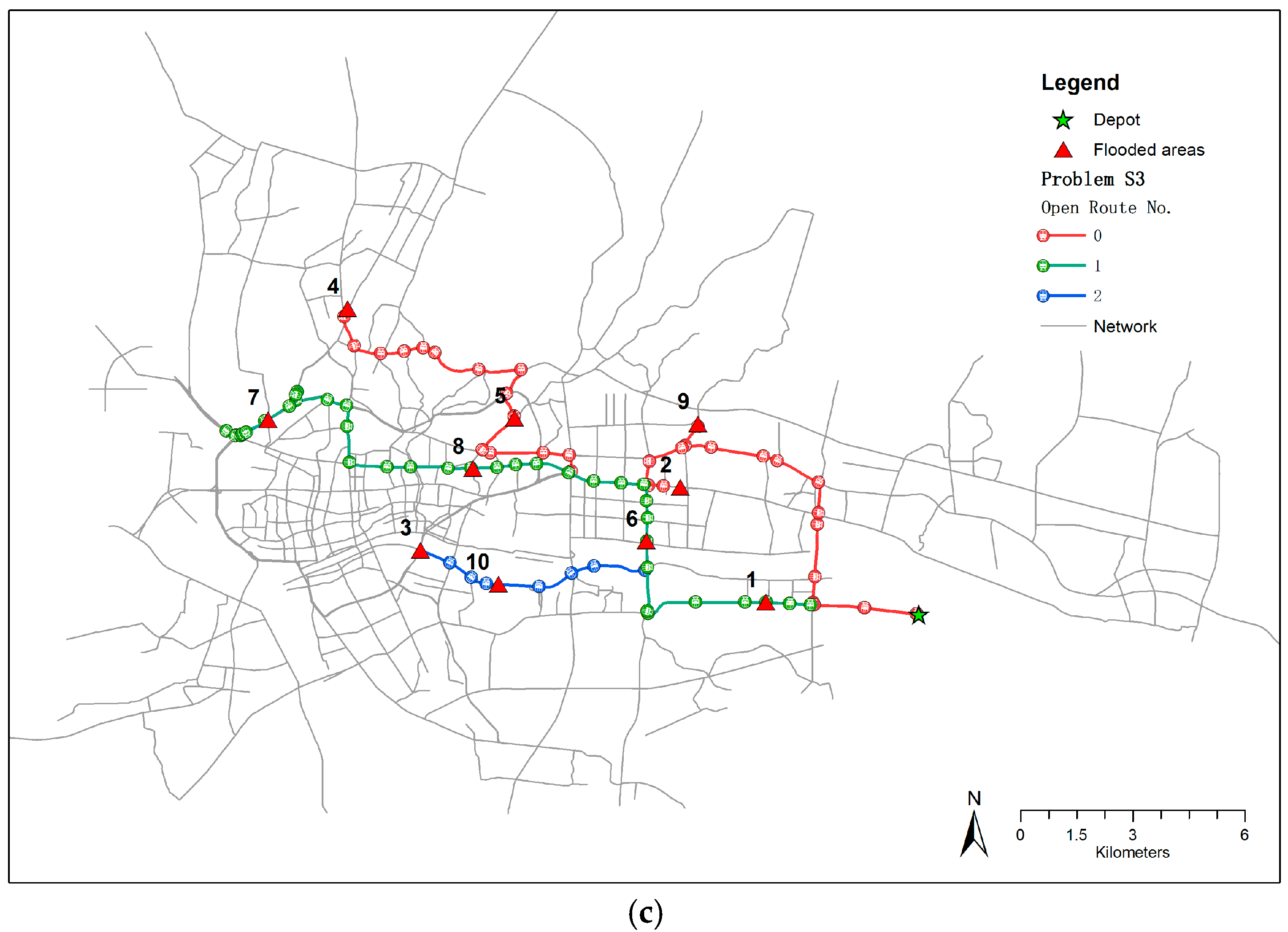
Figure 8a,b, respectively. The three open routes all started from the warehouse, then covered different flooded areas. For S1, the flooded area coverage sequence of open route 0 was 0→8→5→4→7, that of open route 1 was 0→1→2→9, and that of open route 2 was 0→6→10→3. For S2, the flooded area coverage sequence of open route 0 was also 0→8→5→4→7, that of open route 1 was 0→6→2→9, and that of open route 2 was 0→1→10→3. It should be noted that although the flooded area coverage sequence of the first open routes of S1 and S2 were the same, the path details were different between flooded areas 4 and 7. The routes of S2 serve as good guides for rescue vehicles transporting equipment along the fastest paths under a very high on-time arrival reliability (α = 0.9). For S3, the flooded area coverage sequence of open route 0 was 0→9→2→5→4, that of open route 1 was 0→6→8→7, and that of open route 2 was 0→1→10→3. The route details of S3 are displayed on the road network shown in
Figure 8c.
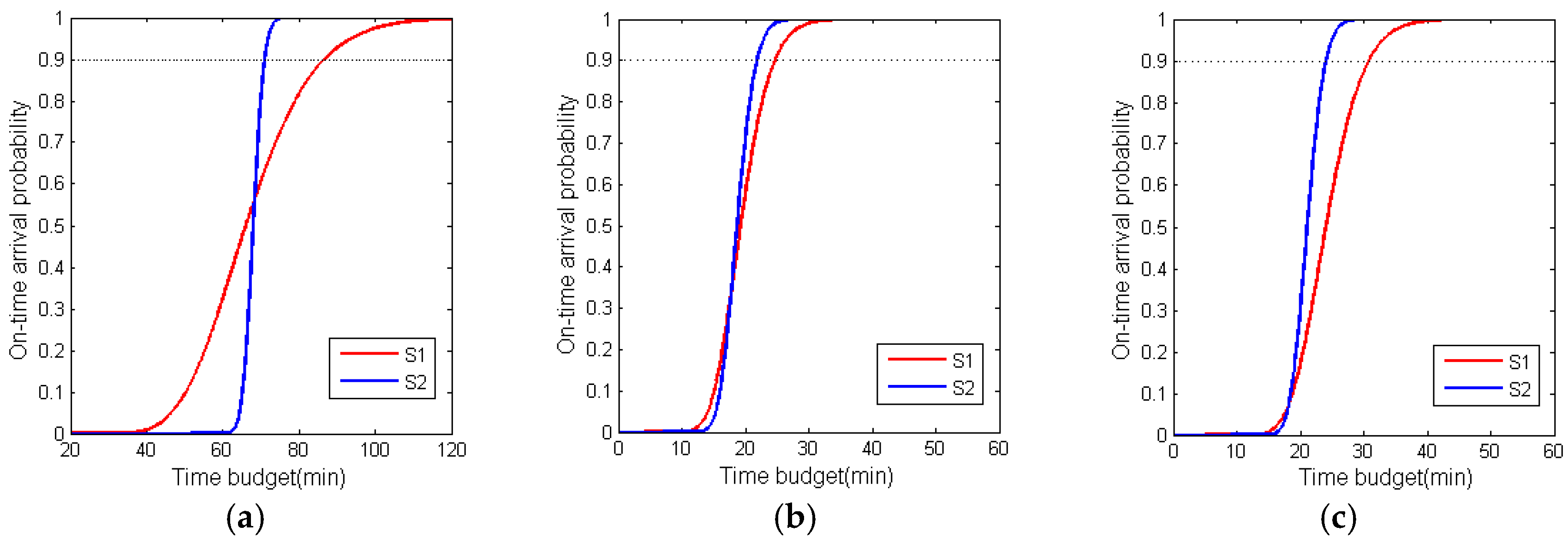
The above analyses and comparisons are all based on an on-time arrival probability of 0.9. The travel time budget of the optimized routes of S1, S2, and S3 may vary with the on-time arrival probability. To answer the question regarding whether the routes of S2 can always achieve a lower travel time budget than the routes of S1 for different on-time arrival probabilities, a comparison of the cumulative probability density curves of the open routes of S1 and S2 was conducted, as shown in
Figure 9. For open route 0, when the on-time arrival probability was above 0.55, the travel time budget of S2 was less than that of S1. For open route 1, when the on-time arrival probability was above 0.3, the travel time budget of S2 was less than that of S1. For open route 2, when the on-time arrival probability was above 0.1, the travel time budget of S2 was less than that of S1. That is, if the on-time arrival probability is required to be larger than 0.55, the routes of S2 are better than those of S1. Therefore, the proposed model considering travel time reliability is important for the flood disaster rescue route planning discussed in this study, for which a high on-time arrival probability should be guaranteed.
Another question is whether the difference in travel time budget between S2 and S3 will change for different on-time arrival probabilities. S2 and S3 are both optimal routing plans derived using the proposed model, and the cumulative probability density curves of their open routes are illustrated in
Figure 10. For open route 0, S3 outperformed S2 regardless of the on-time arrival probability, while for open route 1, S2 outperformed S3. For open route 2, the two curves overlapped. From the curve shapes of S2 and S3, it can be inferred that the difference in travel time budget between S2 and S3 does not seem to change with the variation in on-time arrival probability. Although the sum of the travel time budgets of all three open routes of S3 was larger than that of S2, in terms of balancing the waiting time of people trapped at each flooding point, S3 was better than S2 regardless of the on-time arrival probability.
7. Conclusions
The research presented in this paper introduced a multiobjective rescue routing (MORR) model based on travel time reliability in a stochastic network, for a case in which the road travel time is strongly influenced by urban storm flooding disasters. A hybrid metaheuristic integrating ACO and TS, named ACO-TS, was proposed to solve the MORR model. Experiments based on a real-world case were conducted to evaluate the proposed model and algorithm. The study area was the central urban district of Guangzhou city, which is located in southern China and experiences abundant rainfall during the summer. The objective was to plan routes for rescue vehicles, to guide them to flooding points as quickly as possible under a high on-time arrival probability.
Three problems (S1, S2, and S3) were defined to evaluate the rescue performance of the proposed model. S1 was the basic situation, without consideration of the traffic uncertainty, while the plans of S2 and S3 were derived using the proposed model. By comparing the travel time budgets of S1, S2, and S3, we were able to draw several conclusions. First, when traffic uncertainty was not considered, the on-time arrival probability of the planned routes was low if the rescue vehicles were expected to finish the routes within the average travel time. Second, when the on-time arrival probability was required to be larger than 0.55, the route plan of S2 was better than that of S1. Third, S2 and S3 were non-dominated route plans with different weight combinations of objective F1 and objective F2. In terms of balancing the waiting time at each flooding point, the routing plans of S3 were better than those of S2, regardless of the on-time arrival probability.
Our proposed model and algorithm can help decision makers design reliable and quick rescue routes, and they can also be applied to other emergency rescue events in which the travel time in the transportation network is stochastic. The on-time arrival probability was set to 0.9 for the case study, which is a high on-time arrival probability. Emergency management departments can set higher on-time arrival probabilities according to the urgency of the rescue task. We plan to improve our model and algorithm in the following ways. First, it would be better if the spatial correlation between neighboring road segments is taken into consideration when estimating the values of μ and σ of rescue paths. Second, it is assumed, in this study, that link travel times are stable during the rescue mission. It is necessary to extend the proposed model and the algorithm to a stochastic time-dependent network, in which link travel times vary with time. Third, it is necessary to extend the proposed model and algorithm to the case of multidepot rescue routing problems.