1. Introduction
Historic landscape prospecting via remote sensing and computing technologies has considerably advanced in recent years. Aerial and satellite imagery is a valuable tool for characterizing and locating archeological landscape and structure [
1,
2]. The images can display the data of existing landscape and track changes in time. In addition, these images may contain valuable information about historic features, thereby enhancing the information on the land-use change. Aerial and satellite imagery is considered a critical step toward preserving and restoring a historic property. Recently, emerging techniques of airborne light detection and ranging (LiDAR) help acquire geometric features of landforms [
3]. Many dense point clouds are obtained by using LiDAR scanners. Abstract representation derives from a source dataset to obtain a target dataset with reduced contents and complexity. The structural characteristics of the landscape can be abstractly represented. The representation of the LiDAR data can be possibly derived by extracting line vector features, indicating the suitability for a given application scenario [
4]. Settlement materials may not constantly be visible on the surface. The extraction of concrete feature information from LiDAR data in historic landscape management is crucial, but it is the most time-consuming part. Thus, automating the landscape line extraction is commonly developed in land use and landscape management. Previous studies have extracted artificial architectures, such as buildings and roads, from LiDAR data [
5,
6,
7,
8]. Many dense point clouds are obtained by current airborne LiDAR scanners to derive rasterized digital terrain and surface models.
Highly accurate digital elevation model (DEM) information is obtained from LiDAR data. From this information, landscape line segments, which constitute a much suitable representation (and reduced in terms of data volume) of the LiDAR data for geographic information system (GIS) application scenarios, can be extracted. For example, the building boundary was extracted from the raster DEM data, which are interpolated from the LiDAR points based on image processing techniques [
9,
10]. Therefore, image processing is a direct approach to line extraction from DEM images. Commonly used approaches combine the Canny edge [
11] or Sobel detector [
12] with the Hough transform [
13] for line extraction. Coral low walls protect farm fields (i.e., vegetation gardens) from strong winds that sweep across the Penghu Islands for half the year. However, the anthropogenic features, such as historic vegetation garden walls, can be identified in high-resolution DEMs. The topographic parameters from the DEMs include slope, aspect, and curvatures. These parameters are extensively used in the geomorphology field for providing feature information and mapping land components. The current study was conducted to explore the relationship between topographic properties of parameters and low walls. The high-resolution DEM offers common information for extracting vital topographic data, which are important in studying various landform processes and landscape patterns. Topographic parameters, such as slope and curvature, based on the high-resolution LiDAR DEM demonstrate obvious correspondence with the expected form of features that people recognize, such as a peak with a mountain, channel with a valley, and ridge and pass [
14,
15,
16,
17]. The topographic parameter images contain valuable information on the spatial features and landscape for land use planning and management.
In the current study, we present a rapid method for identifying vegetable garden wall landscapes based on the digital topographic analysis. The model, which uses high-resolution DEM information, is developed for historic wall identification. We propose using multiple topographic parameters in subtle anthropogenic feature detection. The different characteristics of parameters can provide partial information on morphometric landforms and historic features to allow accurate identification. Multiple topographic parameters, such as slope, curvature, and openness, provide the feasibility of distinguishing historic low walls. This detection with multiple parameter approaches was used to improve the overall accuracy of classifying historic anthropogenic features.
2. Materials and Methods
The Xiji Island is part of the Penghu Islands in the Taiwan Strait (
Figure 1). Original settlements are focused on the southern tip of the island. Green grassland was distributed in the island after the migration of people. The study area covers 0.78 km
2. The average elevation and slope of the study area are approximately 6 m and 3.4°, respectively. The maximum elevation and slope are 29 m and 84°, correspondingly. On the Penghu islands, early residents built unique vegetable gardens to protect vegetables from prevailing winds, that is, the strong northeast monsoon. Vegetable gardens consist of low walls built with basalt and coral stones. The average height of these walls is approximately 1 m above the ground, and the wall width is approximately 1 m (
Figure 2).
In the current study, the 1 m spatial resolution elevation was obtained from the LiDAR-derived DEMs. LiDAR measurements were performed during summer on 27 August 2013. Airborne LiDAR data were acquired with a RIEGL LMS-Q680i system [
18]. The position and orientation of the LiDAR data were acquired by using GPS and an inertial measurement unit. The point clouds were processed using TerraScan [
19] and manual procedures. First, TerraScan was applied to automatically filter non-ground points. A manual process of inspection and editing was subsequently conducted to ensure the quality of the ground data points. The maximum vertical error of DEM after validation is 11 cm, and the mean squared error is 6.4 cm in the DEM. The reference data of the low walls were digitized by an operator by using shaded relief maps of DEMs. In the reference data, we only considered the complete and straight walls in the study area. The uncertain and fuzzy information based on the DEM were displayed in the southern area. A color orthophoto at 10 cm spatial resolution was used for visualization and investigation (
Figure 1). From the high-resolution orthophoto, the walls in the southern area were mixed with brush, grass, and trees. Moreover, most of the walls in the southern area were incomplete due to damage.
3. Method
The main processes in this study include derivation of topographic parameters, line extraction, and aggregation (
Figure 3). The rule of low wall extraction is generated from the decision tree to prove the idea extracted from multiple parameters. Moreover, the influence of the feature identification of a location at different scales is critical. Multiple window sizes (multi-scale) are considered, especially with respect to curvature. Finally, a 3 × 3 window size was used in this study.
3.1. Derivation of Topographic Parameters
3.1.1. Slope
A slope reflects the maximal change rate of elevation values. The slope is the angle between the horizontal plane and the angle tangential to the surface, as expressed below:
where x, y, and h represent longitude, latitude, and elevation, respectively [
14].
3.1.2. Maximum Curvature
Curvatures are related to the concavity and convexity of a surface. Many curvatures of a surface at a point that generally vary with orientation are possible. The curvature is a complex terrain derivative to compute and includes maximum, minimum, and average curvatures, or profile and plan curvatures [
20]. In the current study, the maximum curvature is used as the factor for detecting the landscape feature. Numerous detected features were observed from scales (i.e., window sizes) [
18]. The window size used in the current study varied between 3 × 3, 5 × 5, and 7 × 7. The model was fitted to the surface using the window surrounding the target point. The maximum curvature within local formulas is provided based on the quadratic model [
14].
3.1.3. Openness
Terrain openness is a measure of the relationship between surface relief and horizontal distance [
21]. The openness incorporates the terrain line-of-sight principle and is calculated from the zenith and nadir angles along eight azimuths. Positive openness is the mean value of zenith angle along the eight sampling directions (D = 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315°), whereas negative openness is the corresponding mean value of the nadir angle [
22]. In the current study, the openness is the average of positive and negative openness defined as:
where Op is the positive openness, and On is the negative openness [
23].
3.2. Line Detection/Extraction from Image Processing
3.2.1. Edge Detection
Edge detection (e.g., Sobel and zero-cross edge detectors) identifies object boundaries within images. In this study, the edges were detected on the slope map using the zero-cross edge detector; the threshold value is approximately 0 (e.g., 0.008), whereas the edges were detected at the curvature and on the openness maps using the Sobel edge detector. The Sobel edge detector returns edges at these points wherein the gradient of intensity is at the maximum.
3.2.2. Line Segment Extraction Based on the Hough Transform
In this study, the lines in the images were identified using Hough transform. The Hough transform aims to define a mapping between image and parameter spaces. The Hough function uses the parametric representation of a line:
where the function returns rho, which is the distance from the origin to the line along a vector perpendicular to the line, and theta, which is the angle in degrees between the x-axis and the vector.
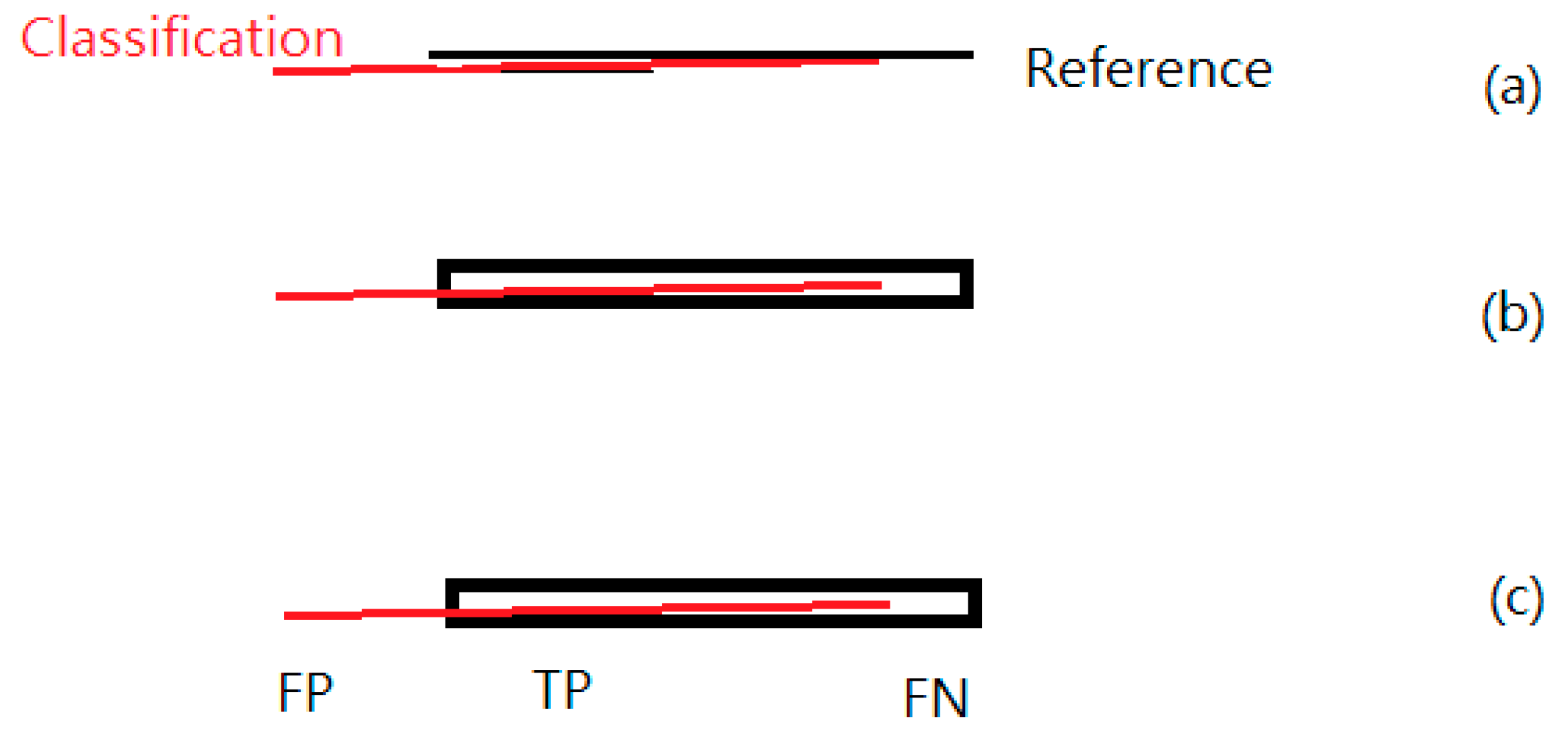
Figure 4 illustrates the reference and classification of a low wall. A 1.5 m buffer along each reference line was generated to compute the accuracy according to the DEM resolution of 1 m. The classified line is within the buffer, that is, a true positive (TP). The classified line is shorter than the buffer of reference, that is, a false negative (FN) (i.e., omission error). The classified line is longer than the buffer of reference, that is, a false positive (FP) (i.e., commission error).
3.2.3. Aggregation
Aggregation function combines three selected line features that are extracted from the slope, curvature, and openness images into an aggregated line feature:
where Line S represents the line set that is extracted from the slope image, Line C represents the line set that is extracted from the curvature image, Line O represents the line set that is extracted from the openness image, and Line Agg represents the line set that is aggregated based on the three line sets. In particular, the steps of aggregation are as follows: (1) create a line segment buffer from the slope, curvature, and openness; (2) merge the line buffers; and (3) create the centerlines with the line-merged buffers.
3.3. Rule Extraction from a Decision Tree
The detection rules are extracted from a decision tree after line detection. The decision tree is a model that predicts the membership of objects in the classes of a categorical dependent variable from their measurements on one or more explanatory variables based on machine learning [
24,
25].
The decision tree produces a tree structure by using a decision at each node based on an inequality, Xi < c, where Xi corresponds to explanatory variable i, and c is a constant value within the range of the Xi values. In this study, decision trees provide responses that are nominal, such as “wall” and “not wall.” The explanatory variables are slope, curvature, and openness in the dataset. Moreover, the classification and regression tree (CART) implementation in MATLAB was used for decision tree learning. A total of 8000 random samples were used for training. A 10-fold cross validation was used for estimating the test correct rate of the models.
4. Results and Discussion
4.1. Topographic Parameter Visualization
Figure 5 depicts the slope, curvature, and openness images based on the DEM geoprocessing. The first- and second-order derivatives of the DEM data, such as slope and curvature, led to the description of spatial features. A slope raster is derived from a DEM. Flat areas will appear white when symbolized with a grayscale, thereby highlighting the dark, steep areas. The line feature (e.g., low wall) was easily detected in the west flat area (
Figure 5a).
Anthropogenic and natural features, such as low wall and channel, became obvious when the maximum curvature was used (
Figure 5b). In natural features, areas of high positive curvature correspond to ridges, whereas areas of high negative curvature correspond to valleys. The anthropogenic features, such as roads, are characterized by low slopes, whereas the natural geomorphologic edges occur in a steep terrain in mountainous areas [
4]. However, the low wall and channel course are easily mixed in the flat area. In a large-scale map, anthropogenic features disturb geomorphometric analysis and have a disturbing effect on automated geomorphological mapping techniques [
4]. However, the low wall and channel are clearly identified from the openness map. The blue area (high negative openness) at the center of the island is a river channel; however, most of the red areas (high positive openness) are the low wall of the vegetable garden (
Figure 5c). Several places are mixed with small channels and low walls, and their blue and red lines are adjacent. In addition, the river channel from the stream flow is also identified by hydrology tools from GIS.
Multiple topographic parameter images can characterize the topographic surface texture and pattern in the study areas. A set of parameters, including shaded relief, slope, curvature, and openness from the high-resolution DEMs, can be enhanced by interpreting geomorphologies [
26]. Therefore, the further feature detection from topographic parameters will provide an effective tool for historic landscape monitoring and management.
4.2. Effect of Scale
Spatial features can be classified as ridges, channels, planes, and crest lines based on maximum curvatures [
14]. However, numerous detected features are observed from scales (i.e., moving window sizes) [
17]. In the current study, the window size may vary from three to seven cells.
Figure 6 presents the maximum curvature maps with various window sizes. The result shows that the wall in the small window size (3 × 3) was clearly marked. The wall and channel course were disorganized in window size 5 × 5 (
Figure 6b). In window size 7 × 7 (
Figure 6c), the wall features were fuzzy. Eventually, the maximum curvature map in window size 3 × 3 was used to identify low wall features.
Current curvature approaches are effective in identifying features at the right scales. For example, the features, such as channels, generally occur at multiple scales in the landscape from small creeks to large rivers. Based on the test of curvature analysis, the openness scale setting is similar to the curvature approach. If the scale of the topographic parameter from DEM correlates to the characteristics of a spatial feature, then accurate information and features can be simply subtracted from the interpolated ground elevation surface in the LiDAR elevations [
20].
Conventionally, the landscape is measured by artificial visual interpretation or by fieldwork. This study uses this approach to select different window sizes and then enhance the automation for line feature detection. The experimental results indicate that the method has the potential performance for wall landscapes, which can effectively preserve line details in the real world.
4.3. Aggregation for Wall Identification
Traditionally, the lines are classified by a user-defined threshold of topographic parameters. However, this study is free for user-defined thresholds of topographic parameters.
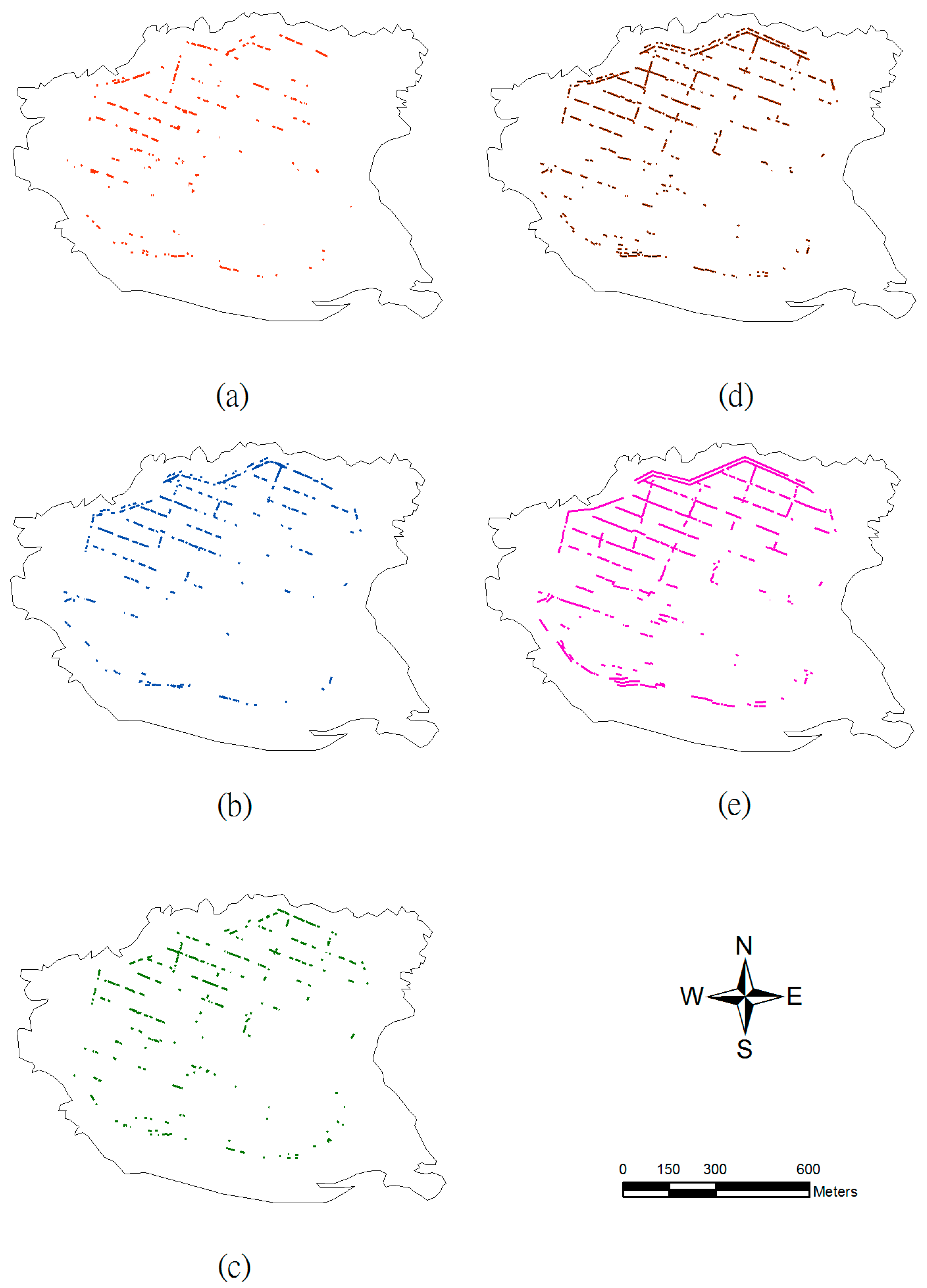
Figure 7a–c depict the wall identification from the three images based on the automatic processes, that is, the Hough transform. The accuracy in the wall detection by using only a slope, curvature, or openness image are 35%, 54%, and 42%, respectively (
Table 1). The results show that the curvature map is most useful to wall feature extraction. The curvature is the most critical factor for recognizing wall lines in the study area. The manual interpretation by an expert based on these topographic and 1 m resolution aerial images is presented in
Figure 7e. This interpretation is more complete and reliable after aggregation from the three extracted lines. The accuracy is improved by 74% (
Table 1). The performance of the automatic interpretation by combining three topographic images is better than when considering only one image (
Figure 7d). Line detection with multiple parameters was used to improve the overall accuracy of low wall identification. Line detection transforms the original image data into line features and maintains nearly adequate information content.
The previous study [
17] indicates that the critical factors of line detection are the density and precision of the LiDAR point cloud and the resolution and quality of the DEM. However, Rutzinger et al. [
17] extracted the break lines only from the curvature image of DEM. Our approach combines the multiple line features from topographic parameter maps (slope, curvature, and openness) in the rapid automatic extraction processes. In the current study, the 2D line was extracted in DEMs from the top view. These studies show the tracing and regularization of building boundary from LiDAR point clouds [
27,
28]. Moreover, the 3D line is extracted and reconstructed in multi-view images from the mobile laser scanner to complete the line segment and enhance its accuracy [
29].
4.4. Rules from the Decision Tree
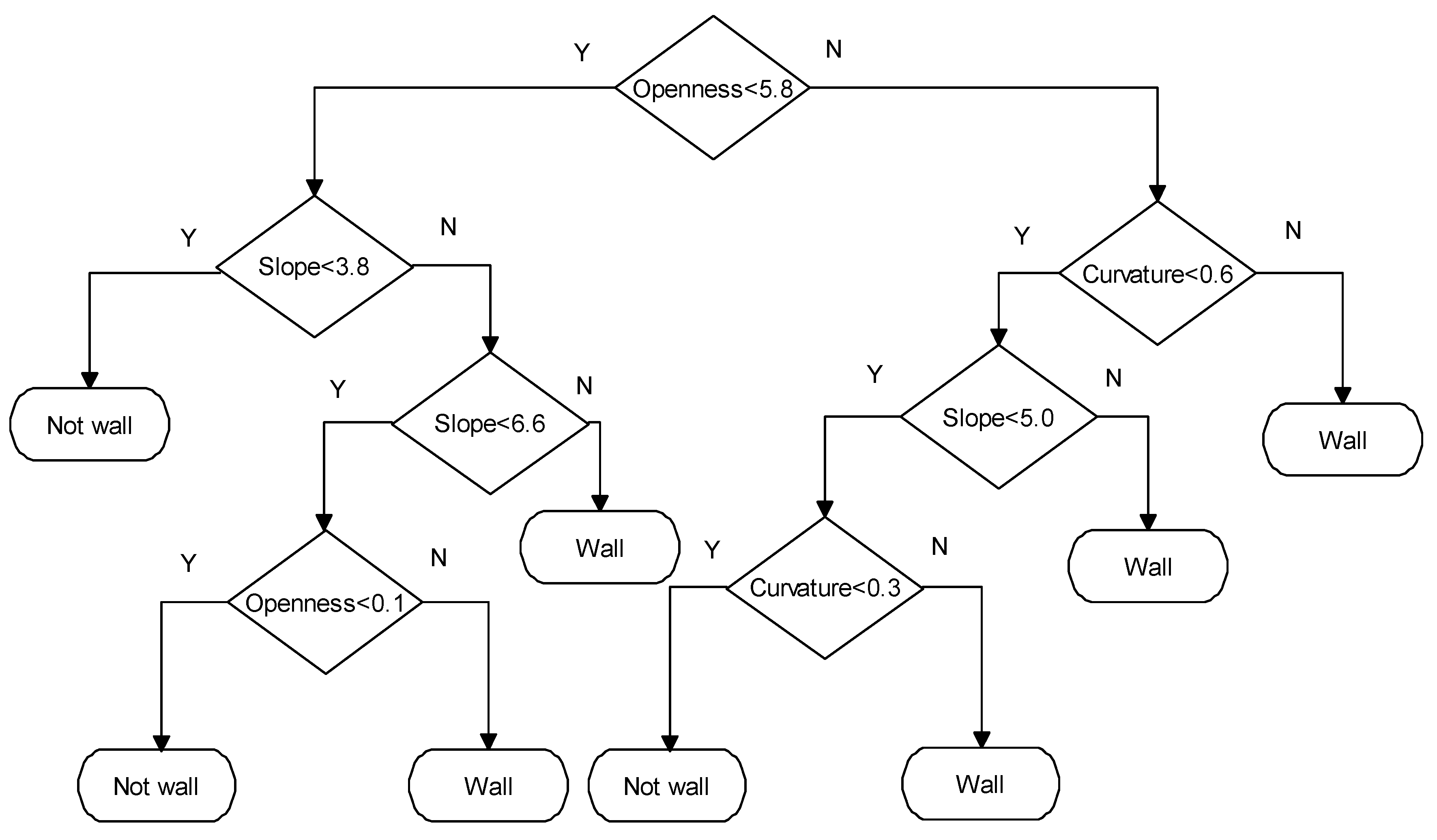
A decision tree is used to automatically classify the low wall.
Figure 8 illustrates the wall detection rule of multiple topographic parameters from the decision tree. The correct rate is 88% based on a 10-fold cross validation. The rule contains not only the single factor, but also the three parameters. The rules from the decision tree explain the necessity for considering the multiple topographical factors. This result matches our finding that multiple topographic parameters can detect the wall features. The rule details are presented in
Figure 8. The decision variable at the first level of the tree is the openness. The leaf node is a wall if the openness and the curvature are greater than 5.7 and 0.6, correspondingly. If the openness is smaller than 5.7, and the slope is smaller than 3.8°, then the leaf node is not a wall.
Table 2 summarizes the descriptive statistics of the low wall features. The average slope, curvature, and openness are 9.25°, 1.63 1/m, and 20.33, respectively. The result also matches the rule from a decision tree. Generally, a wall exists in relatively discrete high slope, positive curvature, and high positive openness when compared with a flat area.
The analysis of the decision tree separates the entire dataset into homogenous subgroups suitable for exploring and modeling through successive binary splits [
24]. The results indicate that the model assesses and provides an effective fit between low wall features and topographic parameters. The use of a decision tree is a non-parametric approach that can accommodate these interactions to avoid any assumption of linear relationships among the variables or homoscedasticity in variances [
30]. The decision tree can be considered appropriate evidence in the presence of complex relationships with multiple parameters and low wall features. A decision tree is generally more interpretable than other classifiers, such as neural networks and support vector machines, because the rules of a decision tree are combined in a cognitive manner [
25].
5. Conclusions
This study presents a rapid scheme for historical vegetable garden wall identification extracted from high-resolution LiDAR DEMs. Selected topographic parameters, such as slope, curvature, and openness, are applied and combined. This study also quantifies the effects of multiple topographic parameters on historic wall feature identification. The topographic parameters can show the features of past geographies that contain valuable information about historic features. Historical feature detection is considered a critical step toward preservation and restoration of a historical property. Generally, landscape line detection with multiple topographic parameters can reduce the confusion of anthropogenic and natural feature identification. The aggregation of three detection results from slope, curvature, and openness increases the accuracy of feature identification. The multiple topographic parameter approaches ensure the identification of historic anthropogenic features from the high-resolution DEMs. Historical feature detection from remote sensing is a powerful tool in land-use change investigations.
The proposed model considers sufficient topographic information that can effectively facilitate the identification of historic wall features. Further study will consider the unmanned aerial vehicle for collecting point clouds and spectral information of image photos. Furthermore, multi-scale parameters can be considered from machine learning for reaching highly accurate performances. Parameters, such as the ruggedness index, standard deviation of elevation, slope variability, and fractal dimension and eigenvector, will be considered additional factors. Moreover, using historical images will introduce interesting opportunities for analyzing the temporal change of the landscapes. The details and relations of the landscape will be determined because similar procedures considering 3D points will be used for extracting digital terrain or ground models from the DSM.
Acknowledgments
Thanks for enhancing the quality of the paper from the editors and anonymous reviewers. This research was funded by the Headquarters of the University Advancement at the National Cheng Kung University, which is sponsored by the Ministry of Education, Taiwan.
Author Contributions
Hone-Jay Chu contributed to idea formulation, study design, result interpretation, and the writing of the manuscript. Yu-Ching Tain and Min-Lang Huang contributed to data analysis, the reporting of results, and result interpretation. Mon-Shieh Yang and Bernhard Höfle contributed to the interpretation of the results, technical consulting, and paper editing. All authors have seen and approved the final version.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kucukkaya, A.G. Photogrammetry and remote sensing in archeology. J. Quant. Spectrosc. Radiat. Transf. 2004, 88, 83–88. [Google Scholar] [CrossRef]
- Campana, S.; Dabas, M.; Marasco, L.; Piro, S.; Zamuner, D. Integration of remote sensing, geophysical surveys and archaeological excavation for the study of a medieval mound (Tuscany, Italy). Archaeol. Prospect. 2009, 16, 167–176. [Google Scholar] [CrossRef]
- Höfle, B.; Rutzinger, M. Topographic airborne LiDAR in geomorphology: A technological perspective. Z. Geomorphol. Suppl. Issues 2011, 55, 1–29. [Google Scholar] [CrossRef]
- Rutzinger, M.; Hoefle, B.; Vetter, M.; Pfeifer, N. Digital terrain models from airborne laser scanning for the automatic extraction of natural and anthropogenic linear structures. Geomorphol. Mapp. Methods Appl. 2011, 15, 475–488. [Google Scholar]
- Tomljenovic, I.; Höfle, B.; Tiede, D.; Blaschke, T. Building Extraction from Airborne Laser Scanning Data: An Analysis of the State of the Art. Remote Sens. 2015, 7, 3826–3862. [Google Scholar] [CrossRef]
- Sohn, G.; Dowman, I. Building extraction using Lidar DEMs and Ikonos images. Int. Arch. Photogramm. Remote Sens. 2003, 34, 37–43. [Google Scholar]
- Poullis, C.; You, S. Delineation and geometric modeling of road networks. ISPRS J. Photogramm. Remote Sens. 2010, 65, 165–181. [Google Scholar] [CrossRef]
- White, R.A.; Dietterick, B.C.; Mastin, T.; Strohman, R. Forest roads mapped using LiDAR in steep forested terrain. Remote Sens. 2010, 2, 1120–1141. [Google Scholar] [CrossRef]
- Ma, R. DEM Generation and Building Detection from LIDAR Data. Photogramm. Eng. Remote Sens. 2005, 71, 847–854. [Google Scholar] [CrossRef]
- Meng, X.; Currit, N. Morphology-Based Building Detection from Airborne LIDAR Data. Photogramm. Eng. Remote Sens. 2009, 75, 437–442. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. A 3 × 3 Isotropic Gradient Operator for Image Processing. In Pattern Classification and Scene Analysis; Sobel, I., Feldman, G., Eds.; Wiley: New York, NY, USA, 1973; pp. 271–272. [Google Scholar]
- Ballard, D.H. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognit. 1981, 13, 111–122. [Google Scholar] [CrossRef]
- Wood, J. The Geomorphological Characterization of Digital Elevation Models; University of Leicester: Leicester, UK, 1996. [Google Scholar]
- Evans, I.S. An integrated system of terrain analysis and slope mapping. Z. Geomorphol. Suppl. 1980, 36, 274–295. [Google Scholar]
- Peucker, T.K.; Douglas, D.H. Detection of surface-specific points by local parallel processing of discrete terrain elevation data. Comput. Graph. Image Process. 1975, 4, 375–387. [Google Scholar] [CrossRef]
- Rutzinger, M.; Hoefle, B.; Kringer, K. Accuracy of automatically extracted geomorphological breaklines from airborne LiDAR curvature images. Geogr. Ann. Ser. A Phys. Geogr. 2012, 94, 33–42. [Google Scholar] [CrossRef]
- Riegl Laser Measurement Systems GmbH. LMS-Q680i Data Sheet. Available online: http://www.riegl.com/uploads/tx_pxpriegldownloads/10_DataSheet_LMS-Q680i_28-09-2012_01.pdf (accessed on 3 November 2017).
- Terrasolid Ltd. Terrascan Data Sheet. Available online: http://www.terrasolid.com/products/terrascanpage.php (accessed on 3 November 2017).
- Koenders, R.; Lindenbergh, R.C.; Storms, J.E.; Menenti, M. Multiscale curvatures for identifying channel locations from DEMs. Comput. Geosci. 2014, 68, 11–21. [Google Scholar] [CrossRef]
- Luo, W.; Li, X.; Di, L.; Stepinski, T.F. Web Service for Extracting Terrain Openness from DEM Data. In Proceedings of the 17th International Conference on Geoinformatics, Fairfax, VA, USA, 12–14 August 2009; pp. 1–5. [Google Scholar]
- Yokoyama, R.; Shirasawa, M.; Pike, R.J. Visualizing topography by openness: a new application of image processing to digital elevation models. Photogramm. Eng. Remote Sens. 2002, 68, 257–266. [Google Scholar]
- Chiba, T.; Kaneta, S.I.; Suzuki, Y. Red relief image map: new visualization method for three dimensional data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1071–1076. [Google Scholar]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Kingsford, C.; Salzberg, S.L. What are decision trees? Nat. Biotechnol. 2008, 26, 1011–1013. [Google Scholar] [CrossRef] [PubMed]
- Chu, H.J.; Wang, C.K.; Huang, M.L.; Lee, C.C.; Liu, C.Y.; Lin, C.C. Effect of point density and interpolation of LiDAR-derived high-resolution DEMs on landscape scarp identification. GIScience Remote Sens. 2014, 51, 731–747. [Google Scholar]
- Sampath, A.; Shan, J. Building boundary tracing and regularization from airborne LiDAR point clouds. Photogramm. Eng. Remote Sens. 2007, 73, 805–812. [Google Scholar] [CrossRef]
- Lee, J.; Han, S.; Byun, Y.; Kim, Y. Extraction and regularization of various building boundaries with complex shapes utilizing distribution characteristics of airborne LIDAR points. ETRI J. 2011, 33, 547–557. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.; Cheng, J.; Chen, B.; Jia, F.; Chen, Z.; Li, J. Line segment extraction for large scale unorganized point clouds. ISPRS J. Photogramm. Remote Sens. 2015, 102, 172–183. [Google Scholar] [CrossRef]
- Chu, H.J.; Lin, C.Y.; Liau, C.J.; Kuo, Y.M. Identifying controlling factors of ground-level ozone levels over southwestern Taiwan using a decision tree. Atmos. Environ. 2012, 60, 142–152. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).