1. Introduction
Real-world traffic flow data play a key role in traffic system analysis and have attracted the attention of researchers from various fields. For example, some studies were focused on modeling traffic models and theories from both microscopic and macroscopic perspectives, (e.g., [
1,
2,
3,
4,
5,
6,
7,
8]), while other studies concentrated on the theoretical urban mobility analysis (e.g., [
9]). However, because of data concerns, many of the early studies were limited to either small scales (small areas in a city or small number of mobile objects) or theoretical levels. That is, such studies could not reach the whole urban scale and are not suitable for overall analysis of a city. Due to recent advances in information technology, particularly with the development and widespread adoption of location-aware devices such as GPS and cell phones, it has become feasible and easier to collect moving object data in a flexible and cost efficient manner. Consequently, many studies have been conducted to capture the characteristics of mobility patterns using such mobility data sets (e.g., [
10,
11,
12]).
The trajectory method is perhaps the most frequently used method under Hägerstrand’s [
4] time geography framework. For example, Spaccapietra
et al. [
11] proposed a conceptual model to structure the whole trajectory of a moving object into countable semantic units, such as moves and stops, where more semantic annotations can be attached. Based on this conceptual model, Bogorny
et al. [
10] aggregated the GPS points at important geographic places as stops, and then aggregated the GPS points between two consecutive stops as moves. In doing so, raw trajectories are decomposed into semantic segments, based on which the authors proposed a data mining query langue to extract meaningful, understandable and useful patterns. Yan
et al. [
12] presented a hybrid model and computing platform to extract and understand the spatio-semantic patterns of whole trajectories. Although the trajectory method is successful in some aspects, when the GPS points are connected together to form one trajectory object, in most existing studies, only the start and end time and spatial attributes of the trajectory were emphasized, while the temporal dimension in other GPS points was not well considered. Thus, the temporal dimension is neglected to some extent. Therefore, this method is unsuitable for spatio-temporal clustering analyses, which dynamically take into account the time dimension of each GPS point [
6].
There has been much research dedicated to generating spatio-temporal clusters. For example, Kalnis
et al. [
6] formally defined a spatio-temporal cluster as a sequence of spatial clusters that are continuous over time and consecutive in space (shares some moving objects). Based on this definition, the authors provided three methods and algorithms to identify spatio-temporal clusters in mobility data set. Hwang
et al. [
13] claimed that the physical meaning of such spatio-temporal clusters could be unclear in cases where the spatial clusters located near the start and end of these spatio-temporal clusters contain totally different sets of objects. Thus, the authors proposed a semantically clear definition of spatio-temporal clusters as well as corresponding approaches to identify them. Rather than to create clusters based on traditional distance, the authors [
14] proposed an improved method to generate spatio-temporal clusters by extending the distance measure to be a function of the position history of the moving objects. However, these studies are limited in applications specific to their methodologies, and do not attempt to analyze urban mobility.
Studies that attempt to analyze spatio-temporal clusters and urban mobility patterns using mobility data set are becoming more prominent. For instance, Cao
et al. [
15] defined the problem of mining periodic patterns and proposed corresponding algorithms to retrieve the periodic patterns in mobility data set. Bazzani
et al. [
16] analyzed the issue of urban mobility by testing the probability distribution of path lengths, the activity downtime and degree of mobility data set in the Florence urban area. Their study found the emergence of robust statistical laws. Hoque
et al. [
17] explored taxicab mobility patterns by analyzing some attributes of yellow cab GPS data in the San Francisco area, such as instantaneous velocity profile, spatio-temporal distribution, clustering and hotspots. However, the instantaneous velocity analysis is based on a single taxicab and cannot reflect the overall traffic trend. Moreover, the clusters were not spatio-temporal because the points were wireless connectivity between mobile taxicabs, pickup and drop off locations.
Although some of the previously mentioned studies were involved in the analysis of traffic mobility patterns, the spatio-temporal clustering method was seldom adopted, especially from the perspectives of traffic congestion and scaling law. Furthermore, the size of collected mobility data set is limited and the taxicabs always stay at preferred locations waiting for phone calls from customers. In this paper, we use an intensive mobility data set, which includes more than 85 million taxicab GPS points. These data were collected from over 11 thousand taxicabs during six days in Wuhan city, Hubei, China. The taxicabs are continuously driven on the road 24 h per day (with drivers changing shifts) to maximize profits for the company. Thus, the mobility data set used in this study are very reliable sensors to traffic behavior and are more unique than previously used data in terms of mobility analysis. We analyzed the overall speed pattern of all taxicabs and selected low-speed and stop taxicab GPS points to generate spatio-temporal clusters. This indicated the stop-and-go movement pattern in real-world traffic congestions. These spatio-temporal clusters were found to demonstrate a scaling property. It means the traffic behavior is a self-organized complex system ([
18,
19,
20]), where global complex mobility patterns are derived from the bottom at the level of the vehicles. The spatio-temporal clusters in the scaling hierarchies indicate the degree of traffic congestions. Combining the scaling law and spatio-temporal clusters, we further analyzed the traffic mobility patterns in a quantitative manner.
The remainder of the paper is organized as follows: in
Section 2, the floating car data is described and the conceptual data model presented; we then conduct GPS error analysis and elimination. In
Section 3, the temporal patterns of the floating car data are analyzed and then the low-speed taxicab GPS points for generating spatio-temporal clusters separated.
Section 4 provides the methodology on how to measure the degree of traffic congestion from the spatio-temporal clusters. In
Section 5, the model is applied to real data and followed by a discussion of the results. Lastly,
Section 6 presents the paper’s conclusions and points to future work.
2. Floating Car Data
Real-world mobility datasets play a key role in this research. The original floating car data were collected from over 11 thousand taxicabs in Wuhan, Hubei, China, at regular intervals (average 20–60 s) during the courses of six days (
c.f., [
21] for more details). There are more than 85 million records in total (over 14 million per day), with attributes of timestamp, car ID, x, y, speed and angle. According to the description of the original mobility dataset, the speed is the instant speed of the taxicab, recorded by the machine equipped on the taxicab. The angle is the azimuth angle of the taxicab, and it is not used in this paper. Because human movement at the city level is constrained by road networks, the urban free space at the city level refers to the space connected by road networks and reached by automobiles. As all the taxicabs are continuously being driven, each road segment in the road network will be passed. Thus, the whole urban free space will be finally covered by the movement of taxicabs. This can be visualized and justified by overlapping all road segments with all GPS points in the city using a GIS spatial analytical function.
2.1. Data Models
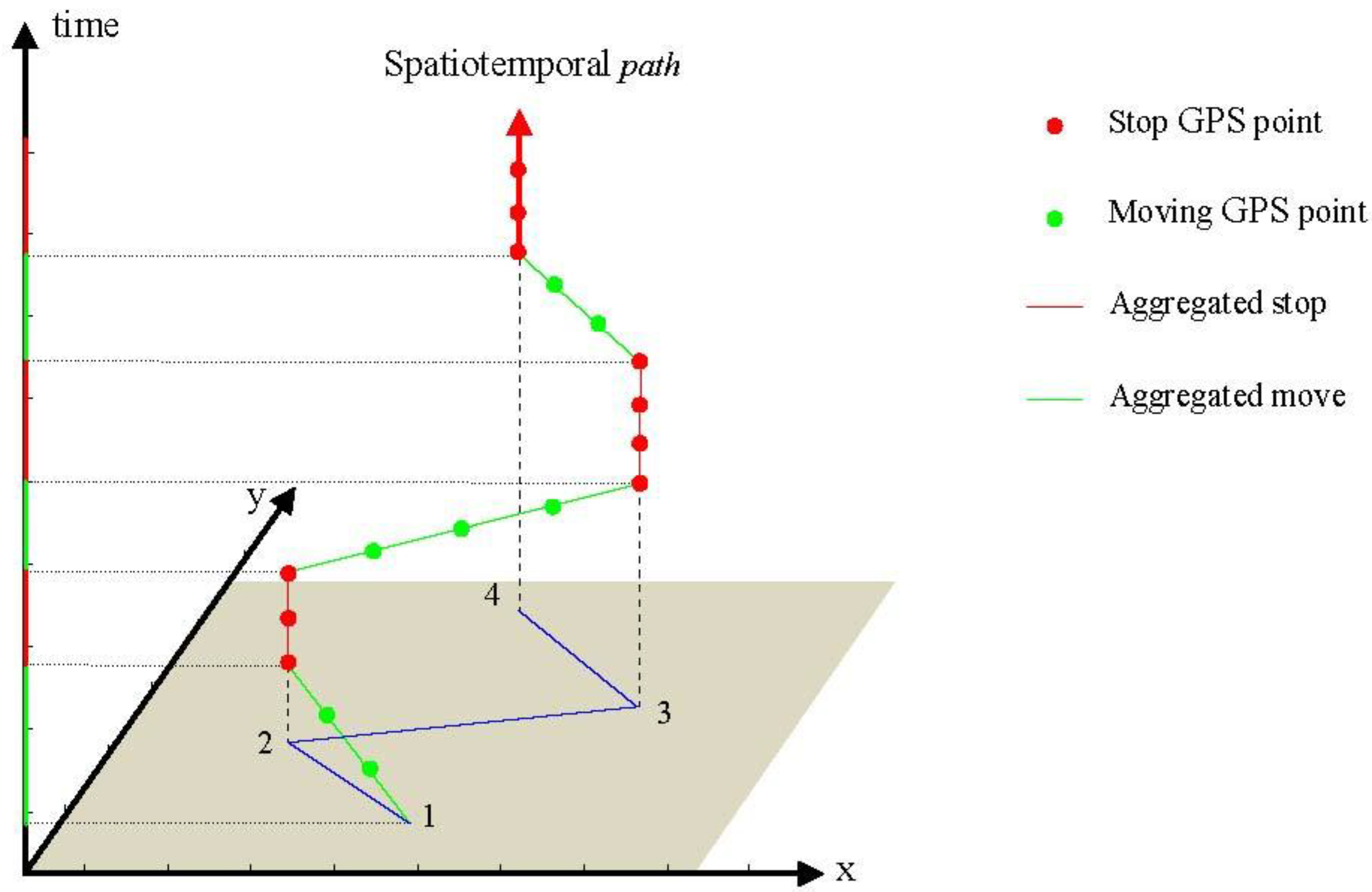
The original floating car data are stored in self-defined text files. Based on the car ID and timestamp, it is simple to filter the sequence of records for each taxicab. The GPS points are strictly sorted by timestamp and connected one by one from the first record. The sorted and connected sequence of records (GPS points) for one taxicab indicate evolving positions in both time and space and is referred to as a trajectory or spatio-temporal path. A spatio-temporal path based on a slice of real taxicab trajectory is visualized in
Figure 1. The green and red points are taxicab GPS points whose instantaneous velocity is greater than and equal to zero, respectively. Accordingly, the three green and three red segment lines represent the aggregated/semantic moves and stops, respectively. For the sake of intuitive visual effects, they are simplified as segment lines.
Figure 1.
Data model representation of a spatio-temporal path of taxicab.
Figure 1.
Data model representation of a spatio-temporal path of taxicab.
It is evident that every aggregated stop or move has a lifetime with two time tags (begin time and end time), which are continuous in time during the entire spatio-temporal path (
Figure 1). For single stop or moving GPS points, there are many coexisting points from floating car data at each time slice of a day, which can be presented in snapshots.
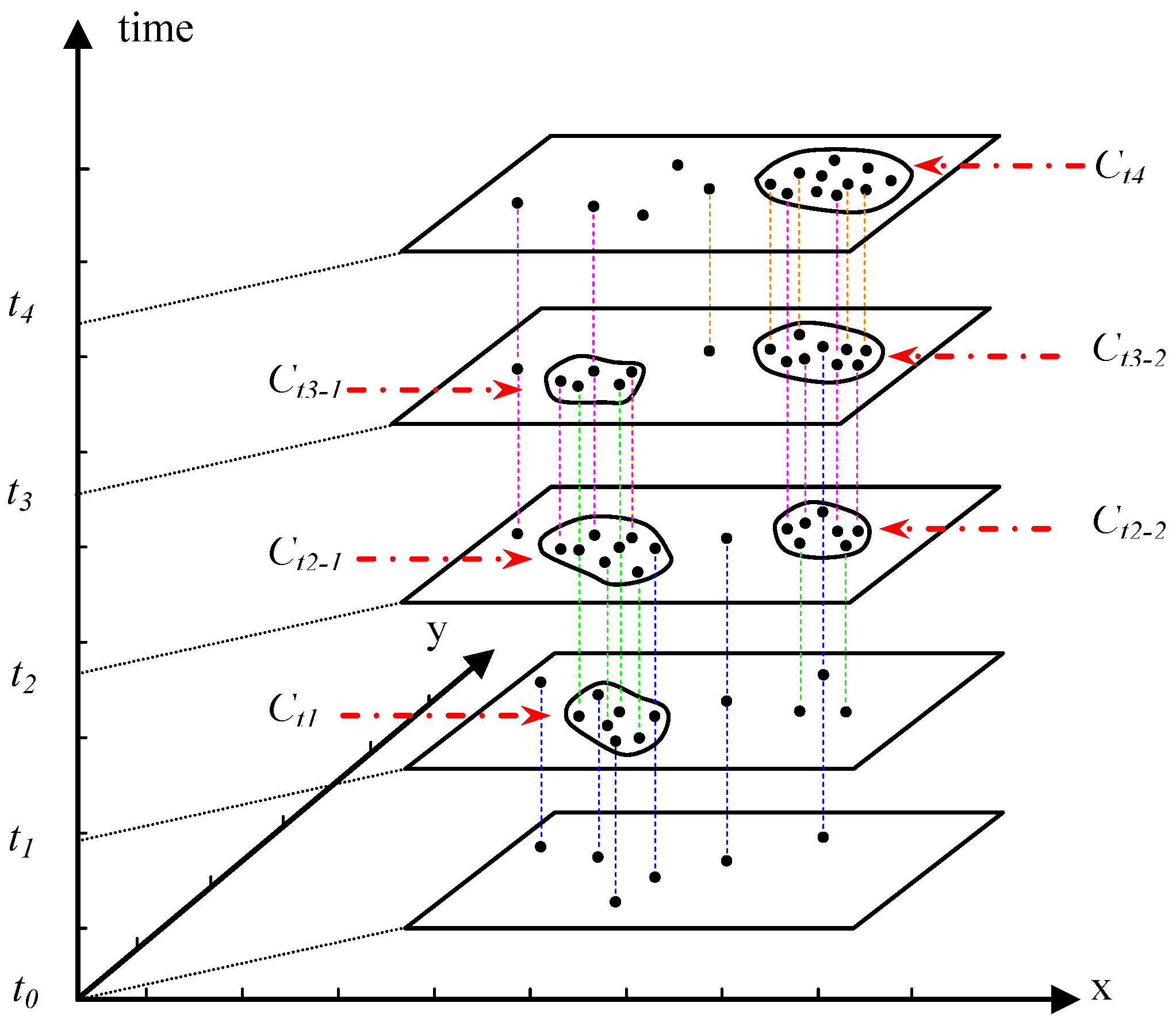
Figure 2 shows five snapshots, where the black points represent coexisting GPS points.
Figure 2.
Notational process of spatio-temporal clustering (Note: the blue, green, pink and orange represent different lifetimes of stops that start from t0, t1, t2 and t3, respectively).
Figure 2.
Notational process of spatio-temporal clustering (Note: the blue, green, pink and orange represent different lifetimes of stops that start from t0, t1, t2 and t3, respectively).
It is easy to understand spatial clusters of static geometric points [
22]: given a prescribed distance/radius, one begins from any geometric point and continues searching for neighbors within the distance until no neighbors remain. In this way, we obtain a serial of grouped points,
i.e., a spatial cluster. By applying this cluster algorithm to the GPS points in each snapshot, we can obtain six spatial clusters at timelines
t1,
t2,
t3 and
t4 (
Figure 2) on the left and right, respectively. These spatial clusters are
Ct1,
Ct2–1,
Ct2–2,
Ct3–1,
Ct3–2 and
Ct4, where C represents cluster and subscript l and r indicate clusters on the left and on the right, respectively. Obviously, clusters [
Ct1,
Ct2–1,
Ct2–2] and [
Ct3–1,
Ct3–2,
Ct4] are not only continuous over time but also overlap in space. The boundaries of spatial clusters can be defined by using the convex hull method. Such groups of clusters are called spatio-temporal clusters. If we connect the boundaries of spatio-temporal clusters, it is similar to distorting three-dimensional cylinders. The evolution of the spatio-temporal cluster can be trackable based on a simple tree-like data model, where the root is the spatio-temporal cluster and the leaves are the sorted spatial clusters.
2.2. GPS Error Analysis and Elimination
The ideal floating car data should be continuous in terms of time intervals between each pair of continuous GPS points and the coordinates of each GPS point should be accurate compared with the actual position of the taxicab. However, there exist GPS errors caused by either blockage of the GPS signal or hardware/software bugs during the data collection process. To eliminate such errors, the following measures were taken.
The GPS points were first filtered that deviate far away from the bounding box of the study area (Wuhan, China). Such error points are outliers and there were 66,658 of them (0.078% of all) in total. Such errors could be caused both by blockage of GPS signal and hardware/software bugs. Then, the GPS points with speed greater than a set limit (such as 150 km/h) were removed, which are obviously errors. There were only 4,174 records (0.005% of all) in six days attributed to high speeds. Although the percentage of such error associated with the GPS points varies with the selection of a different speed limit, the change is too small to be expected to affect the overall analysis significantly.
The sampling time interval for the floating car data is 20–60 s on average. If the time interval between two consecutive GPS points is greater than 60 s, then it could be due to either the loss or delay of a GPS signal, or the driver turning off their GPS device or taxicab. If the time interval between two consecutive GPS points is too long (
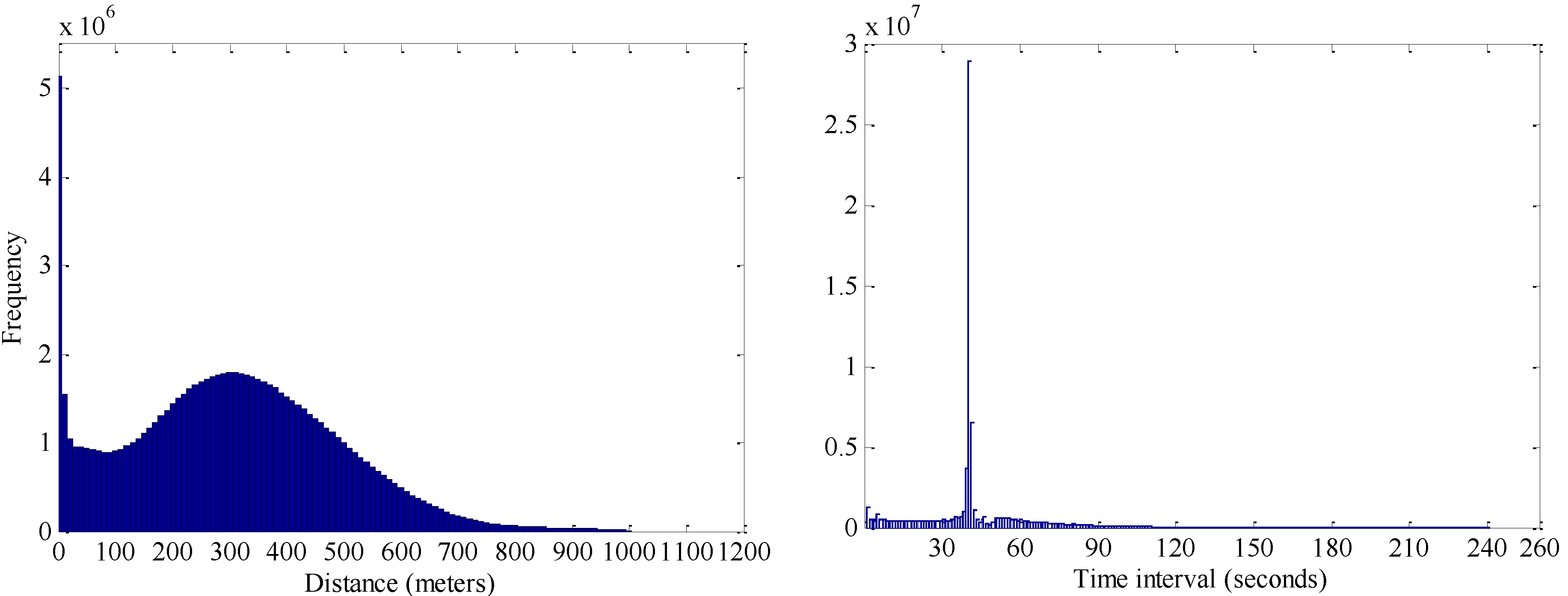
i.e., greater than a time threshold), then one cannot know the movement of the taxicab during this time period. Therefore, the trajectory should be split into different parts at such GPS points. In order to decide what values to choose for such thresholds, we calculated all the time intervals and geometric distances between all pairs of two consecutive GPS points in the trajectories of taxicabs. The mean value of all time intervals is 65 s. It was found that the percentages of the time intervals that were less than 60, 120, 180 and 240 s (
i.e., 1, 2, 3 and 4 min) were 82.2%, 95.8%, 97.8% and 98.4%, respectively. Similarly, the mean value of all geometric distances is 308 m, and the percentages of geometric distances that were less than 300, 500, 800 and 1,000 m were 50.0%, 85.0%, 98.6% and 99.6%, respectively. Obviously, the percentages around the thresholds of 4 min and 1 km are very stable and absolute majorities (
Figure 3).
Figure 3.
Histogram of distances (left panel) and time intervals (right panel) of all pairs of consecutive GPS points less than thresholds.
Figure 3.
Histogram of distances (left panel) and time intervals (right panel) of all pairs of consecutive GPS points less than thresholds.
According to the above analysis, we set up a standard and developed a simple program to eliminate such errors. For instance, if the time interval and geometric distance between two consecutive GPS points were greater than 4 m and 1 km respectively, then it meant that the GPS signal was discontinuous during this time period. If so, then the trajectory was split into different parts, because movement of the taxicab during this time period was unknown. Vice versa, if both time interval and geometric distance are less than their threshold, then they are considered continuous points over time and space. In doing so, the errors in floating care data can be efficiently and effectively reduced.
4. Geographic Hierarchical Structures and Their Implications
In this section, we briefly introduce the concepts of and relationships among heavy-tailed distributions, scaling property and geographic hierarchical structures, with particular focus on how they can be applied to this research. In this paper, heavy-tailed distributions are restricted to some special nonlinear relationships between a quantity and its probability, which can be described as power law, lognormal, exponential, power law with an exponential cutoff and stretched exponential [
23]. In essence, the physical meaning behind a heavy-tailed distribution is that objects with small size are extremely common, while things with large sizes are extremely rare [
24]. The sizes mean the quantified attributes of the objects in a scaling phenomenon. For example, the magnitude of earthquakes. The large and small objects indicate different groups in the head and tail, respectively. As what Adamic [
25] noted, the shared feature of heavy-tailed distributions describes the division of objects into groups, which suggest a hierarchical structure from a statistical perspective.
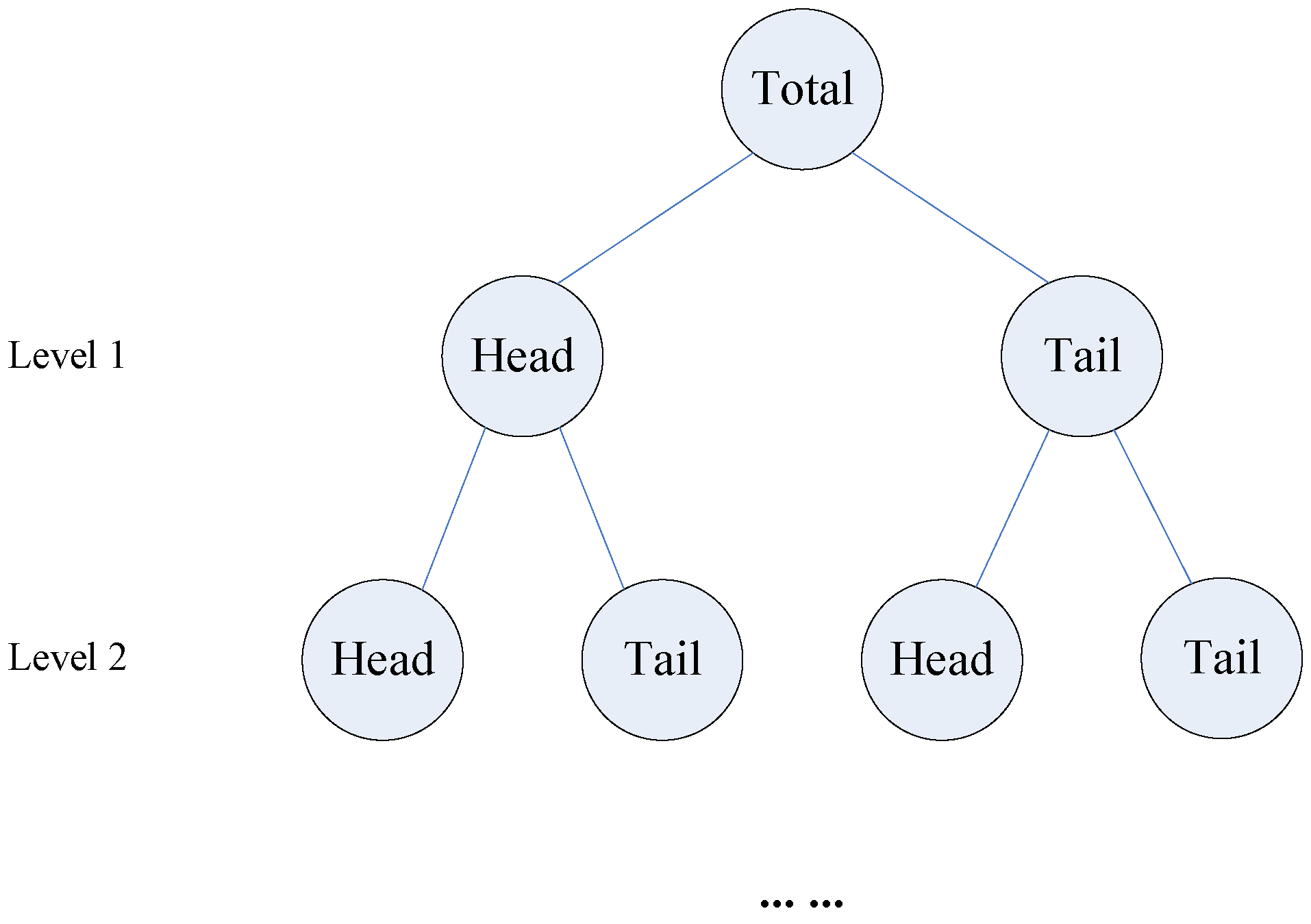
More specifically, Jiang and Liu [
26] proposed that, in the urban environment, if all values of measured geographic objects follow a heavy-tailed distribution, then “the mean (m) of the values can divide all the values into two parts: a high percentage in the tail, and a low percentage in the head”. The regularity is termed as the head/tail division rule. Based on this rule, the two-tier hierarchical structure (head and tail) of geographic objects (or representations) can be objectively and naturally obtained in an iterative way (
Figure 5). The obtained two-tier hierarchical structures (
Figure 5) can reveal geographic implications in different urban environmental contexts. For instance, Liu and Jiang [
27], found that the area and dangling lines of blocks (cellular structure) of road networks in a city followed a heavy-tailed distribution, and thus can be grouped into two-tier hierarchical structures at different levels. The larger the area and more dangling lines a block has, the lower the density and more inconvenient transportation will be, which means urban sprawl is occurring. In doing so, the location of the urban sprawl patches (blocks) and the level of sprawling degree were identified.
Figure 5.
The two-tier hierarchical structure in heavy-tailed distributions.
Figure 5.
The two-tier hierarchical structure in heavy-tailed distributions.
In this paper, spatio-temporal clusters were generated as geographic representations to represent real-world traffic congestion. The attributes of the spatio-temporal clusters are found to follow a power law distribution (for more details, please refer to the middle of next section), which indicated the presence of scaling from a statistical physics perspective [
23]. Therefore, we can obtain the hierarchies of spatio-temporal clusters, and relate them to urban infrastructure such as road networks to explore underlying implications for further analysis in the next section.
5. Results and Discussion
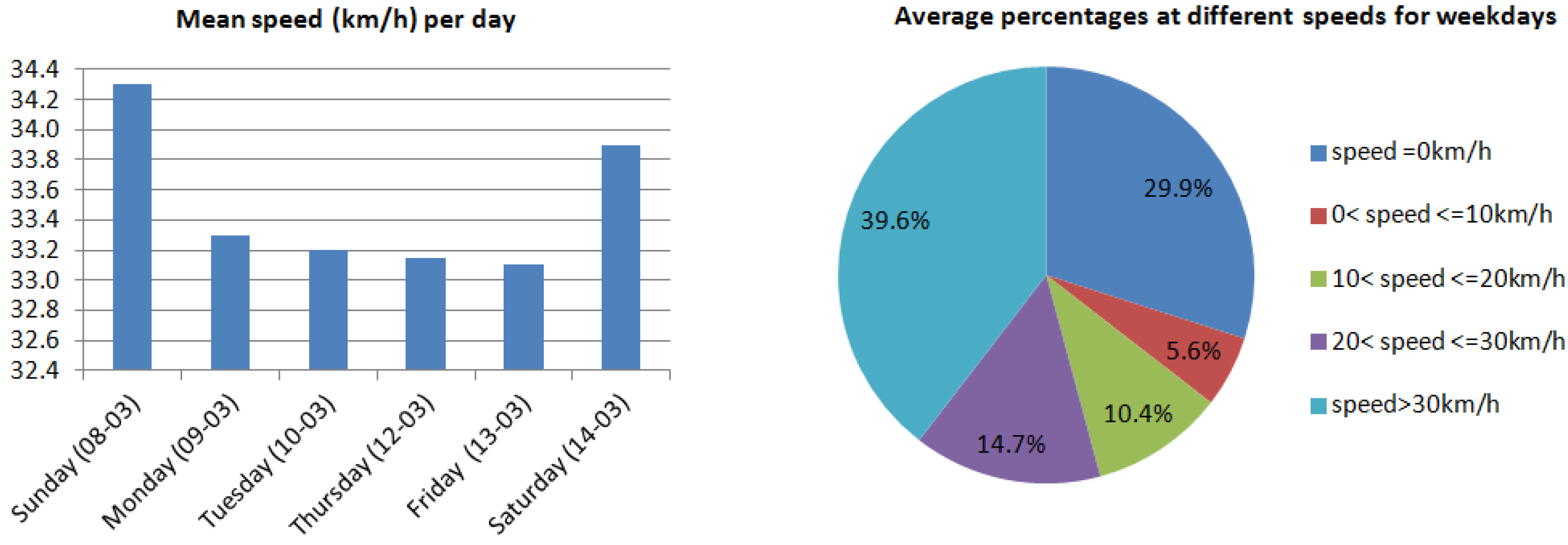
The mean speed of all GPS points as well as the percentage of taxicabs at different speeds for the six days, were calculated per day. The mean speed (on the left panel of
Figure 6) represents the average value of all GPS speed points in each day, where the ones on the weekends are higher than the ones during workdays. It could be the reflection of how traffic is congested. There is also a downward trend between Monday and Friday. We conjecture that it reflects the rhythm of city life: traffic congestion on Fridays is typically higher than that on Mondays. However, the percentage of taxicabs at different speeds during the weekdays (on the right panel of
Figure 6) and weekends are very similar and stable, with no obvious trend. The low-speed GPS points (speed less than 20 km/h) occupied around 16% of all data.
Figure 6.
Mean speeds and average percentages of taxicabs at different speeds.
Figure 6.
Mean speeds and average percentages of taxicabs at different speeds.
As analyzed in
Section 2, a speed of 20 km/h was used as the threshold speed to separate low-speed GPS points from normal-speed ones. Noticeably, in terms of the transferability, the threshold speed is not expected to be universal. Instead, it depends on the result obtained via the above approach applied to the corresponding mobility data set in different urban environments. These low-speed GPS points are not simply selected from the GPS points whose speeds are less than 20 km/h. As shown in
Figure 1, the single GPS points can be aggregated into moves and stops, which are located alternately in the trajectory. If all the speeds of the GPS points in an aggregated move were less than 20 km/h, then these GPS points were selected as low-speed points. Such GPS points were accompanied by stop ones, and therefore reflected the stop-and-go traffic pattern. On the left panel of
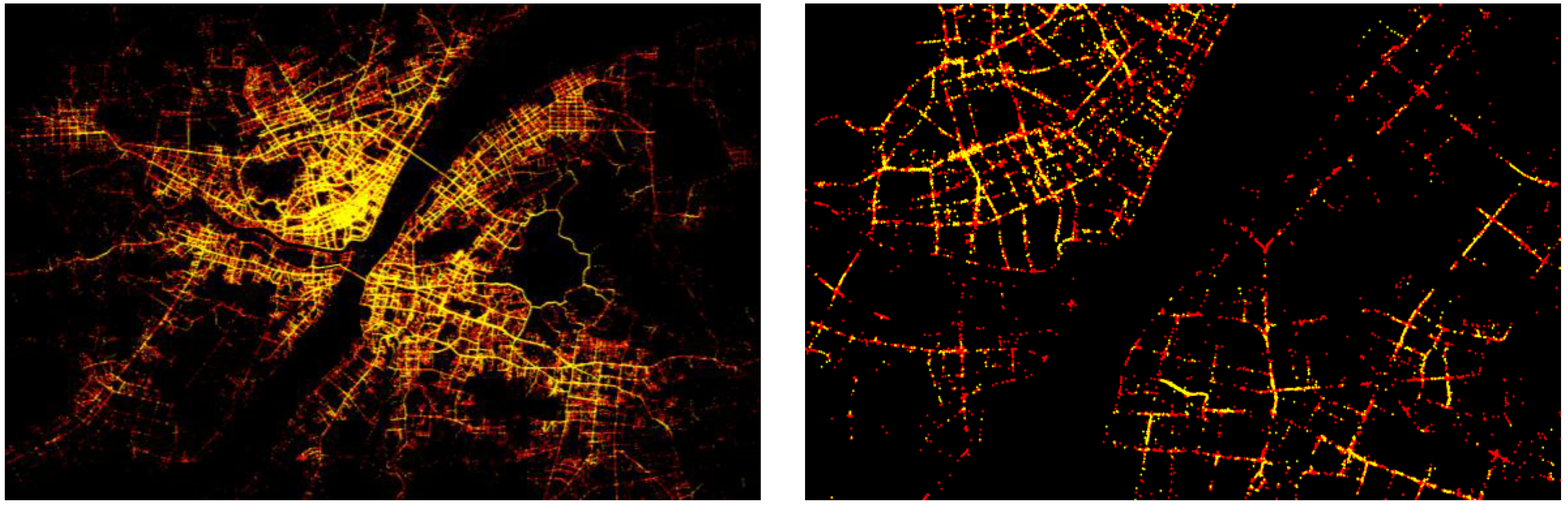
Figure 7 are the geometric points of low-speed and stop GPS points during the daytime on Monday 9 March in Wuhan, China. Although the low-speed and stop points cover the urban space, due to the large amount of points (over 4.6 millions), it is hard to visually tell low-speed points (front in yellow) from the stop points (back in red). On the right panel of
Figure 7 are the low-speed and stop points during rush hour at 8:00 AM at the city center area, where we can clearly see the low-speed and stop points closely accompany one another, indicating the stop-and-go traffic pattern.
Figure 7.
Low-speed (front in yellow) and stop (back in red) GPS points during the time of day on Monday (9 March) (left panel) and at 8:00 AM (right panel).
Figure 7.
Low-speed (front in yellow) and stop (back in red) GPS points during the time of day on Monday (9 March) (left panel) and at 8:00 AM (right panel).
Based on these stop and low-speed GPS points, spatio-temporal clusters can be generated in two steps: first generate spatial clusters based on coexisting GPS points at different time slices (snapshots,
c.f.,
Figure 2), second connect spatial clusters which are continuous over time and space to form spatio-temporal clusters. Taxicabs drive and stop continuously 24 h (
i.e., 24 × 3,600 = 86,400 s) per day. Because the average sampling time interval for the floating car data is 20–60 s, therefore, 20 s is adopted as the minimum time resolution to divide the time of each day into 86,400/20 = 4,320 time slices. That is, all the GPS points in each day can be mapped to 4,320 snapshots according to their lifetime, each of which included a group of coexisting GPS points. Before applying the above algorithms to generate spatial clusters in each group of coexisting GPS points (snapshot), the clustering distance/radius must be defined. Twenty meters was empirically selected as the radius. This is because in real-world traffic congestion, vehicles are very close to each other, and besides taxicabs, there are also other vehicles on the road, such as public buses and personal cars. That is, if the distance between vehicles is longer than 20 m, there is very small chance for vehicles to be congested.
All spatial clusters were generated for Monday 9 March 2009. The maximum size of spatial clusters (i.e., the number of clustered taxicab GPS points) reached 215, which meant that 215 taxicabs stopped at the same time and place. Based on these obtained spatial clusters, we further generated the corresponding spatio-temporal clusters by connecting spatial clusters that were continuous over time and overlapped in space. Two measures can be used to describe a spatio-temporal cluster: (1) the time duration (lifetime), which begins from the timeline of the first spatial cluster and ends at the timeline of the last spatial cluster, and (2) the number of all taxicab GPS points, which is the sum of the number of GPS points of the consecutive spatial clusters inside the spatio-temporal cluster. Generally speaking, a low-density value of vehicles in a short time span implied a normal state of the traffic system. Considering that the average traffic light duration is 2 min, spatio-temporal clusters whose lifetimes are less than 2 min and are of a low density within a short time frame, are considered therefore to be a normal traffic state. Thus, the spatio-temporal clusters whose lifetimes are greater than 2 min were adopted to analyze the mobility patterns.
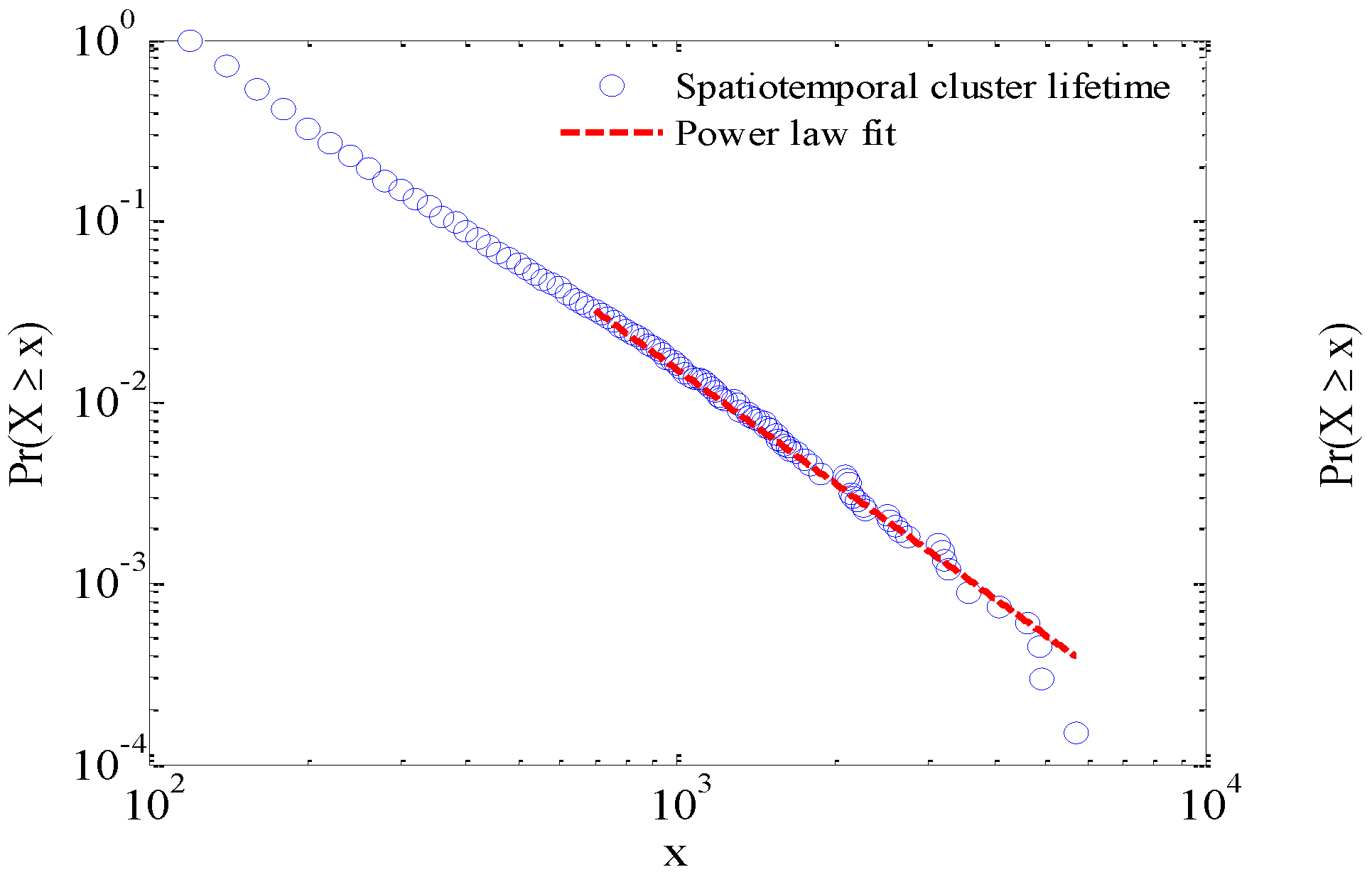
Figure 8.
Power law distribution of lifetime and size of spatio-temporal clusters.
Figure 8.
Power law distribution of lifetime and size of spatio-temporal clusters.
Interestingly, it was found that the lifetime and size of the traffic congestions both demonstrated a power law distribution (
Figure 8), which indicates the presence of scaling as well as a strong hierarchical structure as mentioned in
Section 4. This means that the traffic congestions are not evenly distributed. Instead, it demonstrates a scaling hierarchy, which is a key feature of complex urban systems and that of traffic systems. Traffic congestions were visualized according to their lifetimes during the rush hours on Monday in
Figure 9, where the red represents the longest periods of traffic congestion and the blue means the shortest ones. These traffic congestion periods were generated based on the low-speed and stop GPS points in
Figure 7. In contrast to
Figure 7, the hierarchical structures and spatio-temporal distributions of traffic congestion in urban environments can be visually and quantitatively assessed in
Figure 9.
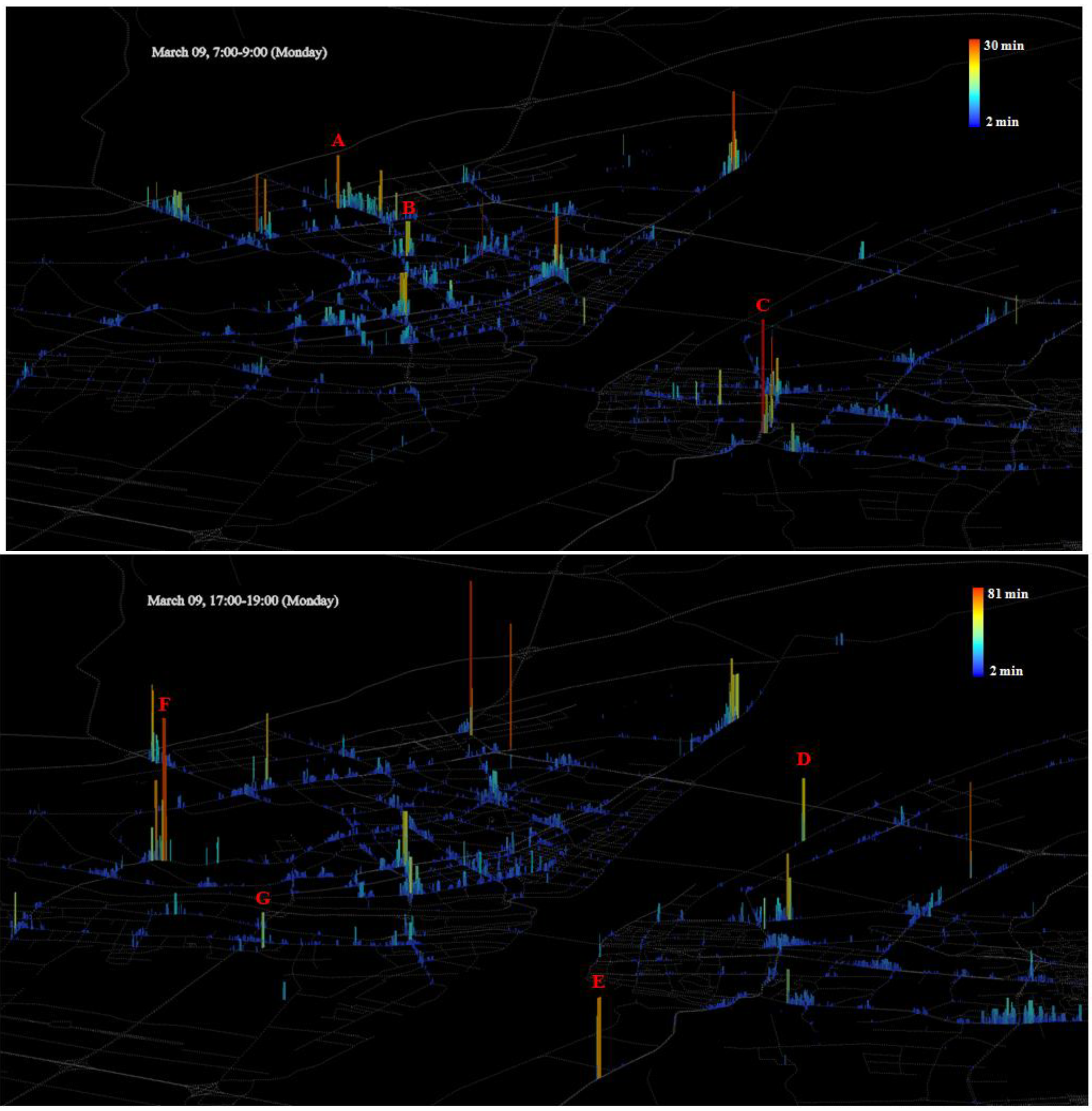
Figure 9.
Spatio-temporal clusters visualized according to their lifetime during rush hour: the more red, the longer the duration of traffic congestion.
Figure 9.
Spatio-temporal clusters visualized according to their lifetime during rush hour: the more red, the longer the duration of traffic congestion.
In
Figure 9, the hierarchies of spatio-temporal clusters are unevenly distributed in a multi-core structure, whose spatial patterns are centralized towards the downtown area during the morning rush hour period from 7:00–9:00 (upper panel in
Figure 9), but decentralized during the rush hour period from 17:00–19:00 (lower panel in
Figure 9). The detected traffic congestions based on traffic GPS points objectively reflect traffic mobility patterns in Wuhan city. The areas of long spatio-temporal clusters indicate heavy traffic congestion, which means that the traffic condition around there is worse than other areas. It was found that areas of long spatio-temporal clusters mostly happened on major roads, such as ErHuanXian, Zhongshan Road, Jinghan Road and Huangpu Road according to their road levels and local popularity. That is, most of the heavily congested areas are coincident with road network structures. Despite that, there exists some difference between morning and afternoon rush hours. For example, some congestion areas such as A and B (upper panel in
Figure 9) in the city center during morning rush hours disappear during afternoon rush hours (lower panel in
Figure 9), while other congestion areas such E and F (lower panel in
Figure 9) emerge in the outward direction of the city during afternoon rush hours. The change of mobility pattern may be due to the movement of people from home to work in the morning, from work to home in the afternoon, and the actual physical difference in location from home and work. Similarly, the long temporal cluster area C (lower right in upper panel in
Figure 9) disappears during afternoon rush hours (lower panel in
Figure 9), while the long temporal cluster area D (middle left in lower panel in
Figure 9) emerges during afternoon rush hours. In actuality, area C is the main train station in Wuhan, and area D is the sub train station. This kind of change probably reflects the temporal regularity of movement of people between Wuhan and other cities. However, not all congestions happened on major roads, such as area G (lower panel in
Figure 9) on Zoo Road. Such areas could be potential developing areas with poor road networks but heavy traffic flows, where the surrounding traffic situation needs to be improved. This could be worth the attention of urban planners and policymakers.
Based on the scaling property (
c.f.,
Figure 8) and the head/tail division rule mentioned in
Section 4, the areas of traffic congestions on Monday 9 March were divided into a series of two-tire hierarchical structures at different levels in time dimension according to their lifetimes (
Table 1). The underlying implication behind the hierarchies indicates the traffic mobility patterns from a temporal perspective. The higher the levels of spatio-temporal clusters, the more serious are the areas of traffic congestion. The mean lifetime of each level (
i.e., 4, 8, 16 and 28 min) could be set up as an index for measuring the degree of traffic congestion, which could provide a useful reference for urban traffic systems. For example, there are 32 areas of traffic congestion whose lifetimes are greater than 28 min, which constitutes areas of serious congestion. Meanwhile, the percentages in
Table 1 are in good agreement with 80/20 percent principle in terms of scaling property, which also means that 20 percent of traffic congestions are serious and 80 percent of them are slight. Therefore, the limited urban human and financial resources should be focused on these seriously congested areas to improve traffic condition around there in an efficient and effective way.
Table 1.
The numbers and percentages of spatio-temporal clusters in the head and tail on Monday.
Table 1.
The numbers and percentages of spatio-temporal clusters in the head and tail on Monday.
| | Mean (minutes) | # of all | # in Head (≥ mean) | % in Head | # in Tail |
|---|
| Level 1 | 4 | 6,711 | 1,525 | 22.7% | 5,186 |
| Level 2 | 8 | 1,525 | 387 | 25.4% | 1138 |
| Level 3 | 16 | 387 | 114 | 29.5% | 273 |
| Level 4 | 28 | 114 | 32 | 28.1% | 82 |