Multi-Robot Item Delivery and Foraging: Two Sides of a Coin
Abstract
:1. Introduction
2. Related Work
3. Problem Definition and Approach
3.1. Motivating Scenario
3.2. Multi-Robot Item Delivery Problem Definition
3.3. Comparison to Multi-Robot Foraging Problem
| Symbol | Item Delivery Problem | Foraging Problem |
|---|---|---|
| Set of locations, spanning the entire space | Discrete set of locations | |
| Types of items to be delivered | A single type of resource | |
| Set of demands | Set of resources | |
| Robot ’s model of demands | Robot ’s model of resources |
3.4. Overview of Approach
- For the FP, resources at the locations replenish following a known model. We detail the different models (Bernoulli, Poisson and stochastic logistic) in Section 4. For the ITP, we focus solely on the Poisson replenishment model;
- The robots’ model of demands, , is updated using the replenishment models, as well as observations made as the robots travel in the environment;
- In the FP, the robots do not share their models , and only share their current destinations. In the ITP, the robots share their models, and we discuss the shared world model in Section 6;
- We contribute the distributed algorithms for the FP and discuss how the algorithms are also applicable to the ITP (Section 5.1).
4. Demand Generation Models
4.1. Resource Replenishment for Multi-Robot Foraging
4.1.1. Bernoulli Replenishment
- The Bernoulli distribution is intuitive and easily understood;
- Resource replenishment is independent of the number of resources already present at the location;
- Even if is known, the number of resources/demands created is probabilistic.
- There is no upper limit to the number of demands generated at a location;
- At most one resource is replenished per time step.
4.1.2. Poisson Replenishment
- The Poisson distribution corresponds to a number of real-life scenarios, e.g., the number of people waiting at a bus stop;
- Resource replenishment is independent of the number of resources/demands already present at the location;
- Even if is known, the number of demands created is probabilistic;
- More than one resource may be replenished every time step.
4.1.3. Stochastic Logistic Replenishment
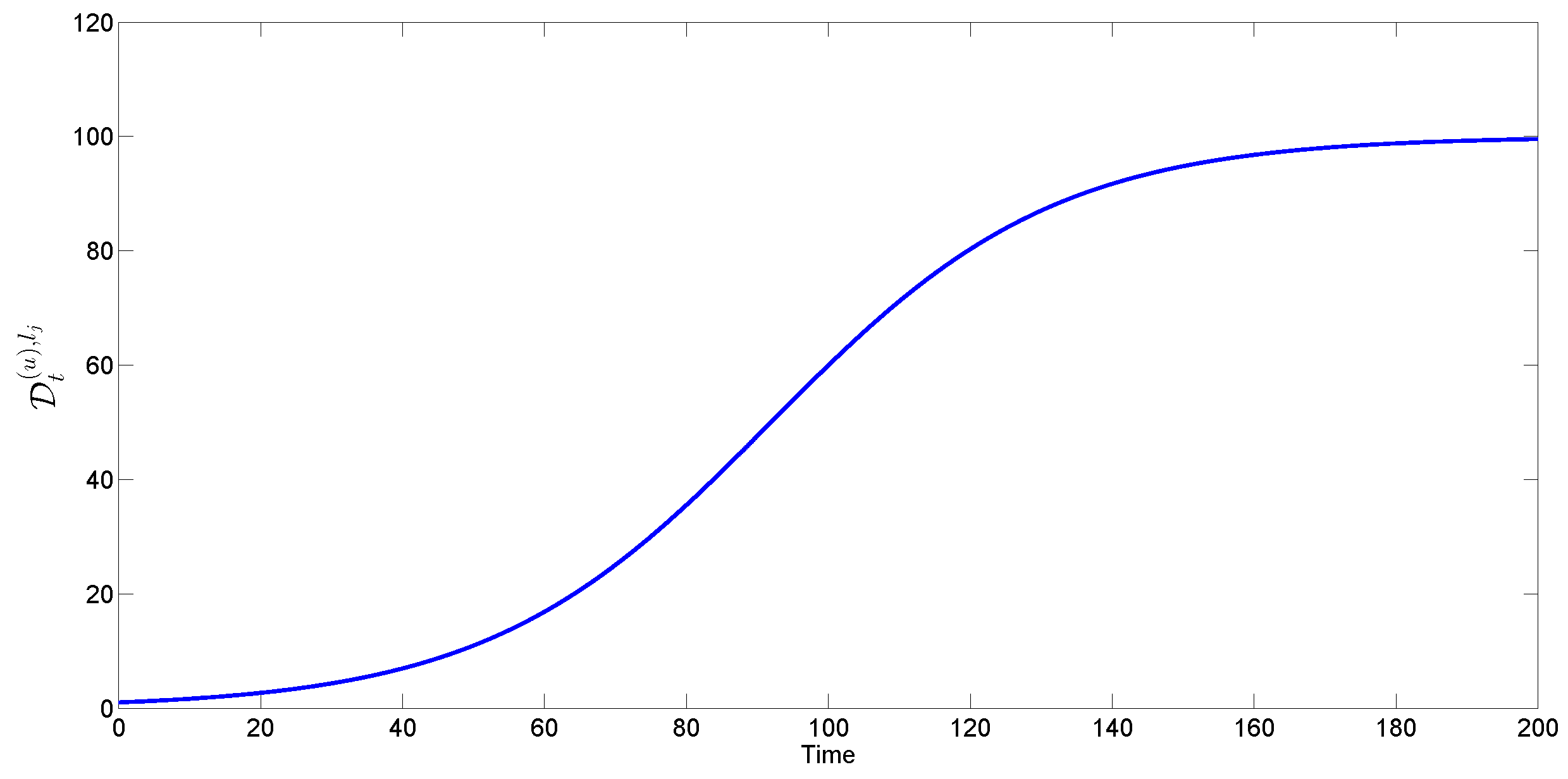
- Independent increments: is independent of ;
- Stationary increments: ;
- Gaussian increments: .
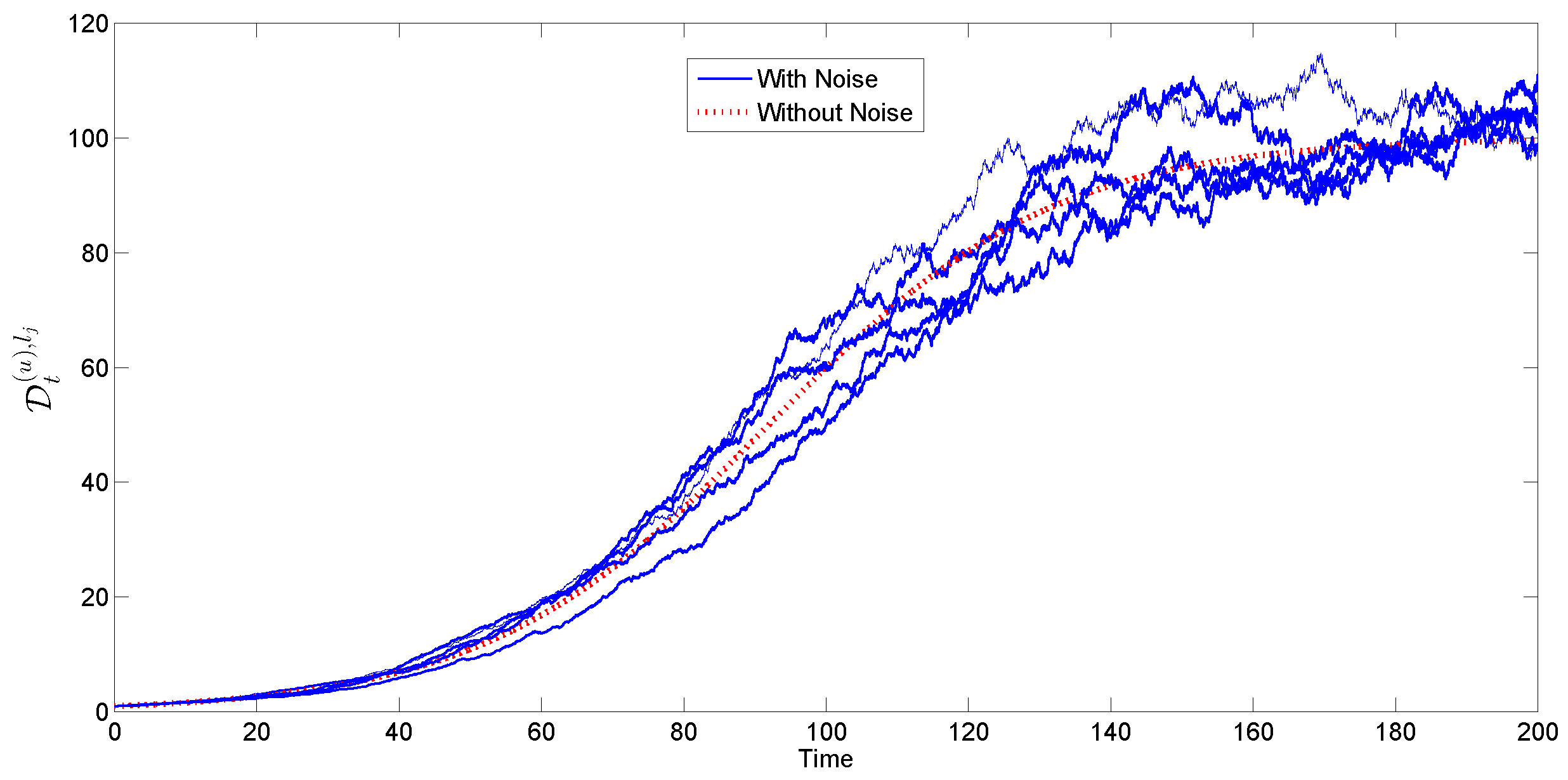
4.2. Applying Resource Replenishment Models to Item Delivery
- Having no upper limit suits the multi-robot item delivery problem, since guests may typically request an unlimited number of refreshments;
- The Poisson distribution is suitable for modeling how demands may be created over time.
5. Distributed Algorithms for Item Delivery
5.1. Multi-Robot Foraging Algorithms
5.1.1. Random
5.1.2. Best Static Loop
5.1.3. Greedy Rate

5.1.4. Adaptive Sleep

5.1.5. Adaptive Sleep with Target Change
5.2. Adapting the Foraging Algorithms for Item Delivery

6. Maintaining a Model of the World
6.1. Modeling Demands at Locations
- Bernoulli replenishment: is not known, and the robots use a preset value for all locations;
- Poisson replenishment: is not known, and the robots use a preset value for all locations;
- Stochastic logistic replenishment: The unconstrained population growth rate and maximum population is known, but the intensity of growth rate fluctuation is not known. The robots assume that , i.e., there is no noise in the growth rate.
6.2. Synchronizing the Shared World Model
- The global position of every robot in the multi-robot team;
- , a model of the number of demands (satisfied and unsatisfied) at location at time t;
- For each robot , which demands have been assigned to ;
- The current destination of every robot .
- ’s global position;
- ’s observations of demands at locations;
- ’s assigned demands;
- ’s current destination.
7. Experiments and Results
7.1. Multi-Robot Foraging Experiments
7.1.1. Experimental Setup
- Space of the world: ;
- Home location: center of the world;
- Number of locations: 20, uniformly distributed in the world;
- Number of robots: 1–10;
- Capacity of each robot: 1–20;
- Maximum speed of each robot: ;
- Length of simulation: 1000 time steps;
- Full communication between robots to share the world model, i.e., perfect communicate with no limits on range and no errors in communication.
- For the Bernoulli replenishment model, ;
- For the Poisson replenishment model, ;
- For the stochastic logistic replenishment model, .
- Bernoulli model: ;
- Poisson model: ;
- Stochastic logistic model: .
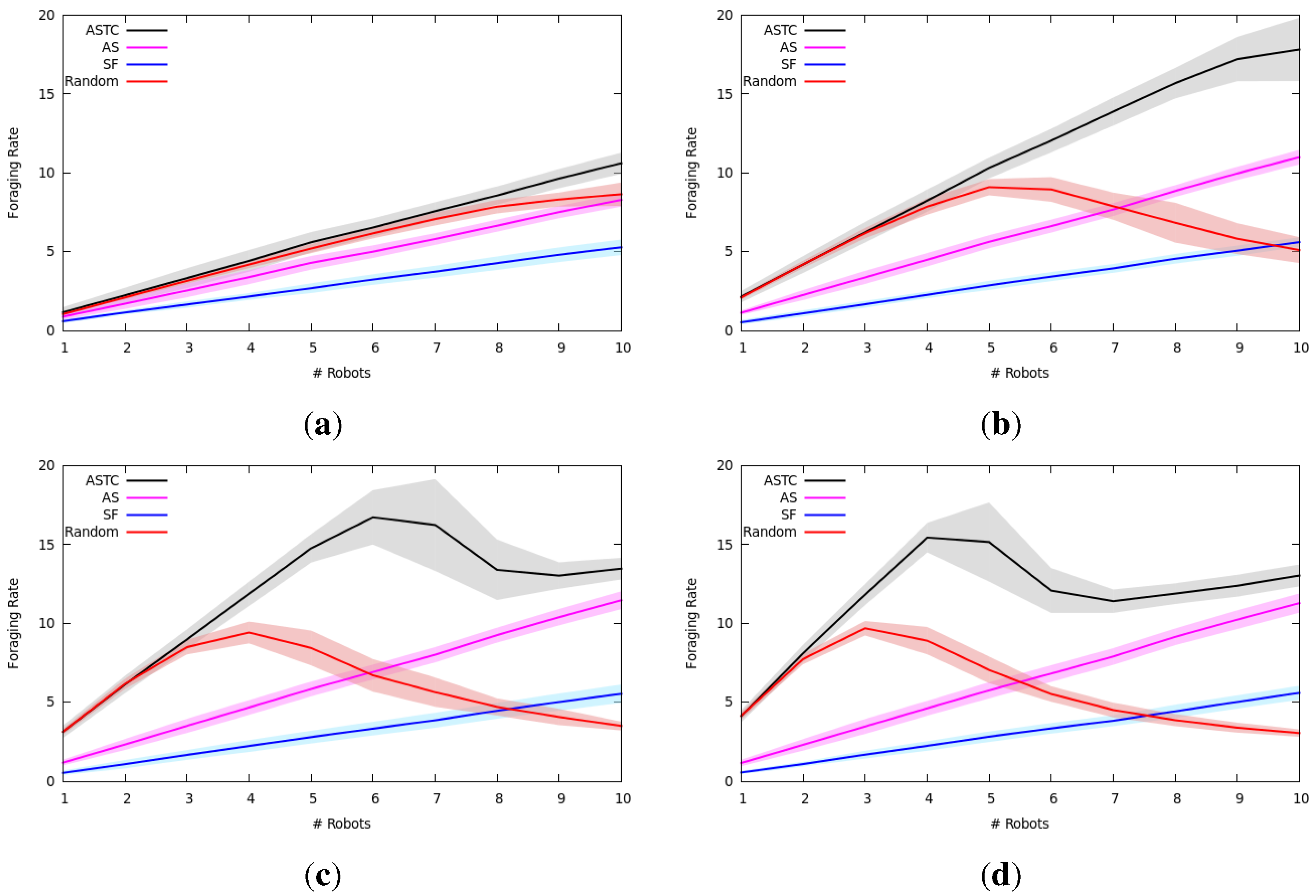
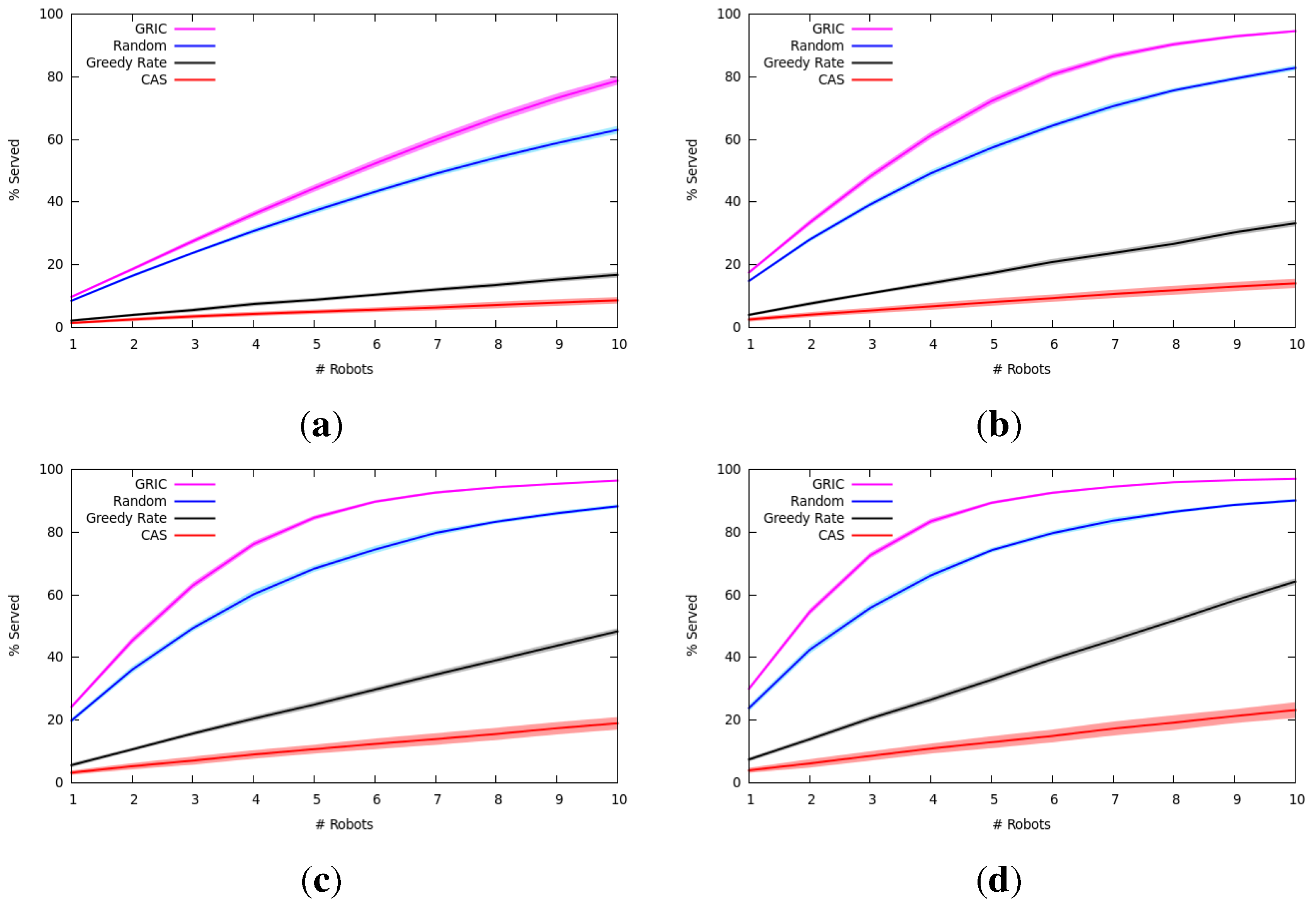
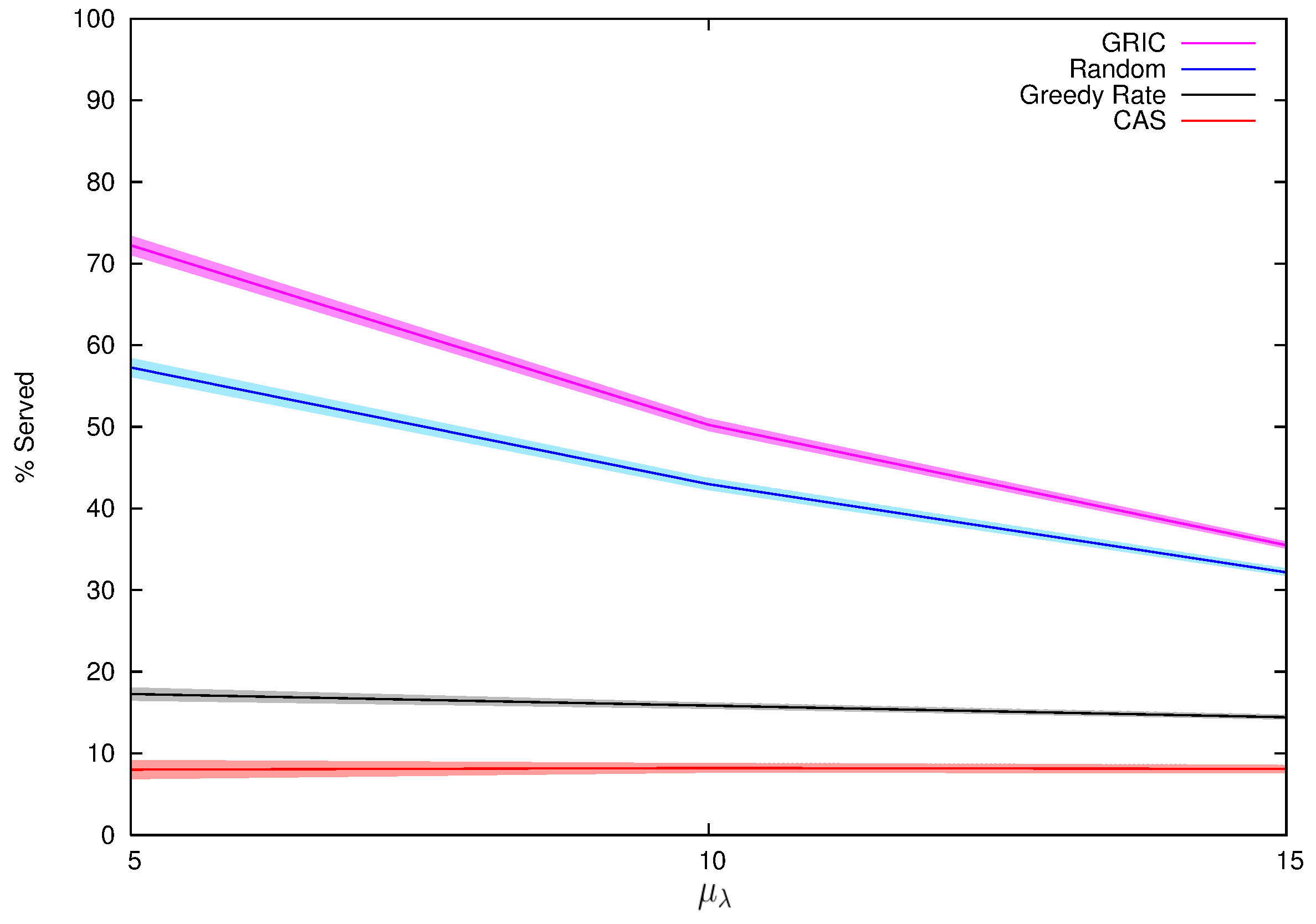
7.1.2. Results and Analysis

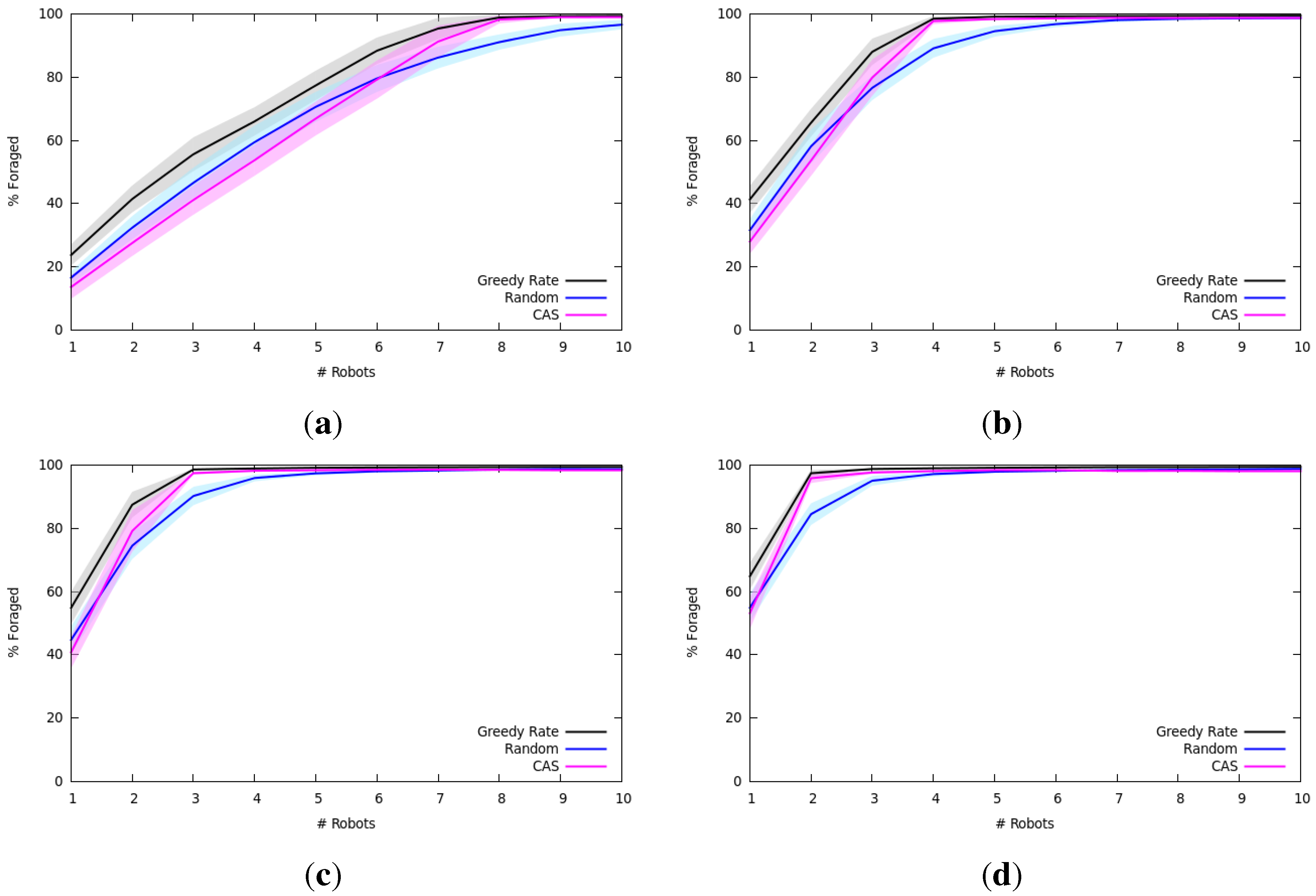
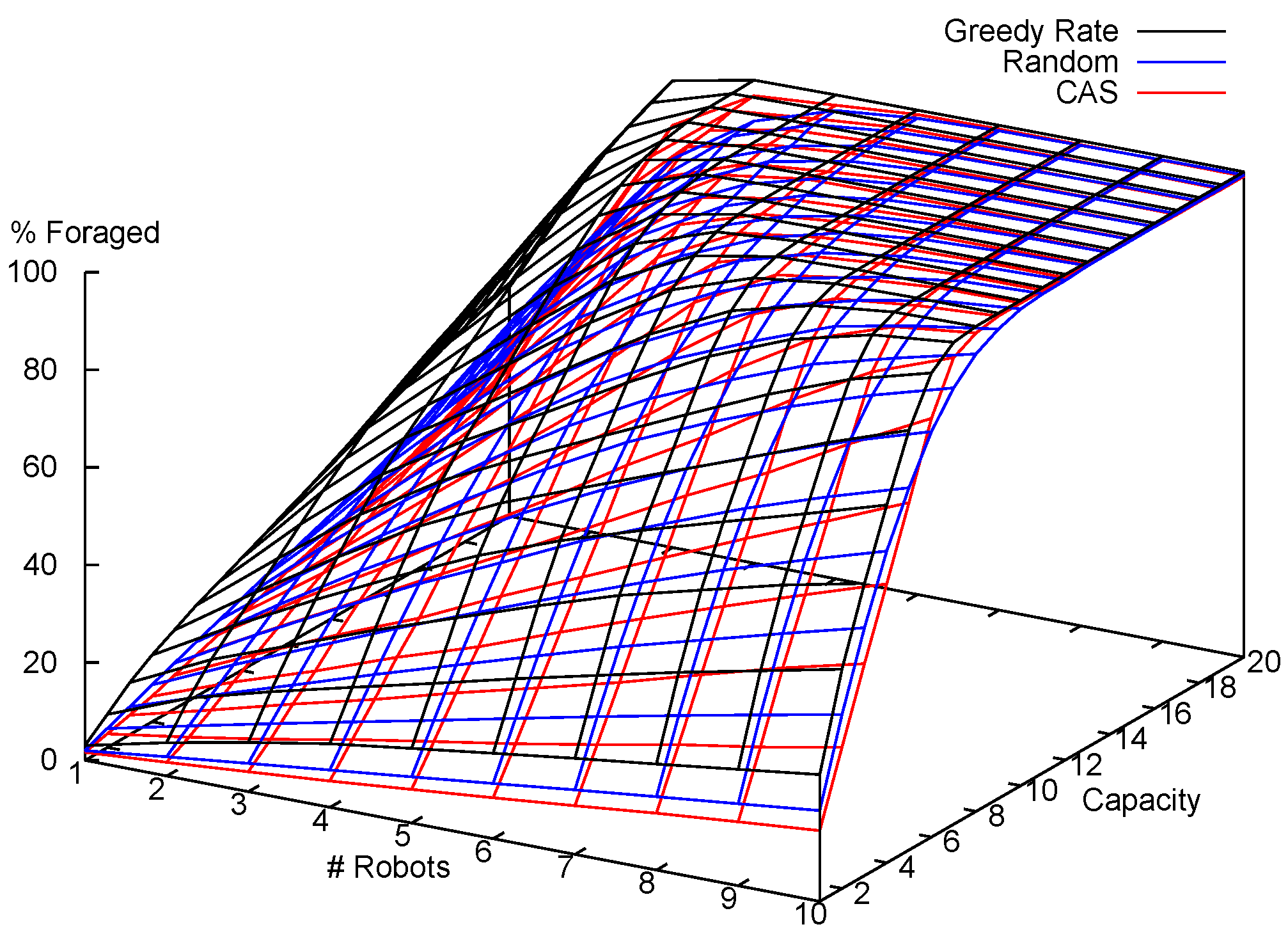
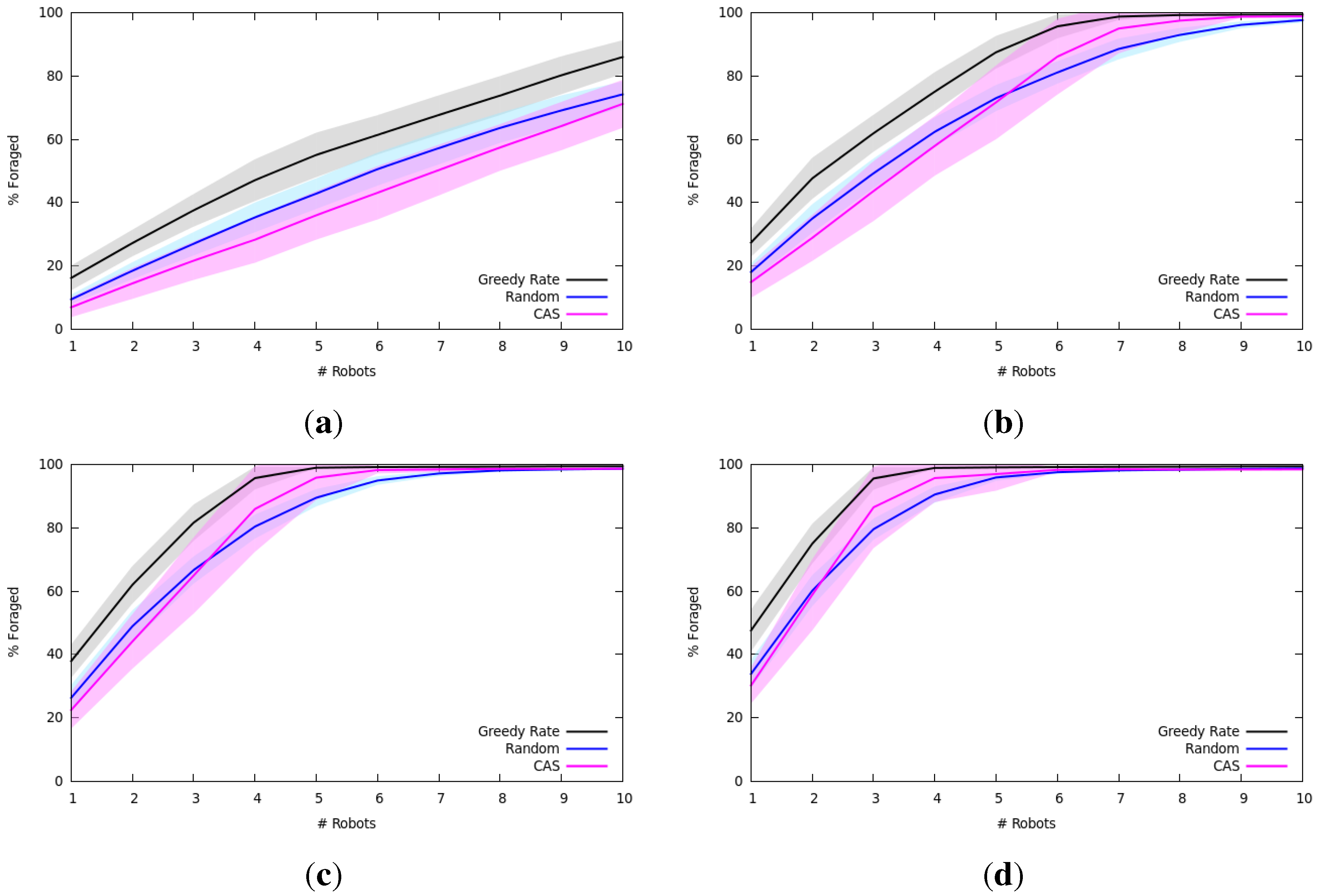
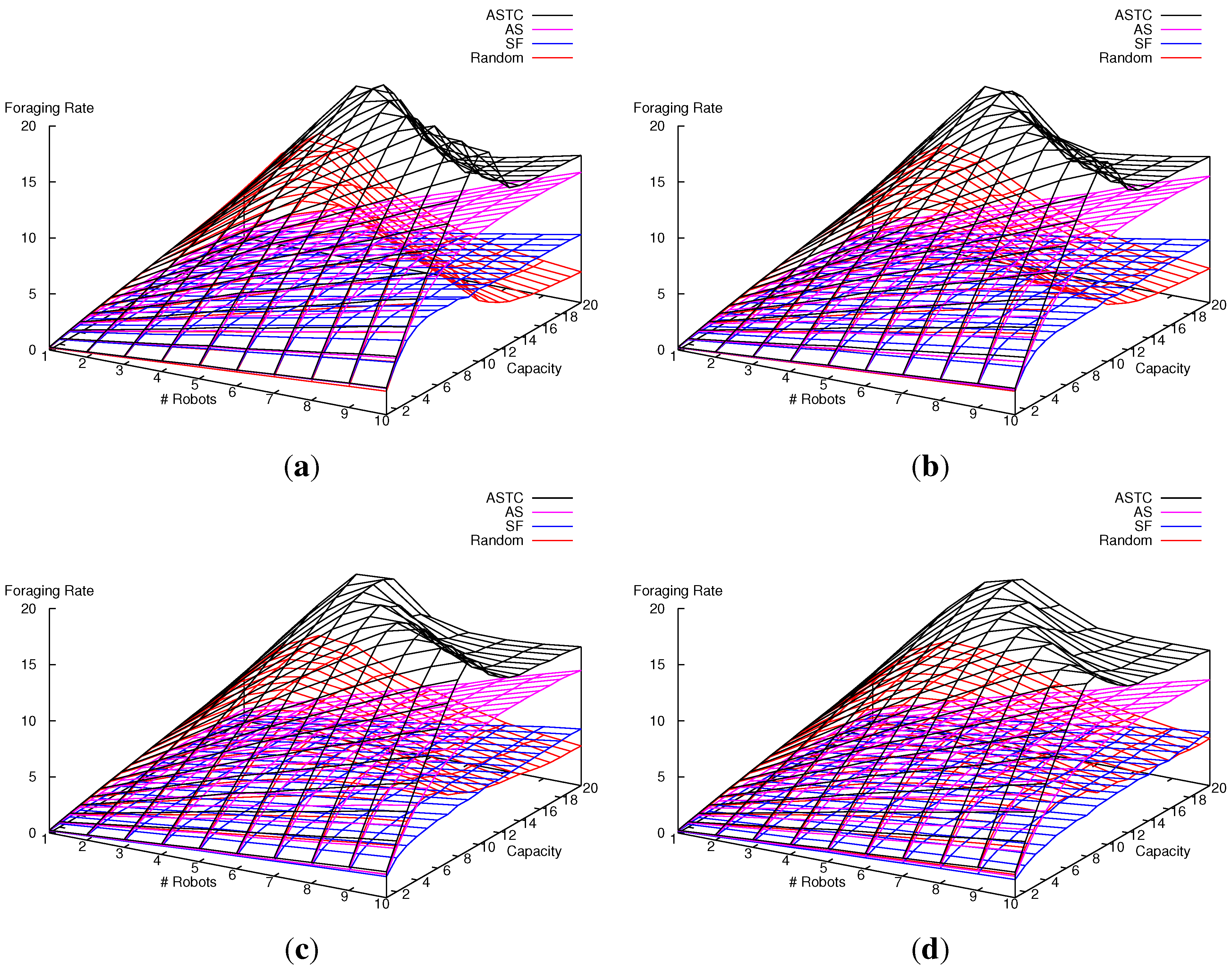
7.2. Multi-Robot Item Delivery Experiments
7.2.1. Experimental Setup
7.2.2. Results and Analysis
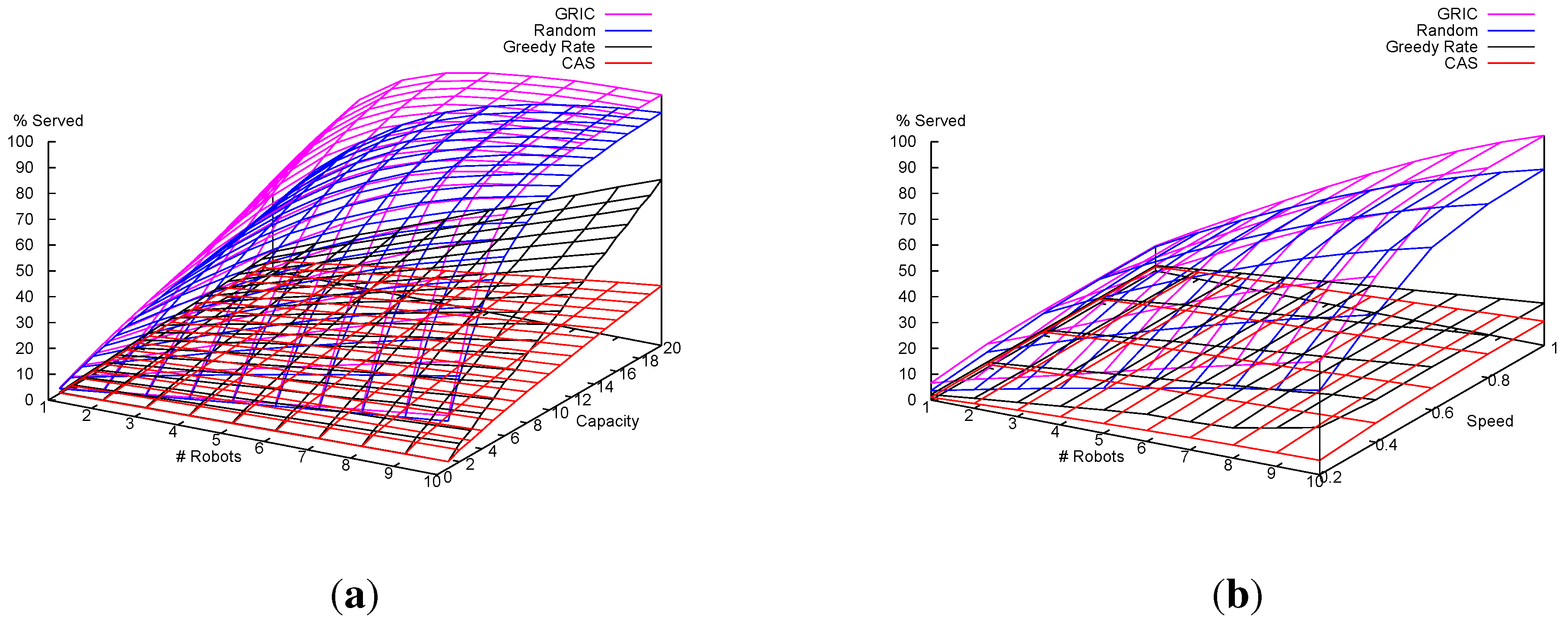

8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liemhetcharat, S.; Yan, R.; Tee, K.P. Continuous foraging and information gathering in a multi-agent team. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Istanbul, Turkey, 4–8 May 2015; pp. 1325–1333.
- Song, Z.; Vaughan, R. Sustainable robot foraging: Adaptive fine-grained multi-robot task Allocation for Maximum Sustainable Yield of Biological Resources. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3309–3316.
- Ahmadi, M.; Stone, P. Continuous area sweeping: A task definition and initial approach. In Proceedings of the International Conference on Advanced Robotics, Seattle, WA, USA, 18–20 July 2005; pp. 316–323.
- Gerkey, B.P.; Mataric, M.J. A formal analysis and taxonomy of task allocation in multi-robot systems. J. Robot. Res. 2004, 23, 939–954. [Google Scholar] [CrossRef]
- Liemhetcharat, S.; Veloso, M. Modeling and learning synergy for team formation with heterogeneous agents. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Valencia, Spain, 4–8 June 2012; pp. 365–375.
- Liemhetcharat, S.; Veloso, M. Weighted synergy graphs for effective team formation with heterogeneous Ad Hoc Agents. J. Artif. Intell. 2014, 208, 41–65. [Google Scholar] [CrossRef]
- Liemhetcharat, S.; Veloso, M. Weighted synergy graphs for role assignment in Ad Hoc Heterogeneous Robot Teams. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 5247–5254.
- Liemhetcharat, S.; Veloso, M. Synergy graphs for configuring robot team members. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Saint Paul, MN, USA, 6–10 May 2013; pp. 111–118.
- Liemhetcharat, S.; Veloso, M. Forming an effective multi-robot team robust to failures. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013.
- Lerman, K.; Jones, C.; Galstyan, A.; Mataric, M.J. Analysis of dynamic task allocation in multi-robot systems. J. Robot. Res. 2006, 25, 225–241. [Google Scholar] [CrossRef]
- Shell, D.A.; Mataric, M.J. Onforaging strategies for large-scale multi-robot systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 2717–2723.
- Modi, P.; Shen, W.; Tambe, M.; Yokoo, M. An asynchronous complete method for distributed constraint optimization. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Melbourne, Australia, 14–18 July 2003.
- Couceiro, M.; Rocha, R.; Figueiredo, C.; Luz, J.; Ferreira, N. Multi-robot foraging based on Darwin’s survival of the fittest. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 801–806.
- Dorigo, M.; Birattari, M. Ant colony optimization. In Encyclopedia of Machine Learning; Springer Science and Business Media: Berlin, Germany, 2011; pp. 37–40. [Google Scholar]
- Panait, L.; Luke, S. A pheromone-based utility model for collaborative foraging. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, New York, NY, USA, 23 July 2004; pp. 36–43.
- Liu, W.; Winfield, A.; Sa, J.; Chen, J.; Dou, L. Towards energy optimization: Emergent task allocation in a swarm of foraging robots. Adapt. Behav. 2007, 15, 289–305. [Google Scholar] [CrossRef]
- Song, Z.; Sadat, S.; Vaughan, R. MO-LOST: Adaptive ant trail untangling in multi-objective multi-colony robot foraging. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Valencia, Spain, 4–8 June 2012; pp. 1199–1200.
- Hoff, N.; Sagoff, A.; Wood, R.; Nagpal, R. Two foraging algorithms for robot swarms using only local communication. In Proceedings of the International Conference on Robotics and Biomimetics, Tianjin, China, 14–18 December 2010; pp. 123–130.
- Lemmens, N.; Jong, S.; Tuyls, K.; Nowe, A. Bee behaviour in multi-agent systems. In Adaptive Agents and Multi-Agent Systems III; Springer Berlin Heidelberg: Berlin, Germany, 2008; pp. 145–156. [Google Scholar]
- Alers, S.; Bloembergen, D.; Hennes, D.; de Jong, S.; Kaisers, M.; Lemmens, N.; Tuyls, K.; Weiss, G. Bee-inspired foraging in an embodied swarm. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Taipei, Taiwan, 2–6 May 2011; pp. 1311–1312.
- Rosenfeld, A.; Kaminka, G.A.; Kraus, S. A study of scalability properties in robotic teams. In Coordination of Large-Scale Multiagent Systems; Springer: New York, NY, USA, 2006; pp. 27–51. [Google Scholar]
- Lerman, K.; Galstyan, A. Mathematical model of foraging in a group of robots: Effect of interference. Auton. Robot. 2002, 13, 127–141. [Google Scholar] [CrossRef]
- Schneider-Fontan, M.; Mataric, M.J. Territorial multi-robot task division. IEEE Trans. Robot. Autom. 1998, 14, 815–822. [Google Scholar] [CrossRef]
- Jager, M.; Nebel, B. Dynamic decentralized area partitioning for cooperating cleaning robots. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA’02, Washington, WA, USA, 11–15 May 2002; pp. 3577–3582.
- Sander, P.V.; Peleshchuk, D.; Grosz, B.J. A scalable, distributed algorithm for efficient task allocation. In Proceedings of the First International Joint Conference on Autonomous Agents and Multiagent Systems, Bologna, Italy, 15–19 July 2002; pp. 1191–1198.
- Rosenfeld, A.; Kaminka, G.A.; Kraus, S. Adaptive robot coordination using interference metrics. In Proceedings of the ECAI, Valencia, Spain, 22–27 August 2004; pp. 910–916.
- Kaminka, G.; Erusalimchik, D.; Kraus, S. Adaptive multi-robot coordination: A game-theoretic perspective. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 328–334.
- Rosenfeld, A.; Kaminka, G.A.; Kraus, S.; Shehory, O. A study of mechanisms for improving robotic group performance. Artif. Intell. 2008, 172, 633–655. [Google Scholar] [CrossRef]
- Dias, M.B.; Stentz, A. Multi-robot exploration controlled by a market economy. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Washington, WA, USA, 11–15 May 2002; pp. 2714–2720.
- Dias, M.B. TraderBots: A New Paradigm for Robust and Efficient Multirobot Coordination in Dynamic Environments. Ph.D. Thesis, The Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, USA, 2004. [Google Scholar]
- Gerkey, B.P.; Matari, M.J. Sold!: Auction methods for multirobot coordination. IEEE Trans. Robot. Autom. 2002, 18, 758–768. [Google Scholar] [CrossRef]
- Choi, H.L.; Brunet, L.; How, J.P. Consensus-based decentralized auctions for robust task allocation. IEEE Trans. Robot. 2009, 25, 912–926. [Google Scholar] [CrossRef]
- Vig, L.; Adams, J. Market-based multi-robot coalition formation. In Proceedings of the International Symposium on Distributed Autonomous Robotics Systems, Minneapolis, MN, USA, 12–14 July 2006; pp. 227–236.
- Akbarimajd, A.; Simzan, G. Application of artificial capital market in task allocation in multi-robot foraging. Int. J. Comput. Intell. Syst. 2013, 7, 401–417. [Google Scholar] [CrossRef]
- Akbarimajd, A.; Jond, H. Multi-Robot Foraging based on Contract Net Protocol. J. Adv. Comput. Res. 2014, 5, 61–67. [Google Scholar]
- Heap, B.; Pagnucco, M. Repeated auctions for reallocation of tasks with pickup and delivery upon robot failure. In PRIMA 2013: Principles and Practice of Multi-Agent Systems; Springer: New York, NY, USA, 2013; pp. 461–469. [Google Scholar]
- Pini, G.; Brutschy, A.; Pinciroli, C.; Dorigo, M.; Birattari, M. Autonomous task partitioning in robot foraging: An approach based on cost estimation. Adapt. Behav. 2013, 21, 118–136. [Google Scholar] [CrossRef]
- Ozgul, E.; Liemhetcharat, S.; Low, K. Multi-Agent Ad Hoc Team partitioning by observing and modeling single-agent performance. In Proceedings of the Asia-Pacific Signal and Information Processing Association Conference, Siem Reap, Cambodia, 9–12 December 2014.
- Castello, E.; Yamamoto, T.; Nakamura, Y.; Ishiguro, H. Foraging optimization in swarm robotic systems based on an adaptive response threshold model. Adv. Robot. 2014, 28, 1343–1356. [Google Scholar] [CrossRef]
- Coltin, B.; Veloso, M. Scheduling for transfers in pickup and delivery problems with very large neighborhood search. In Proceedings of the International Conference on Artificial Intelligence, Las Vegas, NV, USA, 21–24 July 2014; pp. 2250–2256.
- Veloso, M.; Biswas, J.; Coltin, B.; Rosenthal, S.; Kollar, T.; Mericli, C.; Samadi, M.; Brandao, S.; Ventura, R. CoBots: Collaborative Robots Servicing Multi-Floor Buildings. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 5446–5447.
- Veloso, M.; Biswas, J.; Coltin, B.; Rosenthal, S.; Brandao, S.; Mericli, T.; Ventura, R. Symbiotic-autonomous service robots for user-requested tasks in a multi-floor building. In Proceedings of the IROS Workshop on Cognitive Assitive Systems, Algarve, Portugal, 7 October 2012.
- Cordeau, J.; Laporte, G. The dial-a-ride problem: Models and algorithms. Ann. Op. Res. 2007, 153, 29–46. [Google Scholar] [CrossRef]
- Ahmadi, M.; Stone, P. A multi-robot system for continuous area sweeping tasks. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 1724–1729.
- Agmon, N.; Kaminka, G.; Kraus, S. Multi-robot adversarial patrolling: Facing a full-knowledge opponent. J. Artif. Intell. Res. 2011, 412, 5771–5788. [Google Scholar]
- Elmaliach, Y.; Agmon, N.; Kaminka, G. Multi-robot area patrol under frequency constraints. Ann. Math. Artif. Intell. 2009, 57, 292–320. [Google Scholar] [CrossRef]
- Yoshida, E.; Arai, T.; Ota, J.; Miki, T. Effect of grouping in local communication system of multiple mobile robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Munich, Germany, 12–16 September 1994; pp. 808–815.
- Hakoyama, H.; Iwasa, Y. Extinction risk of a density-dependent population estimated from a time series of population size. J. Theor. Biol. 2000, 204, 337–359. [Google Scholar] [CrossRef] [PubMed]
- Coltin, B.; Liemhetcharat, S.; Meriçli, Ç.; Tay, J.; Veloso, M. Multi-humanoid world modeling in standard platform robot soccer. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Nashville, TN, USA, 6–8 December 2010.
- Liemhetcharat, S.; Coltin, B.; Veloso, M. Vision-based cognition of a humanoid robot in standard platform robot soccer. In Proceedings of the International Workshop on Humanoid Soccer Robots, Nashville, TN, USA, 7 December 2010; pp. 47–52.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liemhetcharat, S.; Yan, R.; Tee, K.P.; Lee, M. Multi-Robot Item Delivery and Foraging: Two Sides of a Coin. Robotics 2015, 4, 365-397. https://doi.org/10.3390/robotics4030365
Liemhetcharat S, Yan R, Tee KP, Lee M. Multi-Robot Item Delivery and Foraging: Two Sides of a Coin. Robotics. 2015; 4(3):365-397. https://doi.org/10.3390/robotics4030365
Chicago/Turabian StyleLiemhetcharat, Somchaya, Rui Yan, Keng Peng Tee, and Matthew Lee. 2015. "Multi-Robot Item Delivery and Foraging: Two Sides of a Coin" Robotics 4, no. 3: 365-397. https://doi.org/10.3390/robotics4030365





