Moving Object Localization Using Sound-Based Positioning System with Doppler Shift Compensation
Abstract
:1. Introduction
2. Spread Spectrum Sound-Based Positioning System
2.1. System Configuration
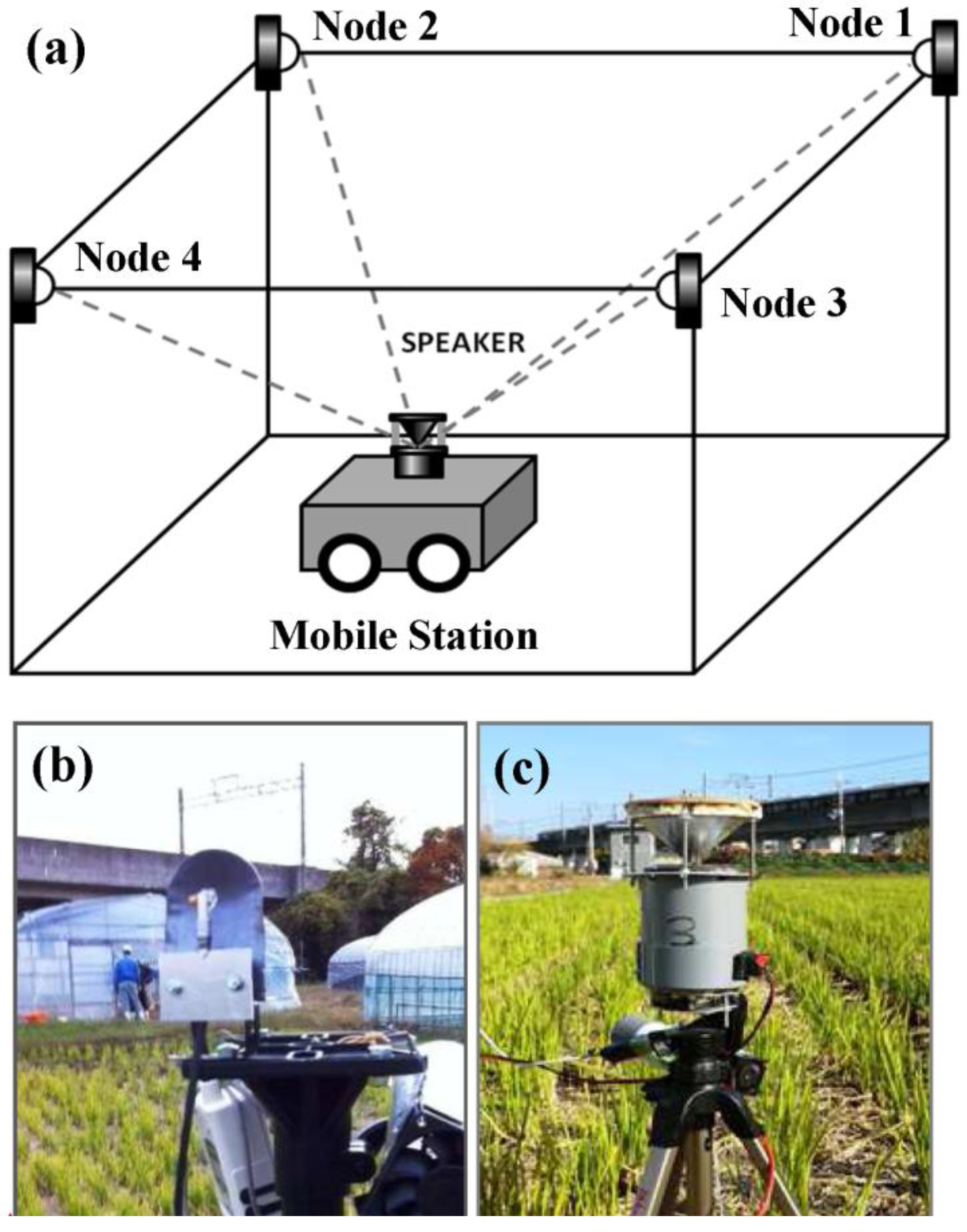
| Property | Value/Remark |
|---|---|
| Number of sound wave | 1 |
| Sampling frequency | 96 kHz |
| Sampling bit | 16 bits |
| M-sequence length | 1,023 |
| Modulation | BPSK |
| Carrier wave frequency | 24 kHz |
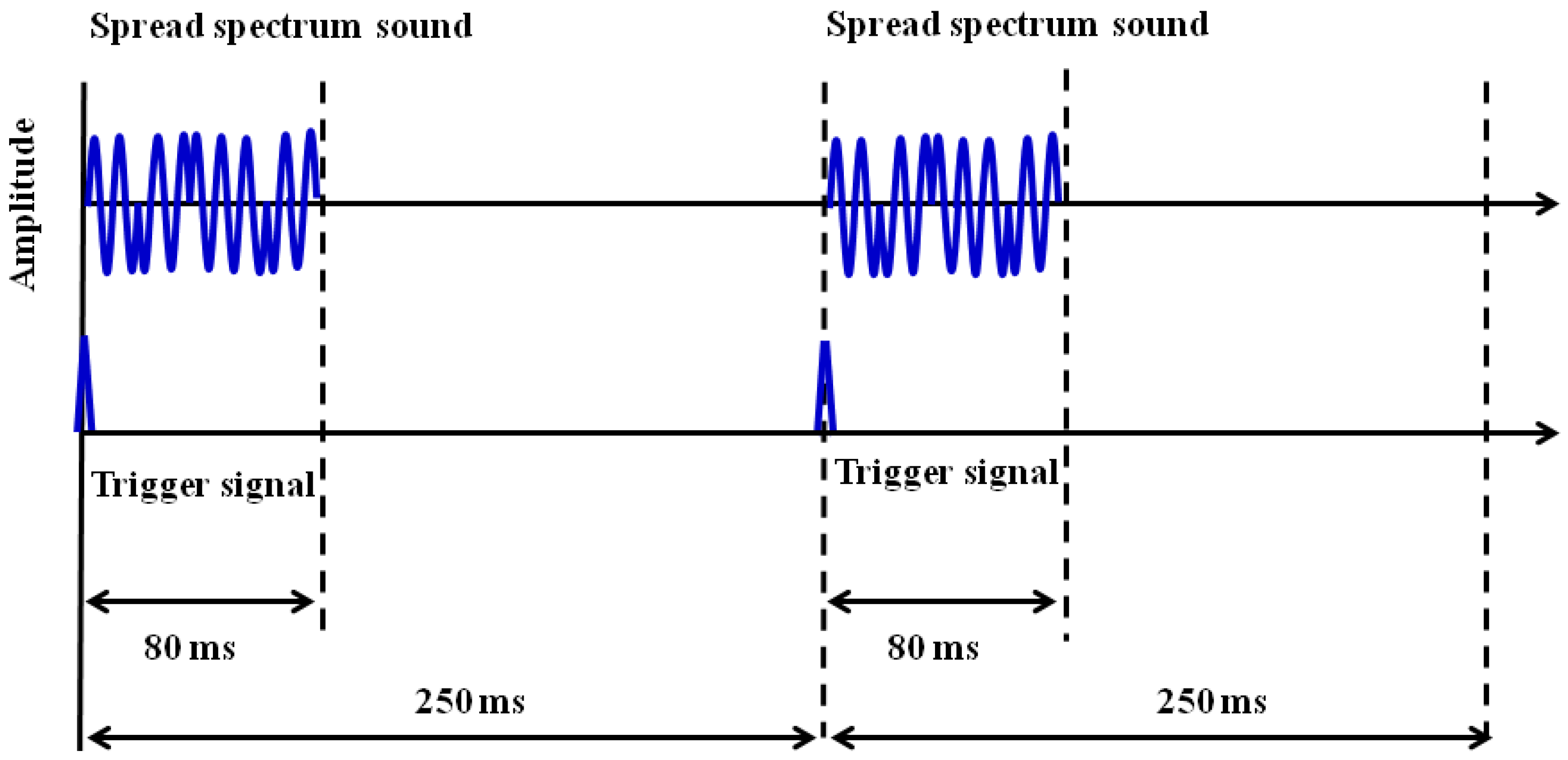
2.2. Position Estimation Method
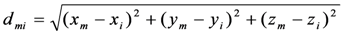
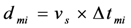
3. Doppler Shift Compensation

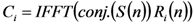
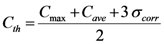
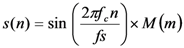
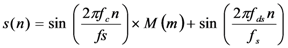
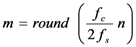
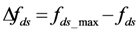
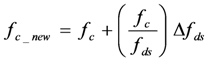
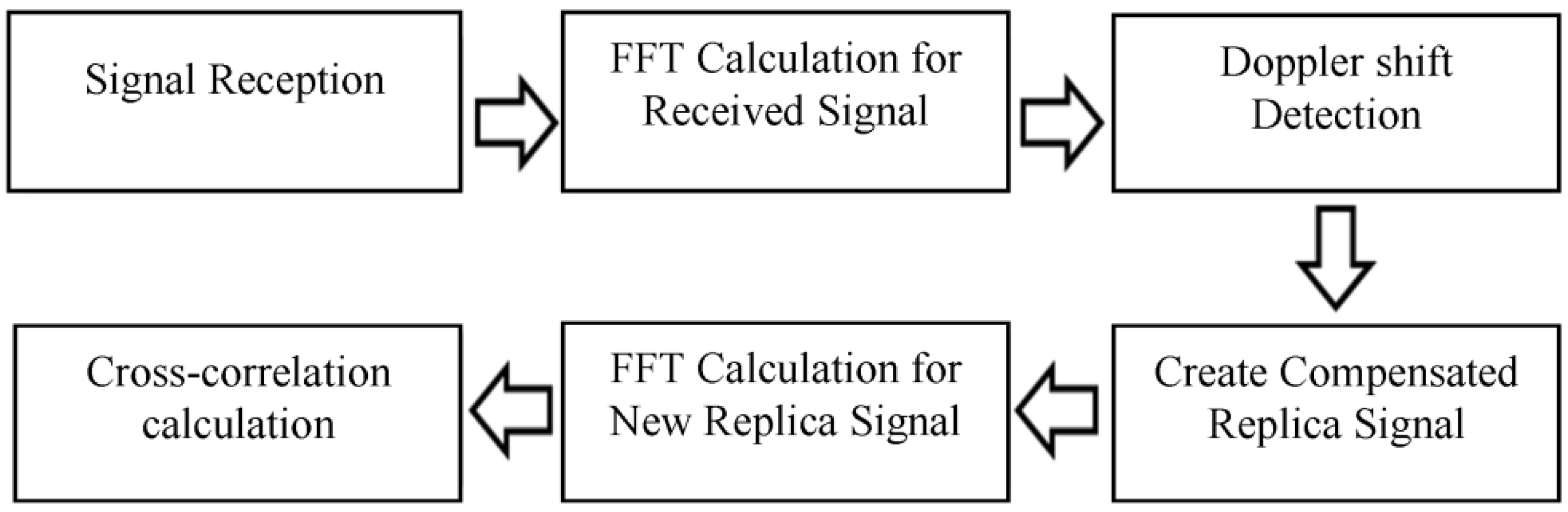
4. Experimental Setup
4.1. The Influence of Moving Speed
 ) was detected for the case of Doppler shift compensation, and correlation SNR was calculated as:
) was detected for the case of Doppler shift compensation, and correlation SNR was calculated as:
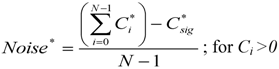
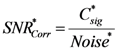
 (the i-th sample, where
(the i-th sample, where  =
=  ), then the same procedure was used to calculate the correlation SNR of the non-compensated system. The experiments were conducted indoors to prevent other undesirable influences, such as wind and noise, from interfering. We also compared the result with theoretical values obtained from numerical simulations.
), then the same procedure was used to calculate the correlation SNR of the non-compensated system. The experiments were conducted indoors to prevent other undesirable influences, such as wind and noise, from interfering. We also compared the result with theoretical values obtained from numerical simulations.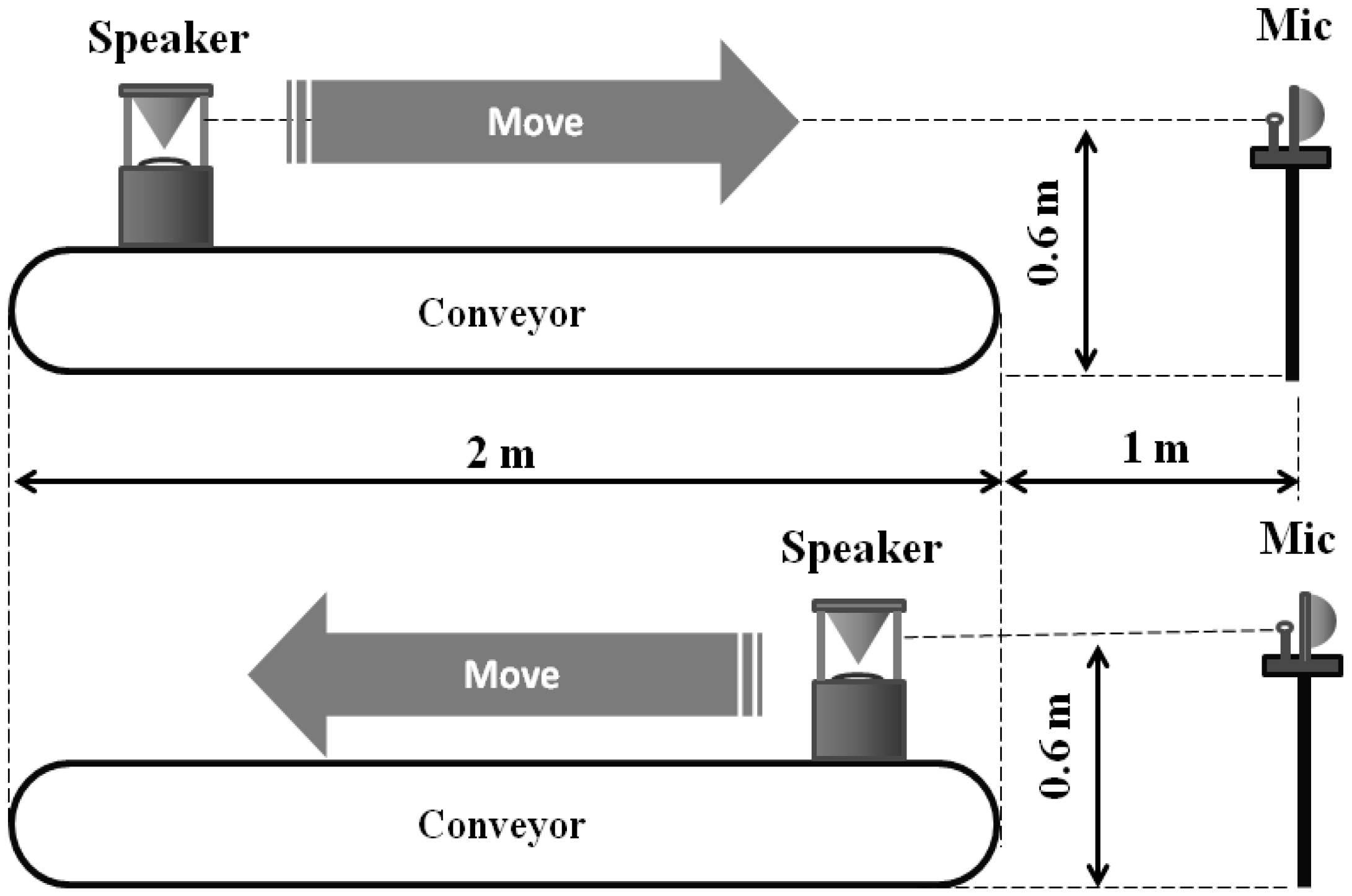
4.2. Moving Object Localization Test
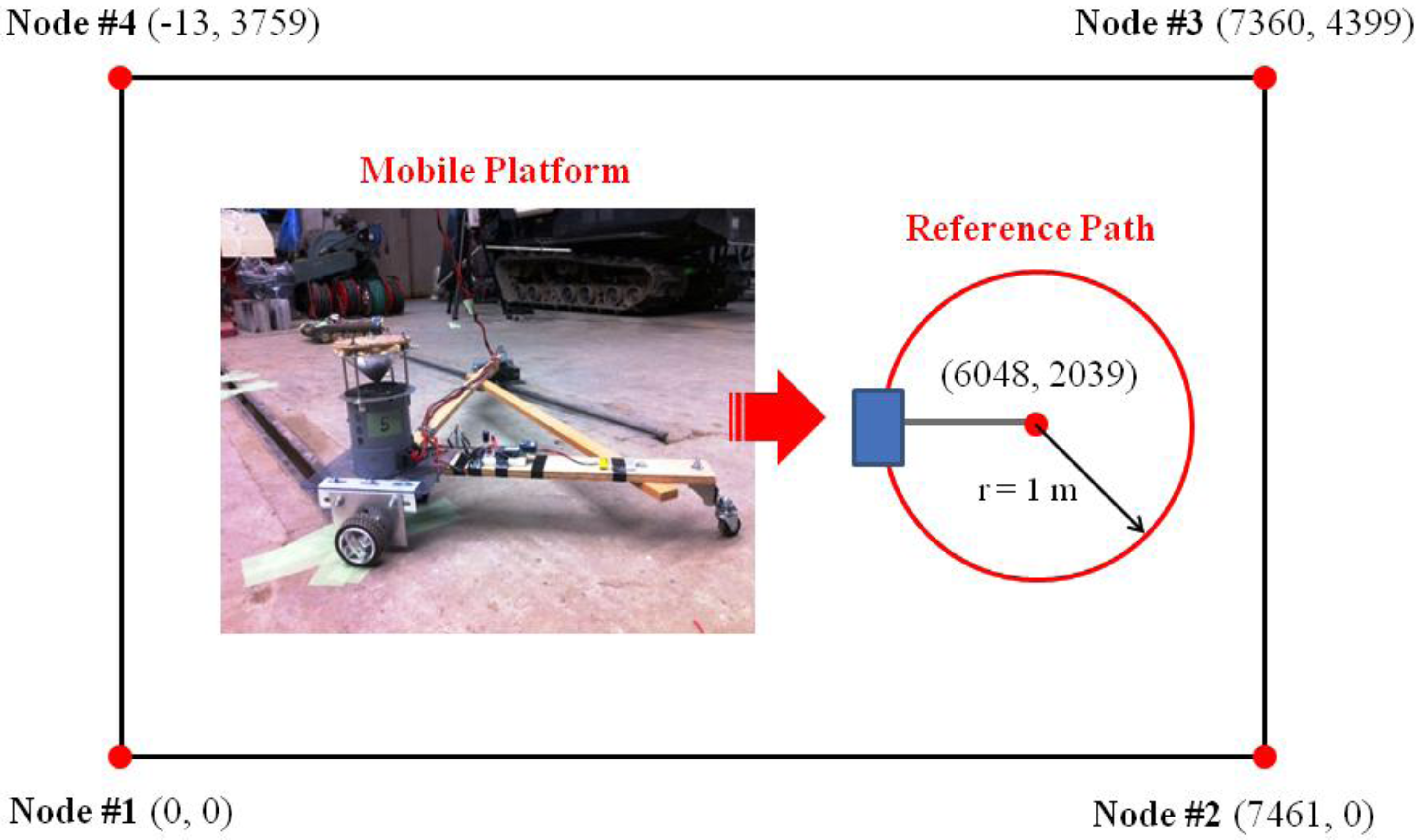
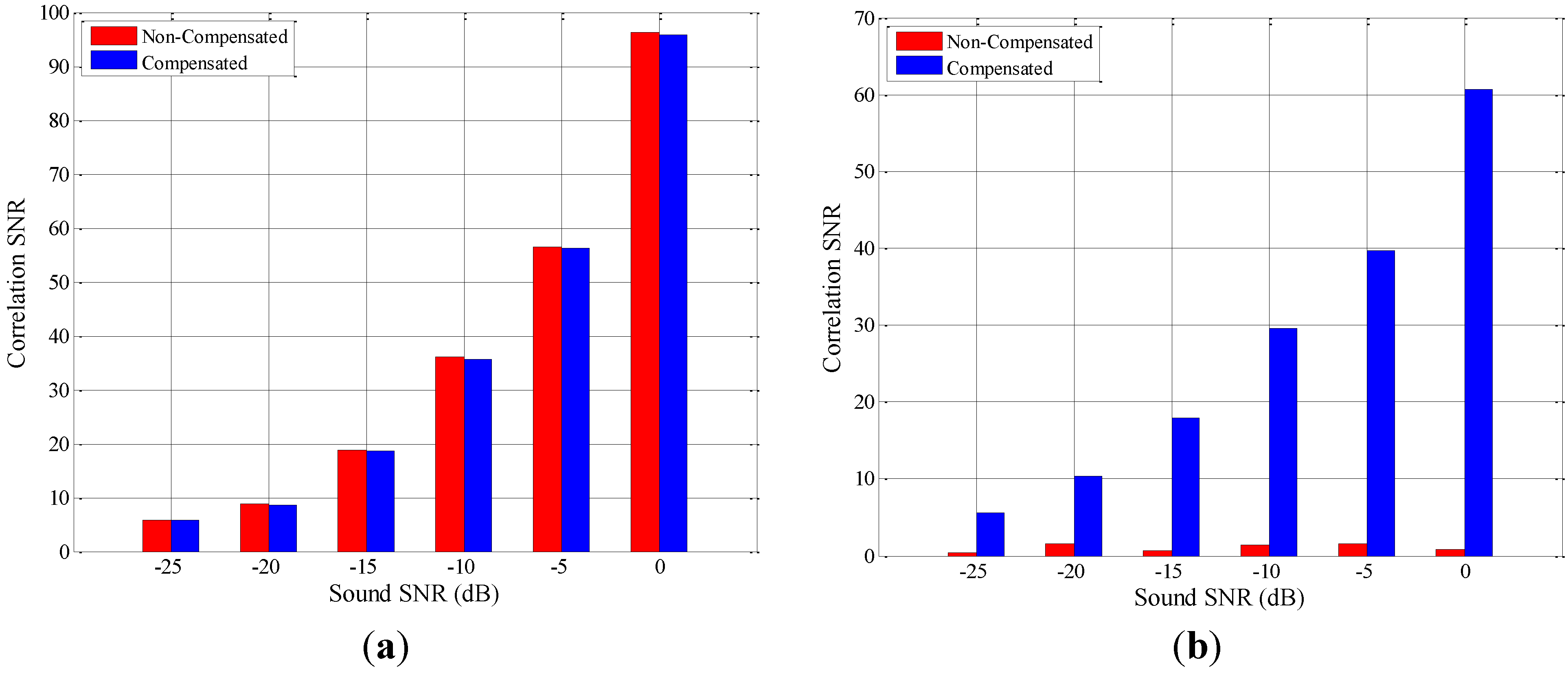
4.3. The Influence of Noise
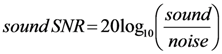
5. Results and Discussion
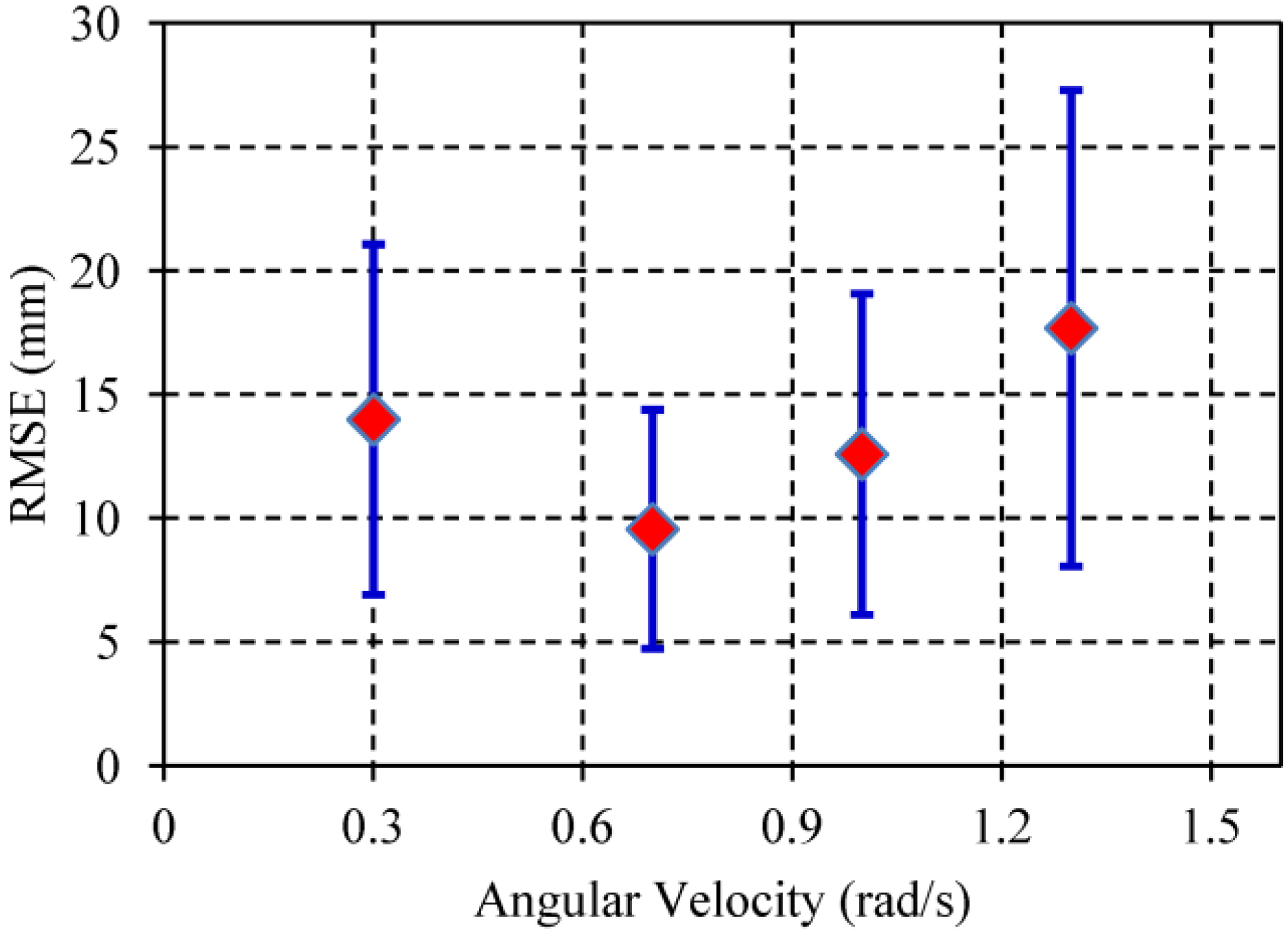
5.1. The Influence of Moving Speed
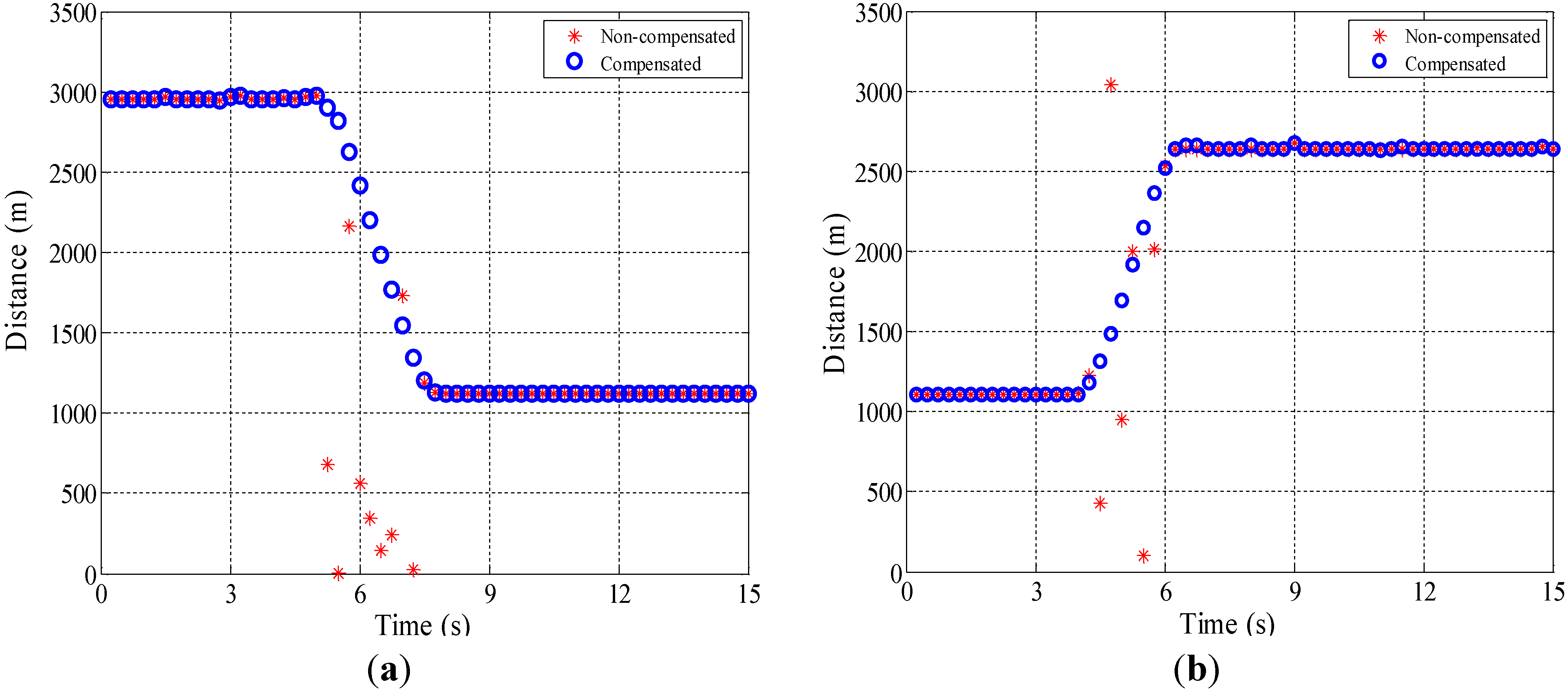
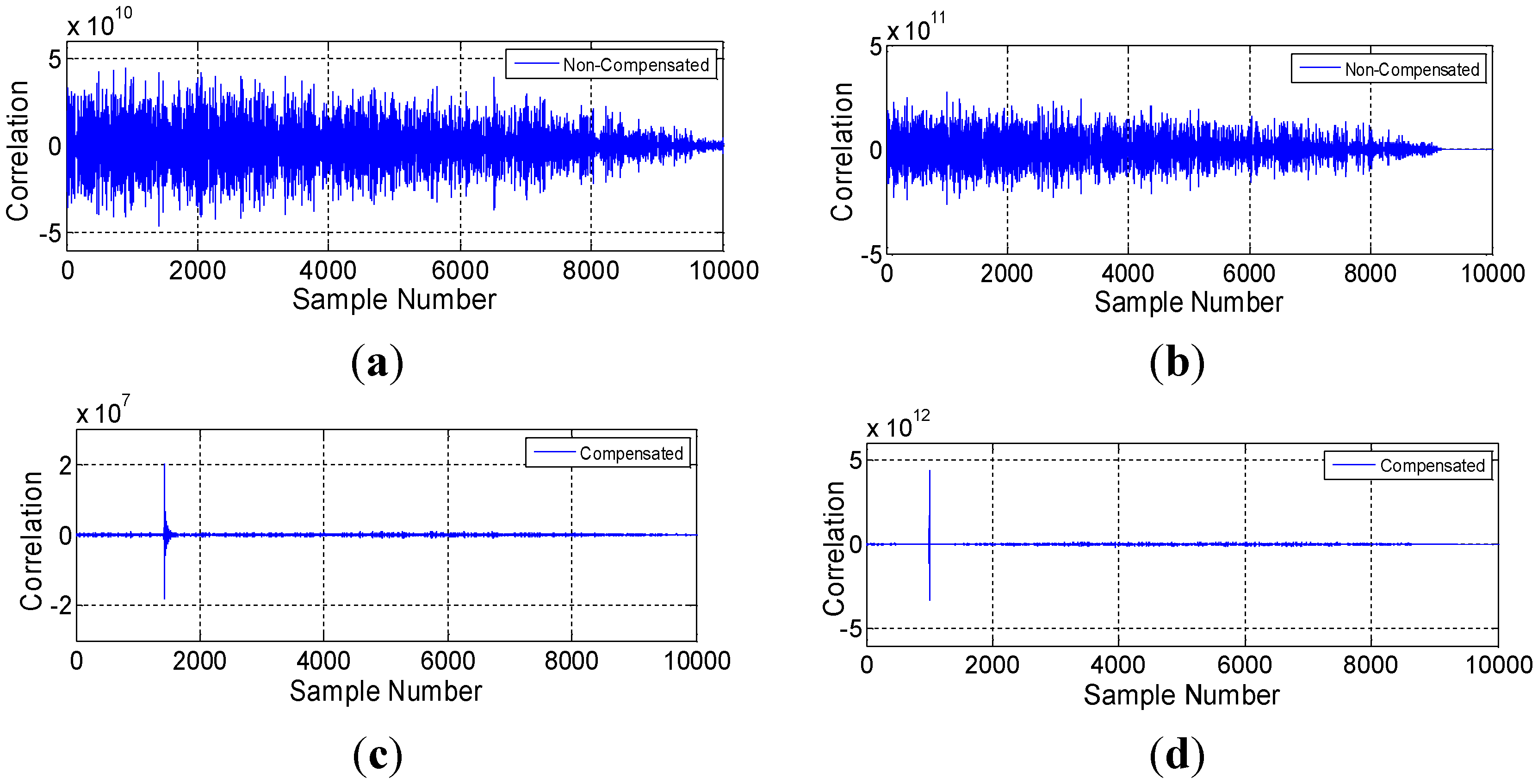

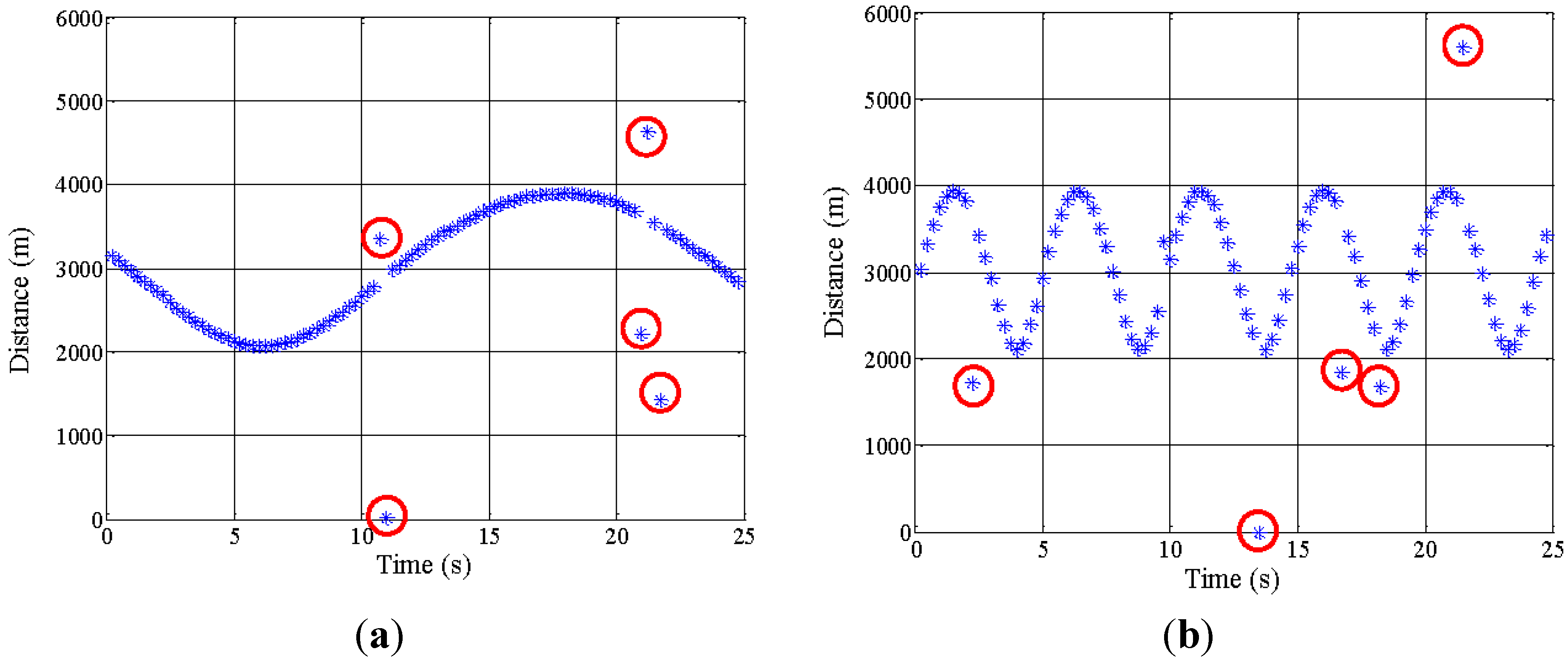
5.2. Moving Object Localization Test
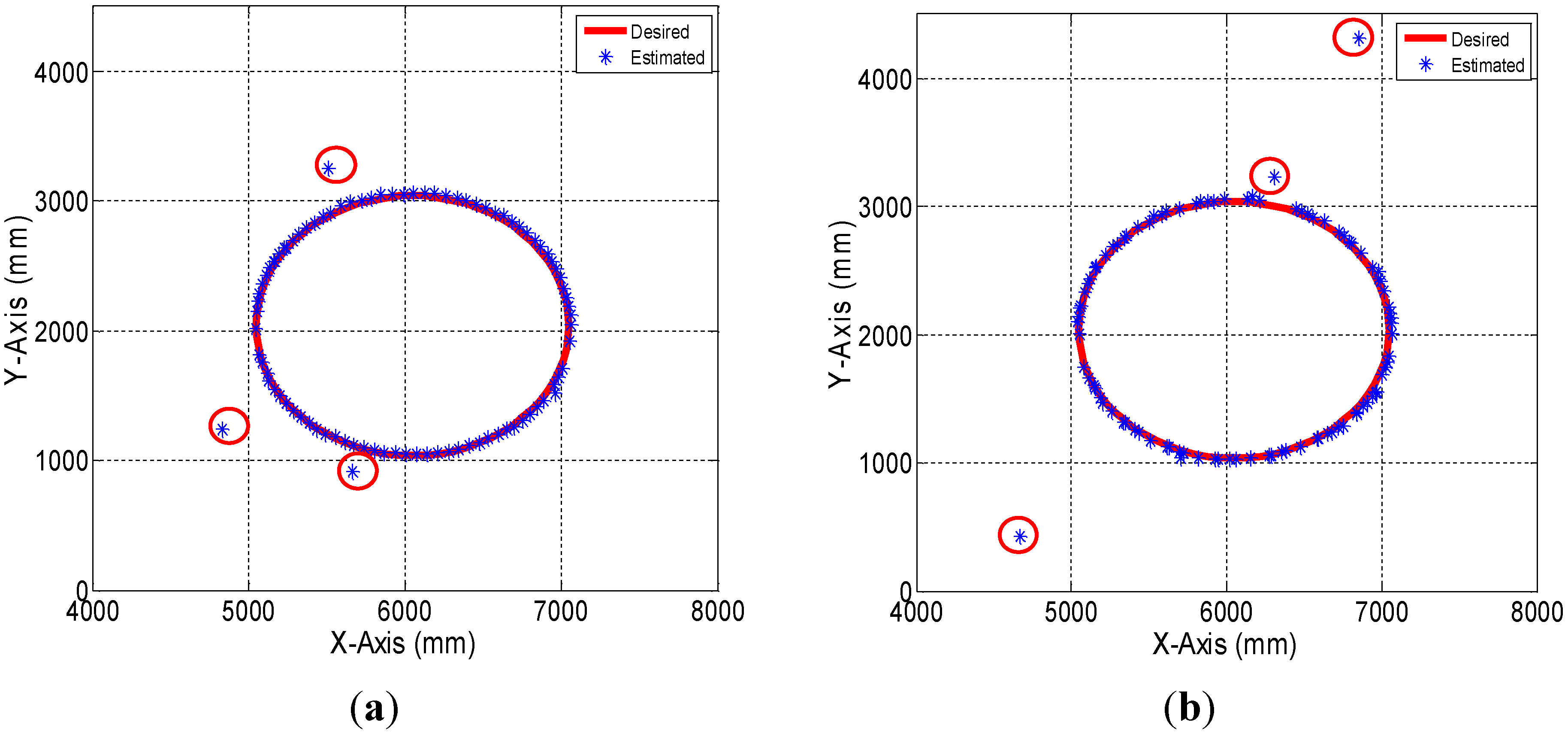
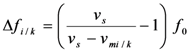
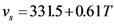
 = [
= [  ,
,  ,
,  ,
,  ] can be estimated using a kinematics model:
] can be estimated using a kinematics model:
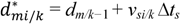
 ). If
). If  – 5σi ≤ dmi/k ≤
– 5σi ≤ dmi/k ≤  +5σi then dmi/k is a valid value, otherwise it is considered an outlier and rejected.
+5σi then dmi/k is a valid value, otherwise it is considered an outlier and rejected.  ± 3σi).
± 3σi).
5.3. The Influence of Noise
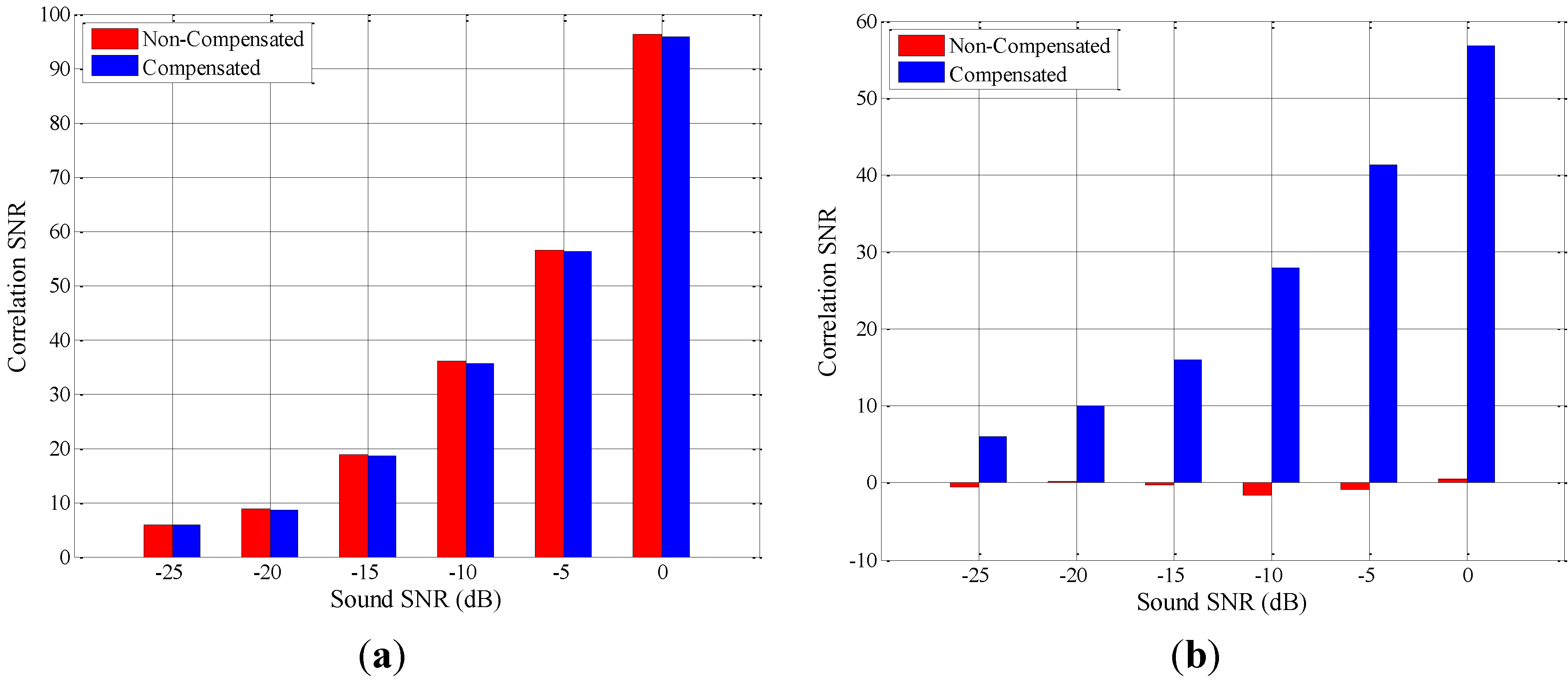
6. Conclusions
Acknowledgments
References
- Kondo, N.; Ting, K.C. Robotics for Bioproduction Systems; American Society of Agricultural Engineers: Ann Arbor, MI, USA, 1998. [Google Scholar]
- Edan, Y.; Han, S.; Kondo, N. Automation in agriculture. In Springer Handbook of Automation; Springer: Berlin, Germany, 2009; pp. 1095–1128. [Google Scholar]
- Bakker, T.; van Asselt, K.; Bontsema, J.; Müller, J.; van Straten, G. An autonomous weeding robot for organic farming. In Field and Service Robotics; Corke, D.P., Sukkariah, D.S., Eds.; Springer: Berlin, Germany, 2006; pp. 579–590. [Google Scholar]
- Slaughter, D.C.; Giles, D.K.; Downey, D. Autonomous robotic weed control systems: A review. Comput. Electron. Agr. 2008, 61, 63–78. [Google Scholar] [CrossRef]
- Acaccia, G.M.; Michelini, R.C.; Molfino, R.M.; Razzoli, R.P. Mobile Robots in Greenhouse Cultivation: Inspection and Treatment of Plants. In Proceesings of the the 1st International Workshop on Advances in Service Robotics, Bardolino, Italy, 13–15 March 2003.
- Søgaard, H.T.; Lund, I. Application accuracy of a machine vision-controlled robotic micro-dosing system. Biosyst. Eng. 2007, 96, 315–322. [Google Scholar] [CrossRef]
- Van Henten, E.J.; van Tuijl, B.A.J.; Hemming, J.; Kornet, J.G.; Bontsema, J.; van Os, E.A. Field test of an autonomous cucumber picking robot. Biosyst. Eng. 2003, 86, 305–313. [Google Scholar] [CrossRef]
- Tanigaki, K.; Fujiura, T.; Akase, A.; Imagawa, J. Cherry-harvesting robot. Comput. Electron. Agr. 2008, 63, 65–72. [Google Scholar] [CrossRef]
- Hayashi, S.; Shigematsu, K.; Yamamoto, S.; Kobayashi, K.; Kohno, Y.; Kamata, J.; Kurita, M. Evaluation of a strawberry-harvesting robot in a field test. Biosyst. Eng. 2010, 105, 160–171. [Google Scholar] [CrossRef]
- Goense, D. The Economics of Autonomous Vehicles. In Proceedings of the VDI-MEG Conference on Agricultural Engineering, VDI-Tagung Landtechnic, Hannover, Germany, 7–8 November 2003.
- Li, M.; Imou, K.; Wakabayashi, K.; Yokoyama, S. Review of research on agricultural vehicle autonomous guidance. Int. J. Agric. Biol. Eng. 2009, 2, 1–16. [Google Scholar]
- Pedersen, S.M.; Fountas, S.; Have, H.; Blackmore, B.S. Agricultural robots—System analysis and economic feasibility. Precis. Agr. 2006, 7, 295–308. [Google Scholar] [CrossRef]
- Harter, A.; Hopper, A.; Steggles, P.; Ward, A.; Webster, P. The anatomy of a context-aware application. Wireless Netw. 2002, 8, 187–197. [Google Scholar] [CrossRef]
- Priyantha, N.B.; Chakraborty, A.; Balakrishnan, H. The Cricket Location-Support System. In Proceeding of the 6th Annual International Conference on Mobile Computing and Networking, Boston, MA, USA, 6–11 August 2000; pp. 32–43.
- Balakrishnan, H.; Priyantha, N.B. The Cricket Indoor Location System: Experience and Status. In Proceedings of the 2003 Workshop on Location-Aware Computing, Seattle, WA, USA, 12 October 2003; pp. 7–9.
- Hazas, M.; Ward, A. A High Performance Privacy-Oriented Location System. In Proceeding of the 1st IEEE International Conference on Pervasive Computing and Communications, Fort Worth, TX, USA, 23–26 March 2003; pp. 216–233.
- Hazas, M.; Hopper, A. Broadband ultrasonic location systems for improved indoor positioning. IEEE Trans. Mobile Comput. 2006, 5, 536–547. [Google Scholar] [CrossRef]
- Prieto, J.C.; Jiménez, A.R.; Guevara, J.I.; Ealo, J.L.; Seco, F.A.; Roa, J.O.; Ramos, J.X. Subcentimeter-Accuracy Localization through Broadband Acoustic Transducers. In Proceeding of IEEE International Symposium on Intelligent Signal Processing 2007, Alcala de Henares, Spain, 3–5 October 2007; pp. 1–6.
- Prieto, J.C.; Jiménez, A.R.; Guevara, J.I.; Ealo, J.L.; Seco, F.A.; Roa, J.O.; Ramos, F. Performance evaluation of 3D-LOCUS advanced acoustic LPS. IEEE Trans. Instrum. Meas. 2009, 58, 2385–2395. [Google Scholar] [CrossRef]
- Girod, L.; Estrin, D. Robust Range Estimation Using Acoustic and Multimodal Sensing. In Proceeding of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2011; pp. 1312–1320.
- Smith, A.; Balakrishnan, H.; Goraczko, M.; Priyantha, N. Tracking Moving Devices with the Cricket Location System. In Proceeding of MobiSYS’04, Boston, MA, USA, 6–9 June 2004.
- Vallidis, N.M. WHISPER: A Spread Spectrum Approach to Occlusion in Acoustic Tracking. Ph.D. Thesis, The University of North Carolina, Chapel Hill, NC, USA, 2002. [Google Scholar]
- Suzuki, A.; Iyota, T.; Choi, Y.; Kubota, Y.; Watanabe, K.; Yamane, A. Measurement Accuracy on Indoor Positioning System Using Spread Spectrum Ultrasonic Waves. In Proceeding of the 4th International Conference on Autonomous Robots and Agents, Wellington, New Zealand, 10–12 February 2009; pp. 294–297.
- Ito, N.; Suzuki, A.; Iyota, T. Verification of CDMA and Accuracy on Echo Ranging System Using Spread Spectrum Ultrasonic Signals. In Proceeding of the 5th International Conference on AutomationRobotics and Applications, Wellington, New Zealand, 6–8 December 2011; pp. 476–479.
- Itagaki, Y.; Suzuki, A.; Iyota, T. Indoor Positioning for Moving Objects Using a Hardware Device with Spread Spectrum Ultrasonic Waves. In Proceeding of the 2012 International Conference on Indoor Positioning and Indoor Navigation, Sydney, Australia, 13–15 November 2012; pp. 1–6.
- Mak, L.C.; Furukawa, T. A time-of-arrival-based positioning technique with non-line-of-sight mitigation using low-frequency sound. Adv. Robot. 2008, 22, 507–526. [Google Scholar]
- Widodo, S.; Shiigi, T.; Than, N.M.; Kikuchi, H.; Yanagida, K.; Nakatsuchi, Y.; Ogawa, Y.; Kondo, N. Wind compensation using base station for spread spectrum sound-based positioning system in open field. EAEF 2013, in press. [Google Scholar]
- Ko, S.I.; Choi, J.S.; Kim, B.H. Indoor mobile localization system and stabilization of localization performance using pre-filtering. Int. J. Contr. Autom. Syst. 2008, 6, 204–213. [Google Scholar]
- Muller, H.L.; McCarthy, M.; Randell, C. Particle Filters for Position Sensing with Asynchronous Ultrasonic Beacons. In Proceeding of the Second International Workshop, Dublin, Ireland, 10–11 May 2006; pp. 1–13.
- Álvarez, F.J.; Hernández, Á.; Moreno, J.A.; Pérez, M.C.; Ureña, J.; de Marziani, C. Doppler-tolerant receiver for an ultrasonic LPS based on Kasami sequences. Sens. Actuator. A Phys. 2013, 189, 238–253. [Google Scholar] [CrossRef]
- Kusy, B.; Ledeczi, A.; Koutsoukos, X. Tracking Mobile Nodes Using RF Doppler Shifts. In Proceeding of the 5th ACM Conference on Embedded Networked Sensor Systems, Sydney, Australia, 6–9 November 2007.
- Amundson, I.; Koutsoukos, X.; Sallai, J. Mobile Sensor Localization and Navigation Using RF Doppler Shifts. In Proceedings of the 1st ACM international Workshop on Mobile Entity Localization and Tracking in GPS-Less Environments, San Francisco, CA, USA, 14–19 September 2008.
- Shiigi, T.; Kondo, N.; Tsuzuki, S.; Okada, S.; Maekawa, A.; Nobara, T.; Sakakibara, M.; Watanabe, K.; Naniwada, Y.; Okada, K. Position Detecting Method Using Spread Spectrum Sound: Correction Method of Measurement Error by Compensating Wind and Temperature. In Proceedings of the 3rd IFAC International Conference Agricontro, Kyoto, Japan, 6–8 December 2010.
- Ohno, K.; Tsubouchi, T.; Shigematsu, B.; Yuta, S. Differential GPS and odometry-based outdoor navigation of a mobile robot. Adv. Robot. 2004, 18, 611–635. [Google Scholar] [CrossRef]
- McBride, D.I.; Firth, H.M.; Herbison, G.P. Noise exposure and hearing loss in agriculture: A survey of farmers and farm workers in the southland region of New Zealand. J. Occup. Environ. Med. 2003, 45, 1281–1288. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Widodo, S.; Shiigi, T.; Hayashi, N.; Kikuchi, H.; Yanagida, K.; Nakatsuchi, Y.; Ogawa, Y.; Kondo, N. Moving Object Localization Using Sound-Based Positioning System with Doppler Shift Compensation. Robotics 2013, 2, 36-53. https://doi.org/10.3390/robotics2020036
Widodo S, Shiigi T, Hayashi N, Kikuchi H, Yanagida K, Nakatsuchi Y, Ogawa Y, Kondo N. Moving Object Localization Using Sound-Based Positioning System with Doppler Shift Compensation. Robotics. 2013; 2(2):36-53. https://doi.org/10.3390/robotics2020036
Chicago/Turabian StyleWidodo, Slamet, Tomoo Shiigi, Naoki Hayashi, Hideo Kikuchi, Keigo Yanagida, Yoshiaki Nakatsuchi, Yuichi Ogawa, and Naoshi Kondo. 2013. "Moving Object Localization Using Sound-Based Positioning System with Doppler Shift Compensation" Robotics 2, no. 2: 36-53. https://doi.org/10.3390/robotics2020036




