A Review of Active Mechanical Driving Principles of Spherical Robots
Abstract
:1. Introduction
2. Barycenter Offset (BCO)
2.1. Governing Principle
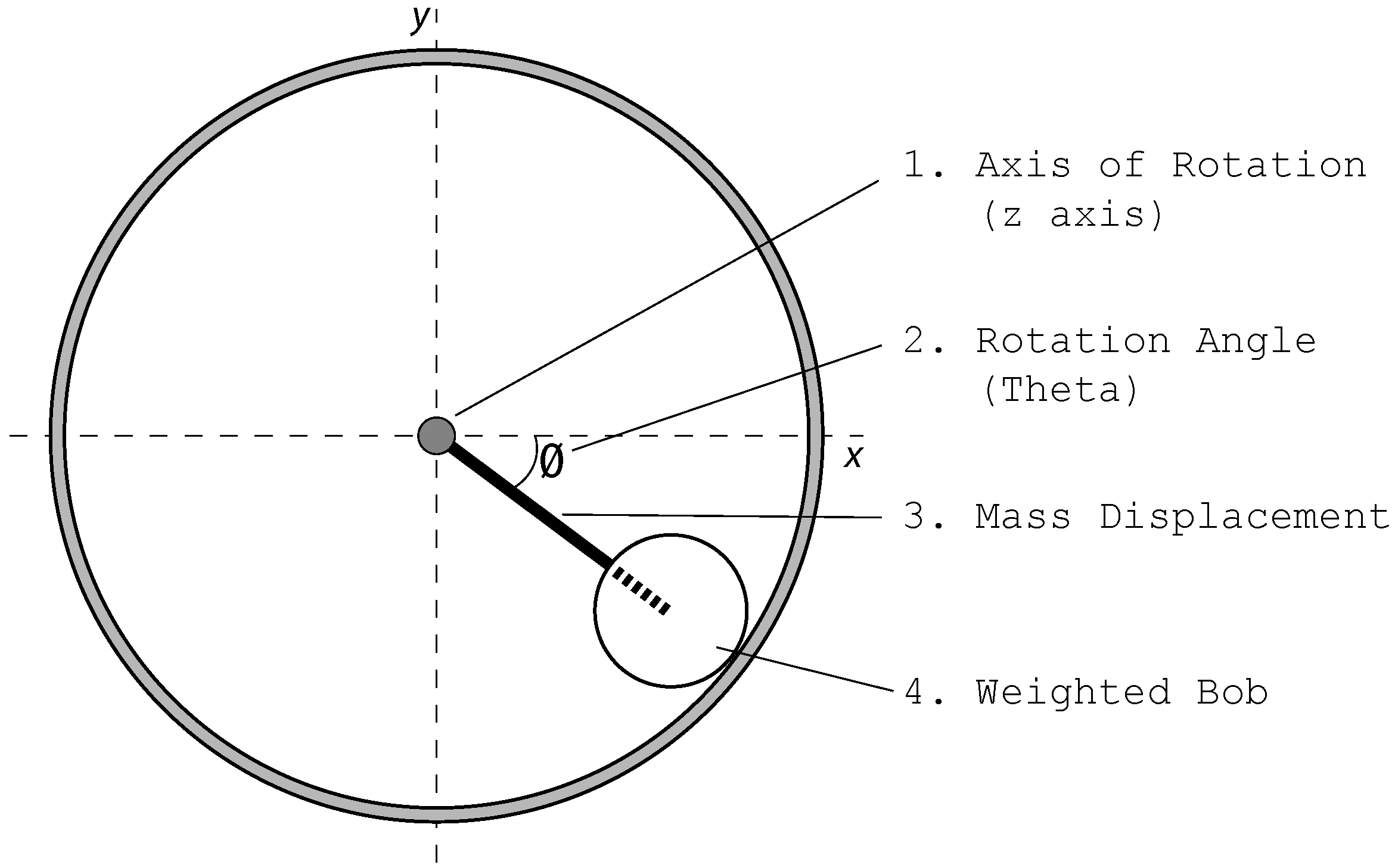
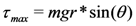
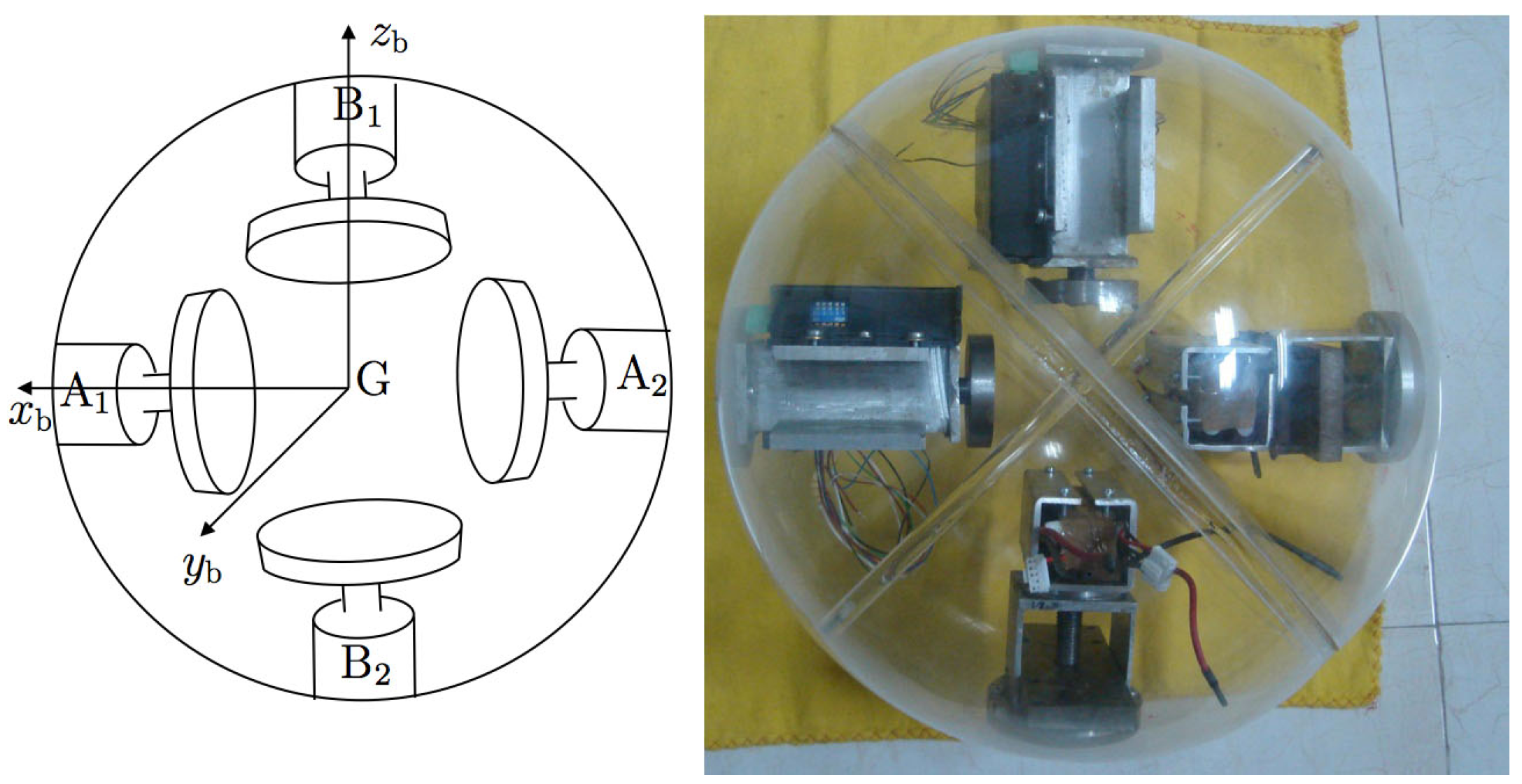
2.2. Implementations of Governing Principle
2.2.1. Hamster Ball

2.2.2. Internal Drive Unit (IDU)
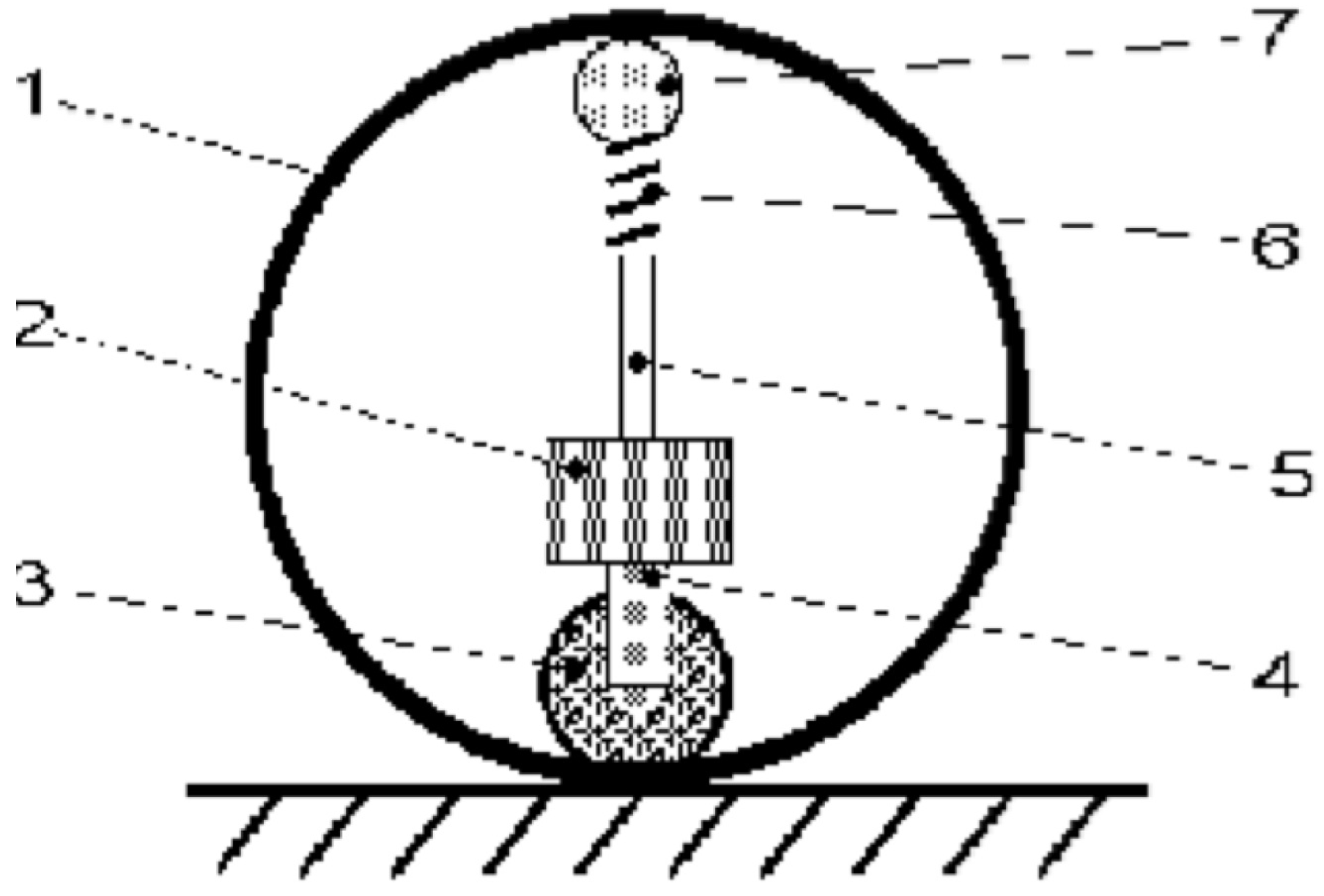
2.2.3. Universal Wheel
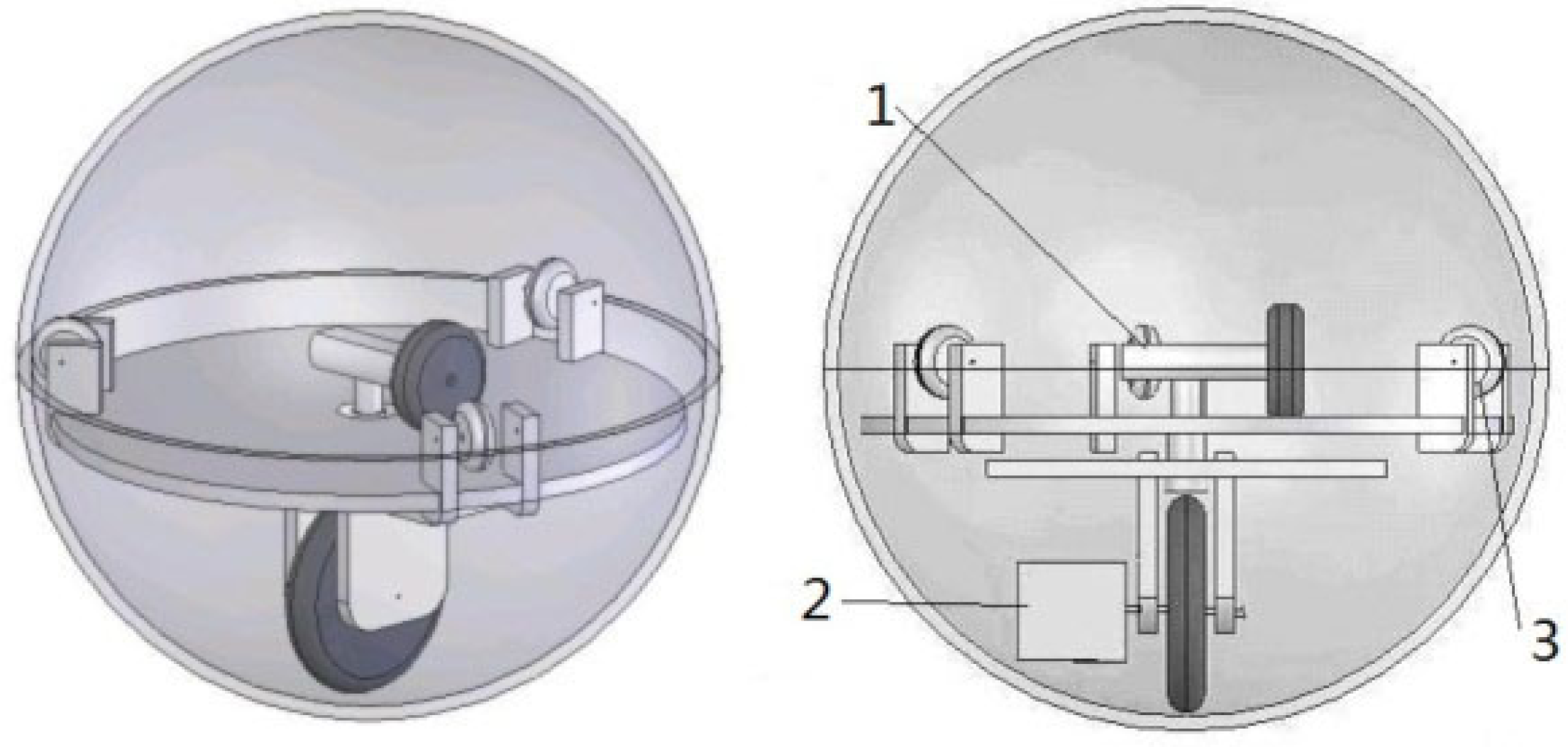

2.2.4. Pendulum Driven
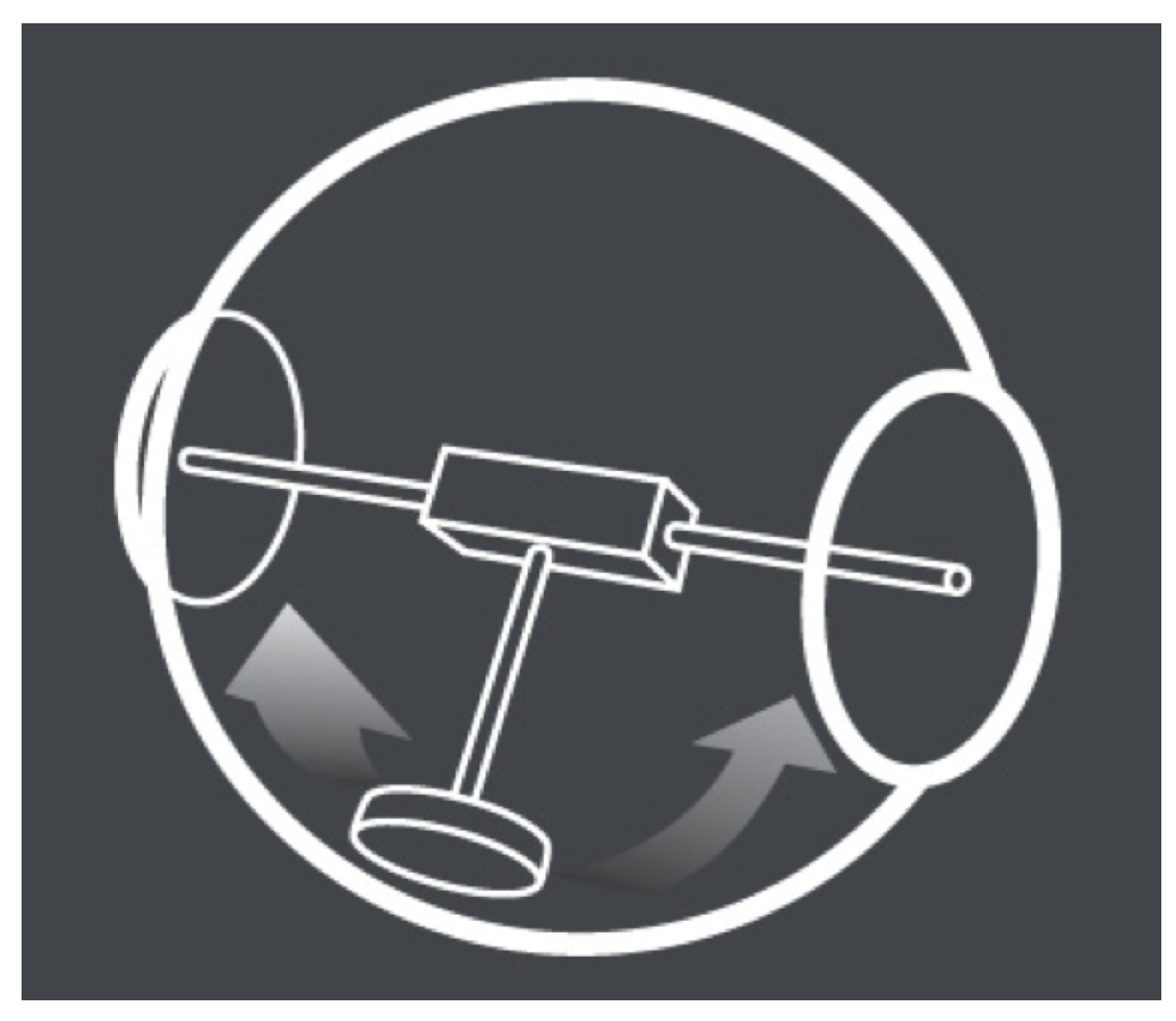
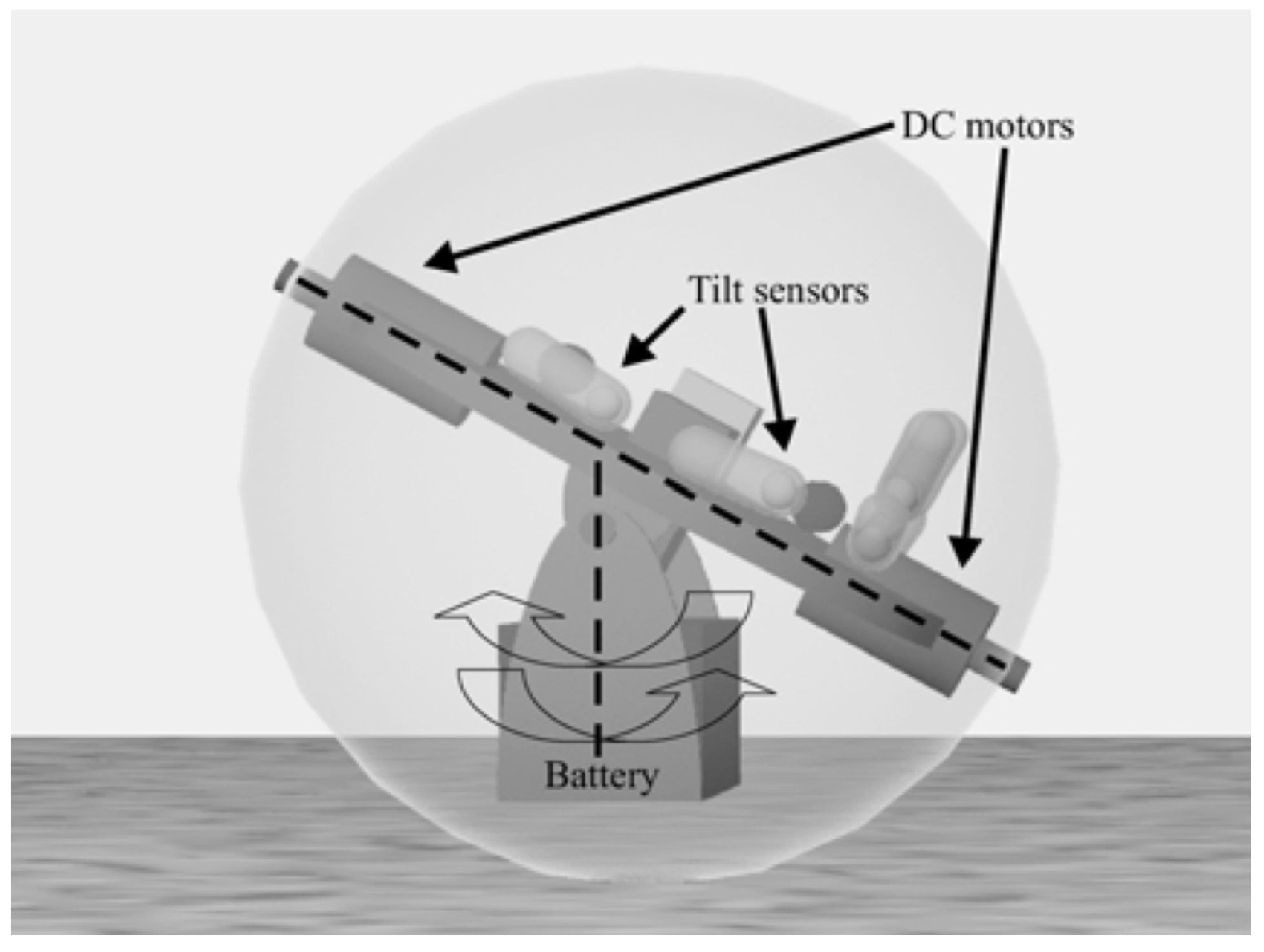
2.2.5. Double Pendulum

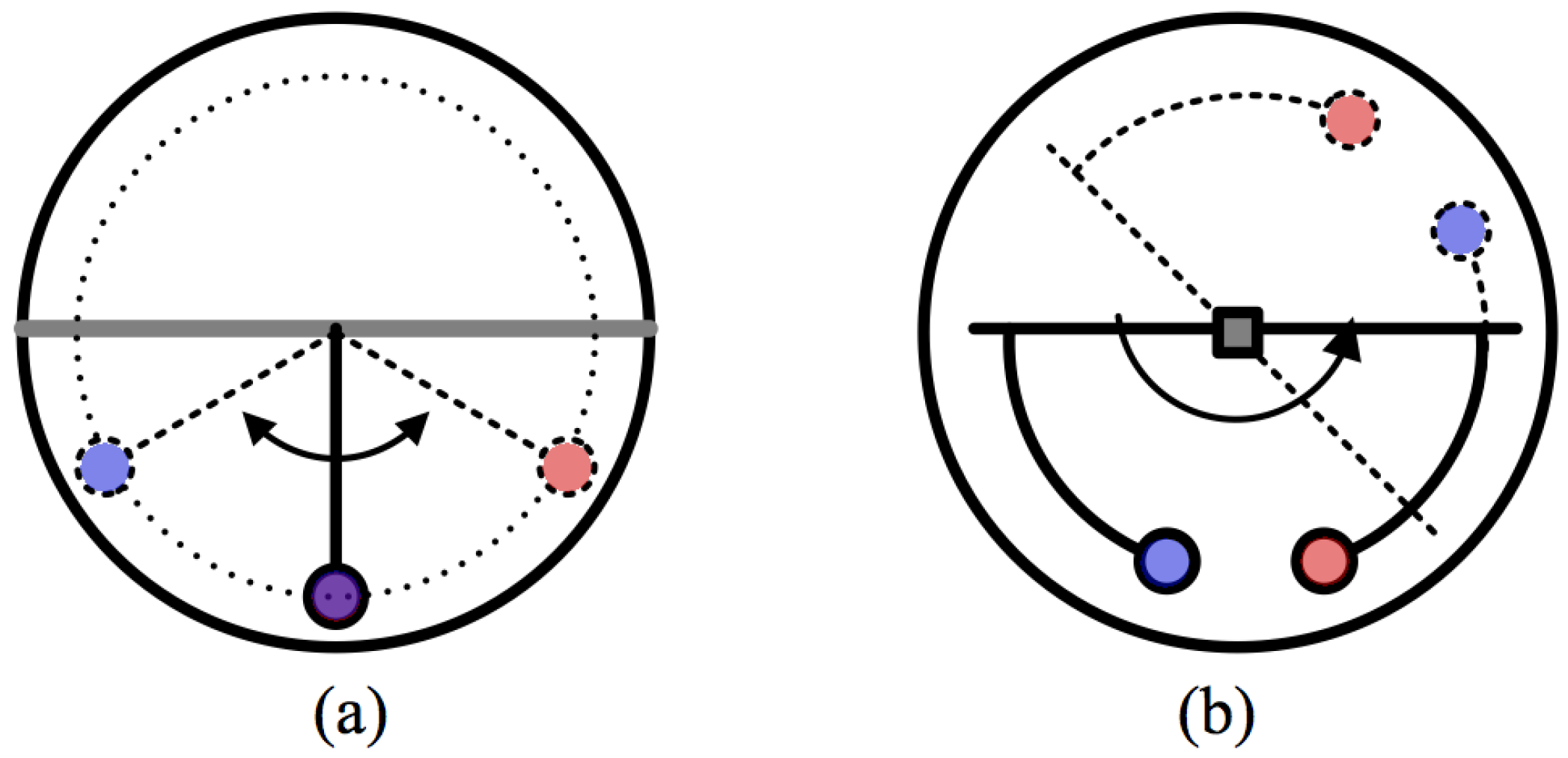
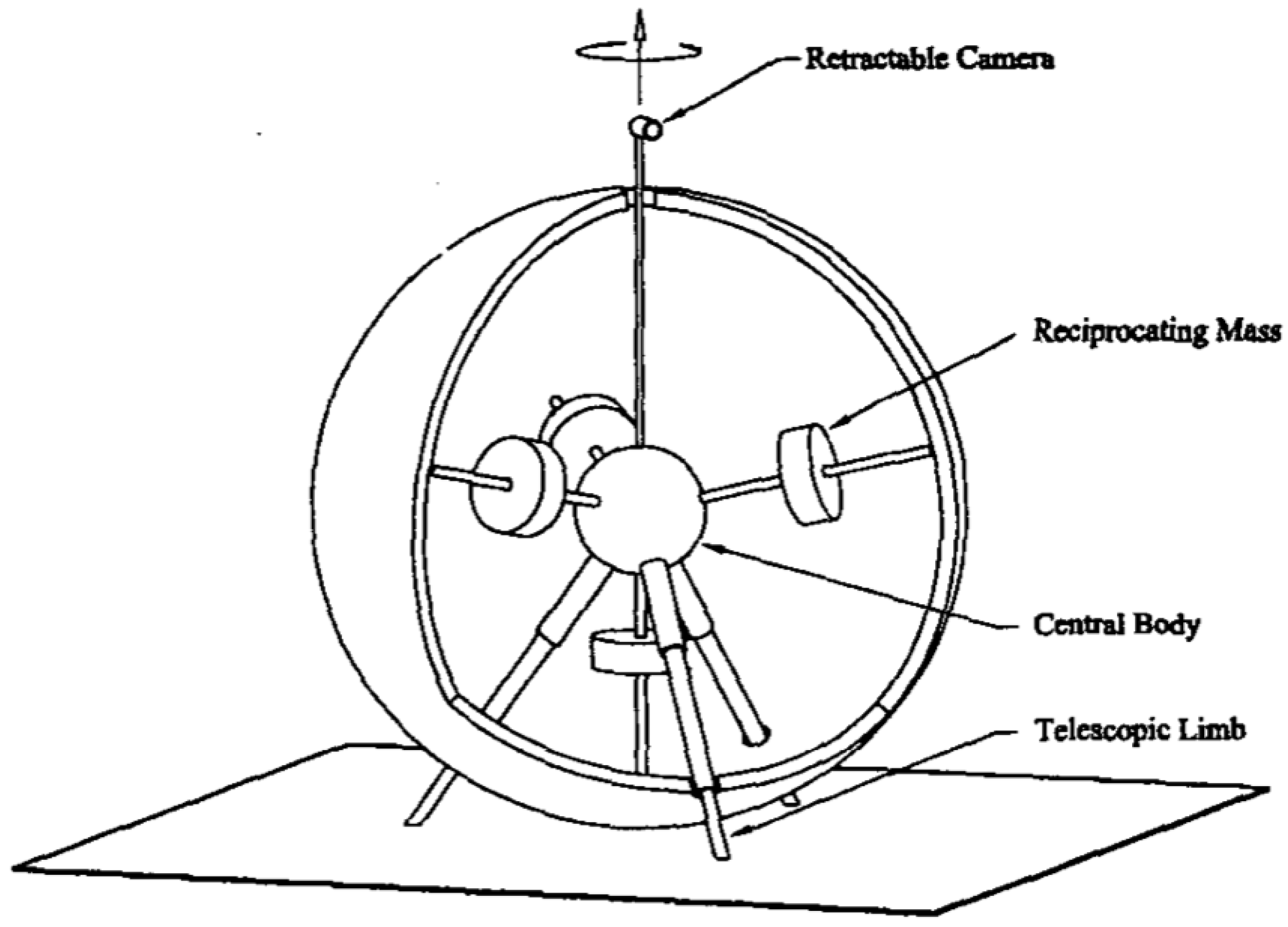
2.2.6. Notable Enhancements



3. Shell Transformation
3.1. Governing Principle
3.2. Implementations of Governing Principle
3.2.1. Pressurized Air Bladders

3.2.2. Shape Memory Alloys

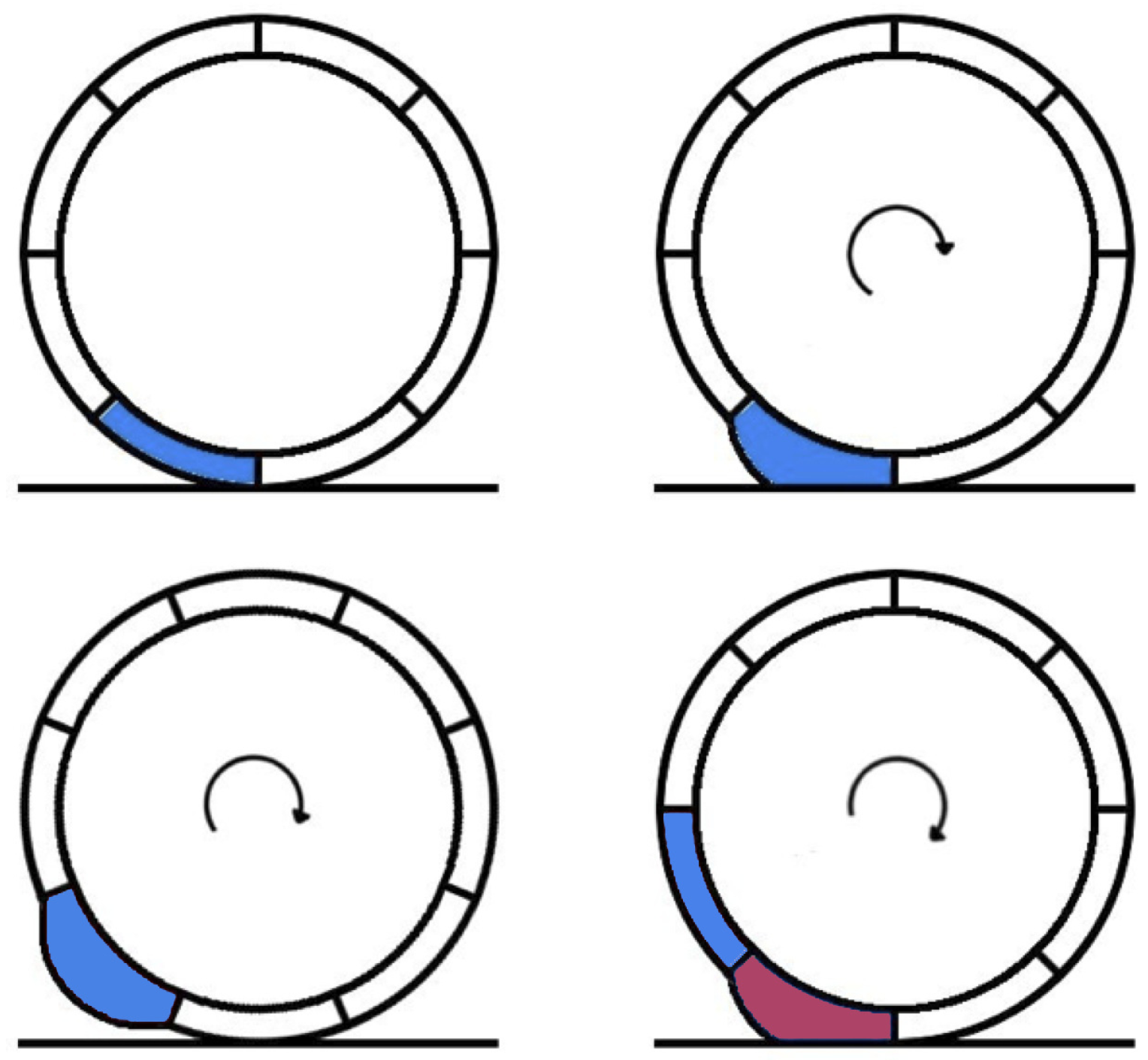
4. Conservations of Angular Momentum (COAM)
4.1. Governing Principle
4.2. Implementations of Governing Principle
4.2.1. Balancing
4.2.2. Uni-Dimensional COAM

4.2.3. Tri-Dimensional COAM

4.2.4. Scissored-Pairs
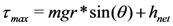

5. Summary and Conclusions
| Type | Principle | Method | Source of Movement | Power Factor | Example |
|---|---|---|---|---|---|
| 1 | BCO | Shifting COG | COG Shift |  | R. Mukherjee et al. [19] |
| 2 | BCO | Single Wheel | Equilibrium Change |  | Halme et al. [1] |
| 3 | BCO | Universal Wheel | Downward Force on Shell |  | Zhan et al. [11] |
| 4 | BCO | Pendulum | Torque about Diameter |  | Michaud et al. [15] |
| 5 | COAM | Single-Axis | Reaction force from spin of CMG |  | Guanghui et al. [30] |
| 6 | COAM | Triple-Axis | Precession Torque |  | Schroll et al. [14,37] |
| 7 | OST | Shell Transformation | Various | Various | Artusi, Wait, Yamanaka, Sugiyama et al. [24,25,26,27] |
References
- Halme, A.; Schonberg, T.; Wang, Y. Motion Control of a Spherical Mobile Robot. In Proceedings of the 4th International Workshop on Advanced Motion Control (AMC’96-MIE), Tsu-City, Japan, March 1996; 1, pp. 259–264.
- Lin, X.; Guo, S.; Tanaka, K.; Hata, S. Development of a Spherical Underwater Robot. In Proceedings of 2011 IEEE/ICME International Conference on Complex Medical Engineering (CME), Harbin, China, May 2011; pp. 662–665.
- Lin, X.; Guo, S.; Tanaka, K.; Hata, S. Underwater Experiments of a Water-Jet-Based Spherical Underwater. Robot. In Proceedings of 2011 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, August 2011; pp. 738–742.
- Michaud, F.; Laplante, J.; Larouche, H.; Duquette, A.; Caron, S.; Létourneau, D.; Masson, P. Autonomous spherical mobile robot for child-development studies. IEEE Trans. Syst. Man Cybern. A 2005, 35, 471–480. [Google Scholar] [CrossRef]
- Kenyon, S.; Creary, D.; Thi, D.; Maynard, J. A small, cheap, and portable reconnaissance robot. Proc. SPIE 2005, 5778, 434–443. [Google Scholar]
- Seeman, M.; Broxvall, M.; Saffiotti, A.; Wide, P. An Autonomous Spherical Robot for Security Tasks. In Proceedings of 2006 IEEE International Conference on Computational Intelligence for Homeland Security and Personal Safety, Orlando, FL, USA, April 2006; pp. 51–55.
- Yili, Z.; Hanxu, S.; Qingxuan, J.; Chenkun, S.; Kailiang, Z. An Omni-Directional Rolling Spherical Robot with Telescopic Manipulator. In Proceedings of the 2nd International Symposium on Systems and Control in Aerospace and Astronautics (ISSCAA 2008), Shenzhen, China, December 2008; pp. 1–6.
- Appelqvist, P. Mechatronics Design of a Robot Society: A Case Study of Minimalist Underwater Robots for Distributed Perception and Task Execution; Helsinki University of Technology: Helsinki, Finland, 2000. [Google Scholar]
- Liu, D.; Sun, H.; Jia, Q. A Family of Spherical Mobile Robot: Driving Ahead Motion Control by Feedback Linearization. In Proceedings of the 2nd International Symposium on Systems and Control in Aerospace and Astronautics (ISSCAA 2008), Shenzhen, China, December 2008; pp. 1–6.
- Alves, J.; Dias, J. Design and control of a spherical mobile robot. Proc IME J. Syst. Contr. Eng. 2003, 217, 457–467. [Google Scholar]
- Zhan, Q.; Cai, Y.; Yan, C. Design, Analysis and Experiments of an Omni-Directional Spherical Robot. In Proceedings of 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, May 2011; pp. 4921–4926.
- Yue, M.; Deng, Z.; Yu, X.; Yu, W. Introducing HIT Spherical Robot: Dynamic Modeling and Analysis Based on Decoupled Subsystem. In Proceedings of IEEE International Conference on Robotics and Biomimetics (ROBIO’06), Kunming, China, December 2006; pp. 181–186.
- Rotundus. Available online: http://www.rotundus.se (accessed on 22 May 2012).
- Schroll, G. Dynamic Model of a Spherical Robot from First Pinciples. M.S. Thesis, Colorado State University, Fort Collins, CO, USA, 2010. [Google Scholar]
- Michaud, F.; Caron, S. Roball, the rolling robot. Auton. Robots 2002, 12, 211–222. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, P.; Hu, H.; Li, M.; Sun, L. Study on Turning in Place of a Spherical Robot Based on Stick-Slip Principle. In Proceedings of 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, December 2009; pp. 771–775.
- Zhao, B.; Li, M.; Yu, H.; Hu, H.; Sun, L. Dynamics and Motion Control of a Two Pendulums Driven Spherical Robot. In Proceedings of 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, October 2010; pp. 147–153.
- Yoon, J.; Ahn, S.; Lee, Y. Spherical Robot with New Type of Two-Pendulum Driving Mechanism. In Proceedings of 2011 15th IEEE International Conference on Intelligent Engineering Systems (INES), Poprad, Slovakia, June 2011; pp. 275–279.
- Mukherjee, R.; Minor, M.; Pukrushpan, J. Simple Motion Planning Strategies for Spherobot: A Spherical Mobile Robot. In Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, December 1999; 3, pp. 2132–2137.
- Chadil, N.; Phadoongsidhi, M.; Suwannasit, K.; Manoonpong, P.; Laksanacharoen, P. A Reconfigurable Spherical Robot. In Proceedings of 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, May 2011; pp. 2380–2385.
- Jearanaisilawong, P.; Laksanacharoen, S.; Piriyawong, V.; Swatdipisal, K. Design of a Three-Legged Reconfigurable Spherical Shape Robot. In Proceedings of IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, July 2009; pp. 1730–1733.
- Kim, Y.; Ahn, S.; Lee, Y. KisBot: New Spherical Robot with Arms. In Proceedings of the 10th WSEAS International Conference on Robotics Control and Manufacturing Technology, Hangzhou, China, April 2010; pp. 63–67.
- Li, B.; Deng, Q.; Liu, Z. A Spherical Hopping Robot for Exploration in Complex Environments. In Proceedings of 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, December 2009; pp. 402–407.
- Artusi, M.; Potz, M.; Aristizabal, J.; Menon, C.; Cocuzza, S.; Debei, S. Electroactive elastomeric actuators for the implementation of a deformable spherical rover. IEEE/ASME Trans. Mechatron. 2011, 16, 50–57. [Google Scholar] [CrossRef]
- Wait, K.; Jackson, P.; Smoot, L. Self Locomotion of a Spherical Rolling Robot Using a Novel Deformable Pneumatic Method. In Proceedings of 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, May 2010; pp. 3757–3762.
- Yamanaka, T.; Nakaura, S.; Sampei, M. Hopping Motion Analysis of “Superball”-Like Spherical Robot Based on Feedback Control. In Proceedings of 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003), Las Vegas, NV, USA, October 2003; 4, pp. 3805–3810.
- Sugiyama, Y.; Shiotsu, A.; Yamanaka, M.; Hirai, S. Circular/Spherical Robots for Crawling and Jumping. In Proceedings of 2005 IEEE International Conference on Robotics and Automation (ICRA 2005), Barcelona, Spain, April 2005; pp. 3595–3600.
- Au, K.; Xu, Y. Decoupled Dynamics and Stabilization of Single Wheel Robot. In Proceedings of 1999 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’99), Kyongju, Korea, October 1999; 1, pp. 197–203.
- Brown, H., Jr.; Xu, Y. A Single-Wheel, Gyroscopically Stabilized Robot. In Proceedings of 1996 IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, April 1996; 4, pp. 3658–3663.
- Shu, G.; Zhan, Q.; Cai, Y. Motion Control of Spherical Robot Based on Conservation of Aangular Momentum. In Proceedings of International Conference on Mechatronics and Automation (ICMA 2009), Changchun, China, August 2009; pp. 599–604.
- Joshi, V.; Banavar, R. Motion analysis of a spherical mobile robot. Robotica 2010, 27, 343–353. [Google Scholar] [CrossRef]
- Joshi, V.; Banavar, R.; Hippalgaonkar, R. Design, Modeling and Controllability of a Spherical Mobile Robot. In Proceedings of the 13th National Conference on Mechanisms and Machines (NaCoMM07), Bangalore, India, 12–13 December 2007.
- Qingxuan, J.; Yili, Z.; Hanxu, S.; Hongyu, C.; Hongyi, L. Motion Control of a Novel Spherical Robot Equipped with a Flywheel. In Proceedings of 2009 International Conference on Information and Automation (ICIA’09), Zhuhai/Macau, China, June 2009; pp. 893–898.
- Carpenter, M.; Peck, M. Dynamics of a High-Agility, Low-Power Coelostat Telescope. In Proceedings of 2006 AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006.
- Aubrun, J.; Margulies, G. Gyrodampers for Large Space Structures; NASA Contractor Report 159171; Lockheed Palo Alto Research Laboratory: Palo Alto, CA, USA, 1979. [Google Scholar]
- Peck, M. Low-Power, High-Agility Space Robotics. In Proceedings of 2005 AIAA GuidanceNavigationand Control Conference and Exhibit, San Francisco, CA, USA, August 2005; pp. 1–12.
- Schroll, G. Angular Momentum Torque Enhancement for Spherical Vehicles. WO Patent WO/2010/057129, May 2010. [Google Scholar]
- 2008 Collegiate Inventors Competition Winners. Available online: http://www.invent.org/collegiate/win2008.htm (accessed on 31 October 2012).
- Carpenter, M. Power-Optimal Steering of a Space Robotic System Driven by Control-Moment Gyroscopes. In Proceedings of 2008 AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chase, R.; Pandya, A. A Review of Active Mechanical Driving Principles of Spherical Robots. Robotics 2012, 1, 3-23. https://doi.org/10.3390/robotics1010003
Chase R, Pandya A. A Review of Active Mechanical Driving Principles of Spherical Robots. Robotics. 2012; 1(1):3-23. https://doi.org/10.3390/robotics1010003
Chicago/Turabian StyleChase, Richard, and Abhilash Pandya. 2012. "A Review of Active Mechanical Driving Principles of Spherical Robots" Robotics 1, no. 1: 3-23. https://doi.org/10.3390/robotics1010003