Protein Association in Solution: Statistical Mechanical Modeling
Abstract
:1. Introduction
2. Solution Experiments Provide Insights on the Driving Forces
3. Background on Modeling the Forces in Protein Solutions
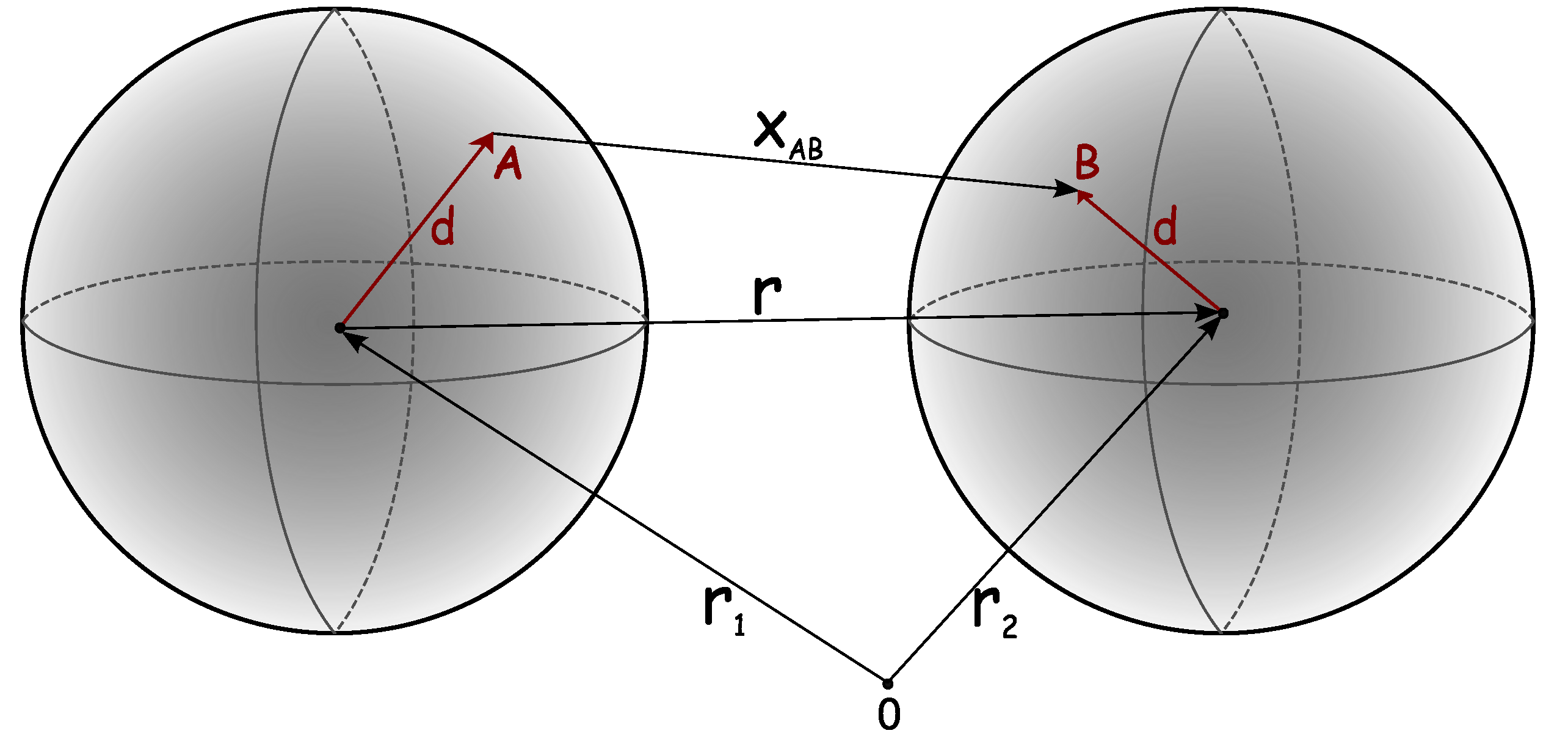
4. Statistical Mechanics-Based Treatments of Protein Interactions
5. The Wertheim Theory Treats Multi-Body Strong and Specific Associations
6. The Wertheim Theory Can Model Globular Protein Association
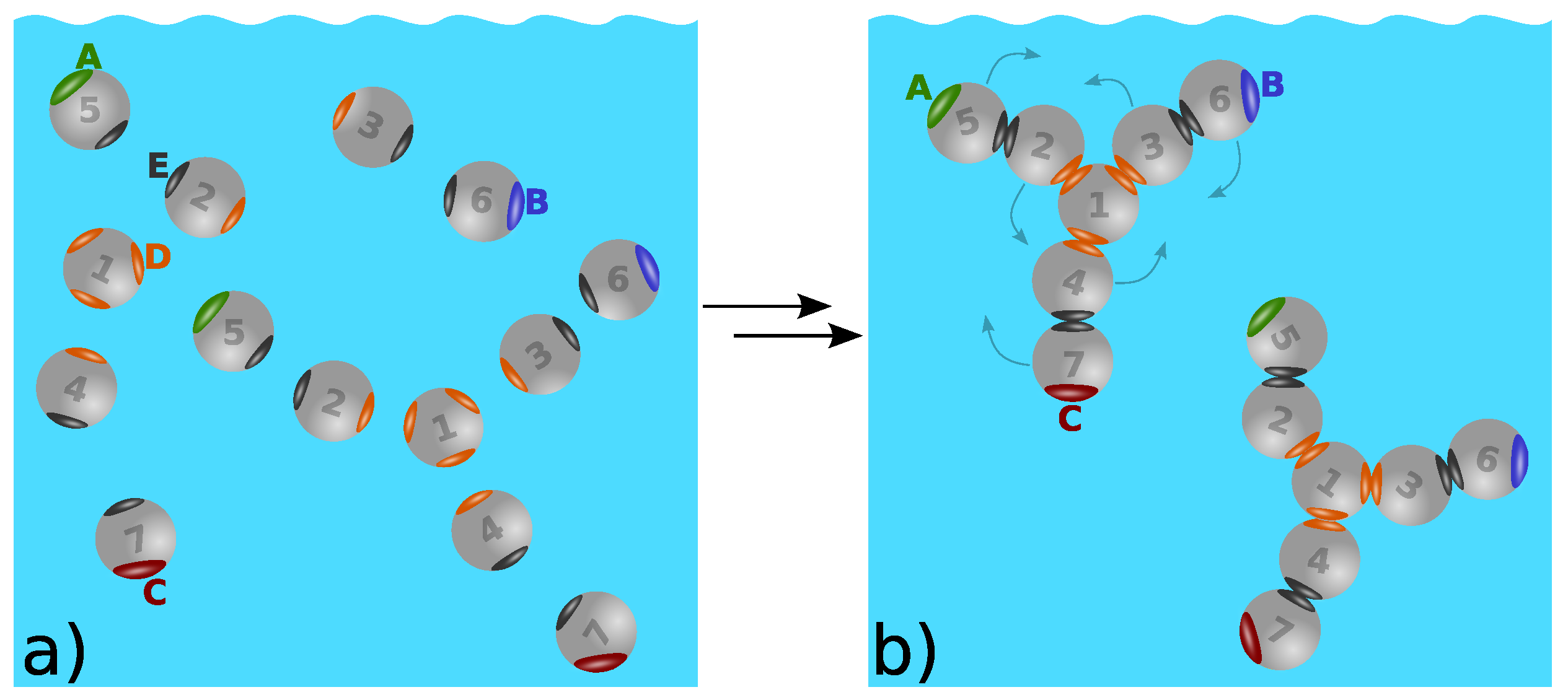
7. Structure–Property Relations of Antibodies: The Seven-Bead Wertheim Model
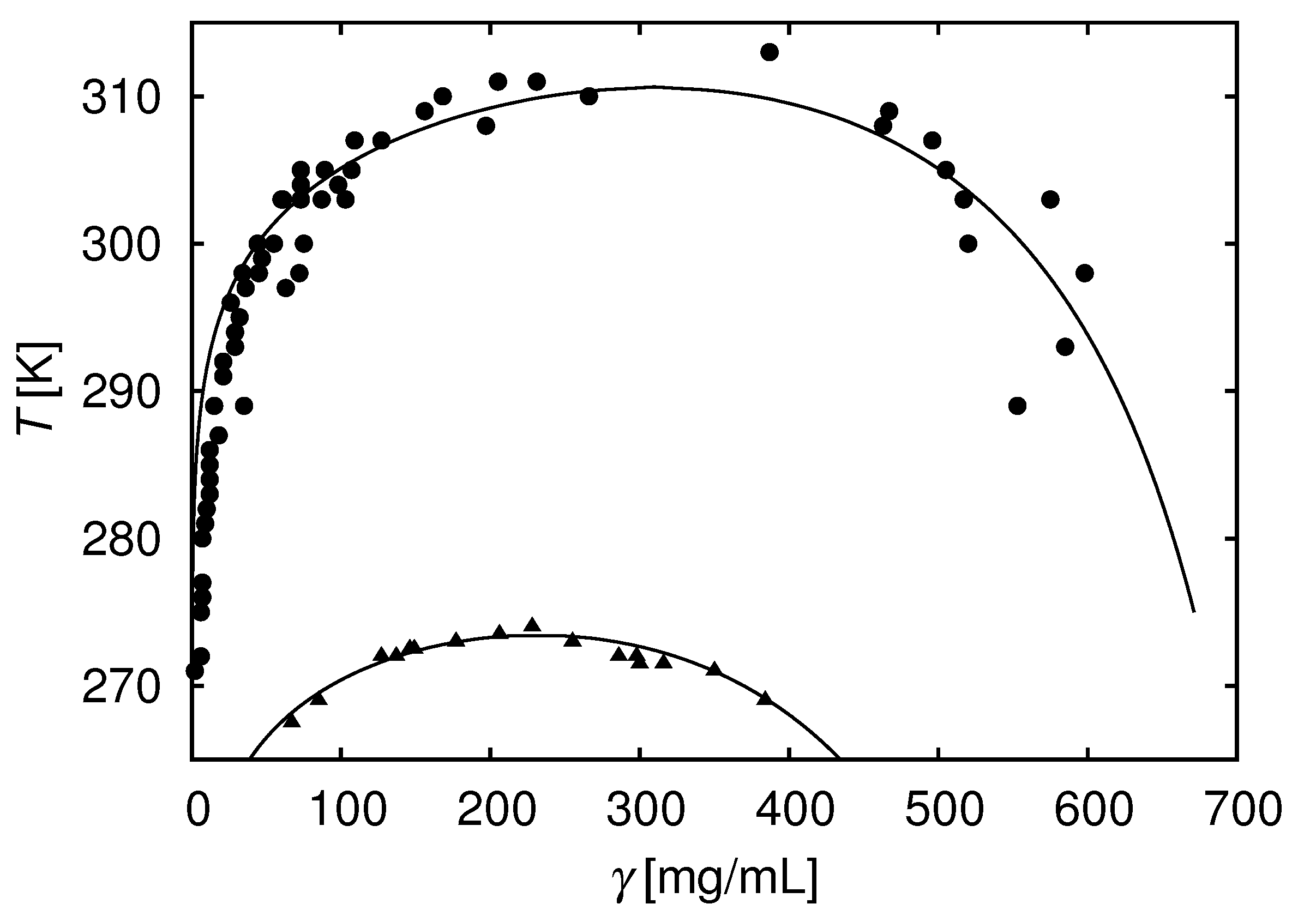
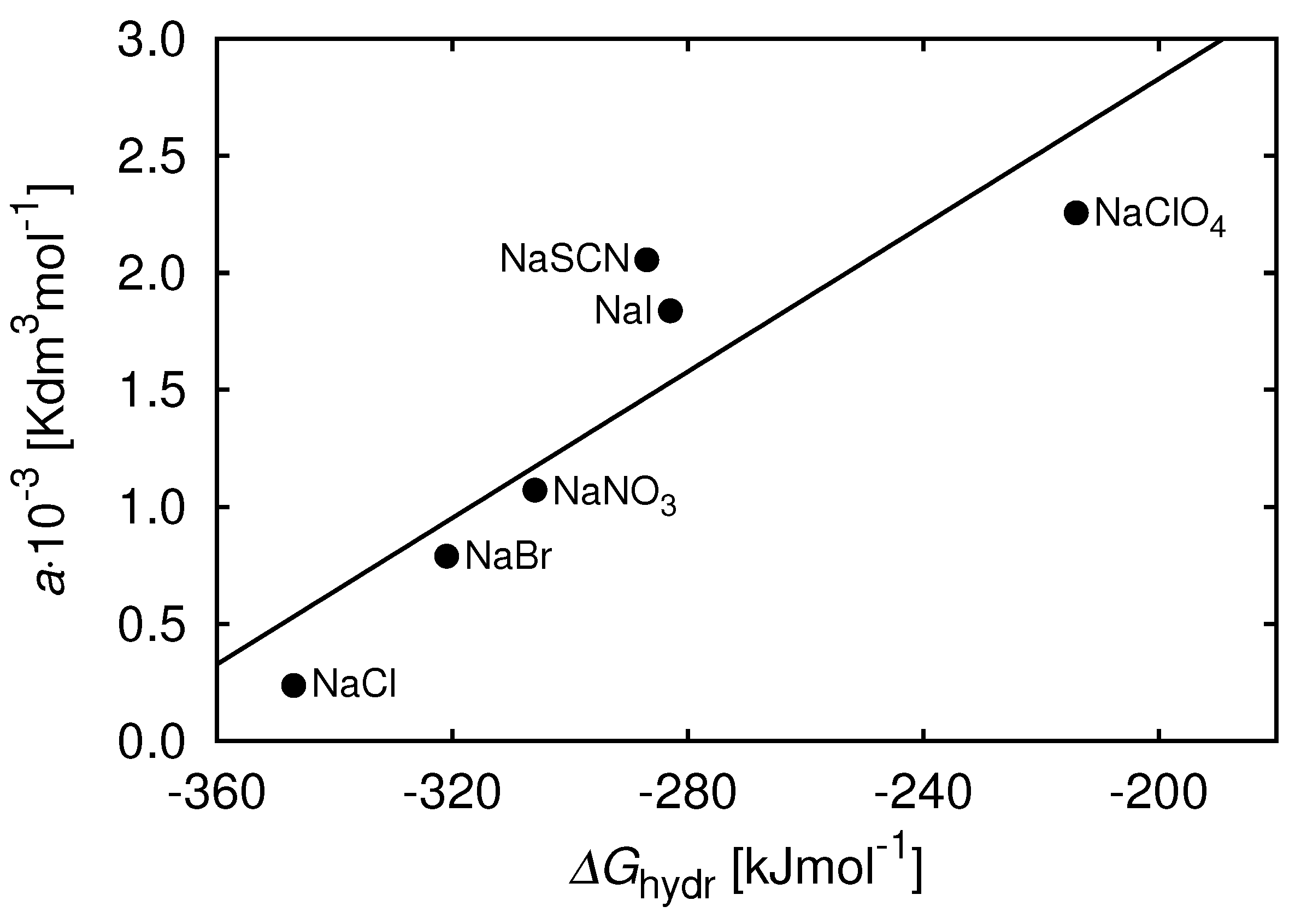
8. Additional Components Can Modulate Protein Associations
9. Crowding Can Alter Protein–Protein Association
10. Limitations and Challenges of Statistical Mechanical Modeling
11. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gunton, J.D.; Shiryayev, A.; Pagan, D.L. (Eds.) Protein Condensation: Kinetic Pathways to Crystallization and Disease; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Hyman, A.A. Phase transitions in cell. Science 2012, 337, 1047. [Google Scholar] [CrossRef] [PubMed]
- Shin, Y.; Brangwynne, C. Liquid phase condensation in cell physiology and disease. Science 2017, 357, 1253. [Google Scholar] [CrossRef] [PubMed]
- Benedek, G.B. Cataract as a protein condensation disease: The proctor lecture. Investig. Ophthalmol. Vis. Sci. 1997, 38, 1911–1921. [Google Scholar]
- Hyman, A.; Weber, C.; Jülicher, F. Liquid-liquid phase separation in biology. Annu. Rev. Cell Dev. Biol. 2014, 30, 39–58. [Google Scholar] [CrossRef]
- Alberti, S.; Dormann, D. Liquid-liquid phase separation in disease. Annu. Rev. Genet. 2014, 53, 171–194. [Google Scholar] [CrossRef]
- Shire, S.J.; Shahrokh, Z.; Liu, L. Challenges in the development of high protein concentration formulations. J. Pharm. Sci. 2004, 93, 1390–1402. [Google Scholar] [CrossRef]
- Schmit, J.D.; He, F.; Mishra, S.; Ketchem, R.R.; Woods, C.E.; Kerwin, B.A. Entanglement model of antibody viscosity. J. Phys. Chem. B 2014, 118, 5044–5049. [Google Scholar] [CrossRef]
- Roberts, D.; Keeling, R.; Tracka, M.; van der Walle, C.F.; Uddin, S.; Warwicker, J.; Curtis, R. Specific ion and buffer effects on protein—protein interactions of a monoclonal antibody. Mol. Pharm. 2015, 12, 179–193. [Google Scholar] [CrossRef]
- Woldeyes, M.A.; Qi, W.; Razinkov, V.I.; Furst, E.; Roberts, C. How well do low- and high- concentration protein interactions predict solution viscosities of monoclonal antibodies? J. Pharm. Sci. 2019, 108, 142–154. [Google Scholar] [CrossRef]
- Chi, E.Y.; Krishnan, S.; Randolph, T.W.; Carpenter, J.F. Physical stability of proteins in aqueous solution: Mechanism and driving forces in nonnative protein aggregation. Pharm. Res. 2003, 20, 1325–1336. [Google Scholar] [CrossRef]
- Randolph, T.W.; Carpenter, J.F. Engineering challenges of protein formulations. AIChE J. 2007, 53, 1902–1907. [Google Scholar] [CrossRef]
- Roberts, C.J. Therapeutic protein aggregation: Mechanisms, design, and control. Trends Biotechnol. 2014, 32, 372–380. [Google Scholar] [CrossRef] [PubMed]
- Cellmer, T.; Bratko, D.; Prausnitz, J.M.; Blanch, H.W. Protein-folding landscapes in multichain systems. Proc. Natl. Acad. Sci. USA 2005, 102, 11692–11697. [Google Scholar] [CrossRef] [PubMed]
- Bratko, D.; Cellmer, T.; Prausnitz, J.M.; Blanch, H.W. Effect of single-point sequence alterations on the aggregation propensity of a model protein. J. Am. Chem. Soc. 2006, 128, 1683–1691. [Google Scholar] [CrossRef] [PubMed]
- Cellmer, T.; Bratko, D.; Prausnitz, J.M.; Blanch, H.W. Protein aggregation in silico. Trends Biotechnol. 2007, 25, 254–261. [Google Scholar] [CrossRef]
- Calero-Rubio, C.; Saluja, A.; Roberts, C.J. Coarse—grained antibody models for “weak” protein—protein interactions from low to high concentrations. J. Phys. Chem. B 2016, 120, 6592–6605. [Google Scholar] [CrossRef]
- Chaudhri, A.; Zarraga, I.E.; Kamerzell, T.J.; Brandt, J.P.; Patapoff, T.W.; Shire, S.J.; Voth, G.A. Coarse—grained modeling of the self—association of therapeutic monoclonal antibodies. J. Phys. Chem. B 2012, 116, 8045–8057. [Google Scholar] [CrossRef]
- Buck, P.M.; Chaudhri, A.; Kumar, S.; Singh, S.K. Highly viscous antibody solutions are a consequence of network formation caused by domain—domain electrostatic complementarities: Insights from coarse—grained simulations. Mol. Pharm. 2014, 12, 127–139. [Google Scholar] [CrossRef]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef]
- Saunders, M.G.; Voth, G.A. Coarse-graining methods for computational biology. Annu. Rev. Biophys. 2013, 42, 73–93. [Google Scholar] [CrossRef]
- Musiani, F.; Giorgetti, A. Protein aggregation and molecular crowding: Perspectives from multiscale simulations. Int. Rev. Cell. Mol. Biol. 2017, 329, 49–77. [Google Scholar] [PubMed]
- Carballo-Pacheco, M.; Strodel, B. Advances in the simulation of protein aggregation at the atomistic scale. J. Phys. Chem. B 2016, 120, 2991–2999. [Google Scholar] [CrossRef] [PubMed]
- Navarro, S.; Ventura, S. Computational methods to predict protein aggregation. Curr. Opin. Struct. Biol. 2022, 73, 102343. [Google Scholar] [CrossRef] [PubMed]
- Brudar, S.; Hribar-Lee, B. The Effect of Arginine on the Phase Stability of Aqueous Hen Egg-White Lysozyme Solutions. Int. J. Mol. Sci. 2023, 24, 1197. [Google Scholar] [CrossRef] [PubMed]
- Brudar, S.; Hribar-Lee, B. The mechanism of self-association of human γ-D crystallin from molecular dynamics simulations. J. Mol. Liq. 2023, 386, 122461. [Google Scholar] [CrossRef]
- Agrawal, N.; Kumar, S.; Wang, X.; Helk, B.; Singh, S.; Trout, B. Aggregation in protein-based biotherapeutics: Computational studies and tools to identify aggregation-prone regions. J. Pharm. Sci. 2011, 100, 5081–5095. [Google Scholar] [CrossRef] [PubMed]
- Dear, B.J.; Bollinger, J.A.; Chowdhury, A.; Hung, J.J.; Wilks, L.R.; Karouta, C.A.; Ramachandran, K.; Shay, T.Y.; Nieto, M.P.; Sharma, A.; et al. X-ray Scattering and Coarse-Grained Simulations for Clustering and Interactions of Monoclonal Antibodies at High Concentrations. J. Phys. Chem. B 2019, 123, 5274–5290. [Google Scholar] [CrossRef]
- Chowdhury, A.; Guruprasad, G.; Chen, A.T.; Karouta, C.A.; Blanco, M.A.; Truskett, T.M.; Johnston, K.P. Protein-protein interactions, clustering, and rheology for bovine IgG up to high concentrations characterized by Small Angle X-Ray Scattering and Molecular Dynamics simulations. J. Pharm. Sci. 2020, 109, 696–708. [Google Scholar] [CrossRef]
- Chowdhury, A.; Bollinger, J.A.; Dear, B.J.; Cheung, J.K.; Johnston, K.P.; Truskett, T.M. Coarse-Grained Molecular Dynamics Simulations for Understanding the Impact of Short-Range Anisotropic Attractions on Structure and Viscosity of Concentrated Monoclonal Antibody Solutions. Mol. Pharm. 2020, 17, 1748–1756. [Google Scholar] [CrossRef]
- Chowdhury, A.; Manohar, N.; Guruprasad, G.; Chen, A.T.; Lanzaro, A.; Blanco, M.; Johnston, K.P.; Truskett, T.M. Characterizing experimental monoclonal antibody interactions and clustering using a coarse-grained simulation library and a viscosity model. J. Phys. Chem. B 2023, 127, 1120–1137. [Google Scholar] [CrossRef]
- Chowdhury, A.A.; Manohar, N.; Witek, M.A.; Woldeyes, M.A.; Majumdar, R.; Qian, K.K.; Kimball, W.D.; Xu, S.; Lanzaro, A.; Truskett, T.M.; et al. Subclass Effects on Self-Association and Viscosity of Monoclonal Antibodies at High Concentrations. Mol. Pharm. 2023, 20, 2991–3008. [Google Scholar] [CrossRef] [PubMed]
- Nagy, G.; Oostenbrink, C.; Hritz, J. Exploring the binding pathways of the 14-3-3ζ protein: Structural and free-energy profiles revealed by Hamiltonian replica exchange molecular dynamics with distancefield distance restraints. PLoS ONE 2017, 12, e0180633. [Google Scholar] [CrossRef] [PubMed]
- Morriss-Andrews, A.; Shea, J.E. Computational studies of protein aggregation: Methods and applications. Annu. Rev. Phys. Chem. 2015, 66, 643–666. [Google Scholar] [CrossRef] [PubMed]
- Brudar, S.; Gujt, J.; Spohr, E.; Hribar-Lee, B. Studying the mechanism of phase separation in aqueous solutions of globular proteins via molecular dynamics computer simulations. Phys. Chem. Chem. Phys. 2021, 23, 415–424. [Google Scholar] [CrossRef]
- McManus, J.J.; Charbonneau, P.; Zaccarelli, E.; Asherie, N. The physics of protein self-assembly. Curr. Opin. Colloid Interf. Sci. 2016, 22, 73–79. [Google Scholar] [CrossRef]
- Fusco, D.; Charbonneau, P. Soft matter perspective on protein crystal assembly. Colloids Surf. B 2016, 137, 22–31. [Google Scholar] [CrossRef]
- Nguemaha, V.; Zhou, H.X. Liquid-liquid phase separation of patchy particles illuminates diverse effects of regulatory components on protein droplet formation. Sci. Rep. 2018, 8, 6728. [Google Scholar] [CrossRef]
- Verwey, E.J.W.; Overbeek, J.T.G. (Eds.) Theory of the Stability of Lyophobic Colloids; Elsevier: Amsterdam, The Netherlands, 1948. [Google Scholar]
- Lyklema, J. (Ed.) Fundamentals of Interface and Colloid Science; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Dahirel, V.; Jardat, M. Effective interactions between charged nanoparticles in water: What is left from the DLVO theory? Curr. Opin. Colloid Interface Sci. 2010, 15, 2–7. [Google Scholar] [CrossRef]
- Sarangapani, P.S.; Hudson, S.D.; Jones, R.L.; Douglas, J.F.; Pathak, J.A. Critical examination of the colloidal particle model of globular proteins. Biophys. J. 2015, 108, 724–737. [Google Scholar] [CrossRef]
- Prausnitz, J.M. The fallacy of misplaced concreteness. Biophys. J. 2015, 108, 453–454. [Google Scholar] [CrossRef]
- Woldeyes, M.A.; Calero-Rubio, C.; Furst, E.; Roberts, C. Predicting protein interactions of concentrated globular protein solutions using colloidal models. J. Phys. Chem. B 2017, 121, 4756–4767. [Google Scholar] [CrossRef] [PubMed]
- Tavares, F.; Bratko, D.; Striolo, A.; Blanch, H.; Prausnitz, J. Phase behavior of aqueous solutions containing dipolar proteins from second-order perturbation theory. J. Chem. Phys. 2004, 120, 9859–9869. [Google Scholar] [CrossRef] [PubMed]
- Lomakin, A.; Asherie, N.; Benedek, G.B. Aeolotopic interactions of globular proteins. Proc. Natl. Acad. Sci. USA 1999, 96, 9465–9468. [Google Scholar] [CrossRef] [PubMed]
- Tavares, T.W.; Bratko, D.; Prausnitz, J.M. The role of salt—macroion van der Waals interactions in the colloid—colloid potential of mean force. Curr. Opin. Colloid Interface Sci. 2004, 9, 81–86. [Google Scholar] [CrossRef]
- Kunz, W. Specific ion effects in colloidal and biological systems. Curr. Opin. Colloid Interface Sci. 2010, 15, 34–39. [Google Scholar] [CrossRef]
- Lima, E.R.A.; Biscaia, E.C.; Bostrom, M.; Tavares, F.W.; Prausnitz, J.M. Osmotic second virial coefficients and phase diagrams for aqueous proteins from a much-improved Poisson—Boltzmann equation. J. Chem. Phys. C 2007, 111, 16055–16059. [Google Scholar] [CrossRef]
- Nostro, P.L.; Ninham, B.W. Hofmeister phenomena: An update on ion specificity in biology. Chem. Rev. 2012, 112, 2286–2322. [Google Scholar] [CrossRef]
- George, A.; Wilson, W.W. Predicting protein crystallization from a dilute-solution property. Acta Crystallogr. D 1994, 50, 361–365. [Google Scholar] [CrossRef]
- George, A.; Chiang, Y.B.; Guo, A.; Arabshahi, Z.C.; Wilson, W.W. Second virial coefficient as predictor in protein crystal growth. Methods Enzymol. 1997, 276, 100–110. [Google Scholar]
- Guo, B.; Kao, S.; McDonald, H.; Asanov, A.; Combs, L.L.; Wilson, W.W. Correlation of second virial coefficients and solubilities useful in protein crystal growth. J. Cryst. Growth 1999, 196, 424–433. [Google Scholar] [CrossRef]
- Himenez, P.C.; Rajagopalan, R. Principles of Colloid and Surface Chemistry, Revised and Expanded, 14th ed.; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Sibanda, N.; Shanmugan, R.K.; Curtis, R. The relationship between protein-protein interactions and liquid-liquid phase separation for monoclonal antibodies. Mol. Pharm. 2023, 20, 2662–2674. [Google Scholar] [CrossRef] [PubMed]
- Kastelic, M.; Kalyuzhnyi, Y.V.; Dill, K.A.; Vlachy, V. Controlling the viscosities of antibody solutions through control of their binding sites. J. Mol. Liquids 2017, 270, 234–242. [Google Scholar] [CrossRef] [PubMed]
- Brudar, S.; Hribar-Lee, B. Effect of Buffer on Protein Stability in Aqueous Solutions: A Simple Protein Aggregation Model. J. Phys. Chem. B 2021, 125, 2504–2512. [Google Scholar] [CrossRef] [PubMed]
- Lomakin, A.; Asherie, N.; Benedek, G.B. Monte Carlo study of phase separation in aqueous protein solutions. J. Chem. Phys. 1996, 104, 1646–1656. [Google Scholar] [CrossRef]
- Wang, Y.; Lomakin, A.; McManus, J.J.; Ogun, O.; Benedek, G.B. Phase behavior of mixtures of human lens proteins γD and βB1. Proc. Natl. Acad. Sci. USA 2010, 107, 13282–13287. [Google Scholar] [CrossRef]
- Wang, Y.; Lomakin, A.; Latypov, R.; Laubach, J.; Hideshima, T.; Richardson, P.; Munshi, N.; Anderson, K.; Benedek, G. Phase transitions in human IgG solutions. J. Chem. Phys. 2013, 139, 121904. [Google Scholar] [CrossRef]
- Wang, Y.; Latypov, R.F.; Lomakin, A.; Meyer, J.A.; Kerwin, B.A.; Vunnum, S.; Benedek, G.B. Quantitative evaluation of colloidal stability of antibody solutions using PEG-induced liquid-liquid phase separation. Mol. Pharm. 2014, 11, 1391–1402. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Y.; Lomakin, A.; Benedek, G.B.; Stanley, H.E.; Xu, L.; Buldyrev, S.V. The phase behavior study of human antibody solution using multi-scale modeling. J. Chem. Phys. 2016, 145, 194901. [Google Scholar] [CrossRef]
- Amin, S.; Barnett, G.V.; Pathak, J.A.; Roberts, C.J.; Sarangapani, P.S. Protein aggregation, particle formation, characterization & rheology. Curr. Opin. Colloid Interface Sci. 2014, 19, 438–449. [Google Scholar]
- Bruinsma, R.; Pincus, P. Protein aggregation in membranes. Curr. Opin. Solid State Mater Sci. 1996, 1, 401–406. [Google Scholar] [CrossRef]
- Fink, A.L. Protein aggregation: Folding aggregates, inclusion bodies and amyloid. Fold Des. 1998, 3, R9–R23. [Google Scholar] [CrossRef] [PubMed]
- Kanai, S.; Liu, J.; Patapoff, T.W.; Shire, S.J. Reversible self-association of a concentrated monoclonal antibody solution mediated by Fab–Fab interaction that impacts solution viscosity. J. Pharm. Sci. 2008, 97, 4219–4227. [Google Scholar] [CrossRef]
- Yadav, S.; Liu, J.; Shire, S.J.; Kalonia, D.S. Specific interactions in high concentration antibody solutions resulting in high viscosity. J. Pharm. Sci. 2010, 99, 1152–1168. [Google Scholar] [CrossRef] [PubMed]
- Yadav, S.; Laue, T.; Kalonia, D.S.; Singh, N.; Shire, S.J. The influence of charge distribution on Self-association and viscosity behavior of monoclonal antibody solutions. Molec. Pharm. 2012, 9, 791–802. [Google Scholar] [CrossRef] [PubMed]
- Nicoud, L.; Lattuada, M.; Yates, A.; Morbidelli, M. Impact of aggregate formation on the viscosity of protein solutions. Soft Matter 2015, 11, 5513. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y. Recent progresses of understanding the viscosity of concentrated protein solutions. Curr. Opin. Chem. Engn. 2017, 16, 48–55. [Google Scholar] [CrossRef]
- Dear, B.J.; Hung, J.J.; Truskett, T.M.; Johnston, K.P. Contrasting the influence of cationic amino acids on the viscosity and stability of a highly concentrated monoclonal antibody. Pharm. Res. 2017, 34, 193–207. [Google Scholar] [CrossRef] [PubMed]
- Inthavong, W.; Chassenieux, C.; Nicolai, T. Viscosity of mixtures of protein aggregates with different sizes and morphologies. Soft Matter 2019, 15, 4682–4688. [Google Scholar] [CrossRef] [PubMed]
- Morriss-Andrews, A.; Shea, J.E. Simulations of protein aggregation: Insights from atomistic and coarse-grained models. J. Phys. Chem. Lett. 2014, 5, 1899–1908. [Google Scholar] [CrossRef]
- Shahfar, H.; Forder, J.K.; Roberts, C.J. Toward a suite of coarse-grained models for molecular simulation of monoclonal antibodies and therapeutic proteins. J. Phys. Chem. B 2021, 125, 3574–3588. [Google Scholar] [CrossRef]
- Calero-Rubio, C.; Saluja, A.; Sahin, E.; Roberts, C.J. Predicting high-concentration interactions of monoclonal antibody solutions: Comparison of theoretical approaches for strongly attractive versus repulsive conditions. J. Phys. Chem. B 2019, 123, 5709–5720. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, G.M.; Calero-Rubio, C.; Sathish, H.A.; Remmele, R.L.; Roberts, C.J. Electrostatically mediated protein-protein interactions for monoclonal antibodies: A combined experimental and coarse-grained molecular modeling approach. J. Pharm. Sci. 2019, 108, 120–132. [Google Scholar] [CrossRef]
- Grünberger, A.; Lai, P.K.; Blanco, M.A.; Roberts, C.J. Coarse-grained modeling of protein second osmotic virial coefficients: Sterics and short-ranged attractions. J. Phys. Chem. B 2013, 117, 763–770. [Google Scholar] [CrossRef]
- Sear, R.P. Phase behavior of a simple model of globular proteins. J. Chem. Phys. 1999, 111, 4800–4806. [Google Scholar] [CrossRef]
- Curtis, R.; Blanch, H.; Prausnitz, J. Calculation of phase diagrams for aqueous protein solutions. J. Phys. Chem. B 2001, 105, 2445–2452. [Google Scholar] [CrossRef]
- Shiryayev, A.; Li, X.; Gunton, J.D. Simple model of sickle hemogloblin. J. Chem. Phys. 2006, 125, 024902. [Google Scholar] [CrossRef]
- Liu, H.; Kumar, S.K.; Sciortino, F. Vapor—liquid coexistence of patchy models: Relevance to protein phase behavior. J. Chem. Phys. 2007, 127, 084902. [Google Scholar] [CrossRef]
- Cheung, J.K.; Shen, V.K.; Errington, J.R.; Truskett, T.M. Coarse-grained strategy for modeling protein stability in concentrated solutions. III: Directional protein interactions. Biophys. J. 2007, 92, 4316–4324. [Google Scholar] [CrossRef]
- Doye, J.P.; Louis, A.A.; Lin, I.C.; Allen, L.R.; Noya, E.G.; Wilber, A.W.; Kok, H.C.; Lyus, R. Controlling crystallization and its absence: Proteins, colloids and patchy models. Phys. Chem. Chem. Phys. 2007, 9, 2197–2205. [Google Scholar] [CrossRef]
- Fantoni, R.; Gazzillo, D.; Giacometti, A.; Miller, M.A.; Pastore, G. Patchy sticky hard spheres: Analytical study and Monte Carlo simulations. J. Chem. Phys. 2007, 127, 234507. [Google Scholar] [CrossRef]
- Gögelein, C.; Nägele, G.; Tuinier, R.; Gibaud, T.; Stradner, A.; Schurtenberger, P. A simple patchy colloid model for the phase behavior of lysozyme dispersions. J. Chem. Phys. 2008, 129, 085102. [Google Scholar] [CrossRef]
- Wentzel, N.; Gunton, J.D. Effect of solvent on the phase diagram of a simple anisotropic model of globular proteins. J. Phys. Chem. B 2008, 112, 7803–7809. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Gunton, J.; Chakrabarti, A. A simple model of directional interactions for proteins. J. Chem. Phys. 2009, 131, 115101. [Google Scholar] [CrossRef]
- Bianchi, E.; Blaak, R.; Likos, C.N. Patchy colloids: State of the art and perspectives. Phys. Chem. Chem. Phys. 2011, 13, 6397–6410. [Google Scholar] [CrossRef]
- Fusco, D.; Charbonneau, P. Crystallization of asymmetric patchy models for globular proteins in solution. Phys. Rev. E 2013, 88, 012721. [Google Scholar] [CrossRef]
- Fusco, D.; Charbonneau, P. Competition between monomeric and dimeric crystals in schematic models for globular proteins. J. Phys. Chem. B 2014, 118, 8034–8041. [Google Scholar] [CrossRef] [PubMed]
- Roosen-Runge, F.; Zhang, F.; Schreiber, F.; Roth, R. Ion-activated attractive patches as a mechanism for controlled protein interactions. Sci. Rep. 2014, 4, 7016. [Google Scholar] [CrossRef] [PubMed]
- Altan, I.; Charbonneau, P. Obtaining soft matter models of proteins and their phase behavior. In Protein Self-Assembly: Methods and Protocols; Humana: New York, NY, USA, 2019; pp. 209–228. [Google Scholar]
- Gnan, N.; Sciortino, F.; Zaccarelli, E. Patchy particle models to understand protein phase behavior. In Protein Self-Assembly: Methods and Protocols; Humana: New York, NY, USA, 2019; pp. 187–208. [Google Scholar]
- Espinosa, J.R.; Joseph, J.A.; Sanchez-Burgos, I.; Garaizar, A.; Frenkel, D.; Collepardo-Guevara, R. Liquid network connectivity regulates the stability and composition of biomolecular condensates with many components. Proc. Natl. Acad. Sci. USA 2020, 117, 13238–13247. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, E.; Largo, J.; Tartaglia, P.; Zaccarelli, E.; Sciortino, F. Phase diagram of patchy colloids: Towards empty liquids. Phys. Rev. Lett. 2006, 97, 168301. [Google Scholar] [CrossRef]
- Bianchi, E.; Tartaglia, P.; Zaccarelli, E.; Scortino, F. Theoretical and numerical study of the phase diagram of patchy colloids: Ordered and disordered patch arrangements. Chem. Rev. 2008, 128, 144504. [Google Scholar] [CrossRef] [PubMed]
- Russo, J.; Leoni, F.; Martelli, F.; Sciortino, F. The physics of empty liquids: From patchy particles to water. Rep. Prog. Phys. 2022, 85, 016601. [Google Scholar] [CrossRef] [PubMed]
- Sciortino, F.; Zaccarelli, E. Equilibrium gels of limited valence colloids. Curr. Opin. Colloid Interface Sci. 2017, 30, 90–96. [Google Scholar] [CrossRef]
- Zhang, F.; Roosen-Runge, F.; Sauter, A.; Wolf, M.; Jacobs, R.M.; Schreiber, F. Reentrant condensation, liquid—liquid phase separation and crystallization in protein solutions induced by multivalent metal ions. Pure Appl. Chem. 2014, 86, 191–202. [Google Scholar] [CrossRef]
- Cai, J.; Townsend, J.P.; Dodson, T.C.; Heiney, P.A.; Sweeney, A.M. Eye patches: Protein assembly of index-gradient squid lenses. Science 2017, 357, 564–569. [Google Scholar] [CrossRef]
- Cai, J.; Sweeney, A.M. The proof is in the pidan: Generalizing proteins as patchy particles. ACS Cent. Sci. 2018, 4, 840–853. [Google Scholar] [CrossRef]
- Altan, I.; Bauernfeind, V.; Sweeney, A.M. Patchy particle insights into self-assembly of transparent, graded index squid lenses. Soft Matter 2023, 19, 4470–4482. [Google Scholar] [CrossRef]
- Kastelic, M.; Kalyuzhnyi, Y.V.; Hribar-Lee, B.; Dill, K.A.; Vlachy, V. Protein aggregation in salt solutions. Proc. Natl. Acad. Sci. USA 2015, 112, 6766–6770. [Google Scholar] [CrossRef]
- Wertheim, M.S. Fluids with highly directional attractive forces. III. Multiple attraction sites. J. Stat. Phys. 1986, 42, 459–476. [Google Scholar] [CrossRef]
- Wertheim, M.S. Fluids with highly directional attractive forces. IV. Equilibrium polymerization. J. Stat. Phys. 1986, 42, 477–492. [Google Scholar] [CrossRef]
- Chapman, W.G.; Jackson, G.; Gubbins, K.E. Phase equilibria of associating fluids chain molecules with multiple bonding sites. Mol. Phys. 1988, 65, 1057–1079. [Google Scholar] [CrossRef]
- Chapman, W.G.; Gubbins, K.E.; Jackson, G.; Radosz, M. SAFT: Equation-of-state solution model for associating fluids. Fluid Phase Equilibria 1989, 52, 31–38. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Application of the perturbed-chain SAFT equation of state to associating systems. Ind. Eng. Chem. Res. 2002, 41, 5510–5515. [Google Scholar] [CrossRef]
- Zmpitas, W.; Gross, J. Detailed pedagogical review and analysis of Wertheim’s thermodynamic perturbation theory. Fluid Phase Equilibria 2016, 428, 121–125. [Google Scholar] [CrossRef]
- Kalyuzhnyi, Y.V.; Holovko, M.; Haymet, A. Integral equation theory for associating liquids: Weakly associating 2–2 electrolytes. J. Chem. Phys. 1991, 95, 9151–9164. [Google Scholar] [CrossRef]
- Wood, R.H.; Lilley, T.H.; Thompson, P.T. Rapidly converging activity expansions for representing the thermodynamic properties of fluid systems: Gases, non-electrolyte solutions, weak and strong electrolyte solutions. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1978, 74, 1301–1323. [Google Scholar] [CrossRef]
- Ebeling, W.; Grigo, M. An analytical calculation of the equation of state and the critical point in a dense classical fluid of charged hard spheres. Ann. Der Phys. 1980, 492, 21–30. [Google Scholar] [CrossRef]
- Wertheim, M. Fluids of dimerizing hard spheres, and fluid mixtures of hard spheres and dispheres. J. Chem. Phys. 1986, 85, 2929–2936. [Google Scholar] [CrossRef]
- Janc, T.; Kastelic, M.; Bončina, M.; Vlachy, V. Salt-specific effects in lysozyme solutions. Condens. Matter Phys. 2016, 19, 23601. [Google Scholar] [CrossRef]
- Kastelic, M.; Kalyuzhnyi, Y.V.; Vlachy, V. Modeling phase transitions in mixtures of β–γ lens crystallins. Soft Matter 2016, 12, 7289–7298. [Google Scholar] [CrossRef]
- Kastelic, M.; Kalyuzhnyi, Y.V.; Vlachy, V. Fluid of fused spheres as a model for protein solution. Condens. Matter Phys. 2016, 19, 23801. [Google Scholar] [CrossRef]
- Taratuta, V.G.; Holschbach, A.; Thurston, G.M.; Blankschtein, D.; Benedek, G.B. Liquid–liquid phase separation of aqueous lysozyme solutions: Effects of pH and salt identity. J. Phys. Chem. 1990, 94, 2140–2144. [Google Scholar] [CrossRef]
- Broide, M.L.; Berland, C.R.; Pande, J.; Ogun, O.O.; Benedek, G.B. Binary-liquid phase separation of lens protein solutions. Proc. Natl. Acad. Sci. USA 1991, 88, 5660–5664. [Google Scholar] [CrossRef]
- Grigsby, J.J.; Blanch, H.W.; Prausnitz, J.M. Cloud-point temperatures for lysozyme in electrolyte solutions: Effect of salt type, salt concentration and pH. Biophys. Chem. 2001, 91, 231–243. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Cremer, P.S. The inverse and direct Hofmeister series for lysozyme. Proc. Natl. Acad. Sci. USA 2009, 106, 15249–15253. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lomakin, A.; Latypov, R.F.; Benedek, G.B. Phase separation in solutions of monoclonal antibodies and the effect of human serum albumin. Proc. Natl. Acad. Sci. USA 2011, 108, 16606–16611. [Google Scholar] [CrossRef]
- Kalyuzhnyi, Y.V.; Vlachy, V. Modeling the depletion effect caused by an addition of polymer to monoclonal antibody solutions. J. Phys. Condens. Matter 2018, 30, 485101. [Google Scholar] [CrossRef]
- Kastelic, M.; Vlachy, V. Theory for the liquid—liquid phase separation in aqueous antibody solutions. J. Phys. Chem. B 2018, 122, 5400–5408. [Google Scholar] [CrossRef] [PubMed]
- Hvozd, T.V.; Kalyuzhnyi, Y.V. Two- and three-phase equilibria of polydisperse Yukawa hard-sphere fluids confined in random porous media: High temperature approximation and scaled particle theory. Soft Matter 2017, 13, 1405–1412. [Google Scholar] [CrossRef]
- Aumiller, W.; Keating, C. Experimental models for dynamic compartmentalization of biomolecules in liquid organelles: Reversible formation and partitioning in aqueous biphasic systems. Adv. Colloid Interface Sci. 2017, 239, 75–87. [Google Scholar] [CrossRef]
- Nakashima, K.K.; Vibhute, M.A.; Spruijt, E. Biomolecular chemistry in liquid phase separated compartment. Front. Mol. Biosci. 2019, 6, 21. [Google Scholar] [CrossRef]
- Larson, N.Y.W.; Cruz, T.; Esfandiary, R.; Kalonia, C.; Forrest, M.; Middaugh, C. Conformational changes and drivers of monoclonal antibody liquid-liquid phase separation. J. Pharm. Sci. 2023, 112, 680–690. [Google Scholar] [CrossRef]
- Mason, B.D.; van Enk, J.Z.; Zhang, L.; Remmele, R.L.; Zhang, J. Liquid-liquid phase separation of a monoclonal antibody and nonmonotonic influence of Hofmeister anions. Biophys. J. 2010, 99, 3792–3800. [Google Scholar] [CrossRef] [PubMed]
- Banani, S.; Lee, H.; Hyman, A.A.; Rosen, M. Biomolecular condensates: Organizers of celular biochemistry. Nat. Rev. Mol. Cell Biol. 2017, 18, 285–298. [Google Scholar] [CrossRef] [PubMed]
- Zeigler, T.M.; Chung, M.C.; Narayana, O.P.; Guana, J. Protein phase separation: Physical models and phase-separation- mediated cancer signaling. Adv. Phys. X 2021, 6, 1936638. [Google Scholar] [CrossRef]
- Kalyuzhnyi, Y.V.; Vlachy, V. Numerical analysis of the liquid-liquid phase separation in the antibody—human serum albumin mixtures in aqueous buffer solution. J. Mol. Liq. 2022, 365, 120006. [Google Scholar] [CrossRef]
- Hribar-Lee, B. The influence of excipients on the viscosity of monoclonal antibody solutions. J. Mol. Liq. 2022, 366, 120349. [Google Scholar] [CrossRef] [PubMed]
- Qin, S.; Zhou, H.X. Protein folding, binding, and droplet formation in cell-like conditions. Curr. Opin. Struct. Biol. 2017, 43, 28–37. [Google Scholar] [CrossRef]
- Hvozd, T.; Kalyuzhnyi, Y.V.; Vlachy, V. Aggregation, liquid–liquid phase separation, and percolation behaviour of a model antibody fluid constrained by hard-sphere obstacles. Soft Matter 2020, 16, 8432–8443. [Google Scholar] [CrossRef] [PubMed]
- Hvozd, T.; Kalyuzhnyi, Y.V.; Vlachy, V. Behaviour of the model antibody fluid constraint by rigid spherical obstacles: Effects of the obstacle-antibody attraction. Soft Matter 2022, 18, 9108–9117. [Google Scholar] [CrossRef]
- Kalyuzhnyi, Y.V.; Holovko, M.; Patsahan, T.; Cummings, P. Phase behavior and percolation properties of the patchy colloidal fluids in the random porous media. J. Phys. Chem. Lett. 2014, 5, 4260–4264. [Google Scholar] [CrossRef]
- Džudžević Čančar, H.; Belak Vivod, M.; Vlachy, V.; Lukšič, M. Phase stability of aqueous mixtures of bovine serum albumin with low molecular mass salts in presence of polyethylene glycol. J. Mol. Liq. 2022, 349, 118477. [Google Scholar] [CrossRef]
- Russo, J.; Tavares, J.M.; Teixeira, P.I.C.; da Gama, M.M.T.; Sciortino, F. Reentrant Phase Diagram of Network Fluids. Phys. Rev. Lett. 2018, 106, 085703. [Google Scholar] [CrossRef] [PubMed]
- Hvozd, T.; Kalyuzhnyi, Y.V.; Vlachy, V.; Cummings, P. Empty liquid state and re-entrant phase behavior of the patchy colloids confined in porous media. J. Chem. Phys. 2022, 156, 161102. [Google Scholar] [CrossRef]
- Banerjee, P.R.; Milin, A.; Moosa, M.M.; Onuchic, P.; Denis, A. Reentrant phase transition drives dynamic substructure formation in ribonucleoprotein droplets. Angew. Chem. Int. Ed. 2017, 56, 11354–11359. [Google Scholar] [CrossRef] [PubMed]
- Arora, J.; Hu, Y.; Esfandiary, R.; Sathish, H.A.; Bishop, S.M.; Joshi, S.B.; Middaugh, C.R.; Volkin, D.B.; Weis, D.D. Charge—mediated Fab–Fc interactions in an IgG1 antibody induce reversible self—association, cluster formation, and elevated viscosity. MAbs 2016, 8, 1561–1574. [Google Scholar] [CrossRef] [PubMed]
- Kalyuzhnyi, Y.V.; Vlachy, V. Model for a mixture of macroions, counterions, and co-ions in a waterlike fluid. Phys. Rev. E 2014, 90, 012308. [Google Scholar] [CrossRef]
- Kalyuzhnyi, Y.V.; Vlachy, V. Explicit-water theory for the salt-specific effects and Hofmeister series in protein solutions. J. Chem. Phys. 2016, 144, 215101. [Google Scholar] [CrossRef]


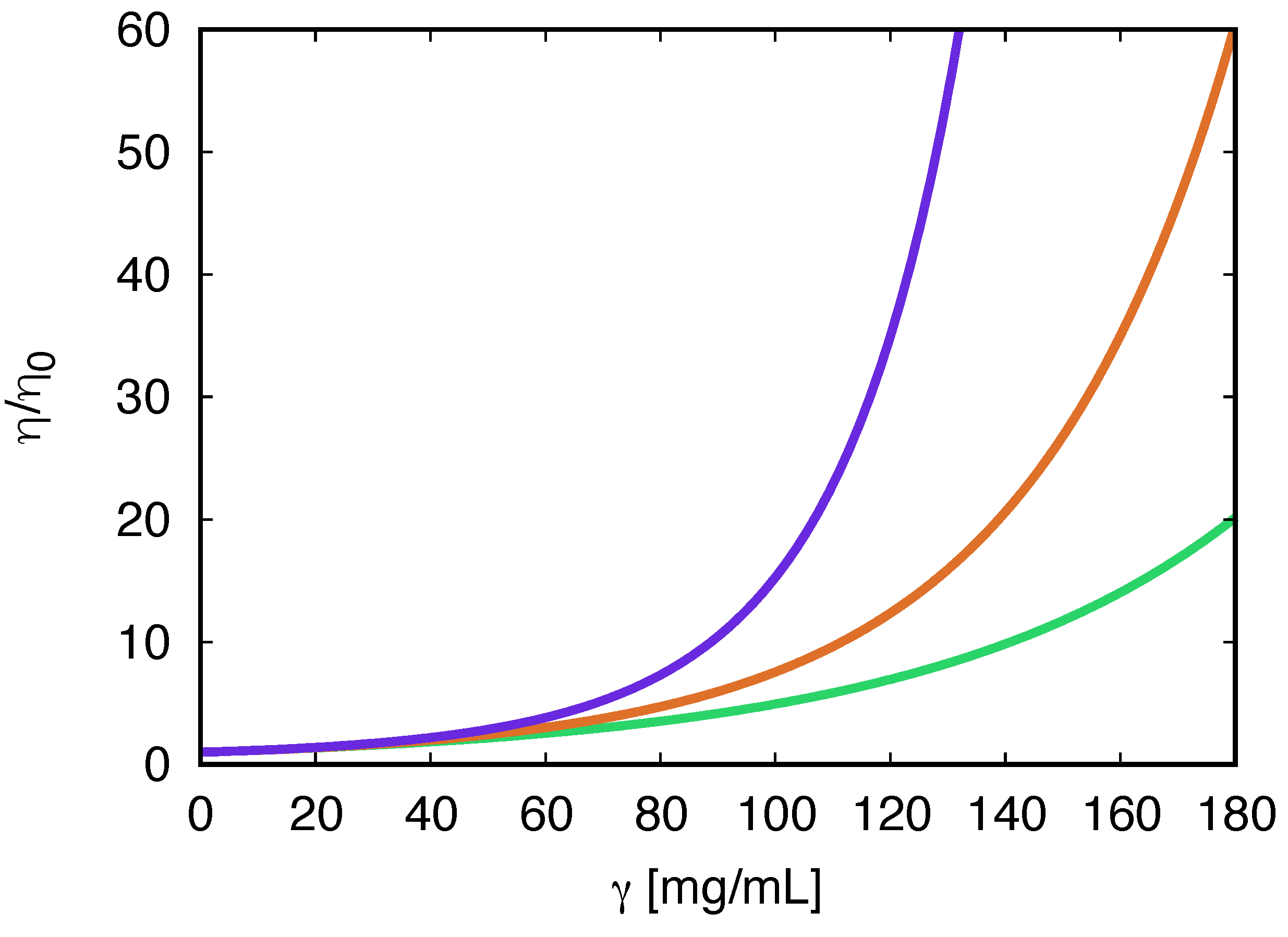
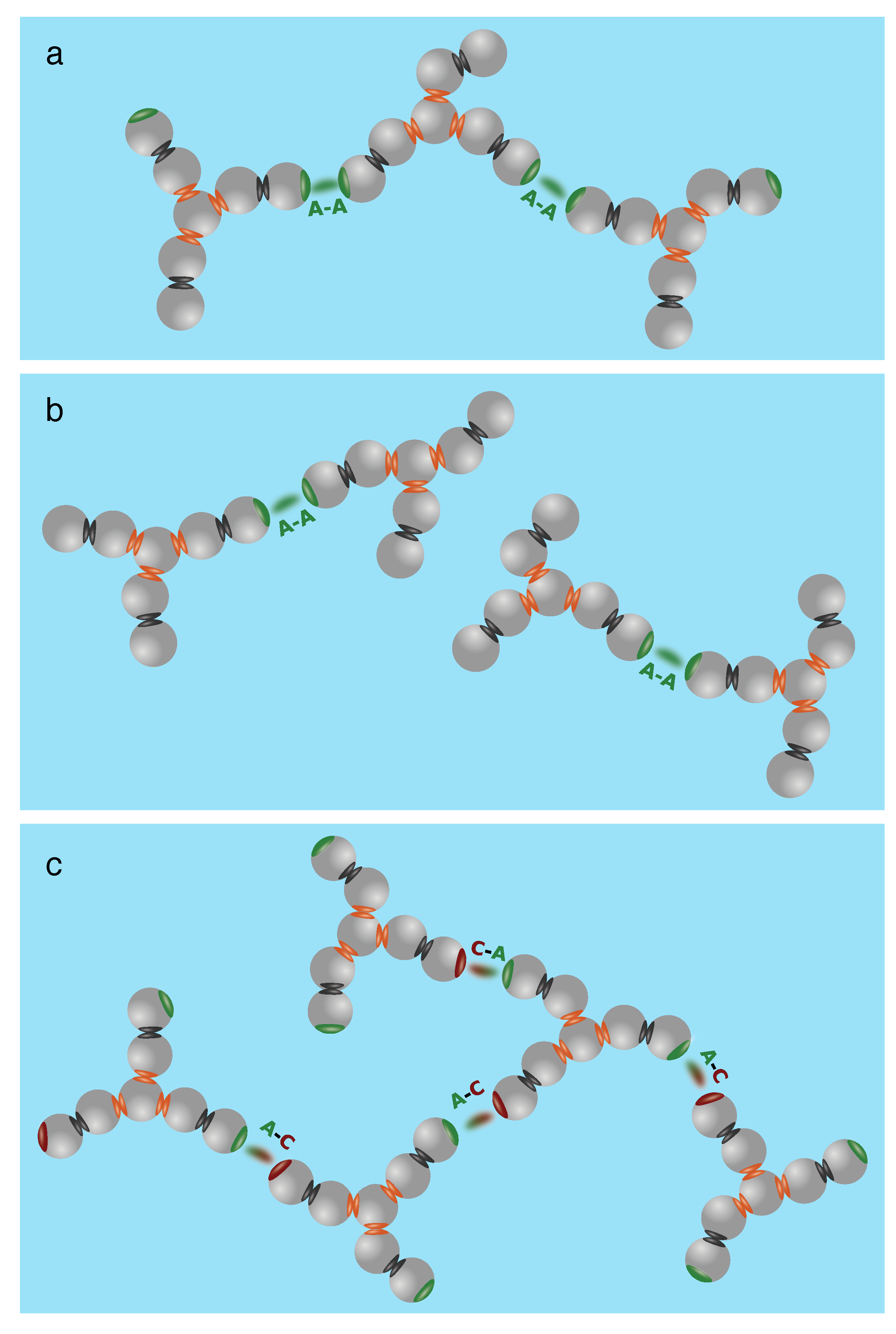

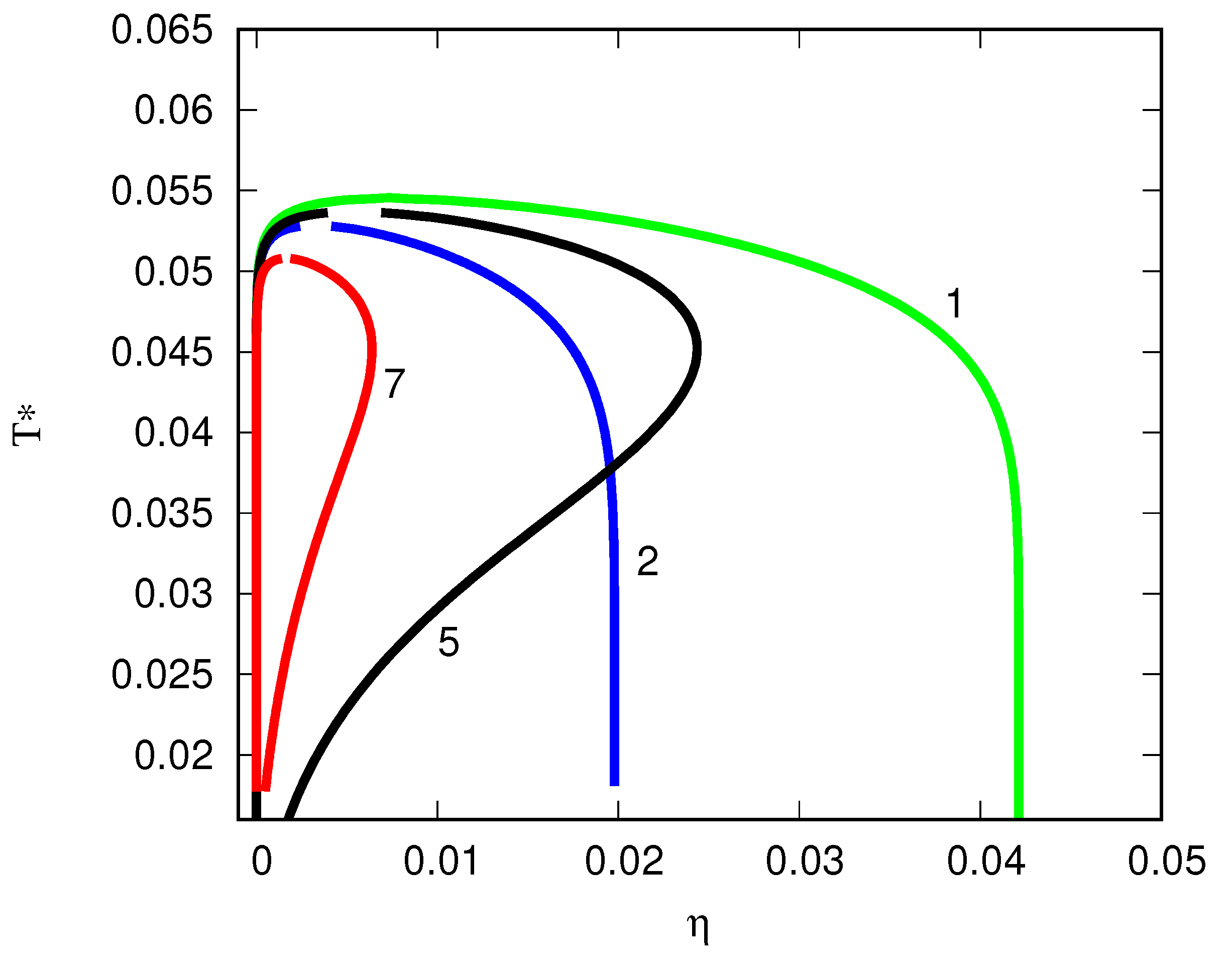
| When | What | Who |
|---|---|---|
| 1990’s | DLVO theories | Prausnitz |
| 1990’s | Liquid phase diagrams | Benedek |
| 1994 | Crystalization, B | George and Wilson |
| 1999 | Wertheim’s theory | Sear |
| 2000’s | Protein stability | Randolph, Carpenter, Shire |
| 2000’s | Salt specific effects | Ninham, Kunz, Tavares |
| 2015 | Aggregation | Kerwin, Roberts |
| 2015 | Molecular structure | Schmitt, Kerwin, Zhou |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vlachy, V.; Kalyuzhnyi, Y.V.; Hribar-Lee, B.; Dill, K.A. Protein Association in Solution: Statistical Mechanical Modeling. Biomolecules 2023, 13, 1703. https://doi.org/10.3390/biom13121703
Vlachy V, Kalyuzhnyi YV, Hribar-Lee B, Dill KA. Protein Association in Solution: Statistical Mechanical Modeling. Biomolecules. 2023; 13(12):1703. https://doi.org/10.3390/biom13121703
Chicago/Turabian StyleVlachy, Vojko, Yurij V. Kalyuzhnyi, Barbara Hribar-Lee, and Ken A. Dill. 2023. "Protein Association in Solution: Statistical Mechanical Modeling" Biomolecules 13, no. 12: 1703. https://doi.org/10.3390/biom13121703







