The Phase Space Analysis of Interacting K-Essence Dark Energy Models in Loop Quantum Cosmology
Abstract
:1. Introduction
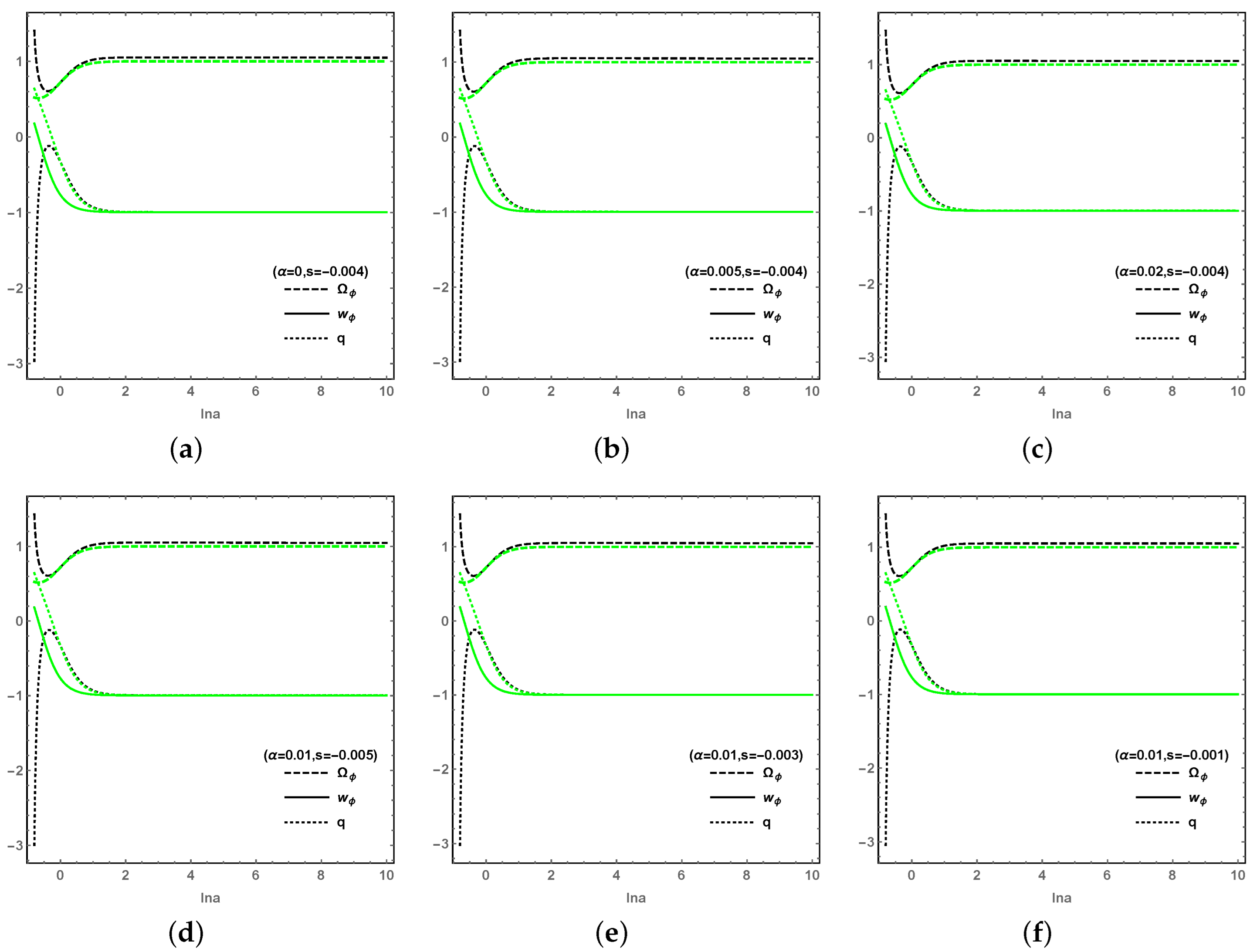
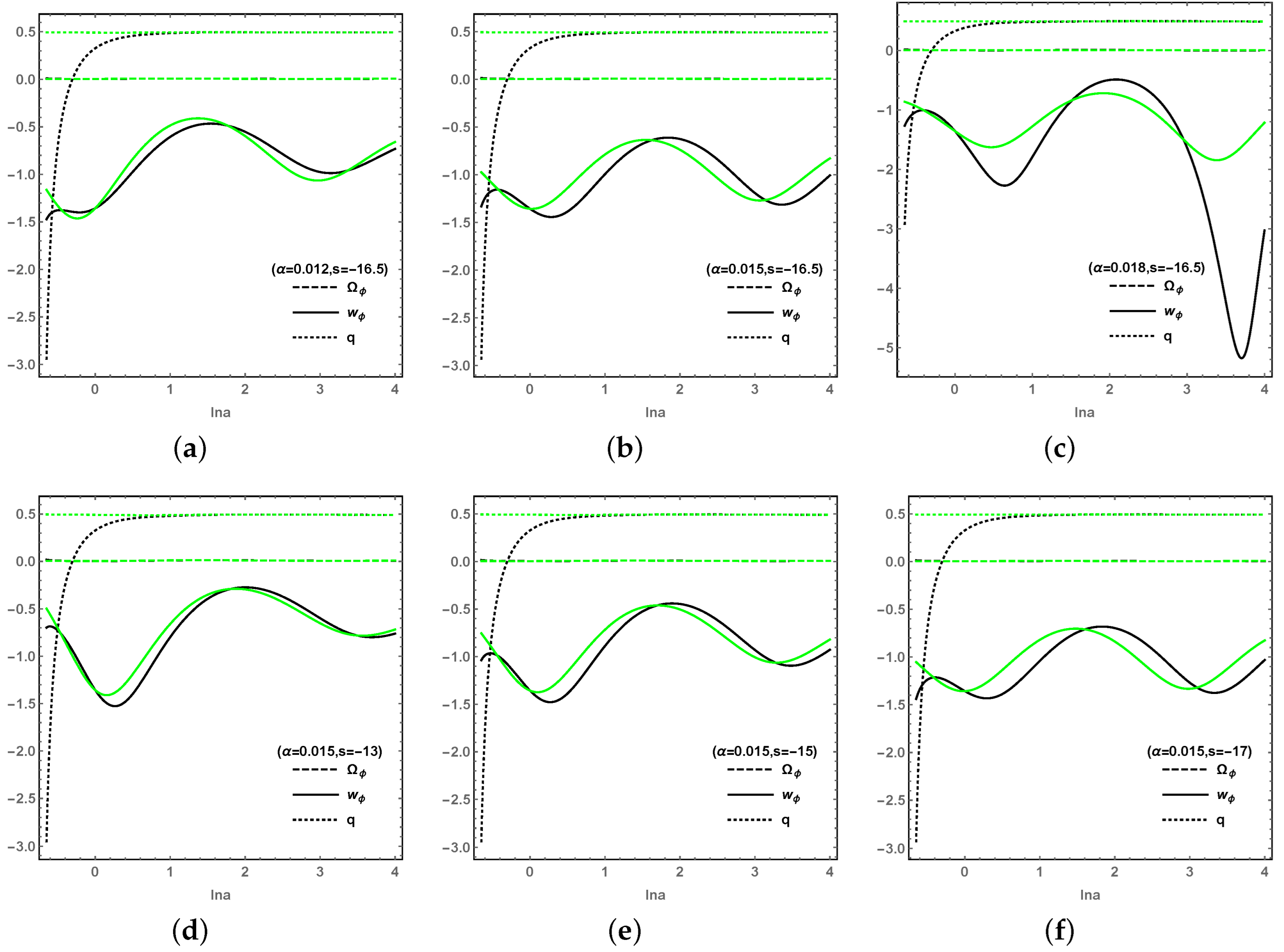
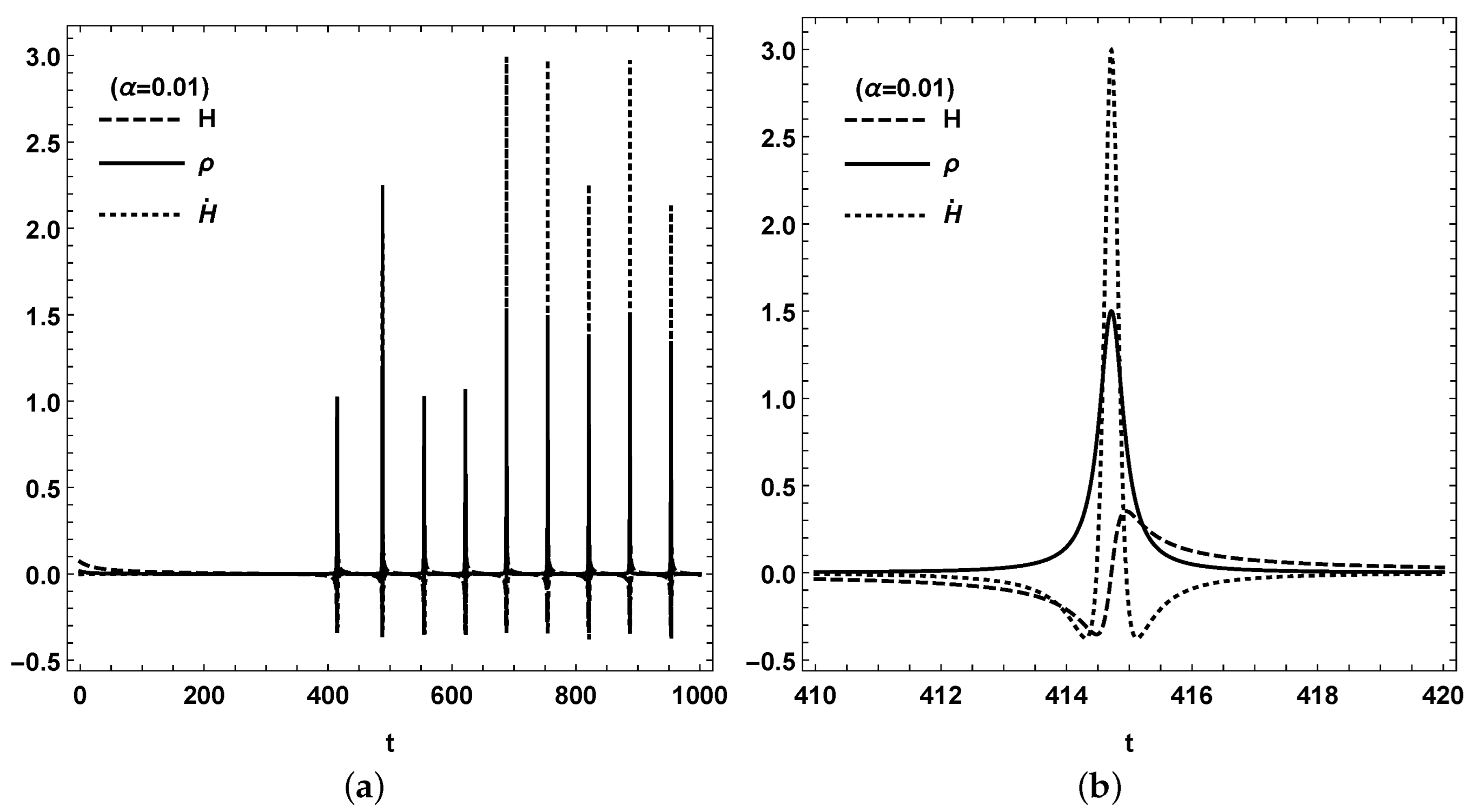
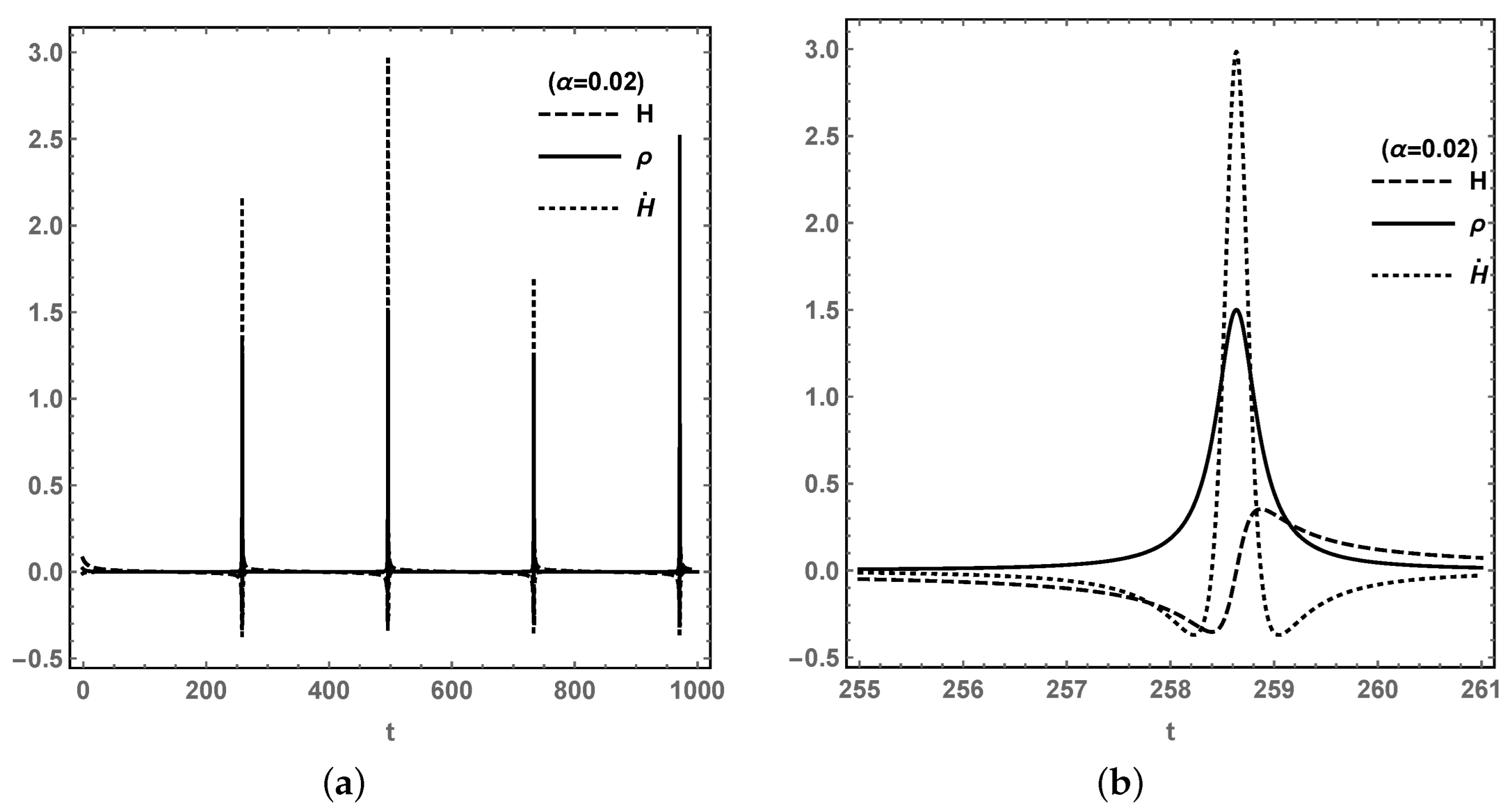
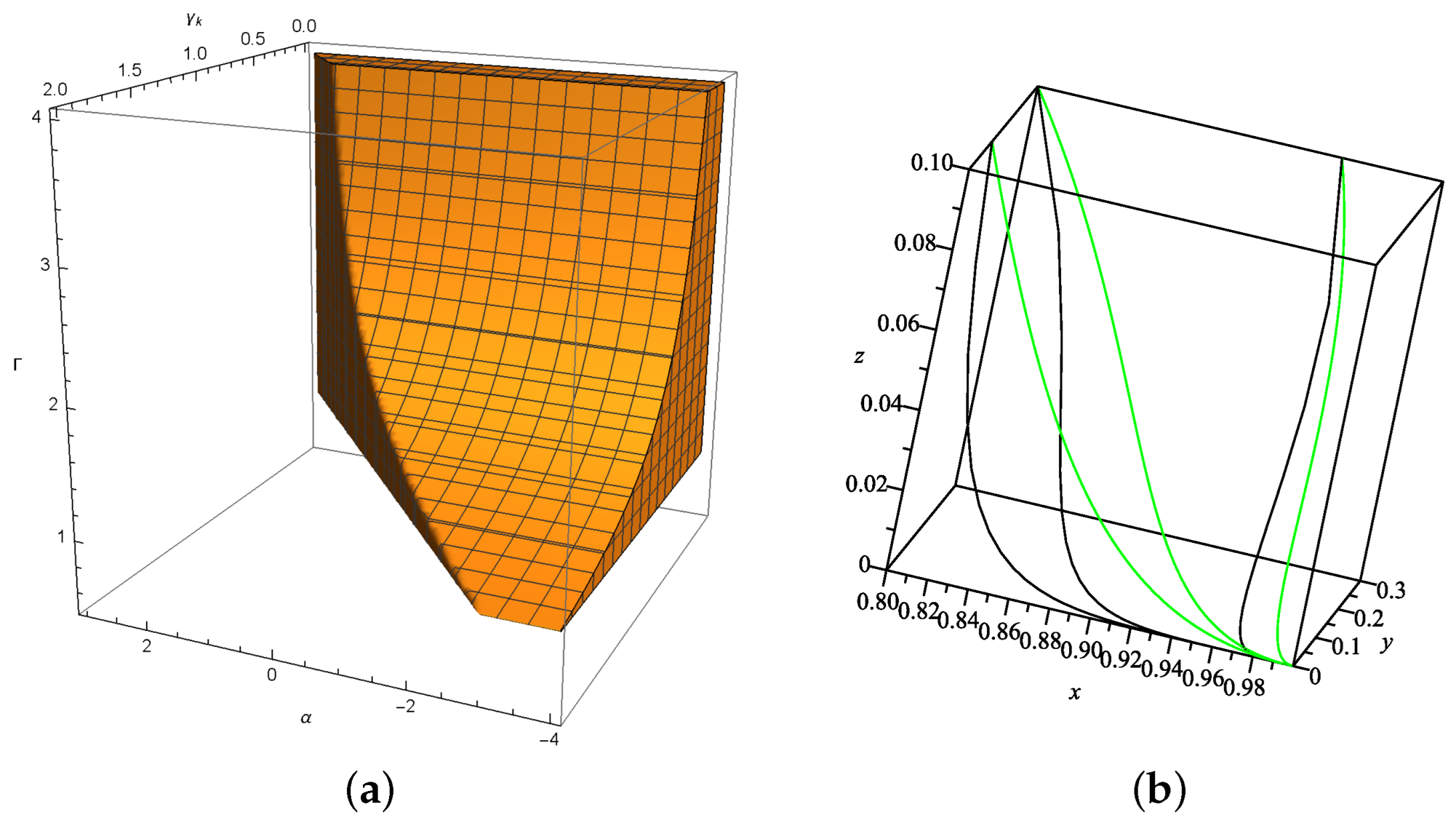
2. Model I: in Loop Quantum Cosmology
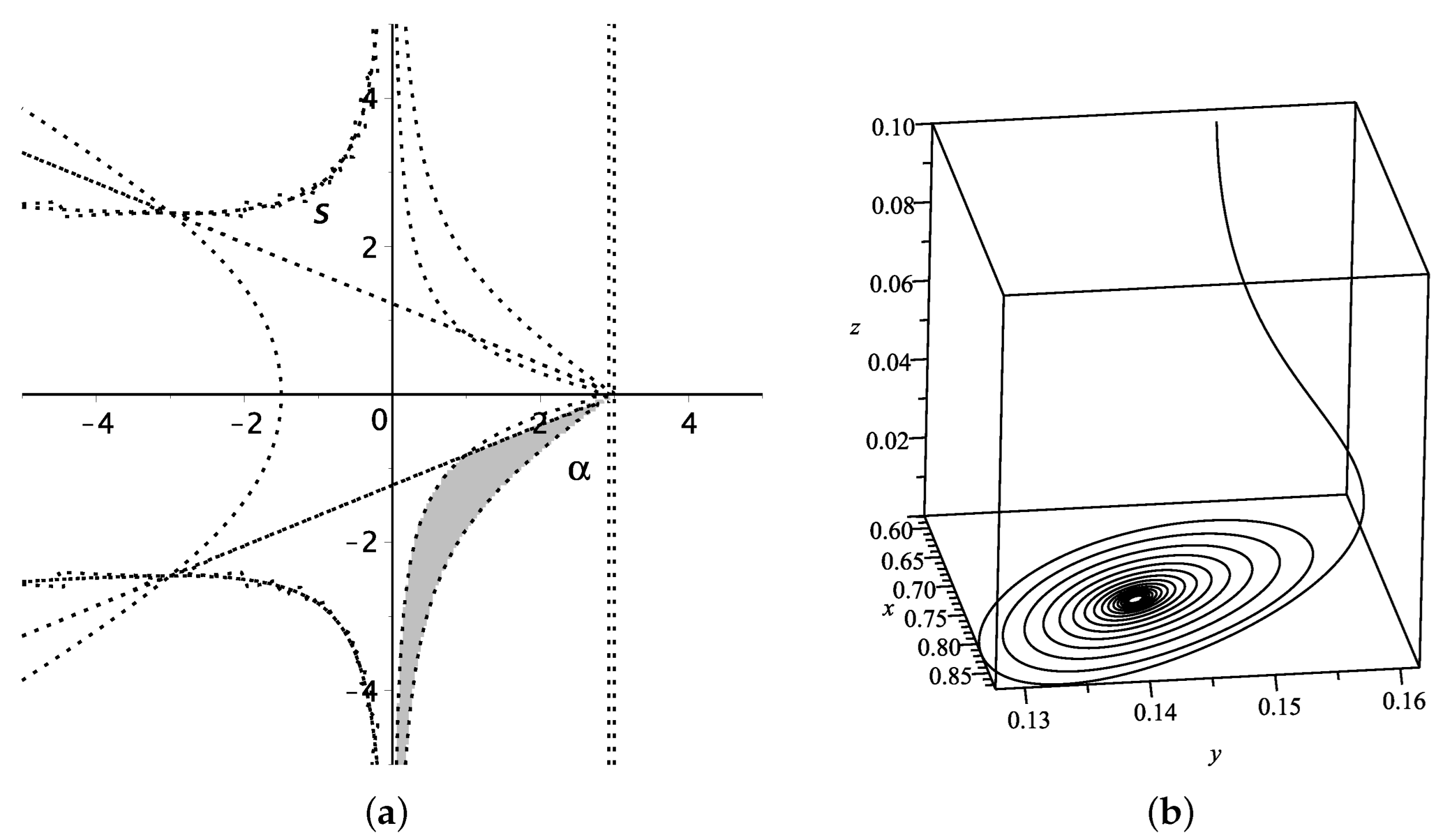
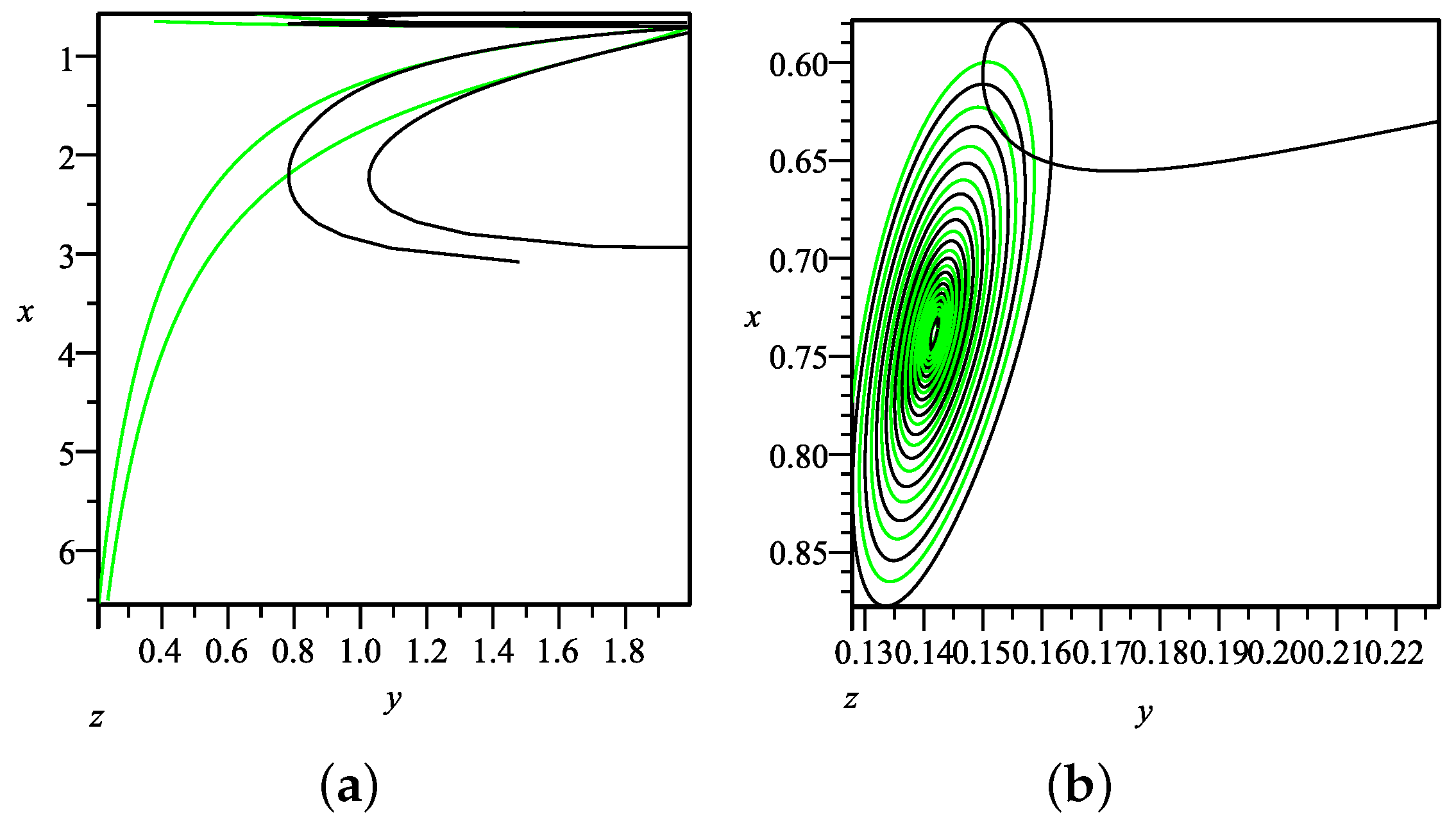
3. Model II: in Loop Quantum Cosmology
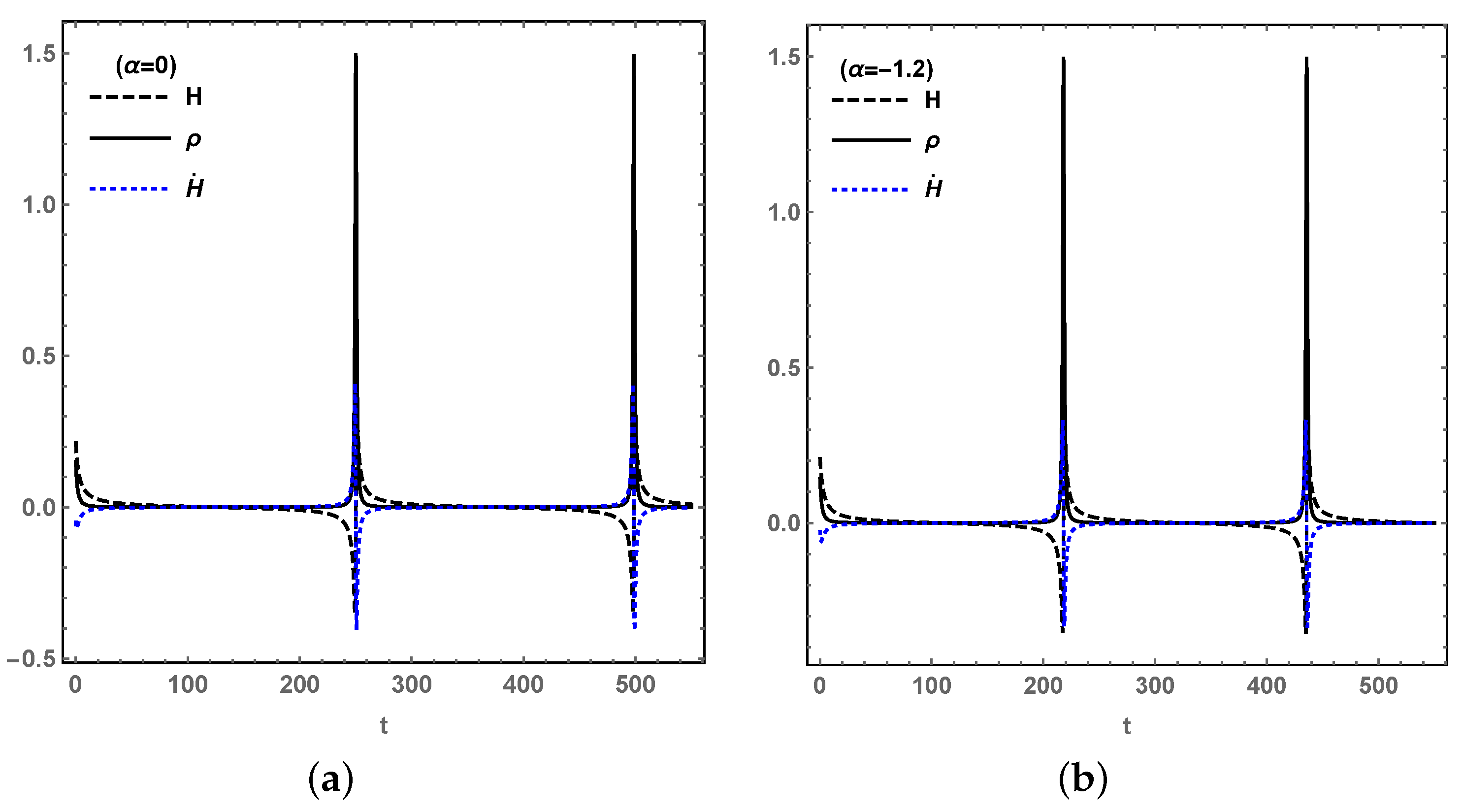
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Spergel, D.N. et al. [WMAP Collaboration]. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. 2003, 148, 175. [Google Scholar] [CrossRef] [Green Version]
- Eisenstein, D.J. et al. [SDSS Collaboration]. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Mission 2018 Collaboration]. Planck 2018 results VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Xu, L.X.; Lu, J.B.; Wang, Y.T. Revisiting generalized Chaplygin gas as a unified dark matter and dark energy model. Eur. Phys. J. C. 2012, 72, 1883. [Google Scholar] [CrossRef]
- Xu, L.X.; Wang, Y.T.; Noh, H. Modified Chaplygin gas as a unified dark matter and dark energy model and cosmic constraints. Eur. Phys. J. C. 2012, 72, 1931. [Google Scholar] [CrossRef]
- Yang, W.Q.; Li, H.; Wu, Y.B.; Lu, J.B. Cosmological implications of the dark matter equation of state. Int. J. Mod. Phys. D 2017, 26, 1750013. [Google Scholar] [CrossRef]
- Du, M.H.; Yang, W.Q.; Xu, L.X.; Pan, S.; Mota, D.F. Future constraints on dynamical dark-energy using gravitational-wave standard sirens. Phys. Rev. D 2019, 100, 043535. [Google Scholar] [CrossRef] [Green Version]
- Sahni, V.; Starobinsky, A.A. The case for a positive cosmological Λ-term. Int. J. Mod. Phys. D 2000, 9, 373. [Google Scholar] [CrossRef]
- Carroll, S.M. The cosmological constant. Living Rev. Relativ. 2001, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Carroll, S.M.; Hoffman, M.; Trodden, M. Can the dark energy equation-of-state parameter w be less than −1? Phys. Rev. D 2003, 68, 023509. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Li, X.D.; Wang, S.; Wang, Y. Dark Energy. Commun. Theor. Phys. 2011, 56, 525–604. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.J.; Zhang, S.N. The age problem in the ΛCDM model. Mon. Not. R. Astron. Soc. 2010, 407, 1835–1841. [Google Scholar] [CrossRef] [Green Version]
- Tsujikawa, S. Quintessence: A Review. Class. Quant. Gravit. 2013, 30, 214003. [Google Scholar] [CrossRef] [Green Version]
- Feng, B.; Wang, X.L.; Zhang, X.M. Dark Energy Constraints from the Cosmic Age and Supernova. Phys. Lett. B 2005, 607, 35–41. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark Energy: Theory and Observations; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Goswami, G.K.; Pradhan, A.; Beesham, A. A Dark Energy Quintessence Model of the Universe. Mod. Phys. Lett. A 2020, 35, 2050002. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, N.; Pradhan, A. Crossing the phantom divide line in universal extra dimensions. New Astron. 2020, 80, 101406. [Google Scholar] [CrossRef]
- Varshney, G.; Sharma, U.K.; Pradhan, A.; Kumar, N. Reconstruction of Tachyon, Dirac-Born-Infeld-essence and Phantom model for Tsallis holographic dark energy in f (R, T) gravity. Chin. J. Phys. 2021, 73, 56–73. [Google Scholar] [CrossRef]
- Dixit, A.; Maurya, D.C.; Pradhan, A. Phantom dark energy nature of bulk-viscosity universe in modified f (Q)-gravity. Int. J. Geom. Meth. Mod. Phys. 2022, 2250198. [Google Scholar] [CrossRef]
- Guo, Z.K.; Cai, R.G. Cosmological Evolution of Interacting Phantom Energy with Dark Matter. J. Cosmol. Astropart. Phys. 2005, 5, 2. [Google Scholar] [CrossRef]
- Bojowald, M. Loop Quantum Cosmology. Living Rev. Relativ. 2005, 8, 11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, B.F.; Singh, P.; Wang, A. Towards cosmological dynamics from loop quantum gravity. Phys. Rev. D 2018, 97, 084029. [Google Scholar] [CrossRef] [Green Version]
- Li, B.F.; Singh, P.; Wang, A. Qualitative dynamics and inflationary attractors in loop cosmology. Phys. Rev. D 2018, 98, 066016. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A. Gravity, Geometry and Quantum. AIP Conf. Proc. 2006, 3, 861. [Google Scholar]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum Nature of the Big Bang. Phys. Rev. Lett. 2006, 96, 141301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sami, M.; Singh, P.; Tsujikawa, S. Avoidence of future singularities in loop quantum cosmology. Phys. Rev. D 2007, 74, 043514. [Google Scholar] [CrossRef] [Green Version]
- Samart, D.; Gumjudpai, B. Phantom field dynamics in loop quantum cosmology. Phys. Rev. D 2007, 76, 043514. [Google Scholar] [CrossRef] [Green Version]
- Cailleteau, T.; Cardoso, A.; Vandersloot, K.; Wands, D. Singularity in loop quantum cosmology. Phys. Rev. Lett. 2008, 101, 251302. [Google Scholar] [CrossRef] [Green Version]
- Haro, J. Future singularity avoidence in semiclassical cosmology. Gen. Relativ. Gravit. 2012, 44, 2215–2238. [Google Scholar] [CrossRef]
- Kleidis, K.; Oikonomou, V.K. Loop quantum cosmology scalar field models. Int. J. Geom. Meth. Mod. Phys. 2018, 15, 1850071. [Google Scholar] [CrossRef] [Green Version]
- Novello, M.; Bergliaffa, S.E.P. Bouncing cosmologies. Phys. Rep. 2008, 463, 127–213. [Google Scholar] [CrossRef]
- Brandenberger, R.; Peter, P. Bouncing Cosmologies: Progress and Problems. Found. Phys. 2017, 47, 797–850. [Google Scholar] [CrossRef] [Green Version]
- Wu, P.X.; Zhang, S.N. Cosmological evolution of interacting phantom (quintessence) model in loop quantum cosmology. J. Cosmol. Astropart. Phys. 2008, 6, 7. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.B.; Wang, B.; Jing, J.L. Dynamics of interacting dark energy model in Einstein and loop quantum cosmology. Phys. Rev. D 2008, 78, 123503. [Google Scholar] [CrossRef]
- Fu, X.Y.; Yu, H.W.; Wu, P.X. Dynamics of interacting phantom in loop quantum cosmology. Phys. Rev. D 2008, 78, 063001. [Google Scholar] [CrossRef] [Green Version]
- Zonunmawia, H.; Khyllep, W.; Roy, N.; Dutta, J.; Tamanini, N. Extended phase space analysis of interacting DE models in loop quantum cosmology. Phys. Rev. D 2017, 96, 083527. [Google Scholar] [CrossRef] [Green Version]
- Oikonomou, V.K. The classical and loop quantum cosmology phase space of interacting dark energy and superfliud dark matter. Phys. Rev. D 2019, 99, 104042. [Google Scholar] [CrossRef] [Green Version]
- Oikonomou, V.K. Generalised logarithmic equation of state in classical and loop quantum cosmology dark energy-dark matter coupled system. Ann. Phys. 2019, 409, 167934. [Google Scholar] [CrossRef] [Green Version]
- Garriga, J.; Mukhanov, V.F. Perturbations in k-inflation. Phys. Lett. B 1999, 458, 219–225. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, S.; Sharma, U.K.; Pradhan, A. New holographic dark energy in Bianchi-III universe with k-essence. New Astron. 2018, 68, 57–64. [Google Scholar] [CrossRef]
- Varshney, G.; Sharma, U.K.; Pradhan, A. Reconstructing the k-essence and the dilation field models of the THDE in f (R, T) gravity. Eur. Phys. J. Plus 2020, 135, 541. [Google Scholar] [CrossRef]
- Bhardwaj, V.K.; Pradhan, A.; Dixit, A. Compatibility between the scalar field models of tachyon, k-essence and quintessence in f (R, T) gravity. New Astron. 2021, 83, 101478. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V. K-inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef] [Green Version]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. A Dynamical Solution to the Problem of a Small Cosmological Constant and Late-time Cosmic Acceleration. Phys. Rev. Lett. 2000, 85, 4438–4441. [Google Scholar] [CrossRef] [Green Version]
- Rendall, A.D. Dynamics of k-essence. Class. Quant. Gravit. 2006, 23, 1557–1570. [Google Scholar] [CrossRef] [Green Version]
- Bose, N.; Majumdar, A.S. A k-essence Model of Inflation, Dark Matter and Dark Energy. Phys. Rev. D 2009, 79, 103517. [Google Scholar] [CrossRef] [Green Version]
- Bose, N.; Majumdar, A.S. Unified Model of k-Inflation, Dark Matter and Dark Energy. Phys. Rev. D 2009, 80, 103508. [Google Scholar] [CrossRef] [Green Version]
- De-Santiago, J.; Cervantes-Cota, J.L.; Wands, D. Cosmological phase space analysis of the F (X)-V (ϕ) scalar field bouncing solutions. Phys. Rev. D 2013, 87, 023502. [Google Scholar] [CrossRef] [Green Version]
- De-Santiago, J.; Cervantes-Cota, J.L. Phase space analysis of the F (X)-V (ϕ) scalar field Lagrangian and scaling solutions in flat cosmology. J. Phys. Conf. Ser. 2014, 485, 012017. [Google Scholar] [CrossRef] [Green Version]
- Dutta, J.; Khyllep, W.; Tamanini, N. Cosmological dynamics of scalar fields with kinetic corrections: Beyond the exponential potential. Phys. Rev. D 2016, 93, 063004. [Google Scholar] [CrossRef] [Green Version]
- Scherrer, R.J. Purely kinetic k-essence as unified dark matter. Phys. Rev. Lett. 2004, 93, 011301. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically Driven Quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef] [Green Version]
- Chimento, L.P.; Feinstein, A. Power-law expansion in k-essence cosmology. Mod. Phys. Lett. A 2004, 19, 761–768. [Google Scholar] [CrossRef]
- Chimento, L.P. Extended tachyon field, Chaplygin gas and solvable k-essence cosmologies. Phys. Rev. D 2004, 69, 123517. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, A.; Ghosh, A.; Banerjee, N. Dynamical systems analysis of a k-essence model. Phys. Rev. D 2019, 99, 103513. [Google Scholar] [CrossRef] [Green Version]
- Battye, R.A.; Pace, F. Approximation of the potential in scalar field dark energy models. Phys. Rev. D 2016, 94, 063513. [Google Scholar] [CrossRef] [Green Version]
- Bolotin, Y.L.; Kostenko, A.; Lemets, O.A. Cosmological evolution with interaction between dark energy and dark matter. Int. J. Mod. Phys. D 2015, 24, 1530007. [Google Scholar] [CrossRef] [Green Version]
- Wang, B. Dark Matter and Dark Energy Interactions: Theoretical Challenges, Cosmological Implications and Observational Signatures. Rep. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef] [Green Version]
- Chimento, L.P. Linear and nonlinear interactions in the dark sector. Phys. Rev. D 2010, 81, 043525. [Google Scholar] [CrossRef] [Green Version]
- Goswami, G.K.; Pradhan, A.; Beesham, A. FLRW Accelerating Universe with Interactive Dark Energy. Pramana-J. Phys. 2019, 93, 89. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, A.; Goswami, G.K.; Beesham, A.; Dixit, A. An FLRW interacting dark energy model of the Universe. New Astron. 2020, 78, 101368. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Pan, S.; Yang, W.Q. Dynamics of nonlinear interacting dark energy models. Int. J. Mod. Phys. D 2019, 28, 1950161. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.Q.; Pan, S.; Barrow, J.D. Large-scale stability and astronomical constraints for coupled dark-energy models. Phys. Rev. D 2018, 97, 043529. [Google Scholar] [CrossRef] [Green Version]
- Zhang, N.; Wu, Y.B.; Chi, J.N.; Yu, Z.; Xu, D.F. Diagnosing Tsallis holographic dark energy models with interactions. Mod. Phys. Lett. A 2020, 33, 2050044. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.J.; Chen, B.H.; Li, J.; Qi, J.Z. The evolution of the power law k-essence cosmology. Astrophys. Space Sci. 2015, 356, 399–405. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.B.; Jing, J.L. Dark energy model interacting with dark matter and unparticle. Class. Quant. Gravit. 2009, 26, 155006. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.H.; Wu, Y.B.; Xu, D.F.; Dong, W.; Nan, Z. Dynamical stability and geometrical dianostic of the power law k-essence dark energy model with interaction. Universe 2020, 6, 244. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef] [Green Version]
- Bahamonde, S.; Boehmer, C.G.; Carloni, S.; Copeland, E.J.; Fang, W.; Tamanini, N. Dynamical systems applied to cosmology: Dark energy and modified gravity. Phys. Rep. 2018, 775–777, 1–122. [Google Scholar]
- Leon, G.; Saridakis, E.N. Phase-space analysis of Horava-Lifshitz cosmology. J. Cosmol. Astropart. Phys. 2009, 11, 6. [Google Scholar] [CrossRef]
- Shi, J.L.; Wu, J.P. Dynamics of k-essence in loop quantum cosmology. Chin. Phys. C 2021, 4, 451–461. [Google Scholar] [CrossRef]
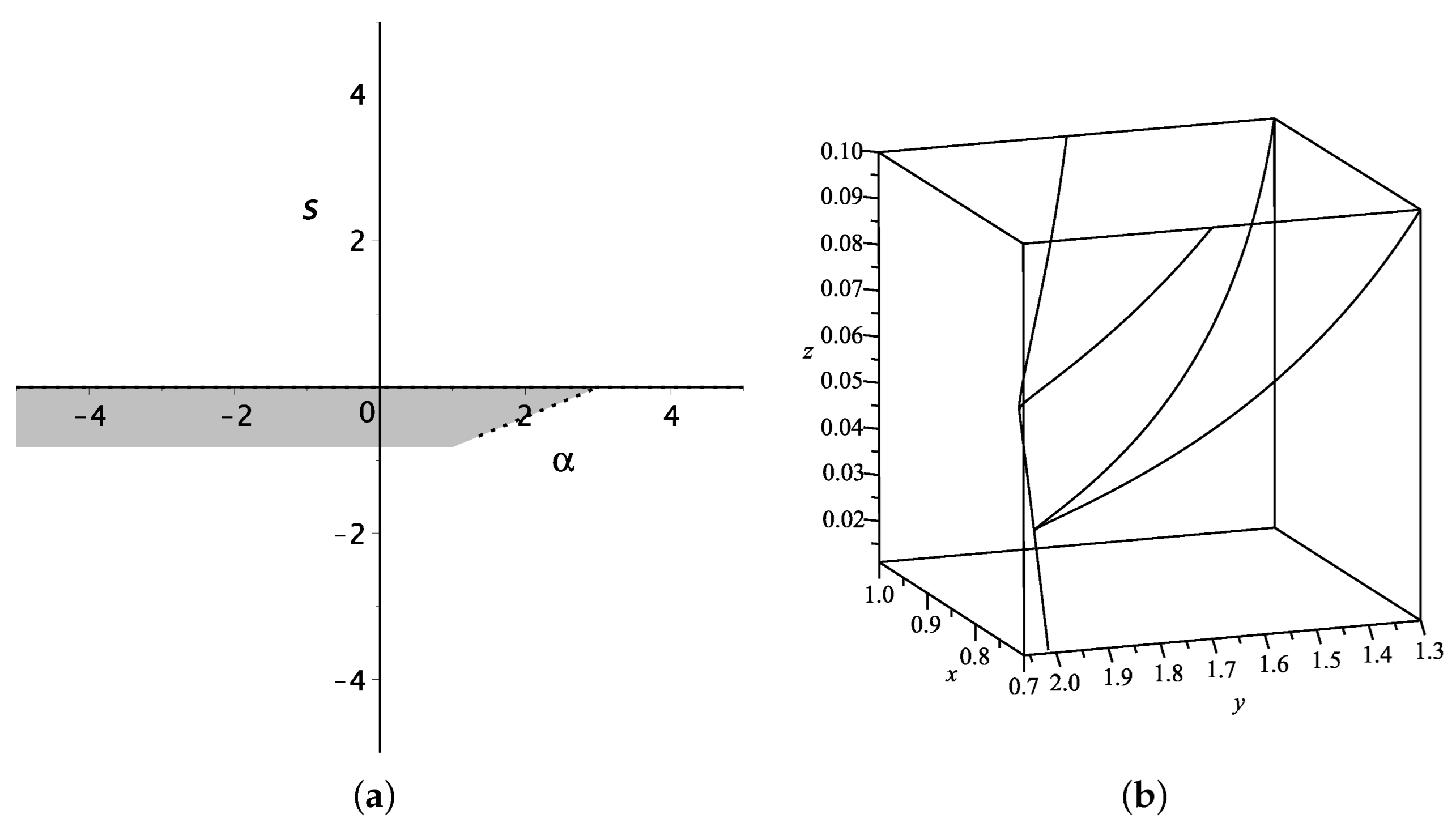
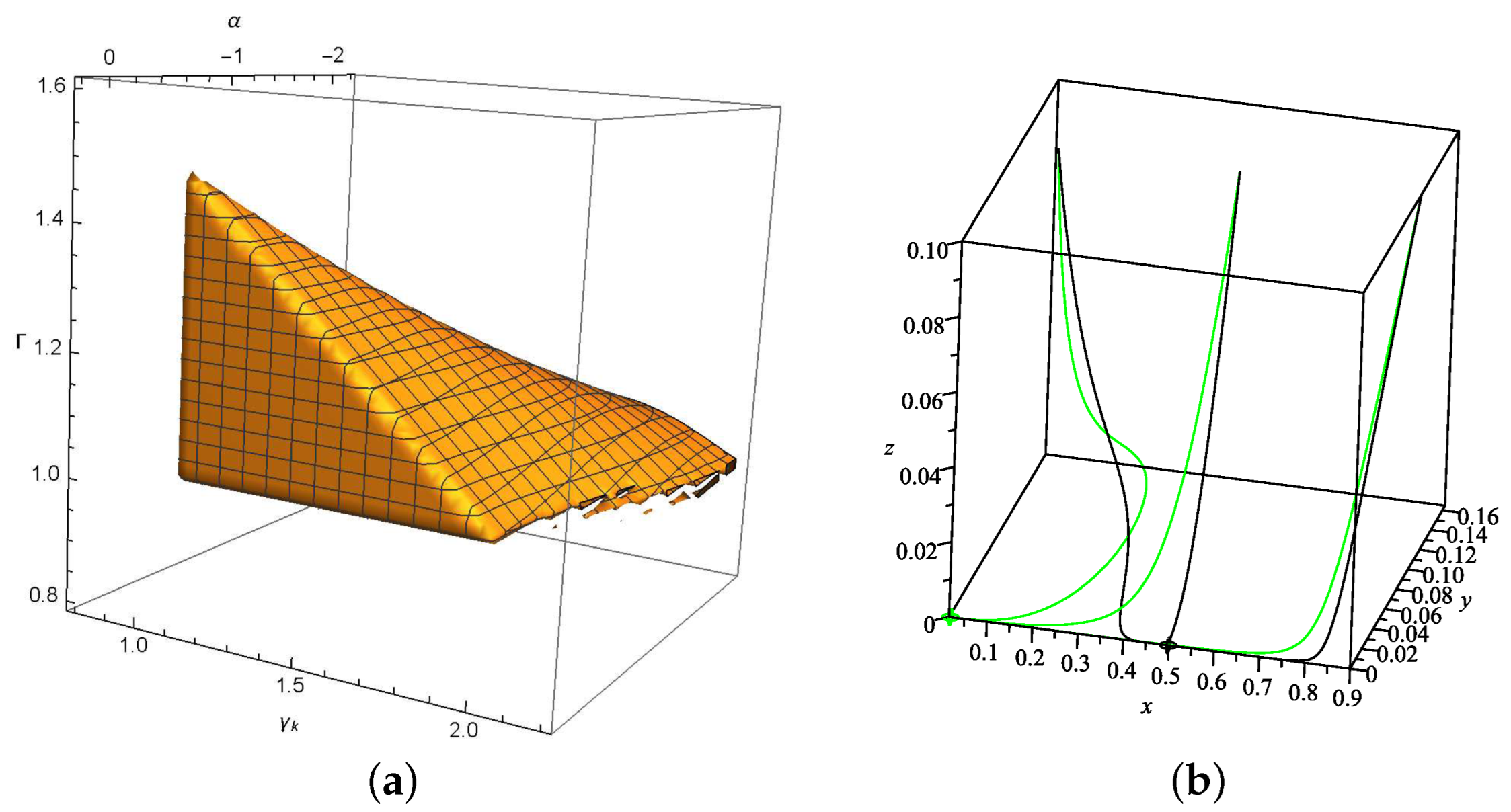
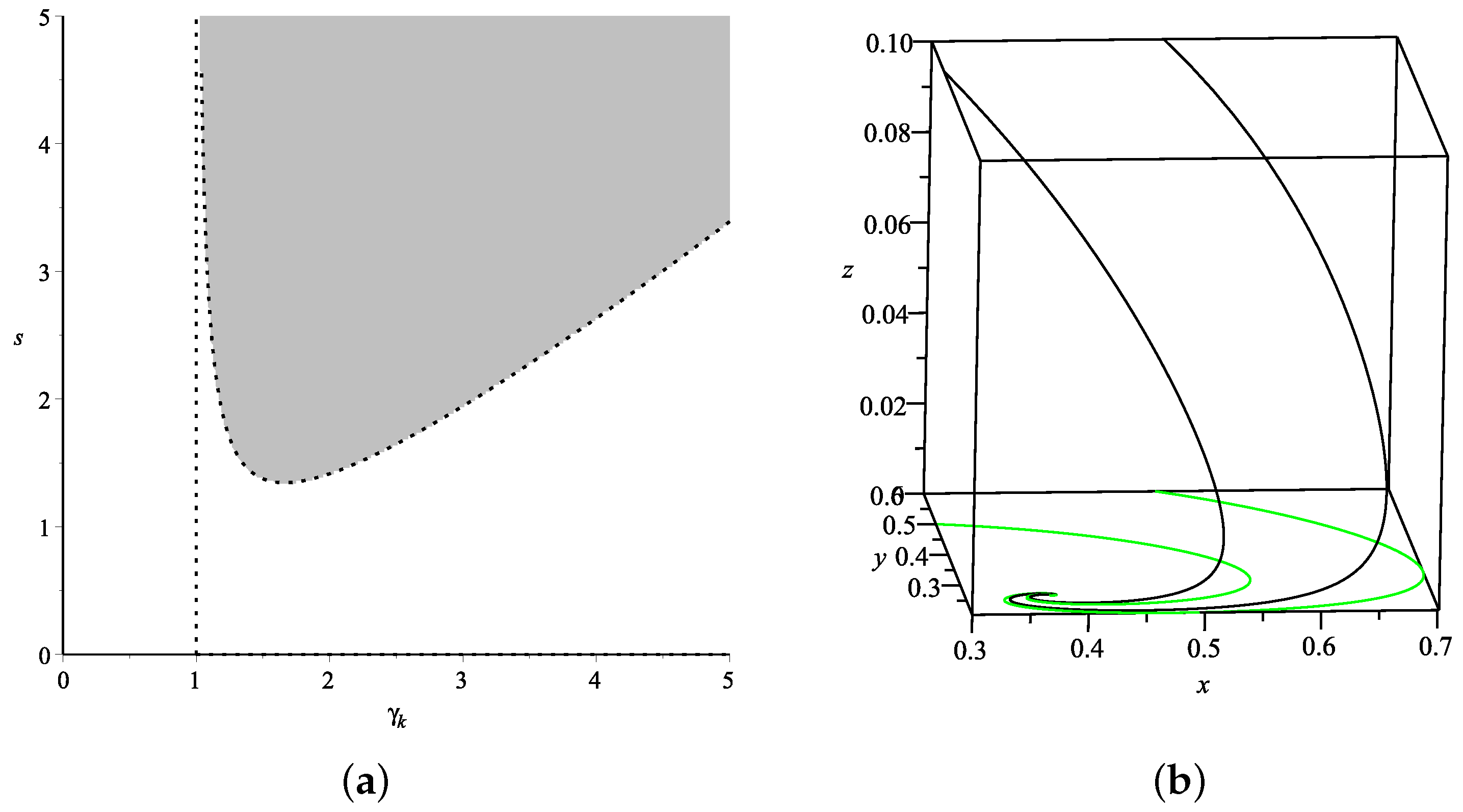
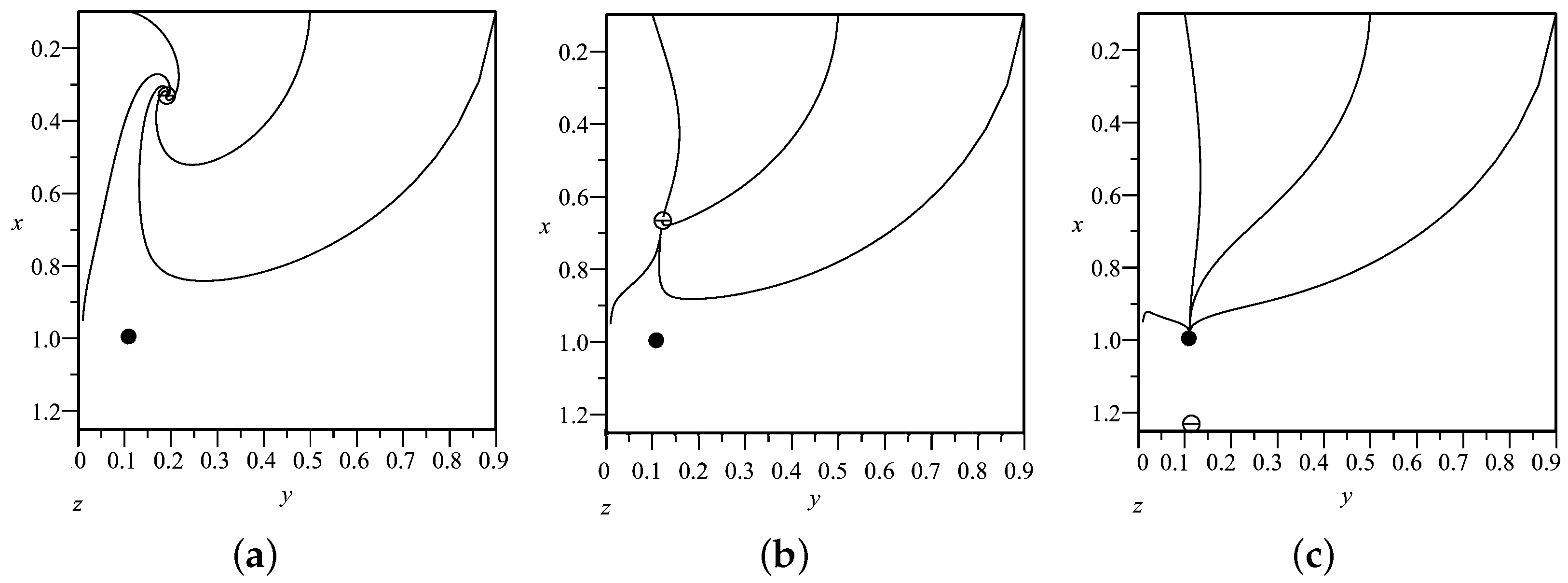
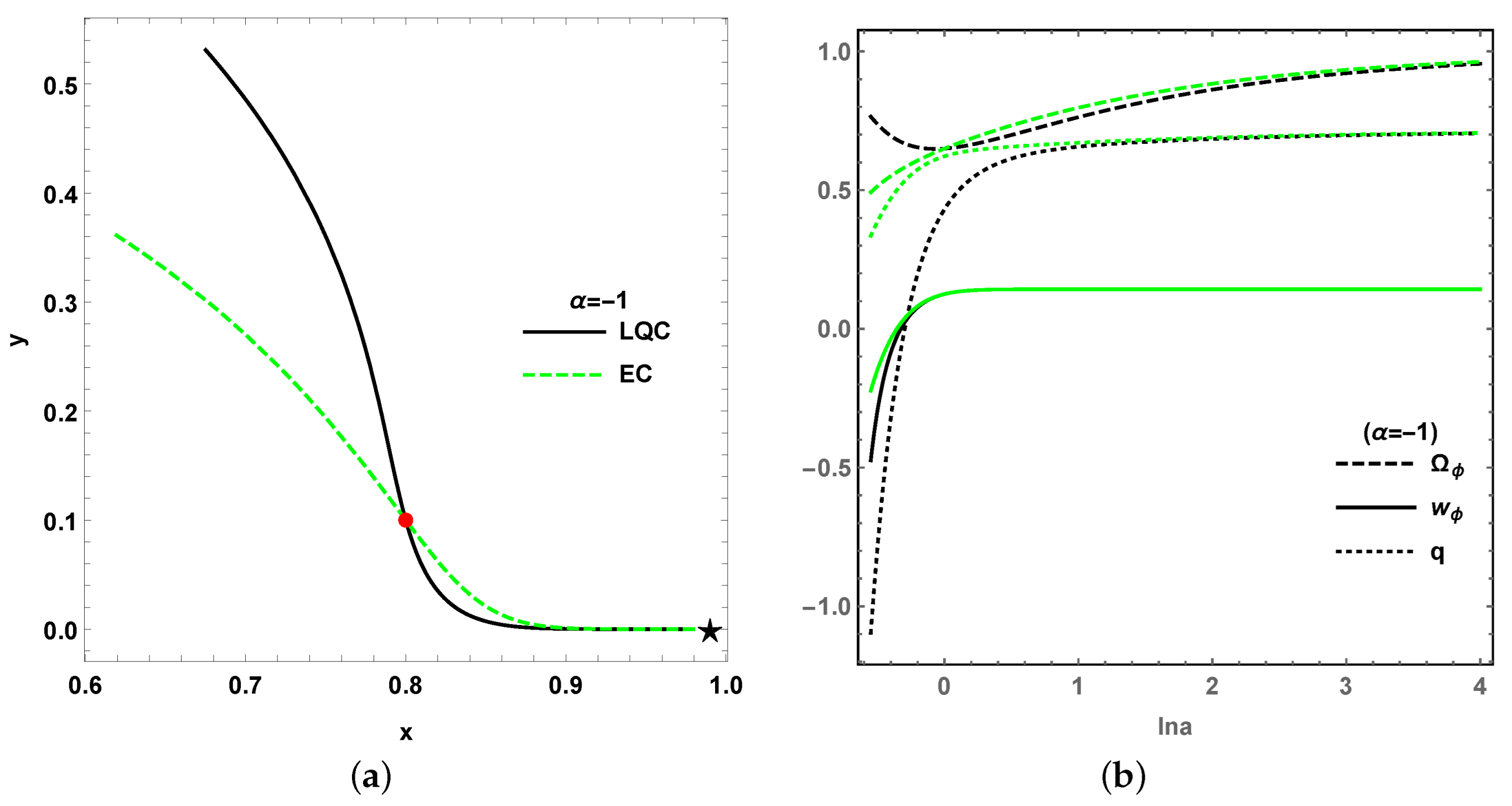
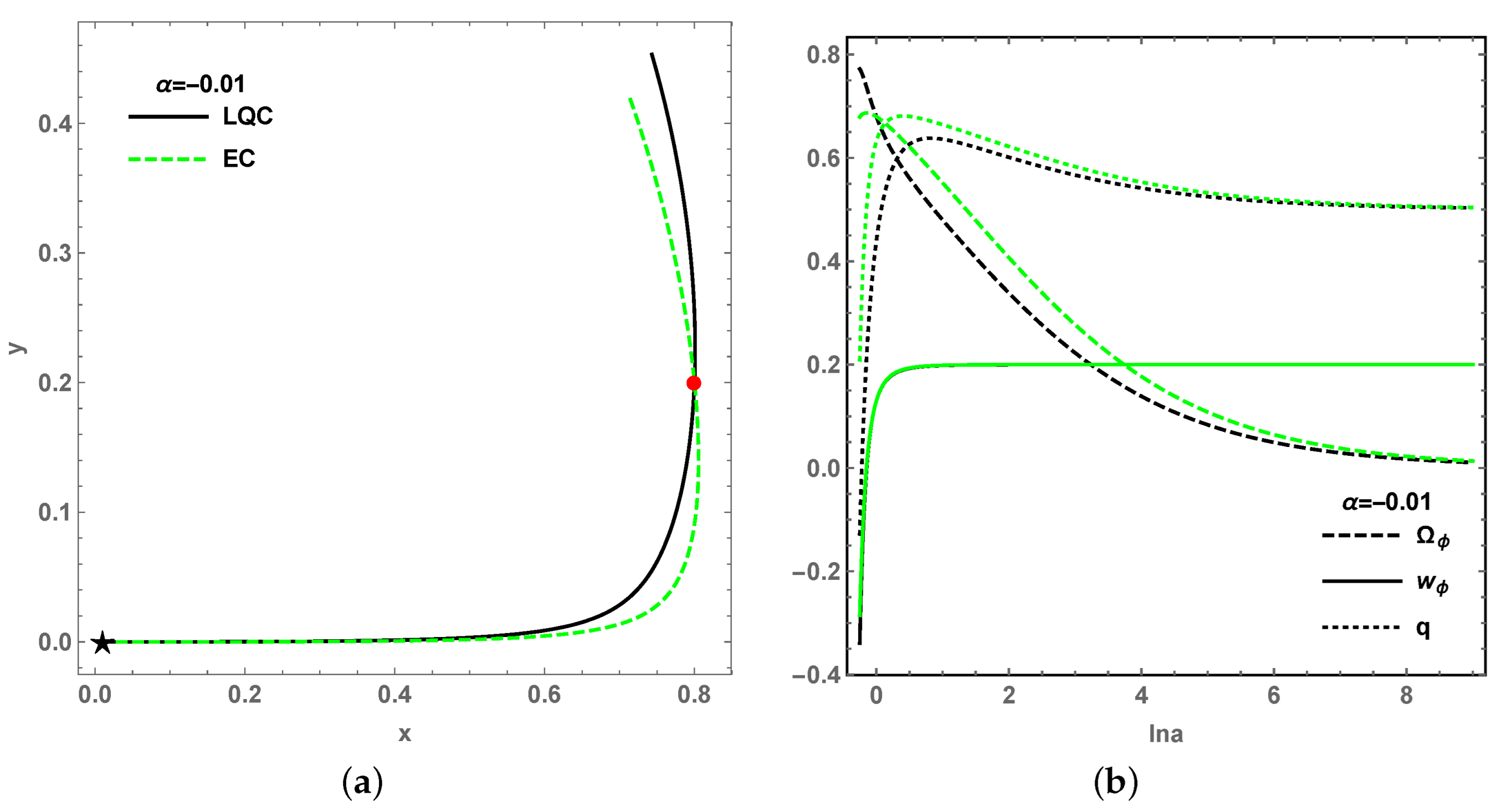
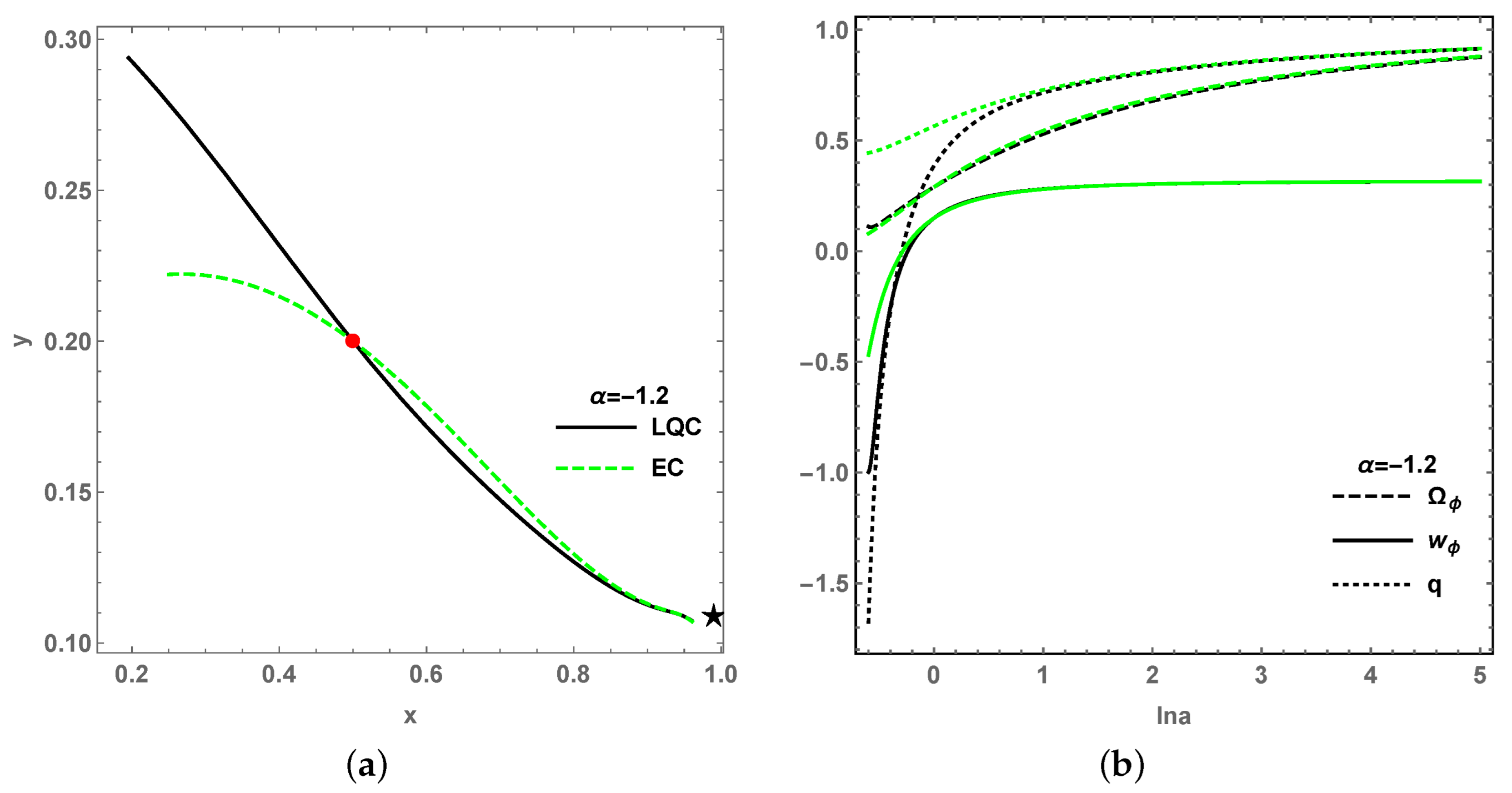
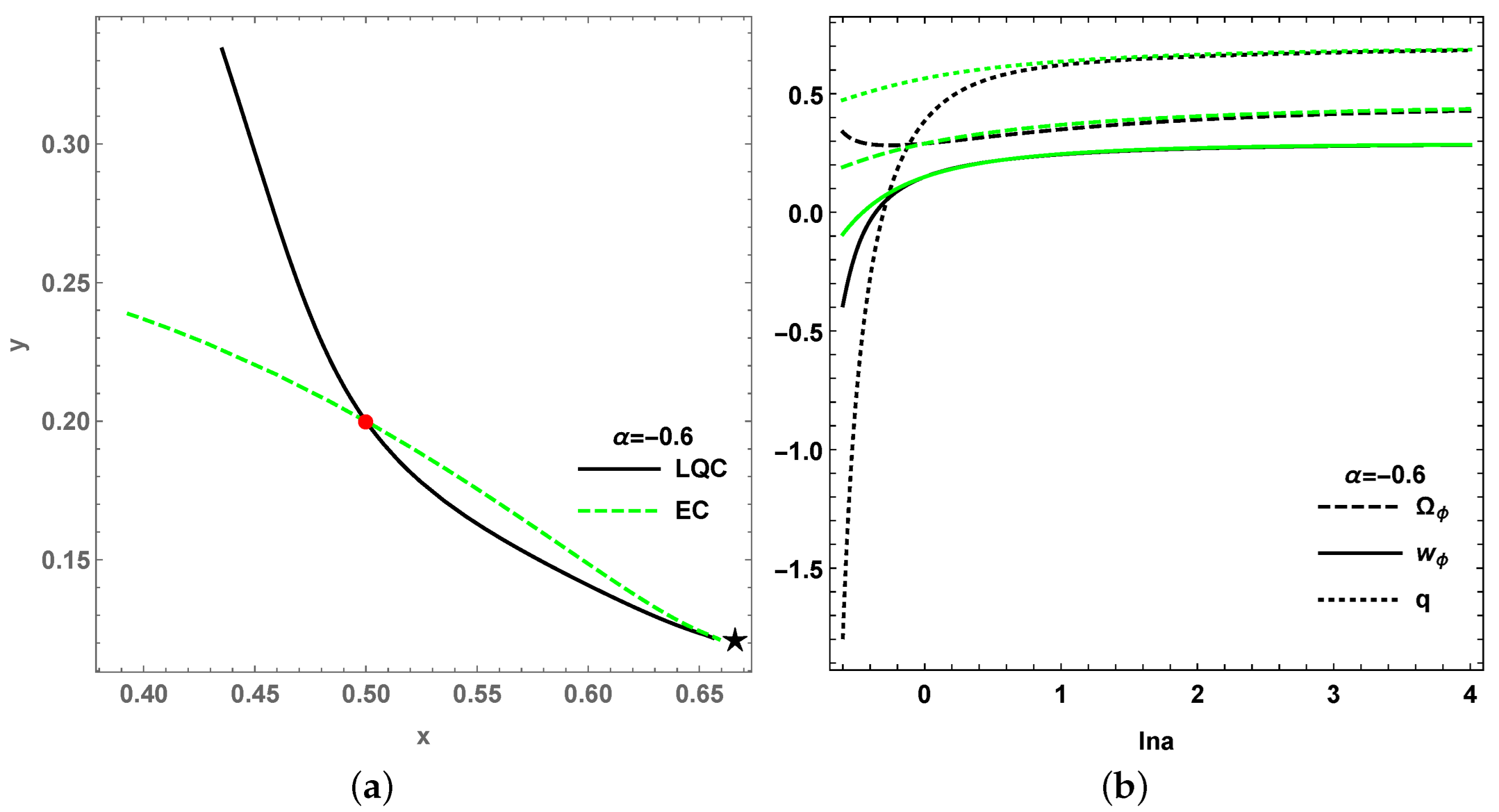
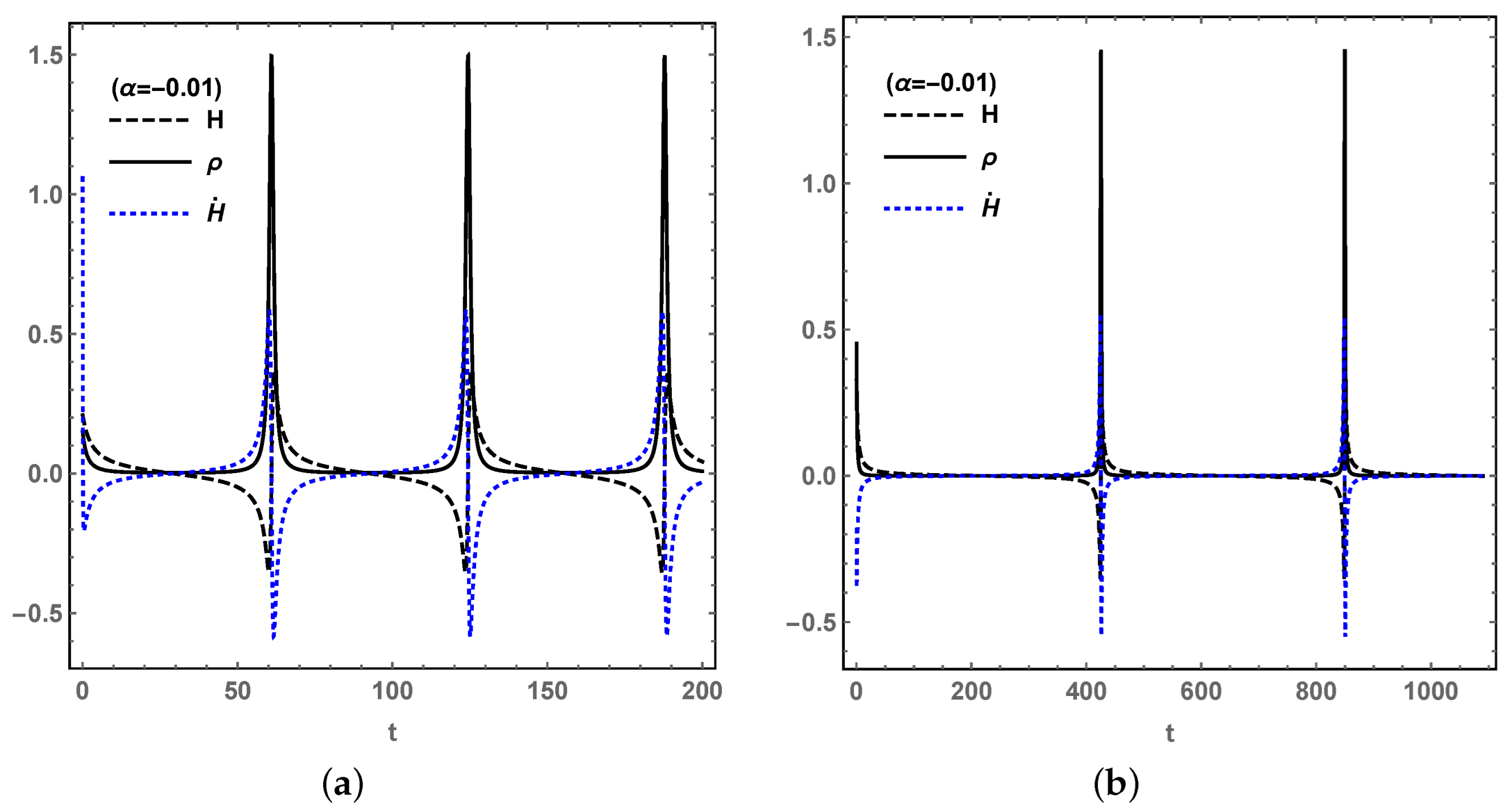
| Name | Existence | Stability | |||
|---|---|---|---|---|---|
| none | 1 | ||||
| 1 | |||||
| none | 1 | ||||
| 1 | |||||
| Name | Existence | Stability | |||
|---|---|---|---|---|---|
| unstable | 0 | none | |||
| always | unstable | 1 | |||
| always | unstable | 1 | |||
| always | 1 | ||||
| unstable | |||||
| none | stable | ||||
| none | unstable |
| Name | Existence | Stability | q | |||
|---|---|---|---|---|---|---|
| 1 | ||||||
| 0 | 0 | 1/2 | ||||
| 0 | 0 | 1/2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Wu, Y.; Chi, J.; Liu, W.; Hu, Y. The Phase Space Analysis of Interacting K-Essence Dark Energy Models in Loop Quantum Cosmology. Universe 2022, 8, 520. https://doi.org/10.3390/universe8100520
Chen B, Wu Y, Chi J, Liu W, Hu Y. The Phase Space Analysis of Interacting K-Essence Dark Energy Models in Loop Quantum Cosmology. Universe. 2022; 8(10):520. https://doi.org/10.3390/universe8100520
Chicago/Turabian StyleChen, Bohai, Yabo Wu, Jianan Chi, Wenzhong Liu, and Yiliang Hu. 2022. "The Phase Space Analysis of Interacting K-Essence Dark Energy Models in Loop Quantum Cosmology" Universe 8, no. 10: 520. https://doi.org/10.3390/universe8100520






