Topological Aspects of Dense Matter: Lattice Studies
Abstract
:1. Introduction
2. Topology and Strong Interactions
2.1. Topology, from Low to High Temperatures
2.2. Symmetries of QCD, and Topology
2.3. Conserved Charges and
2.4. Instantons and Zero Modes
2.5. Detecting Topology—The Chiral Magnetic Effect and
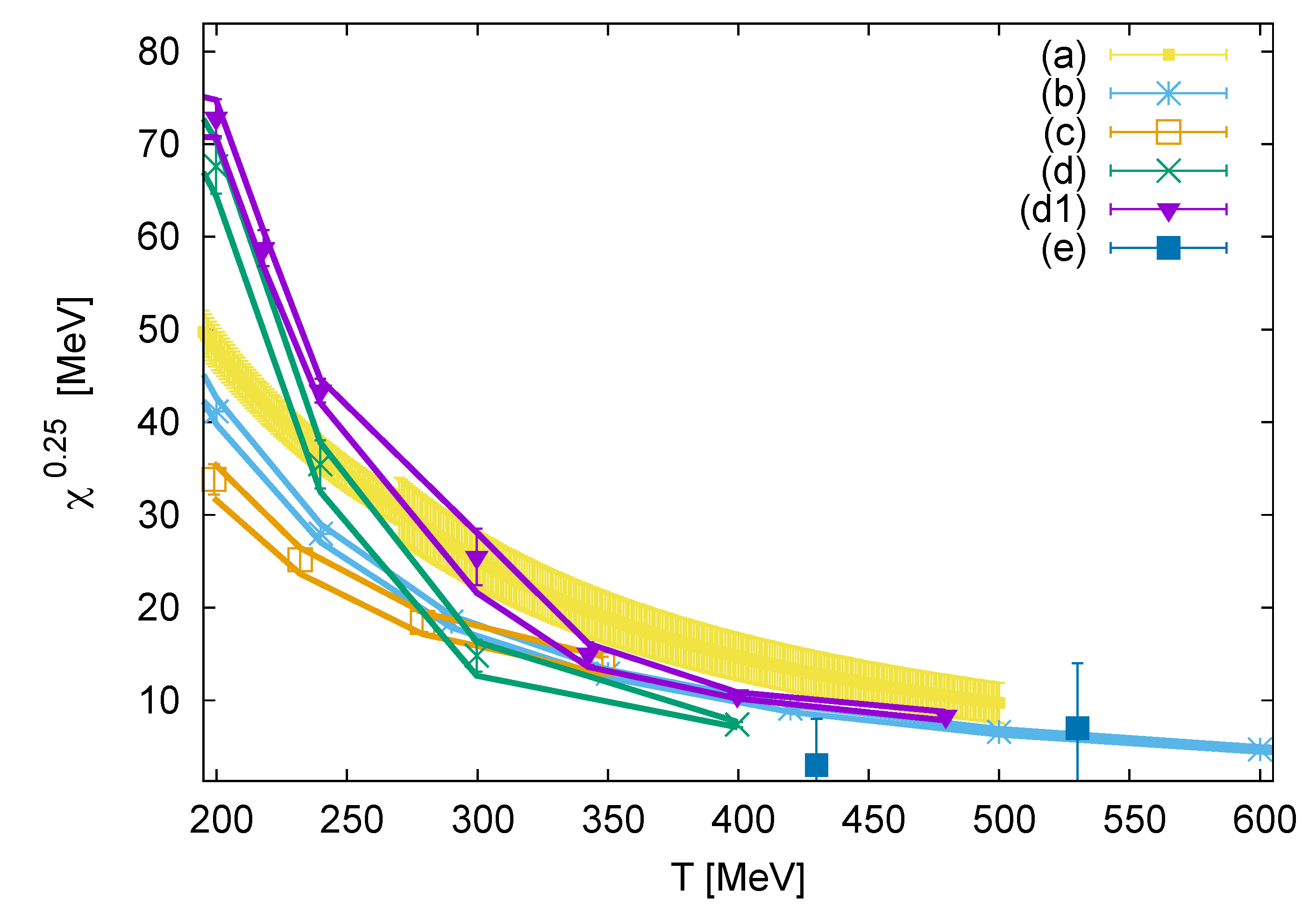
3. Lattice Results—Topology and Dense Matter
3.1. Baryon Density
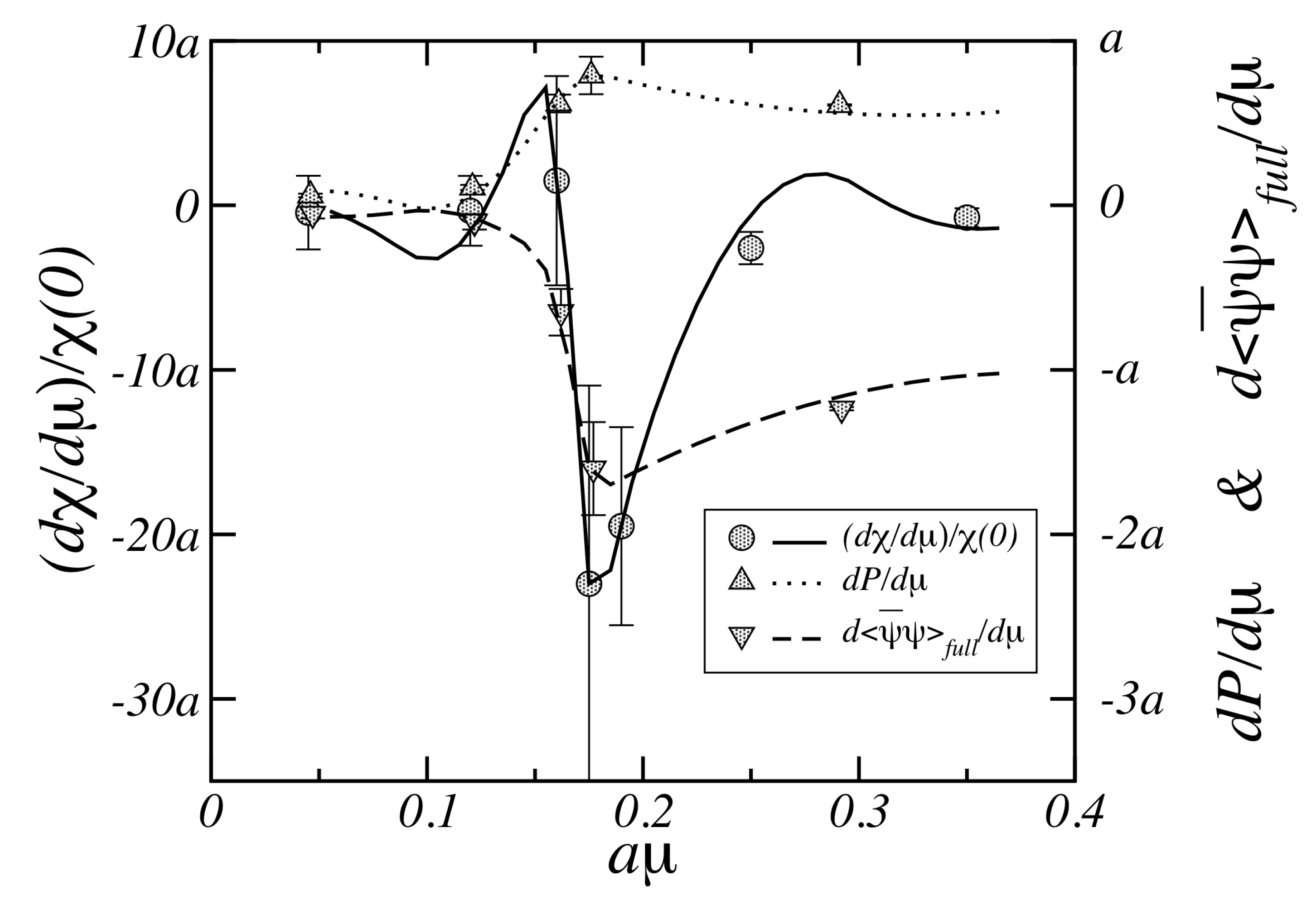
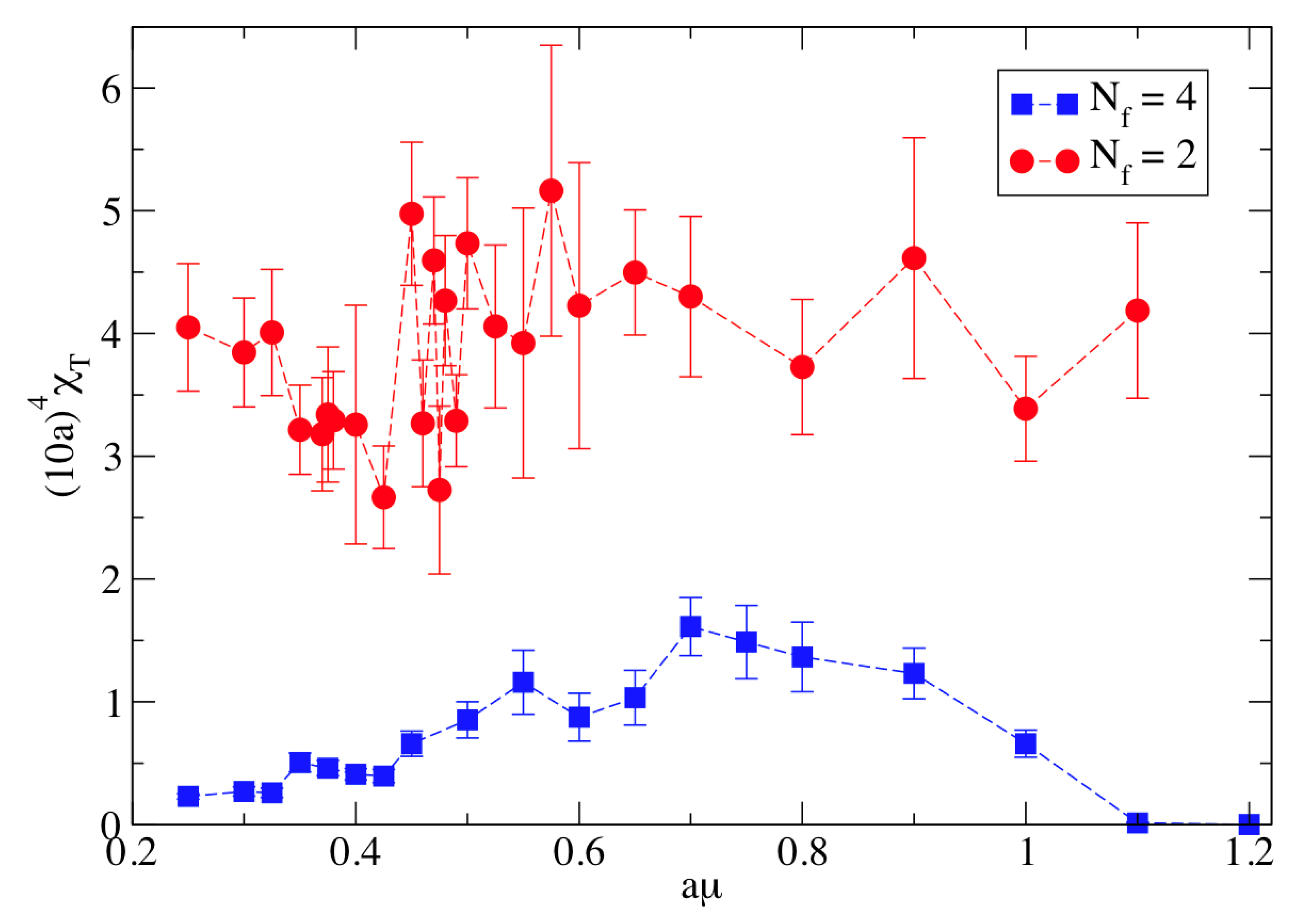
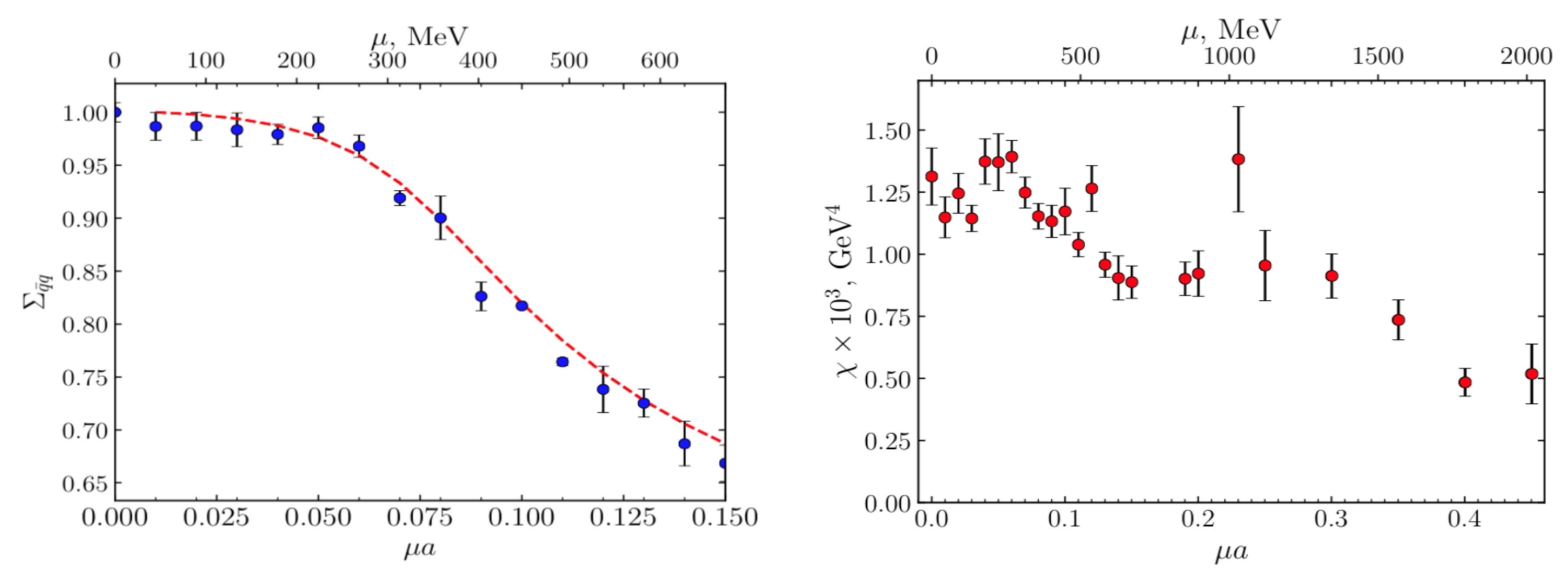
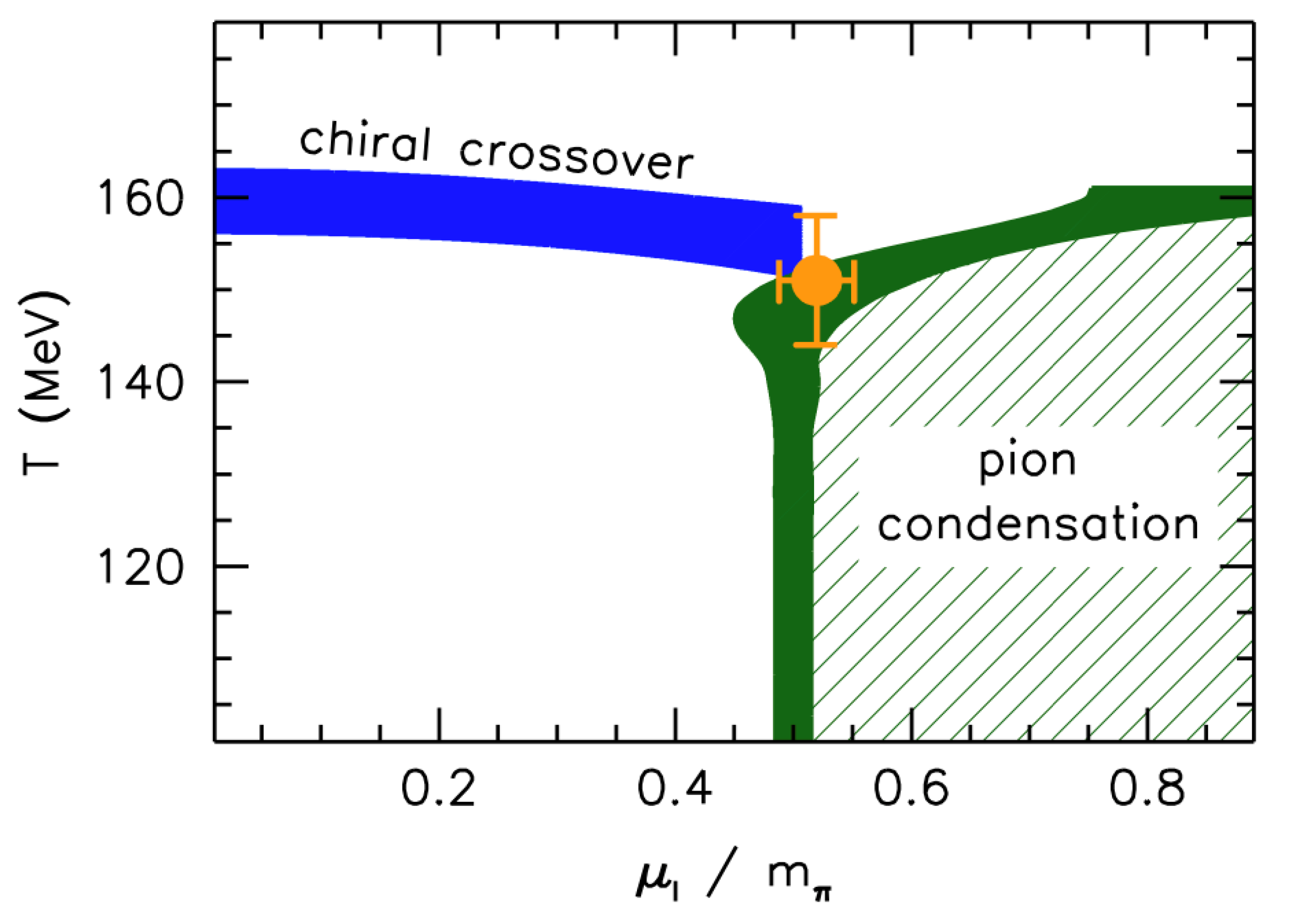
3.2. Isospin Density
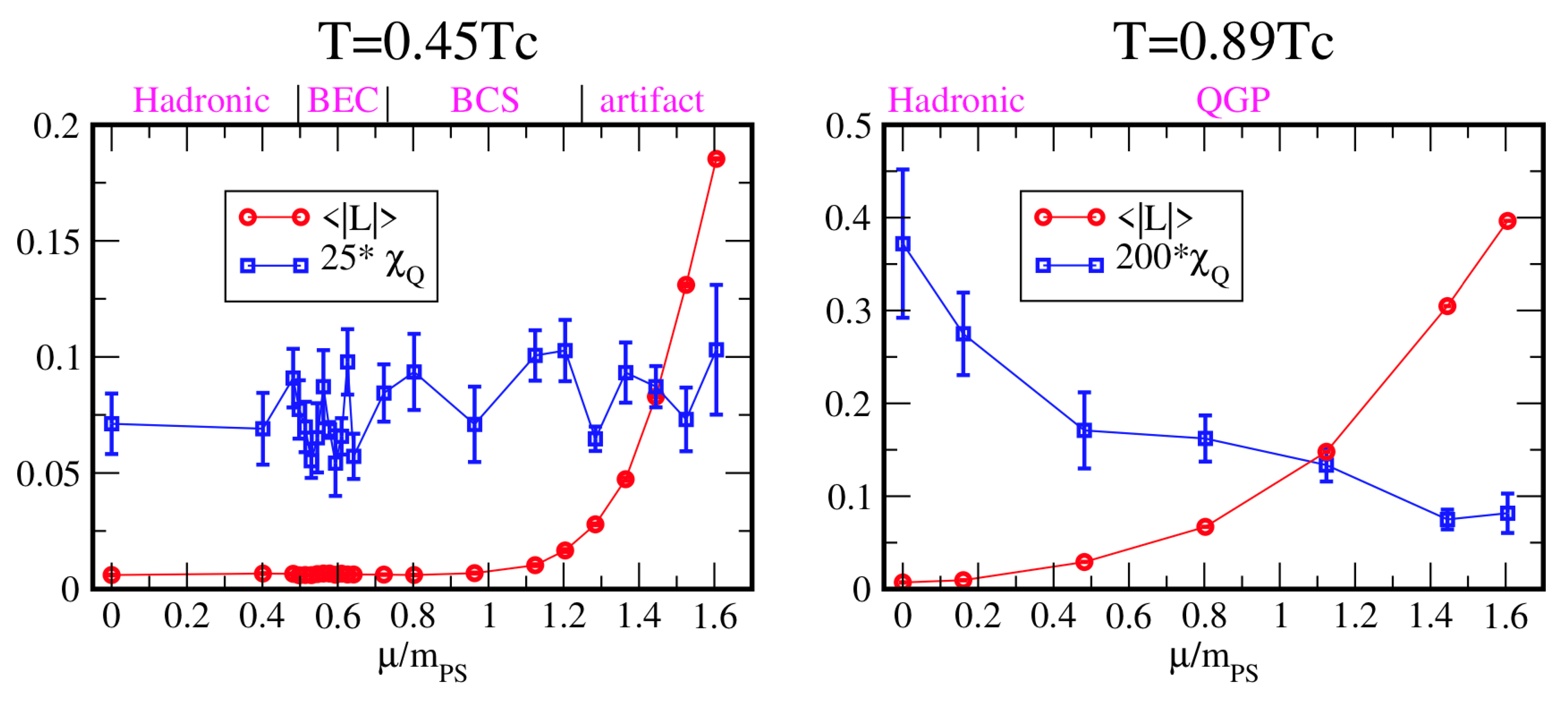
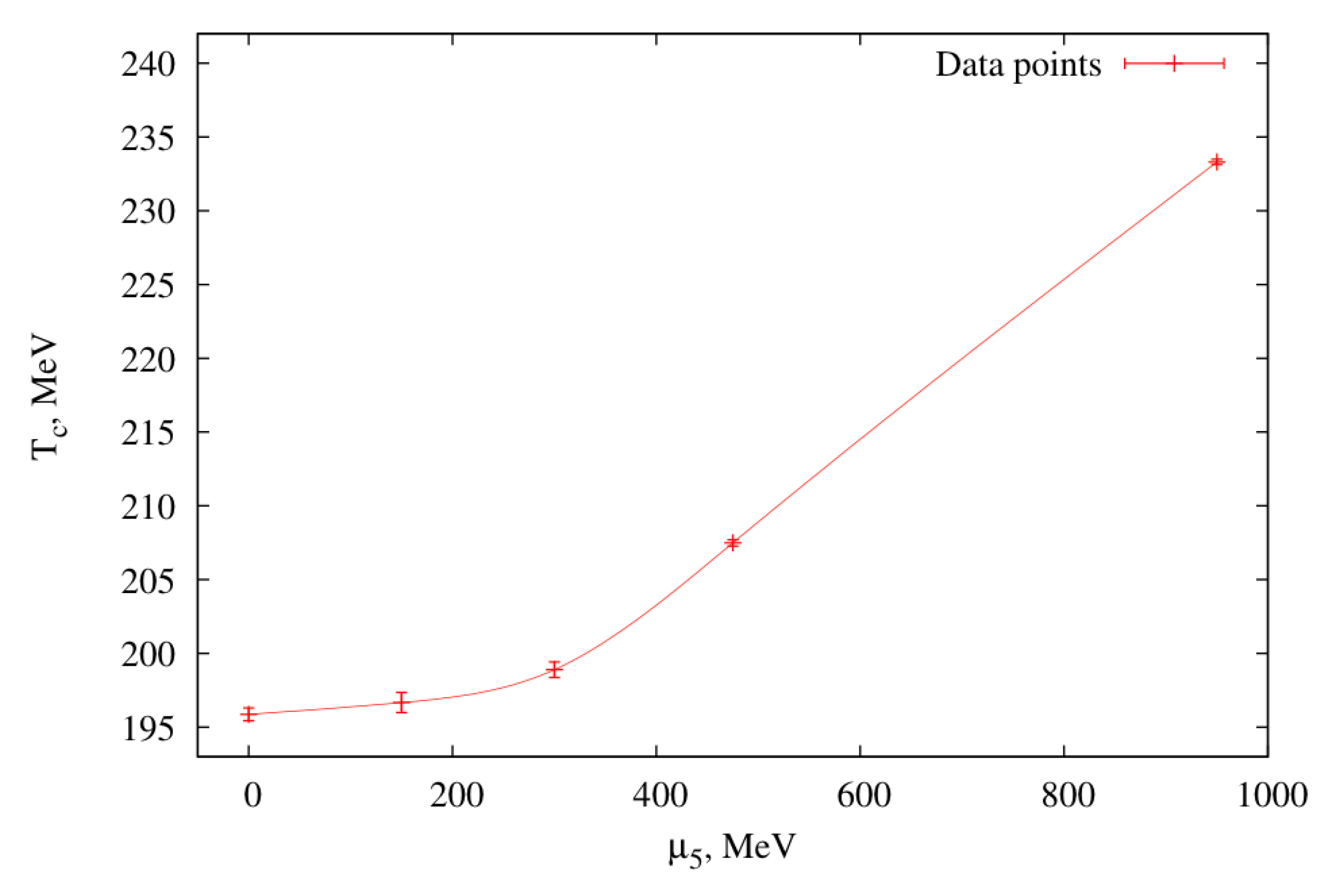
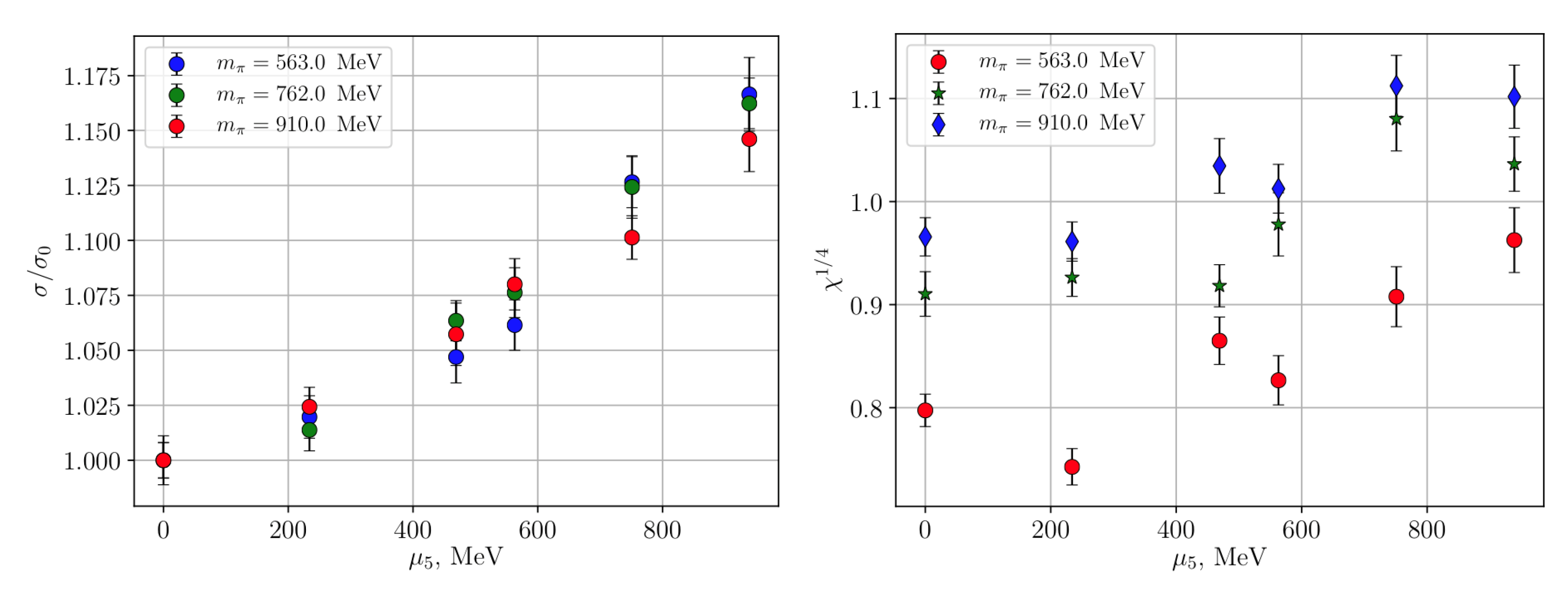
3.3. Chiral Density
4. Summarising
Funding
Conflicts of Interest
References
- Dexheimer, V.; Constantinou, C.; Most, E.R.; Jens Papenfort, L.; Hanauske, M.; Schramm, S.; Stoecker, H.; Rezzolla, L. Neutron-Star-Merger Equation of State. Universe 2019, 5, 129. [Google Scholar] [CrossRef] [Green Version]
- Ratti, C. Lattice QCD and heavy ion collisions: A review of recent progress. Rept. Prog. Phys. 2018, 81, 084301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guenther, J.N. Overview of the QCD phase diagram: Recent progress from the lattice. Eur. Phys. J. A 2021, 57, 136. [Google Scholar] [CrossRef] [PubMed]
- Rajagopal, K.; Wilczek, F. The Condensed matter physics of QCD. Front. Part. Phys. Handb. QCD 2000, 11, 2061–2151. [Google Scholar]
- Mannarelli, M. Meson condensation. Particles 2019, 2, 25. [Google Scholar] [CrossRef] [Green Version]
- Pisarski, R.D.; Rennecke, F. Multi-instanton contributions to anomalous quark interactions. Phys. Rev. D 2020, 101, 114019. [Google Scholar] [CrossRef]
- McLerran, L.; Redlich, K.; Sasaki, C. Quarkyonic Matter and Chiral Symmetry Breaking. Nucl. Phys. A 2009, 824, 86–100. [Google Scholar] [CrossRef] [Green Version]
- Buballa, M.; Carignano, S. Inhomogeneous chiral condensates. Prog. Part. Nucl. Phys. 2015, 81, 39–96. [Google Scholar] [CrossRef] [Green Version]
- Buballa, M.; Kurth, L.; Wagner, M.; Winstel, M. Regulator dependence of inhomogeneous phases in the (2+1)-dimensional Gross-Neveu model. Phys. Rev. D 2021, 103, 034503. [Google Scholar] [CrossRef]
- Jackiw, R.W. Axial anomaly. Scholarpedia 2008, 3, 7302. [Google Scholar] [CrossRef]
- Pospelov, M.; Ritz, A. Theta vacua, QCD sum rules, and the neutron electric dipole moment. Nucl. Phys. B 2000, 573, 177–200. [Google Scholar] [CrossRef] [Green Version]
- Pich, A.; de Rafael, E. Strong CP violation in an effective chiral Lagrangian approach. Nucl. Phys. B 1991, 367, 313–333. [Google Scholar] [CrossRef] [Green Version]
- Abel, C.; Afach, S.; Ayres, N.J.; Baker, C.A.; Ban, G.; Bison, G.; Bodek, K.; Bondar, V.; Burghoff, M.; Chanel, E.; et al. Measurement of the permanent electric dipole moment of the neutron. Phys. Rev. Lett. 2020, 124, 081803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef] [Green Version]
- Peccei, R.D.; Quinn, H.R. Constraints Imposed by CP Conservation in the Presence of Instantons. Phys. Rev. D 1977, 16, 1791–1797. [Google Scholar] [CrossRef]
- Pospelov, M.; Ritz, A. Electric dipole moments as probes of new physics. Ann. Phys. 2005, 318, 119–169. [Google Scholar] [CrossRef] [Green Version]
- Alexandrou, C.; Athenodorou, A.; Hadjiyiannakou, K.; Todaro, A. Neutron electric dipole moment using lattice QCD simulations at the physical point. Phys. Rev. D 2021, 103, 054501. [Google Scholar] [CrossRef]
- Lombardo, M.P.; Trunin, A. Topology and axions in QCD. Int. J. Mod. Phys. A 2020, 35, 2030010. [Google Scholar] [CrossRef]
- Borsanyi, S.; Dierigl, M.; Fodor, Z.; Katz, S.D.; Mages, S.W.; Nogradi, D.; Redondo, J.; Ringwald, A.; Szabo, K.K. Axion cosmology, lattice qcd and the dilute instanton gas. Phys. Lett. 2016, 752, 175–181. [Google Scholar] [CrossRef]
- Bonati, C.; D’Elia, M.; Martinelli, G.; Negro, F.; Sanfilippo, F.; Todaro, A. Topology in full QCD at high temperature: A multicanonical approach. J. High Energy Phys. 2018, 11, 170. [Google Scholar] [CrossRef] [Green Version]
- Petreczky, P.; Schadler, H.; Sharma, S. The topological susceptibility in finite temperature QCD and axion cosmology. Phys. Lett. B 2016, 762, 498–505. [Google Scholar] [CrossRef] [Green Version]
- Burger, F.; Ilgenfritz, E.-M.; Lombardo, M.P.; Trunin, A. Chiral observables and topology in hot QCD with two families of quarks. Phys. Rev. D 2018, 98, 094501. [Google Scholar] [CrossRef] [Green Version]
- Borsányi, S.; Fodor, Z.; Guenther, J.; Kampert, K.H.; Katz, S.D.; Kawanai, T.; Kovacs, T.G.; Mages, S.W.; Pasztor, A.; Pittler, F.; et al. Calculation of the axion mass based on high-temperature lattice quantum chromodynamics. Nature 2016, 539, 69–71. [Google Scholar] [CrossRef] [Green Version]
- Taniguchi, Y.; Kanaya, K.; Suzuki, H.; Umeda, T. Topological susceptibility in finite temperature ( 2+1 )-flavor QCD using gradient flow. Phys. Rev. D 2017, 95, 054502. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. The U(1) Problem. Phys. Rev. D 1975, 11, 3583–3593. [Google Scholar] [CrossRef]
- Vecchia, P.D.; Veneziano, G. Chiral Dynamics in the Large n Limit. Nucl. Phys. B 1980, 171, 253–272. [Google Scholar] [CrossRef] [Green Version]
- Vecchia, P.D.; Giannotti, M.; Lattanzi, M.; Lindner, A. Round Table on Axions and Axion-like Particles. PoS Confin. 2019, 2018, 034. [Google Scholar]
- Veneziano, G. U(1) Without Instantons. Nucl. Phys. B 1979, 159, 213–224. [Google Scholar] [CrossRef] [Green Version]
- Kapusta, J.I.; Kharzeev, D.; McLerran, L.D. The Return of the prodigal Goldstone boson. Phys. Rev. D 1996, 53, 5028–5033. [Google Scholar] [CrossRef] [Green Version]
- Kotov, A.Y.; Lombardo, M.P.; Trunin, A.M. Fate of the η′ in the quark gluon plasma. Phys. Lett. B 2019, 794, 83–88. [Google Scholar] [CrossRef]
- Alford, M.G.; Kapustin, A.; Wilczek, F. Imaginary chemical potential and finite fermion density on the lattice. Phys. Rev. D 1999, 59, 054502. [Google Scholar] [CrossRef] [Green Version]
- Gorghetto, M.; Villadoro, G. Topological Susceptibility and QCD Axion Mass: QED and NNLO corrections. J. High Energy Phys. 2019, 2019, 033. [Google Scholar] [CrossRef] [Green Version]
- Son, D.T.; Stephanov, M.A. QCD at finite isospin density. Phys. Rev. Lett. 2001, 86, 592–595. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Astrakhantsev, N.; Braguta, V.V.; Ilgenfritz, E.M.; Kotov, A.Y.; Nikolaev, A.A. Lattice study of thermodynamic properties of dense QC2D. Phys. Rev. D 2020, 102, 074507. [Google Scholar] [CrossRef]
- Brandt, B.B.; Cuteri, F.; Endrodi, G.; Schmalzbauer, S. The Dirac spectrum and the BEC-BCS crossover in QCD at nonzero isospin asymmetry. Particles 2020, 3, 7. [Google Scholar] [CrossRef] [Green Version]
- Brandt, B.B.; Endrodi, G.; Schmalzbauer, S. QCD phase diagram for nonzero isospin-asymmetry. Phys. Rev. D 2018, 97, 054514. [Google Scholar] [CrossRef] [Green Version]
- Brandt, B.B.; Cuteri, F.; Endrodi, G.; Schmalzbauer, S. Exploring the QCD phase diagram via reweighting from isospin chemical potential. PoS LATTICE 2019, 2019, 189. [Google Scholar]
- Braguta, V.V.; Kotov, A.Y.; Nikolaev, A.A. Lattice Simulation Study of the Properties of Cold Quark Matter with a Nonzero Isospin Density. JETP Lett. 2019, 110, 1–4. [Google Scholar] [CrossRef]
- Detmold, W.; Orginos, K.; Shi, Z. Lattice QCD at non-zero isospin chemical potential. Phys. Rev. D 2012, 86, 054507. [Google Scholar] [CrossRef] [Green Version]
- Cea, P.; Cosmai, L.; D’Elia, M.; Papa, A. Francesco Sanfilippo The critical line of two-flavor QCD at finite isospin or baryon densities from imaginary chemical potentials. Phys. Rev. D 2012, 85, 094512. [Google Scholar] [CrossRef] [Green Version]
- Toublan, D.; Kogut, J.B. Isospin chemical potential and the QCD phase diagram at nonzero temperature and baryon chemical potential. Phys. Lett. B 2003, 564, 212–216. [Google Scholar] [CrossRef] [Green Version]
- Schäfer, T.; Shuryak, E.V. Instantons in qcd. Rev. Mod. Phys. 1998, 70, 323–425. [Google Scholar] [CrossRef]
- Rapp, R.; Schäfer, T.; Shuryak, E.V.; Velkovsky, M. Diquark Bose condensates in high density matter and instantons. Phys. Rev. Lett. 1998, 81, 53–56. [Google Scholar] [CrossRef] [Green Version]
- Rapp, R.; Schäfer, T.; Shuryak, E.V.; Velkovsky, M. High density QCD and instantons. Ann. Phys. 2000, 280, 35–99. [Google Scholar] [CrossRef] [Green Version]
- Atiyah, M.F.; Singer, I.M. The Index of elliptic operators. 5. Ann. Math. 1971, 93, 139–149. [Google Scholar] [CrossRef]
- Atiyah, M.F.; Singer, I.M. Dirac Operators Coupled to Vector Potentials. Proc. Natl. Acad. Sci. USA 1984, 81, 2597–2600. [Google Scholar] [CrossRef] [Green Version]
- Bzdak, A.; Esumi, S.; Koch, V.; Liao, J.; Stephanov, M.; Xu, N. Mapping the Phases of Quantum Chromodynamics with Beam Energy Scan. Phys. Rept. 2020, 853, 1–87. [Google Scholar] [CrossRef] [Green Version]
- Kharzeev, D.E.; Levin, E.M. Color Confinement and Screening in the θ Vacuum of QCD. Phys. Rev. Lett. 2015, 114, 242001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kharzeev, D.E. The chiral magnetic effect and anomaly-induced transport. Prog. Part. Nucl. Phys. 2014, 75, 133–151. [Google Scholar] [CrossRef] [Green Version]
- Ruggieri, M.; Chernodub, M.N.; Lu, Z. Topological susceptibility, divergent chiral density, and phase diagram of chirally imbalanced QCD medium at finite temperature. Phys. Rev. 2020, 102, 014031. [Google Scholar] [CrossRef]
- Astrakhantsev, N.Y.; Braguta, V.V.; Kotov, A.Y.; Kuznedelev, D.D.; Nikolaev, A.A. Lattice study of QCD at finite chiral density: Topology and confinement. Eur. Phys. J. A 2021, 57, 15. [Google Scholar] [CrossRef]
- Yamamoto, A. Chiral magnetic effect in lattice qcd with a chiral chemical potential. Phys. Rev. Lett. 2011, 107, 031601. [Google Scholar] [CrossRef] [Green Version]
- Braguta, V.V.; Kotov, A.Y. Catalysis of dynamical chiral symmetry breaking by chiral chemical potential. Phys. Rev. 2016, 93, 105025. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Luo, X.; Segovia, J.; Zong, H. A Brief Review of Chiral Chemical Potential and Its Physical Effects. Symmetry 2020, 12, 2095. [Google Scholar] [CrossRef]
- Müller-Preussker, M. Recent results on topology on the lattice (in memory of Pierre van Baal). PoS LATTICE 2015, 2014, 003. [Google Scholar]
- Hands, S.; Kogut, J.B.; Lombardo, M.; Morrison, S.E. Symmetries and spectrum of SU(2) lattice gauge theory at finite chemical potential. Nucl. Phys. B 1999, 558, 327–346. [Google Scholar] [CrossRef] [Green Version]
- Alles, B.; D’Elia, M.; Giacomo, A.D. Topological susceptibility at zero and finite T in SU(3) Yang-Mills theory. Nucl. Phys. B 1997, 494, 281–292, Erratum in 2004, 679, 397–399. [Google Scholar] [CrossRef] [Green Version]
- Alles, B.; D’Elia, M.; Lombardo, M.P. Behaviour of the topological susceptibility in two colour QCD across the finite density transition. Nucl. Phys. B 2006, 752, 124–139. [Google Scholar] [CrossRef] [Green Version]
- Lombardo, M.; Paciello, M.L.; Petrarca, S.; Taglienti, B. Glueballs and the superfluid phase of Two-Color QCD. Eur. Phys. J. C 2008, 58, 69–81. [Google Scholar] [CrossRef]
- Hands, S.; Kim, S.; Skullerud, J. A Quarkyonic Phase in Dense Two Color Matter? Phys. Rev. D 2010, 81, 091502. [Google Scholar] [CrossRef] [Green Version]
- Hands, S.; Kenny, P. Topological Fluctuations in Dense Matter with Two Colors. Phys. Lett. B 2011, 701, 373–377. [Google Scholar] [CrossRef] [Green Version]
- Hands, S.; Kenny, P.; Kim, S.; Skullerud, J. Lattice Study of Dense Matter with Two Colors and Four Flavors. Eur. Phys. J. A 2011, 47, 60. [Google Scholar] [CrossRef] [Green Version]
- Astrakhantsev, N.Y.; Bornyakov, V.G.; Braguta, V.V.; Ilgenfritz, E.M.; Kotov, A.Y.; Nikolaev, A.A.; Rothkopf, A. Lattice study of static quark-antiquark interactions in dense quark matter. J. High Energy Phys. 2019, 2019, 171. [Google Scholar] [CrossRef] [Green Version]
- Iida, K.; Itou, E.; Lee, T. Two-colour QCD phases and the topology at low temperature and high density. J. High Energy Phys. 2020, 2020, 181. [Google Scholar] [CrossRef] [Green Version]
- Boz, T.; Giudice, P.; Hands, S.; Skullerud, J. Dense two-color QCD towards continuum and chiral limits. Phys. Rev. D 2020, 101, 074506. [Google Scholar] [CrossRef] [Green Version]
- Appelquist, T.; Ratnaweera, A.; Terning, J.; Wijewardhana, L.C.R. The Phase structure of an SU(N) gauge theory with N(f) flavors. Phys. Rev. D 1998, 58, 105017. [Google Scholar] [CrossRef] [Green Version]
- Appelquist, T.; Sannino, F. The Physical spectrum of conformal SU(N) gauge theories. Phys. Rev. D 1999, 59, 067702. [Google Scholar] [CrossRef] [Green Version]
- Orlando, D.; Reffert, S.; Sannino, F. Charging the Conformal Window. Phys. Rev. D 2021, 103, 105026. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G. QCD phase diagram with isospin chemical potential. PoS LATTICE 2016, 2016, 039. [Google Scholar]
- Bornyakov, V.G.; Nikolaev, A.A.; Rogalyov, R.N.; Terentev, A.S. Gluon Propagators in 2+1 Lattice QCD with Nonzero Isospin Chemical Potential. arXiv 2021, arXiv:2102.07821. [Google Scholar]
- Bali, G.S.; Endrodi, G.; Gavai, R.V.; Mathur, N. Probing the nature of phases across the phase transition at finite isospin chemical potential. arXiv 2016, arXiv:1610.00233. [Google Scholar] [CrossRef] [Green Version]
- Endrődi, G. Magnetic structure of isospin-asymmetric qcd matter in neutron stars. Phys. Rev. 2014, 90, 094501. [Google Scholar] [CrossRef] [Green Version]
- Braguta, V.V.; Goy, V.A.; Ilgenfritz, E.M.; Kotov, A.Y.; Molochkov, A.V.; Muller-Preussker, M.; Petersson, B. Two-Color QCD with Non-zero Chiral Chemical Potential. J. High Energy Phys. 2015, 2015, 094. [Google Scholar] [CrossRef] [Green Version]
- Espriu, D.; Nicola, A.G.; Vioque-Rodríguez, A. Chiral perturbation theory for nonzero chiral imbalance. J. High Energy Phys. 2020, 2020, 062. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lombardo, M.P. Topological Aspects of Dense Matter: Lattice Studies. Universe 2021, 7, 336. https://doi.org/10.3390/universe7090336
Lombardo MP. Topological Aspects of Dense Matter: Lattice Studies. Universe. 2021; 7(9):336. https://doi.org/10.3390/universe7090336
Chicago/Turabian StyleLombardo, Maria Paola. 2021. "Topological Aspects of Dense Matter: Lattice Studies" Universe 7, no. 9: 336. https://doi.org/10.3390/universe7090336





