Analogue Hawking Radiation in Nonlinear LC Transmission Lines
Abstract
:1. Introduction
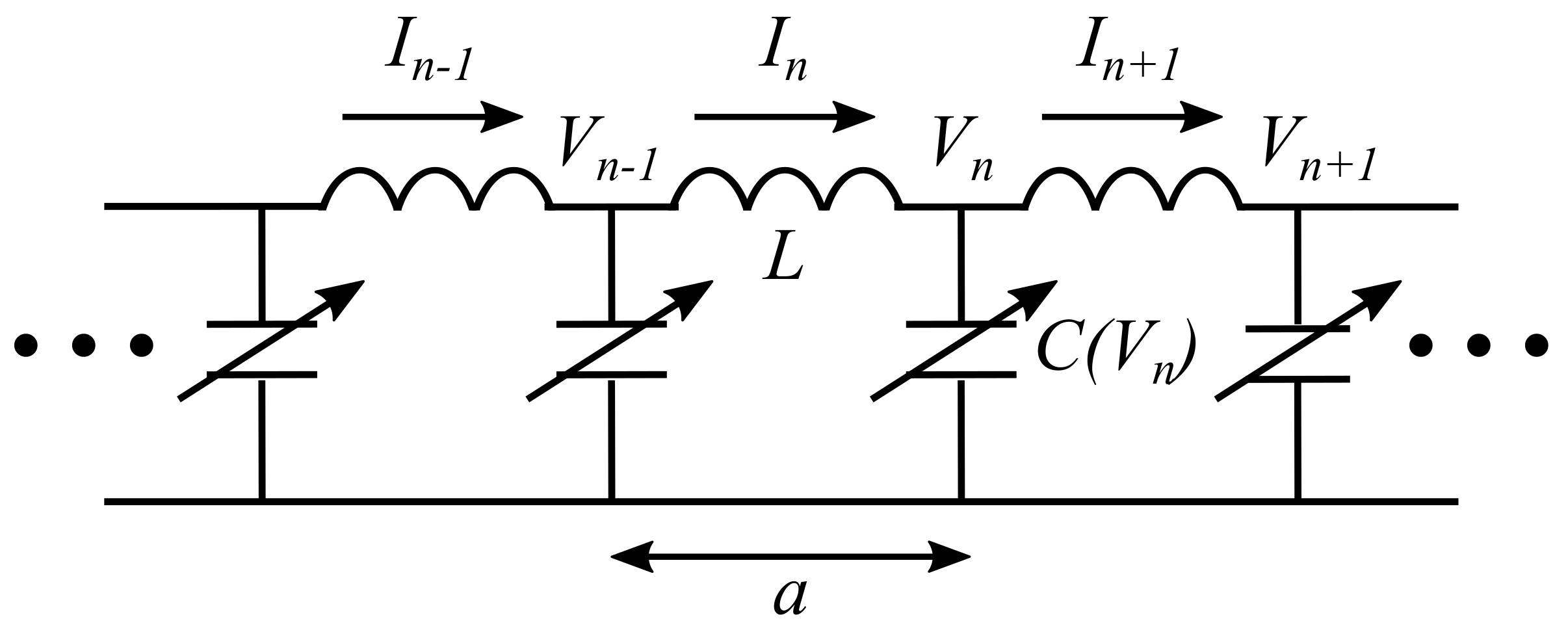
2. Model and Methods
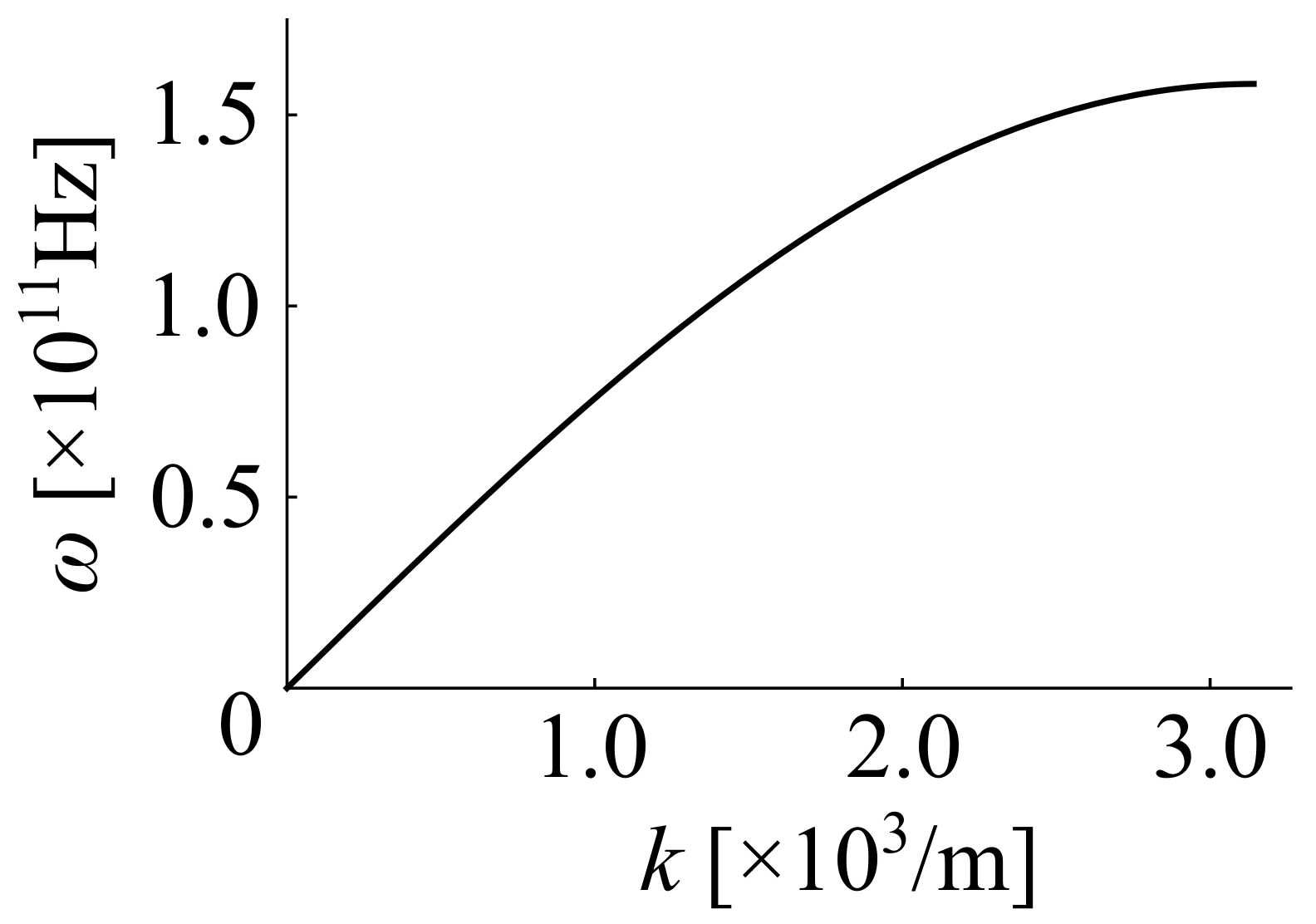
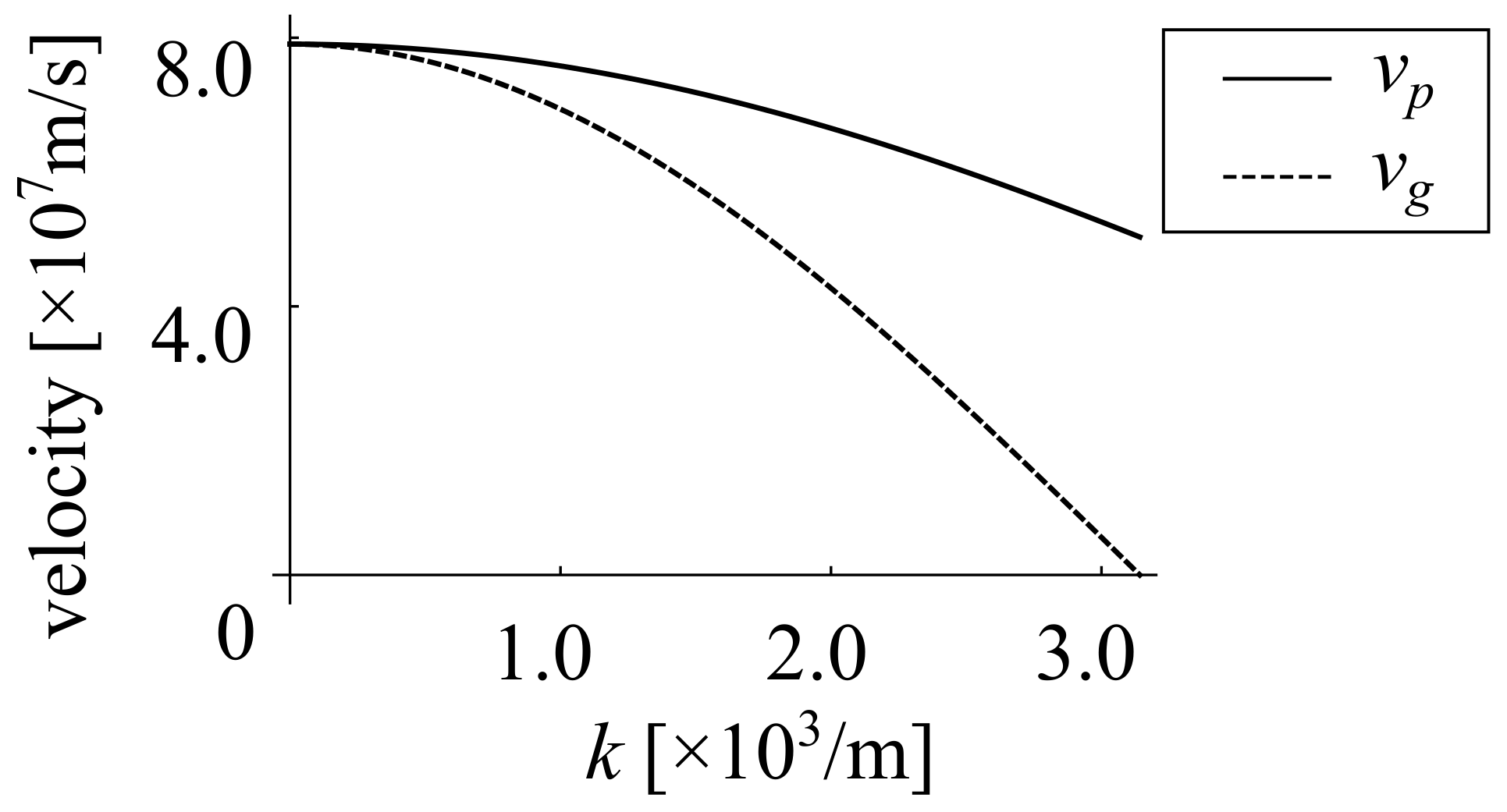
3. Results
3.1. Nonlinear Schrödinger Soliton
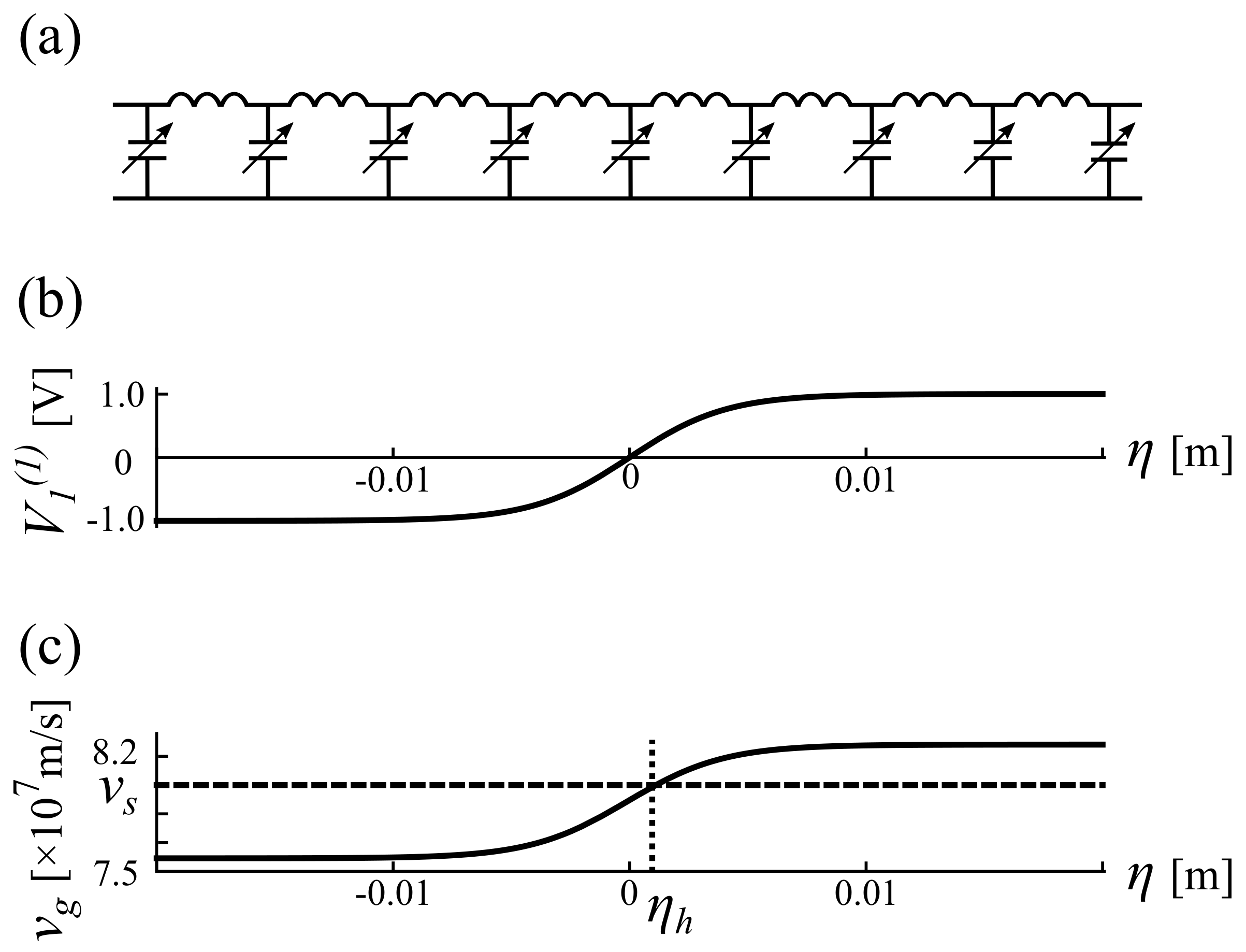
3.2. Analogue Black Hole
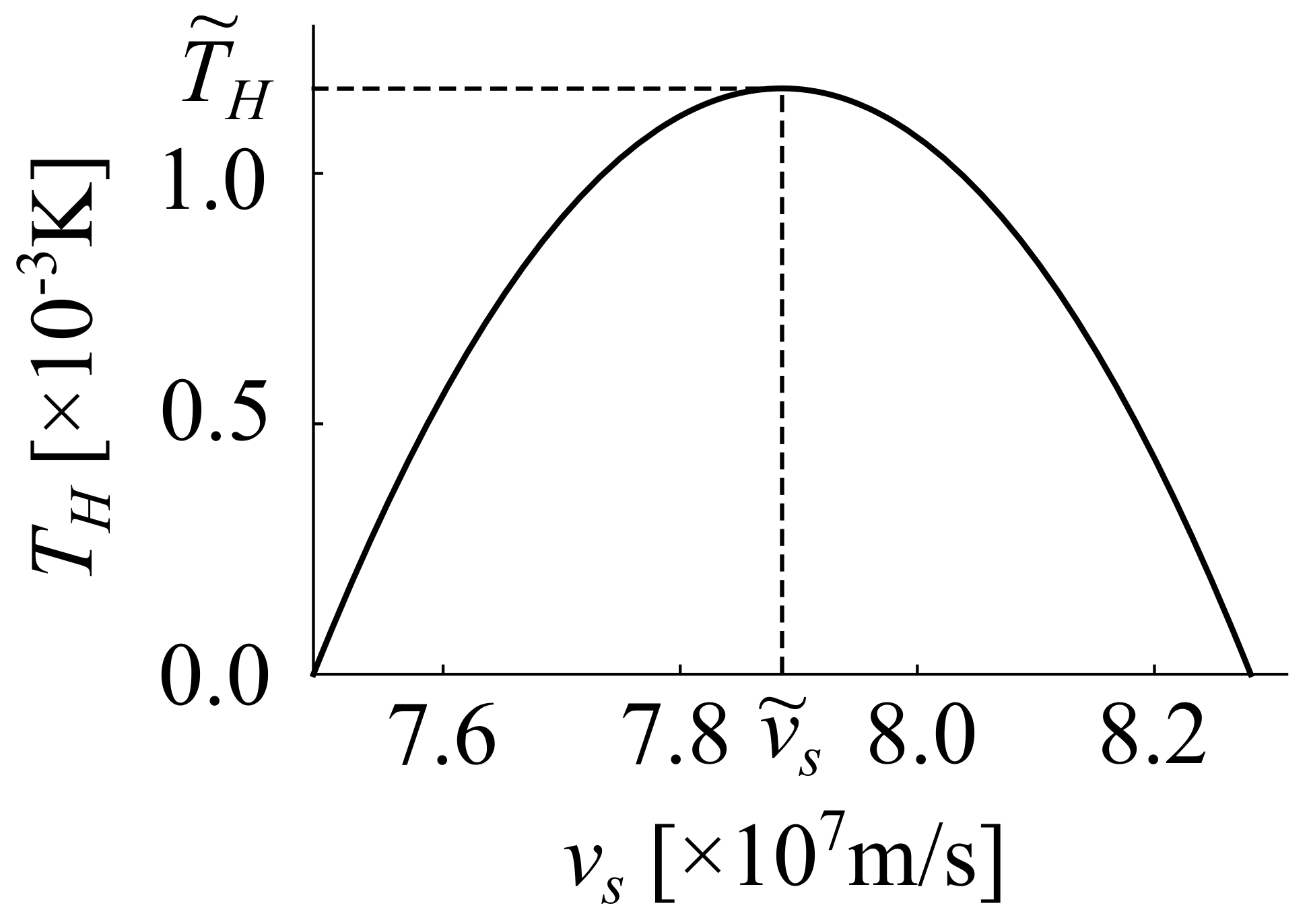
3.3. Hawking Temperature
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Discrete Reductive Perturbation Method
References
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Unruh, W.G. Experimental Black-Hole Evaporation? Phys. Rev. Lett. 1981, 46, 1351–1353. [Google Scholar] [CrossRef]
- Jacobson, T.A.; Volovik, G.E. Event horizons and ergoregions in 3He. Phys. Rev. D 1998, 58, 064021. [Google Scholar] [CrossRef] [Green Version]
- Garay, L.J.; Anglin, J.R.; Cirac, J.I.; Zoller, P. Sonic Analog of Gravitational Black Holes in Bose-Einstein Condensates. Phys. Rev. Lett. 2000, 85, 4643–4647. [Google Scholar] [CrossRef] [Green Version]
- Philbin, T.G.; Kuklewicz, C.; Robertson, S.; Hill, S.; König, F.; Leonhardt, U. Fiber-Optical Analog of the Event Horizon. Science 2008, 319, 1367–1370. [Google Scholar] [CrossRef] [Green Version]
- Schützhold, R.; Unruh, W.G. Hawking Radiation in an Electromagnetic Waveguide? Phys. Rev. Lett. 2005, 95, 031301. [Google Scholar] [CrossRef] [Green Version]
- Nation, P.D.; Blencowe, M.P.; Rimberg, A.J.; Buks, E. Analogue Hawking Radiation in a dc-SQUID Array Transmission Line. Phys. Rev. Lett. 2009, 103, 087004. [Google Scholar] [CrossRef] [Green Version]
- Katayama, H.; Hatakenaka, N.; Fujii, T. Analogue Hawking radiation from black hole solitons in quantum Josephson transmission lines. Phys. Rev. D 2020, 102, 086018. [Google Scholar] [CrossRef]
- Katayama, H.; Ishizaka, S.; Hatakenaka, N.; Fujii, T. Solitonic black holes induced by magnetic solitons in a dc-SQUID array transmission line coupled with a magnetic chain. Phys. Rev. D 2021, 103, 066025. [Google Scholar] [CrossRef]
- Katayama, H. Designed Analogue Black Hole Solitons in Josephson Transmission Lines. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Nation, P.D.; Johansson, J.R.; Blencowe, M.P.; Nori, F. Colloquium: Stimulating uncertainty: Amplifying the quantum vacuum with superconducting circuits. Rev. Mod. Phys. 2012, 84, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Russell, J.S. Report on waves. In Proceedings of the the Fourteenth Meeting of the British Association for the Advancement of Science, York, UK, September 1844; pp. 311–390. [Google Scholar]
- Zabusky, N.J.; Kruskal, M.D. Interaction of “Solitons” in a Collisionless Plasma and the Recurrence of Initial States. Phys. Rev. Lett. 1965, 15, 240–243. [Google Scholar] [CrossRef] [Green Version]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for Solving the Korteweg-deVries Equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Hasegawa, A.; Tappert, F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl. Phys. Lett. 1973, 23, 142–144. [Google Scholar] [CrossRef]
- Toda, M. Vibration of a Chain with Nonlinear Interaction. J. Phys. Soc. Jpn. 1967, 22, 431–436. [Google Scholar] [CrossRef]
- Taniuti, T.; Yajima, N. Perturbation Method for a Nonlinear Wave Modulation. I. J. Math. Phys. 1969, 10, 1369–1372. [Google Scholar] [CrossRef]
- Kengne, E. and Bame, C. Dynamics of Modulated Wave Trains in a Discrete Nonlinear-dispersive Dissipative Bi-inductance Transmission Line. Czechoslov. J. Phys. 2005, 55, 609–630. [Google Scholar] [CrossRef]
- Kengne, E.; Lakhssassi, A. Analytical study of dynamics of matter-wave solitons in lossless nonlinear discrete bi-inductance transmission lines. Phys. Rev. E 2015, 91, 032907. [Google Scholar] [CrossRef]
- Kengne, E.; Lakhssassi, A. Analytical studies of soliton pulses along two-dimensional coupled nonlinear transmission lines. Chaos Solitons Fractals 2015, 73, 191–201. [Google Scholar] [CrossRef]
- Kengne, E.; Liu, W.M. Transmission of rogue wave signals through a modified Noguchi electrical transmission network. Phys. Rev. E 2019, 99, 062222. [Google Scholar] [CrossRef]
- Abdoulkary, S.; English, L.; Mohamadou, A. Envelope solitons in a left-handed nonlinear transmission line with Josephson junction. Chaos Solitons Fractals 2016, 85, 44–50. [Google Scholar] [CrossRef]
- Ghafouri-Shiraz, H.; Shum, P. Narrow pulse formation using nonlinear LC ladder networks. Fiber Integr. Opt. 1996, 15, 305–323. [Google Scholar] [CrossRef]
- Taniuti, T. Reductive Perturbation Method and Far Fields of Wave Equations. Prog. Theor. Phys. Suppl. 1974, 55, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Corley, S.; Jacobson, T. Hawking spectrum and high frequency dispersion. Phys. Rev. D 1996, 54, 1568–1586. [Google Scholar] [CrossRef] [Green Version]
- Corley, S. Computing the spectrum of black hole radiation in the presence of high frequency dispersion: An analytical approach. Phys. Rev. D 1998, 57, 6280–6291. [Google Scholar] [CrossRef] [Green Version]
- Corley, S.; Jacobson, T. Black hole lasers. Phys. Rev. D 1999, 59, 124011. [Google Scholar] [CrossRef] [Green Version]
- Steinhauer, J. Observation of self-amplifying Hawking radiation in an analogue black-hole laser. Nat. Phys. 2014, 10, 864–869. [Google Scholar] [CrossRef]
- Gaona-Reyes, J.L.; Bermudez, D. The theory of optical black hole lasers. Ann. Phys. 2017, 380, 41–58. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katayama, H.; Hatakenaka, N.; Matsuda, K.-i. Analogue Hawking Radiation in Nonlinear LC Transmission Lines. Universe 2021, 7, 334. https://doi.org/10.3390/universe7090334
Katayama H, Hatakenaka N, Matsuda K-i. Analogue Hawking Radiation in Nonlinear LC Transmission Lines. Universe. 2021; 7(9):334. https://doi.org/10.3390/universe7090334
Chicago/Turabian StyleKatayama, Haruna, Noriyuki Hatakenaka, and Ken-ichi Matsuda. 2021. "Analogue Hawking Radiation in Nonlinear LC Transmission Lines" Universe 7, no. 9: 334. https://doi.org/10.3390/universe7090334





