Constraints on Dark Energy Models from Galaxy Clusters and Gravitational Lensing Data
Abstract
:1. Introduction
2. Galaxy Clusters
2.1. Angular Diameter Distance Using the SZ/X-Ray Method
2.2. The Gas Mass Fraction
2.3. Gravitational Lensing
2.4. Statistic Analysis
3. Dark Energy Models and Results
3.1.
3.2. Model
3.3. Chevalier–Polarski–Linder Model
3.4. Interacting Dark Energy Model
3.5. Early Dark Energy Model
3.6. Statistical Discrimination Models
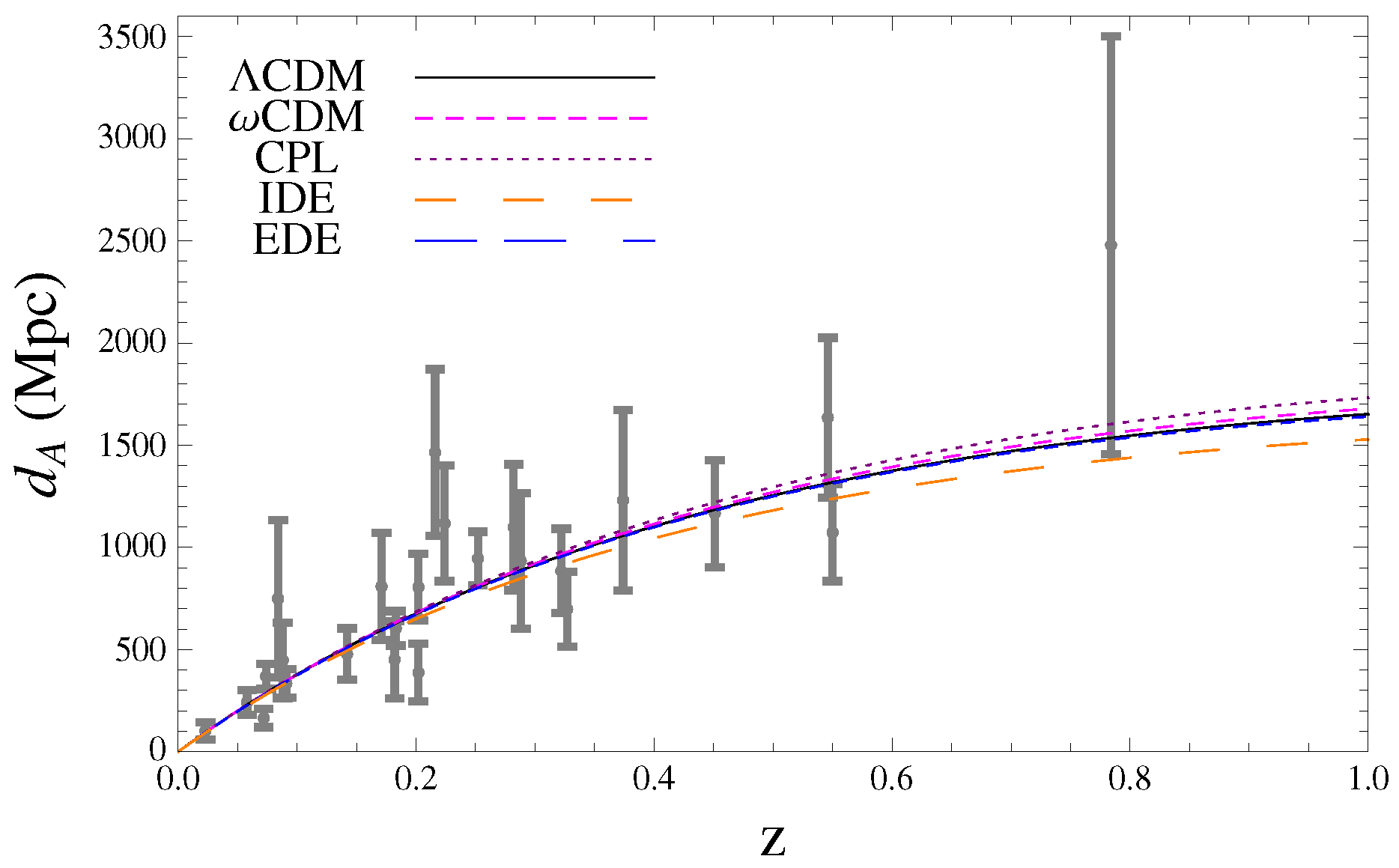
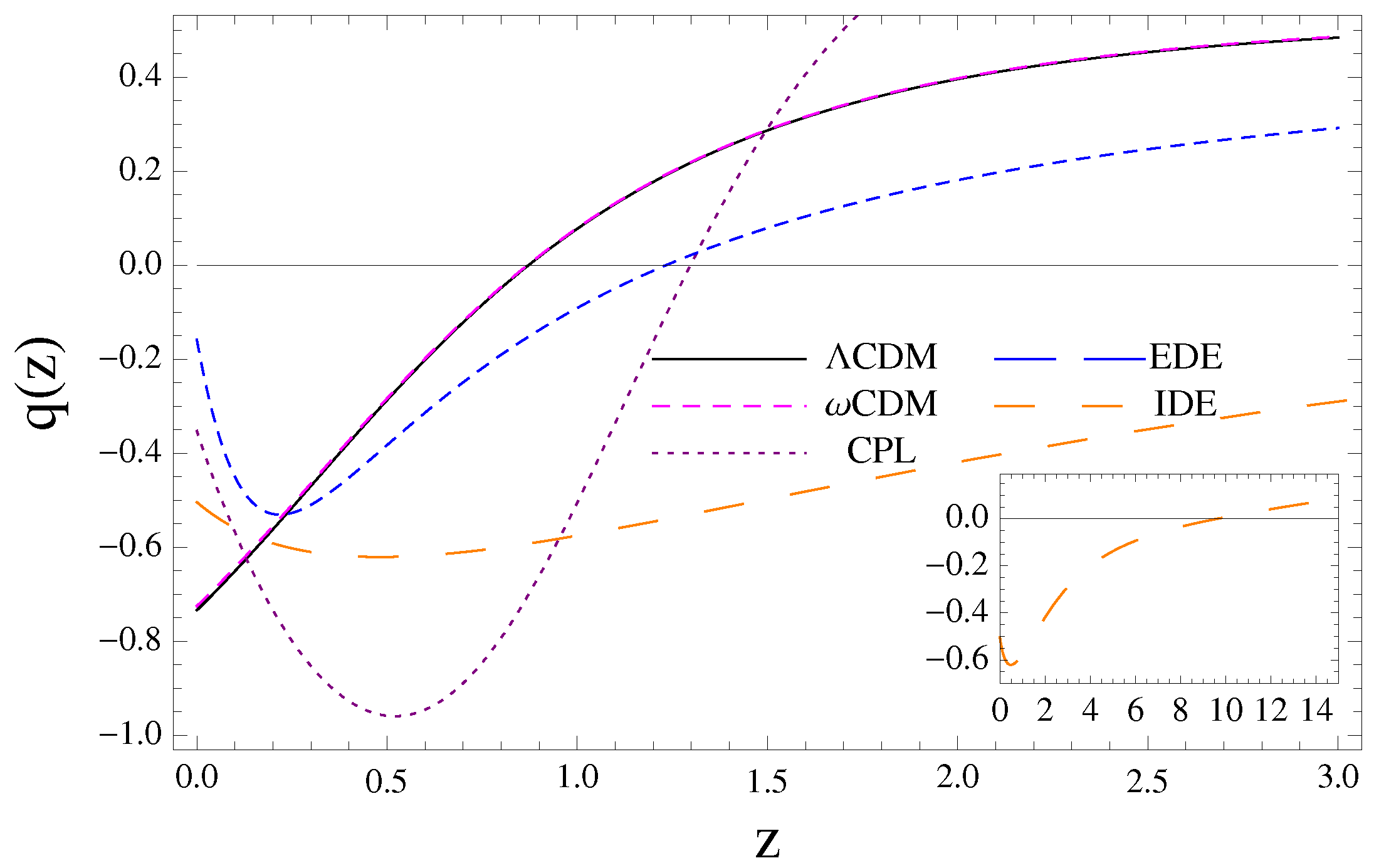
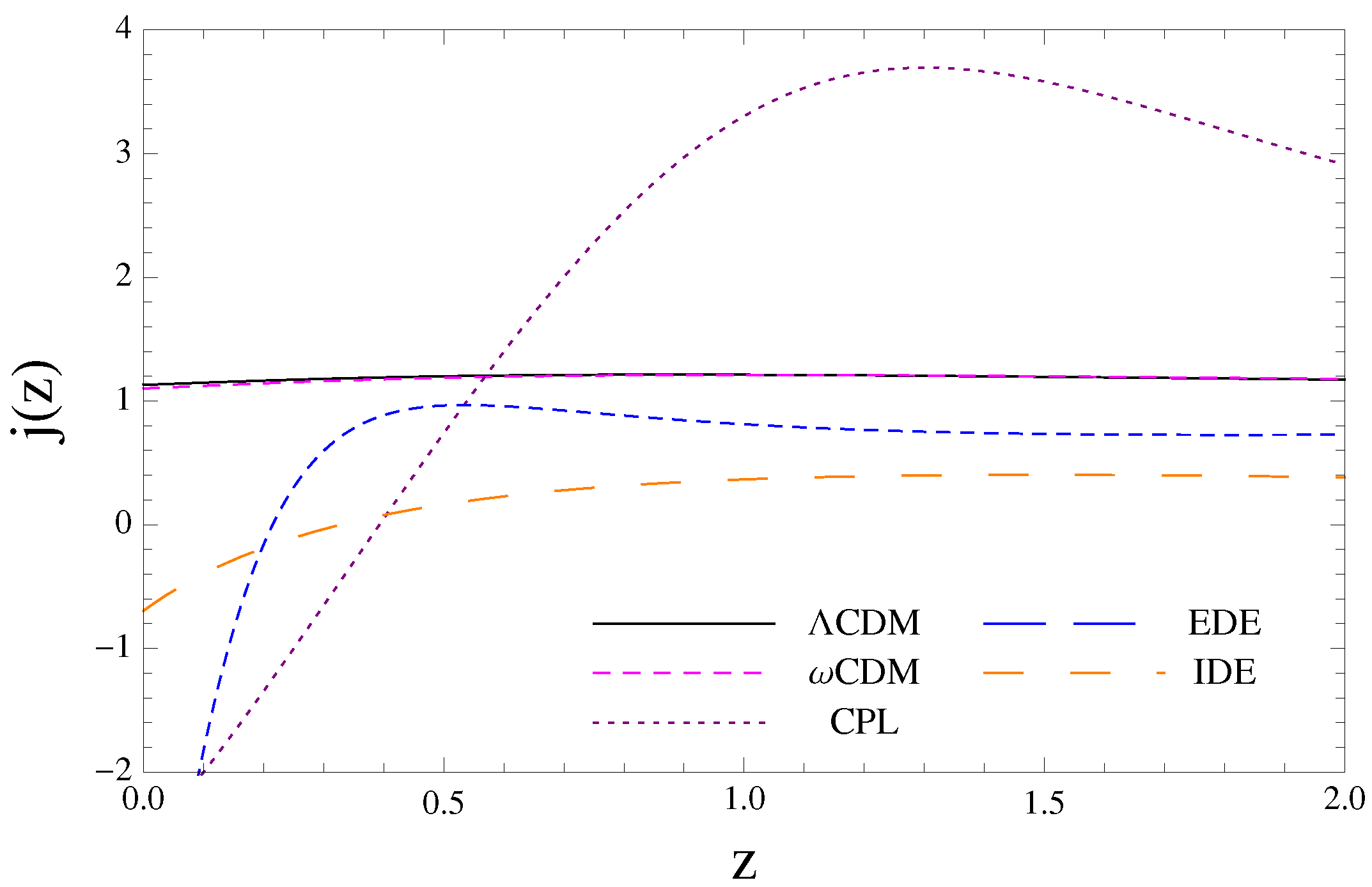
4. History of the Expansion and Cosmography
5. Summary and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. β-Model and Triaxial Ellipsoids
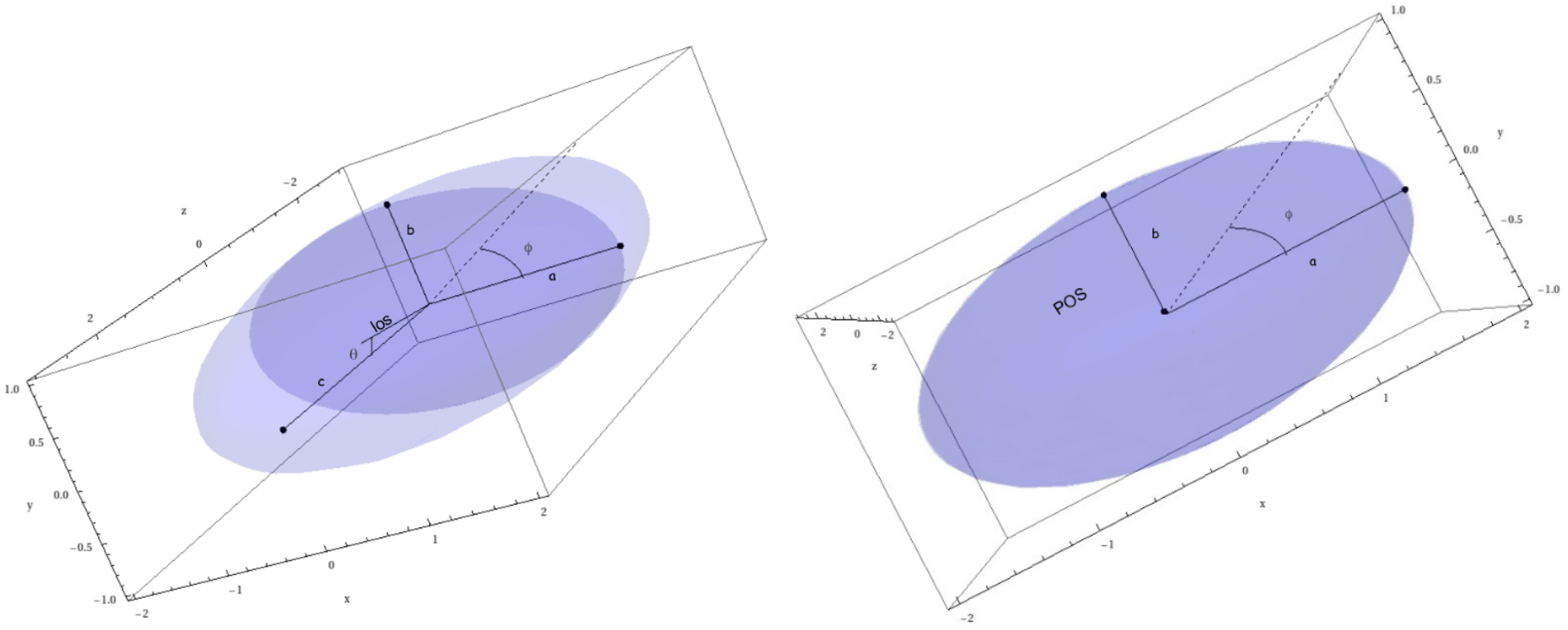
Appendix A.2. Galaxy Clusters Data
| Cluster | (keV) | (K) | (Mpc) | ||
|---|---|---|---|---|---|
| MS 1137.5 + 6625 | 0.784 | 2.00 | |||
| MS 0451.6 − 0305 | 0.550 | 1.87 | |||
| Cl 0016 + 1609 | 0.546 | 1.89 | |||
| RXJ1347.5 − 1145 | 0.451 | 1.91 | |||
| A 370 | 0.374 | 1.96 | |||
| MS 1358.4 + 6245 | 0.327 | 1.88 | |||
| A 1995 | 0.322 | 1.91 | |||
| A 611 | 0.288 | 1.76 | |||
| A 697 | 0.282 | 1.89 | |||
| A 1835 | 0.252 | 1.93 | |||
| A 2261 | 0.224 | 1.87 | |||
| A 773 | 0.216 | 1.76 | |||
| A 2163 | 0.202 | 1.90 | |||
| A 520 | 0.202 | 1.93 | |||
| A 1689 | 0.183 | 1.86 | |||
| A 665 | 0.182 | 1.87 | |||
| A 2218 | 0.171 | 1.95 | |||
| A 1413 | 0.142 | 1.88 | |||
| A 2142 | 0.091 | 1.87 | |||
| A 478 | 0.088 | 1.91 | |||
| A 1651 | 0.084 | 1.75 | |||
| A 401 | 0.074 | 1.78 | |||
| A 399 | 0.072 | 1.81 | |||
| A 2256 | 0.058 | 1.96 | |||
| A 1656 | 0.023 | 1.96 |
Appendix B
Appendix B.1. SNIa
Appendix B.2. CMB
Appendix B.3. BAO
References
- De Filippis, E.; Sereno, M.; Bautz, M.W.; Longo, G. Measuring the Three-dimensional Structure of Galaxy Clusters. I. Application to a Sample of 25 Clusters. Astrophys. J. 2005, 625, 108–120. [Google Scholar] [CrossRef] [Green Version]
- Bonamente, M.; Joy, M.K.; LaRoque, S.J.; Carlstrom, J.E.; Reese, E.D.; Dawson, K.S. Determination of the Cosmic Distance Scale from Sunyaev-Zel’dovich Effect and Chandra X-ray Measurements of High-redshift Galaxy Clusters. Astrophys. J. 2006, 647, 25–54. [Google Scholar] [CrossRef]
- Biesiada, M.; Piórkowska, A.; Malec, B. Cosmic equation of state from strong gravitational lensing systems. Mon. Not. R. Astron. Soc. 2010, 406, 1055–1059. [Google Scholar] [CrossRef]
- Campigotto, M.C.; Diaferio, A.; Hernandez, X.; Fatibene, L. Strong gravitational lensing in f (χ) = χ3/2 gravity. J. Cosmol. Astropart. Phys. 2017, 2017, 057. [Google Scholar] [CrossRef]
- Albrecht, A.; Bernstein, G.; Cahn, R.; Freedman, W.L.; Hewitt, J.; Hu, W.; Huth, J.; Kolb, E.W.; Knox, L.; Mather, J.C.; et al. Report of the Dark Energy Task Force. arXiv, 2006; arXiv:astro-ph/0609591. [Google Scholar]
- Frieman, J.A.; Turner, M.S.; Huterer, D. Dark Energy and the Accelerating Universe. Annu. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–22. [Google Scholar] [CrossRef]
- Bartelmann, M.; Steinmetz, M.; Weiss, A. Arc statistics with realistic cluster potentials. 2: Influence of cluster asymmetry and substructure. Astron. Astrophys. 1995, 297, 1–12. [Google Scholar]
- Sunyaev, R.A.; Zel’dovich, Y.B. The Spectrum of Primordial Radiation, its Distortions and their Significance. Comment Astrophys. Space Phys. 1970, 2, 66–74. [Google Scholar]
- Sunyaev, R.A.; Zel’dovich, Y.B. Microwave background radiation as a probe of the contemporary structure and history of the universe. Annu. Rev. Astron. Astrophys. 1980, 18, 537–560. [Google Scholar] [CrossRef]
- Itoh, N.; Kohyama, Y.; Nozawa, S. Relativistic Corrections to the Sunyaev–Zeldovich Effect for Clusters of Galaxies. Astrophys. J. 1998, 502, 7–15. [Google Scholar] [CrossRef]
- Nozawa, S.; Itoh, N.; Suda, Y.; Ohhata, Y. An improved formula for the relativistic corrections to the kinematical Sunyaev-Zeldovich effect for clusters of galaxies. Nuovo Cimento B 2006, 121, 487–500. [Google Scholar]
- Vikhlinin, A.; Kravtsov, A.V.; Burenin, R.A.; Ebeling, H.; Forman, W.R.; Hornstrup, A.; Jones, C.; Murray, S.S.; Nagai, D.; Quintana, H.; et al. Chandra Cluster Cosmology Project III: Cosmological Parameter Constraints. Astrophys. J. 2009, 692, 1060–1074. [Google Scholar] [CrossRef]
- Sasaki, S. A New method to estimate cosmological parameters using baryon fraction of clusters of galaxies. Publ. Astron. Soc. Jpn. 1996, 48, L119–L122. [Google Scholar] [CrossRef]
- Allen, S.W.; Schmidt, R.W.; Ebeling, H.; Fabian, A.C.; van Speybroeck, L. Constraints on dark energy from Chandra observations of the largest relaxed galaxy clusters. Mon. Not. R. Astron. Soc. 2004, 353, 457–467. [Google Scholar] [CrossRef]
- Nesseris, S.; Perivolaropoulos, L. Crossing the Phantom Divide: Theoretical Implications and Observational Status. J. Cosmol. Astropart. Phys. 2007, 2007, 189–198. [Google Scholar] [CrossRef]
- Allen, S.W.; Rapetti, D.A.; Schmidt, R.W.; Ebeling, H.; Morris, G.; Fabian, A.C. Improved constraints on dark energy from Chandra X-ray observations of the largest relaxed galaxy clusters. Mon. Not. R. Astron. Soc. 2008, 383, 879–896. [Google Scholar] [CrossRef]
- Limousin, M.; Morandi, A.; Sereno, M.; Meneghetti, M.; Ettori, S.; Bartelmann, M.; Verdugo, T. The Three- Dimensional Shapes of Galaxy Clusters. Space Sci. Rev. 2013, 177, 155–194. [Google Scholar] [CrossRef]
- Cao, S.; Pan, Y.; Biesiada, M.; Godlowski, W.; Zhu, Z.-H. Constraints on cosmological models from strong gravitational lensing systems. J. Cosmol. Astropart. Phys. 2012, 2012, 140–143. [Google Scholar] [CrossRef]
- White, R.E., III; Davis, D.S. X-ray Properties of a Complete Sample of Elliptical Galaxies. Bull. Am. Astron. Soc. 1996, 28, 1323. [Google Scholar]
- Narayan, R.; Bartelmann, M. Lectures on Gravitational Lensing. arXiv, 1996; arXiv:astro-ph/9606001. [Google Scholar]
- Sereno, M.; Longo, G. Determining cosmological parameters from X-ray measurements of strong lensing clusters. Mon. Non. R. Astron. Soc. 2004, 354, 1255–1262. [Google Scholar] [CrossRef] [Green Version]
- Cavaliere, A.; Fusco-Femiano, R. X-rays from hot plasma in clusters of galaxies. Astron. Astrophys. 1976, 49, 137–144. [Google Scholar]
- Rosati, P.; Borgani, S.; Norman, C. The Evolution of X-ray Clusters of Galaxies. Annu. Rev. Astron. Astrophys. 2002, 40, 539–577. [Google Scholar] [CrossRef]
- Schneider, P.; Ehlers, J.; Falco, E.E. Gravitational Lenses; XIV 560; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1992; p. 112. [Google Scholar]
- Ono, T.; Masai, K.; Sasaki, S. Cluster Mass Estimate Using Strong Gravitational Lenses Revisited. Publ. Astron. Soc. Jpn. 1999, 51, 91–94. [Google Scholar] [CrossRef]
- Yu, H.; Zhu, Z.-H. Combining optical and X-ray observations of galaxy clusters to constrain cosmological parameters. Res. Astron. Astrophys. 2011, 11, 776–786. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope Cluster Supernova Survey: V. Improving the Dark Energy Constraints Above z>1 and Building an Early-Type-Hosted Supernova Sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S. Distance priors from Planck and dark energy constraints from current data. Phys. Rev. D 2013, 88, 043522. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, E.; Bailey, S.; Bizyaev, D.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Burden, A.; Cuesta, A.J.; Brownstein, J.R.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon Acoustic Oscillations in the Data Release 9 Spectroscopic Galaxy Sample. Mon. Non. R. Astron. Soc. 2012, 427, 3435–3467. [Google Scholar] [CrossRef] [Green Version]
- Blake, C.; Kazin, E.A.; Beutler, F.; Davis, T.M.; Parkinson, D.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; et al. The WiggleZ Dark Energy Survey: mapping the distance-redshift relation with baryon acoustic oscillations. Mon. Non. R. Astron. Soc. 2011, 418, 1707–1724. [Google Scholar] [CrossRef]
- Shi, K.; Huang, Y.; Lu, T. A comprehensive comparison of cosmological models from latest observational data. Mon. Non. R. Astron. Soc. 2012, 426, 2452–2462. [Google Scholar] [CrossRef]
- Andrae, R.; Schulze-Hartung, T.; Melchior, P. Dos and don’ts of reduced chi-squared. arXiv, 2010; arXiv:1012.3754. [Google Scholar]
- Albrecht, A.; Amendola, L.; Bernstein, G.; Clowe, D.; Eisenstein, D.; Guzzo, L.; Hirata, C.; Huterer, D.; Kirshner, R.; Kolb, E.; et al. Findings of the Joint Dark Energy Mission Figure of Merit Science Working Group. arXiv, 2009; arXiv:0901.0721. [Google Scholar]
- Wolz, L.; Kilbinger, M.; Weller, J.; Giannantonio, T. On the validity of cosmological Fisher matrix forecasts. J. Cosmol. Astropart. Phys. 2012, 2012, 009. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 471–474. [Google Scholar] [CrossRef]
- Liddle, A.R. How many cosmological parameters? Mon. Non. R. Astron. Soc. 2004, 351, L49–L53. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference. Technometrics 2003, 45, 181. [Google Scholar]
- Hogg, D.W. Distance measures in cosmology. arXiv, 1999; arXiv:astro-ph/9905116. [Google Scholar]
- Planck Collaboration; Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar]
- Chevallier, M.; Polarski, D. Accelerating Universes with Scaling Dark Matter. Int. J. Mod. Phys. D 2001, 10, 213–223. [Google Scholar] [CrossRef]
- Linder, E.V. Mapping the Dark Energy Equation of State. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Abdalla, E.; Atrio-Barandela, F.; Pavón, D. Dark Matter and Dark Energy Interactions: Theoretical Challenges, Cosmological Implications and Observational Signatures. Rep. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef] [PubMed]
- Bolotin, Y.L.; Kostenko, A.; Lemets, O.A.; Yerokhin, D.A. Cosmological Evolution With Interaction Between Dark Energy And Dark Matter. Int. J. Mod. Phys. D 2015, 24, 1530007. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C. Probing the interaction between dark matter and dark energy in the presence of massive neutrinos. Phys. Rev. D 2016, 94, 123511. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C. Echo of interactions in the dark sector. Phys. Rev. D 2017, 96, 103511. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pan, S.; Saridakis, E.N. New constraints on interacting dark energy from cosmic chronometers. Phys. Rev. D 2016, 94, 023508. [Google Scholar] [CrossRef]
- Richarte, M.G.; Xu, L. Exploring a new interaction between dark matter and dark energy using the growth rate of structure. arXiv, 2015; arXiv:1506.02518. [Google Scholar]
- Sharov, G.S.; Bhattacharya, S.; Pan, S.; Nunes, R.C.; Chakraborty, S. A new interacting two fluid model and its consequences. Mon. Non. R. Astron. Soc. 2017, 466, 3497–3506. [Google Scholar] [CrossRef]
- Salvatelli, V.; Said, N.; Bruni, M.; Melchiorri, A.; Wands, D. Indications of a late-time interaction in the dark sector. Phys. Rev. Lett. 2014, 113, 181301. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Meng, X.-H. Can vacuum decay in our universe? Class. Quantum Gravity 2005, 22, 283–294. [Google Scholar] [CrossRef]
- Costa, F.E.M.; Barboza, E.M., Jr.; Alcaniz, J.S. Cosmology with interaction in the dark sector. Phys. Rev. D 2009, 79, 127302. [Google Scholar] [CrossRef]
- Nunes, R.C.; Barboza, E.M. Dark matter-dark energy interaction for a time-dependent equation of state. Gen. Relativ. Gravit. 2014, 46, 1820. [Google Scholar] [CrossRef]
- Yang, W.; Banerjee, N.; Pan, S. Constraining a dark matter and dark energy interaction scenario with a dynamical equation of state. arXiv, 2017; arXiv:1705.09278. [Google Scholar]
- Steinhardt, P.J.; Wang, L.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. D 1999, 59, 123504. [Google Scholar] [CrossRef]
- Doran, M.; Robbers, G. Early Dark Energy Cosmologies. J. Cosmol. Astropart. Phys. 2006, 6, 573–583. [Google Scholar] [CrossRef]
- Sandage, A. The Change of redshift and Apparent Luminosity of Galaxies due to the Deceleration of Selected Expanding Universes. Astrophys. J. 1962, 136, 319–333. [Google Scholar] [CrossRef]
- Bolotin, Y.L.; Erokhin, D.A.; Lemets, O.A. Expanding Universe: Slowdown or speedup? Phys. Uspekhi 2012, 55, 941–986. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Barrow, J.D.; Bean, R.; Magueijo, J. Can the Universe escape eternal acceleration? Mon. Non. R. Astron. Soc. 2000, 316, L41–L44. [Google Scholar] [CrossRef]
- Guimarães, A.C.C.; Lima, J.A.S. Could the cosmic acceleration be transient? A cosmographic evaluation. Class. Quantum Gravity 2011, 28, 125026. [Google Scholar] [CrossRef]
- Li, Z.; Wu, P.; Yu, H. Examining the cosmic acceleration with the latest Union2 supernova data. Phys. Lett. B 2011, 695, 1–8. [Google Scholar] [CrossRef]
- Shafieloo, A.; Sahni, V.; Starobinsky, A.A. Is cosmic acceleration slowing down? Phys. Rev. D 2009, 80, 101301. [Google Scholar] [CrossRef]
- Cárdenas, V.H.; Bernal, C.; Bonilla, A. Cosmic slowing down of acceleration using fgas. Mon. Non. R. Astron. Soc. 2013, 433, 3534–3538. [Google Scholar] [CrossRef]
- Magaña, J.; Motta, V.; Cárdenas, V.H.; Foëx, G. Testing cosmic acceleration for w(z) parameterizations using fgas measurements in galaxy clusters. Mon. Non. R. Astron. Soc. 2017, 469, 47–61. [Google Scholar] [CrossRef]
- Bonilla Rivera, A.; García Farieta, J. Exploring the Dark Universe: Constraint on dynamical dark energy models from CMB, BAO and Growth Rate Measurements. arXiv, 2016; arXiv:1605.01984. [Google Scholar]
- Pan, S.; Chakraborty, S. Will there be future deceleration? A study of particle creation mechanism in non-equilibrium thermodynamics. Adv. High Energy Phys. 2015, 2015, 654025. [Google Scholar] [CrossRef]
- Chen, X.-M.; Gong, Y.; Saridakis, E.N. The Transient Acceleration from Time-Dependent Interacting Dark Energy Models. Int. J. Theor. Phys. 2014, 53, 469–481. [Google Scholar] [CrossRef]
- Carvalho, F.C.; Alcaniz, J.S.; Lima, J.A.S.; Silva, R. Scalar-field-dominated cosmology with a transient accelerating phase. Phys. Rev. Lett. 2006, 97, 081301. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Sugiyama, N. Small Scale Cosmological Perturbations: An Analytic Approach. Astrophys. J. 1996, 471, 542–570. [Google Scholar] [CrossRef]
- Bond, J.R.; Efstathiou, G.; Tegmark, M. Forecasting Cosmic Parameter Errors from Microwave Background Anisotropy Experiments. Mon. Non. R. Astron. Soc. 1997, 291, L33–L41. [Google Scholar]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Percival, W.J.; Reid, B.A.; Eisenstein, D.J.; Bahcall, N.A.; Budavari, T.; Frieman, J.A.; Fukugita, M.; Gunn, J.E.; Lupton, R.H.; Mckay, T.A.; et al. Baryon Acoustic Oscillations in the Sloan Digital Sky Survey Data Release 7 Galaxy Sample. Mon. Non. R. Astron. Soc. 2010, 401, 2148–2168. [Google Scholar] [CrossRef] [Green Version]
- Eisenstein, D.J.; Hu, W. Baryonic Features in the Matter Transfer Function. Astrophys. J. 1998, 496, 605–614. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Heath Jones, D.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: baryon acoustic oscillations and the local Hubble constant. Mon. Non. R. Astron. Soc. 2011, 416, 3017–3032. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, E.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Non. R. Astron. Soc. 2014, 441, 24–60. [Google Scholar] [CrossRef] [Green Version]
| 1 | Even though GC forms at the same time, they can have different evolution and thus different gas fractions. To preserve the constancy of the baryon fraction with redshift to mimic the relative cosmic abundance, GCs have to be selected among the most massive and relaxed ones at each epoch. |
| 2 | The pressure gradient force of an isothermal gas with temperature is balanced by the gravity in GC. |
| 3 | Specifically, a hydrostatic isothermal spherical symmetric . |
| 4 | For an unbiased estimator, If all the parameters are assumed to be known (in other words, if we don’t marginalize over any other parameters), then the minimal expected error is . |
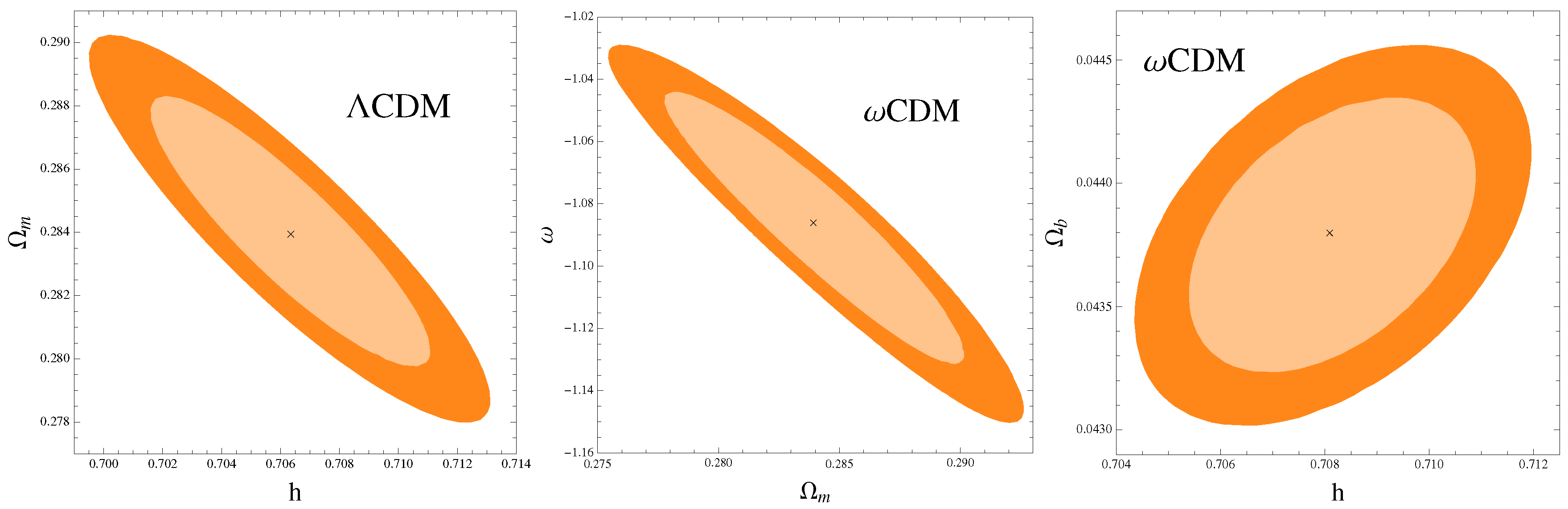

| Parameter | CMB + BAO + SNIa | CMB + BAO + SNIa + + + SGL |
|---|---|---|
| h | ||
| 565.686 | 777.256 |
| Parameter | CMB + BAO + SNIa | CMB + BAO + SNIa + + + SGL |
|---|---|---|
| h | ||
| 563.953 | 772.283 |
| Parameter | CMB + BAO + SNIa | CMB + BAO + SNIa + + + SGL |
|---|---|---|
| h | ||
| 563.854 | 771.481 |
| Parameter | CMB + BAO + SNIa | CMB + BAO + SNIa + + + SGL |
|---|---|---|
| h | ||
| 563.960 | 771.442 |
| Parameter | CMB + BAO + SNIa | CMB + BAO + SNIa + + + SGL |
|---|---|---|
| h | ||
| 564.275 | 771.697 |
| Model | d | AIC | BIC | |||
|---|---|---|---|---|---|---|
| 4 | 1.060 | 785.256 | 2.973 | 803.666 | 0.000 | |
| 5 | 1.055 | 782.283 | 0.000 | 805.295 | 1.626 | |
| CPL | 6 | 1.055 | 783.481 | 1.198 | 811.096 | 7.430 |
| IDE | 6 | 1.055 | 783.442 | 1.159 | 811.057 | 7.391 |
| EDE | 6 | 1.055 | 783.697 | 1.414 | 811.312 | 7.646 |
| Model | Parameters | |
|---|---|---|
| 1.11 | , , , | |
| 1.11 | , , , , . | |
| CPL | 1.14 | , , , , , . |
| IDE | 1.14 | , , , , , . |
| EDE | 1.14 | , , , , , . |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonilla, A.; Castillo, J.E. Constraints on Dark Energy Models from Galaxy Clusters and Gravitational Lensing Data. Universe 2018, 4, 21. https://doi.org/10.3390/universe4010021
Bonilla A, Castillo JE. Constraints on Dark Energy Models from Galaxy Clusters and Gravitational Lensing Data. Universe. 2018; 4(1):21. https://doi.org/10.3390/universe4010021
Chicago/Turabian StyleBonilla, Alexander, and Jairo E. Castillo. 2018. "Constraints on Dark Energy Models from Galaxy Clusters and Gravitational Lensing Data" Universe 4, no. 1: 21. https://doi.org/10.3390/universe4010021





