Weak Lensing Data and Condensed Neutrino Objects
Abstract
:1. Introduction
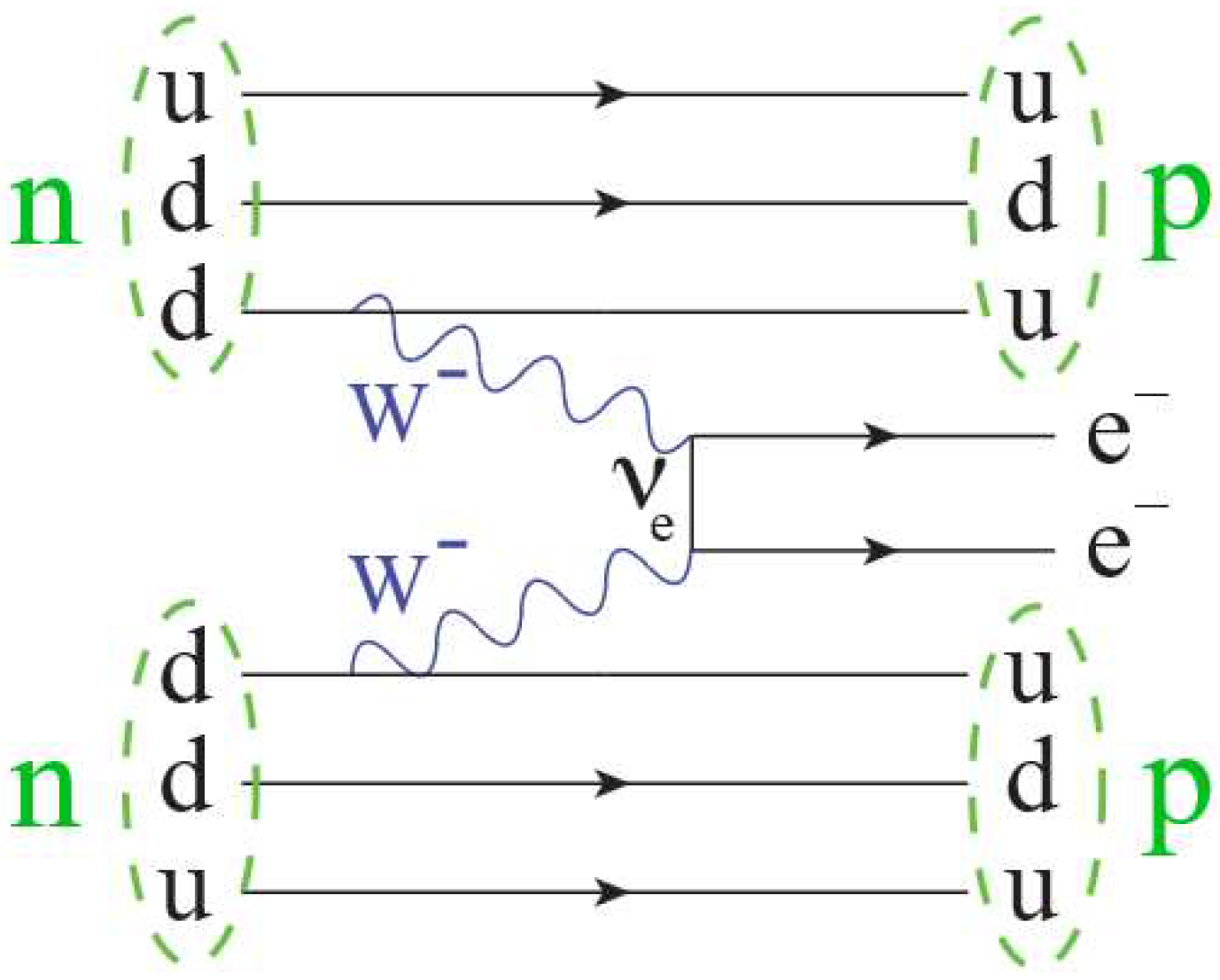
2. Neutrino Magnetic Moment Power Loss
3. Condensed Neutrinos is an Idea Many Decades Old
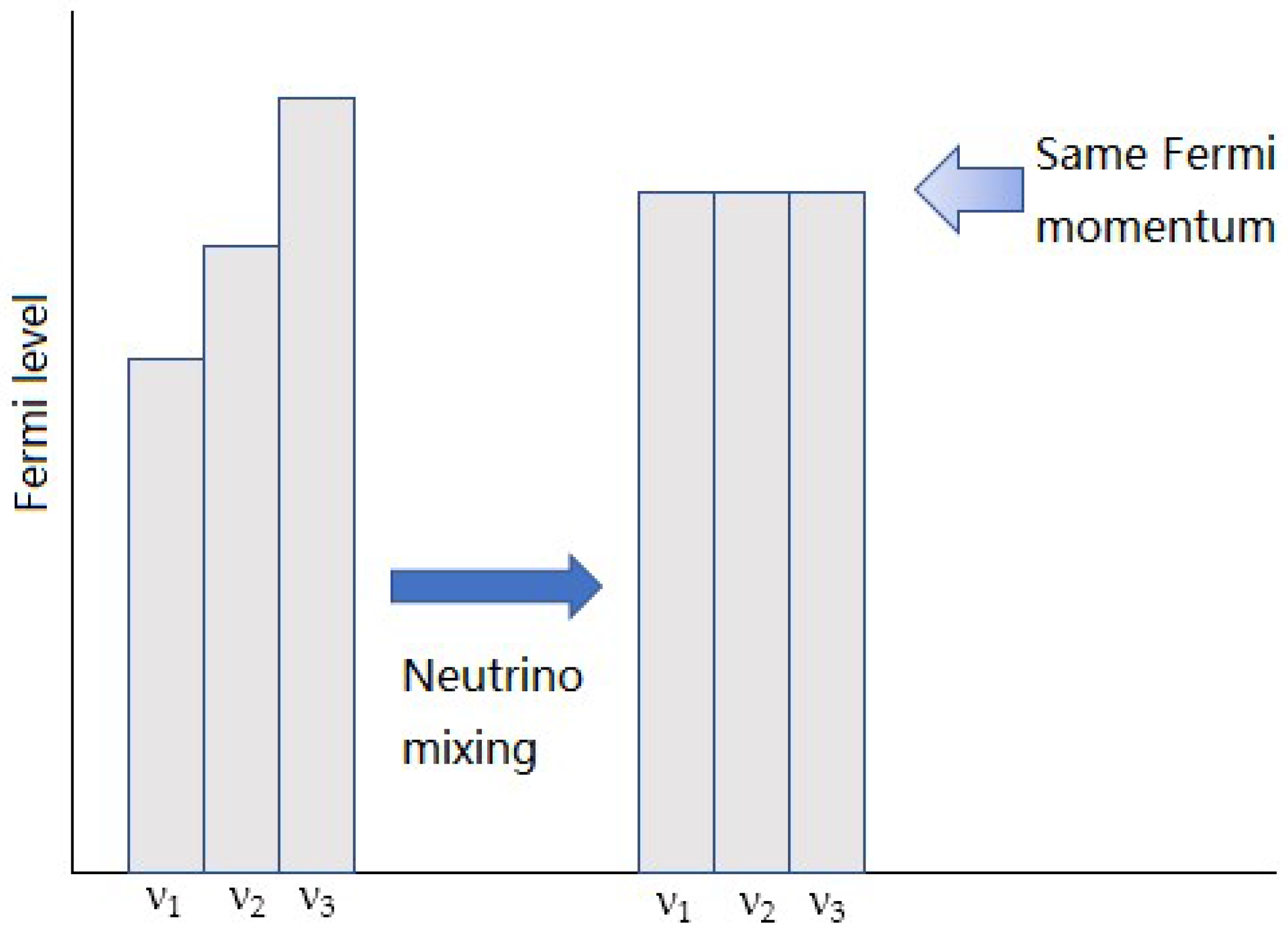
4. Neutrino Equation of State
5. CNO are Stable Objects
6. Materials and Methods
7. Updated and New Results
7.1. Einasto Density Profile Fits
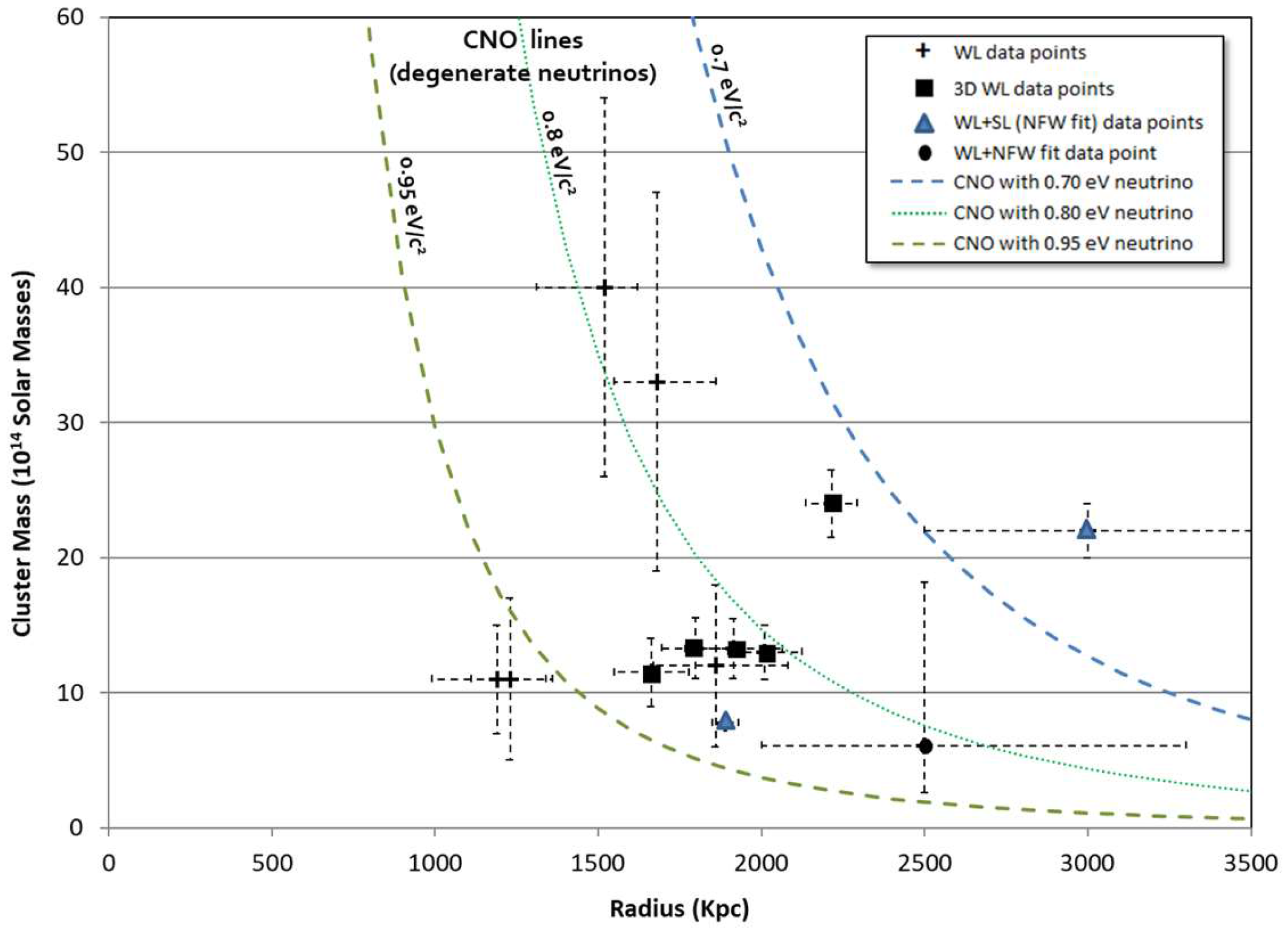
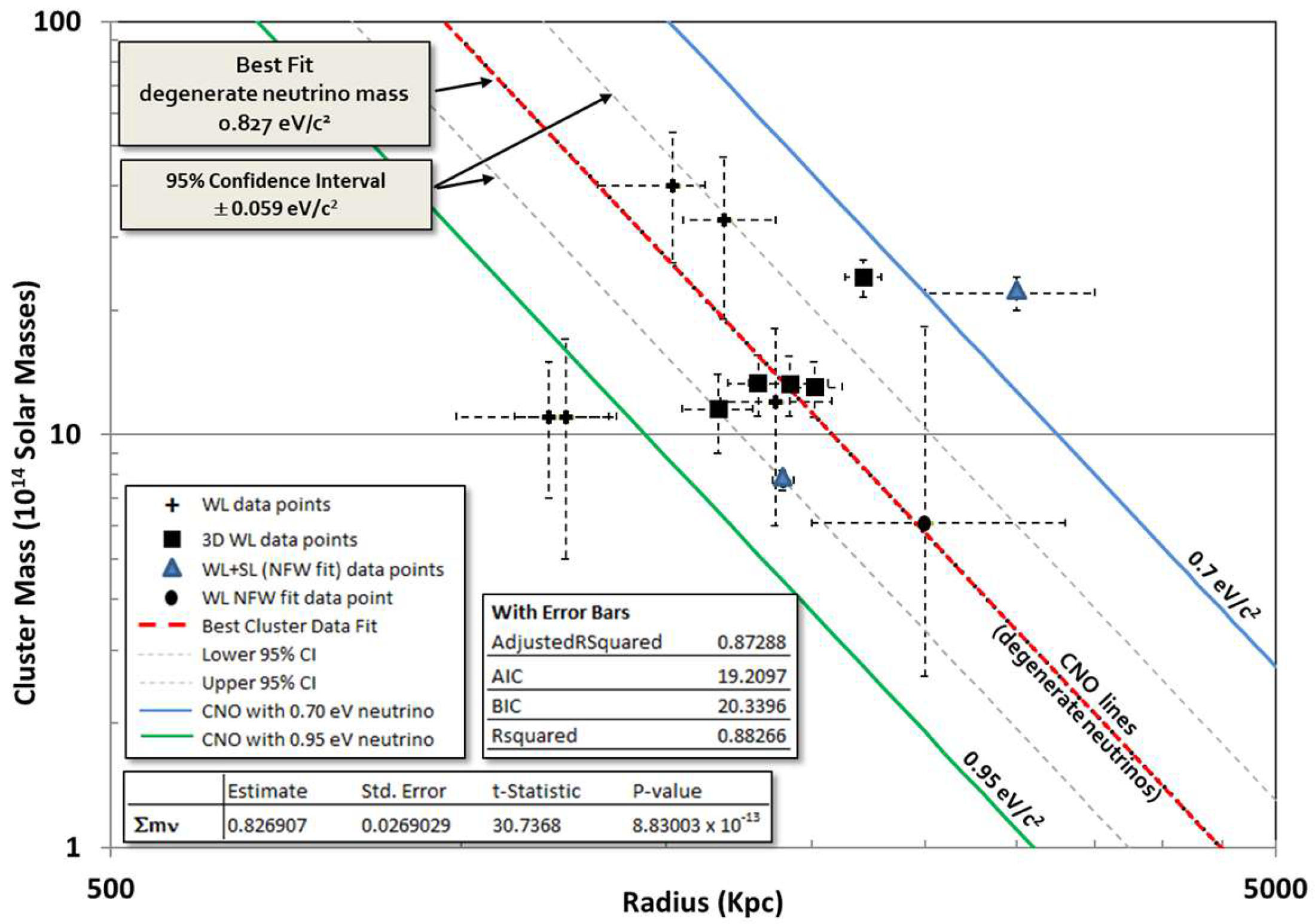
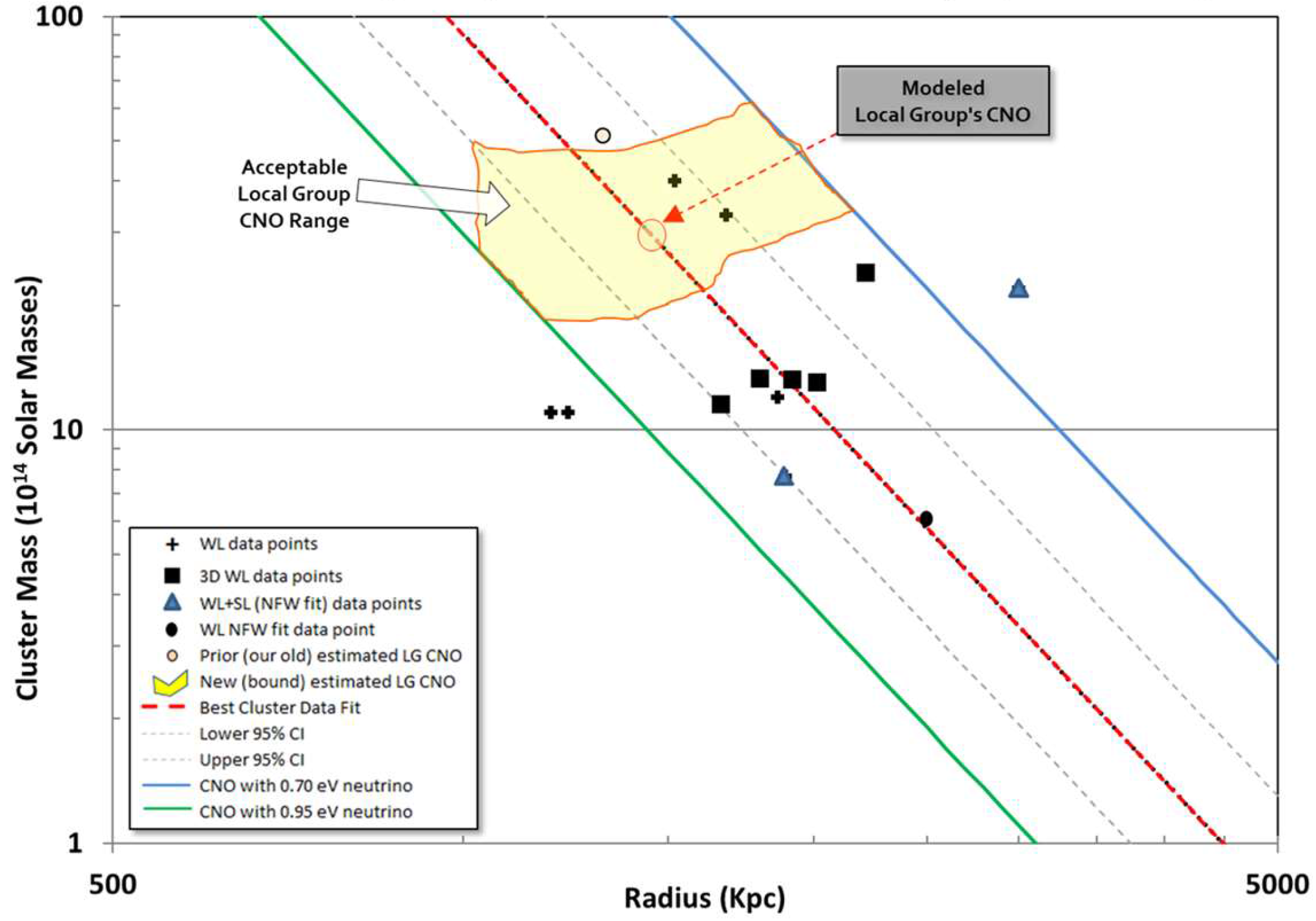
7.2. Dark Matter Galaxy Cluster Data
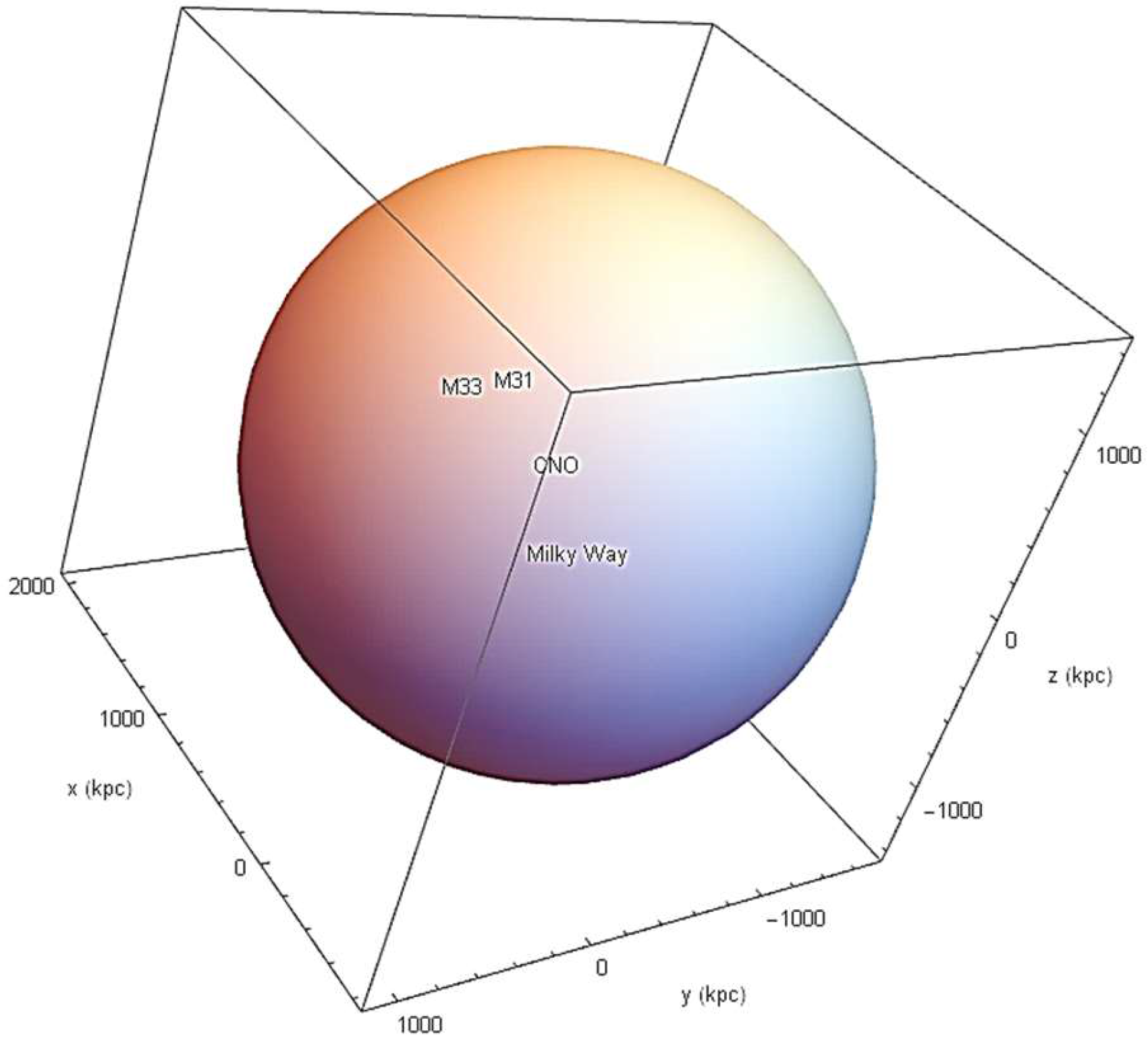
7.3. Monte Carlo and Latin Hypercube Local Group CNO Center Locations
8. Discussion
Author Contributions
Conflicts of Interest
References
- Einstein, A. Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes. Ann. Phys. 1911, 340, 898–908. (In Germany) [Google Scholar] [CrossRef]
- Einstein, A. Die Grundlage der allgemeinen Relativitätstheorie. Ann. Phys. 1916, 49, 769–822. (In Germany) [Google Scholar] [CrossRef]
- Einstein, A. Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie. Sitzungsberichte der Königlich Preussischen Akad. d. Wissenschaften (Berlin) 1917, 1, 142–152. (In Germany) [Google Scholar]
- Wilkinson Microwave Anisotropy Prob. Available online: https://en.wikipedia.org/wiki/Wilkinson_Microwave_Anisotropy_Prob (accessed on 20 November 2017).
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. (In Germany) [Google Scholar]
- Kitching, T.D.; Rhodes, J.; Heymans, C.; Massey, R.; Liu, Q.; Cobzarenco, M.; Cragin, B.L.; Hassaine, A.; Kirkby, D.; Lok, E.J.; et al. Image Analysis for Cosmology: Shape Measurement Challenge Review & Results from the Mapping Dark Matter Challenge. Astron. Comput. 2015, 10, 9–21. [Google Scholar]
- Kahlhoefer, F. Review of LHC Dark Matter Searches. Int. J. Mod. Phys. A 2017, 32, 1730006. [Google Scholar] [CrossRef]
- López-Corredoira, M. Tests and Problems of the Standard Model in Cosmology. Found. Phys. 2017, 47, 711–768. [Google Scholar] [CrossRef]
- Roos, M. Dark Matter: The evidence from astronomy, astrophysics and cosmology. arXiv, 2010; arXiv:1001.0316. [Google Scholar]
- Lukovic, V.; Cabella, P.; Vittorio, N. Dark matter in cosmology. Int. J. Mod. Phys. A 2014, 29, 1443001. [Google Scholar] [CrossRef]
- Particle Data Group. Review of Particle Physics. Chin. Phys. C 2016, 40, 100001. [Google Scholar]
- Morley, P.D.; Buettner, D.J. Instantaneous power radiated from magnetic dipole moments. Astropart. Phys. 2015, 62, 7–11. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Grasso, D.; Rubinstein, H.R. Magnetic Fields in the Early Universe. Phys. Rep. 2001, 348, 163–266. [Google Scholar] [CrossRef]
- Morley, P.D.; Buettner, D.J. SHM of galaxies embedded within condensed neutrino matter. Int. J. Mod. Phys. D 2015, 24, 1550004. [Google Scholar] [CrossRef]
- Milky Way. Available online: https://en.wikipedia.org/wiki/Milky_Way (accessed on 20 November 2017).
- KATRIN. Available online: https://www.katrin.kit.edu/ (accessed on 20 November 2017).
- GERDA Collaboration. Background-free search for neutrinoless double-β decay of 76Ge with GERDA. Nature 2017, 544, 47–52. [Google Scholar]
- The Nobel Prize in Physics 2015. Available online: https://www.nobelprize.org/nobel_prizes/physics/laureates/2015/ (accessed on 20 November 2017).
- Morley, P.D.; Buettner, D.J. A dark matter signature for condensed neutrinos. Int. J. Mod. Phys. D 2016, 25, 1650089. [Google Scholar] [CrossRef]
- Morley, P.D.; Buettner, D.J. Dark matter in the local group of galaxies. Int. J. Mod. Phys. D 2017, 26, 1750069. [Google Scholar] [CrossRef]
- Sereno, M.; Fedeli, C.; Moscardini, L. Comparison of weak lensing by NFW and Einasto halos and systematic errors. J. Cosmol. Astropart. Phys. 2016, 2016, 042. [Google Scholar] [CrossRef]
- Retana-Montenegro, E.; Frutos-Alfaro, F. The lensing properties of the Einasto profile. arXiv, 2011; arXiv:1108.4905v1 [astro-ph.CO]. [Google Scholar]
- Gavazzi, R. Projection effects in cluster mass estimates: The case of MS2137-23. Astron. Astrophys. 2005, 443, 793–804. [Google Scholar] [CrossRef]
- Gavazzi, R.; Adami, C.; Durret, F.; Cuillandre, J.-C.; Ilbert, O.; Mazure, A.; Pelló, R.; Ulmer, M.P. A weak lensing study of the Coma cluster. Astron. Astrophys. 2009, 498, L33–L36. [Google Scholar] [CrossRef]
- Irgens, R.J.; Lilje, P.B.; Dahle, H.; Maddox, S.J. Weak Gravitational Lensing by a Sample of X-ray-luminous Clusters of Galaxies. II. Comparison with Virial Masses. Astrophys. J. 2002, 579, 227–235. [Google Scholar] [CrossRef]
- Coe, D.; Umetsu, K.; Zitrin, A.; Donahue, M.; Medezinski, E.; Postman, M.; Carrasco, M.; Anguita, T.; Geller, M.J.; Rineset, K.J.; et al. Clash: Precise New Constraints on the Mass Profile of the Galaxy Cluster A2261. Astrophys. J. 2012, 757, 22. [Google Scholar] [CrossRef]
- Umetsu, K.; Broadhurst, T.; Zitrin, A.; Medezinski, E.; Hsu, L. Cluster Mass Profiles from a Bayexian Analysis of Weak-Lensing Distortion and Magnificantion Measurements: Applications to Subaru Data. Astrophys. J. 2011, 729, 127. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A Test of Goodness of Fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Choulakian, V.; Lockhart, R.A.; Stephens, M.A. Cramér-von Mises Statistics for Discrete Distributions. Can. J. Stat. 1994, 22, 125–137. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Pearson’s chi-squared test. Available online: https://en.wikipedia.org/wiki/Pearson%27s_chi-squared_test (accessed on 20 November 2017).
- Burkardt, J. IHS—Improved Distributed Hypercube Sampling. Available online: https://people.sc.fsu.edu/~jburkardt/cpp_src/ihs/ihs.html (accessed on 20 November 2017).
- Stodden, D.Y.; Galasso, G.D. Space system visualization and analysis using the Satellite Orbit Analysis Program (SOAP). In Proceedings of the IEEE Aerospace Applications Conference, Aspen, CO, USA, 4–11 February 1995. [Google Scholar]
- Corbelli, E.; Salucci, P. The extended rotation curve and the dark matter halo of M33. Mon. Not. R. Astron. Soc. 2000, 311, 441–447. [Google Scholar] [CrossRef]
- Carignan, C.; Chemin, L.; Huchtmeier, W.K.; Lockman, F.J. The Extended H1 Rotation Curve and Mass Distribution of M31. Astrophys. J. 2006, 641, L109–L112. [Google Scholar] [CrossRef]
- Xin, X.; Zheng, X. A Revised Rotation Curve of the Milky Way with Maser Astrometry. Res. Astron. Astrophys. 2013, 13, 849–861. [Google Scholar] [CrossRef]
- Ade1, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Neutrino decoupling. Available online: https://en.wikipedia.org/wiki/Neutrino_decoupling (accessed on 20 November 2017).
- Heavens, A.; Fantaye, Y.; Sellentin, E.; Eggers, H.; Hosenie, Z.; Kroon, S.; Mootoovaloo, A. No Evidence for Extensions to the Standard Cosmological Model. Phys. Rev. Lett. 2017, 119, 101301. [Google Scholar] [CrossRef] [PubMed]
| 1 | The authors performed a rough order of magnitude calculation on the number of expected CNOs in [11]. |
| 2 | v is the neutrino speed, c is the speed of light. |
| 3 | MRI (magnetic resonance imaging) uses this radiation physics. |
| 4 | |
| 5 | eV/c2 is electron Volts divided by the speed of light squared. |
| 6 | The authors are aware of efforts to use lensing of the Cosmic Microwave Background for mapping Dark Matter distributions (https://arxiv.org/pdf/1707.09369.pdf). However, we are awaiting appropriate data to include in future analysis. |
| 7 | For a definition of M200, R200, Mvir and Rvir. please see https://en.wikipedia.org/wiki/Virial_mass. |
| 8 | Coordinates obtained from Wolfram Research’s Mathematica® 11.2. |
| 9 | See for example https://en.wikipedia.org/wiki/Latin_hypercube_sampling for a description of Latin hypercube sampling. |
| 10 | |
| 11 | The rotation speed of a spiral arm is relative to the spiral galaxy’s center. |




| x(0) (for mνc2 = 1 eV) | Mtotal (MΘ) | R0 (ly) | Ω (joules) | R0 (RS) |
|---|---|---|---|---|
| 0.001 | 3.100 × 1013 | 13.01 × 106 | −1.764 × 1054 | 1.344 × 106 |
| 0.01 | 9.809 × 1014 | 4.12 × 106 | −5.569 × 1057 | 1.345 × 104 |
| 0.1 | 3.077 × 1016 | 1.30 × 106 | −1.739 × 1061 | 135.3 |
| 1.0 | 5.27 × 1017 | 3.72 × 105 | −1.969 × 1064 | 2.254 |
| Interesting Property | Consequence |
|---|---|
| CNO obey Pauli Exclusion Principle | CNO cannot grow from fusion (like Black Holes)—CNO repel each other |
| Embedded matter (galaxies and gas) undergo simple harmonic motion | Embedded gas is not in thermodynamic equilibrium, contrary to assumptions in x-ray data analysis |
| CNO can be internally excited (lowest excited state is a quadrupole oscillation) | CNO do not necessarily have a spherical shape |
| CNO are primarily composed of the original cosmological neutrinos and anti-neutrinos formed in the Big Bang | CNO are common objects (not rare) |
| Spherical CNO Properties | Einasto Density Parameters | |||||
|---|---|---|---|---|---|---|
| mν (eV/c2) | x(0) | M(Rmax) (1014 Mo) | Rmax (Kpc) | ρ−2 (per Mo/Kpc3) | r−2 (Kpc) | α |
| 0.7 | 0.005 | 7.07563 | 3646.02 | 8336.41 | 1853.96 | 2.2081 |
| 0.006 | 9.30115 | 3329 | 14,409.6 | 1692.09 | 2.20887 | |
| 0.007 | 11.7211 | 3082.04 | 22,878.5 | 1566.69 | 2.20832 | |
| 0.008 | 14.3206 | 2883.2 | 34,148.4 | 1465.54 | 2.20801 | |
| 0.009 | 17.0877 | 2718.57 | 48,638.3 | 1381.42 | 2.20893 | |
| 0.01 | 20.0131 | 2579.16 | 66,700.5 | 1310.7 | 2.20801 | |
| 0.015 | 37.4921 | 2107 | 22,5235 | 1069.76 | 2.20918 | |
| 0.02 | 56.5911 | 1823.84 | 533,578 | 926.671 | 2.20704 | |
| 0.8 | 0.005 | 5.41728 | 2794 | 14,219.9 | 1419.48 | 2.20743 |
| 0.006 | 7.12107 | 2550 | 24,564.9 | 1295.97 | 2.20644 | |
| 0.007 | 8.97393 | 2360 | 39,046.8 | 1199.14 | 2.20924 | |
| 0.008 | 10.9657 | 2208 | 58,287.6 | 1121.65 | 2.20922 | |
| 0.009 | 13.0828 | 2081.46 | 82,932 | 1057.9 | 2.20699 | |
| 0.01 | 15.3225 | 1974.72 | 113,784 | 1003.47 | 2.20745 | |
| 0.015 | 28.1461 | 1612.37 | 384,147 | 819.097 | 2.20792 | |
| 0.02 | 73.6874 | 1397 | 909,020 | 709.983 | 2.20246 | |
| 0.95 | 0.005 | 3.84162 | 1983 | 28,278.5 | 1006.5 | 2.20706 |
| 0.006 | 5.04993 | 1808 | 48,899.8 | 918.405 | 2.20894 | |
| 0.007 | 7.27676 | 1674 | 77,601.6 | 850.565 | 2.20691 | |
| 0.008 | 7.77518 | 1565.37 | 115,867 | 795.492 | 2.20753 | |
| 0.009 | 9.42287 | 1477 | 164,901 | 750.167 | 2.20606 | |
| 0.01 | 10.9897 | 1401 | 226,441 | 711.225 | 2.209 | |
| 0.015 | 19.9595 | 1143.38 | 762,388 | 581.445 | 2.2013 | |
| 0.02 | 31.1658 | 990.5 | 1,807,020 | 503.513 | 2.20053 | |
| Cluster | z | Mvir (1014 Mo) | Rvir (Mpc) | Type | Reference |
|---|---|---|---|---|---|
| MS2137-23 * | 0.310 | 1.89 ± 0.04 | SL+WL (NFW fit) | [24] | |
| Coma (Abell 1656) ** | 0.024 | WL NFW | [25] | ||
| A914 | 0.193 | 11 ± 6 | WL | [26] | |
| A1351 | 0.328 | 33 ± 14 | WL | [26] | |
| A1576 | 0.299 | 40 ± 14 | WL | [26] | |
| A1722 | 0.326 | 12 ± 6 | WL | [26] | |
| A1995 | 0.321 | 11 ± 4 | WL | [26] | |
| A2261 | 0.225 | 22 ± 2 | ~3 | SL+WL (NFW fit) | [27] |
| A1689 | 0.183 | 13 ± 2.05 | 2.011 ± 0.113 | 3D WL | [28] |
| A1703 | 0.281 | 13.25 ± 2.21 | 1.915 ± 0.148 | 3D WL | [28] |
| A370 | 0.375 | 23.99 ± 2.49 | 2.215 ± 0.079 | 3D WL | [28] |
| Cl0024 + 17 | 0.395 | 13.29 ± 2.24 | 1.799 ± 0.105 | 3D WL | [28] |
| RXJ1347 − 11 | 0.451 | 11.5 ± 2.50 | 1.663 ± 0.115 | 3D WL | [28] |
| Goodness-of-Fit statistics mν = 0.8269 (5000 Monte Carlo iterations) | Mean p-value | Mean CI | Variance | Median p-value | IQR |
|---|---|---|---|---|---|
| Anderson-Darling [29] | 0.464 | ±0.006 | 0.049 | 0.415 | 0.397 |
| Cramér-von Mises [30] | 0.446 | ±0.006 | 0.048 | 0.379 | 0.384 |
| Kolmogorov-Smirnov [31] | 0.513 | ±0.007 | 0.063 | 0.379 | 0.403 |
| Pearson χ2 [32] | 0.564 | ±0.005 | 0.031 | 0.53 | 0.304 |
| Watson U2 [30] | 0.33 | ±0.006 | 0.041 | 0.261 | 0.313 |
| Name | Distance (kpc) | Dec (°) | RA (°) |
|---|---|---|---|
| M31 | 788.333 | 41.2689 | 10.685 |
| M33 | 862.417 | 30.6581 | 23.466 |
| Milky Way | 7.61113 | −29.0078 | 266.417 |
| Quantity | Predicted Value |
|---|---|
| Center CNO-LG distance from MW | 673.422 kpc |
| Center CNO-LG distance from M33 | 740.423 kpc |
| Center CNO-LG distance from M31 | 656.015 kpc |
| Algorithm error center CNO-LG | 0.000706162 kpc |
| Right ascension of CNO-LG center | −26.6588° |
| Declination of CNO-LG center | 0.91773° |
| Galactic longitude of CNO-LG center | 62.83928785° |
| Galactic latitude of CNO-LG center | −42.77834848° |
| Milky way cant angle | 47.221° |
| Local Group Galaxy | Distance from Center (kpc) | VDM Low (km/s) | VDM High (km/s) | Reference |
|---|---|---|---|---|
| M33 | 15 | ~65 | ~110 | [35] |
| M31 | 30 | ~50 | ~110 | [36] |
| Milky Way | 8 | ~80 | ~260 | [37] |
| Milky Way | 20 | ~250 | ~400 | [37] |
| 0.768290 eV/c2 | 0.826907 eV/c2 | 0.88552 eV/c2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| x(0) boundary values → | 0.014 | 0.017 | 0.021 | 0.013 | 0.017 | 0.022 | 0.013 | 0.019 | 0.025 |
| M33 (@ 15 kpc) (km/s) | 26 | 31 | 38 | 24 | 30 | 35 | 23 | 27 | 16 |
| M31 (@ 30 kpc) (km/s) | 56 | 70 | 88 | 54 | 71 | 88 | 54 | 73 | 76 |
| MW (@ 8 kpc) (km/s) | 162 | 203 | 253 | 155 | 204 | 250 | 156 | 203 | 201 |
| MW (@ 20 kpc) (km/s) | 257 | 321 | 399 | 246 | 322 | 393 | 246 | 319 | 310 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morley, P.; Buettner, D. Weak Lensing Data and Condensed Neutrino Objects. Universe 2017, 3, 81. https://doi.org/10.3390/universe3040081
Morley P, Buettner D. Weak Lensing Data and Condensed Neutrino Objects. Universe. 2017; 3(4):81. https://doi.org/10.3390/universe3040081
Chicago/Turabian StyleMorley, Peter, and Douglas Buettner. 2017. "Weak Lensing Data and Condensed Neutrino Objects" Universe 3, no. 4: 81. https://doi.org/10.3390/universe3040081




