Getting Your Peaks in Line: A Review of Alignment Methods for NMR Spectral Data
Abstract
:1. Introduction

2. A Generic NMR Spectrum Alignment Framework
3. Working on Extracted Peaks Instead of Full Spectra
| Short Name | Full Name | Reference | Technique | Target Function | Peak Picking? | Number of Parameters | Original Applied Data | Segment-Wise? | Pair-Wise? | Correction Method | Software |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PLF | Partial Linear Fit | [11] | Segmentation model by consecutive peaks distances less than window size D | Sum of squared differences in intensity | No | 2 (window D and shift S) | 1D NMR | Yes | Yes | Shift | NA |
| COW | Correlation Optimized Warping | [12] | Dynamic programming | Pearson correlation coefficient | No | 2 (m: length of segments and t: slack or the max. allowable shift) | Chromatograpic data | yes | Yes | Insert and deletion | (1) |
| PAGA | Peak alignment by genetic algorithn | [13] | Genetic Algorithm | Pearson correlation coefficient | No | 6 - Based on GA (normalize geometric ranking q=0.8, population size, number of generations, segment size, max. allowable shift, linear interpolation ra) | 1D NMR | Yes | Yes | Shift & Insert and deletion | NA |
| PARS | Peak alignment using Reduced Set | [14] | Breadth first search (BFS), Dynamic Programming (DP), complexity reduced dynamic programming (crDP) | Euclidean distances | Yes | 2 (search window size, mismatch weight) | 1D NMR, Gas Chromatography | No | Yes | Shift | (+) |
| DTW | Dynamic Time Warping | [15] | Dynamic programming | Squared Euclidean distance | No | 2 (T(x,y) local continuity constraint; x = largest block distance covered by any of the rules, y = max. number of horizontal / vertical consecutive transition allowed for) | Chromatograpic data | No | Yes | Insert and deletion | (1) |
| PABS | Peak alignment by Beam search | [16] | Beam search algorithm | Pearson correlation coefficient | No | 3 (ranges of segment number, sideway movement and interpolation) | 1D NMR | Yes | Yes | Shift & Insert and deletion | (+) |
| PAPCA (*) | Peak alignment by PCA | [17] | Principle Component Analysis | CORREL | No | 1 (correlation threshold 0.8) | 1D NMR | No | No | Shift | (+) |
| PTW | Parametric Time Warping | [18] | Global polynominal model | Root mean squared (RMS) | No | 1 (degree of polynomial warping function) | Chromatograpic data | No | Yes | Polynominal model | (2) |
| PAFFT | Peak alignment by FFT | [19] | FFT + segmentation model by equal size segments | FFT cross-correlation | No | 2 (segment size: segsize, max. allowable shift) | Chromatograpic data | Yes | Yes | Shift | (3) |
| RAFFT | Recursive alignment by FFT | [19] | FFT + Recursive segmentation model from global to local | FFT cross-correlation | No | 1 (max. allowable shift) | Chromatograpic data | Yes | Yes | Shift | (3) |
| SpecAlign | NA | [20] | Sliding windows | Minimal matched peak distances | No | 1 (window size w) | Mass Spectrometry | No | Yes | Insert and deletion | (3) |
| FW | Fuzzy Warping | [21] | Fuzzy logic for matching most intense peaks | Maximize fuzzy membership Gaussian function | Yes | 1 (the number of most intense peaks) | 1D NMR | No | Yes | Insert and deletion | (4) |
| GFHT | Generlized Fuzzy Hought Transform | [22] | Hough transform | Hough score | Yes | 3 (expansion factor alpha, step size, lower vote threshold) | 1D NMR | No | No | NA | NA |
| RSPA | Recursive segment-wise peak alignment | [23] | Recursive segmentation model | FFT cross-correlation | Yes | 6 (peak height threshold, splitting threshold, min. segment size, validation of segment alignment, max. allowable shift, alignment acceptance) | 1D NMR | Yes | Yes | Shift & Insert and deletion | (+) |
| PCANS | Progressive Consensus Alignment of NMR Spectra | [24] | Segmentation model+Dynamic programming + progressive consensus alignment | Scoring by similarity between peaks calculated by height, half height and position of peaks | Yes | 5 (minScoreN, minScoreD, gap penalty, boundary penalty, max. allowable shift maxCS) | 1D NMR | Yes | No | Shift | (5) |
| BAA (*) | Bayesian approach for alignment | [25] | Bayesian modeling | Bayesian estimation | No | 3 (noise variance, two parameter values in diagonal entries of diagonal covariance matrix) | 1D NMR | No | Yes | Polynomial model | NA |
| icoshift | interval correlation shifting | [10] | Segmentation model by equal size segments or manually selecting segments | FFT cross-correlation | No | 2 (the number of intervals or the length of interval l, max. allowable shift) | 1D NMR | Yes | Yes | Shift & Insert and deletion | (6) |
| CluPA | hierarchial Cluster-based Peak Alignment | [8] | Segmentation model by hierarchical clustering | FFT cross-correlation | Yes | 1 (max. allowable shift) | 1D NMR | Yes | Yes | Shift | (7) |

4. Alignment with or without a Reference Spectrum
4.1. Pairwise Methods, Based on a Selected Reference Spectrum
4.2. Inter-Sample Methods, without Using a Reference Spectrum
5. Alignment of Whole Spectra or Alignment of Spectrum Segments?
6. Criteria or Target Function
7. Correction Methods
8. Alignment Assessment and Evaluation
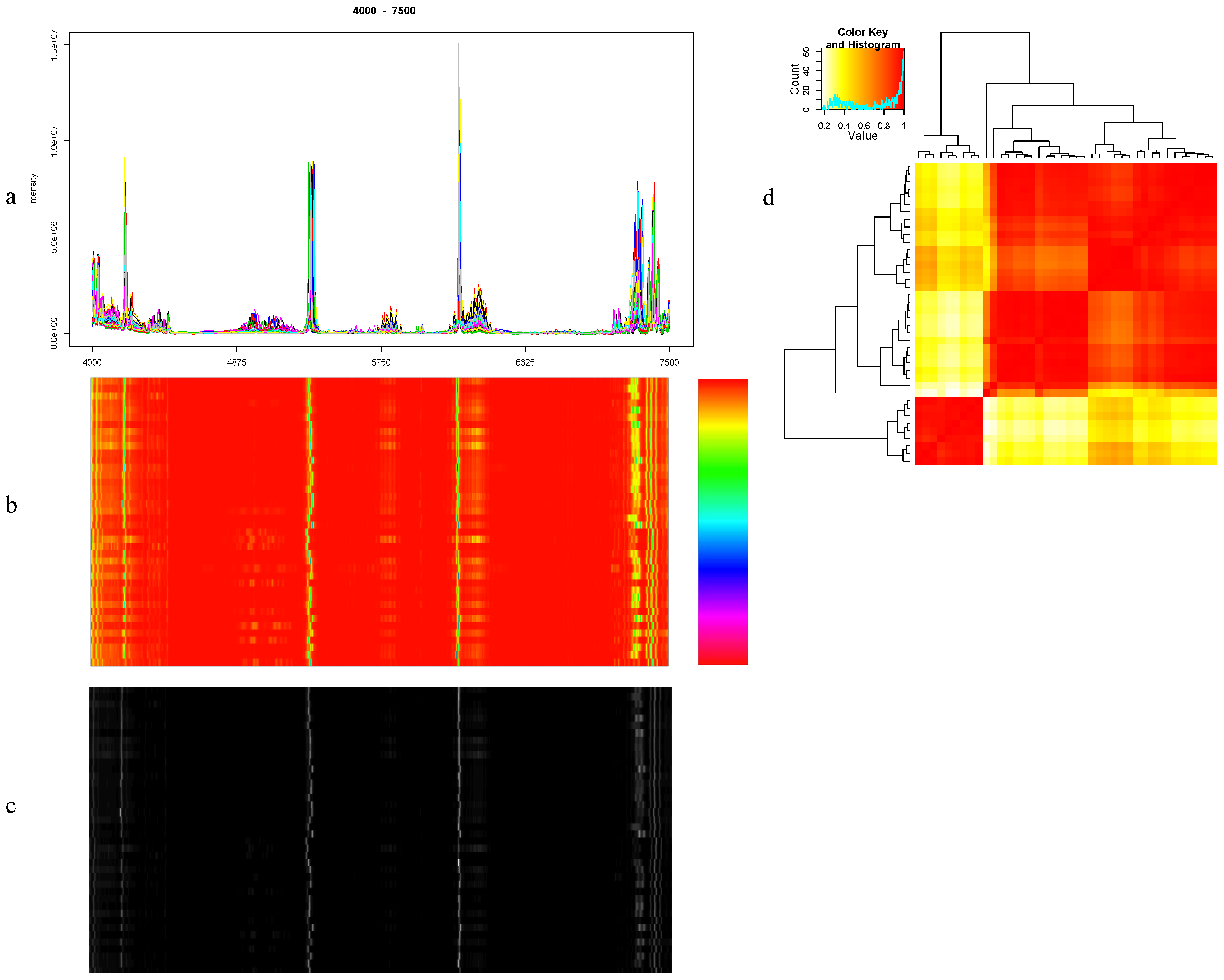
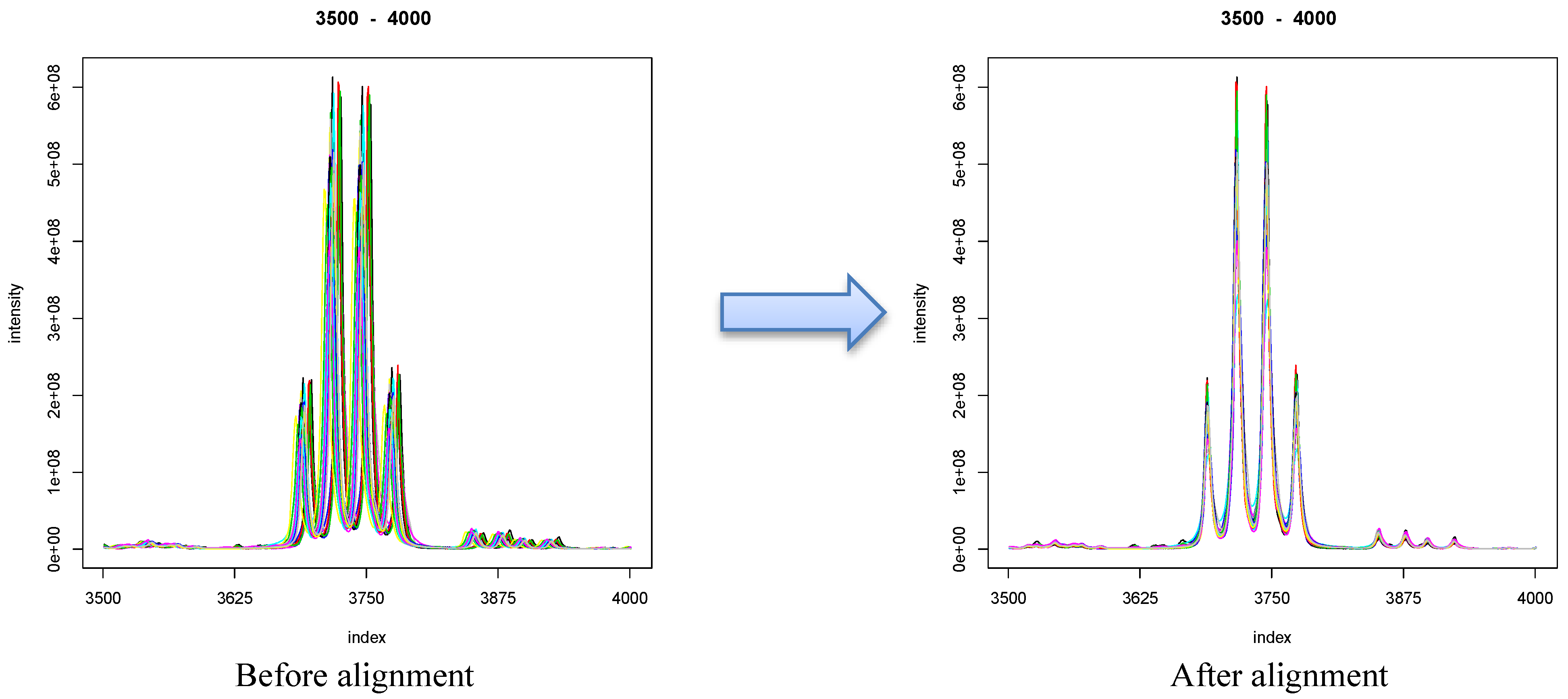
8.1. Visualization
8.2. Quantitation of Similarity between Spectra
8.3. PCA Analysis
8.4. Classification Model Analysis
8.5. Other Evaluation Approaches
9. Method Complexities
9.1. Computational Complexity
9.2. Usage Complexity (Method Meta-Parameters)
10. Alignment of 2D NMR Data
11. Conclusion and Future Work
Acknowledgments
Conflict of Interest
References
- Beneduci, A.; Chidichimo, G.; Dardo, G.; Pontoni, G. Highly routinely reproducible alignment of 1H NMR spectral peaks of metabolites in huge sets of urines. Anal. Chim. Acta 2011, 685, 186–195. [Google Scholar] [CrossRef]
- Giskeødegård, G.F.; Bloemberg, T.G.; Postma, G.; Sitter, B.; Tessem, M.-B.; Gribbestad, I.S.; Bathen, T.F.; Buydens, L.M. C. Alignment of high resolution magic angle spinning magnetic resonance spectra using warping methods. Anal. Chim. Acta 2010, 683, 1–11. [Google Scholar] [CrossRef]
- Lindon, J.C.; Holmes, E.; Nicholson, J.K. Pattern recognition methods and applications in biomedical magnetic resonance. Prog. Nucl. Mag. Res. Sp. 2001, 39, 1–40. [Google Scholar] [CrossRef]
- Davis, R.A.; Charlton, A.J.; Godward, J.; Jones, S.A.; Harrison, M.; Wilson, J.C. Adaptive binning: An improved binning method for metabolomics data using the undecimated wavelet transform. Chemometr. Intell. Lab. Syst. 2007, 85, 144–154. [Google Scholar] [CrossRef]
- De Meyer, T.; Sinnaeve, D.; Van Gasse, B.; Tsiporkova, E.; Rietzschel, E.R.; De Buyzere, M.L.; Gillebert, T.C.; Bekaert, S.; Martins, J.C.; Van Criekinge, W. NMR-based characterization of metabolic alterations in hypertension using an adaptive, intelligent binning algorithm. Anal. Chem. 2008, 80, 3783–3790. [Google Scholar] [CrossRef]
- Anderson, P.E.; Reo, N.V.; DelRaso, N.J.; Doom, T.E.; Raymer, M.L. Gaussian binning: A new kernel-based method for processing NMR spectroscopic data for metabolomics. Metabolomics 2008, 4, 261–272. [Google Scholar] [CrossRef]
- Sousa, S.A.A.; Magalhães, A.; Ferreira, M.M.C. Optimized bucketing for NMR spectra: Three case studies. Chemometr. Intell. Lab. Syst. 2013, 122, 93–102. [Google Scholar] [CrossRef]
- Vu, T.N.; Valkenborg, D.; Smets, K.; Verwaest, K.A.; Dommisse, R.; Lemière, F.; Verschoren, A.; Goethals, B.; Laukens, K. An integrated workflow for robust alignment and simplified quantitative analysis of NMR spectrometry data. BMC Bioinformatics 2011, 12, 405. [Google Scholar]
- Larsen, F.H.; Van den Berg, F.; Engelsen, S.B. An exploratory chemometric study of 1H NMR spectra of table wines. J. Chemometr. 2006, 20, 198–208. [Google Scholar] [CrossRef]
- Savorani, F.; Tomasi, G.; Engelsen, S.B. icoshift: A versatile tool for the rapid alignment of 1D NMR spectra. J. Magn. Reson. 2010, 202, 190–202. [Google Scholar] [CrossRef]
- Vogels, J.T.W.E.; Tas, A.C.; Venekamp, J.; Van der Greef, J. Partial linear fit: A new NMR spectroscopy preprocessing tool for pattern recognition applications. J. Chemometr. 1996, 10, 425–438. [Google Scholar] [CrossRef]
- Nielsen, N.P.V.; Carstensen, J.M.; Smedsgaard, J. Aligning of single and multiple wavelength chromatographic profiles for chemometric data analysis using correlation optimised warping. J. Chromatogr. A 1998, 805, 17–35. [Google Scholar] [CrossRef]
- Forshed, J.; Schuppe-Koistinen, I.; Jacobsson, S.P. Peak alignment of NMR signals by means of a genetic algorithm. Analytica. Chimica. Acta 2003, 487, 189–199. [Google Scholar] [CrossRef]
- Torgrip, R.J.O.; Åberg, M.; Karlberg, B.; Jacobsson, S.P. Peak alignment using reduced set mapping. J. Chemometr. 2003, 17, 573–582. [Google Scholar] [CrossRef]
- Tomasi, G.; Van den Berg, F.; Andersson, C. Correlation optimized warping and dynamic time warping as preprocessing methods for chromatographic data. J. Chemometr. 2004, 18, 231–241. [Google Scholar] [CrossRef]
- Lee, G.C.; Woodruff, D.L. Beam search for peak alignment of NMR signals. Analytica. Chimica. Acta 2004, 513, 413–416. [Google Scholar] [CrossRef]
- Stoyanova, R.; Nicholls, A.W.; Nicholson, J.K.; Lindon, J.C.; Brown, T.R. Automatic alignment of individual peaks in large high-resolution spectral data sets. J. Magn. Reson. 2004, 170, 329–335. [Google Scholar]
- Eilers, P.H.C. Parametric Time Warping. Anal. Chem. 2004, 76, 404–411. [Google Scholar] [CrossRef]
- Wong, J.W.H.; Durante, C.; Cartwright, H.M. Application of fast Fourier transform cross-correlationfor the alignment of large chromatographic and spectral datasets. Anal. Chem. 2005, 77, 5655–5661. [Google Scholar] [CrossRef]
- Wong, J.W.H.; Cagney, G.; Cartwright, H.M. SpecAlign—processing and alignment of mass spectra datasets. Bioinformatics 2005, 21, 2088–2090. [Google Scholar] [CrossRef]
- Wu, W.; Daszykowski, M.; Walczak, B.; Sweatman, B.C.; Connor, S.C.; Haselden, J.N.; Crowther, D.J.; Gill, R.W.; Lutz, M.W. Peak alignment of urine NMR spectra using fuzzy warping. J. Chem. Inf. Model. 2006, 46, 863–875. [Google Scholar] [CrossRef]
- Csenki, L.; Alm, E.; Torgrip, R.J.O.; Aberg, K.M.; Nord, L.I.; Schuppe-Koistinen, I.; Lindberg, J. Proof of principle of a generalized fuzzy Hough transform approach to peak alignment of one-dimensional 1H NMR data. Anal. Bioanal. Chem. 2007, 389, 875–885. [Google Scholar] [CrossRef]
- Veselkov, K.A.; Lindon, J.C.; Ebbels, T.M. D.; Crockford, D.; Volynkin, V.V.; Holmes, E.; Davies, D.B.; Nicholson, J.K. Recursive segment-wise peak alignment of biological 1H NMR spectra for improved metabolic biomarker recovery. Anal. Chem. 2009, 81, 56–66. [Google Scholar] [CrossRef]
- Staab, J.M.; O’Connell, T.M.; Gomez, S.M. Enhancing metabolomic data analysis with Progressive Consensus Alignment of NMR Spectra (PCANS). BMC Bioinformatics 2010, 11, 123. [Google Scholar]
- Kim, S.B.; Wang, Z.; Hiremath, B. A Bayesian approach for the alignment of high-resolution NMR spectra. Ann. Oper. Res. 2010, 174, 19–32. [Google Scholar]
- Wang, T.; Shao, K.; Chu, Q.; Ren, Y.; Mu, Y.; Qu, L.; He, J.; Jin, C.; Xia, B. Automics: an integrated platform for NMR-based metabonomics spectral processing and data analysis. BMC Bioinformatics 2009, 10, 83. [Google Scholar]
- Yang, C.; He, Z.; Yu, W. Comparison of public peak detection algorithms for MALDI mass spectrometry data analysis. BMC Bioinformatics 2009, 10, 4. [Google Scholar] [CrossRef]
- Skov, T.; Van den Berg, F.; Tomasi, G.; Bro, R. Automated alignment of chromatographic data. J. Chemometr. 2006, 20, 484–497. [Google Scholar] [CrossRef]
- MacKinnon, N.; Ge, W.; Khan, A.P.; Somashekar, B.S.; Tripathi, P.; Siddiqui, J.; Wei, J.T.; Chinnaiyan, A.M.; Rajendiran, T.M.; Ramamoorthy, A. Variable reference alignment: An improved peak alignment protocol for NMR spectral data with large intersample variation. Anal. Chem. 2012, 84, 5372–5379. [Google Scholar] [CrossRef]
- Alm, E.; Torgrip, R.J.O.; Aberg, K.M.; Schuppe-Koistinen, I.; Lindberg, J. A solution to the 1D NMR alignment problem using an extended generalized fuzzy Hough transform and mode support. Anal. Bioanal. Chem. 2009, 395, 213–223. [Google Scholar] [CrossRef]
- Clifford, D.; Stone, G.; Montoliu, I.; Rezzi, S.; Martin, F.P.; Guy, P.; Bruce, S.; Kochhar, S. Alignment using variable penalty dynamic time warping. Anal. Chem. 2009, 81, 1000–1007. [Google Scholar]
- Burges, C.J.C. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Vapnik, V.N. The nature of statistical learning theory; Springer-Verlag New York, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Barker, M.; Rayens, W. Partial least squares for discrimination. J. Chemometr. 2003, 17, 166–173. [Google Scholar] [CrossRef]
- Smolinska, A.; Blanchet, L.; Buydens, L.M. C.; Wijmenga, S.S. NMR and pattern recognition methods in metabolomics: from data acquisition to biomarker discovery: a review. Anal. Chim. Acta 2012, 750, 82–97. [Google Scholar] [CrossRef]
- Cloarec, O.; Dumas, M.E.; Trygg, J.; Craig, A.; Barton, R.H.; Lindon, J.C.; Nicholson, J.K.; Holmes, E. Evaluation of the orthogonal projection on latent structure model limitations caused by chemical shift variability and improved visualization of biomarker changes in 1H NMR spectroscopic metabonomic studies. Anal. Chem. 2005, 77, 517–526. [Google Scholar] [CrossRef]
- Forshed, J.; Torgrip, R.J.O.; Åberg, K.M.; Karlberg, B.; Lindberg, J.; Jacobsson, S.P. A comparison of methods for alignment of NMR peaks in the context of cluster analysis. J Pharmaceut. Biomed. Anal. 2005, 38, 824–832. [Google Scholar] [CrossRef]
- Cloarec, O.; Dumas, M.E.; Craig, A.; Barton, R.H.; Trygg, J.; Hudson, J.; Blancher, C.; Gauguier, D.; Lindon, J.C.; Holmes, E.; et al. Statistical Total Correlation Spectroscopy: An exploratory approach for latent biomarker identification from metabolic 1H NMR data sets. Anal. Chem. 2005, 77, 1282–1289. [Google Scholar] [CrossRef]
- Holmes, E.; Cloarec, O.; Nicholson, J.K. Probing Latent Biomarker Signatures and in Vivo Pathway Activity in Experimental Disease States via Statistical Total Correlation Spectroscopy (STOCSY) of Biofluids: Application to HgCl2 toxicity. J. Proteome Res. 2006, 5, 1313–1320. [Google Scholar] [CrossRef]
- Torgrip, R.J.O.; Alm, E.; Åberg, K.M. Warping and alignment technologies for inter-sample feature correspondence in 1D H-NMR, chromatography-, and capillary electrophoresis-mass spectrometry data. Bioanal. Rev. 2010, 1, 105–116. [Google Scholar]
- Zheng, M.; Lu, P.; Liu, Y.; Pease, J.; Usuka, J.; Liao, G.; Peltz, G. 2D NMR metabonomic analysis: a novel method for automated peak alignment. Bioinformatics 2007, 23, 2926–2933. [Google Scholar] [CrossRef]
- Robinette, S.L.; Ajredini, R.; Rasheed, H.; Zeinomar, A.; Schroeder, F.C.; Dossey, A.T.; Edison, A.S. Hierarchical alignment and full resolution pattern recognition of 2D NMR Spectra: application to nematode chemical ecology. Anal. Chem. 2011, 83, 1649–1657. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Vu, T.N.; Laukens, K. Getting Your Peaks in Line: A Review of Alignment Methods for NMR Spectral Data. Metabolites 2013, 3, 259-276. https://doi.org/10.3390/metabo3020259
Vu TN, Laukens K. Getting Your Peaks in Line: A Review of Alignment Methods for NMR Spectral Data. Metabolites. 2013; 3(2):259-276. https://doi.org/10.3390/metabo3020259
Chicago/Turabian StyleVu, Trung Nghia, and Kris Laukens. 2013. "Getting Your Peaks in Line: A Review of Alignment Methods for NMR Spectral Data" Metabolites 3, no. 2: 259-276. https://doi.org/10.3390/metabo3020259
APA StyleVu, T. N., & Laukens, K. (2013). Getting Your Peaks in Line: A Review of Alignment Methods for NMR Spectral Data. Metabolites, 3(2), 259-276. https://doi.org/10.3390/metabo3020259