Abstract
Numerous works focus on the data privacy issue of the Internet of Things (IoT) when training a supervised Machine Learning (ML) classifier. Most of the existing solutions assume that the classifier’s training data can be obtained securely from different IoT data providers. The primary concern is data privacy when training a -Nearest Neighbour (-NN) classifier with IoT data from various entities. This paper proposes secure -NN, which provides a privacy-preserving -NN training over IoT data. It employs Blockchain technology with a partial homomorphic cryptosystem (PHC) known as Paillier in order to protect all participants (i.e., IoT data analyst C and IoT data provider P) data privacy. When C analyzes the IoT data of P, both participants’ privacy issue arises and requires a trusted third party. To protect each candidate’s privacy and remove the dependency on a third-party, we assemble secure building blocks in secure -NN based on Blockchain technology. Firstly, a protected data-sharing platform is developed among various P, where encrypted IoT data is registered on a shared ledger. Secondly, the secure polynomial operation (SPO), secure biasing operations (SBO), and secure comparison (SC) are designed using the homomorphic property of Paillier. It shows that secure -NN does not need any trusted third-party at the time of interaction, and rigorous security analysis demonstrates that secure -NN protects sensitive data privacy for each P and C. The secure -NN achieved , , and precisions on BCWD, HDD, and DD datasets. The performance of secure -NN is precisely similar to the general -NN and outperforms all the previous state of art methods.
1. Introduction
At present, smart cities include more innumerable superior IoT infrastructures [1] to manage their component efficiently [2]. A tremendous volume of information accumulated from numerous IoT devices stationed in different city areas, such as medical health, agriculture, transportation, and energy transmission [3]. A large volume of reforms prompted by ML technology were proposed to handle the issues emerging from processing obligations of IoT data [4]. -means [5] and -NN [6] are pre-eminent unsupervised and supervised learning models, respectively, that can effectively implement data classification amid all ML models [7]. Therefore, these ML models have been used in various specialties to answer real-world classification dilemmas in IoT-enabled smart health. Considering the synopsis of individual fitness and healthcare records observed by wearable IoT sensors, Refs. [8,9,10] could be fed to a -NN classifier for fitness analysis. -NN clustering classifier is also deployed in the field of network interference apprehension to recognize abnormalities from a group of traffic data derived from interactions among IoT devices [11].
The structure of supervised ML classifiers such as -NN or Support Vector Machine (SVM) is denoted as the training stage, which trains a specific classifier to find underlying patterns with a defined output variable. The higher the significance of training samples increased, the more the performance of the ML classifier enhanced [12,13]. An individual such as a network provider or a hospital entity often owns the dataset required for training. It is generally bounded in courses of sample distinctiveness and amount. It is necessary to train the ML model classifiers with an efficient and effective mechanism using a unification of sample sets collected from various entities. Various entities are generally opposed to sharing their datasets for training as there are many safety concerns in terms of ownership, integrity, and data privacy:
- Most of the training phases manipulate intimate data samples such as medical data reported from clinical wearable IoT devices, resulting in the leakage of private or sensitive and confidential information at the time of training tasks.
- Latent invaders may cause unauthorized modification of data records by altering or tampering at the time of the data sharing process, resulting in an inaccurate classification of the ML model.
- The data provider may lose authority, and replication of the shared datasets may occur as datasets are available to the associates.
To secure the data privacy issue of individual data providers, most of the present solutions [14,15,16,17] focused on cryptography and differential privacy. Those solutions assumed that the data required for training could be obtained securely from various data providers to classify and analyze. Issues of ownership and data integrity were focused on trivially. However, solutions are invalid due to potential attacks, for most cases, in reality. This paper uses the Blockchain technology to build a reliable data-sharing terrace, which can cover the gap between realistic confinement and typical prediction. In general, a shared filing scheme intended to permit the distribution of tamper-proof records among various individuals is called a Blockchain [18]. Auditing is enabled on Blockchain for immutable records, which confirms the ownership of recorded data.
Some works are focused on privacy-preserving -NN computation, search, query, and classification [19,20,21,22,23,24,25,26,27,28]. None of these works used Homomorphic encryption with Blockchain in order to secure sensitive information. To consolidate Blockchain into ML training method is laborious but encouraging. The first difficulty is to outline a suitable training data format convenient for adjusting on Blockchain to secure each data provider’s privacy. The second difficulty is to develop the training algorithm that establishes an accurate -NN classifier using the Blockchain’s recorded data and secures sensitive information. Secure SVM [29] was proposed to address the problems mentioned earlier. In the proposed method, they employed a Blockchain-based, privacy-preserving training algorithm for the SVM using encrypted data of IoT devices from Smart Cities. A public-key cryptosystem is applied by Secure SVM to protect the privacy of the data, which are encrypted by the private keys of data providers. However, Secure SVM requires too many calculations, comparison, time, and space in order to analyze the health data. In most medical health research, -NN outperformed SVM in terms of performance and time complexity [30,31,32].
To handle the above challenges, we propose secure -NN, a privacy-preserving -NN schema based on Blockchain and encrypted data of IoT devices. A public-key cryptosystem called Paillier has been employed to shield the IoT data privacy, which is encrypted by the own private key of the respected data providers. Paillier is an additive homomorphic cryptosystem (HC), which is very efficient in terms of time complexity for encryption and decryption than any other algorithm, such as Rabin, RSA, and Goldwasser-Micali [33]. Handling encrypted data could be a problem because of the tremendous amount of intercommunications. However, -NN can handle these circumstances as there is no separate optimization algorithm. -NN has essential procedures such as polynomial operations and comparison. We design secure building blocks SPO (addition and subtraction), SC, and SBO by using the homomorphic properties of Paillier for secure -NN. With the above building blocks, all iterations of secure -NN do not need any trusted third party at the time of interaction, which significantly lessens the risk of a data breach.
The main contribution of this paper is as follows.
- To establish protected and trustworthy IoT data sharing, Blockchain technology is employed. All the IoT data are encrypted locally by the own private key of the respected data provider. The encrypted data are recorded on a Blockchain by uniquely formatted transactions.
- We designed protected building blocks, such as SPO (addition, subtraction), SBO, and SC using the PHC, i.e., Paillier, and developed a secure -NN training algorithm. There is no requirement for a trusted third-party.
- Rigorous analysis has been done to prove that the secure -NN can protect data privacy at the time of training, achieve similar accuracy as general -NN and outperform all the previous state of the art method.
The rest of the paper is articulated as follows. Related work and preliminaries are discussed in Section 2 and Section 3, respectively. The system overview is presented in Section 4. Section 5 summarized the proposed method. Analyzation of confidentiality issues and evaluation of the proposed scheme are explained in Section 6 and Section 7, respectively. Finally, in Section 8, the paper is concluded.
2. Related Work
Supervised learning contains two phases: the training phase, where the ML model learns from a given set of labeled specimens, and the classification phase, where labels are the result for a given sample with maximum possibility. Thus, current research on privacy-preserving ML can be divided into two sections, namely privacy-preserving ML training and privacy-preserving ML classification.
2.1. Privacy-Preserving ML Training
In most cases, multiple parties are involved when training an ML model, which results in the privacy issue of the IoT data. The main goal is to protect the data provider’s IoT data from being discovered by others at the time of training an ML model. During the last decade, numerous work have been done on this category [15,34,35,36,37,38,39,40] and our work focus here.
There are many methods used to secure data privacy in the publishing stage [41,42,43], but the most common approach is Differential privacy (DP) [15]. It assures the protection of published data by combining vigilantly computed distress to the fundamental data. The DP-based deep learning method was proposed by Abadi [15]. They developed a system to jointly train a neural network with preserving the sensitive information of their datasets. DP-based solutions can achieve more excellent computational performance. These solutions can execute calculations over plain text data. There are some limitations also: Firstly, due to perturbations, the quality and integrity of the training data are reduced significantly. Secondly, each training data’s sensitive information is publicly exhibited, so only disruptions are not enough to effectively secure data privacy. The privacy budget parameter is inversely proportional to the model accuracy but directly proportional to data privacy protection.
ML training achieves reliability and provides privacy guarantee on encrypted IoT data using homomorphic encryption, and it allows calculations on ciphertext and preserves the correctness of the data. In order to train various ML models, different protected methods based on HC have been proposed, such as SVM [29,34], Logistic Regression [35,36], Decision Tree [38], and Naive Bayes [37]. Secure protocols [34] have been developed for secure addition and subtraction depending on Paillier, which results in a Secure SVM training algorithm. Due to the computational limitation of Paillier, the authors developed an authorization server which worked as a trusted third-party.
PHC method can reach higher data privacy with more efficiency than the Fully homomorphic encryption (FHE) system. The PHC is much more practical than FHE for the addition and multiplication operations. Complicated calculations can be employed with a trusted third-party [34]. Without that, the model will be inaccurate due to the approximation of complex equations with an individual computational operation [39,40]. On the other hand, the calculations of FHE is costly in terms of time and space complexity. Therefore, existing uses of FHE is prohibitive from the scenario of encryption and forecast. As a result, they are unrealistic in terms of application.
2.2. Privacy-Preserving ML Classification
Usually, two different parties interact in a classification as a service scenario. One holds the data sample, and the other holds the ML model. It is not safe to reveal sensitive data to an unreliable ML model owner for a data owner who wants to know the classification result. On the other hand, the model owner may decline to share the classification result as the asset value is too high for the service provider.
Some existing solutions are [14,17,44,45,46] for developing an effective solution in order to secure the privacy of both parties. A method was proposed by Wang et al. [45] to classify encrypted images based on multi-layer learning. The authors used a public classifier but considered that the image data should be secure. A privacy-preserving nonlinear SVM method was proposed by Zhu et al. [46] for online-based medical prediagnosis. The authors can protect both individual information of the health record and the SVM model with their design. Rahulamathavan et al. [17] proposed a privacy-preserving SVM data classification system. It can securely classify multiclass datasets. In this schema, the client input data samples are anonymous to the server. At the same time, clients are also unaware of the server-side classifier during the classification process. A group of classification protocols was developed using the HC techniques for employing ML’s simple classifiers on encrypted data, such as Naive Bayes, hyperplane decision, and decision trees [14,44].
All the above studies employed standard ML classifiers and developed building blocks to assemble a privacy-preserving classification method. The calculations at the time of training an ML classifier are much complex compared to the classification phase. Those building blocks might be useless due to the complexity of the training algorithm.
2.3. The Novelty of This Paper
Earlier research on secure -NN focused on any specific domain such as data confidentiality, secure query, secure search, secure computation, and secure classification [19,20,21,22,23,24,25,26,27,28]. None of them keep track of all the transactions, and most of them considered that the -NN model is already trained. In this study, a partial cryptosystem known as Paillier is employed with Blockchain technology to handle the issues related to ownership, integrity, and data privacy at the time of training -NN classifiers based on the data from various data providers. To be specific, all IoT data from individual data providers is encrypted using Paillier then registered on a distributed ledger. Any data analyst can obtain encrypted data by interacting with the respective data provider and train the -NN classifier. The data analysts can never obtain the plaintext of IoT data on the Blockchain. The secure protocol of operation in -NN is developed to conduct training tasks with encrypted data, i.e., SPO (addition/subtraction), SBO, and SC. A privacy-preserving -NN training algorithm, secure -NN, is proposed based on this building block, and there is no need for a trusted third party. The secure -NN can train -NN classifiers without the loss of accuracy as the training is based on Paillier.
Two well-known security definitions are used as security goals: secure two-party computation [47] and modular sequential composition [48]. The propose method illustrates that the individual data provided is inadequate to acquire any information about other data provider’s data. Simultaneously, the model parameters of data analysts are secure from the knowledge of any data providers during the training process.
3. Preliminaries
This section describes all notations, background ideas, and related technologies of this research.
3.1. Notation
A dataset D, which consists of m records, where and is the i-th record in D and is the label of the corresponding and . Define d and as two relevant parameters of -NN. In this paper, we use a PHC named Paillier as the cryptosystem, and let represent the encryption of message under Paillier. Notations are summarized in Table 1.

Table 1.
Notations.
3.2. Homomorphic Cryptosystem
Cryptosystems are mainly based on three algorithms: Generation of key (KeyGen), data encryption (Enc), and data decryption (Dec). In public-key cryptosystems, a pair of keys (PK; SK) is used, such as for encryption and decryption public key (PK) and private key (SK) are used respectively. A cryptosystem property, which can map the operations over ciphertext to the corresponding plaintext without being aware of the decryption key, is known as Homomorphic. Definition 1 describes the homomorphic property of the cryptosystem.
Definition 1.
(homomorphic [33]) A method of public-key encryption (Gen, Enc, Dec) can be homomorphic only if for all n and all (PK; SK) output by (), it is possible to define groups (depending on PK only) such that:
- and are the message space and all ciphertexts outcome respectively by are elements of .
- is held for any , any output by , and any output by .
A partial homomorphic cryptosystem known as Paillier is being used in the proposed schema. It is a public key cryptography method with the partial homomorphic property as it allows only two operations, secure addition and subtraction. Let p and q are n-bit primes, . N and (Let, be an integer. Then is an abelian group under multiplication modulo N. Define , the order of the group .) are the public key and private key, respectively. is the encryption function in Paillier, where and is the decryption function. More details about Paillier is explained in [32].
3.3. -Nearest Neighbors (-NN)
-nearest neighbors (-NN) [6] clustering is a type of supervised ML algorithm, used for classification and predictive regression problems. There is no specific training phase and uses whole training data [49] during classification because of that, it is called a lazy learning algorithm. It does not assume anything about the underlying data. Distance d needs to be calculated in order to find the designated centroid . There are different methods to find the distance in -NN algorithm, i.e., Euclidean distance (Equation (1)), Manhattan distance (Equation (2)), Cosine distance (Equation (3)), etc. methods. In this study, we will use Manhattan distance . Let, . Algorithm 1 illustrate the entire process.
| Algorithm 1: Basic NN |
 |
3.4. Blockchain System
Blockchain is a public and shared ledger, consists of a list of blocks. It is developed in cryptocurrency systems for registering transactions such as Bitcoin. It ensures secure transactions among untrusted participants. Various Blockchain platforms are: Ethereum, HyperLedger, etc., have been employed in different real-life sectors. According to the access restriction of users in Blockchain, Blockchain platforms are classified into consortium Blockchains, private Blockchains, and public Blockchains.
There are various advantages of Blockchain:
- Decentralized: It is developed on a peer-to-peer network as a shared ledger, and there is no requirement of a trusted third-party.
- Tamper-proof: Consensus protocols are employed by Blockchain, such as Proof-of-Work (PoW). Thus, Data manipulation is impractical.
- Traceability: The rest participants can easily verify the transactions between two parties in a Blockchain system.
Despite having many advantages, Blockchain has the vulnerability of data privacy to skilled attackers. Initially, all transactions are registered as plain texts in blocks, which exposes the transaction’s vital information to other participants, and adversaries [50]. Therefore, privacy and security issues must be handled cautiously when using Blockchain in terms of data sharing platform.
4. Problem Description
This segment illustrates the issues of secure -NN training across encrypted IoT data accumulated from various parties, which includes the system design, threat type, and design purposes.
4.1. System Design
A data flow IoT ecosystem is developed and shown in Figure 1, including IoT devices, data providers, the Blockchain platform, and data analysts.
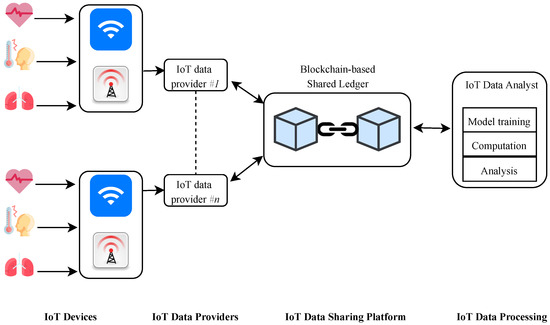
Figure 1.
System model of a data-driven IoT ecosystem.
- ZigBee, 3rd generation (3G)/4th generation (4G), and Wireless Fidelity (WiFi) are examples of the wired or wireless network through which IoT devices can sense and transmit valuable information, including medical data, smart cities, etc. In this study, due to the lack of computational capabilities, IoT devices will not participate in the data sharing and analysis processes.
- Data providers gather all the data from IoT devices within their range. All the data comprises sensitive information, so all the data are encrypted using partially homomorphic encryption by the data provider and registered in a Blockchain.
- To gather the encrypted IoT data from all data providers, the Blockchain-based IoT platform serves as a distributed database, where protocols are maintained, and all data are recorded in a shared ledger. The built-in consensus mechanism ensures the sharing of IoT data in a secure and tamper-proof way.
- IoT data analysts intend to get a rooted perspicacity within the data registered in the Blockchain-based platform by using the existing analyzing techniques. Data analysts will obtain encrypted data from corresponding data providers in order to train the NN classifiers.
4.2. Threat Type
Various latent threats exist over individual entities and at the time of their interactions, according to the system model description in Figure 1. This study focuses on the threats related to data privacy throughout the interaction between the data provider and data analysts. It is assumed that the data analyst is a curious but honest foe. To be more specific, the data analyst is honest for maintaining the protocol of predesigned ML training and curious regarding the contents of the data. Moreover, the data analyst strives to acquire further knowledge by analyzing the intermediate data at the time of computation on encrypted data.
The subsequent models of threat are considered based on the data analyst’s collected vital information with various attack inclinations mostly employed in the literature [51,52]. On the other hand, the data provider may also try to identify the data analyst’s model parameter from the intermediate data.
- Recognized Ciphertext Model. The data analyst can merely obtain the encrypted IoT data registered in the Blockchain Platform. The IoT data analysts can record intermediate outputs when training the secure algorithm, such as iteration steps.
- Recognized Background Model. The IoT data analyst expects to know more further details of shared data. However, from the shared ciphertext model, an IoT data analyst may gather more information by using her previous knowledge. To be more specific, the IoT data analyst can conspire with distinct IoT data providers to infer the sensitive information of other participants.
4.3. Design Purposes
Consider more than one IoT data provider and data analyst conspire to steal other participant’s privacy. Assume that all the participants as a curious-but-honest foe who executes protocol honestly but has an interest in other’s private information. Any number of participants may conspire with each other. The proposed method aims to shield the individual participant’s privacy and securely train the -NN classifiers. The security goals are as follows:
- At the time of encountering curious-but-honest foe, the data analyst and individual data provider’s data are protected from disclosure.
- At the time of encountering more than one parties conspire with each other, the data analyst and individual data provider’s privacy also will be protected from disclosure.
5. The Construction of Secure -NN
This section illustrates the system specifications of the proposed privacy-preserving -NN training method over block-chain-based encrypted IoT data.
5.1. System Overview
For clearness, consider that a data analyst intents to train -NN classifier based on the data gathered from various IoT data providers. Figure 2 illustrates the system overview, where the individual data provider preprocessed IoT data instances, encrypts them locally using their own private key, and register those encrypted data in the Blockchain-based distributed ledger. Present key supervision mechanisms [53,54,55] can be applied to handle the encryption abilities of data providers. The IoT data analyst can train a -NN classifier by collecting the encrypted data registered in the public ledger and erect a protected algorithm with the building blocks of SPO, SBO, and SC. At the time of the training process, it is essential to interact between IoT data analyst and IoT data provider for reciprocating intermediate outcomes.
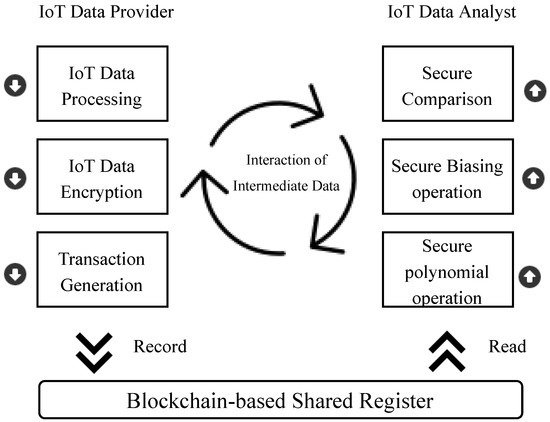
Figure 2.
System overview of Secure -NN.
However, it is essential to mention that many comparison tasks are necessary to perform the training on an -NN model. To accomplish the comparison task on encrypted data is extremely expensive, costly, and time-consuming. On the other hand, accurate intermediate data cannot be shared because the parameters of -NN algorithm are easy to guess. There is a high possibility that in this situation, data analysts can be successful at guessing the original data. Therefore, to reduce the algorithm’s complexity, to make the method more realistic and protected from the privacy breach of both data providers and data analysts, we introduce a SBO. The data provider adds a small amount of bias () to secure the data’s privacy at the time of sharing the intermediate data. This small amount of discrimination does not cause any significant change in the classification process.
5.2. Encrypted Data Sharing via Blockchain
To aid model training, without the sacrifice of generality, consider that the same training task’s data instances have been locally preprocessed and designated with the corresponding feature vectors [16].
A unique transaction arrangement is defined in order to save the encrypted IoT data in the Blockchain. The proposed transaction structure primarily consists of two fields: input and output.
The input terminal comprises:
- The address of the data provider
- The encrypted version of data
- Name of the IoT device from where the data is generated
The corresponding output terminal holds:
- The address of the data analyst
- The encrypted version of data
- Name of the IoT device from where the data is generated
Hash value will be the addresses of the data provider and data analyst, and the encrypted data is determined from the homomorphic encryption, i.e., Paillier. Depending on the consideration that the length of the private key is 128 bytes, the length of the individual encrypted data instance is set to 128 bytes and stored in the Blockchain. The segment length of the IoT device type is 4 bytes.
The node serving as the data provider in the Blockchain network broadcasts it in a P2P system after assembling a new transaction, where the miner nodes will validate the correctness of the operation. A specific miner node can package the transaction in a new block and adding the block to the existing chain using current consensus algorithms, i.e., the PoW mechanism. Multiple transactions can be registered in a single block.
5.3. Building Blocks
Section 4 already specified that the goal is to secure the privacy of various IoT providers and design a privacy-preserving algorithm for training -NN models over multiple private datasets afforded by diverse IoT providers.
5.3.1. -NN
Several methods are available in order to calculate the distance, which is a model parameter of the -NN. In this research, Manhattan distance (Equation (2)) is considered due to its simplicity in calculation. Algorithm 1 illustrate the entire process.
5.3.2. Secure Polynomial Operations (SPO)
In the proposed secure -NN training schema, we develop secure polynomial addition and subtraction to securely train the -NN model using the homomorphic property of Paillier’s. Reliable additions, secure subtractions and multiplication can be achieved straightforward. The homomorphic properties in Paillier can be defined as: , and the homomorphic properties in case of subtraction can be described as:. is known as the modular multiplicative inverse, which can calculate in Paillier. function can compute , . Therefore, using ciphertext manipulation, the secure polynomial multiplication can be achieved, as shown in Equation (4).
Similarly, the secure polynomial division can be achieved, as shown in Equation (5).
However, this research need only secure polynomial addition and subtraction. Thus, the secure polynomial addition and subtraction are statistically indistinguishable, as Paillier is statistically indistinguishable [33].
5.3.3. Secure Biasing Operations (SBO)
In line no. 6 of Algorithm 2, data provider P calculate distance using SPO. Next step is to send the encrypted distance to the data analyst C. If the data provider P sent the encrypted distance to the data analyst C then C will decrypt it and try to guess the private data of the data provider. There is a high possibility of success as the data analyst C initiated the clustering point. Therefore, to protect the privacy of the data provider P’s data at the time of training the -NN algorithm, we introduce the secure biasing operation (SBO). P will add a small amount of bias using SPO before sending the data to C in order to protect the data privacy. The bias will be unknown to C.
| Algorithm 2: Secure Comparison |
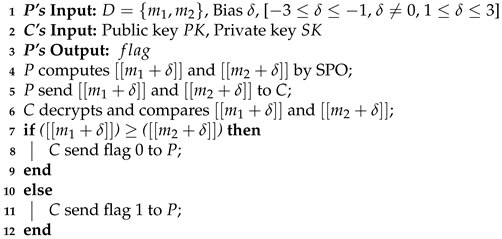 |
In this study, the range of bias will depend on the coefficient of variation (), where = = . Standard Deviation and Mean is computed using, = and = respectively. Here n is the total number of data and stands for each data of the data-set. CV value greater than or equal to one, means that the data is scattered. CV value less than one, means that the is not scattered. Therefore, at the time of the experiment, various values for bias were chosen. The range was within , when and , when . We found that bias range and , gives proper classification results, when CV ≥ 1 and CV < 1, respectively. Therefore, If the coefficient of variation is greater than or equal to 1, , than set the range of to [] and On the other hand, if the coefficient of variation is less than 1, , than set the range of to []. Note that the value of will never be equal to ().
5.3.4. Secure Comparison (SC)
The secure comparison in the proposed method is illustrated as the comparison between two encrypted numbers and . For participants A and B engage in the secure comparison algorithm, neither parties can obtain real information. Our secure comparison algorithm protocol is exhibited in Algorithm 2, and the security proof is described in Section 6.
Proposition 1.
(Security of Secure Comparison Algorithm). Algorithm 2 is secure in the curious-but-honest model.
To develop SBO, we use the secure polynomial operation (mainly addition and subtraction) based on the homomorphic property of Paillier’s. A small amount of bias (where [, , ]) is encrypted and added with by data provider P using SPO (addition/subtraction). However, the data analyst C will never be able to extract the exact value of the bias value, or of the range, and this small amount of bias does not affect the classification task, which is shown in the performance evaluation Section 7. SBO ensures the privacy of the data provider P. If is positive, the definition will be:
Again, when is negative, the definition will be:
5.4. Training Algorithm of Secure -NN
For protected optimum design parameters, we outline a privacy-preserving -NN training algorithm. Assume there is a single IoT data analyst C and n number of data providers P. Algorithm 3 specifies the training algorithm for secure -NN. In Algorithm 3, the -NN model parameters and sensitive data of IoT data providers are confidential. At the time of facing any collusion or curious-but-honest adversaries, individual members cannot infer any vital information of another member from the algorithm’s execution process’s intermediate outcomes. Section 6 illustrates the security proofs for Algorithm 3.
Proposition 2.
(Security of Privacy-Preserving NN Training Algorithm). Algorithm 3 is secure in the curious-but-honest model.
| Algorithm 3: Secure NN Training Algorithm |
 |
6. Security Analysis
The security analysis manifests in this section under the identified ciphertext model and the public background model. Two security definitions were followed: secure two-party computation [47] and modular sequential composition [48]. A satisfied, protected two-party calculation protocol is safe in the face of curious-but-honest foes, and modular sequential composition implements a way to develop secret protocols in a modular way. Security proof of the proposed algorithm is described based on these two definitions.
6.1. Background of Security Proof
The notation in the article [14] was followed: Let, F is computed by a protocol and be a polynomial function; Input of A’s and B’s are a and b respectively using , desire to calculate ; A’s view is the tuple = where are the message received by A at the time of execution. B’s view is defined in a similar manner. and are the outputs of A and B respectively. ’s global outcome is =.
Definition 2.
(Secure Two-Party Computation [47]). If for all possible inputs and simulators and holds the following properties (≈ denotes computational indistinguishability against probabilistic polynomial-time adversaries with the negligible advantage in the security parameter λ.), only then a protocol π privately computes f with statistical security:
The sequential modular composition’s fundamental idea is that: protocol is run to call an ideal functionality F by n participants, e.g., to calculate F privately, A and B send their inputs to a trusted third-party and receive the result. If the secure two-party computation is satisfied by the protocol , and the same functionality as F can be achieved by protocol privately, then the protocol of in can replace the ideal protocol for the functionality F; Then, the latest protocol is protected and safe under the curious-but-honest model [14,48].
Theorem 1.
(Modular Sequential Composition [37]). Let the two-party probabilistic polynomial time functionalities be and is calculated by the protocols in the presence of curious-but-honest adversaries. Let, two-party probabilistic polynomial time functionality be G and G is securely computed in the by a protocol π - hybrid model in the presence of curious-but-honest adversaries. Then, securely calculate G in the presence of curious-but-honest adversaries.
6.2. Security Proof for Secure Comparison
Two entities are involved in Algorithm 2: P and C. The function is
Proof of Proposition 1.
The view of P is
Hence, the simulator:
where and are encrypted by and the confidentiality of and are equivalent to the Paillier cryptosystem. Therefore, P cannot infer the value directly.
The view of C is
Then, runs as follows:
The bias is unknown to C, for that reason C would never be able to get the real and from and . After comparison bewteen and , C will return a flag with a value 0, if ≥ , other wise value of flag will be 1. C is honest in following the method’s protocols. Therefore, C would never infer the value directly. □
6.3. Security Proof for Secure -NN Training Algorithm
IoT data providers P and an IoT data analyst C, are the roles involved in Algorithm 2. Individual IoT data providers function in the same manner. Every one of the data providers will meet the security requirements if we can prove that one of them meets the security requirements. The function is:
Proof of Proposition 2.
Individual IoT data provider’s P view is
where and are encrypted by , the confidentiality of and will be equivalent to the cryptosystem Paillier. So none of the IoT data providers can infer the value directly.
The view of C is
Now, the confidentiality of needs to be discussed, i.e., whether the IoT data analyst can predict the private data of individuals IoT data providers from the value. Clearly, the value is no-solution for the unknown . The IoT data analyst may try to calculate unknown using the known distance and centroid . It is not possible for IoT data analysts to identify the point of IoT data providers because the distance is added with bias value and the data analyst has no idea about the bias value or its range. Even with the brute force cracking, it is not possible to get the real value of dataset D. Consider that individual IoT data provider consists of a small dataset, which is dimensional, 100 instances, and each dimension is 32 bits (Typically, 4 bytes (32-bit) memory space is occupied by single-precision floating-point ). Under this situation, the probability of IoT data analyst successful guessing is , which is a negligible success probability [33]. □
We obtain the security of Algorithm 3 using modular sequential composition, as SPO, SBO, and SC are used in Algorithm 3, so it is secure in the curious-but-honest model.
7. Performance Evaluation
In this section, the performance of secure -NN is evaluated based on efficiency and accuracy through extensive analysis using real-world dataset. Firstly, experiment settings are described, and the effectiveness and efficiency are demonstrated by the experimental results.
7.1. Experiment Setup
This segment discusses the testbed, dataset, and all other tasks for data preprocessing and experimental environment.
7.1.1. Testbed
In the proposed model, individual IoT data providers gather all the data in their domain from the IoT devices and perform data encryption. The experiments are executed on MacBook Pro equipped with an Intel Core i5 processor (2.5 GHz), memory (4 GB 1600 MHz DDR3), serving as IoT data providers and IoT data analysts simultaneously. The SPO, SBO, SC, and the Secure -NN are implemented in the Platform: Google’s Colaboratory; Language: Python 3; Browser: Google Chrome.
7.1.2. Dataset
This study uses three real-world datasets, namely Breast Cancer Wisconsin Data Set (BCWD), Heart Disease Data Set (HDD), and Diabetes Data Set (DD) [56,57]. These datasets are publicly available from the UCI machine learning repository. The features of BCWD resembled a digitalized image of a breast mass and described characteristics of the cell nuclei present in the image. Each of the data instances is labeled as benign or malignant. The HDD and DD contain 13 and 9 numeric attributes, respectively. Instances are classified based on the types of heart diseases and diabetes symptoms. Table 2 represents the statistics of the dataset. We run 10-fold cross-validation to avoid overfitting or contingent results, and average results are recorded. 80% of the data has been selected for the model training and the remaining 20% for testing.

Table 2.
Statistics of Datasets.
7.1.3. Float Format Conversion
The general K-NN training algorithms perform on both integer and floating-point numbers based on the data set. However, all the operations of cryptosystems are done on integers. Therefore for safety purposes, we should perform format conversion into an integer representation. Let, D is a binary floating-point number, which is represented as, , according to the global standard IEEE 754 [where the sign bit is s, significant number is M and exponential bit E]. A data analyst may perform this format conversion during the implementation of secure -NN based on the dataset type.
7.1.4. Key Length Setting
The security of the public key cryptosystem is closely associated with the length, and a compact key may cause vulnerable encryption. A long key reduces the homomorphic operation’s efficiency, and a too-short key may cause the overflow of plaintext space during the homomorphic operations (i.e., the secure polynomial operation and secure biasing operation) on the ciphertext. Therefore, it is crucial to consider the length of the key in order to bypass the possibility of overflow. The Key of Paillier cryptosystem N is set to -bit in secure -NN.
7.2. Evaluation Parameters
We use three commonly used criteria for evaluating ML classifiers (Accuracy (6), Precision (7), Recall (8)).
where is the number of relevant ( the positive class) that are labeled precisely, is the numbers of irrelevant (the negative class) that are labeled correctly, is the numbers of relevant that are mislabeled and is the number of irrelevant that are mislabeled in the test outcomes.
The general -NN was implemented using raw Python language in order to demonstrate that secure -NN does not lessen the accuracy upon preserving the individual IoT data provider’s privacy and securely training the classifier. The main focus is to train the classifier securely. For that reason, the train parameters are not adjusted, and default parameters are used. The results of precision and recall are summarized in Table 3.

Table 3.
Summary of performance.
The performance of Secure -NN is almost similar to standard -NN and has better performance than SVM [29]. However, the data provider must be careful about the bias value because a larger bias may reduce the classifier’s performance. The proposed design shows better robustness on both (discrete attributes and numerical attributes) datasets.
7.3. Efficiency
7.3.1. Building Blocks Evaluation
Table 4 illustrates the running time of the SPO with encrypted datasets on Algorithm 3. Table 4 also gives the time consumption of IoT data providers P and data analysis C, the total time consumption.

Table 4.
Performance of the building blocks in Secure -NN against Secure SVM.
According to the performance results in Table 4, secure -NN spend less than an hour with encrypted dataset BCWD, HDD, and DD at the time of training, which is an acceptable time consumption as a stand-alone algorithm. It is essential to mention that the general -NN is comparatively slower, so it is better not to train a -NN algorithm with a larger dataset at a time. We recommend that the reader convert the larger dataset into small portions and train the secure -NN. In our implementation, we used multi-threading in Python to control the run time of a larger dataset.
In this experiment, various P is simulated linearly. Therefore the P time shown in Table 4 is the accumulation of time consumed by different P. In a real-world application, various P can run their algorithms parallelly so that the time consumption of P and the total time consumption can be reduced. We believe Algorithm 3 to be useful for real-world sensitive applications. Confronting various datasets such as BCWD, DD (numerical attributes), and HDD (discrete attributes), secure -NN manifests satisfying robustness in time consumption.
7.3.2. Scalability Evaluation
Secure -NN believes that various IoT data providers are engaging and contributing data. We distribute the dataset into various identical sections to mimic the situation of different IoT data providers. We observe the fluctuations in time consumption to evaluate the scalability of the proposed scheme when various data IoT providers strive for the calculation. Cases are simulated during the number of IoT data providers rises from 1 to 5. The outcomes are represented in Figure 3. The X-axis represents the number of IoT data providers associated with the calculation, and the Y-axis represents the time consumption.
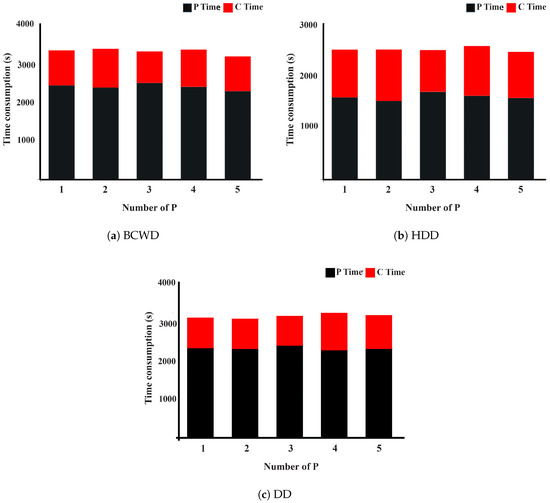
Figure 3.
Time consumption of secure -NN with different numbers of data providers P.
Theoretically, The time consumption of secure -NN is proportional to the amount of data and number of iterations in the comparison portion. If the total amount of data and data quality are fixed, the rise in the number of P will not affect the time consumption, and the time consumption of P or C remains the same at different numbers of P. There is a small vibration in the total time consumption when the number of P rises from 1 to 5 because the program’s run time gets disturbed as other host processes are used for the simulation.
8. Conclusions
This paper introduced a novel privacy-preserving -NN training method called secure -NN, which can handle data privacy and data integrity concerns. It employs Blockchain technology to train the algorithm in a multi-party scenario where the IoT data is received from various data providers. A partial homomorphic cryptosystem known as Paillier is applied to assemble an effective and reliable method. Efficiency and security of secure -NN are demonstrated in this study. The proposed method achieves almost similar accuracy to general -NN and outperforms the earlier state of the art. Future work includes developing a versatile structure that allows assembling a broad range of privacy-preserving ML training algorithms on a multi-party scenario with encrypted datasets.
Author Contributions
Data curation, R.U.H.; Funding acquisition, Q.J. and Q.Q.; Investigation, R.U.H.; Methodology, R.U.H. and A.S.M.T.H.; Project administration, A.S.M.T.H.; Software, R.U.H.; Supervision, A.S.M.T.H.; Validation, A.S.M.T.H., Q.J. and Q.Q.; Writing—original draft, R.U.H.; Writing—review & editing, R.U.H., A.S.M.T.H., Q.J. and Q.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research work is supported by Key-Area Research and Development Program of Guangdong Province under Grant No. 2019B010137002, and the National Key Research and Development Program of China under Grant No. 2020YFA0909100, the National Natural Science Foundation of China under Grants No. 61902385 and 61762062.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hasan, A.S.M.T.; Qu, Q.; Li, C.; Chen, L.; Jiang, Q. An Effective Privacy Architecture to Preserve User Trajectories in Reward-Based LBS Applications. ISPRS Int. J. Geo-Inf. 2018, 7, 53. [Google Scholar] [CrossRef]
- Vongsingthong, S.; Smanchat, S. Internet of Things: A review of applications & technologies. Suranaree J. Sci. Technol. 2014, 1, 359–374. [Google Scholar]
- Zhang, Y.; Yu, R.; Nekovee, M.; Liu, Y.; Xie, S.; Gjessing, S. Cognitive machine-to-machine communications: Visions and potentials for the smart grid. IEEE Netw. 2012, 26, 6–13. [Google Scholar] [CrossRef]
- Provost, F.; Kohavi, R. On applied research in machine learning. Mach. Learn. Boston 1998, 30, 127–132. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Soucy, P.; Mineau, G.W. A simple K-NN algorithm for text categorization. In Proceedings of the 2001 IEEE International Conference on Data Mining IEEE, San Jose, CA, USA, 29 November–2 December 2001. [Google Scholar]
- Barlow, H.B. Unsupervised learning. Neural Comput. 1989, 1, 295–311. [Google Scholar] [CrossRef]
- Anliker, U.; Ward, J.A.; Lukowicz, P.; Troster, G.; Dolveck, F.; Baer, M.; Keita, F.; Schenker, E.B.; Catarsi, F.; Coluccini, L.; et al. AMON: A wearable multiparameter medical monitoring and alert system. IEEE Trans. Inf. Technol. Biomed. 2004, 8, 415–427. [Google Scholar] [CrossRef]
- Baig, M.M.; Gholamhosseini, H. Smart health monitoring systems: An overview of design and modeling. J. Med. Syst. 2013, 37, 1–14. [Google Scholar] [CrossRef]
- Lee, H.; Choi, T.K.; Lee, Y.B.; Cho, H.R.; Ghaffari, R.; Wang, L.; Choi, H.J.; Chung, T.D.; Lu, N.; Hyeon, T.; et al. A graphene-based electrochemical device with thermoresponsive microneedles for diabetes monitoring and therapy. Nat. Nanotechnol. 2016, 11, 556–572. [Google Scholar] [CrossRef]
- Shen, M.; Wei, M.; Zhu, L.; Wang, M. Classification of encrypted traffic with second-order markov chains and application attribute bigrams. IEEE Trans. Inf. Forensics Secur. 2017, 12, 1830–1843. [Google Scholar] [CrossRef]
- Sun, C.; Shrivastava, A.; Singh, S.; Gupta, A. Revisiting unreasonable effectiveness of data in deep learning era. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 843–852. [Google Scholar]
- Shen, M.; Ma, B.; Zhu, L.; Mijumbi, R.; Du, X.; Hu, J. Cloud-based approximate constrained shortest distance queries over encrypted graphs with privacy protection. IEEE Trans. Inf. Forensics Secur. 2018, 13, 940–953. [Google Scholar] [CrossRef]
- Bost, R.; Popa, R.A.; Tu, S.; Goldwasser, S. Machine learning classification over encrypted data. In Proceedings of the Network and Distributed System Security Symposium, San Diego, CA, USA, 23–26 February 2014. [Google Scholar]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security; ACM: New York, NY, USA, 2016; pp. 308–318. [Google Scholar]
- Wang, Q.; Hu, S.; Du, M.; Wang, J.; Ren, K. Learning privately: Privacy-preserving canonical correlation analysis for cross-media retrieval. In Proceedings of the IEEE INFOCOM 2017—IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Rahulamathavan, Y.; Phan, R.C.W.; Veluru, S.; Cumanan, K.; Rajarajan, M. Privacy-preserving multi-class support vector machine for outsourcing the data classification in cloud. IEEE Trans. Dependable Secure Comput. 2014, 11, 467–479. [Google Scholar] [CrossRef]
- Li, H.; Zhu, L.; Shen, M.; Gao, F.; Tao, X.; Liu, S. Blockchain-based data preservation system for medical data. J. Med. Syst. 2018, 42, 141. [Google Scholar] [CrossRef]
- Qi, Y.; Atallah, M.J. Efficient privacy-preserving k-nearest neighbor search. In Proceedings of the 28th International Conference on Distributed Computing Systems, Beijing, China, 17–20 June 2008; pp. 311–319. [Google Scholar]
- Zhan, J.Z.; Chang, L.; Matwin, S. Privacy preserving k-nearest neighbor classification. IJ Netw. Secur. 2005, 1, 46–51. [Google Scholar]
- Ni, W.; Gu, M.; Chen, X. Location privacy-preserving k nearest neighbor query under user’s preference. Knowl. Based Syst. 2016, 103, 19–27. [Google Scholar] [CrossRef]
- Rong, H.; Wang, H.M.; Liu, J.; Xian, M. Privacy-preserving k-nearest neighbor computation in multiple cloud environments. IEEE Access 2016, 4, 9589–9603. [Google Scholar] [CrossRef]
- Songhori, E.M.; Hussain, S.U.; Sadeghi, A.R.; Koushanfar, F. Compacting privacy-preserving k-nearest neighbor search using logic synthesis. In Proceedings of the 2015 52nd ACM/EDAC/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 8–12 June 2015; pp. 1–6. [Google Scholar]
- Wu, W.; Parampalli, U.; Liu, J.; Xian, M. Privacy preserving k-nearest neighbor classification over encrypted database in outsourced cloud environments. World Wide Web 2019, 22, 101–123. [Google Scholar] [CrossRef]
- Park, J.; Lee, D.H. Privacy preserving k-nearest neighbor for medical diagnosis in e-health cloud. J. Healthc. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Yang, S.; Tang, S.; Zhang, X. Privacy-preserving k nearest neighbor query with authentication on road networks. J. Parallel Distrib. Comput. 2019, 134, 25–36. [Google Scholar] [CrossRef]
- Xiong, L.; Chitti, S.; Liu, L. K nearest neighbor classification across multiple private databases. In Proceedings of the 15th ACM International Conference on Information and Knowledge Management, New York, NY, USA, 5–11 November 2006; pp. 840–841. [Google Scholar] [CrossRef]
- Zhang, F.; Zhao, G.; Xing, T. Privacy-preserving distributed k-nearest neighbor mining on horizontally partitioned multi-party data. In International Conference on Advanced Data Mining and Applications; Springer: Berlin/Heidelberg, Germany, 2009; pp. 755–762. [Google Scholar]
- Shen, M.; Tang, X.; Zhu, L.; Du, X.; Guizani, M. Privacy-Preserving Support Vector Machine Training Over Blockchain-Based Encrypted IoT Data in Smart Cities. IEEE Internet Things J. 2019, 6, 7702–7712. [Google Scholar] [CrossRef]
- Huang, M.; Han, H.; Wang, H.; Li, L.; Zhang, Y.; Bhatti, U.A. A Clinical Decision Support Framework for Heterogeneous Data Sources. IEEE J. Biomed. Health Inform. 2018, 22, 1824–1833. [Google Scholar] [CrossRef] [PubMed]
- Can, Y.S.; Chalabianloo, N.; Ekiz, D.; Ersoy, C. Continuous stress detection using wearable sensors in real life: Algorithmic programming contest case study. Sensors 2019, 19, 1849. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.; Jha, N.K. A health decision support system for disease diagnosis based on wearable medical sensors and machine learning ensembles. IEEE Trans. Multi-Scale Comput. Syst. 2017, 3, 228–241. [Google Scholar] [CrossRef]
- Katz, J.; Lindell, Y. Introduction to modern cryptography. In CRC Cryptography and Network Security Series; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- FG-Serrano, F.-J.; N-Vzquez, A.; A-Martn, A. Training Support Vector Machines with privacy-protected data. Pattern Recognit. 2017, 72, 93–107. [Google Scholar] [CrossRef]
- Cock, M.; Dowsley, R.; Nascimento, A.C.A.; Newman, S.C. Fast, privacy preserving linear regression over distributed datasets based on pre-distributed data. In Proceedings of the 8th ACM Workshop on Artificial Intelligence and Security, AISec ’15; ACM: New York, NY, USA, 2015; pp. 3–14. [Google Scholar]
- Graepel, T.; Lauter, K.; Naehrig, M. Ml confidential: Machine learning on encrypted data. In International Conference on Information Security and Cryptology—ICISC 2012; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–21. [Google Scholar]
- Liu, X.; Lu, R.; Ma, J.; Chen, L.; Qin, B. Privacy-preserving patientcentric clinical decision support system on naive bayesian classification. IEEE J. Biomed. Health Inform. 2016, 20, 655–668. [Google Scholar] [CrossRef]
- Vaidya, J.; Shafiq, B.; Fan, W.; Mehmood, D.; Lorenzi, D. A random decision tree framework for privacy-preserving data mining. IEEE Trans. Dependable Secure Comput. 2014, 11, 399–411. [Google Scholar] [CrossRef]
- Aono, Y.; Hayashi, T.; Phong, L.T.; Wang, L. Privacy-preserving logistic regression with distributed data sources via homomorphic encryption. IEICE Trans. Inf. Syst. 2016, 99, 2079–2089. [Google Scholar] [CrossRef]
- Aono, Y.; Hayashi, T.; P, L.T.; Wang, L. Scalable and secure logistic regression via homomorphic encryption. In Proceedings of the Sixth ACM Conference on Data and Application Security and Privacy, CODASPY ’16; ACM: New York, NY, USA, 2016; pp. 142–144. [Google Scholar]
- Hasan, A.S.M.T.; Jiang, Q.; Chen, H.; Wang, S. A New Approach to Privacy-Preserving Multiple Independent Data Publishing. Appl. Sci. 2018, 8, 783. [Google Scholar] [CrossRef]
- Hasan, A.S.M.T.; Jiang, Q.; Li, C. An Effective Grouping Method for Privacy-Preserving Bike Sharing Data Publishing. Future Internet 2017, 9, 65. [Google Scholar] [CrossRef]
- Hasan, A.S.M.T.; Jiang, Q.; Luo, J.; Li, C.; Chen, L. An effective value swapping method for privacy preserving data publishing. Secur. Comm. Netw. 2016, 9, 3219–3228. [Google Scholar] [CrossRef]
- De Cock, M.; Dowsley, R.; Horst, C.; Katti, R.; Nascimento, A.; Poon, W.; Truex, S. Efficient and Private Scoring of Decision Trees, Support Vector Machines and Logistic Regression Models based on PreComputation. IEEE Trans. Dependable Secure Comput. 2017, 16, 217–230. [Google Scholar] [CrossRef]
- Wang, W.; Vong, C.; Yang, Y.; Wong, P. Encrypted image classification based on multilayer extreme learning machine. Multidimens. Syst. Signal Process. 2017, 28, 851–865. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, X.; Lu, R.; Li, H. Efficient and privacy-preserving online medical prediagnosis framework using nonlinear svm. IEEE J. Biomed. Health Inform. 2017, 21, 838–850. [Google Scholar] [CrossRef] [PubMed]
- Goldreich, O. Foundations of Cryptography: Volume 2, Basic Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Canetti, R. Security and composition of multiparty cryptographic protocols. J. Cryptol. 2000, 13, 143–202. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Gao, F.; Zhu, L.; Shen, M.; Sharif, K.; Wan, Z.; Ren, K. A Blockchain-based privacy-preserving payment mechanism for vehicleto-grid networks. IEEE Netw. 2018, 32, 184–192. [Google Scholar] [CrossRef]
- Shen, M.; Ma, B.; Zhu, L.; Du, X.; Xu, K. Secure phrase search for intelligent processing of encrypted data in cloud-based iot. IEEE Internet Things J. 2018, 6, 1998–2008. [Google Scholar] [CrossRef]
- Zhu, L.; Tang, X.; Shen, M.; Du, X.; Guizani, M. Privacy-preserving ddos attack detection using cross-domain traffic in software defined networks. IEEE J. Selec. Areas Commun. 2018, 36, 628–643. [Google Scholar] [CrossRef]
- Du, X.; Guizani, M.; Xiao, Y.; Chen, H. A routing-driven elliptic curve cryptography based key management scheme for heterogeneous sensor networks. IEEE Trans. Wirel. Commun. 2009, 8, 1223–1229. [Google Scholar] [CrossRef]
- Xiao, Y.; Rayi, V.K.; Sun, B.; Du, X.; Hu, F.; Galloway, M. A survey of key management schemes in wireless sensor networks. Comput. Commun. 2007, 30, 2314–2341. [Google Scholar] [CrossRef]
- Du, X.; Xiao, Y.; Guizani, M.; Chen, H.H. An effective key management scheme for heterogeneous sensor networks. Ad Hoc Netw. 2007, 5, 24–34. [Google Scholar] [CrossRef]
- Dheeru, D.; Karra, T.E. UCI Mach Learning Repository; University of California, School of Information and Computer Science: Irvine, CA, USA, 2017. [Google Scholar]
- Detrano, R.; Janosi, A.; Steinbrunn, W.; Pfisterer, M.; Schmid, J.; Sandhu, S.; Guppy, K.H.; Lee, S.; Froelicher, V. International application of a new probability algorithm for the diagnosis of coronary artery disease. Am. J. Cardiol. 1989, 64, 304–310. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).