Abstract
This work presents a new concept to implement the elliptic curve point multiplication (PM). This computation is based on a new modular arithmetic over Gaussian integer fields. Gaussian integers are a subset of the complex numbers such that the real and imaginary parts are integers. Since Gaussian integer fields are isomorphic to prime fields, this arithmetic is suitable for many elliptic curves. Representing the key by a Gaussian integer expansion is beneficial to reduce the computational complexity and the memory requirements of secure hardware implementations, which are robust against attacks. Furthermore, an area-efficient coprocessor design is proposed with an arithmetic unit that enables Montgomery modular arithmetic over Gaussian integers. The proposed architecture and the new arithmetic provide high flexibility, i.e., binary and non-binary key expansions as well as protected and unprotected PM calculations are supported. The proposed coprocessor is a competitive solution for a compact ECC processor suitable for applications in small embedded systems.
1. Introduction
Many resource-constrained systems, such as embedded systems, still rely on symmetric cryptography for message authentication. For digital signatures and key exchange protocols, asymmetric cryptography is required. However, software implementations of public-key algorithms such as the Rivest-Shamir-Adleman (RSA) algorithm or elliptic curve cryptography (ECC) may be too slow on small embedded systems. Such systems benefit from hardware assistance, i.e., coprocessors optimized for public-key operations. For applications in embedded systems, ECC algorithms dominate, because shorter key lengths are required [1,2,3,4,5,6].
In this work, we investigate the elliptic curve cryptography over Gaussian integers. Gaussian integers are a subset of complex numbers such that the real and imaginary parts are integers. Due to the isomorphism between Gaussian integer rings and rings over ordinary integers [7,8], this principle is suitable for many cryptographic systems. It was shown in [9,10,11,12] that a significant complexity reduction can be achieved for the RSA cryptographic system using Gaussian integers. Similarly, Rabin cryptographic system was previously considered over Gaussian integers in [13,14]. In the context of ECC, arithmetic over complex numbers was proposed to speed up the point multiplication [15,16,17,18,19]. However, to the best of our knowledge, no ECC hardware implementation over Gaussian integers exists. We propose a compact ECC processor design and demonstrate that the Gaussian integer arithmetic provides high flexibility.
The operation that dominates the execution time of ECC algorithms is the point multiplication, i.e., , where P is a point on the elliptic curve and k is an integer. The point multiplication is typically implemented based on the binary expansion of the integer k with binary digits , where r is the length in bits and is the binary representation of the key (the integer k). Using the Horner scheme the point multiplication can be calculated as
with the double-and-add method [17]. This method requires two different point operations, the point addition and the point doubling operation.
Alternatively, -adic expansions of the integer k with a non-binary basis were proposed to speed up the point multiplication (PM) and to improve the resistance against attacks [20,21,22,23,24,25]. This -adic expansion results in the point multiplication
where the digits can be elements from complex number fields such as Gaussian, Eisenstein, or Kleinian integers depending on the basis . Publications on hardware designs for non-binary-base expansions mainly consider implementations for extension fields [26,27,28]. In [27], a multiple-base expansion and arithmetic over Kleinian integers are used. The approach in [26,28] is based on a ternary instead of a binary expansion. The corresponding point multiplication has a run-time of point additions and Frobenius mappings . This point multiplication with the ternary basis is much faster than with a binary basis because the point-doubling operation is replaced by a simple Frobenius mapping (Frobenius endomorphism) . For any point this mapping operation results in the point , which requires only squaring of the field elements x and y. In [26,28], arithmetic over binary extension field is considered, where the squaring operation is very efficient [29,30].
It was demonstrated in [22,24,25,31,32,33,34] that non-binary expansions are beneficial to harden ECC implementations against attacks (SCA). Hardware implementations of the elliptic curve point multiplication are prone to SCA. There exist different attacks in the literature such as timing attacks (TA), simple power analysis (SPA), differential power analysis (DPA), refined power analysis (RPA), zero value analysis, and methods based on machine learning [17,34,35,36,37,38,39,40].
In this work, we consider an endomorphism for prime fields [17], where the prime field is represented by Gaussian integers. Hardware implementations can benefit from arithmetic over Gaussian integers and non-binary expansion. In particular, we consider the PM for Gaussian integers, where both the key as well as are Gaussian integers. The material in this paper was presented in part at the Zooming Innovation in Consumer Electronics International Conference 2020 [41]. In [41] a new algorithm for the -adic expansion of the key k was presented. The resulting expansion increases the robustness against TA and SPA and reduces the required memory size and the computational complexity for a protected PM. In this study, we propose an ECC coprocessor design for resource-constrained systems which employs a new concept for the Montgomery modular arithmetic [42]. The proposed processor provides high flexibility, because it supports binary and -adic key expansions and different PM algorithms. An unprotected PM with binary key expansions can reduce the latency for applications where only a public key is employed, e.g., the verification of digital signatures according to the NIST standard [43]. On the other hand, -adic expansions can reduce the computational complexity and memory requirements for calculations protected against SCA. This is beneficial for applications where the secret key is used, e.g., for the elliptic curve Diffie-Hellman key exchange [17]. We demonstrate that the arithmetic over Gaussian integers can be implemented as efficiently as ordinary Montgomery modular arithmetic over prime fields. The main aim of this work is to demonstrate that Gaussian integer arithmetic is a competitive solution for compact ECC processor designs.
This publication is organized as follows. In Section 2, we review the Gaussian integers as well as the ECC point multiplication for binary and -adic expansions. The resistance of the PM implementation against attacks is discussed in Section 3. The Montgomery arithmetic over Gaussian integers is considered in Section 4. It is demonstrated that the key expansion employing Gaussian integers reduces the memory requirements and computational complexity compared with other -adic expansions. In Section 5, we introduce the architecture of the hardware implementation that supports Gaussian integer arithmetic. We discuss area requirements and throughput results for field-programmable gate array (FPGA) implementations in Section 6. Finally, we conclude our work in Section 7.
2. Point Multiplication over Gaussian Integers
In this section, we briefly review the Gaussian integers and the elliptic curve point multiplication for the ordinary binary representation of the key. We demonstrate that the point multiplication over Gaussian integers with a -adic key expansion can reduce the computational complexity. Furthermore, we discuss suitable projective coordinates.
2.1. Gaussian Integers
Many ECC applications [5,6,32,44,45,46,47,48] consider arithmetic operations over ordinary integer fields. On the other hand, it was previously shown that Gaussian integers are suitable for ECC applications [42]. In this section, we review some important properties of the Gaussian integers.
Gaussian integers are a subset of the complex numbers with integers as real and imaginary parts. The set of Gaussian integers is typically denoted by . The modulo function of a Gaussian integer with and is defined as
where is the complex divisor and its conjugate. The brackets denote rounding to the closest Gaussian integer [7], i.e., for we have .
For primes p of the form , the set
is a finite field isomorphic to a prime field over ordinary integers [7]. Hence, these sets are suitable for ECC applications. In this case, p is the sum of two perfect squares, i.e., and with integers a, b. An algorithm for finding a, b for a given prime is provided in [7].
The inverse mapping of a Gaussian integer to an element of the prime field is defined as
where the parameters u and v are calculated using the extended Euclidean algorithm [7]. Next, we consider an example to illustrate the modular arithmetic over Gaussian integer fields.
Example 1.
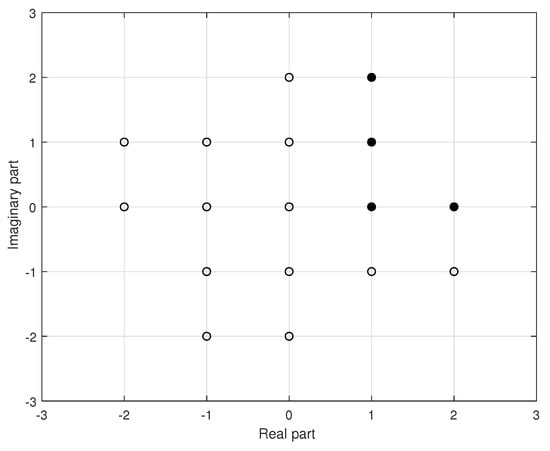
Consider the set with . The elements of the Gaussian integer field according to (4) are shown in Figure 1. Pleas note that the black markings are relevant for Example 3 and will be discussed in Section 3.

Figure 1.
The set of Gaussian integers for .
For the ordinary integers and the corresponding Gaussian integers are and . The sum can also be calculated as . Similarly, the product can also be expressed as . Any Gaussian integer can be mapped to an element of the prime field using the parameters and . For instance, for we have .
The complex multiplication of two Gaussian integers and can be efficiently calculated as
where , , and . Hence, the complex multiplication requires three integer multiplications. We call such an integer multiplication an atomic multiplication. While the complex multiplication over Gaussian integers does not provide a significant complexity reduction in comparison with the multiplication over ordinary integers, the squaring of a Gaussian integer can be simplified to
where only two atomic multiplications and three additions are required [11,12].
2.2. Elliptic Curve Point Multiplication for Binary Keys
The public-key cryptosystems using elliptic curves were introduced in [1,2]. In this work, we consider the curve
which is recommended for prime fields [3,17]. The parameters and are non-zero constant coefficients. The pair x and y defines the coordinates of a point on the curve.
The main operation of ECC is the PM , i.e., multiplying a point on the elliptic curve with a scalar k. There exist different algorithms for the ECC point multiplication [17,49]. These multiplication algorithms are based on two point operations, the point addition (ADD) and the point doubling (DBL). Both operations depend on the form of the curve [17]. Let and be two distinct points on an elliptic curve (8), then the ADD operation is calculated as
Similarly, the DBL operation is defined as
The calculations in (9) and (10) are typically performed using arithmetic over prime fields. However, we consider arithmetic over Gaussian integer fields, where .
The number of required ADD and DBL operations per point multiplication depends on the field size, but also on the PM algorithm. We first consider a binary representation of the key , where r is the number of binary digits of the key. The subscript indicates the binary basis, i.e., . One example for the PM is presented in Algorithm 1, which requires DBL and at most ADD operations per PM, whereas the number of ADD operations varies with the key. We focus on the worst-case complexity because most implementations will try to balance the number of ADD operations in ordered to harden the calculation against timing attacks [32,33].
| Algorithm 1 Point multiplication with binary key representation [32]. | |
| input:P, | |
| output: | |
| 1: | |
| 2: for ( down to 0) do | |
| 3: | // DBL R |
| 4: if () then | |
| 5: | // ADD R and P |
| 6: end if | |
| 7: end for | |
| 8: return R | |
2.3. Elliptic Curve Point Multiplication for -Adic Expansion
Next, we consider Algorithm 2 which calculates the -adic expansion of an integer k [19]. Algorithm 2 is the ordinary division algorithm for base conversion when k and are both integers. In this case, the algorithm results in an expansion with digits. However, we consider the expansion where k and are Gaussian integers. In this case, the modulo function is calculated according to (3) and the number of digits can be estimated as
To see this, note that the division results in a quotient which is a Gaussian integer. Hence, the absolute value of the enumerator is diminished by a factor in each iteration.
From the estimate (11) follows that it is advantageous to represent the key as a Gaussian integer. For any Gaussian integer ring the absolute value is bounded by [41]. Hence, we can estimate the maximum number of digits l for the -adic expansion of a key as
Note that the size of the keyspace is determined by the order of the elliptic curve. For a curve of order n, we choose a Gaussian integer key from or a smaller ring. The size of this ring should equal the order to retain the size of the keyspace. Consequently, using approximately halves the number of digits compared with an expansion of an ordinary integer , which has a maximum key length .
| Algorithm 2-adic expansion of integers or Gaussian integers. | |
| input: Gaussian integer k and base | |
| output:-adic expansion | |
| 1: | |
| 2: | |
| 3: while () do | |
| 4: | // remainder |
| 5: | // quotient |
| 6: | |
| 7: end while | |
| 8: return | |
In [17,50] several endomorphisms for different curves over prime fields were presented. To demonstrate that a -adic expansion can reduce the computational complexity, we consider an example based on the curve (8) with and . The -adic expansion according to (2) results in digits . For the products we use the endomorphism for prime fields [17,50]. Note that is a point on the curve (8) if is a valid point. The negation of any point is according to [17]. Hence, for the products with non-zero we have
Similarly, we can calculate the mapping as . This product requires a DBL and an ADD operation. The operation of the PM with this expansion is summarized in Algorithm 3, where denotes the pentavalent representation of the integer k.
| Algorithm 3 Point multiplication with expansion. | |
| input:P, | |
| output: | |
| 1: ; | |
| 2: for ( down to 0) do | |
| 3: | // DBL R |
| 4: | // ADD Q and |
| 5: if then | |
| 6: | // ADD R and |
| 7: end if | |
| 8: end for | |
| 9: return R | |
Example 2.
We consider the curve over the field from Example 1. Using the generator point we obtain a subgroup of order 13, which comprises the neutral element and the following points
| . |
Due to the order of the subgroup we choose a key from , i.e., . Using Algorithm 2 with , we obtain the expansion . With the starting point , the PM from Algorithm 3 results in the point .
Each iteration of Algorithm 3 is more complex than a single iteration of Algorithm 1. However, the -adic expansion reduces the number of iterations that are required to calculate the PM. Again let r be the number of bits for the binary key representation, and l the number of digits . We have because of (12). Algorithm 1 requires a maximum of iterations with one DBL and one ADD operation in each iteration. Similarly, the point multiplication based on the -adic expansion requires a maximum of iterations, with one DBL and two ADD operations in each iteration. This results in DBL operations and at most ADD operations. Hence, the number of both operations is reduced compared with the binary case. Similar considerations hold for the Montgomery PM [49]. A comparison of the latencies of the PM using binary and -adic expansion of the key are given in Section 6.
As proposed in [25], the non-binary expansions are beneficial to harden ECC implementations against attacks based on power analysis. The products can be precomputed and stored in memory. This minimizes the dependencies between arithmetic operations and the key.
2.4. Projective Coordinates
ADD and DBL are calculated using modular arithmetic operations, i.e., addition, subtraction, multiplication, and inversion over prime or Gaussian integer fields. The most expensive operation is the multiplicative inverse. To speed up the PM calculation, several point representation methods were considered, such as the projective homogeneous coordinates [51] and the Jacobian coordinates [17,52]. These methods transform each point from affine to projective coordinates , where the computation of ADD and DBL is applied without inversion. After the computation of a PM, the result is transformed back into affine coordinates by applying a single inversion. The number of required modular arithmetic operations depends on the representation of the projective coordinates. In this work, we consider the Jacobian coordinates [17,52], because fewer modular multiplications are required.
A drawback of the representation in the projective coordinates is that many interim results have to be stored. We can reduce the number of interim values by exploiting some properties of the Jacobian coordinates. Consider the calculation of the ADD operation or in Algorithms 1 and 3. In both cases, the second argument does not change throughout the PM algorithm. Hence, the point P can be represented in affine coordinates with as . Similarly, for holds and so on. This enables a special ADD operation with reduced complexity [17,51,52]. In the following, this operation is denoted by SADD.
Transforming the result from projective to affine coordinates requires a single inversion. This transformation is defined for the Jacobian coordinates as
3. Resistance Against Side-Channel Attacks
In Section 5, we will discuss a flexible architecture for the PM calculation that can be used with binary and non-binary key expansions and with different PM algorithms. A PM according to Algorithm 1 with binary key expansions can be useful for applications where only a public key is employed, e.g., the verification of digital signatures according to the NIST standard [43]. On the other hand, applications, where the secret key is used, require protection against side-channel attacks. In this section, we discuss the resistance of the PM implementation against SCA. In particular, we consider the key expansion algorithm from [41] which improves the resistance against TA and SPA. We demonstrate that this key expansion employing Gaussian integers reduces the memory requirements and computational complexity compared with other -adic expansions. Algorithm 3 is an example for such a point multiplication.
The SADD operation in Algorithm 1 is only calculated if the current bit of the binary key . Moreover, the DBL and SADD operations employ different numbers of arithmetic operations. Hence, the power consumption and the execution time of an iteration depend on the current bit of the secret key. Consequently, an attacker can estimate the current bit of the secret key by observing the power consumption over time. To avoid TA and SPA attacks, many publications balance the number of applied point operations using additional dummy ADD operations [22,24,31,32,33,34].
Similar to the binary PM, the conditional SADD operation is computed if for the PM with -adic expansion in Algorithm 3. Note that the product is a point multiplication, where the associated number of DBL and SADD operations depends on the actual value of . Hence, an attacker can infer by estimating the number of calculated DBL and SADD from the power consumption of the device.
Improved robustness against SPA can be achieved by precomputing all possible products and storing these values in a memory [21,22,24,31]. Hence, by processing the PM according to Algorithm 3, the corresponding product is read from the memory. This results in fixed calculation times for the SADD operation with any product . Nonetheless, this concept is not protected against TA or SPA. An attacker still can detect all values in an expansion, where the conditional SADD operation is skipped.
To protect the PM against such attacks, Algorithm 4 was recommended in [41] for the key expansions. This algorithm replaces all values by . Hence, it determines a new base conversion of the key excluding all zero elements. Consequently, the SADD operation in step 6 of the PM in Algorithm 3 is calculated in each iteration independent of the value of and without the need for dummy additions. This results in a constant calculation time for a PM and increases the robustness against SPA and timing attacks. It was shown in [41] that the key expansions according to Algorithm 2 and Algorithm 4 result in the same point multiplication.
| Algorithm 4 SPA resistance -adic expansion of a Gaussian integers (or an integer) k according to [41]. | |
| input: Gaussian integer k and base | |
| output:-adic expansion | |
| 1: | |
| 2: | |
| 3: while () do | |
| 4: | // remainder |
| 5: if () then | |
| 6: | |
| 7: end if | |
| 8: | // quotient |
| 9: | |
| 10: end while | |
| 11: return | |
Algorithm 4 is suitable for ordinary integers and Gaussian integers. However, using Gaussian integers reduces memory requirements and computational complexity. This complexity reduction results from the symmetry of the Gaussian integer field. We illustrate this with the following example.
Example 3.
We consider expansions with . The set of all possible digits is depicted in Figure 1. The corresponding precomputations can be obtained as follows. First, the product is calculated using a DBL operation. Next, we calculate the products for the remaining digits in the first quadrant, i.e., and , where we use two SADD operations and the endomorphism (15). The corresponding digits are depicted with filled points in Figure 1. For the Gaussian integer we have to calculate , which requires additionally one DBL and one SADD operation.
Similarly, the number of stored precomputed points can be reduced using Gaussian integers. For the hardware implementation, we use the sign-magnitude binary format for the real and imaginary parts of a Gaussian integer. With this representation, it is sufficient to store the value and all values corresponding to the values from the first quadrant. These values are represented with filled points in Figure 1 for . The different signs for real and imaginary parts resulting from (13) to (16) are implicitly stored as parts of the values in the expansion, i.e., each value contains bits addressing a value from the first quadrant and two bits for the signs of the real and imaginary parts. This representation does not increase the number of bits for the expansion, but reduces the number of stored precomputed points to for the products and one point for the value .
We provide results for different values in Table 1. This table contains the number of stored points, the number of iterations l per PM, and the number of multiplications M per PM. Table 1 illustrates the number of required multiplications M for the DBL and SADD point operations with and without precomputations. Note that the parameter M denotes the number of multiplication equivalent operations. For Gaussian integers, this number is approximated based on the complex squaring (7) and multiplication (6), where the complexity of a complex squaring is about of the complexity of a complex multiplication.

Table 1.
Performance results for different -adic expansions in comparison with [21] for a binary key length according to [41].
Furthermore, results from [21] are included in the lower part of Table 1 for comparison. The concept from [21] aims on reducing the required memory for the precomputed points. For instance, compare for example with digits and the base with digits from [21]. The proposed approach reduces the number of stored points from 8 to 5. Moreover, the number of multiplications is decreased by .
Finally, we note that the robustness against DPA attacks can be improved for -adic expansion with with the randomized initial point approach proposed in [21]. This approach increases the number of the stored precomputed points, but still achieves a complexity reduction compared with other non-binary expansions.
4. Montgomery Arithmetic over Gaussian Integers
In this section, we consider the Montgomery arithmetic over Gaussian integer fields. Furthermore, we discuss some important properties of the proposed concept for hardware implementations.
4.1. Montgomery Reduction over Gaussian Integers
After each complex multiplication or squaring operation, a reduction step is required to map the result in a valid field representative. However, the modulo operation according to (3) is computationally expensive. Alternatively, the Montgomery method can be applied to efficiently determine this modulo operation [53].
Typically, the Montgomery reduction is considered in ECC applications to design arithmetic that supports arbitrary prime fields [32,33,48,54]. In this case, the Montgomery multiplication is based on arithmetic over a ring that is isomorphic to the prime field . Due to the isomorphism between prime fields and Gaussian integer fields , the concept of Montgomery multiplication is applicable for Gaussian integers. This was previously considered in [11,12,42].
Similar to [42] and without loss of generality, we consider with . Then we can reduce the complexity of the modulo reduction by replacing the expensive calculation with , where the integer R is a power of two that satisfies . Note that is a simple bitwise AND operation of the real and imaginary parts of with , because R is a power of two. Each Gaussian integer is mapped to the Montgomery domain as
The complex addition and subtraction in the Montgomery domain are equal to the modular arithmetic of Gaussian integers, because
However, the multiplication in the Montgomery domain requires a special reduction function
where the result is again in the Montgomery domain. The Montgomery reduction function also determines the inverse mapping, since . The generalization of the Montgomery reduction algorithm from ordinary integers to Gaussian integers is not trivial. The final reduction step of the algorithm uses the total order of integers. However, such an order relation does not exist for complex numbers.
Two Montgomery reduction algorithms were presented in [42]. These algorithms differ in the norm used for the final reduction step, where one uses the absolute value of and the other is based on the Manhattan weight . Calculating the Manhattan weight is less complex than calculating the absolute value because only addition is required, whereas squaring is necessary to determine . To achieve a low complexity implementation of the proposed coprocessor, we apply the algorithm based on the Manhattan weight.
Note that holds for any x which can be seen from squaring both sides of the inequality. Furthermore, it was shown in [42] that for each Gaussian integer holds.
The algorithm based on the Manhattan weight calculates a result satisfying this bound. This precision reduction is described in Algorithm 5, where
and can be calculated using the extended Euclidean algorithm [7].
| Algorithm 5 Precision reduction for Gaussian integers using the Manhattan weight according to [42]. | |
| input:, , | |
| output: | |
| 1: | // bitwise AND of real and imaginary part with |
| 2: | // shift real and imaginary part right by l |
| 3: if () then | |
| 4: | |
| 5: else | |
| 6: determine according to (22) | |
| 7: | |
| 8: end if | |
This algorithm is useful when many successive multiplications have to be calculated which is the case in ECC applications. However, not every Gaussian integer satisfying the bound in (21) is necessarily an element of the set . Hence, in the final calculation step, the correct representative can be determined by minimizing absolute value as
This step is more complex but has to be performed only once per PM.
4.2. Simplifying the Reduction
The number of comparisons to calculate the offsets in (22) and (23) can be reduced based on the signs of the real and imaginary parts of the Gaussian integer q, i.e., we can first determine the corresponding quadrant and reduce the number of possible offsets [42].
For all interim results in the PM calculation, we can use the reduction based on the Manhattan weight in Algorithm 5. Note that the reduction for interim results does not necessarily require the offset that minimizes the Manhattan weight in (22). The aim of this reduction is finding a Gaussian integer that is congruent to the actual representative x and has a Manhattan weight satisfying (21). Hence, the reduction can be stopped once a value with is found. We implement an iterative reduction in microcode. Hence, the latency depends on the number of reduction steps required until such a congruent is found.
To estimate the latency, a Monte Carlo simulation is conducted. Table 2 shows the results of this simulation. This table provides the percentage of the number of required reduction steps for Gaussian integers of different sizes. Each simulation considered 100.000 random values. The four columns on the right in Table 2 present the percentage for the number of required offset reductions after an arithmetic operation. Note that no reduction is required if the result q already satisfies . These results illustrate that sequential processing of the offset reduction is reasonable because of all operations satisfy and require no reduction. Approximately 4–5% of all operations require a single reduction step. Only in about of all cases, two or three calculation steps were required.

Table 2.
Examples of primes of the form suitable for ECC applications, and the percentage of the number of required offset reductions for 100 k samples.
4.3. Bit Width for the Gaussian Integer Representation
Next, we determine the number of bits that are required to represent a Gaussian integer with and . In particular, we show that
bits for the real as well as for the imaginary part are sufficient, where denotes the floor function.
In the following, and denote the real and the imaginary parts of the complex number x, respectively. For , we have . Let c and d be the real and the imaginary parts of . From (3) follows
This implies and , . Hence, we have
because and are integers. With the binary logarithm of these bounds, we can determine the required number of bits considering an extra bit in (24) for the signs.
5. Hardware Architecture
In this section, we present an area-efficient processor architecture supporting Gaussian integer arithmetic. We propose an application-specific instruction set processor based on a Harvard architecture. This architecture aims at high flexibility, i.e., it supports different algorithms for point multiplications. With this architecture, we can demonstrate that a protected PM using Gaussian integers can be as fast as an unprotected binary PM.
The main components of the proposed Harvard architecture are depicted in Figure 2. The coprocessor is divided into three main components, which are interconnected and controlled by a control unit. The uppermost component in this block diagram is a program memory. The processor is controlled by microcode instead of a finite state machine to enable different PM algorithms. The undermost components are a data memory that stores the operands, interim, and final results of the PM, and an arithmetic unit, which performs all required arithmetic operations. Since the carry chains in the arithmetic unit limits the operating frequency, this unit determines the performance of the whole coprocessor.
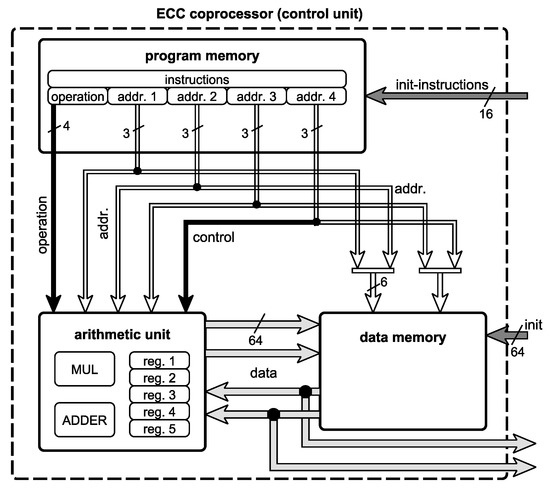
Figure 2.
Block diagram of the ECC processor.
Figure 2 includes four types of buses. The operation path, shown in black, defines the operation to be performed by the arithmetic unit. The address paths define either the register addresses for the arithmetic unit or the addresses for the data memory. For the data memory, two address paths are concatenated to obtain 6-bit addresses. Please note the path, connected to the address 4 of the program memory, can either be used as part of a data memory address or for further specification of arithmetic instructions, depending on the operation.
The 64-bit data paths are shown in light gray. These directly connect the arithmetic unit and the data memory to omit multiplexing in the control unit. The dark gray paths are for the initialization of the memories before the processing of a PM. The data memory has to be initialized with necessary values for computing the PM such as the domain parameters , , the point P, and the key k, while the program memory has to be initialized with the microcode for the PM processing.
As mentioned above, the calculation in projective coordinates significantly reduces the computational complexity. However, the computation with projective coordinates requires storage for many interim results. Typically, these results are stored in registers to enable fast data access. The proposed architecture stores these interim results in random accessible memory (RAM) because RAM is more compact than registers. This also results in a compact control logic with very simple data paths.
The data paths connect the RAM and the arithmetic unit. All data passes through the RAM, hence no multiplexers are required to control the data flow. However, additional clock cycles are required for each operation to read and store data. On the other hand, some arithmetic operations for the PM processing are multicycle operations, where the additional cycles for data transfer are only a small overhead. Moreover, reducing the logic results in a higher operating frequency that shortens the latency for a PM.
The address of the program memory is defined by a program counter in the control unit, which is not shown in Figure 2. Hence, each instruction is available for exactly one clock cycle. For multicycle operations, as the multiplication a dummy operation no op is available. For branches, the program counter can be set to a value specified in the corresponding instruction. For function calls within the microcode a register is available, which can store the current value of the counter as return address. After the function, the counter can be set to the value of this register using a return operation. Next, we specify the three components of the proposed ECC coprocessor in more detail.
5.1. Instruction Set Architecture
Table 3 presents all instructions for the proposed application-specific instruction set processor using arithmetic over Gaussian integers. In total, 11 instructions are sufficient to control all necessary operations for calculating a PM. Therefore, only four bits are considered to indicate the requested operation.

Table 3.
Definition of the instruction set.
The operations read, store, branch, return, and no op are control instructions that are processed in the control unit, while add, multiply, complement, shift, rotate, and mod R are arithmetic instructions that are executed in the arithmetic unit.
The instruction read is used to read data from the RAM to the two input registers 1 and 2 in the arithmetic unit. Similarly, the store instruction saves the two output registers 4 and 5 to the RAM. Both operations require two addresses for the data memory. The data memory stores up to 64 variables, hence six address bits are required. In Table 3 these addresses are represented by the combination of two fields of three bits width.
The branch instruction is used for branches, loops, and function calls. By calling the branch instruction, we set the program counter to the address defined in the memory addr. field if a specific condition is fulfilled. Depending on the control bits this condition can be the carry bit or the sign of the first register. For function calls no condition is required. Instead, the current program counter value is written to a register as return address. Using the return operation this address can be written to the program counter. The instruction no op is used when the arithmetic unit is busy. This is required for multicycle operations.
The add instruction adds two m-bit numbers, which allows for a complex addition in two clock cycles. Depending on the control bits this instruction can also add the absolute values to determine the Manhattan weight in one clock cycle. The complement calculates the two’s complement of an m-bit number. This complement instruction is required to transform to or from sign-magnitude representation used for the multiplication. Moreover, it can change the sign of a number in sign-magnitude representation by flipping the sign bit of a register. For subtraction, the complement instruction is called before the add instruction. Subtraction could also be implemented as a combined adder-subtractor logic requiring an additional subtraction instruction.
The multiply instruction performs an -bit multiplication which requires four clock cycles. The rotate instruction is used to shift the last two registers by bits, which allows for a faster m-bit multiplication using accumulation on these two registers. Each m-bit multiplication requires four -bit multiplications and some additions, i.e., for two m-bit numbers we have
where and denote the least significant half-words, and the most significant half-words of a and b, respectively. The term could be written as , which would reduce the number of multiplications to three. On the other hand, this would require subtraction and a representation of negative numbers in the half-words. To avoid this we implement the multiplication according to (26). To allow for a complex multiplication three m-bit multiplications and some additions and subtractions are required according to (6).
The shift instruction is required for the division by R and can right-shift the last two registers by either one or eight bits, depending on the control bits. For the modulo reduction, the mod R instruction is used to perform bit-wise AND of the first and the last register. While the modulo R operation could be implemented by truncating the result, we require the ability to use arbitrary R. Hence, we can load to the first register and call the mod R operation to calculate the last register modulo R.
5.2. Data Memory
We employ dual-port RAM (DP-RAM) to store variables and intermediate results, which enables accessing the real and imaginary parts of each Gaussian integer simultaneously. Alternatively, two smaller single port memories could be used in parallel. However, this would result in more complicated microcode. We store the results of complex additions and subtractions before the reduction in RAM. Hence, an additional carry bit is necessary, which increases the required bits for the real and imaginary parts of Gaussian integers and consequently the word width of the RAM from (24) to
for the whole design.
For embedded systems, where the proposed architecture is supported as a coprocessor to a primary processor, this DP-RAM may be shared with the primary processor. Note that a smaller word width increases the likelihood that this DP-RAM can be shared because small embedded systems typically do not provide memories with large word width. Consequently, using Gaussian integers increases the likelihood that the RAM can be shared, due to the reduced word width of .
5.3. Arithmetic Unit for Gaussian Integer Fields
The arithmetic unit consists of five registers (reg.) of the length m, an adder, and a multiplier (MUL), as shown in Figure 2. The adder is used for the instructions add, multiply, and complement to minimize the area requirements.
The multiplication of two unsigned -bit integers is implemented using the Karatsuba principal (cf. (26)) as depicted in Figure 3. The operands are stored in the first two registers, which are connected to the multipliers. We use four multipliers with a width of which achieves a good trade-off between area requirements and latency. Register 2 is shifted by bits in each iteration to perform a -bit multiplication in four clock cycles. The partial results of the four multipliers are stored in register 3. These results are then added to registers 4 and 5, which are used as accumulator registers. As shown in Figure 3, registers 4 and 5 are applied to the adder with an -bit shift, corresponding to the -bit shift of the input register. After an -bit multiplication the accumulator registers can be shifted by -bit using the rotate instruction. This allows for an accumulation of the next -bit multiplication.
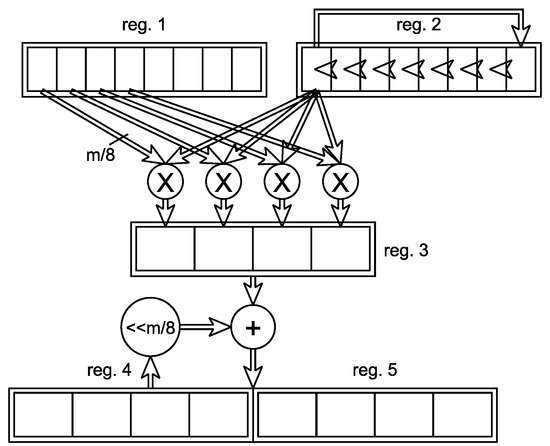
Figure 3.
Structure of the Karatsuba multiplier.
6. Results and Discussion
In this section, we present implementation results for the proposed processor architecture for the Xilinx Virtex 7 FPGA. To the best of our knowledge, no ECC hardware implementation over Gaussian integers exists. Hence, we compare these results with implementations over prime fields from the literature. This comparison illustrates that the proposed architecture is a competitive solution for a compact ECC processor. Yet more important, we compare the latency of a PM with binary keys, according to Algorithm 1, with a PM using -adic key expansions, according to Algorithm 3, to demonstrate that a protected PM using Gaussian integers can be as fast as an unprotected binary PM or even faster.
All results are presented in Table 4, which is divided into two parts. In the upper part, the results for the proposed architecture with different bit lengths are summarized. The lower part contains results from the literature for comparison. The parameter r denotes the maximum key length in bits. The hardware requirements are represented by the number of look-up tables (LUT), flip-flops (FF), slices, and DSP units, as well as the RAM size. The maximum clock frequency is denoted by . Note that the number of inputs per LUT as well as the number of LUTs and registers per slice vary for different FPGA devices. However, we can compare the total number of registers and memory size.

Table 4.
Results and comparison with other area efficient implementations.
The proposed architectures were synthesized with and without the FPGA’s DSP units. However, the architectures were not optimized for the provided DSP units. The number of flip-flops is dominated by the five registers of the arithmetic unit which have a size of m bits. The RAM size is the sum of the data and program memory sizes. A data memory with 38 words of m bits and a program memory with 950 words of length 16 bits are sufficient. Hence, the RAM requirements are dominated by the program memory, since the arithmetic unit performs only very simple operations. Multiple instructions are required to perform a complete arithmetic operation over complex numbers.
The proposed architecture is suitable for binary key representations and -adic expansions. Hence, the latency values are provided for both representations, where we use and for the -adic expansion. Similarly, we consider two different PM algorithms. One algorithm is protected against timing and SPA attacks by balancing the number of ADD and DBL operations. The latency for this algorithm is denoted by protected in Table 4. The results denoted by unprotected correspond to the PM with the minimum number of ADD and DBL operations.
To evaluate the proposed architecture, we compare the implementation results with other designs that employ the Montgomery modular arithmetic over ordinary integer fields [33,55]. The design in [33] support primes up to 521 bits. It requires a smaller number of LUT, but more flip-flops and a larger memory due to the larger key. For longer keys, the design in [33] results in higher latency. Consider for example the key length . The protected PM from [33] requires 55.87 ms. The proposed design without DSP units requires only 17.87 ms for the protected PM with and 9.9 ms for .
The design in [55] considers key lengths up to and the unprotected PM. This design is optimized for the use of DSP units which reduces the number of LUT. The number of LUT is similar to the proposed design with key length using DSP units. It employs much more flip-flops and memory. The proposed architecture for with 4 DSP units is faster for all considered PM calculations.
The implementation results demonstrate that the latency of a protected PM with ()-adic expansion is similar to the latency of an unprotected binary PM. The latency of the protected -adic expansion is only 10% higher than the latency of unprotected binary PM. On the other hand, the protected binary PM has latency values that are 25% larger than the results for the protected -adic expansion. Note that the latency with -adic expansions can be further reduced with other bases , i.e, the choice of enables a trade-off between speed and memory size. According to Table 1, the base with =17 reduces the computational complexity by 29% compared with , at the cost of memory for three additional precomputed points. For instance, with and the implementation with DSP units achieves a latency of 5.58 ms for the protected PM and 5.5 ms for the unprotected PM, respectively. The memory size increases from 18.5 kbits to 20.4 kbits. This PM is significantly faster than the results from [33,55]. In [32], an implementation for the Virtex 7 FPGA is reported that achieves a latency of only 1.96 ms for a protected PM with . However, this implementation employs a much higher parallelization degree using 20 DSP units, i.e., five times more DSP units than with the proposed design.
7. Conclusions
In this work, we have presented a new concept to implement the elliptic curve point multiplication. This computation is based on a new modular arithmetic over Gaussian integer fields [42]. The proposed coprocessor is flexible, i.e., it supports different point multiplication algorithms over prime fields. The implementation results illustrate that the proposed concept is a competitive solution for a compact ECC processor for applications in small embedded systems.
Moreover, the proposed architecture supports different ECC key representations with binary and -adic expansions. We have demonstrated that it is beneficial to represent the key and the base as Gaussian integers. This representation speeds up the PM computation. Furthermore, such -adic expansions improve the robustness against TA and SPA attacks. The randomized initial point method from [56] can be applied to further strengthen the robustness against DPA, and RPA attacks. We have demonstrated that the Gaussian integer representation reduces the number of stored points and the computational complexity of such a protected point multiplication compared with other non-binary key representations.
Gaussian integer fields can only be constructed for primes of the form , hence a generalization of this work to Eisenstein integers could be beneficial. Eisenstein integers are complex numbers of the form , where , and Eisenstein integer fields can be constructed for primes of the form . An elliptic curve point multiplication using Eisenstein integers was considered in [57] showing similar properties as the PM over Gaussian integers. However, up to now no efficient modulo operation for Eisenstein integers is known. We believe that a generalization of the Montgomery modular multiplication to Eisenstein integers would be a promising direction for further research.
Author Contributions
The research for this article was exclusively undertaken by M.S., J.-P.T. and J.F. Conceptualization and investigation, M.S. and J.F.; software and validation, M.S. and J.-P.T.; writing—review and editing, M.S., J.-P.T. and J.F.; writing—original draft preparation and hardware, M.S.; supervision, project administration, and funding acquisition J.F.; All authors have read and agreed to the published version of the manuscript.
Funding
The German Federal Ministry of Economics and Technology (ZF4559701ED8) supported the research for this article.
Acknowledgments
The authors would like to thank Hyperstone GmbH, Konstanz for supporting the research for this article.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Miller, V.S. Use of Elliptic Curves in Cryptography. In Advances in Cryptology—CRYPTO ’85 Proceedings; Williams, H.C., Ed.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 417–426. [Google Scholar]
- Koblitz, N. Elliptic Curve Cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Krisell, M. Elliptic Curve Digital Signatures in RSA Hardware; Scholar’s Press: Mexico City, Mexico, 2012. [Google Scholar]
- Esmaeildoust, M.; Schinianakis, D.; Javashi, H.; Stouraitis, T.; Navi, K. Efficient RNS Implementation of Elliptic Curve Point Multiplication Over GF(p). IEEE Trans. Very Large Scale Integr. Syst. 2013, 21, 1545–1549. [Google Scholar] [CrossRef]
- Li, L.; Li, S. High-Performance Pipelined Architecture of Elliptic Curve Scalar Multiplication Over GF(2m). IEEE Trans. Very Large Scale Integr. Syst. 2016, 24, 1223–1232. [Google Scholar] [CrossRef]
- Rashidi, B.; Sayedi, S.M.; Rezaeian Farashahi, R. Efficient and low-complexity hardware architecture of Gaussian normal basis multiplication over GF(2m) for elliptic curve cryptosystems. IET Circuits Devices Syst. 2017, 11, 103–112. [Google Scholar] [CrossRef]
- Huber, K. Codes over Gaussian integers. IEEE Trans. Inf. Theory 1994, 40, 207–216. [Google Scholar] [CrossRef]
- Freudenberger, J.; Ghaboussi, F.; Shavgulidze, S. New Coding Techniques for Codes over Gaussian Integers. IEEE Trans. Commun. 2013, 61, 3114–3124. [Google Scholar] [CrossRef]
- Elkamchouchi, H.; Elshenawy, K.; Shaban, H. Extended RSA cryptosystem and digital signature schemes in the domain of Gaussian integers. In Proceedings of the 8th International Conference on Communication Systems (ICCS), Singapore, 28–28 November 2002; Volume 1, pp. 91–95. [Google Scholar]
- Koval, A.; Verkhovsky, B.S. Analysis of RSA over Gaussian Integers Algorithm. In Proceedings of the Fifth International Conference on Information Technology: New Generations (ITNG), Las Vegas, NV, USA, 7–9 April 2008; pp. 101–105. [Google Scholar]
- Koval, A. Security Systems Based on Gaussian Integers: Analysis of Basic Operations and Time Complexity of Secret Transformations. Ph.D. Thesis, New Jersey Institute of Technology, Newark, NJ, USA, 2011. [Google Scholar]
- Koval, A. Algorithm for Gaussian Integer Exponentiation. In Information Technology: New Generations; Springer International Publishing: Manhattan, NY, USA, 2016; pp. 1075–1085. [Google Scholar]
- Bhargava, K.; Soni, V. A novice cryptosystem based on nth root of Gaussian integers. In Proceedings of the 2017 International Conference on Computer, Communications and Electronics (Comptelix), Jaipur, India, 1–2 July 2017; pp. 271–274. [Google Scholar]
- Awad, Y.; El-Kassar, A.N.; Kadri, T. Rabin Public-Key Cryptosystem in the Domain of Gaussian Integers. In Proceedings of the International Conference on Computer and Applications (ICCA), Beirut, Lebanon, 25–26 July 2018; pp. 336–340. [Google Scholar]
- Koblitz, N. An elliptic curve implementation of the finite field digital signature algorithm. In Proceedings of the Advances in Cryptology (CRYPTO), Santa Barbara, CA, USA, 23–27 August 1998; pp. 327–337. [Google Scholar]
- Solinas, J. Efficient Arithmetic on Koblitz Curves. Des. Codes Cryptogr. 2000, 19, 195–249. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer: New York, NY, USA, 2003. [Google Scholar]
- Roberto Avanzi, C.H.; Prodinger, H. Redundant τ-adic expansions I: Non-adjacent digit sets and their applications to scalar multiplication. Des. Codes Cryptogr. 2011, 58, 173–202. [Google Scholar] [CrossRef]
- Heuberger, C.; Mazzoli, M. Symmetric digit sets for elliptic curve scalar multiplication without precomputation. Theor. Comput. Sci. 2014, 547, 18–33. [Google Scholar] [CrossRef]
- Jarvinen, K.; Tommiska, M.; Skytta, J. A scalable architecture for elliptic curve point multiplication. In Proceedings of the IEEE International Conference on Field- Programmable Technology, Brisbane, NSW, Australia, 6–8 December 2004; pp. 303–306. [Google Scholar]
- Hedabou, M.; Pinel, P.; Bénéteau, L. Countermeasures for Preventing Comb Method Against SCA Attacks. In Information Security Practice and Experience; Deng, R.H., Bao, F., Pang, H., Zhou, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 85–96. [Google Scholar]
- Okeya, K.; Takagi, T.; Vuillaume, C. Efficient Representations on Koblitz Curves with Resistance to Side Channel Attacks. In Information Security and Privacy; Boyd, C., Gonza’lez Nieto, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 218–229. [Google Scholar]
- Thériault, N. SPA Resistant Left-to-Right Integer Recodings. In Selected Areas in Cryptography; Preneel, B., Tavares, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 345–358. [Google Scholar]
- Tao, Z.; Mingyu, F.; Xiaoyu, Z. Secure and efficient elliptic curve cryptography resists side-channel attacks. J. Syst. Eng. Electron. 2009, 20, 660–665. [Google Scholar]
- Liu, S.; Yao, H.; Wang, X.A. SPA Resistant Scalar Multiplication Based on Addition and Tripling Indistinguishable on Elliptic Curve Cryptosystem. In Proceedings of the 10th International Conference on P2P, Parallel, Grid, Cloud and Internet Computing (3PGCIC), Krakow, Poland, 4–6 November 2015; pp. 785–790. [Google Scholar]
- Lutz, J.; Hasan, A. High performance FPGA based elliptic curve cryptographic co-processor. In Proceedings of the International Conference on Information Technology: Coding and Computing (ITCC), Las Vegas, NV, USA, 5–7 April 2004; Volume 2, pp. 486–492. [Google Scholar]
- Dimitrov, V.S.; Järvinen, K.U.; Jacobson, M.J.; Chan, W.F.; Huang, Z. FPGA Implementation of Point Multiplication on Koblitz Curves Using Kleinian Integers. In Cryptographic Hardware and Embedded Systems—CHES 2006; Goubin, L., Matsui, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 445–459. [Google Scholar]
- Li, L.; Li, S. Improved Algorithms and Implementations for Integer to τ NAF Conversion for Koblitz Curves. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 154–162. [Google Scholar] [CrossRef]
- Hossain, M.S.; Saeedi, E.; Kong, Y. High-Speed, Area-Efficient, FPGA-Based Elliptic Curve Cryptographic Processor over NIST Binary Fields. In Proceedings of the IEEE International Conference on Data Science and Data Intensive Systems, Sydney, Australia, 11–13 December 2015; pp. 175–181. [Google Scholar]
- Safieh, M.; Thiers, J.P.; Freudenberger, J. Area Efficient Coprocessor for the Elliptic Curve Point Multiplication. In Proceedings of the 12th International ITG Conference on Systems, Communications and Coding (SCC), Rostock, Germany, 11–14 February 2019; pp. 1–6. [Google Scholar]
- Möller, B. Securing elliptic curve point multiplication against side-channel attacks. In International Conference on Information Security; Springer: Berlin/Heidelberg, Germany, 2001; pp. 324–334. [Google Scholar]
- Amiet, D.; Curiger, A.; Zbinden, P. Flexible FPGA-Based Architectures for Curve Point Multiplication over GF(p). In Proceedings of the Euromicro Conference on Digital System Design (DSD), Limassol, Cyprus, 31 August–2 September 2016; pp. 107–114. [Google Scholar]
- Salman, A.; Ferozpuri, A.; Homsirikamol, E.; Yalla, P.; Kaps, J.; Gaj, K. A scalable ECC processor implementation for high-speed and lightweight with side-channel countermeasures. In Proceedings of the International Conference on ReConFigurable Computing and FPGAs (ReConFig), Cancun, Mexico, 4–6 December 2017; pp. 1–8. [Google Scholar]
- Goubin, L. A refined power-analysis attack on elliptic curve cryptosystems. In International Workshop on Public Key Cryptography; Springer: Berlin/Heidelberg, Germany, 2003; pp. 199–211. [Google Scholar]
- Kocher, P. Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 1996. [Google Scholar]
- Kocher, P.; Jaffe, J.; Jun, B. Differential Power Analysis. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 1999. [Google Scholar]
- Akishita, T.; Takagi, T. Zero-Value Point Attacks on Elliptic Curve Cryptosystem. In Information Security; Boyd, C., Mao, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 218–233. [Google Scholar]
- Mulder, E.D.; Örs, S.B.; Preneel, B.; Verbauwhede, I. Differential power and electromagnetic attacks on a FPGA implementation of elliptic curve cryptosystems. Comput. Electr. Eng. 2007, 33, 367–382. [Google Scholar] [CrossRef]
- Lerman, L.; Bontempi, G.; Markowitch, O. Side channel attack: An approach based on machine learning. In Proceedings of the 2nd International Workshop Constructive Side-Channel Analysis and Security Design, Darmstadt, Germany, 13–14 April 2011; pp. 29–41. [Google Scholar]
- Maghrebi, H.; Portigliatti, T.; Prouff, E. Breaking cryptographic implementations using deep learning techniques. In Proceedings of the International Conference on Security, Privacy, and Applied Cryptography Engineering, Hyderabad, India, 14–18 December 2016; pp. 3–26. [Google Scholar]
- Safieh, M.; Thiers, J.; Freudenberger, J. Side Channel Attack Resistance of the Elliptic Curve Point Multiplication using Gaussian Integers. In Proceedings of the Zooming Innovation in Consumer Technologies Conference (ZINC), Novi Sad, Serbia, 26–27 May 2020; pp. 231–236. [Google Scholar]
- Safieh, M.; Freudenberger, J. Montgomery Modular Arithmetic over Gaussian Integers. In Proceedings of the 24th International Information Technology Conference (IT), Zabljak, Montenegro, 18–22 February 2020. [Google Scholar]
- Locke, G.; Gallagher, P. Digital Signature Standard (DSS); Standard FIPS PUB 186-3; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2009. [Google Scholar]
- Schmalisch, M.; Timmermann, D. A reconfigurable arithmetic logic unit for elliptic curve cryptosystems over GF(2m). In Proceedings of the 46th Midwest Symposium on Circuits and Systems, Cairo, Egypt, 27–30 December 2003; Volume 2, pp. 831–834. [Google Scholar]
- Chelton, W.N.; Benaissa, M. Fast Elliptic Curve Cryptography on FPGA. IEEE Trans. Very Large Scale Integr. Syst. 2008, 16, 198–205. [Google Scholar] [CrossRef]
- Khan, Z.U.A.; Benaissa, M. Throughput/Area-efficient ECC Processor Using Montgomery Point Multiplication on FPGA. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 1078–1082. [Google Scholar] [CrossRef]
- Khan, Z.U.A.; Benaissa, M. High-Speed and Low-Latency ECC Processor Implementation Over GF(2m) on FPGA. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 165–176. [Google Scholar] [CrossRef]
- Roy, D.B.; Mukhopadhyay, D. High-Speed Implementation of ECC Scalar Multiplication in GF(p) for Generic Montgomery Curves. IEEE Trans. Very Large Scale Integr. Syst. 2019, 27, 1587–1600. [Google Scholar]
- Montgomery, P.L. Speeding the Pollard and elliptic curve methods of factorization. Math. Comput. 1987, 48, 243–264. [Google Scholar] [CrossRef]
- Gallant, R.; Lambert, R.; Vanstone, S. Faster Point Multiplication on Elliptic Curves with Efficient Endomorphisms. In Advances in Cryptology—CRYPTO 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 190–200. [Google Scholar]
- Brier, É.; Joye, M. Weierstraß Elliptic Curves and Side-Channel Attacks. In Public Key Cryptography; Naccache, D., Paillier, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 335–345. [Google Scholar]
- Schinianakis, D.M.; Fournaris, A.P.; Michail, H.E.; Kakarountas, A.P.; Stouraitis, T. An RNS Implementation of an Fp Elliptic Curve Point Multiplier. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 1202–1213. [Google Scholar] [CrossRef]
- Montgomery, P.L. Modular multiplication without trial division. Math. Comput. 1985, 44, 519–521. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Q.; Liu, Z.; Tu, C.; Lin, J. Low-Cost Hardware Implementation of Elliptic Curve Cryptography for General Prime Fields. In Information and Communications Security; Lecture Notes in Computer Science; Lam, K.Y., Chi, C.H., Qing, S., Eds.; Springer International Publishing: Manhattan, NY, USA, 2016; pp. 292–306. [Google Scholar]
- Matutino, P.M.; Araújo, J.; Sousa, L.; Chaves, R. Pipelined FPGA coprocessor for elliptic curve cryptography based on residue number system. In Proceedings of the International Conference on Embedded Computer Systems: Architectures, Modeling, and Simulation (SAMOS), Pythagorio, Greece, 16–20 July 2017; pp. 261–268. [Google Scholar]
- Itoh, K.; Izu, T.; Takenaka, M. Efficient Countermeasures Against Power Analysis for Elliptic Curve Cryptosystems. In Smart Card Research and Advanced Applications VI; Quisquater, J.J., Paradinas, P., Deswarte, Y., El Kalam, A.A., Eds.; Springer: Boston, MA, USA, 2004; pp. 99–113. [Google Scholar]
- Thiers, J.P.; Safieh, M.; Freudenberger, J. Side Channel Attack Resistance of the Elliptic Curve Point Multiplication using Eisenstein Integers. In Proceedings of the IEEE 10th International Conference on Consumer Electronics (ICCE), Berlin, Germany, 9–13 November 2020. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).