Beyond Snap-In: A Hybrid Nonlinear Control Approach for Actuators Possessing a Square-Law Characteristic
Abstract
:1. Introduction
2. Kinematics of Actuators Possessing a Square Characteristic
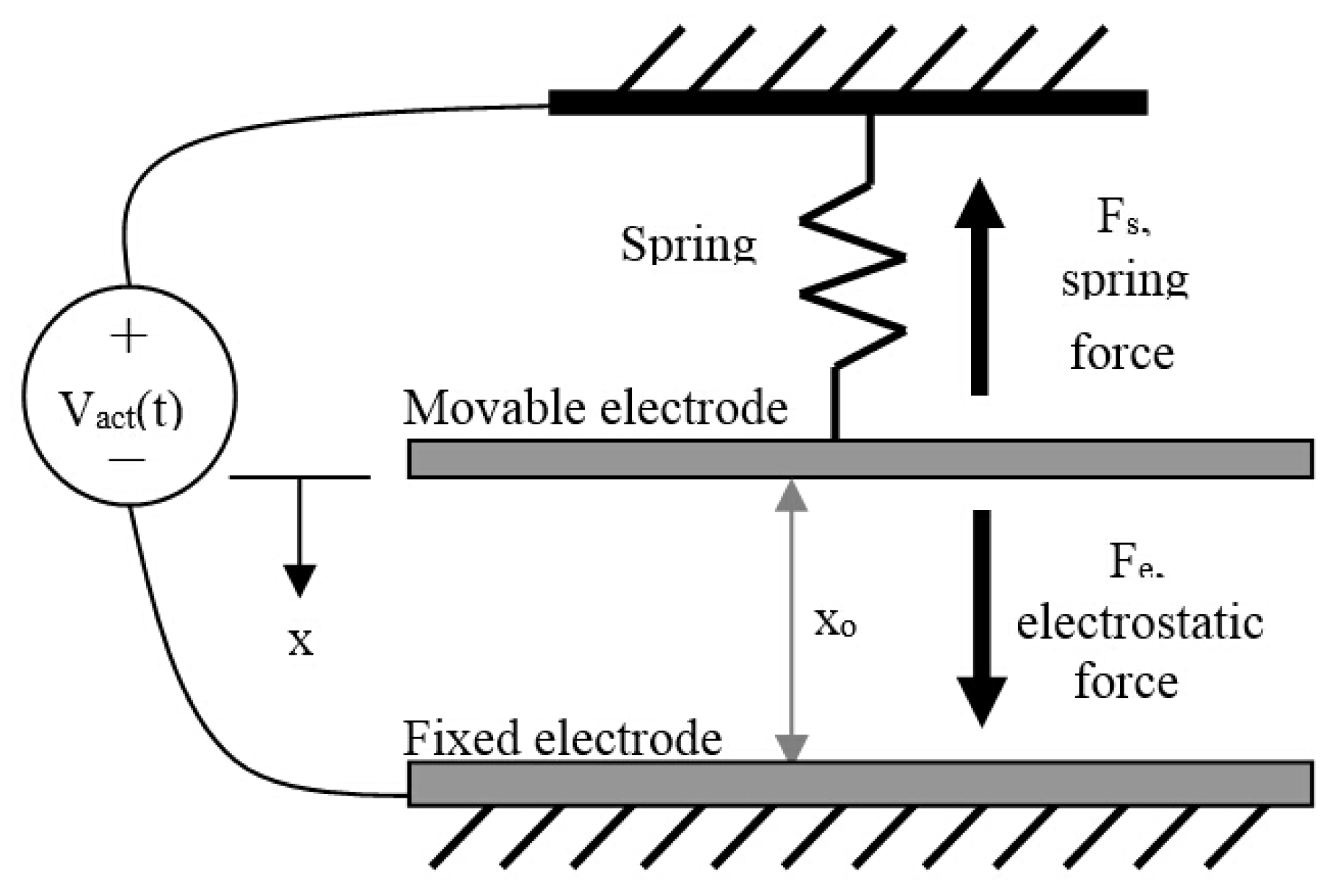
2.1. Kinematics of PPAs
2.2. Kinematics of Solenoids
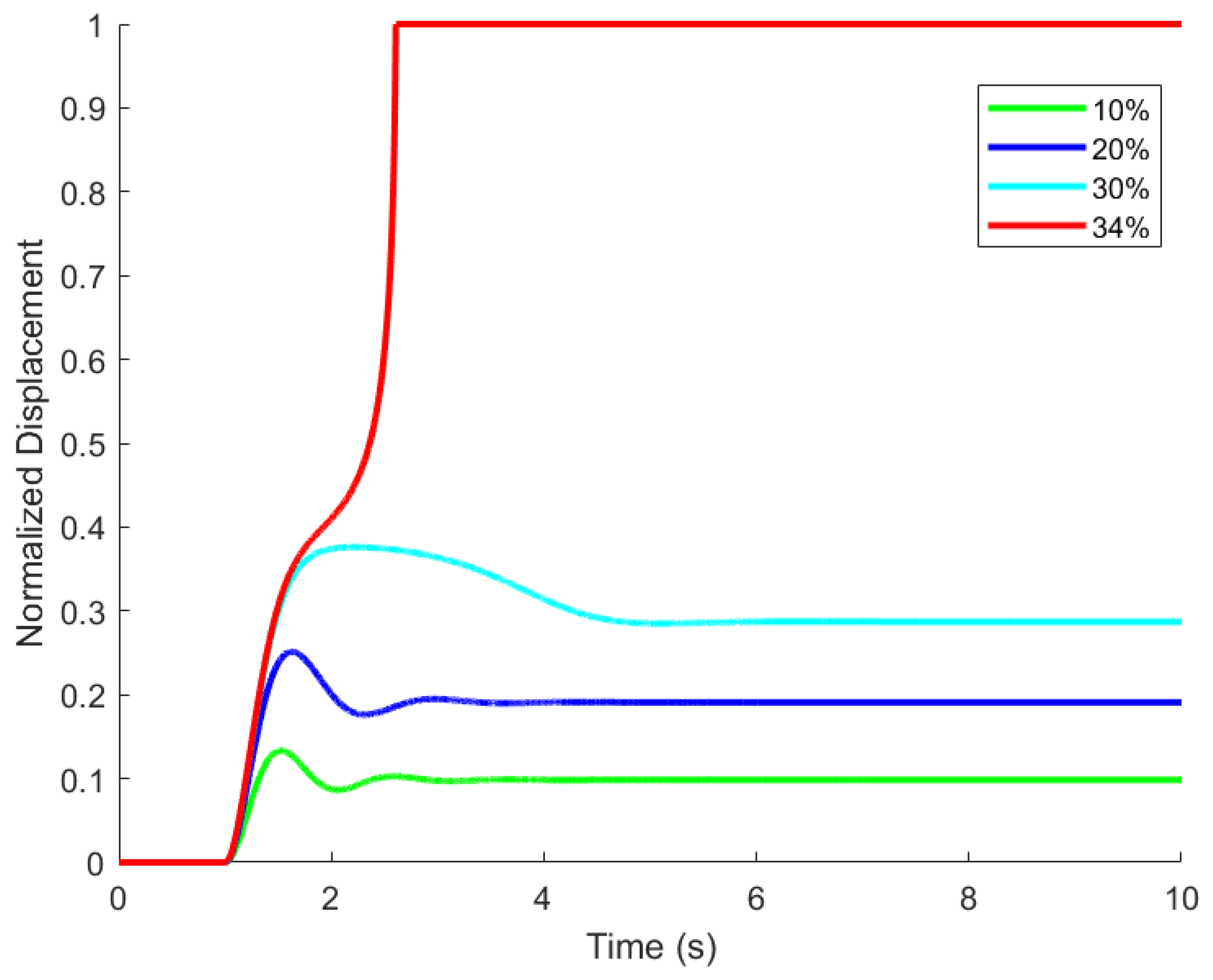
2.3. The Pull-in Effect and Stable Range of PPAs
2.4. The Pull-In Effect and Stable Range of Solenoids
3. Characteristics of Square-Law Actuator Systems in Circuits
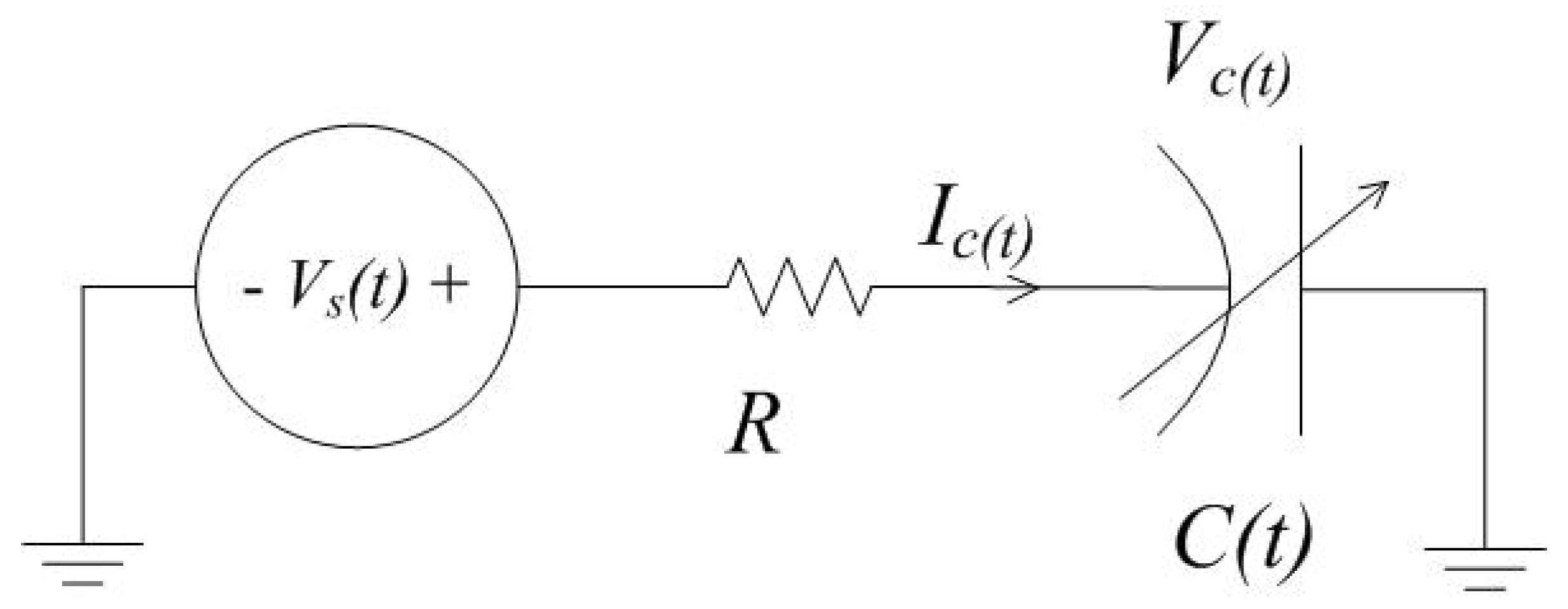
3.1. PPAs with a Series Resistor
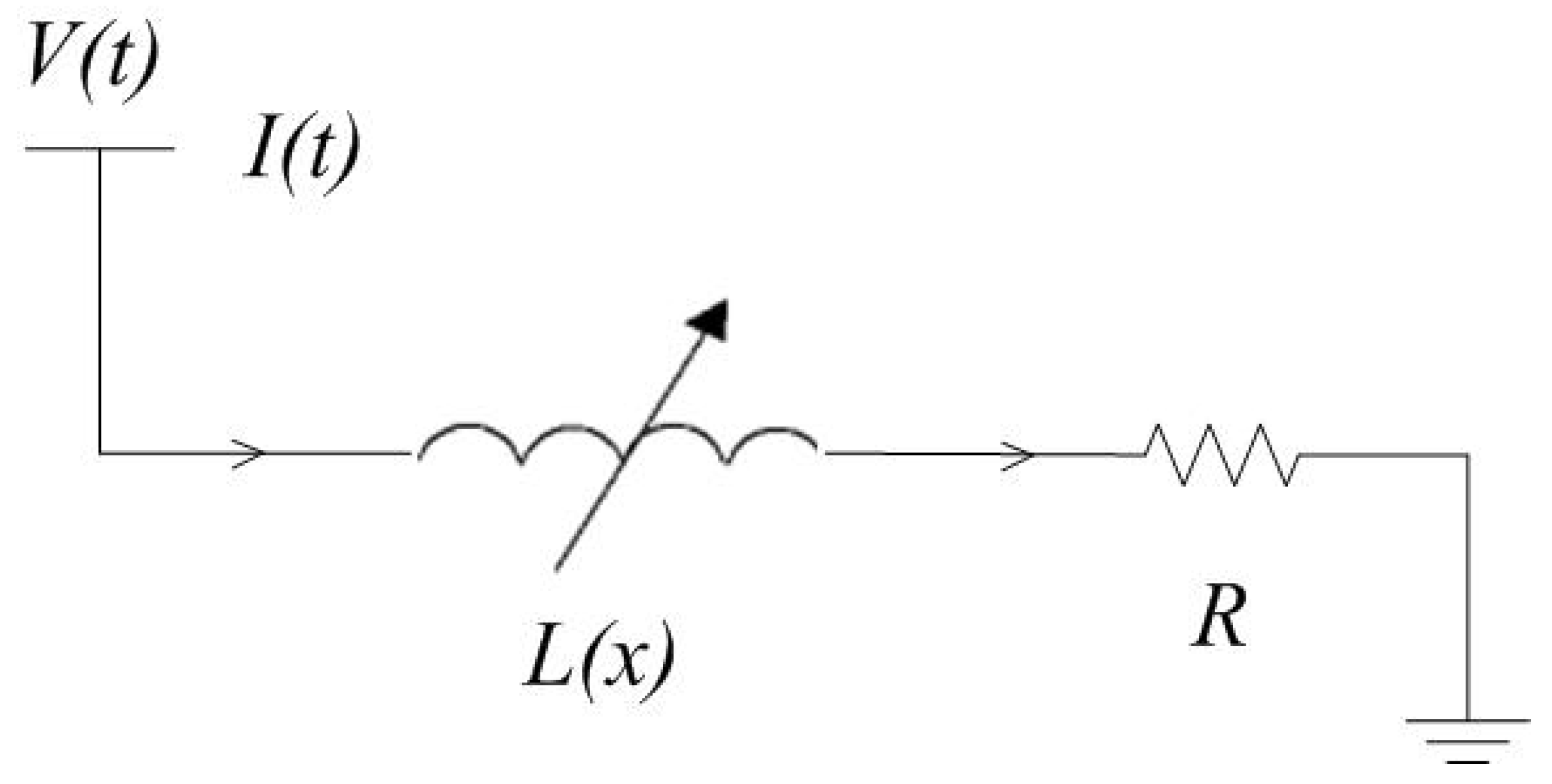
3.2. Solenoids with a Series Resistor
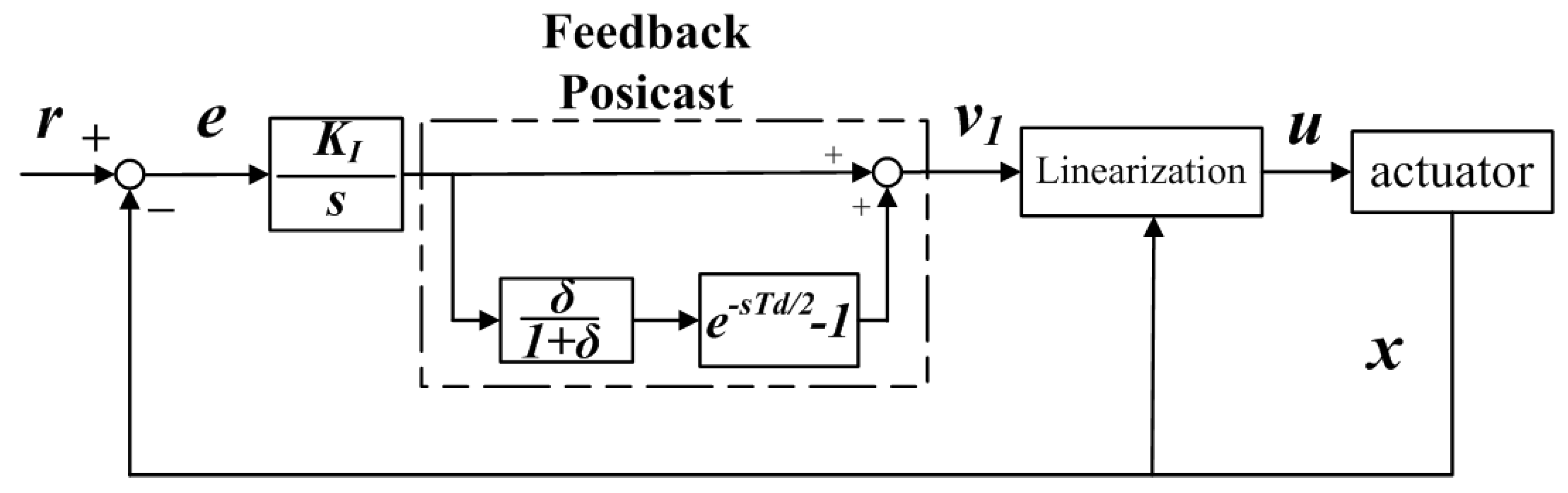
4. Control Scheme
4.1. Dynamic System Formulation
4.2. Hybrid Nonlinear Control Scheme
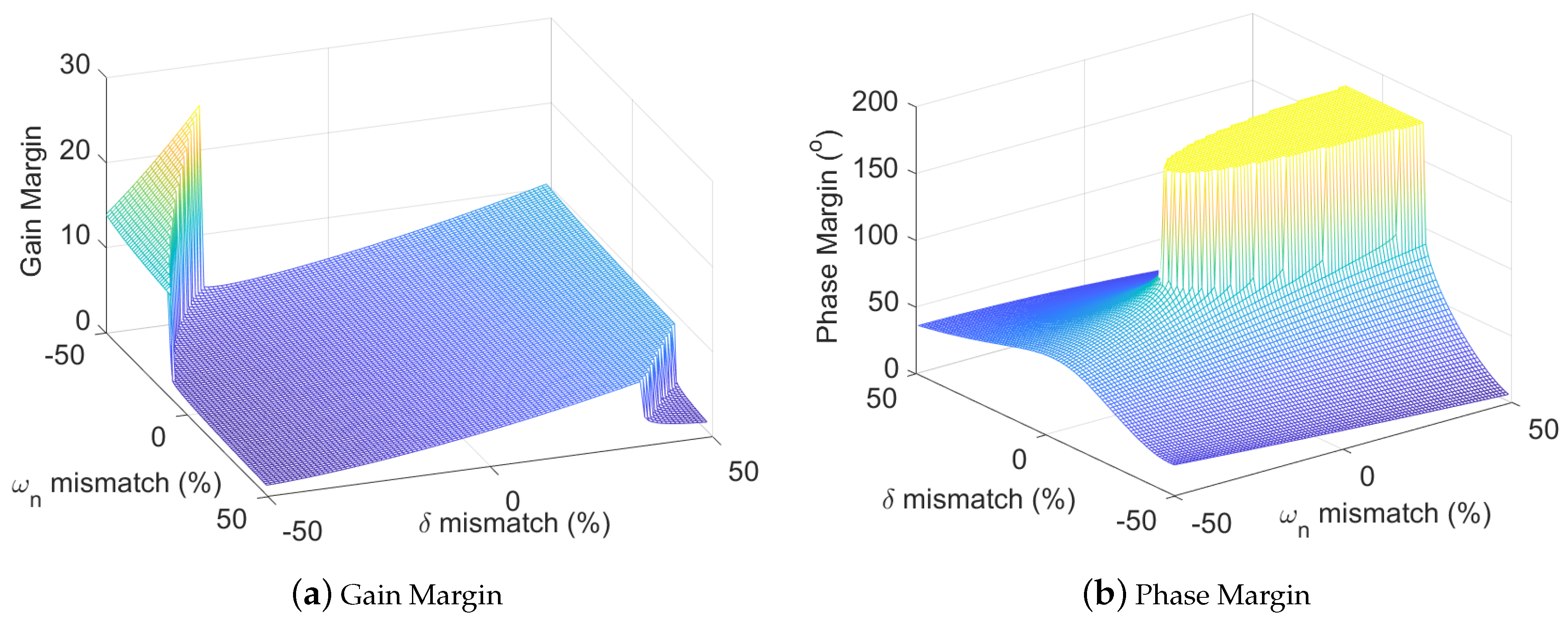
4.3. Stability Analysis
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PPA | Parallel-Plate Actuator |
| MEMS | Micro-Electro-Mechanical Systems |
| IOL | Input–Output Linearization |
| FPIOL | Feedback Posicast Input–Output Linearization |
| PID | Proportional–Integral–Derivative |
References
- Sundaram, A.; Maddela, M.; Ramadoss, R.; Feldner, L.M. MEMS-based electronically steerable antenna array fabricated using PCB technology. J. Microelectromech. Syst. 2008, 17, 356–362. [Google Scholar] [CrossRef]
- Langfelder, G.; Caspani, A.; Tocchio, A. Design criteria of low-power oscillators for consumer-grade MEMS resonant sensors. IEEE Trans. Ind. Electron. 2013, 61, 567–574. [Google Scholar] [CrossRef]
- Yan, S.; Xie, Y.; Zhang, M.; Deng, Z.; Tu, L. A subnano-g electrostatic force-rebalanced flexure accelerometer for gravity gradient instruments. Sensors 2017, 17, 2669. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Sun, Y.; Luo, G.; Wu, G.; Zhang, T. Recent Advancements in Inertial Micro-Switches. Electronics 2019, 8, 648. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Z.; Lee, Y.; Bright, V.M.; Neff, J. Design and investigation of multi-level digitally positioned micromirror for open-loop controlled applications. Sens. Actuators A Phys. 2003, 103, 271–283. [Google Scholar] [CrossRef]
- Giner, J.; Maeda, D.; Ono, K.; Shkel, A.M.; Sekiguchi, T. MEMS Gyroscope With Concentrated Springs Suspensions Demonstrating Single Digit Frequency Split and Temperature Robustness. J. Microelectromech. Syst. 2018, 28, 25–35. [Google Scholar] [CrossRef]
- Stork, M.; Mayer, D. Peristaltic pump with magnetoelastic drive. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Nga, T.; Lee, D.; Kim, S.; Lee, M.; Hwang, K.; Yang, Y.; Lee, K.Y. 40 dB-Isolation, 1.85 dB-Insertion Loss Full CMOS SPDT Switch with Body-Floating Technique and Ultra-Small Active Matching Network Using On-Chip Solenoid Inductor for BLE Applications. Electronics 2018, 7, 297. [Google Scholar] [CrossRef]
- Howe, D. Magnetic actuators. Sens. Actuators A Phys. 2000, 81, 268–274. [Google Scholar] [CrossRef]
- Li, C. Modelling, Control and Estimation Techniques For Micromachined Electrostatic Actuators Using Macro Magnetic Actuators. Ph.D. Dissertation, Auburn University, Montgomery, AL, USA, 2016. [Google Scholar]
- Rocha, L.; Cretu, E.; Wolffenbuttel, R. Behavioural analysis of the pull-in dynamic transition. J. Micromech. Microeng. 2004, 14, S37. [Google Scholar] [CrossRef]
- Weinberg, M.S.; Kourepenis, A. Error sources in in-plane silicon tuning-fork MEMS gyroscopes. J. Microelectromech. Syst. 2006, 15, 479–491. [Google Scholar] [CrossRef]
- Tan, J.; Sun, W.; Yeow, J. Internal model-based robust tracking control design for the MEMS electromagnetic micromirror. Sensors 2017, 17, 1215. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Yang, H.; Jenkins, L.L.; Dean, R.N.; Flowers, G.T.; Hung, J.Y. Enhanced-performance control of an electromagnetic solenoid system using a digital controller. IEEE Trans. Control. Syst. Technol. 2015, 24, 1805–1811. [Google Scholar] [CrossRef]
- Seeger, J.I.; Crary, S.B. Stabilization of electrostatically actuated mechanical devices. In Proceedings of the International Solid State Sensors and Actuators Conference (Transducers’97), Chicago, IL, USA, 19 June 1997; Volume 2, pp. 1133–1136. [Google Scholar]
- Li, C.; Dean, R.N.; Flowers, G.T. Analysis and dynamic simulation of the synthetic voltage division controller for extending the parallel plate actuator stable range of motion. Microsyst. Technol. 2017, 23, 1125–1130. [Google Scholar] [CrossRef]
- Chiou, J.; Lin, Y. A novel capacitance control design of tunable capacitor using multiple electrostatic driving electrodes. In Proceedings of the 2001 1st IEEE Conference on Nanotechnology, IEEE-NANO 2001 (Cat. No. 01EX516), Maui, HI, USA, 30 October 2001; pp. 319–324. [Google Scholar]
- Seeger, J.I.; Boser, B.E. Charge control of parallel-plate, electrostatic actuators and the tip-in instability. J. Microelectromech. Syst. 2003, 12, 656–671. [Google Scholar] [CrossRef] [Green Version]
- Seeger, J.I.; Boser, B.E. Negative capacitance for control of gap-closing electrostatic actuators. In Proceedings of the TRANSDUCERS’03, 12th International Conference on Solid-State Sensors, Actuators and Microsystems, Digest of Technical Papers (Cat. No. 03TH8664), Boston, MA, USA, 8–12 June 2003; Volume 1, pp. 484–487. [Google Scholar]
- Nagai, S.; Kawamura, A. Sensorless Position Control for Compact Dual Solenoid Actuator Using Disturbance Observer. In Proceedings of the 2019 IEEE International Conference on Mechatronics (ICM), Ilmenau, Germany, 18–20 March 2019; Volume 1, pp. 97–101. [Google Scholar]
- Kang, J.Y.; Jeon, Y.H. Position Control for Solenoid Valve using the Fractional Order Controller. J. Korea Inst. Electron. Commun. Sci. 2018, 13, 101–106. [Google Scholar]
- Poletkin, K.; Lu, Z.; Wallrabe, U.; Badilita, V. A new hybrid micromachined contactless suspension with linear and angular positioning and adjustable dynamics. J. Microelectromech. Syst. 2015, 24, 1248–1250. [Google Scholar] [CrossRef]
- Poletkin, K.; Korvink, J. Modeling a Pull-In Instability in Micro-Machined Hybrid Contactless Suspension. Actuators 2018, 7, 11. [Google Scholar] [CrossRef]
- Hosseini, M.; Zhu, G.; Peter, Y.A. A new formulation of fringing capacitance and its application to the control of parallel-plate electrostatic micro actuators. Analog. Integr. Circ. Signal Process. 2007, 53, 119–128. [Google Scholar] [CrossRef]
- Beeby, S. MEMS Mechanical Sensors; Artech House: Norwood, MA, USA, 2004. [Google Scholar]
- Yu, L.; Chang, T.N. Zero vibration on–off position control of dual solenoid actuator. IEEE Trans. Ind. Electron. 2010, 57, 2519–2526. [Google Scholar]
- Taghizadeh, M.; Ghaffari, A.; Najafi, F. Modeling and identification of a solenoid valve for PWM control applications. C. R. Mec. 2009, 337, 131–140. [Google Scholar] [CrossRef]
- Prudenziati, M. Handbook of sensors and actuators. In Thick Film Sensors; Elsevier: Amsterdam, The Netherlands, 1994; Volume 1. [Google Scholar]
- Hung, J.Y. Feedback control with posicast. IEEE Trans. Ind. Electron. 2003, 50, 94–99. [Google Scholar] [CrossRef]
- Roldán-Pérez, J.; García-Cerrada, A.; Rodríguez-Cabero, A.; Zamora-Macho, J. Comprehensive Design and Analysis of a State-Feedback Controller for a Dynamic Voltage Restorer. Energies 2018, 11, 1972. [Google Scholar] [CrossRef]
- Lu, M.C.; Fedder, G.K. Position control of parallel-plate microactuators for probe-based data storage. J. Microelectromech. Syst. 2004, 13, 759–769. [Google Scholar] [CrossRef]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Wang, X.; Hou, R.; Dean, R.N.; Zhou, L.; Dong, Y.; Song, D. Beyond Snap-In: A Hybrid Nonlinear Control Approach for Actuators Possessing a Square-Law Characteristic. Electronics 2019, 8, 863. https://doi.org/10.3390/electronics8080863
Li C, Wang X, Hou R, Dean RN, Zhou L, Dong Y, Song D. Beyond Snap-In: A Hybrid Nonlinear Control Approach for Actuators Possessing a Square-Law Characteristic. Electronics. 2019; 8(8):863. https://doi.org/10.3390/electronics8080863
Chicago/Turabian StyleLi, Chong, Xinning Wang, Renyu Hou, Robert N. Dean, Liqin Zhou, Yuhang Dong, and Dalei Song. 2019. "Beyond Snap-In: A Hybrid Nonlinear Control Approach for Actuators Possessing a Square-Law Characteristic" Electronics 8, no. 8: 863. https://doi.org/10.3390/electronics8080863



