Constant Envelope Modulation Techniques for Limited Power Millimeter Wave Links
Abstract
:1. Introduction
2. Communication Links in Millimeter Waves
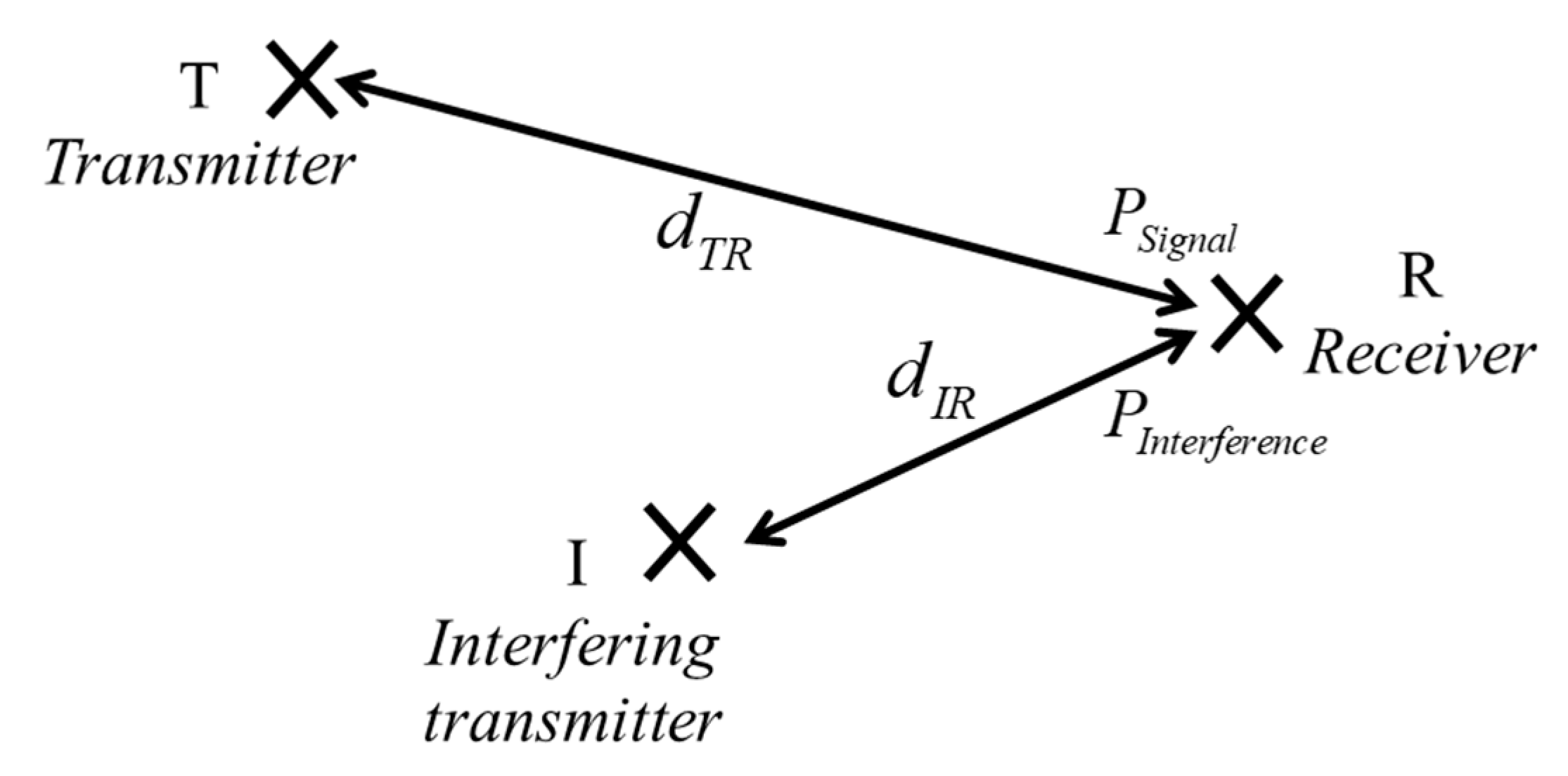
3. Error Rate Degradation in the Presence of Co-Channel Interference
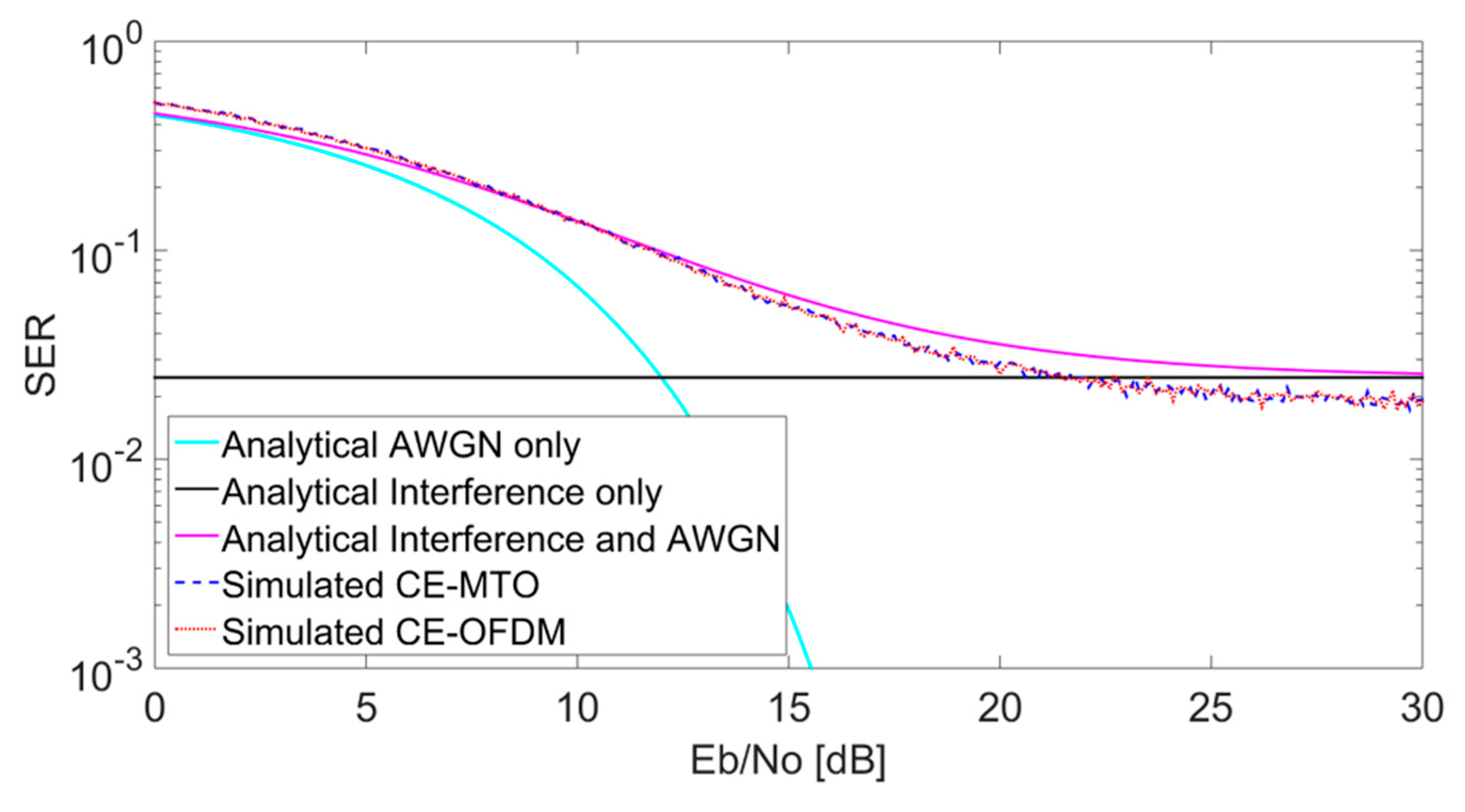
4. Performance of AWGN Channel in the Presence of CCI
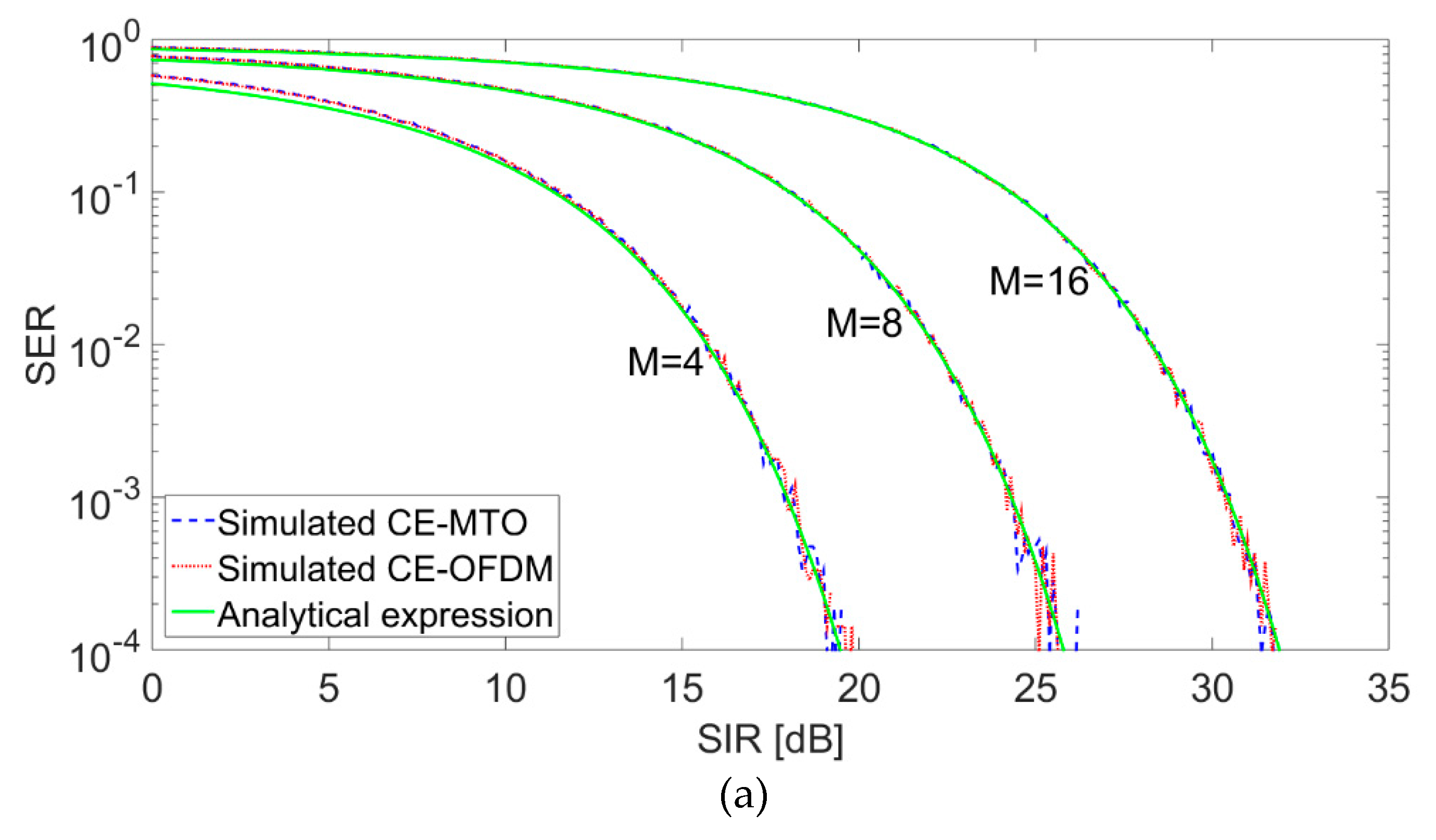
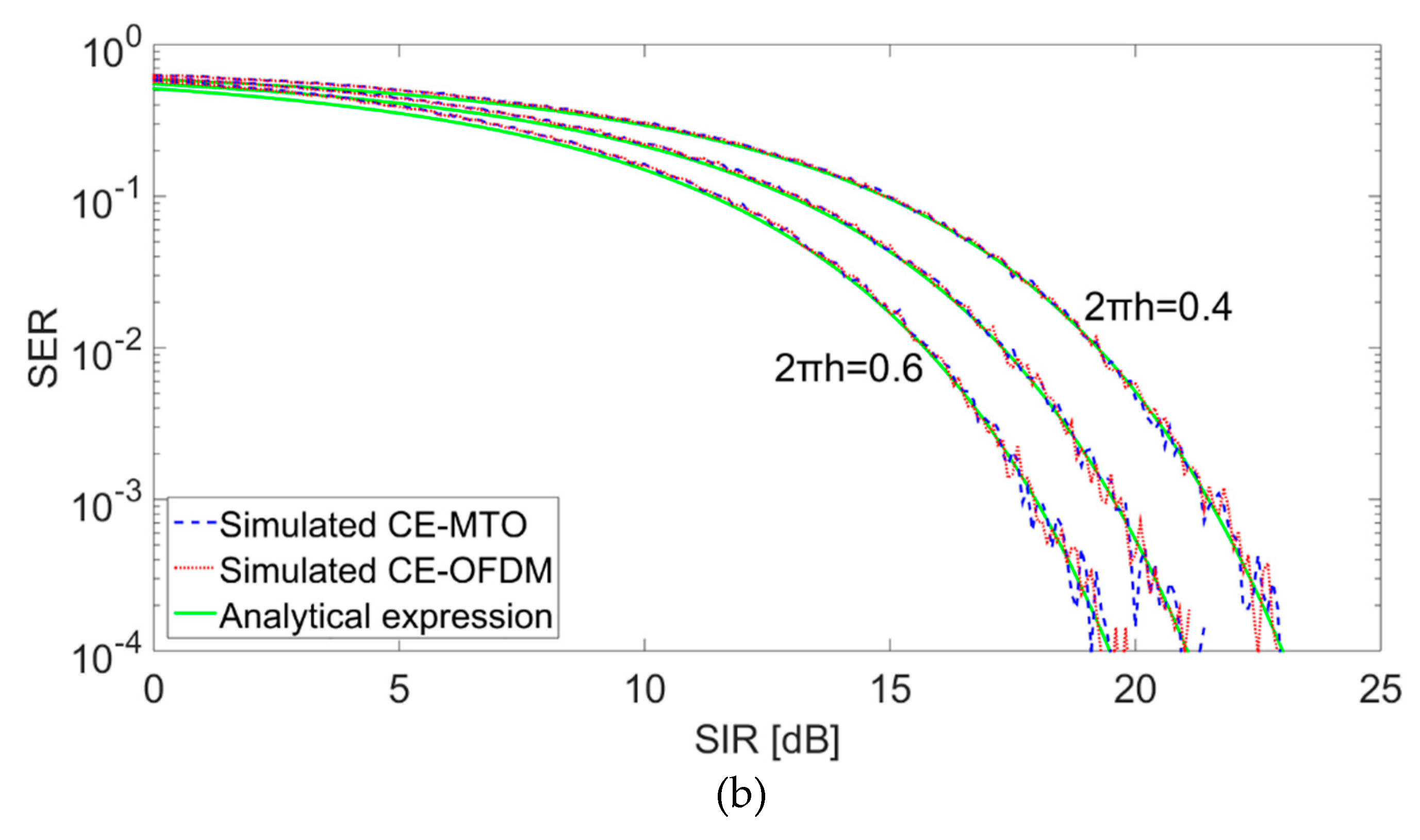
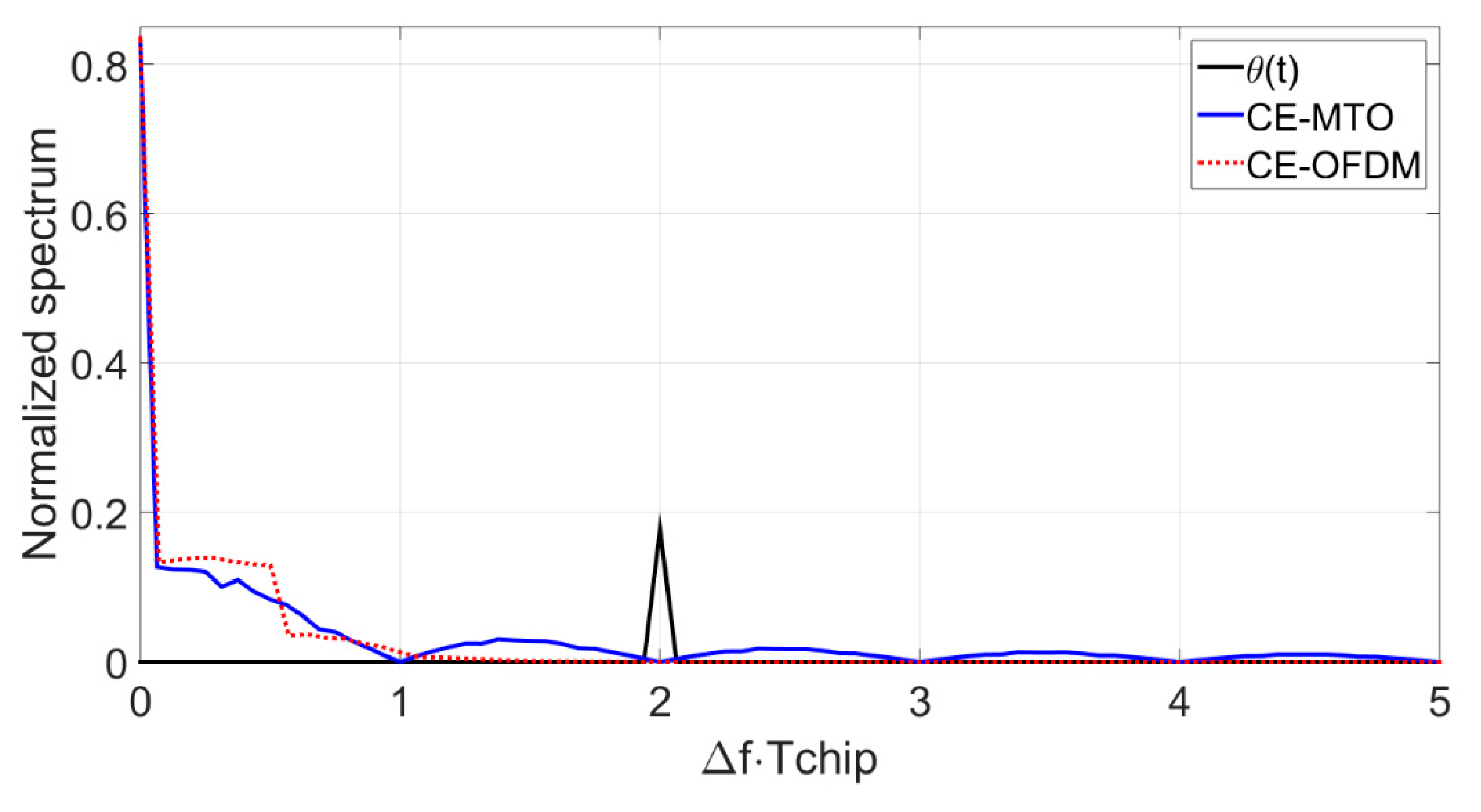
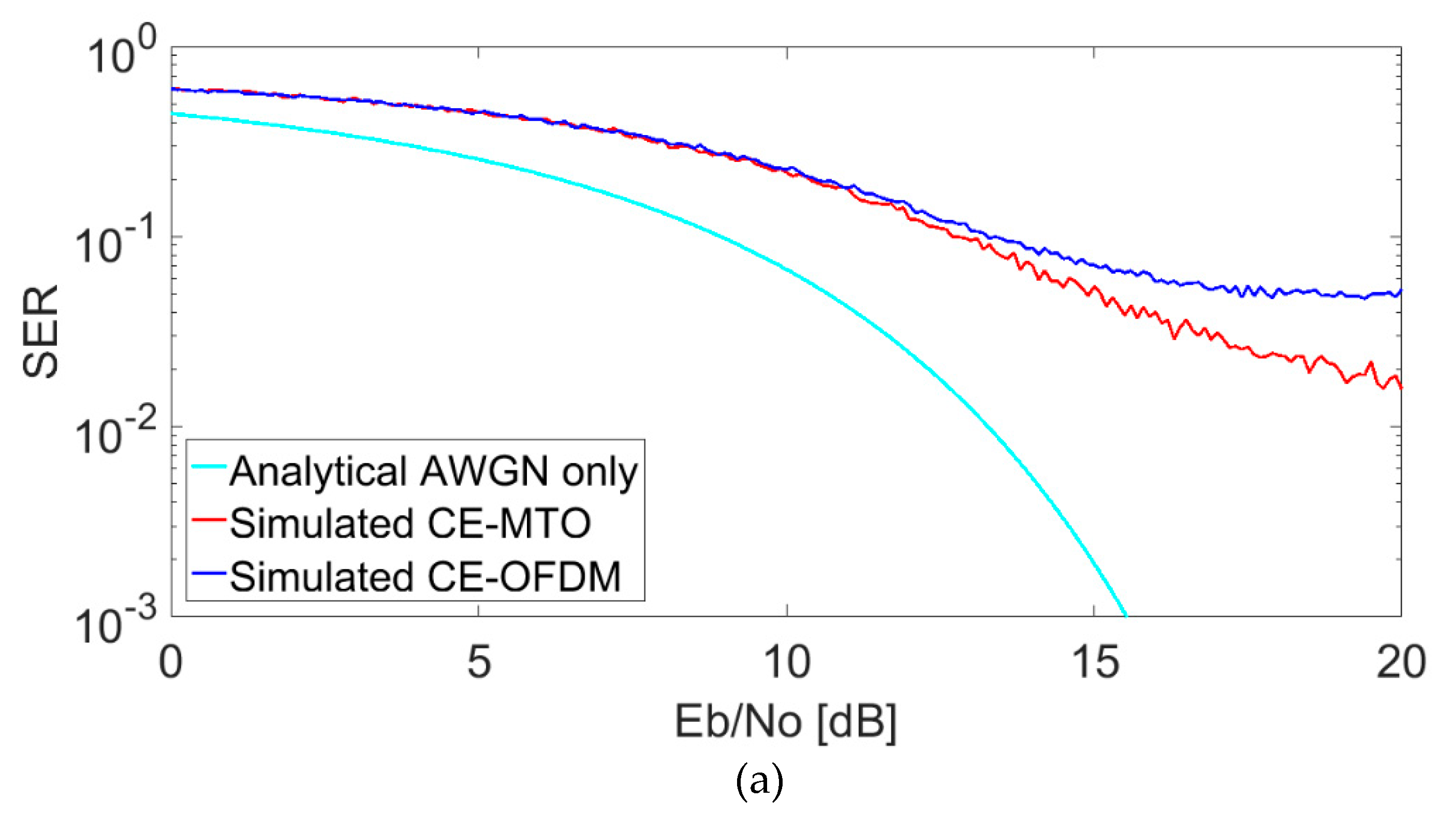
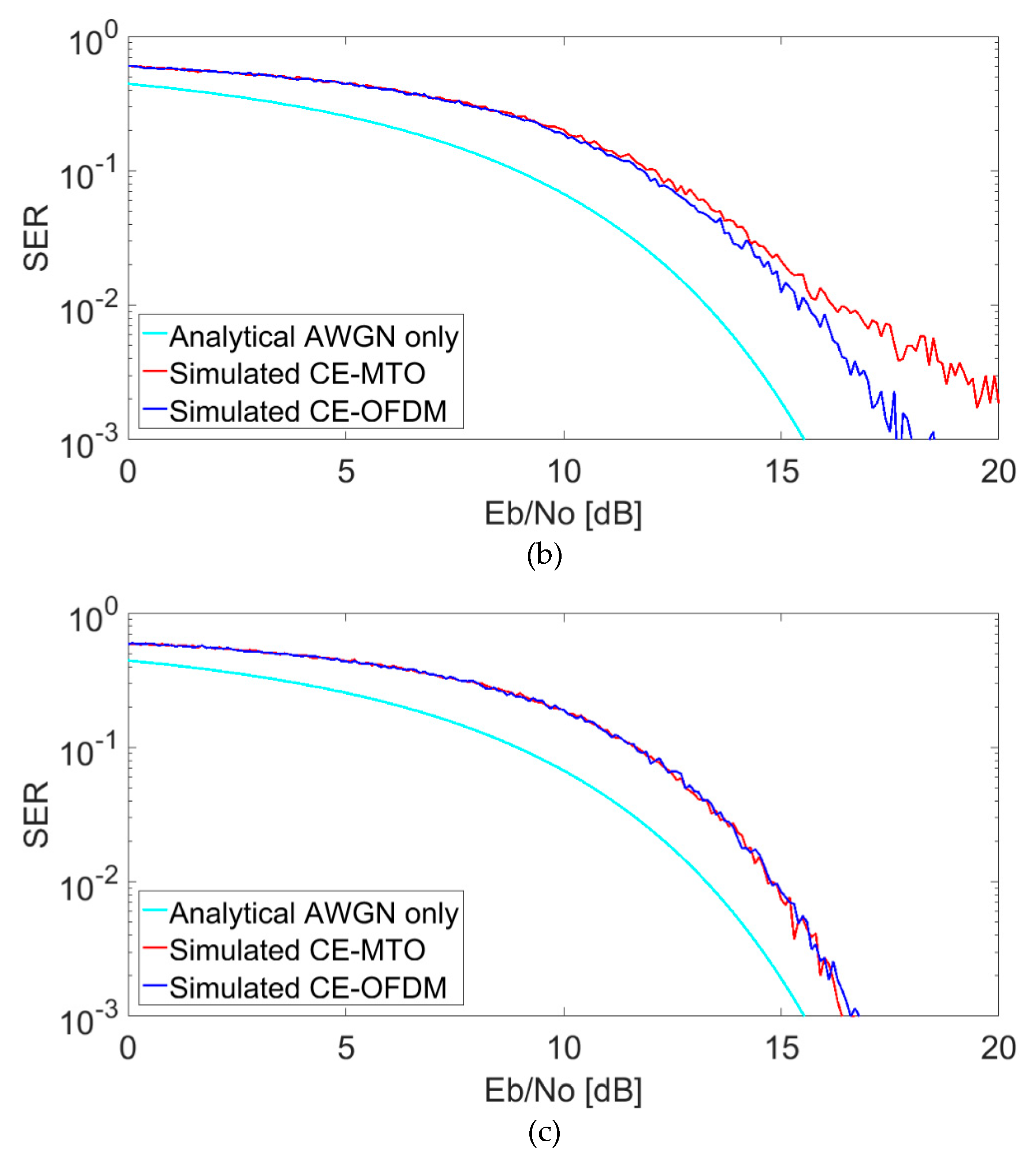
5. Results for Different CCI Scenarios
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Almeida, M.P.; Vargas, C.E.O.; Tamo, A.; Mello, L.S. Interference simulation between 5G and GSO–NGSO networks at 27–30 GHz range. In Proceedings of the 2019 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications (APWC), Granada, Spain, 9–13 September 2019; pp. 202–205. [Google Scholar]
- Cianca, E.; Rossi, T.; Yahalom, A.; Pinhasi, Y.; Farserotu, J.; Sacchi, C. EHF for Satellite Communications: The New Broadband Frontier. Proc. IEEE 2011, 99, 1858–1881. [Google Scholar] [CrossRef]
- Lutz, E.; Bischl, H.; Ernst, H.; Giggenbach, D.; Holzbock, M.; Jahn, A.; Werner, M. Development and Future Applications of Satellite Communications. In Emerging Location Aware Broadband Wireless Ad Hoc Networks; Ganesh, R., Kota, S.L., Pahlavan, K., Agustí, R., Eds.; Springer: Boston, MA, USA, 2004. [Google Scholar]
- Etinger, A.; Balal, N.; Litvak, B.; Einat, M.; Kapilevich, B.; Pinhasi, Y. Non-Imaging MM-Wave FMCW Sensor for Pedestrian Detection. IEEE Sens. J. 2014, 14, 1232–1237. [Google Scholar] [CrossRef]
- Yang, X.; Yang, J. A research on millimeter wave LFMCW radar for airfield object imaging. Int. J. Infrared Millim. Waves 2001, 22, 247–253. [Google Scholar] [CrossRef]
- Lin, S.K. Microwave and Millimeter-Wave Remote Sensing for Security Applications. Remote Sens. 2013, 5, 367–373. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.S.; Wu, L.; Ying, X.H. A Receiver in a Millimeter Wave Radiometer for Atmosphere Remote Sensing. Int. J. Infrared Millim. Waves 2009, 30, 259–269. [Google Scholar] [CrossRef]
- Byeon, C.W.; Park, C.S. Low-cost compact millimeter-wave antenna-in-package for short-range wireless communications. Microw. Opt. Technol. Lett. 2017, 59, 329–333. [Google Scholar] [CrossRef]
- Lin, W.; Chen, J.; Zhu, Y.; Kong, F.; Xu, J.; Kuai, L.; Yu, C.; Yan, P.; Hong, W. Wide band compact rf receiver for millimeter wave 5g mobile communication. In Proceedings of the 2016 IEEE International Conference on Ubiquitous Wireless Broadband (ICUWB), Nanjing, China, 16–19 October 2016; pp. 1–4. [Google Scholar]
- Balal, Y.; Pinhasi, Y. Atmospheric effects on millimeter and sub-millimeter (THz) Satellite Communication Paths. J. Infrared Millim. Terahertz Waves 2019, 40, 219–230. [Google Scholar] [CrossRef]
- Antes, J.; Kallfass, I. Performance Estimation for Broadband Multi-Gigabit Millimeter- and Sub-Millimeter-Wave Wireless Communication Links. IEEE Trans. Microw. Theory Tech. 2015, 63, 3288–3299. [Google Scholar] [CrossRef]
- Balal, N.; Pinhasi, G.A.; Pinhasi, Y. Atmospheric and Fog Effects on Ultra-Wide Band Radar Operating at Extremely High Frequencies. Sensors 2016, 16, 751. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M. Millimeter Wave Mobile Communications for 5G Cellular: It Will Work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef]
- Nordrum, A.; Clark, K. Everything you need to know about 5G. In IEEE Spectrum Magazine; Institute of Electrical and Electronic Engineers: Piscataway, NJ, USA, 2019. [Google Scholar]
- Zhu, J.; Wang, Z.; Li, Q.; Chen, H.; Ansari, N. Mitigating Intended Jamming in mmWave MIMO by Hybrid Beamforming. IEEE Wirel. Commun. Lett. 2019, 8, 1617–1620. [Google Scholar] [CrossRef]
- Hoffman, C. What is 5G, and how fast will it be? In How-To Geek website. How-To Geek LLC; Retrieved: 23 February 2019; Available online: https://www.howtogeek.com/340002/what-is-5g-and-how-fast-will-it-be/ (accessed on 3 December 2019).
- Chen, H.; Shao, H.; Chen, H. Angle-range-polarization-dependent beamforming for polarization sensitive frequency diverse array. EURASIP J. Adv. Signal Process. 2019, 2019, 23. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Chen, H.; Lam, W.H. Optimality of beamforming condition for multiple antenna systems with mean feedback. J. Wirel. Commun. Netw. 2011, 2011, 160. [Google Scholar] [CrossRef] [Green Version]
- Miller, S.L.; O’Dea, R.J. Peak power and bandwidth efficient linear modulation. IEEE Trans. Commun. 1998, 46, 1639–1648. [Google Scholar] [CrossRef]
- Ochiai, H. Power efficiency comparison of OFDM and single-carrier signals. Proc. IEEE VTC 2002, 2, 899–903. [Google Scholar]
- Wulich, D. Definition of efficient PAPR in OFDM. IEEE Commun. Lett. 2005, 9, 832–834. [Google Scholar] [CrossRef]
- Yixuan, H.; Su, H.; Shiyong, M.; Qu, L.; Dan, H.; Yuan, G.; Rong, S. Constant envelope OFDM RadCom fusion system. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 104. [Google Scholar]
- Qian, R.; Jiang, D.; Fu, W. Digital constant-envelope modulation scheme for radar using multicarrier OFDM signals. IET Signal Process. 2017, 11, 861–868. [Google Scholar] [CrossRef]
- Zou, W.Y.; Wu, Y. COFDM: An overview. IEEE Trans. Broadcast. 1995, 41, 1–8. [Google Scholar] [CrossRef]
- Thompson, S.C.; Ahmed, A.U.; Proakis, J.G.; Zeidler, J.R.; Geile, M.J. Constant envelope OFDM. IEEE Trans. Commun. 2008, 56, 1300–1312. [Google Scholar] [CrossRef]
- Balal, Y.; Pinchas, M.; Pinhasi, Y. Constant Envelope Phase Modulation Inspired by Orthogonal Waveforms. IEEE Commun. Lett. 2016, 20, 2169–2172. [Google Scholar] [CrossRef]
- Jadav, N.K. A Survey on OFDM Interference Challenge to improve its BER. In Proceedings of the 2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 29–31 March 2018; pp. 1052–1058. [Google Scholar]
- Aladwani, A.; Erdogan, E.; Gucluoglu, T. Impact of Co-Channel Interference on Two-Way Relaying Networks with Maximal Ratio Transmission. Electronics 2019, 8, 392. [Google Scholar] [CrossRef] [Green Version]
- Liolis, K.P.; Panagopoulos, A.D.; Cottis, P.G. Use of cell-site diversity to mitigate co-channel interference in 10-66 GHz broadband fixed wireless access networks. In Proceedings of the 2006 IEEE Radio and Wireless Symposium, San Diego, CA, USA, 17–19 October 2006; pp. 283–286. [Google Scholar]
- Ohwatari, Y.; Miki, N.; Asai, T.; Abe, T.; Taoka, H. Performance of advanced receiver employing interference rejection combining to suppress inter-cell interference in LTE-Advanced downlink. In Proceedings of the 2011 IEEE VTC—Fall, San Francisco, CA, USA, 5–8 September 2011; pp. 1–7. [Google Scholar]
- Sun, S.; Gao, Q.; Peng, Y.; Wang, Y.; Song, L. Interference management through CoMP in 3GPP LTE-Advanced networks. IEEE Wirel. Commun. Mag. 2013, 20, 59–66. [Google Scholar] [CrossRef]
- Kiyani, N.F.; Sridharan, V.; Dolmans, G. Co-Channel Interference Mitigation Technique for Non-Coherent OOK Receivers. IEEE Wirel. Commun. Lett. 2014, 3, 189–192. [Google Scholar]
- Li, T.; Mow, W.-H.; Lau, V.K.N.; Siu, M.; Cheng, R.; Murch, R. Robust joint interference detection and decoding for OFDM-based cognitive radio systems with unknown interference. IEEE J. Sel. Areas Commun. 2007, 25, 566–575. [Google Scholar] [CrossRef]
- Crane, R.K. Propagation phenomena affecting satellite communication systems operating in the centimeter and millimeter wavelength bands. Proc. IEEE 1971, 59, 173–188. [Google Scholar] [CrossRef]
- Crane, R.K. Fundamental limitations caused by RF propagation. Proc. IEEE 1981, 69, 196–209. [Google Scholar] [CrossRef]
- Ippolito, L.J. Radio propagation for space communication systems. Proc. IEEE 1981, 69, 697–727. [Google Scholar] [CrossRef]
- Liebe, H.J. Atmospheric EHF window transparencies near 35, 90, 140 and 220 GHz. IEEE Trans. Antennas Propag. 1983, 31, 127–135. [Google Scholar] [CrossRef]
- Bohlander, R.A.; McMillan, R.W. Atmospheric effects on near millimeter wave propagation. Proc. IEEE 1985, 73, 49–60. [Google Scholar] [CrossRef]
- Currie, N.C.; Brown, C.E. Principles and Applications of Millimeter-Wave Radar; Artech House: London, UK, 1987. [Google Scholar]
- Attenuation by atmospheric gases ITU-R P.676-11, 09/2016. Available online: https://www.itu.int/rec/R-REC-P.676-11-201609-I/en (accessed on 3 December 2019).
- Liebe, H.J. An updated model for millimeter wave propagation in moist air. Radio Sci. 1985, 20, 1069–1089. [Google Scholar] [CrossRef] [Green Version]
- Liebe, H.J. MPM—An atmospheric millimeter-wave propagation model. Int. J. Infrared Millim. Waves 1989, 10, 631–650. [Google Scholar] [CrossRef]
- Liebe, H.J.; Manabe, T.; Hufford, G.A. Millimeter-wave attenuation and delay rates due to fog / cloud conditions. IEEE Trans. Antennas Propag. 1989, 37, 1617–1623. [Google Scholar] [CrossRef]
- Liebe, H.J.; Hufford, G.A.; Manabe, T. A model for the complex permittivity of water at frequencies below 1THz. Int. J. Infrared Millim. Waves 1991, 12, 659–675. [Google Scholar] [CrossRef]
- Pinhasi, Y.; Yahalom, A.; Pinhasi, G.A. Propagation Analysis of Ultra-Short Pulses in Resonant Dielectric Media. J. Opt. Soc. Am. B 2009, 26, 2404–2413. [Google Scholar] [CrossRef]
- van Vleck, J.H. The absorption of microwaves by oxygen. Phys. Rev. 1947, 71, 413–424. [Google Scholar] [CrossRef]
- Rosenkranz, P.W. Shape of the 5 mm oxygen band in the atmosphere. IEEE Trans. Antennas Propag. 1975, 23, 498–506. [Google Scholar] [CrossRef]
- Liebe, H.J.; Rosenkranz, P.W.; Hufford, G.A. Atmospheric 60 GHz oxygen spectrum: New laboratory measurements and line parameters. J. Quant. Spectrosc. Radiat. Transf. 1992, 48, 629–643. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balal, Y.; Pinchas, M.; Pinhasi, Y. Constant Envelope Modulation Techniques for Limited Power Millimeter Wave Links. Electronics 2019, 8, 1521. https://doi.org/10.3390/electronics8121521
Balal Y, Pinchas M, Pinhasi Y. Constant Envelope Modulation Techniques for Limited Power Millimeter Wave Links. Electronics. 2019; 8(12):1521. https://doi.org/10.3390/electronics8121521
Chicago/Turabian StyleBalal, Yael, Monika Pinchas, and Yosef Pinhasi. 2019. "Constant Envelope Modulation Techniques for Limited Power Millimeter Wave Links" Electronics 8, no. 12: 1521. https://doi.org/10.3390/electronics8121521




