Site-Specific Propagation Loss Prediction in 4.9 GHz Band Outdoor-to-Indoor Scenario
Abstract
:1. Introduction
2. Proposal of Propagation Loss Prediction Method for Outdoor-to-Indoor Scenario
2.1. Proposed Extension Method for Ray-Tracing Simulation
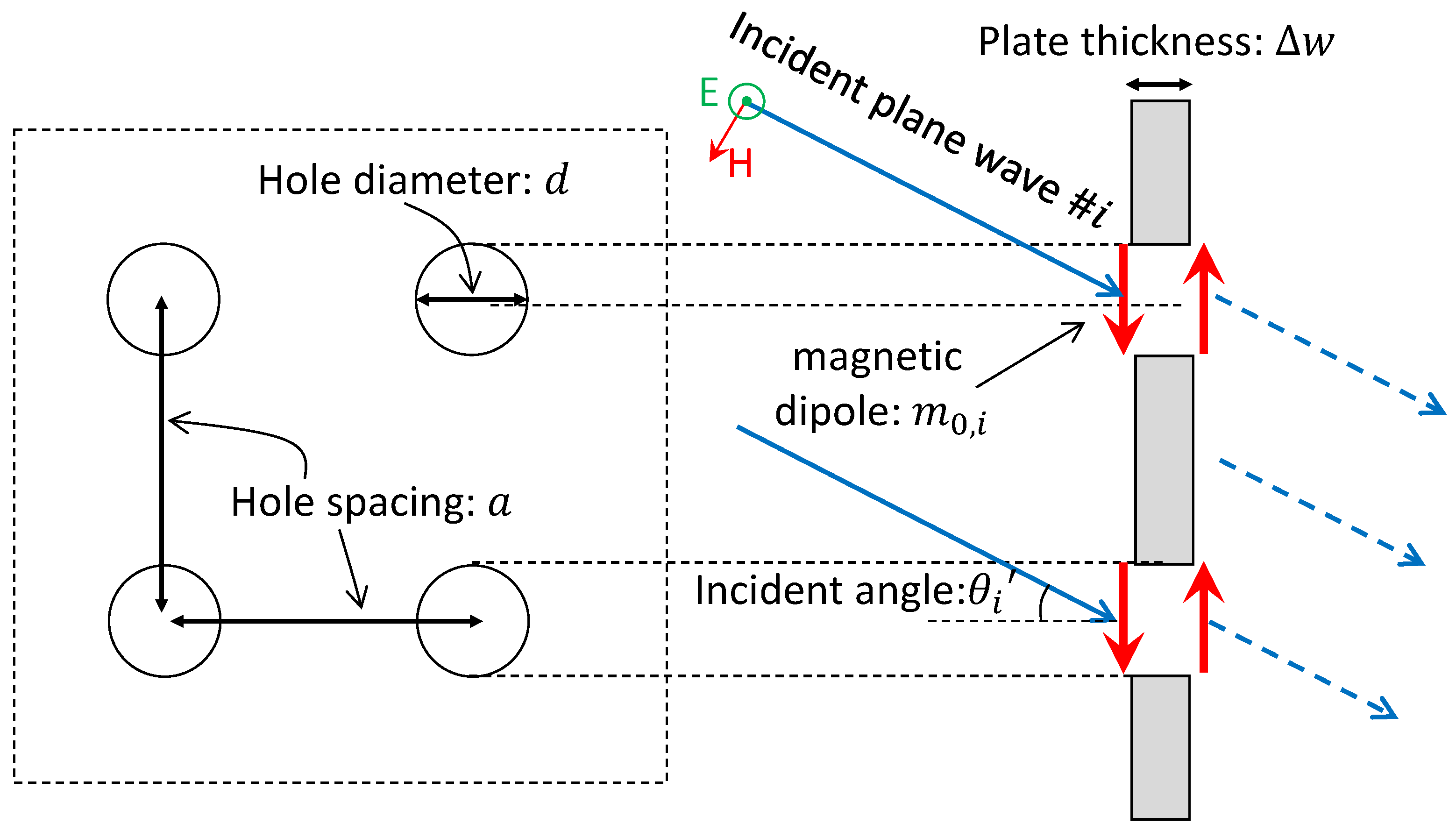
2.2. Fresnel Zone Shielding Loss Calculation
2.3. Transmission Loss Calculation by Equivalent Dielectric Plate
3. 4.9 GHz Band Radio Measurement for Penetration Loss Characteristics from Window
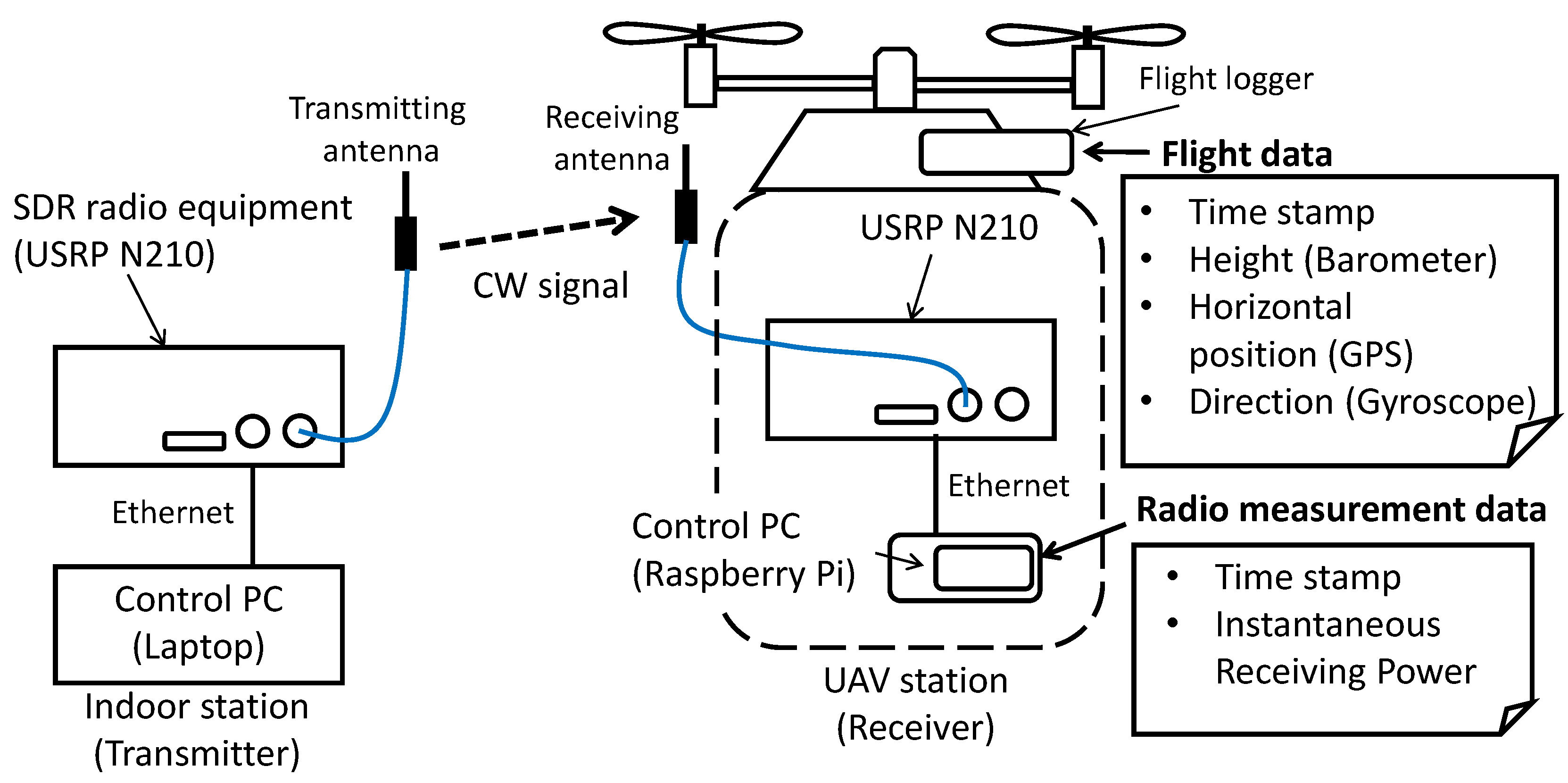
3.1. Radio Measurement System Using UAV
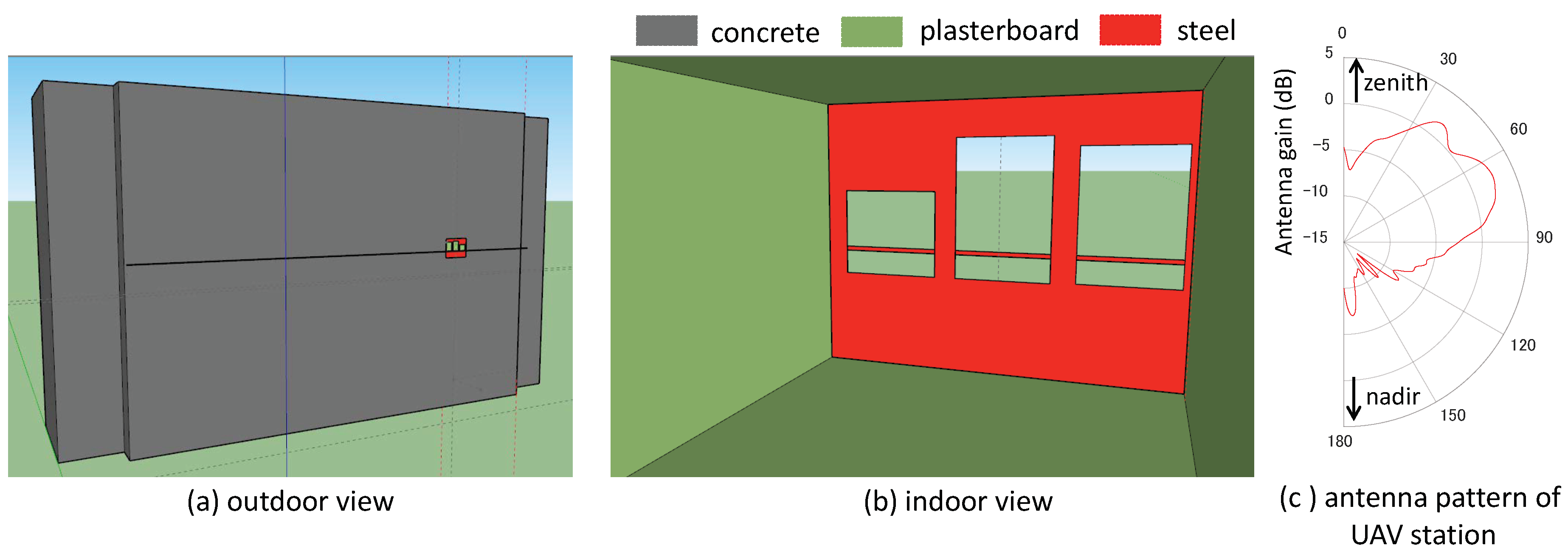
3.2. Measurement Method
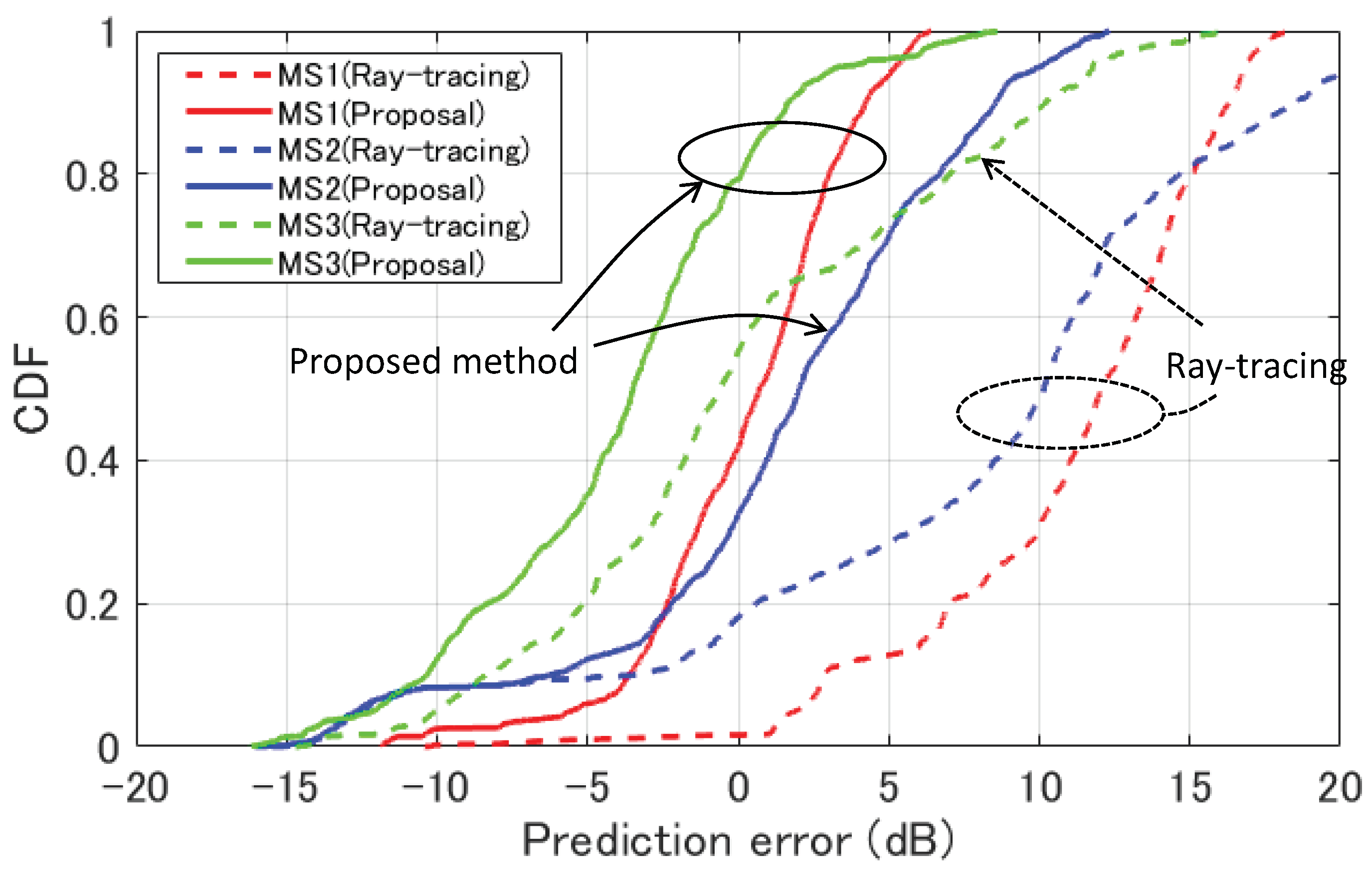
4. Penetration Loss Prediction Results
4.1. Ray-Tracing Simulation Method
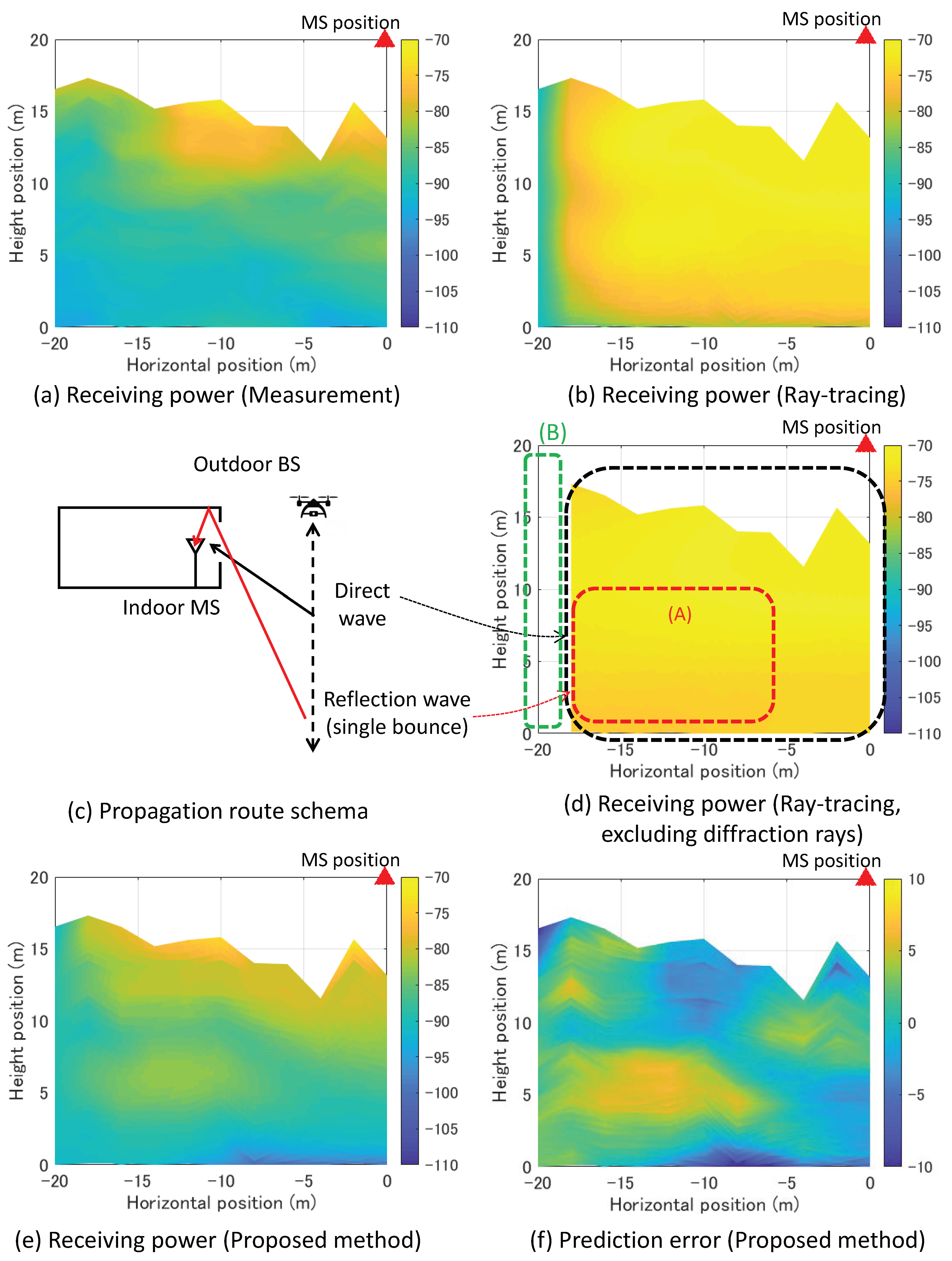
4.2. Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Omote, H.; Miyashita, M.; Yamaguchi, R. Measurement of time-spatial characteristics between indoor spaces in different LOS buildings. In Proceedings of the 2015 International Symposium on Antennas and Propagation (ISAP), Hobart, Australia, 9–12 November 2015; pp. 1–4. [Google Scholar]
- de Jong, Y.L.C.; Koelen, M.H.J.L.; Herben, M.H.A.J. A building-transmission model for improved propagation prediction in urban microcells. IEEE Trans. Veh. Technol. 2004, 53, 490–502. [Google Scholar] [CrossRef]
- Axiotis, D.I.; Theologou, M.E. An empirical model for predicting building penetration loss at 2 GHz for high elevation angles. IEEE Antennas Wirel. Propag. Lett. 2003, 2, 234–237. [Google Scholar] [CrossRef]
- Chee, K.L.; Anggraini, A.; Kaiser, T.; Kurner, T. Outdoor-to-indoor propagation loss measurements for broadband wireless access in rural areas. In Proceedings of the 5th European Conference on Antennas and Propagation (EUCAP), Rome, Italy, 11–15 April 2011; pp. 1376–1380. [Google Scholar]
- Alatossava, M.; Suikkanen, E.; Veli-Matti, J.M.H.; Ylitalo, J. Extension of COST 231 Path Loss Model in Outdoor-to-Indoor Environment to 3.7 GHz and 5.25 GHz. In Proceedings of the 11th International Symposium on Wireless Personal Multimedia Communications, Saariselkä, Finland, 23–27 September 2008; pp. 1–4. [Google Scholar]
- Medbo, J.; Furuskog, J.; Riback, M.; Berg, J.E. Multi-frequency path loss in an outdoor to indoor macrocellular scenario. In Proceedings of the 2009 3rd European Conference on Antennas and Propagation, Berlin, Germany, 23–27 March 2009; pp. 3601–3605. [Google Scholar]
- Okamoto, H.; Kitao, K.; Ichitsubo, S. Outdoor-to-Indoor Propagation Loss Prediction in 800-MHz to 8-GHz Band for an Urban Area. IEEE Trans. Veh. Technol. 2009, 58, 1059–1067. [Google Scholar] [CrossRef]
- Roivainen, A.; Hovinen, V.; Tervo, N.; Latva-aho, M. Outdoor-to-indoor path loss modeling at 10.1 GHz. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Imai, T.; Kitao, K.; Tran, N.; Omaki, N.; Okumura, Y.; Nishimori, K. Outdoor-to-Indoor path loss modeling for 0.8 to 37 GHz band. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–4. [Google Scholar] [CrossRef]
- COST 231. COST Action 231—Digital Mobile Radio Towards Future Generation Systems—Final Report; Office for Official Publications of the European Communities: Luxembourg, 1999. [Google Scholar]
- ITU-R Recommendation P. 2109. Prediction of Building Entry Loss. 2017. Available online: https://www.itu.int/rec/R-REC-P.2109/en (accessed on 21 November 2019).
- McKown, J.W.; Hamilton, R.L. Ray tracing as a design tool for radio networks. IEEE Netw. 1991, 5, 27–30. [Google Scholar] [CrossRef]
- Seidel, S.Y.; Rappaport, T.S. Site-specific propagation prediction for wireless in-building personal communication system design. IEEE Trans. Veh. Technol. 1994, 43, 879–891. [Google Scholar] [CrossRef]
- Costa, E. Ray tracing based on the method of images for propagation simulation in cellular environments. In Proceedings of the Tenth International Conference on Antennas and Propagation (Conf. Publ. No. 436), Edinburgh, UK, 14–17 April 1997; Volume 2, pp. 204–209. [Google Scholar] [CrossRef]
- Rodriguez, I.; Nguyen, H.C.; Sorensen, T.B.; Zhao, Z.; Guan, H.; Mogensen, P. A novel geometrical height gain model for line-of-sight urban micro cells below 6 GHz. In Proceedings of the 2016 International Symposium on Wireless Communication Systems (ISWCS), Poznan, Poland, 20–23 September 2016; pp. 393–398. [Google Scholar] [CrossRef]
- Inomata, M.; Sasaki, M.; Onizawa, T.; Kitao, K.; Imai, T. Effect of reflected waves from outdoor buildings on outdoor-to-indoor path loss in 0.8 to 37 GHz band. In Proceedings of the 2016 International Symposium on Antennas and Propagation (ISAP), Okinawa, Japan, 24–28 October 2016; pp. 62–63. [Google Scholar]
- Hasegawa, K.; Taga, T. A proposal of double aperture field method, and its experimental confirmation. In Proceedings of the 2015 International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Hsinchu, Taiwan, 16–18 November 2015; pp. 1–2. [Google Scholar] [CrossRef]
- Imai, T.; Okumura, Y. Study on hybrid method of ray-tracing and physical optics for outdoor-to-indoor propagation channel prediction. In Proceedings of the 2014 IEEE International Workshop on Electromagnetics (iWEM), Sapporo, Japan, 4–6 August 2014; pp. 249–250. [Google Scholar] [CrossRef]
- Saito, K.; Fan, Q.; Keerativoranan, N.; Takada, J. Vertical and Horizontal Building Entry Loss Measurement in 4.9 GHz Band by Unmanned Aerial Vehicle. IEEE Wirel. Commun. Lett. 2019, 8, 444–447. [Google Scholar] [CrossRef]
- Saito, K.; Fan, Q.; Keerativoranan, N.; Takada, J. 4.9 GHz Band Outdoor to Indoor Propagation Loss Analysis in High Building Environment Using Unmanned Aerial Vehicle. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–4. [Google Scholar]
- Saito, K.; Fan, Q.; Keerativoranan, N.; Takada, J. 4.9 GHz Band Outdoor-to-Indoor Radio Propagation Measurement by an Unmanned Aerial Vehicle. In Proceedings of the 2018 IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Nagoya, Japan, 29–31 August 2018. [Google Scholar] [CrossRef]
- 3GPP TS38.913 V14.3.0. Access, Evolved Universal Terrestrial Radio. Study on Scenarios and Requirements for Next Generation Access Technologies. 2017. Available online: https://www.3gpp.org/DynaReport/38-series.htm (accessed on 21 November 2019).
- 3GPP TS38.101-1 16.1.0 Access, Evolved Universal Terrestrial Radio. NR: User Equipment (UE) Radio Transmission and Reception; Part 1: Range 1 Standalone. 2019. Available online: https://www.3gpp.org/DynaReport/38-series.htm (accessed on 21 November 2019).
- Bethe, H.A. Theory of Diffraction by Small Holes. Phys. Rev. 1944, 66, 163–182. [Google Scholar] [CrossRef]
- Culshaw, W. Reflectors for a Microwave Fabry-Perot Interferometer. IRE Trans. Microw. Theory Tech. 1959, 7, 221–228. [Google Scholar] [CrossRef]
- McNamara, D.A.; Pistorius, C.W.I.; Malherbe, J.A.G. Introduction to the Uniform Geometrical Theory of Diffraction; Artech House on Demand: Boston, MA, USA, 1990. [Google Scholar]
- Kouyoumjian, R.G.; Pathak, P.H. A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface. Proc. IEEE 1974, 62, 1448–1461. [Google Scholar] [CrossRef]
- Molisch, A.F. Wireless Communications, 2nd ed.; Wiley Publishing: Hoboken, NJ, USA, 2011. [Google Scholar]
- Otoshi, T.Y. A Study of Microwave Leakage through Perforated Flat Plates (Short Papers). IEEE Trans. Microw. Theory Tech. 1972, 20, 235–236. [Google Scholar] [CrossRef]
- Yamamoto, S.; Hamano, A.; Hatakeyama, K.; Iwai, T. EM-wave transmission characteristic of periodically perforated metal plates. In Proceedings of the 2016 IEEE 5th Asia-Pacific Conference on Antennas and Propagation (APCAP), Kaohsiung, Taiwan, 26–29 July 2016; pp. 7–8. [Google Scholar] [CrossRef]
- McDonald, N.A. Electric and Magnetic Coupling through Small Apertures in Shield Walls of Any Thickness. IEEE Trans. Microw. Theory Tech. 1972, 20, 689–695. [Google Scholar] [CrossRef]
- Ettus Research. Universal Software Radio Peripheral N210. Available online: https://www.ettus.com/product/details/UN210-KIT (accessed on 21 November 2019).
- The Raspberry Pi Foundation. Raspberry Pi 2 Model B. Available online: https://www.raspberrypi.org/products/raspberry-pi-2-model-b/ (accessed on 21 November 2019).
- Kozo Keikaku Enginerring Inc. RapLab, Radio Wave Propagation Analysis Tool. Available online: https://www.kke.co.jp/en/solution/theme/raplab.html/ (accessed on 21 November 2019).





| Radio Equipment | |
|---|---|
| Center frequency | 4.89 GHz |
| Transmit power | 11.5 dBm |
| Transmit signal | CW |
| Receiver dynamic range | From −120 dBm to −30 dBm |
| Tx/Rx antennas | Dipole (2.14 dBi) |
| Polarization | Vertical polarization |
| Antenna height (UAV) | From 0 m to 15 m |
| Indoor floor height | 20 m (building), 7 m (cafeteria) |
| Antenna height (indoor) | 1.7 m from floor |
| Receiver sampling rate | 100 Hz |
| Moving average | 2 m (horizontal) 1 m (vertical) |
| UAV equipment | |
| Flight controller | DJI NAZA-M v2 |
| Flight recorder | DJI iOSD MARK II |
| UAV sensor | 100 Hz |
| recording rate | |
| Ray-Tracing Simulation | |
|---|---|
| Calculation Method | Method of Imaging |
| Number of reflections | 3 |
| Number of diffractions | 1 |
| Number of transmissions | 1 |
| Material parameters | Concrete: |
| (: relative permittivity | Ground: |
| : conductivity) | Metal: |
| Plaster board: | |
| Equivalent dielectric plate calculation | |
| Plate width | 3 mm |
| Hole diameter d | 20 mm |
| Hole spacing a | 30 mm |
| Ray-Tracing | Proposed Method | |||||||
|---|---|---|---|---|---|---|---|---|
| MS1 | MS2 | MS3 | Total | MS1 | MS2 | MS3 | Total | |
| mean (dB) | 11.1 | 8.0 | 0.4 | 7.0 | 0.3 | 1.5 | −3.9 | −0.5 |
| standard deviation (dB) | 4.8 | 8.8 | 6.7 | 8.2 | 3.4 | 6.0 | 4.8 | 5.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saito, K.; Fan, Q.; Keerativoranan, N.; Takada, J.-i. Site-Specific Propagation Loss Prediction in 4.9 GHz Band Outdoor-to-Indoor Scenario. Electronics 2019, 8, 1398. https://doi.org/10.3390/electronics8121398
Saito K, Fan Q, Keerativoranan N, Takada J-i. Site-Specific Propagation Loss Prediction in 4.9 GHz Band Outdoor-to-Indoor Scenario. Electronics. 2019; 8(12):1398. https://doi.org/10.3390/electronics8121398
Chicago/Turabian StyleSaito, Kentaro, Qiwei Fan, Nopphon Keerativoranan, and Jun-ichi Takada. 2019. "Site-Specific Propagation Loss Prediction in 4.9 GHz Band Outdoor-to-Indoor Scenario" Electronics 8, no. 12: 1398. https://doi.org/10.3390/electronics8121398





