Analog Memristive Characteristics and Conditioned Reflex Study Based on Au/ZnO/ITO Devices
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Confirmation of Memristor and I–V Characteristics
3.2. Memorizing Characteristics
3.3. LTspice Models and Simulation
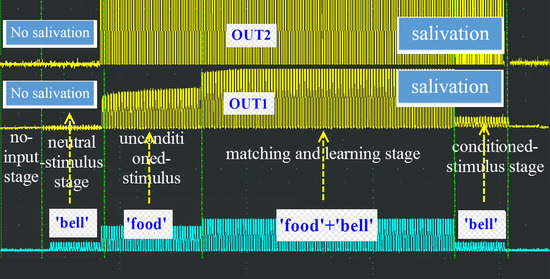
3.4. Conditioned Reflex Simulation and Circuit Experiments
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lv, F.; Yang, R.; Guo, X. Analog and digital reset processes observed in Pt/CuO/Pt memristive devices. Solid State Ion. 2017, 303, 161–166. [Google Scholar] [CrossRef]
- Ravichandran, V.; Li, C.; Banagozar, A.; Yang, J.J.; Xia, Q.F. Artificial neural networks based on memristive devices. Sci. China Inform. Sci. 2018, 61, 1–14. [Google Scholar] [CrossRef]
- Pershin, Y.V.; Ventra, D.M. Practical approach to programmable analog circuits with memristors. IEEE Trans. Circuits Syst. I Reg. Pap. 2010, 57, 1857–1864. [Google Scholar] [CrossRef]
- Jo, S.H.; Chang, T.; Ebong, I.; Bhadviya, B.B.; Mazumder, P.; Lu, W. Nanoscale memristor device as synapse in neuromorphic systems. Nano Lett. 2010, 10, 1297–1301. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Sah, M.P.; Yang, C.; Roska, T.; Chua, L.O. Neural synaptic weighting with a pulse-based memristor circuit. Trans. Circuits Syst. I Reg. Pap. 2012, 59, 148–158. [Google Scholar] [CrossRef]
- Ouyang, J.; Chu, C.W.; Szmanda, C.R.; Ma, L.; Yang, Y. Programmable polymer thin film and non-volatile memory device. Nat. Mater. 2004, 3, 918–922. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Mccreery, R.L. Solid-state electrochemistry in molecule/TiO2 molecular heterojunctions as the basis of the TiO2 “memristor”. J. Electrochem. Soc. 2009, 156, 29–37. [Google Scholar] [CrossRef]
- Batas, D.; Fiedler, H. A memristor spice implementation and a new approach for magnetic flux controlled memristor modeling. IEEE Trans. Nanotechnol. 2011, 10, 250–255. [Google Scholar] [CrossRef]
- Rak, A.; Cserey, G. Macromodeling of the memristor in SPICE. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2010, 29, 632–636. [Google Scholar] [CrossRef]
- Hu, X.; Feng, G.; Li, H.; Chen, Y.; Duan, S. An adjustable memristor model and its application in small-world neural networks. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014. [Google Scholar]
- Sun, Y.; Yan, X.; Zheng, X.; Liu, Y.; Shen, Y.; Ding, Y.; Zhang, Y. Effect of carrier screening on ZnO-based resistive switching memory devices. Nano Res. 2017, 10, 77–86. [Google Scholar] [CrossRef]
- Murali, S.; Rajachidambaram, J.S.; Han, S.Y.; Chang, C.H.; Herman, G.S.; Conley, J.F.J. Resistive switching in zinc–tin-oxide. Solid State Electron. 2013, 79, 248–252. [Google Scholar] [CrossRef]
- Xu, Z.; Jin, K.; Gu, L.; Jin, Y.; Ge, C.; Wang, C.; Guo, H.; Lu, R.; Zhao, H.; Yang, G. Evidence for a crucial role played by oxygen vacancies in LaMnO3 resistive switching memories. Small. 2012, 8, 1279–1284. [Google Scholar] [CrossRef] [PubMed]
- Fullam, S.; Ray, N.J.; Karpov, E.G. Cyclic resistive switching effect in plasma electrolytically oxidized mesoporous Pt/TiO2 structures. Superlatt. Microstruct. 2015, 82, 378–383. [Google Scholar] [CrossRef]
- Adhikari, S.P.; Sah, M.P.; Kim, H.; Chua, L. Three fingerprints of memristor. Trans. Circuits Syst. I Reg. Pap. 2013, 60, 3008–3021. [Google Scholar] [CrossRef]
- Chua, L. Resistance switching memories are memristors. Appl. Phys. A 2011, 102, 765–781. [Google Scholar] [CrossRef]
- Simanjuntak, F.M.; Panda, D.; Wei, K.H.; Tseng, T.Y. Status and prospects of ZnO-based resistive switching memory devices. Nanoscale Res. Lett. 2016, 11, 368–385. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Shen, Z.; Wu, Y.; Wang, X.; Zhang, S.; Shi, X.; Zeng, H. Amorphous ZnO based resistive random access memory. RSC Adv. 2016, 6, 7867–7872. [Google Scholar] [CrossRef]
- Huang, C.H.; Huang, J.S.; Lai, C.C.; Huang, H.W.; Lin, S.J.; Chueh, Y.L. Manipulated transformation of filamentary and homogeneous resistive switching on ZnO thin film memristor with controllable multistate. ACS Appl. Mater. Interfaces 2013, 5, 6017–6023. [Google Scholar] [CrossRef] [PubMed]
- Shang, D.S.; Wang, Q.; Chen, L.D.; Dong, R.; Li, X.M.; Zhang, W.Q. Effect of carrier trapping on the hysteretic current-voltage characteristics in Ag/La0.7Ca0.3MnO3/Pt heterostructures. Phys. Rev. B 2006, 73, 245427. [Google Scholar] [CrossRef]
- Nüesch, F.; Forsythe, E.W.; Le, Q.T.; Gao, Y.; Rothber, L.J. Importance of indium tin oxide surface acido basicity for charge injection into organic materials based light emitting diodes. J. Appl. Phys. 2000, 87, 7973–7980. [Google Scholar]
- Fang, Y.J.; Sha, J.; Wang, Z.L.; Wan, Y.T.; Xia, W.W.; Wang, Y.W. Behind the change of the photoluminescence property of metal-coated ZnO nanowire arrays. Appl. Phys. Lett. 2011, 98, 033103. [Google Scholar] [CrossRef]
- Ielmini, D. Brain-inspired computing with resistive switching memory (RRAM): Devices, synapses and neural networks. Microelectron. Eng. 2018, 190, 44–53. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.; Jo, S.H.; Kim, K.H.; Sheridan, P.; Gaba, S.; Lu, W. Synaptic behaviors and modeling of a metal oxide memristive device. Appl. Phys. A 2011, 102, 857–863. [Google Scholar] [CrossRef]
- Pan, R.; Li, J.; Zhuge, F.; Zhu, L.; Liang, L.; Zhang, H.; Gao, J.; Cao, H.; Fu, B.; Li, K. Synaptic devices based on purely electronic memristors. Appl. Phys. Lett. 2016, 108, 382001. [Google Scholar] [CrossRef]
- Biolek, Z.; Biolek, D.; Biolkova, V. SPICE model of memristor with nonlinear dopant drift. Radioengeering 2009, 18, 210–214. [Google Scholar]
- Pershin, Y.V.; Ventra, M.D. Experimental demonstration of associative memory with memristive neural networks. Neural Netw. 2010, 23, 881–886. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yakopcic, C.; Taha, T.M. Subramanyam, G.; Pino, R.E.; Rogers, S. A memristor device model. IEEE Electron Device Lett. 2011, 32, 1436–1438. [Google Scholar] [CrossRef]
- Laiho, M.; Lehtonen, E.; Russel, A.; Dudek, P. Memristive synapses are becoming reality. Neuromorphic Eng. 2010. [Google Scholar] [CrossRef]
- Lehtonen, E.; Poikonen, J.; Laiho, M.; Wei, L. Time-dependency of the threshold voltage in memristive devices. IEEE Int. Symp. Circuits Syst. 2011, 19, 2245–2248. [Google Scholar]
- Yu, J.; Mu, X.; Xi, X.; Wang, S. A memristor model with piecewise window function. Radioengineering 2013, 22, 969–974. [Google Scholar]
- Prodromakis, T.; Peh, B.; Papavassiliou, C.; Toumazou, C. A versatile memristor model with nonlinear dopant kinetics. IEEE Trans. Electron Devices 2011, 58, 3099–3105. [Google Scholar] [CrossRef]
- Wang, F.Z.; Helian, N.; Wu, S.; Yang, X.; Guo, Y.K.; Lim, G.; Rashid, M.M. Delayed switching applied to memristor neural networks. J. Appl. Phys. 2012, 111, 07E317. [Google Scholar] [CrossRef]
- Ziegler, M.; Soni, R.; Patelczyk, T.; Ignatov, M.; Bartsch, T.; Meuffels, P.; Kohlstedt, H. An electronic version of pavlov’s dog. Adv. Funct. Mater. 2012, 22, 2744–2749. [Google Scholar] [CrossRef]




| No | Structure | Current | Endurance | Roff/Ron | Retention |
|---|---|---|---|---|---|
| 1 | Pt/ZnO/Pt | 30 mA | 100 | 103–104 | not available |
| 2 | Ru/ZnO/Pt | 10 mA | 200 | 61 | 104 |
| 3 | Ag/ZnO/Pt | 10 mA | 40 | 100 | not available |
| 4 | Cu/ZnO/ITO | not available | 300 | >20 | not available |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, T.; Rao, J.; Tang, X.; Yang, L.; Liu, N. Analog Memristive Characteristics and Conditioned Reflex Study Based on Au/ZnO/ITO Devices. Electronics 2018, 7, 141. https://doi.org/10.3390/electronics7080141
Cheng T, Rao J, Tang X, Yang L, Liu N. Analog Memristive Characteristics and Conditioned Reflex Study Based on Au/ZnO/ITO Devices. Electronics. 2018; 7(8):141. https://doi.org/10.3390/electronics7080141
Chicago/Turabian StyleCheng, Tiedong, Jingjing Rao, Xingui Tang, Lirong Yang, and Nan Liu. 2018. "Analog Memristive Characteristics and Conditioned Reflex Study Based on Au/ZnO/ITO Devices" Electronics 7, no. 8: 141. https://doi.org/10.3390/electronics7080141