Super-Twisting Extended State Observer and Sliding Mode Controller for Quadrotor UAV Attitude System in Presence of Wind Gust and Actuator Faults
Abstract
:1. Introduction
- Propose a STESO to accurately estimate the disturbance torque caused by wind gust and actuator faults in finite time, and give the parameter selection rule of the observer;
- Design a fast convergence attitude control law based on STSMC, and give a comprehensive stability analysis on the entire system.
2. Mathematical Model and Problem Formulation
2.1. Notation
2.2. Quaternion Operations
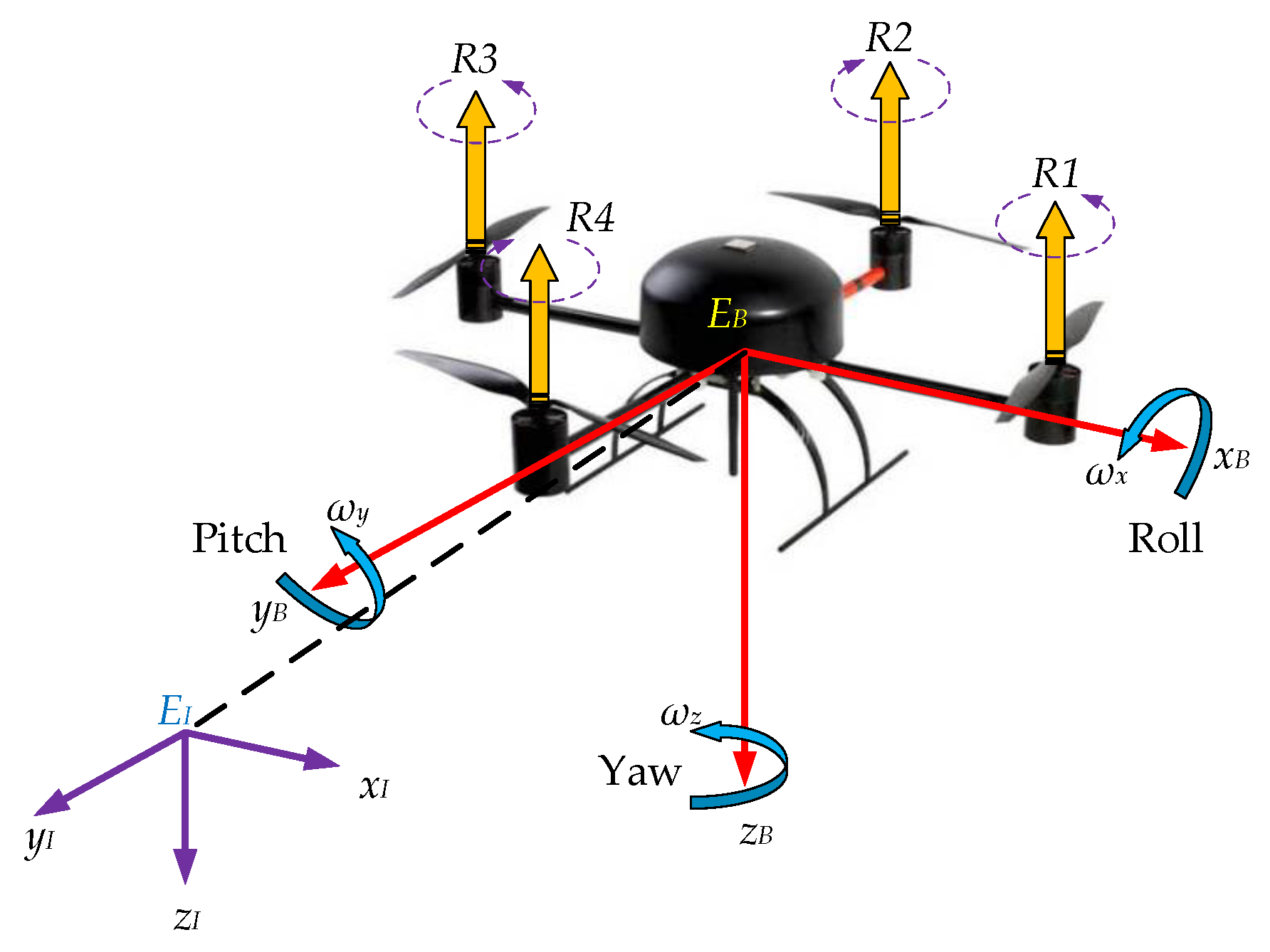
2.3. Kinematics and Dynamics of Quadrotor
2.4. Lumped Disturbaces
2.4.1. Wind Gust
2.4.2. Actuator Faults
2.5. Problem Formulation
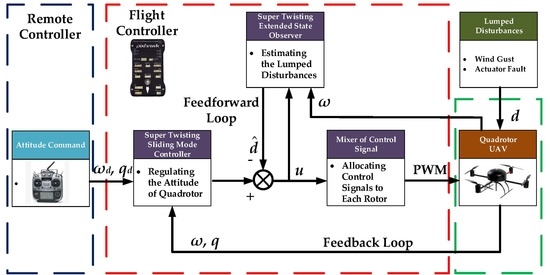
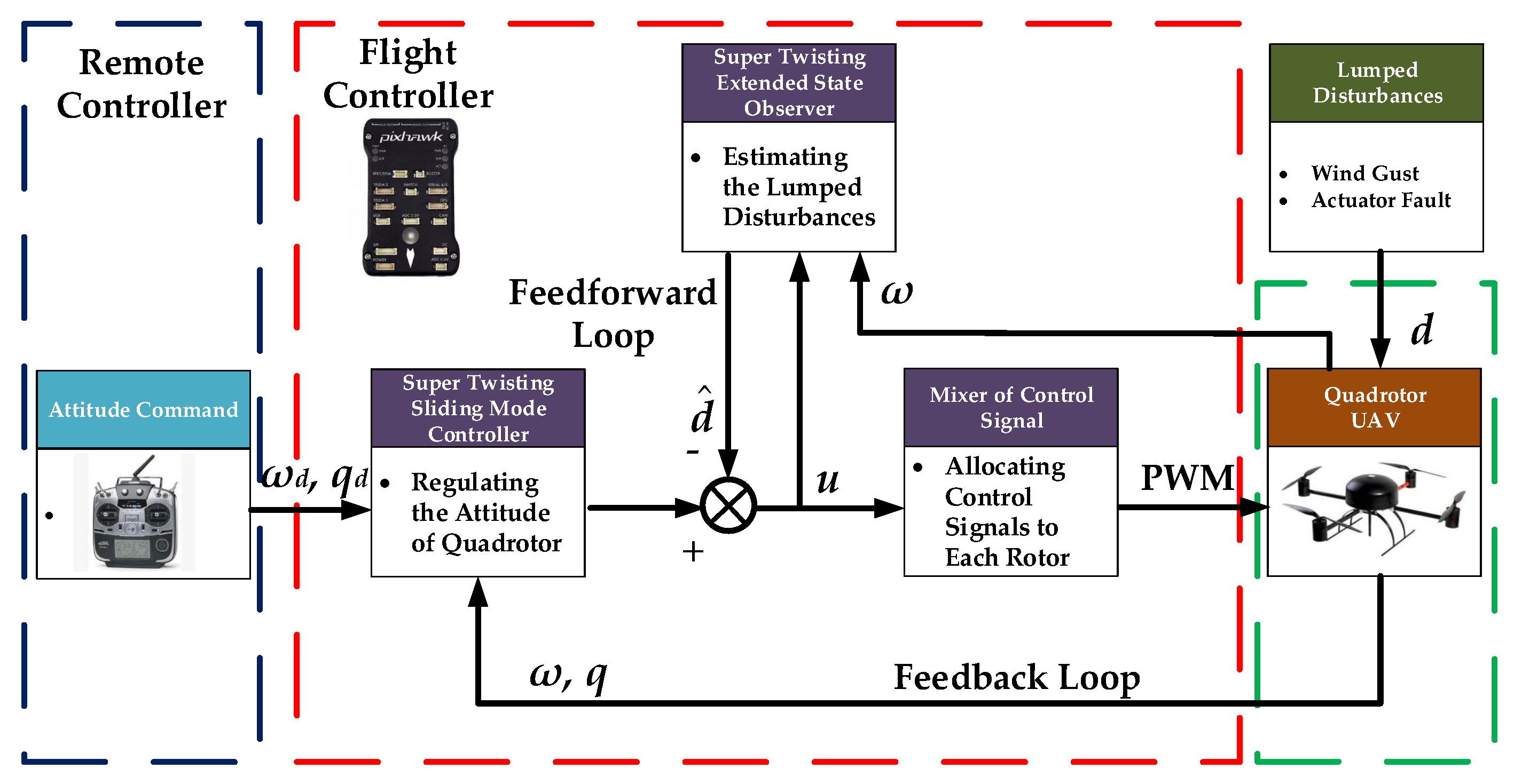
- Design the feedforward loop so that the lumped disturbances are estimated by STESO and compensated this way.
- Design the feedback loop that regulates the orientation of quadrotor to track the desired attitude produced by the commander timely.
3. Design and Analysis of Super Twisting Extended State Observer
3.1. Design of STESO
3.2. Convergence Analysis and Parameter Selection Rule
4. Design of Super Twisting Sliding Mode Controller
5. Simulation and Experimental Results
5.1. Simulation Results
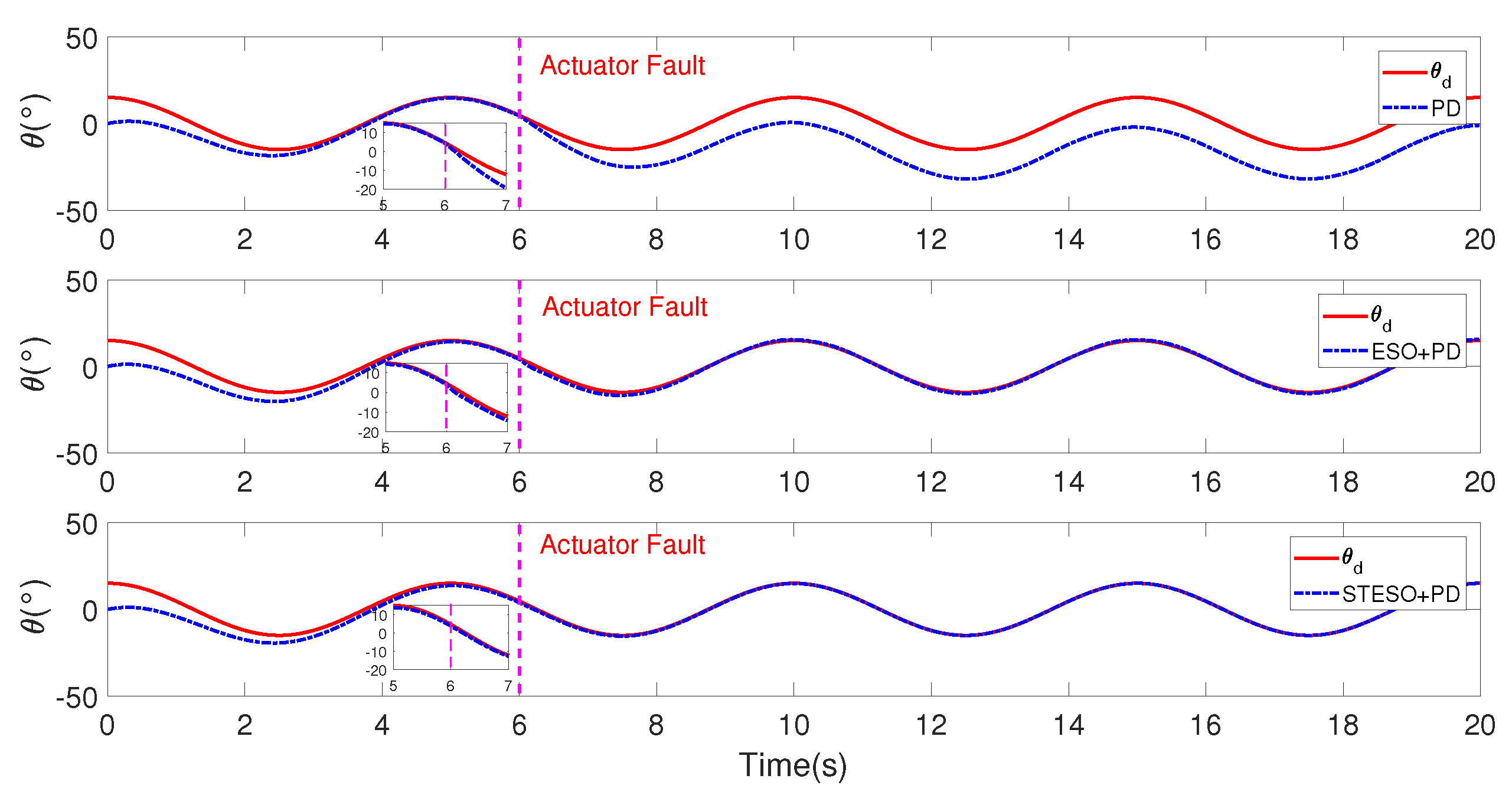
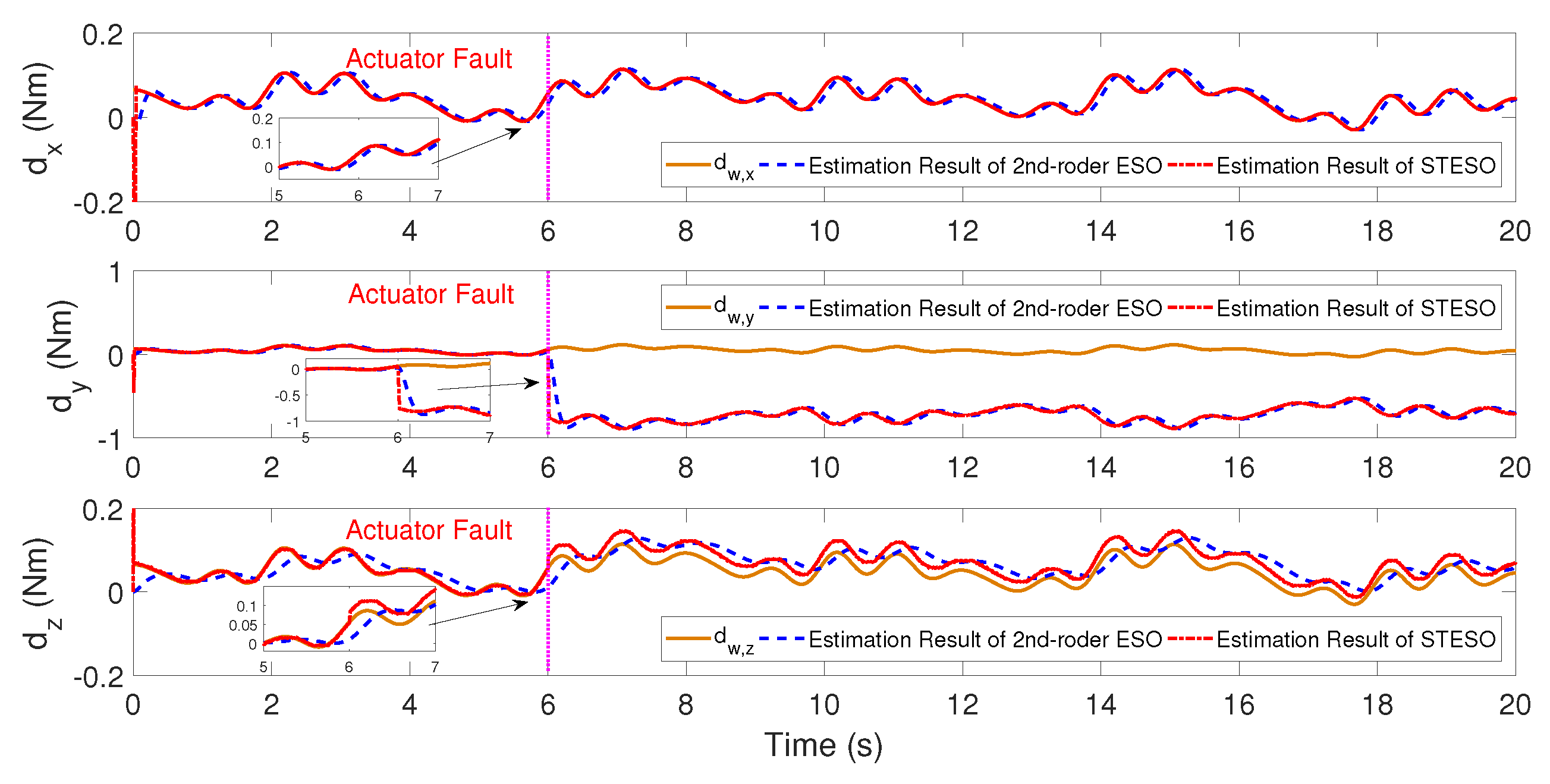
5.1.1. Case A: STESO vs. 2nd-Order ESO
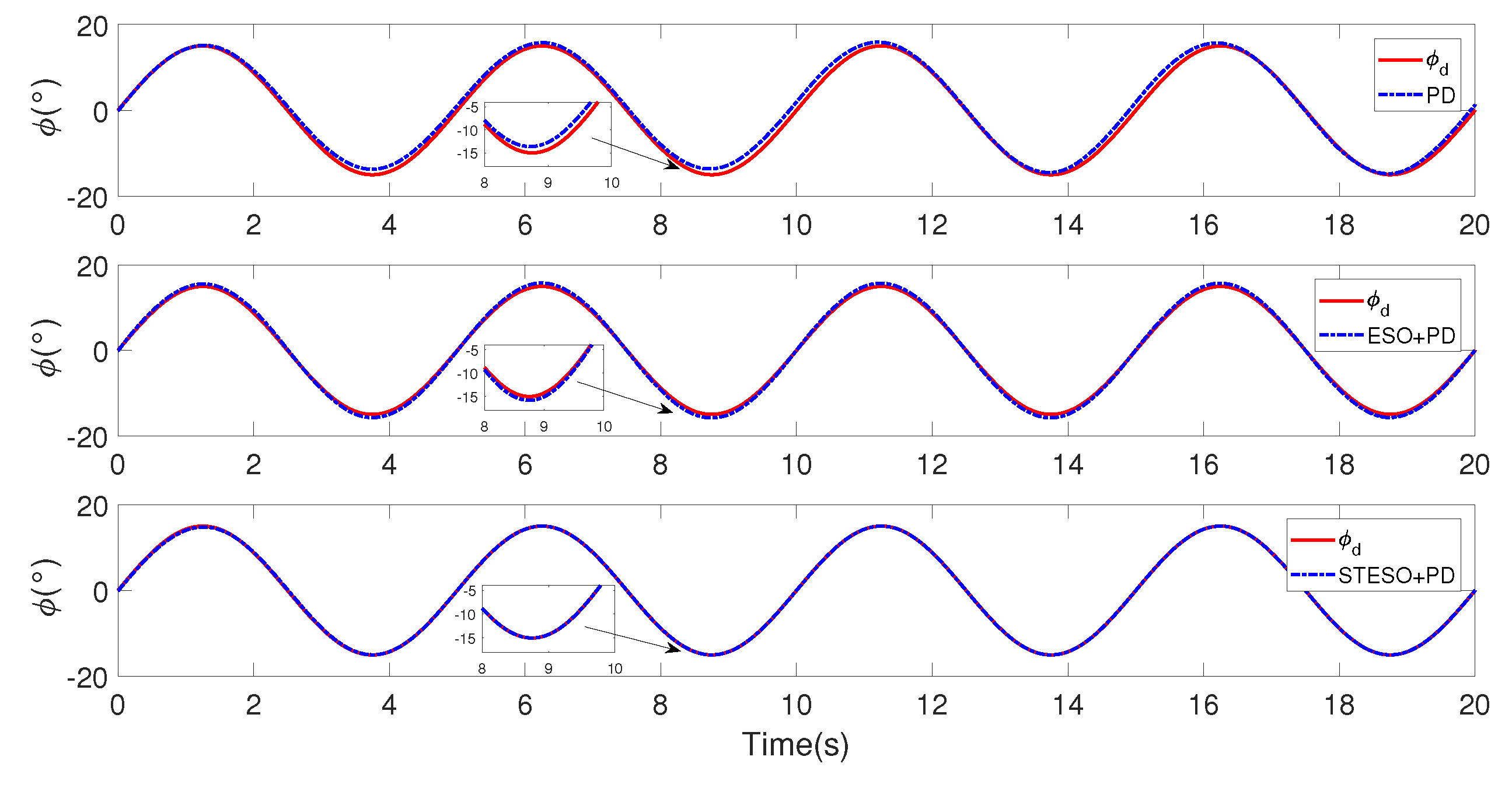
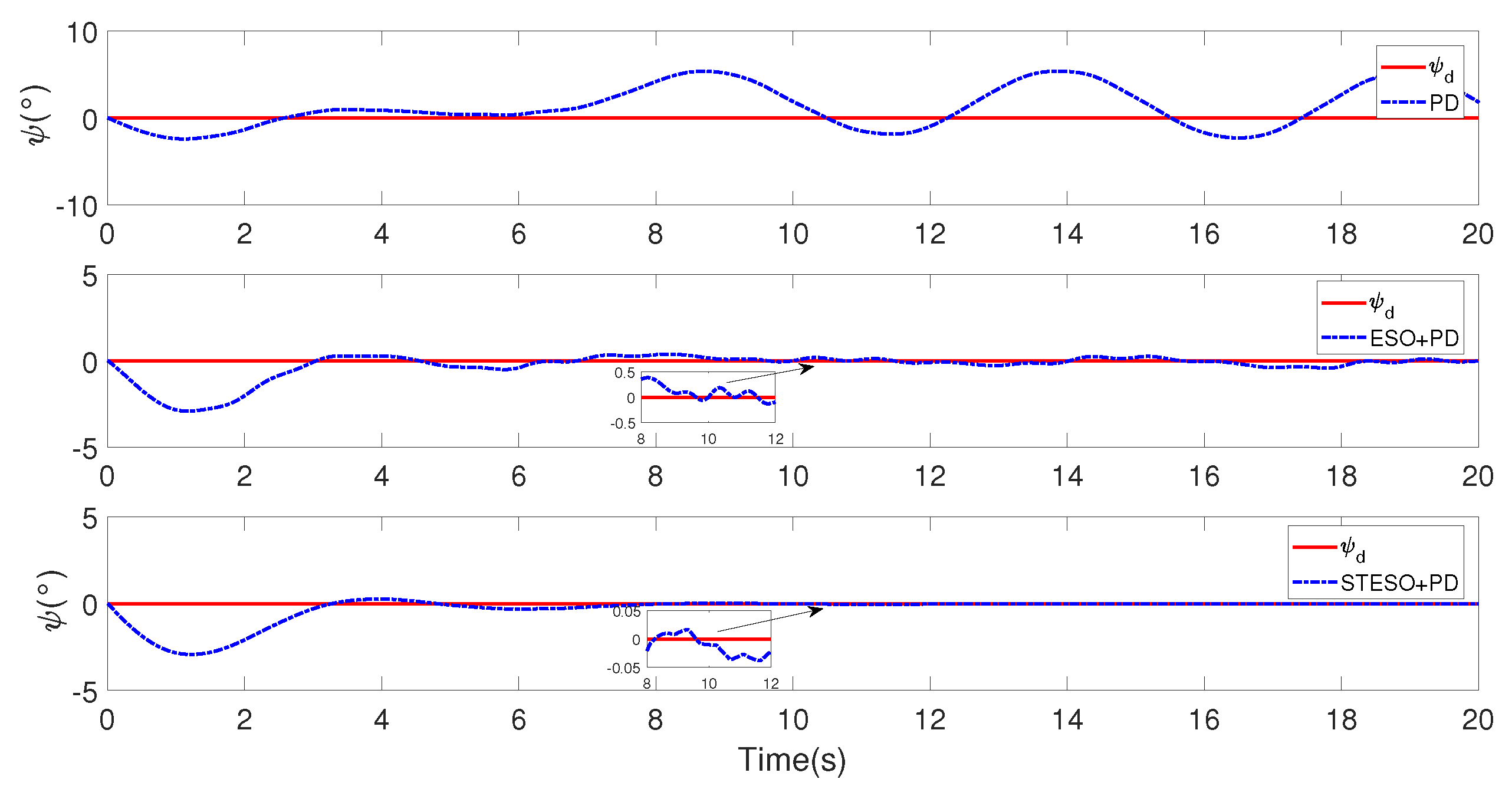
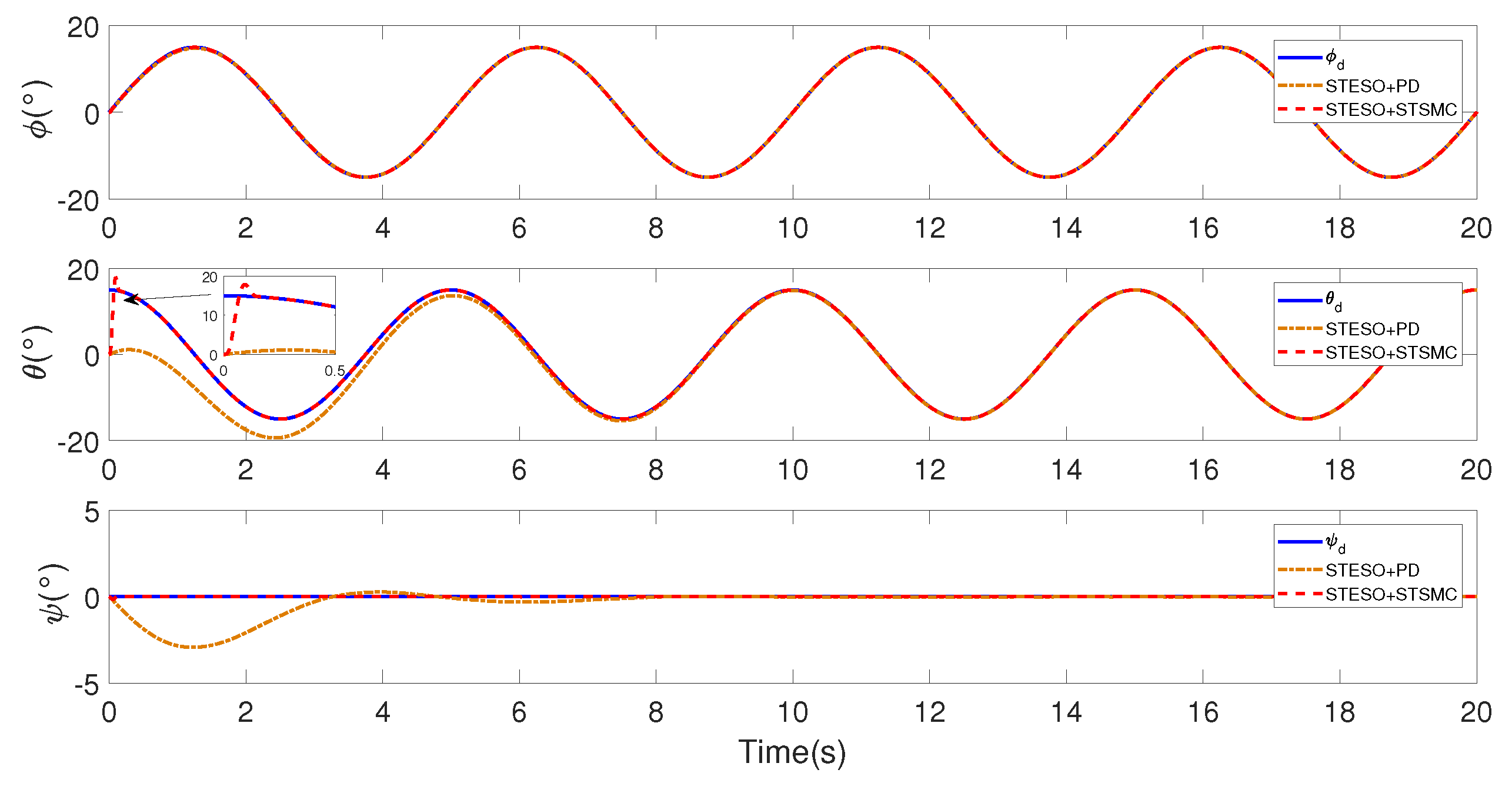
5.1.2. Case B. STSMC vs. Nonlinear PD
5.2. Experimental Results
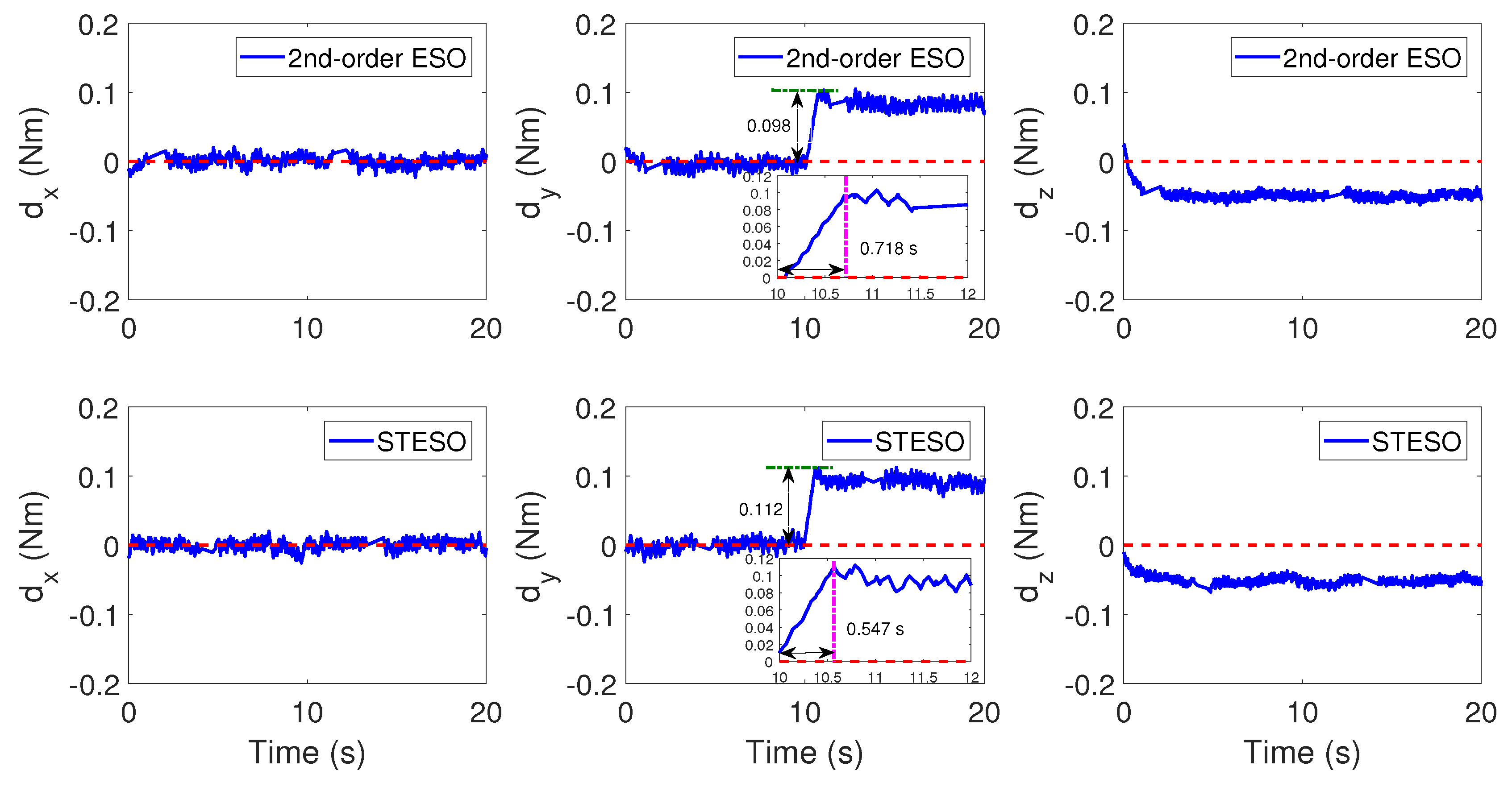
5.2.1. Case A: STESO vs. 2nd-Order ESO
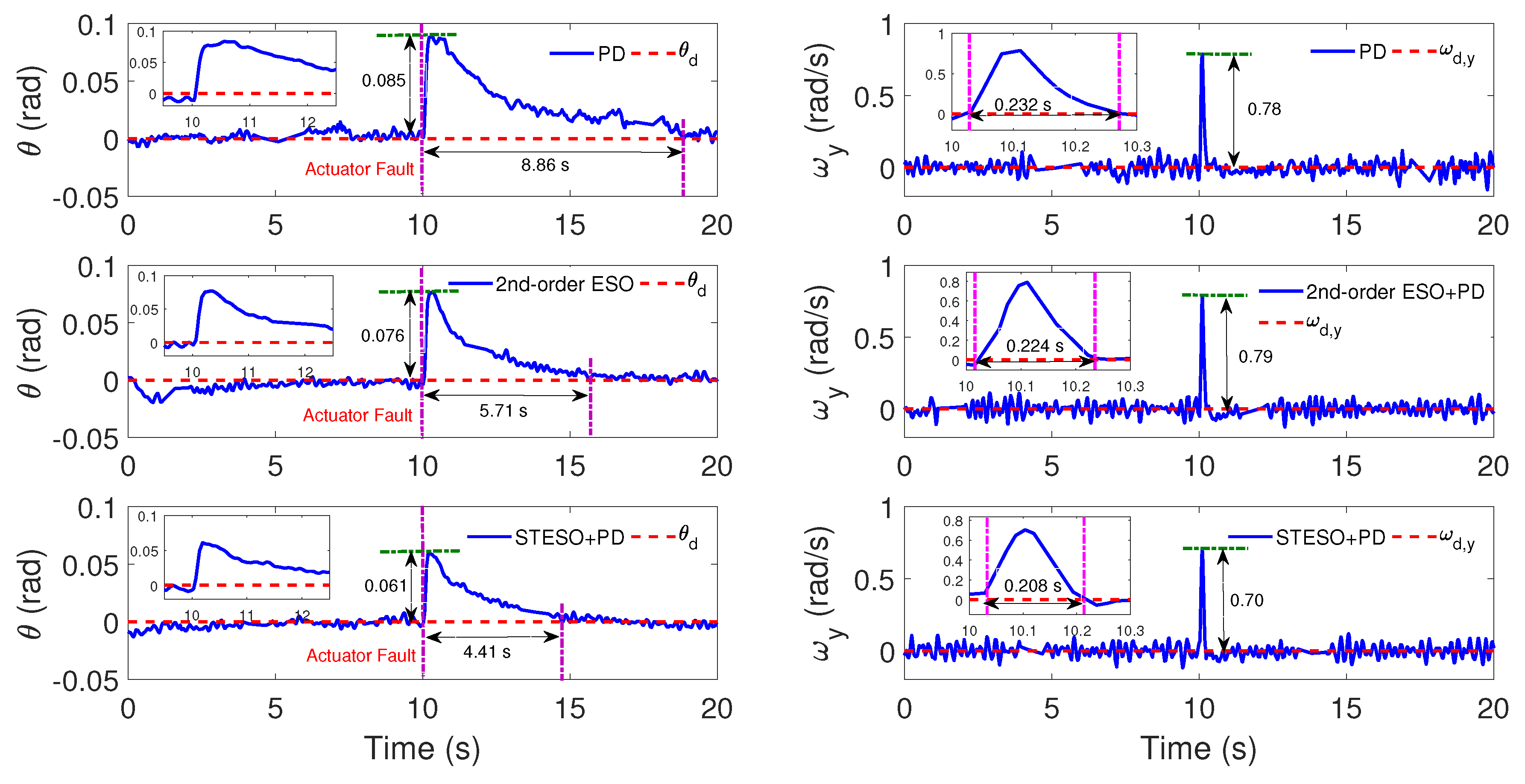
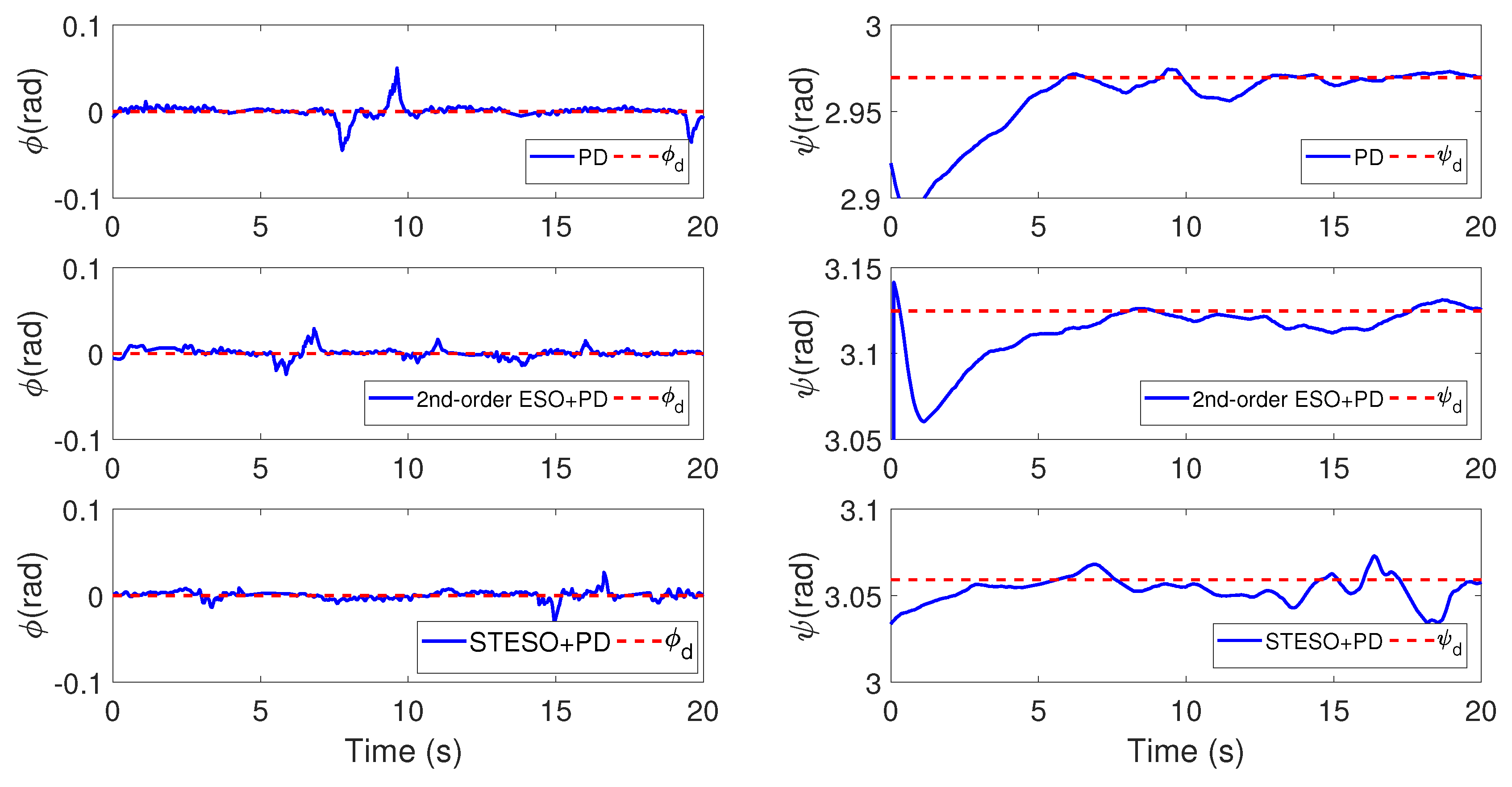
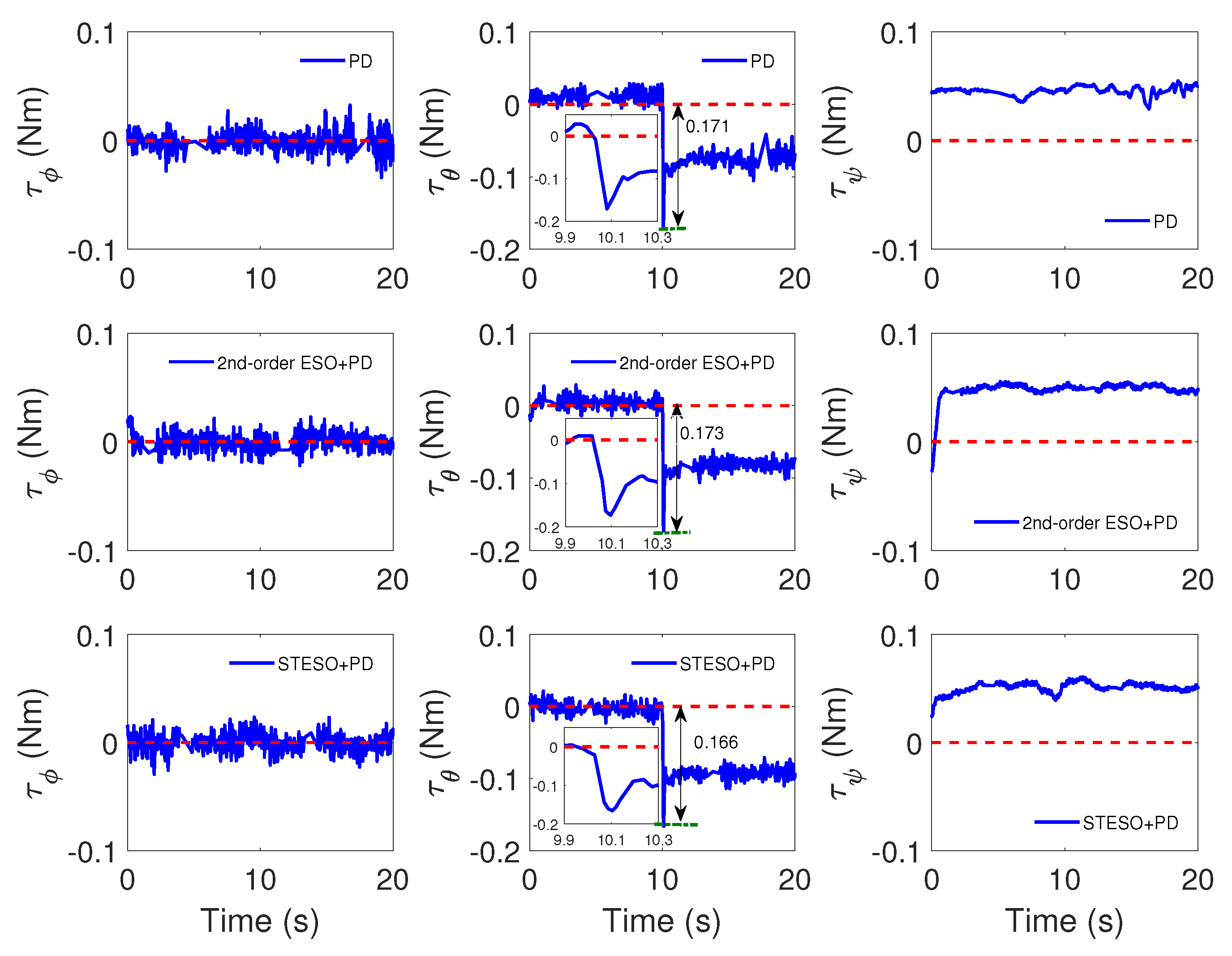
5.2.2. Case B: Proposed Method vs. Nonlinear PD
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Stepaniak, M.J.; van Graas, F.; de Haag, M.U. Design of an Electric Propulsion System for a Quadrotor Unmanned Aerial Vehicle. J. Aircr. 2009, 46, 1050–1058. [Google Scholar] [CrossRef]
- Gupte, S.; Mohandas, P.I.T.; Conrad, J.M. A Survey of Quadrotor Unmanned Aerial Vehicles. In Proceedings of the IEEE Southeastcon, Orlando, FL, USA, 15–18 March 2012. [Google Scholar]
- Ozbek, N.S.; Onkol, M.; Efe, M.O. Feedback control strategies for quadrotor-type aerial robots: A survey. Trans. Inst. Meas. Control 2016, 38, 529–554. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Becker, M.; Siegwart, R. Autonomous miniature flying robots: Coming soon! IEEE Robot Autom Mag. 2007, 14, 88–98. [Google Scholar] [CrossRef]
- Han, W.X.; Wang, Z.H.; Shen, Y. Fault estimation for a quadrotor unmanned aerial vehicle by integrating the parity space approach with recursive least squares. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 783–796. [Google Scholar] [CrossRef]
- Tian, B.L.; Ma, Y.X.; Zong, Q. A Continuous Finite-Time Output Feedback Control Scheme and Its Application in Quadrotor UAVs. IEEE Access 2018, 6, 19807–19813. [Google Scholar] [CrossRef]
- Huang, M.; Xian, B.; Diao, C.; Yang, K.Y.; Feng, Y. Adaptive Tracking Control of Underactuated Quadrotor Unmanned Aerial Vehicles via Backstepping. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 2076–2081. [Google Scholar]
- Salih, A.L.; Moghavvemi, M.; Mohamed, H.A.F.; Gaeid, K.S. Flight PID controller design for a UAV quadrotor. Sci. Res. Essays 2010, 5, 3660–3667. [Google Scholar]
- Lee, K.U.; Kim, H.S.; Park, J.B.; Choi, Y.H. Hovering Control of a Quadrotor. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems (Iccas), JeJu Island, Korea, 17–21 October 2012; pp. 162–167. [Google Scholar]
- González-Vázquez, S.; Moreno-Valenzuela, J. A New Nonlinear PI/PID Controller for Quadrotor Posture Regulation. In Proceedings of the 2010 IEEE Electronics, Robotics and Automotive Mechanics Conference, Morelos, Mexico, 28 September–1 October 2010; pp. 642–647. [Google Scholar]
- González-Vázquez, S.; Moreno-Valenzuela, J. Motion Control of a Quadrotor Aircraft via Singular Perturbations. Int. J. Adv. Robot. Syst. 2013, 10, 368. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Lu, G.; Zhong, Y.S. Robust LQR Attitude Control of a 3-DOF Laboratory Helicopter for Aggressive Maneuvers. IEEE Trans. Ind. Electron. 2013, 60, 4627–4636. [Google Scholar] [CrossRef]
- Munoz, F.; Gonzalez-Hernandez, I.; Salazar, S.; Espinoza, E.S.; Lozano, R. Second order sliding mode controllers for altitude control of a quadrotor UAS: Real-time implementation in outdoor environments. Neurocomputing 2017, 233, 61–71. [Google Scholar] [CrossRef]
- Avram, R.C.; Zhang, X.D.; Muse, J. Nonlinear Adaptive Fault-Tolerant Quadrotor Altitude and Attitude Tracking With Multiple Actuator Faults. IEEE Trans. Control Syst. Technol. 2018, 26, 701–707. [Google Scholar] [CrossRef]
- Wang, C.; Song, B.F.; Huang, P.F.; Tang, C.H. Trajectory Tracking Control for Quadrotor Robot Subject to Payload Variation and Wind Gust Disturbance. J. Intell. Robot. Syst. 2016, 83, 315–333. [Google Scholar] [CrossRef]
- Basri, M.A.M.; Husain, A.R.; Danapalasingam, K.A. Stabilization and trajectory tracking control for underactuated quadrotor helicopter subject to wind-gust disturbance. Sadhana Acad. Proc. Eng. Sci. 2015, 40, 1531–1553. [Google Scholar] [CrossRef]
- Chen, W.H.; Ohnishi, K.; Guo, L. Advances in Disturbance/Uncertainty Estimation and Attenuation. IEEE Trans. Ind. Electron. 2015, 62, 5758–5762. [Google Scholar] [CrossRef]
- Yang, J.; Chen, W.H.; Li, S.H.; Guo, L.; Yan, Y.D. Disturbance/Uncertainty Estimation and Attenuation Techniques in PMSM Drives-A Survey. IEEE Trans. Ind. Electron. 2017, 64, 3273–3285. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z. Nonlinear attitude control scheme with disturbance observer for flexible spacecrafts. Nonlinear Dyn. 2015, 81, 257–264. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z.; Du, Y.J. Adaptive sliding mode backstepping control for entry reusable launch vehicles based on nonlinear disturbance observer. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 19–29. [Google Scholar] [CrossRef]
- Pu, Z.Q.; Yuan, R.Y.; Yi, J.Q.; Tan, X.M. A Class of Adaptive Extended State Observers for Nonlinear Disturbed Systems. IEEE Trans. Ind. Electron. 2015, 62, 5858–5869. [Google Scholar] [CrossRef]
- Wang, H.D.; Huang, Y.B.; Xu, C. ADRC Methodology for a Quadrotor UAV Transporting Hanged Payload. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 1–3 August 2016; pp. 1641–1646. [Google Scholar]
- Xia, Y.Q.; Pu, F.; Li, S.F.; Gao, Y. Lateral Path Tracking Control of Autonomous Land Vehicle Based on ADRC and Differential Flatness. IEEE Trans. Ind. Electron. 2016, 63, 3091–3099. [Google Scholar] [CrossRef]
- Dou, J.X.; Kong, X.X.; Wen, B.C. Altitude and attitude active disturbance rejection controller design of a quadrotor unmanned aerial vehicle. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 1732–1745. [Google Scholar] [CrossRef]
- Busawon, K.K.; Kabore, P. Disturbance attenuation using proportional integral observers. Int. J. Control 2001, 74, 618–627. [Google Scholar] [CrossRef]
- Gao, Z.W.; Breikin, T.; Nang, H. Discrete-time proportional and integral observer and observer-based controller for systems with both unknown input and output disturbances. Opt. Control Appl. Meth. 2008, 29, 171–189. [Google Scholar] [CrossRef]
- Alcan, G.; Unel, M. Robust Hovering Control of a Quadrotor Using Acceleration Feedback. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (Icuas’17), Miami, FL, USA, 13–16 June 2017; pp. 1455–1462. [Google Scholar]
- Han, J.Q. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Wang, W.; Gao, Z. A comparison study of advanced state observer design techniques. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 6, pp. 4754–4759. [Google Scholar]
- Madonski, R.; Herman, P. Survey on methods of increasing the efficiency of extended state disturbance observers. ISA Trans. 2015, 56, 18–27. [Google Scholar] [CrossRef] [PubMed]
- Godbole, A.A.; Kolhe, J.P.; Talole, S.E. Performance Analysis of Generalized Extended State Observer in Tackling Sinusoidal Disturbances. IEEE Trans. Control Syst. Technol. 2013, 21, 2212–2223. [Google Scholar] [CrossRef]
- Madani, T.; Benallegue, A. Sliding mode observer and backstepping control for a quadrotor unmanned aerial vehicles. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; Volume 1–13, pp. 2462–2467. [Google Scholar]
- Chuei, R.; Cao, Z.W.; Man, Z.H. Super Twisting Observer based Repetitive Control for Aperiodic Disturbance Rejection in a Brushless DC Servo Motor. Int. J. Control Autom. Syst. 2017, 15, 2063–2071. [Google Scholar] [CrossRef]
- Utkin, V. On Convergence Time and Disturbance Rejection of Super-Twisting Control. IEEE Trans. Autom. Control 2013, 58, 2013–2017. [Google Scholar] [CrossRef]
- Li, P.; Ma, J.J.; Zheng, Z.Q. Disturbance-observer-based fixed-time second-order sliding mode control of an air-breathing hypersonic vehicle with actuator faults. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 344–361. [Google Scholar] [CrossRef]
- Tian, B.L.; Liu, L.H.; Lu, H.C.; Zuo, Z.Y.; Zong, Q.; Zhang, Y.P. Multivariable Finite Time Attitude Control for Quadrotor UAV: Theory and Experimentation. IEEE Trans. Ind. Electron. 2018, 65, 2567–2577. [Google Scholar] [CrossRef]
- Chovancova, A.; Fico, T.; Hubinsky, P.; Duchon, F. Comparison of various quaternion-based control methods applied to quadrotor with disturbance observer and position estimator. Robot. Auton. Syst. 2016, 79, 87–98. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Siegwart, R. Full control of a quadrotor. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; Volume 9, pp. 153–158. [Google Scholar]
- Waslander, S.; Wang, C. Wind Disturbance Estimation and Rejection for Quadrotor Position Control. In Proceedings of the AIAA Infotech@Aerospace Conference and AIAA Unmanned...Unlimited Conference, Seattle, WA, USA, 6–9 April 2009. [Google Scholar]
- Chen, Y.M.; He, Y.L.; Zhou, M.F. Decentralized PID neural network control for a quadrotor helicopter subjected to wind disturbance. J. Cent. South Univ. 2015, 22, 168–179. [Google Scholar] [CrossRef]
- Önder, E.M. Battery power loss compensated fractional order sliding mode control of a quadrotor UAV. Asian J. Control 2012, 14, 413–425. [Google Scholar]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: New York, NY, USA, 2014. [Google Scholar]
- Quan, Q.; Dai, X. Flight Performance Evaluation of UAVs. Available online: http://flyeval.com/ (accessed on 20 April 2018).
- Shi, D.; Wu, Z.; Chou, W. Harmonic Extended State Observer Based Anti-Swing Attitude Control for Quadrotor with Slung Load. Electronics 2018, 7, 83. [Google Scholar] [CrossRef]
- Shi, D.; Wu, Z.; Chou, W. Generalized Extended State Observer Based High Precision Attitude Control of Quadrotor Vehicles Subject to Wind Disturbance. IEEE Access 2018, 6, 2169–3536. [Google Scholar] [CrossRef]
- Meier, L.; Tanskanen, P.; Heng, L.; Lee, G.H.; Fraundorfer, F.; Pollefeys, M. PIXHAWK: A micro aerial vehicle design for autonomous flight using onboard computer vision. Auton. Robot. 2012, 33, 21–39. [Google Scholar] [CrossRef]
- Meier, L.; Tanskanen, P.; Fraundorfer, F.; Pollefeys, M. The Pixhawk Open-Source Computer Vision Framework for Mavs. In Proceedings of the International Conference on Unmanned Aerial Vehicle in Geomatics (UAV-G), New York, NY, USA, 14–16 September 2011; Volume 38-1, pp. 13–18. [Google Scholar]


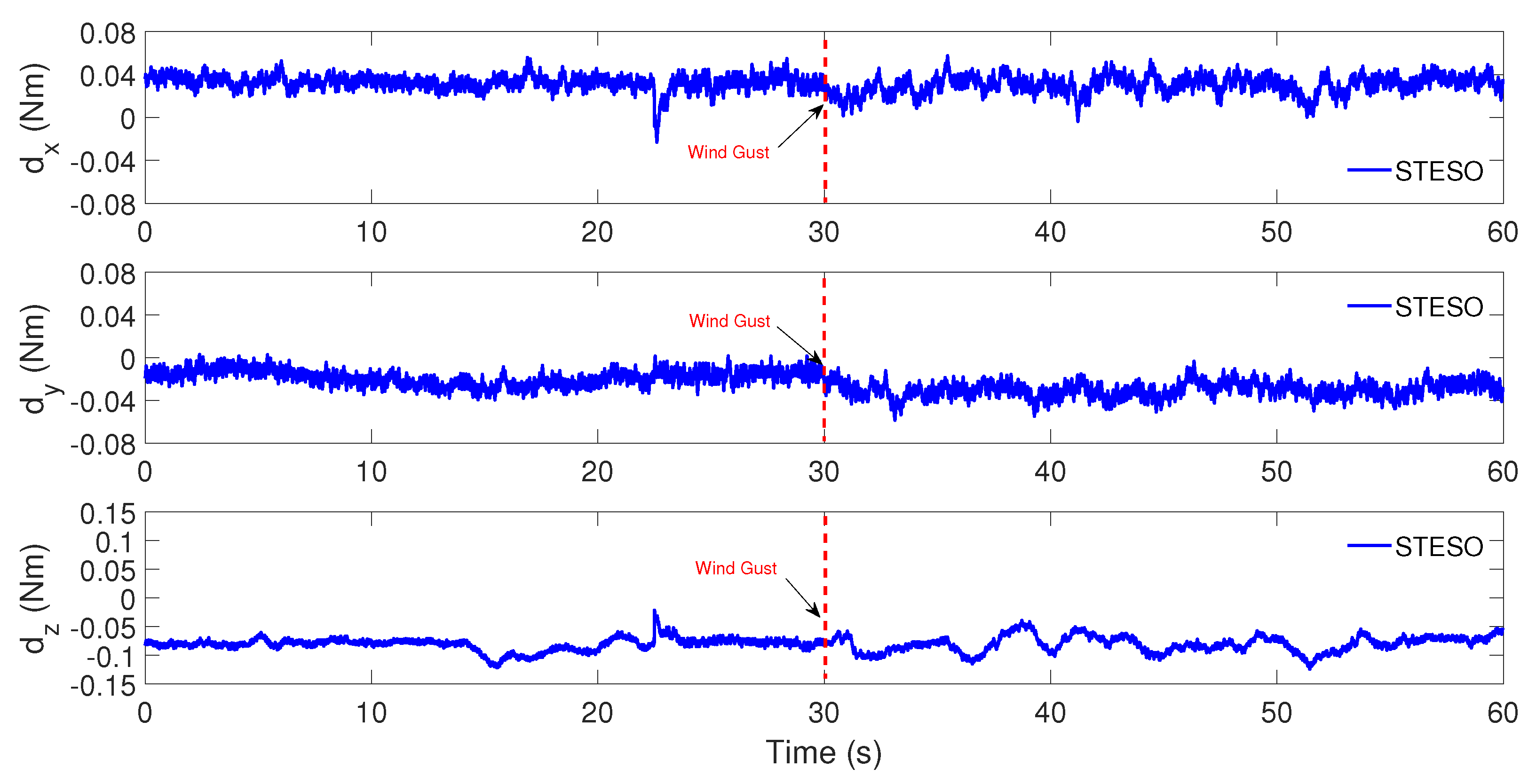
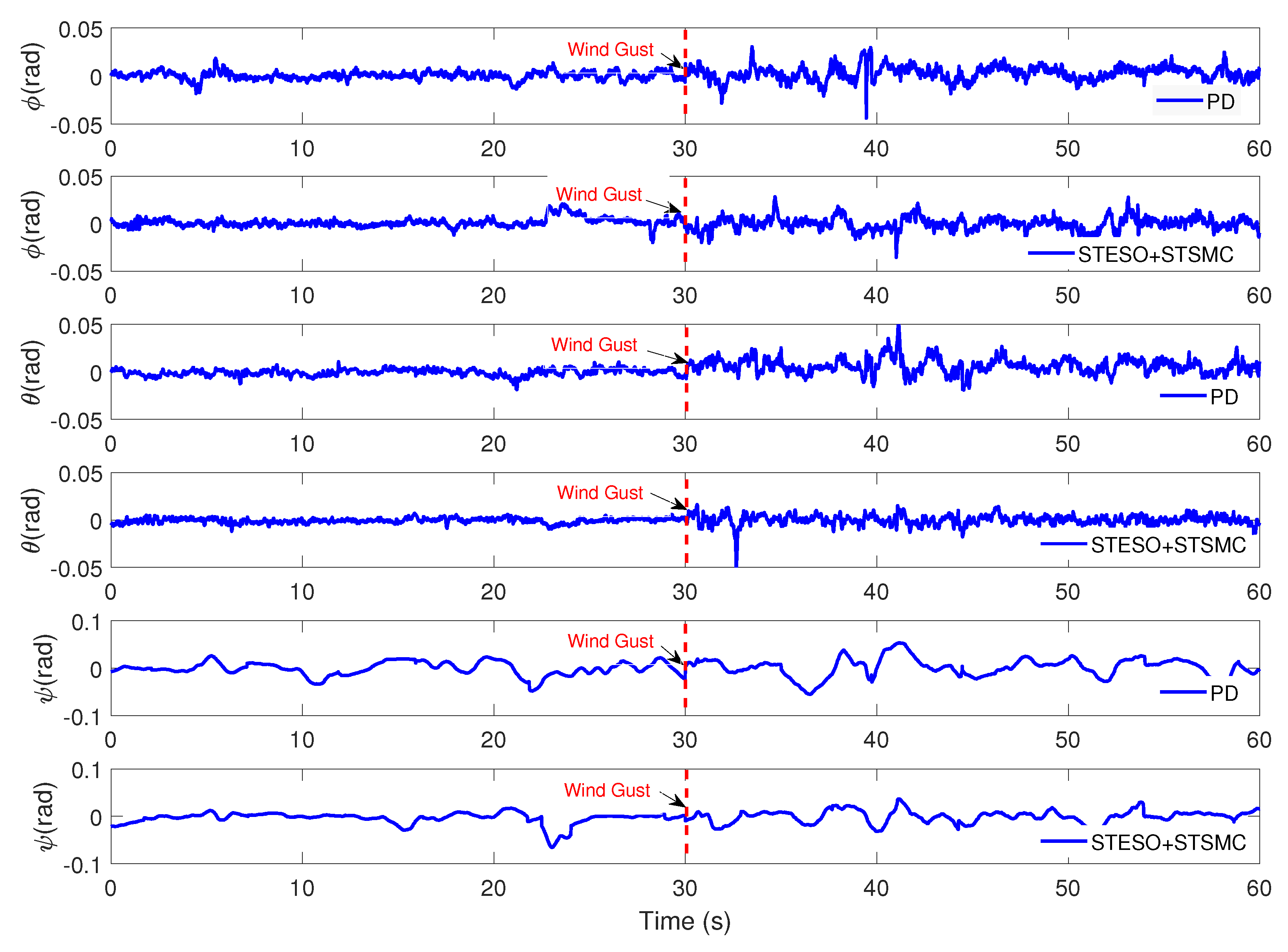
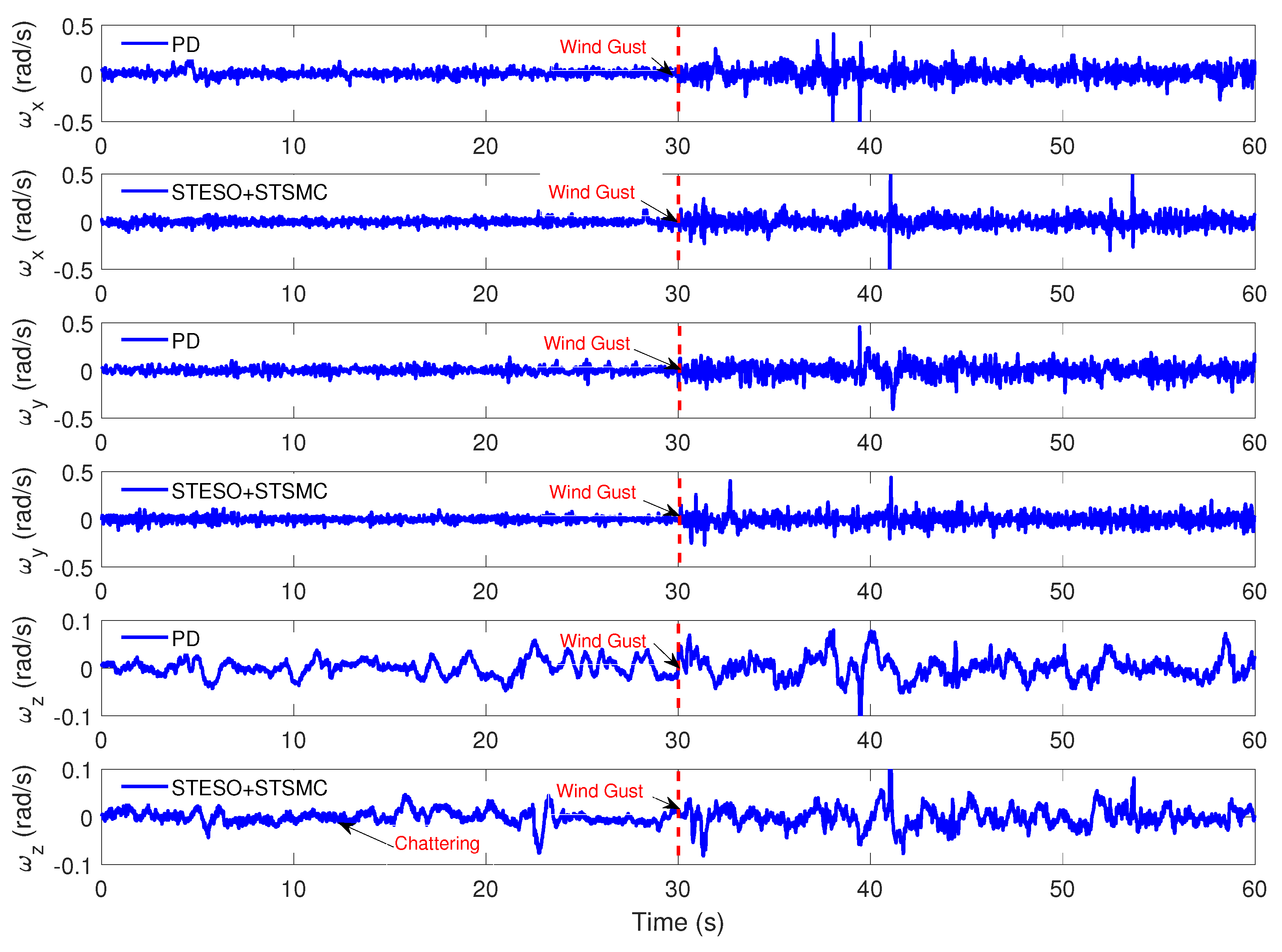
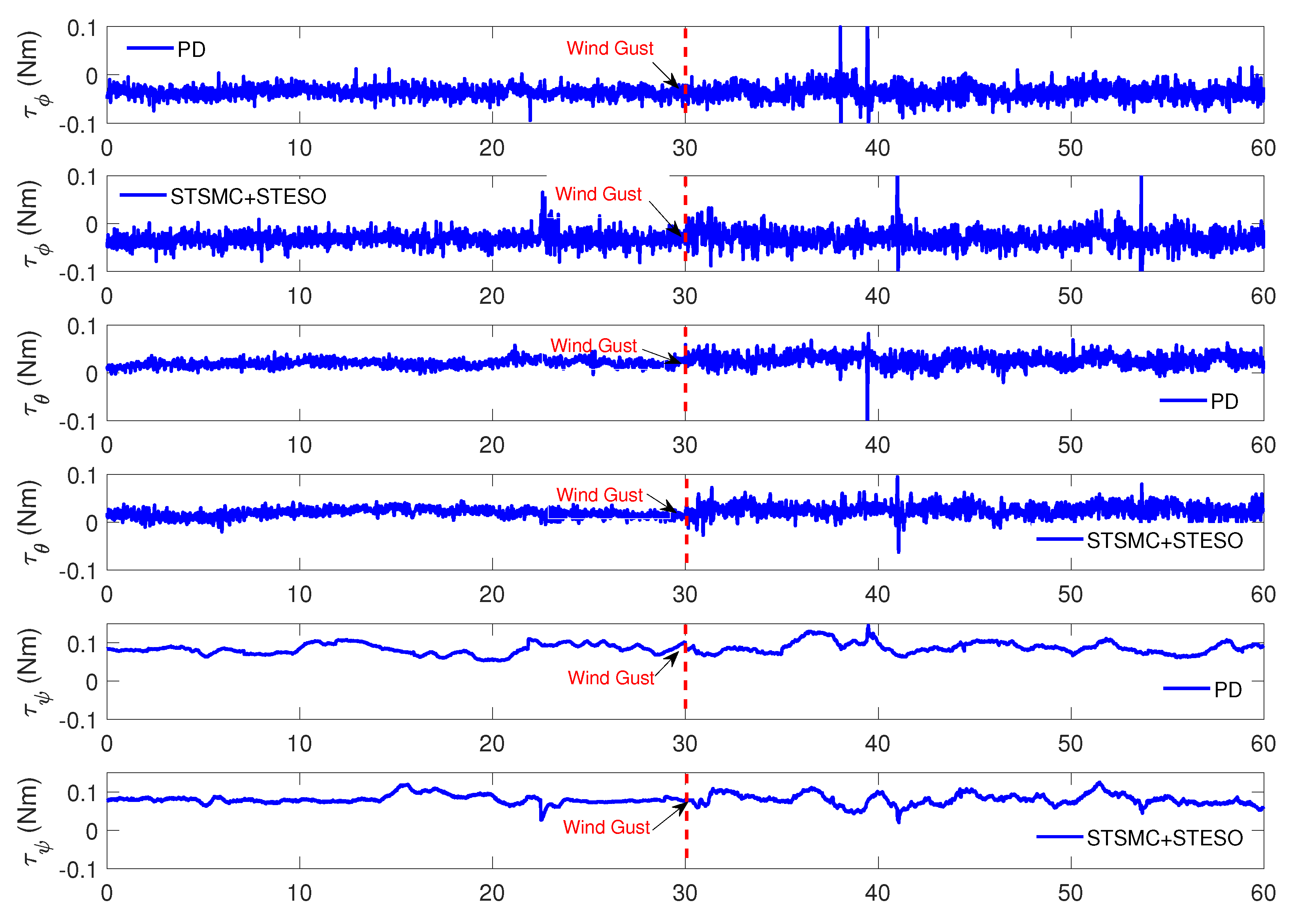
| Parameter | Description | Value |
|---|---|---|
| m | Mass | kg |
| Roll inertia | ||
| Pitch inertia | ||
| Yaw inertia | ||
| l | Motor moment arm | m |
| g | Gravity acceleration | |
| Aerodynamic coefficient | ||
| Drag coefficient | ||
| Maximum rotational speed | 8214 r/min | |
| Minimum rotational speed | 100 r/min |
| Deflection | Recovery Time | Convergence Time | |||
|---|---|---|---|---|---|
| Without Estimator | 0.085 rad | 0.78 rad/s | 8.86 s | 0.232 s | / |
| 2nd-order ESO + PD | 0.076 rad | 0.79 rad/s | 5.71 s | 0.224 s | 0.718 s |
| STESO + PD | 0.061 rad | 0.70 rad/s | 4.41 s | 0.208 s | 0.547 s |
| Actuator Fault Only | Actuator Fault+Wind Gust | |||||
|---|---|---|---|---|---|---|
| nonlinear PD | 0.0082 | 0.0072 | 0.0187 | 0.0160 | 0.0202 | 0.0204 |
| STESO + STSMC | 0.0094 | 0.0052 | 0.0135 | 0.0136 | 0.0116 | 0.0132 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, D.; Wu, Z.; Chou, W. Super-Twisting Extended State Observer and Sliding Mode Controller for Quadrotor UAV Attitude System in Presence of Wind Gust and Actuator Faults. Electronics 2018, 7, 128. https://doi.org/10.3390/electronics7080128
Shi D, Wu Z, Chou W. Super-Twisting Extended State Observer and Sliding Mode Controller for Quadrotor UAV Attitude System in Presence of Wind Gust and Actuator Faults. Electronics. 2018; 7(8):128. https://doi.org/10.3390/electronics7080128
Chicago/Turabian StyleShi, Di, Zhong Wu, and Wusheng Chou. 2018. "Super-Twisting Extended State Observer and Sliding Mode Controller for Quadrotor UAV Attitude System in Presence of Wind Gust and Actuator Faults" Electronics 7, no. 8: 128. https://doi.org/10.3390/electronics7080128