A Multiple-Sensor Fault-Tolerant Control of a Single-Phase Pulse-Width Modulated Rectifier Based on MRAS and GPI Observers
Abstract
:1. Introduction
- (1)
- The proposed method is capable of tolerating single- or multiple-sensor faults, and the rectifier’s control loop can be driven by the single survivable sensor. For this purpose, two multiple-sensor fault-tolerant controls are investigated. In the first scenario, a DC-link voltage sensor fault followed by a grid voltage sensor fault is discussed. In the second scenario, a DC-link voltage sensor fault followed by a grid current sensor fault is investigated.
- (2)
- For this purpose, a residual generation-based FDI approach is presented. Hence, a bank of two Generalized Proportional Integral Observers (GPIO) and one Model Reference Adaptive System (MRAS) observer are developed in order to accurately estimate the grid voltage, the DC-link voltage and the grid current, respectively. Once the residual exceeds its corresponding threshold, a fault flag switches from 0 to 1 and the faulty sensor is identified. Thereafter, the faulty measurement is substituted by the virtual sensor into the rectifier’s control loop, to guarantee the continuous work of the rectifier.
- (3)
- The proposed FTC approach does not need any additional sensors, in particular load current sensors. Hence, in this work, the load current is considered as an unknown disturbance. It should not have any impact on the performance of the proposed FTC approach, neither in healthy operation nor during sensor post-fault operation of the system. Moreover, the system’s parameters’ mismatch, including grid-side filter inductor and DC-link capacitance, does not affect the robustness of the proposed method.
- (4)
- During sensor post-fault operation, the proposed FTC method allows the start-up of the process with the single survivable sensor with good accuracy and the same performance of the closed-loop control as in healthy operation mode.
- (5)
- The effectiveness of the proposed method is demonstrated through extensive simulation and experimental studies. The proposed FDI/FTC approach can be deployed on the commonly used digital controllers, improving the cost and the performance of real-time control of single-phase PWM converters in several industrial applications.
2. Mathematical Model of the Single-Phase PWM Rectifier and Control Strategy
- –
- DC-Link Voltage Control Loop: The main purpose of the DC-link voltage loop is to maintain this voltage at a constant reference value. The voltage control loop is based on a PI controller due to its simplicity, easy implementation and good regulation results of DC quantities.
- –
- PR-Based Grid Current Control: The grid current controller allows ig to track its reference ig* with good accuracy. For this purpose, a proportional resonant (PR) controller is employed [15].
- –
- SOGI-PLL-Based Grid Synchronization: To ensure grid-side unity power factor, the phase angle of the grid current ig should be synchronized with the grid voltage Vg. Different synchronization techniques are presented in the literature [40]. Among these, the second-order generalized integrator-based phase-locked loop (SOGI-PLL) is an effective approach due to its fast dynamic response and high filtering capacity [15].
3. Design of GPI and MRAS Observers
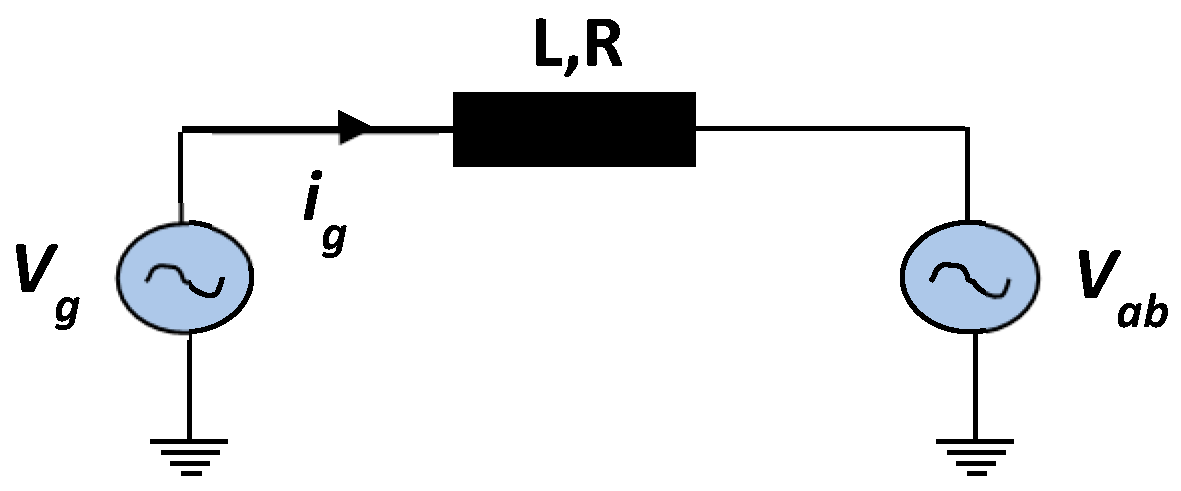
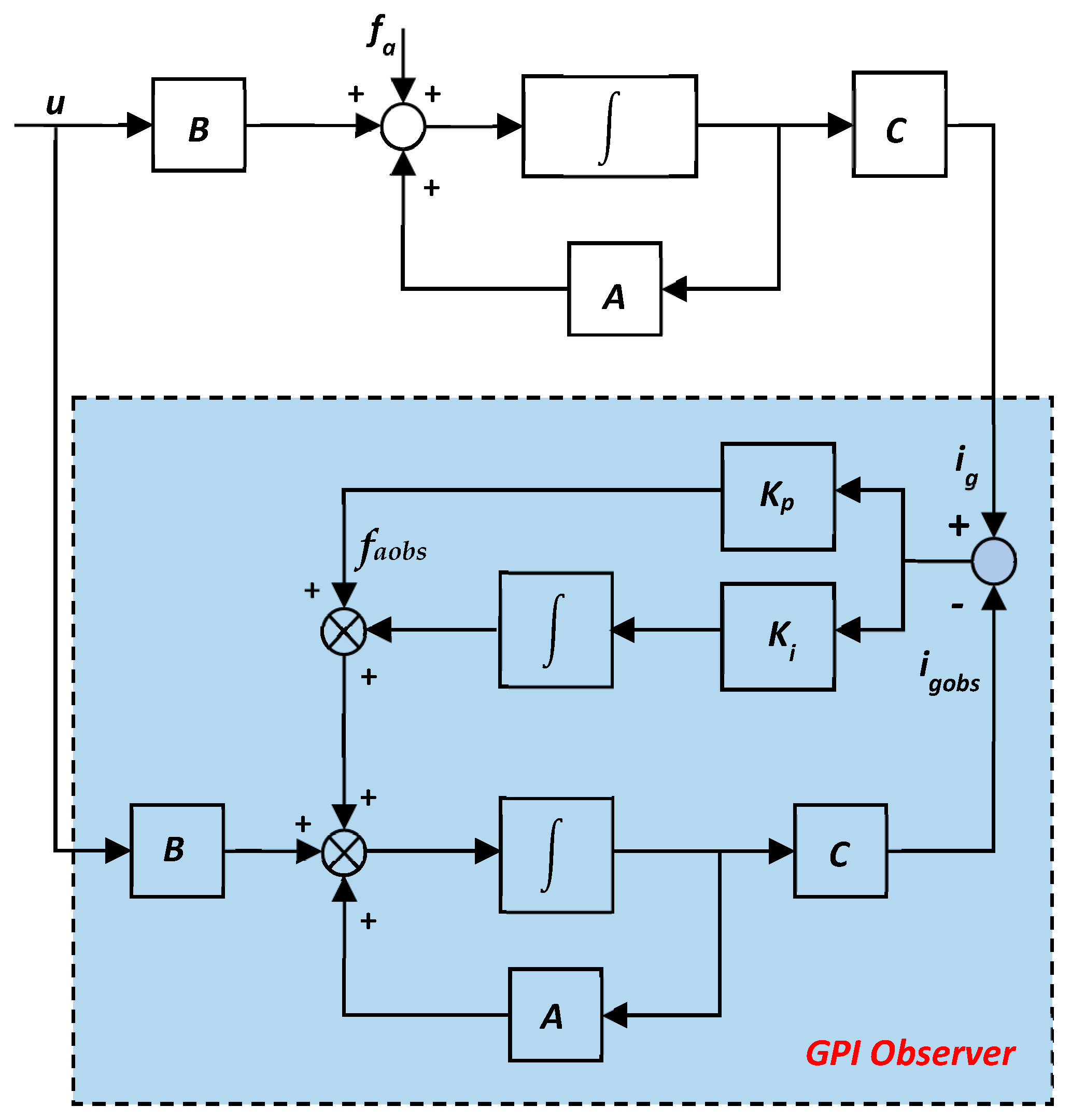
3.1. Grid Voltage GPI Observer Design
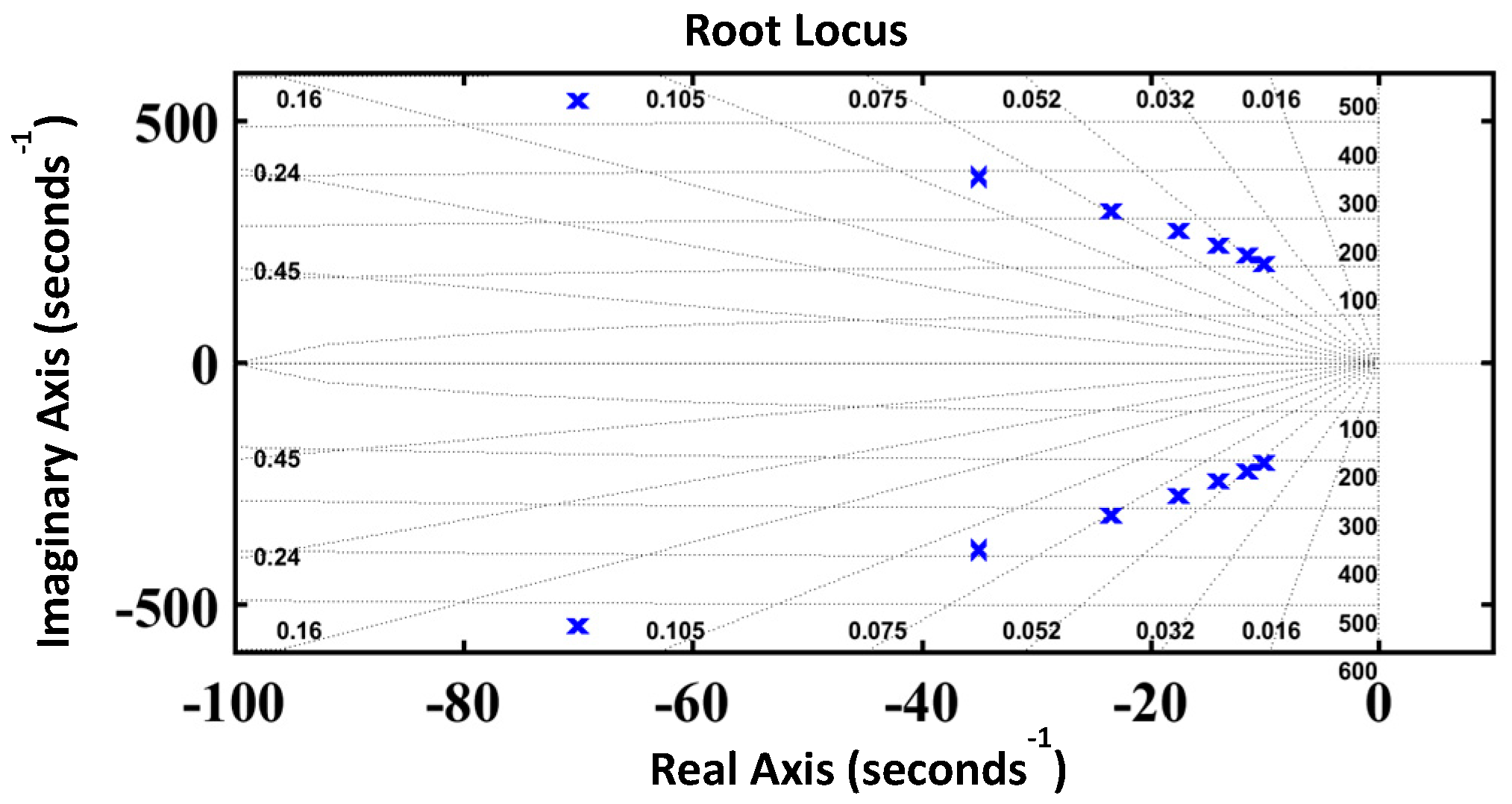
3.2. Observer Stability Analysis
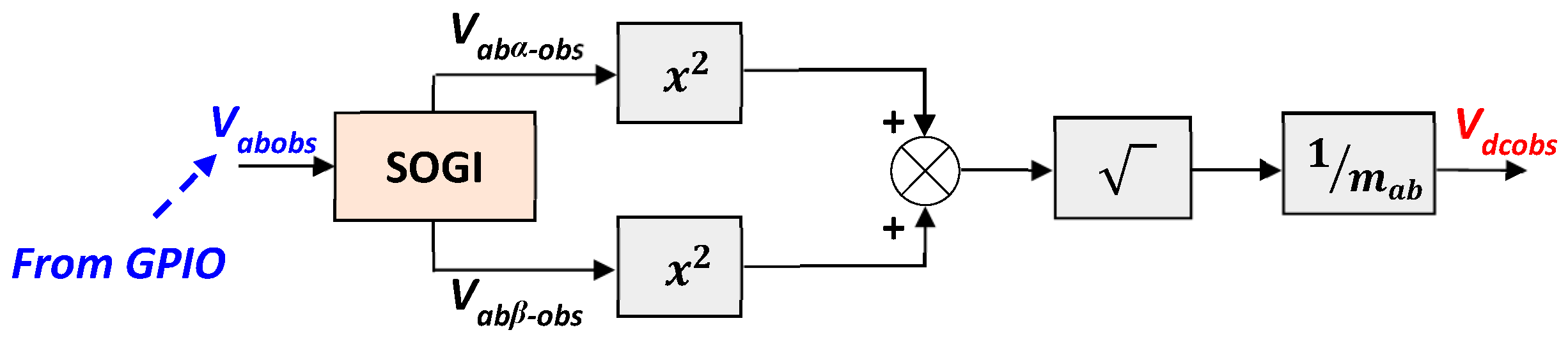
3.3. DC-Link Voltage Estimation Based on SOGI-GPIO
3.4. Virtual Flux MRAS-Based Grid Current Estimation
4. Proposed Sensor FDI and FTC Strategy
5. Simulation Results
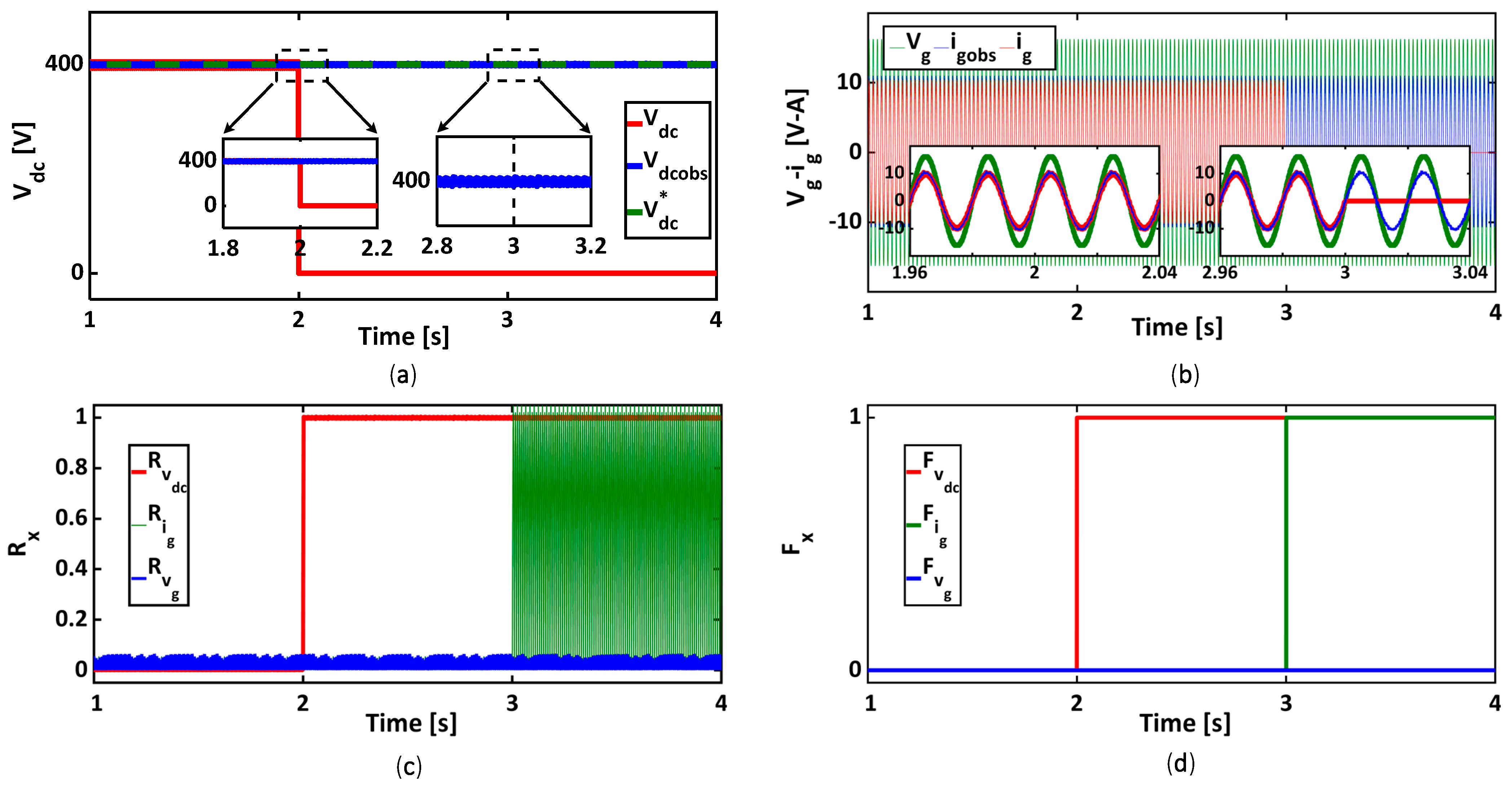
5.1. Multiple-Sensor Fault-Tolerant Control
5.2. Post-Fault System Restart with the Single Survivable Sensor
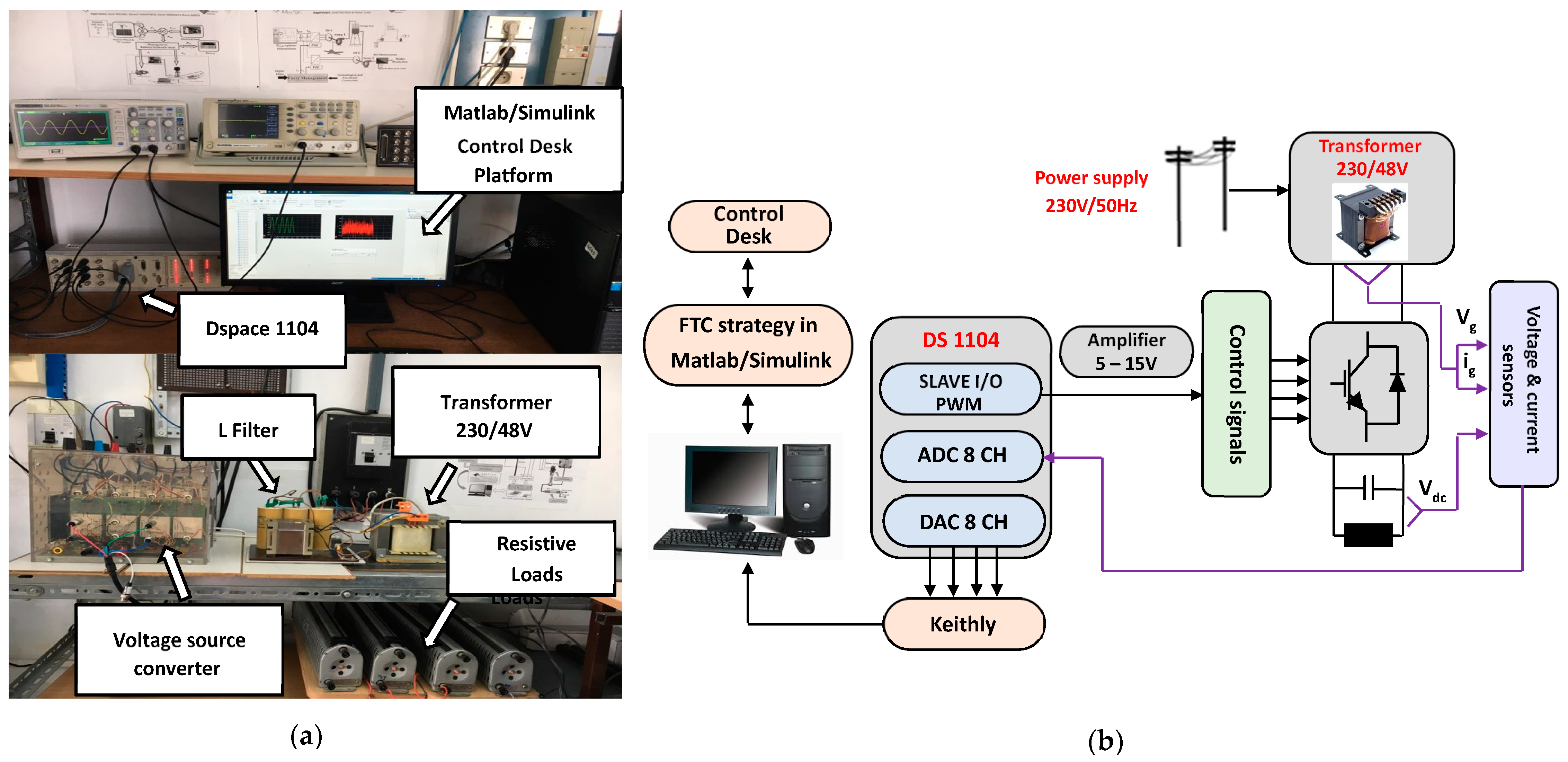
6. Experimental Results
6.1. Residual Robustness Analysis and Threshold Selection
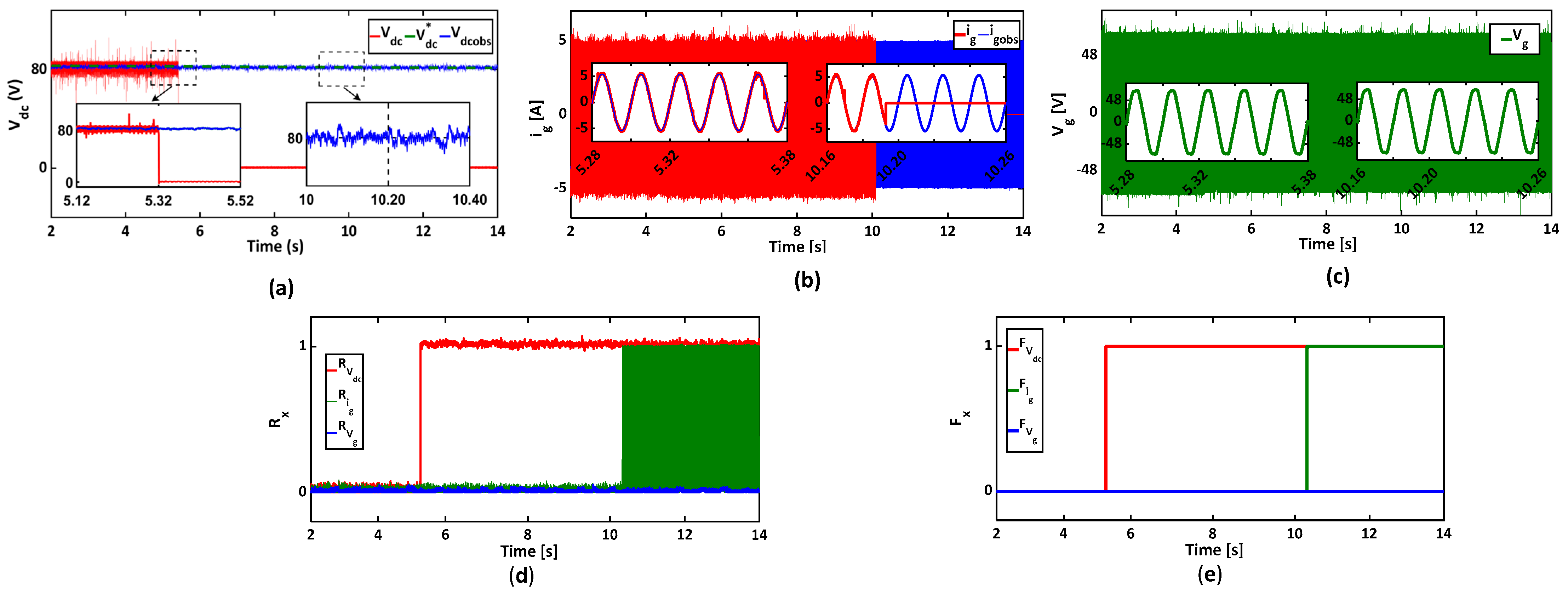
6.2. Multiple-Sensor Fault-Tolerant Control
6.3. Post-Fault System Restart with the Single Survivable Sensor
6.4. Comparative Study with Previously Proposed Methods
7. Conclusions
- (1)
- The proposed approach is a unified sensor fault detection method for the main three sensors used in the closed-loop control of the single-phase PWM rectifier without any extra hardware.
- (2)
- In addition to single-sensor fault detection, the proposed approach is able to diagnose multiple-sensor faults and ensure a post-fault operation of the PWM rectifier with the single survivable sensor.
- (3)
- It has the capability to guarantee the start-up of the single-phase PWM rectifier with a single survivable sensor and with the same performance as in healthy operation, even under DC-link load variations or system’s parameters’ mismatch.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ADC | Analogue to Digital Converter |
| C | DC-link capacitor |
| d1, d3 | Duty Cycle |
| DAC | Digital to Analogue Converter |
| DSOGI | Dual Second-Order Generalized Integrator |
| EVs | Electric Vehicles |
| fa | Disturbance and/or unknown input |
| faobs | Observed value of the disturbance and/or unknown input |
| FDI | Fault Detection and Isolation |
| FE | Fault Estimation |
| FTC | Fault-Tolerant Control |
| fsw | Switching frequency |
| Fx | Fault Flag, x = {ig, Vg, Vdc} |
| GPIO | Generalized Proportional Integral Observer |
| ic | Current in the DC-side capacitor |
| idc | DC-side output current |
| ig | Grid current |
| igobs | Observed value of the grid current |
| ig* | Reference value of the grid current |
| ignom | Nominal value of the grid current |
| iL | Load current |
| Tf | Grid current fundamental period |
| Ki | Integral Gain |
| Kp | Proportional Gain |
| L | Line inductance |
| LO | Luenberger observer |
| mab | Modulation index |
| MRAS | Model Reference Adaptive System |
| PI | Proportional Integral |
| PR | Proportional Resonant |
| PWM | Pulse-Width Modulated |
| R | Line resistance |
| RL | Rated Load resistance |
| Rx | Residual, x = {ig, Vg, Vdc} |
| SMO | Sliding-Mode Observer |
| SOGI | Second-Order Generalized Integrator |
| SOGI-PLL | Second-Order Generalized Integrator Phase-Locked Loop |
| S1, S3 | Binary Switching Control Signal |
| Ts | Sampling Time |
| Tx | Threshold, x = {ig, Vg, Vdc} |
| Vab | Rectifier input voltage |
| Vabobs | Estimated value of the rectifier input voltage |
| Vabobsα, Vabobsβ | Estimated orthogonal components of the rectifier input voltage |
| Vdc | DC-link voltage |
| Vdc* | Reference value of the DC-link voltage |
| Vdcobs | Observed value of the DC-link voltage |
| Vin* | Reference value of the rectifier voltage |
| Vg | Grid voltage |
| Vgnom | Nominal value of the grid voltage |
| Vgobs | Observed value of the grid voltage |
| θg | Phase angle |
| ϕg | Grid virtual flux |
| ϕgobs | Observed value of the grid virtual flux |
| φab | Phase difference |
References
- Ndabarushimana, E.; Qin, N.; Ma, L. Disturbance Decoupling for a Single-Phase Pulse Width Modulation Rectifier Based on an Extended H-Infinity Filter. Electronics 2023, 12, 2765. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Z.; Wang, C.; Zhu, Y.; Cao, X. A Novel Improved Coordinate Rotated Algorithm for PWM Rectifier THD Reduction. Electronics 2022, 11, 1435. [Google Scholar] [CrossRef]
- Kang, L.; Zhang, J.; Zhou, H.; Zhao, Z.; Duan, X. Model predictive current control with fixed switching frequency and dead-time compensation for single-phase PWM rectifier. Electronics 2021, 10, 426. [Google Scholar] [CrossRef]
- Bi, Y.; Wu, C.; Zhao, T.; Li, H.; Xu, J.; Shu, G.; Wang, Y. Modified deadbeat predictive current control method for single-phase AC–DC PFC converter in EV charging system. IEEE Trans. Ind. Electron. 2023, 70, 286–297. [Google Scholar] [CrossRef]
- Ramos, L.A.; Van Kan, R.F.; Mezaroba, M.; Batschauer, A.L. A Control Strategy to Smooth Power Ripple of a Single-Stage Bidirectional and Isolated AC-DC Converter for Electric Vehicles Chargers. Electronics 2022, 11, 650. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J.; Wang, C.; You, X.; Yu, S.; Su, P. Tuning method of resonant current controller with DC elimination for PWM rectifiers in electric multiple units. IEEE Trans. Transp. Electrif. 2020, 6, 740–751. [Google Scholar] [CrossRef]
- Tasiu, I.A.; Liu, Z.; Wu, S.; Yu, W.; Al-Barashi, M.; Ojo, J.O. Review of recent control strategies for the traction converters in high-speed train. IEEE Trans. Transp. Electrif. 2022, 8, 2311–2333. [Google Scholar] [CrossRef]
- Liu, H.; Ma, L.; Peng, L.; Song, W.; Cheng, S. Robust current control scheme for single-phase PWM rectifiers based on improved μ-synthesis in electric locomotive. IET Power Electron. 2020, 13, 4068–4078. [Google Scholar] [CrossRef]
- Peng, L.; Ma, L.; Song, W.; Liu, H. A simple model predictive instantaneous current control for single-phase PWM converters in stationary reference frame. IEEE Trans. Power Electron. 2022, 37, 7629–7639. [Google Scholar] [CrossRef]
- Lee, G.-Y.; Park, H.-C.; Ji, M.-W.; Kim, R.-Y. Digitalized Control Algorithm of Bridgeless Totem-Pole PFC with a Simple Control Structure Based on the Phase Angle. Electronics 2023, 12, 4449. [Google Scholar] [CrossRef]
- Deng, Q.; Gou, B.; Ge, X.; Lin, C.; Xie, D.; Feng, X. A High-accuracy-light-AI Data-driven Diagnosis Method for Open-circuit Faults in Single-Phase PWM Rectifiers. IEEE Trans. Transp. Electrif. 2023, 9, 4352–4365. [Google Scholar] [CrossRef]
- Qin, N.; Wang, T.; Huang, D.; You, Y.; Zhang, Y. VWM-DCRNN: A Method of Combining Signal Processing With Deep Learning for Fault Diagnosis in Single-Phase PWM Rectifier. IEEE Trans. Power Electron. 2023, 38, 8894–8906. [Google Scholar] [CrossRef]
- Zhang, K.; Gou, B.; Feng, X. Online Fault Diagnosis for Single-Phase PWM Rectifier Using Data-Driven Method. CPSS Trans. Power Electron. Appl. 2022, 7, 49–57. [Google Scholar] [CrossRef]
- Li, Z.; Wang, B.; Ren, Y.; Wang, J.; Bai, Z.; Ma, H. L- and LCL-Filtered Grid-Tied Single-Phase Inverter Transistor Open-Circuit Fault Diagnosis Based on Post-Fault Reconfiguration Algorithms. IEEE Trans Power Electron. 2019, 34, 10180–10192. [Google Scholar] [CrossRef]
- Youssef, A.B.; El Khil, S.K.; Slama-Belkhodja, I. State Observer-Based Sensor Fault Detection and Isolation, and Fault Tolerant Control of a Single-Phase PWM Rectifier for Electric Railway Traction. IEEE Trans Power Electron. 2013, 28, 5842–5853. [Google Scholar] [CrossRef]
- Poon, J.; Jain, P.; Konstantakopoulos, I.C.; Spanos, C.; Panda, S.K.; Sanders, S.R. Model-Based Fault Detection and Identification for Switching Power Converters. IEEE Trans Power Electron. 2017, 32, 1419–1430. [Google Scholar] [CrossRef]
- Yu, Y.; Song, Y.; Tao, H.; Hu, J. Voltage and Current Sensor Fault Diagnosis Method for Traction Rectifier in High-Speed Trains. Electronics 2024, 13, 197. [Google Scholar] [CrossRef]
- Ndrabarushimana, E.; Ma, L. Robust Sensor Fault Detection for a Single-Phase Pulse Width Modulation Rectifier. Electronics 2023, 12, 2366. [Google Scholar] [CrossRef]
- Xie, D.; Lin, C.; Zhang, Y.; Sangwongwanich, A.; Ge, X.; Feng, X.; Wang, H. Diagnosis and Resilient Control for Multiple Sensor Faults in Cascaded H-Bridge Multilevel Converters. IEEE Trans. Power Electron. 2023, 38, 11435–11450. [Google Scholar] [CrossRef]
- Xia, J.; Guo, Y.; Dai, B.; Zhang, X. Sensor Fault Diagnosis and System Reconfiguration Approach for an Electric Traction PWM Rectifier Based on Sliding Mode Observer. IEEE Trans Ind. Appl. 2017, 53, 4768–4778. [Google Scholar] [CrossRef]
- Xia, J.; Li, Z.; Gao, X.; Guo, Y.; Zhang, X. Real-time sensor fault identification and remediation for single-phase grid-connected converters using hybrid observers with unknown input adaptation. IEEE Trans. Ind. Electron. 2023, 70, 2407–2418. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Yan, X.-G.; Mao, Z. Incipient Voltage Sensor Fault Isolation for Rectifier in Railway Electrical Traction Systems. IEEE Trans Ind. Electron. 2017, 64, 6763–6774. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Yan, X.-G.; Shen, J. Interval Sliding Mode Observer Based Incipient Sensor Fault Detection with Application to a Traction Device in China Railway High-Speed. IEEE Trans Veh. Technol. 2019, 68, 2585–2597. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, J.; Xu, Z.; Din, Z.; Zheng, Y. Active power decoupling control for PWM converter considering sensor failures. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 2236–2245. [Google Scholar] [CrossRef]
- Chowdhury, V.R.; Kimball, J.W. Robust Control Scheme for a Three Phase Grid-Tied Inverter with LCL Filter During Sensor Failures. IEEE Trans Ind. Electron. 2021, 68, 8253–8264. [Google Scholar] [CrossRef]
- Merai, M.; Naouar, M.W.; Slama-Belkhodja, I.; Monmasson, E. FPGA-Based Fault-Tolerant Space Vector-Hysteresis Current Control for Three-Phase Grid-Connected Converter. IEEE Trans Ind. Electron. 2016, 63, 7008–7017. [Google Scholar] [CrossRef]
- Mehmood, F.; Papadopoulos, P.M.; Hadjidemetriou, L.; Charalambous, A.; Polycarpou, M.M. Model-based fault diagnosis scheme for current and voltage sensors in grid side converters. IEEE Trans. Power Electron. 2023, 38, 5360–5375. [Google Scholar] [CrossRef]
- Ben Youssef, A.; El Khil, S.K.; Belkhodja, I.S. Open-circuit fault diagnosis and voltage sensor fault tolerant control of a single phase pulsed width modulated rectifier. Math. Comput. Simul. 2017, 131, 234–252. [Google Scholar] [CrossRef]
- Xia, Y.; Gou, B.; Xu, Y. Current sensor fault diagnosis and fault tolerant control for single-phase PWM rectifier based on a hybrid model-based and data driven method. IET Power Electron. 2020, 13, 4150–4157. [Google Scholar] [CrossRef]
- Gong, Z.; Huang, D.; Jadoon, H.U.K.; Ma, L.; Song, W. Sensor-Fault-Estimation-Based Tolerant Control for Single-Phase Two-Level PWM Rectifier in Electric Traction System. IEEE Trans Power Electron. 2020, 35, 12274–12284. [Google Scholar] [CrossRef]
- Dardouri, M.; El Khil, S.K.; Jelassi, K. Current Sensor Fault Reconstruction and Compensation of an AC-Voltage Sensorless Controlled Single Phase Grid Connected Converter using PI-Observers. Int. J. Renew. Energy Res. (IJRER) 2022, 12, 248–258. [Google Scholar]
- Gong, Z.; Huang, D.; Ma, L.; Qin, N.; Jadoon, H.U.K. Grid voltage sensor fault-tolerant control for single-phase two-level PWM rectifier. IET Electr. Power Appl. 2021, 16, 776–788. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, W.; Fan, X.; Peng, T.; Yang, C. JITL-MBN: A realtime causality representation learning for sensor fault diagnosis of traction drive system in high-speed trains. IEEE Trans. Neural Netw. Learn. Syst. 2022. early access. [Google Scholar] [CrossRef] [PubMed]
- Ni, Q.; Zhan, Z.; Li, X.; Zhao, Z.; Lai, L.L. A Real-time Fault Diagnosis Method for Grid-Side Overcurrent in Train Traction System using Signal Time Series Feature Pattern Recognition. IEEE Trans. Ind. Electron. 2023, 71, 4210–4218. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, H. Automatic damage detection and diagnosis for hydraulic structures using drones and artificial intelligence techniques. Remote Sens. 2023, 15, 615. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, M.; Zhang, K.; Li, Z. A Dam Deformation Residual Correction Method for High Arch Dams Using Phase Space Reconstruction and an Optimized Long Short-Term Memory Network. Mathematics 2023, 11, 2010. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Chakraborty, C.; Verma, V. Speed and Current Sensor Fault Detection and Isolation Technique for Induction Motor Drive Using Axes Transformation. IEEE Trans. Ind. Electron. 2015, 62, 1943–1954. [Google Scholar] [CrossRef]
- Kommuri, S.K.; Bin Lee, S.; Veluvolu, K.C. Robust Sensors-Fault-Tolerance with Sliding Mode Estimation and Control for PMSM Drives. IEEE/ASME Trans. Mechatron. 2018, 23, 17–28. [Google Scholar] [CrossRef]
- Han, Y.; Luo, M.; Zhao, X.; Guerrero, J.M.; Xu, L. Comparative Performance Evaluation of Orthogonal-Signal-Generators-Based Single-Phase PLL Algorithms—A Survey. IEEE Trans. Power Electron. 2016, 31, 3932–3944. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Deng, J.; Chen, Z.; Li, S. The State of Charge Estimation of Lithium-Ion Batteries Based on a Proportional-Integral Observer. IEEE Tans Veh. Technol. 2014, 63, 1614–1621. [Google Scholar]
- Lu, J.; Savaghebi, M.; Ghias, A.M.Y.M.; Hou, X.; Guerrero, J.M. A reduced-order generalized proportional integral observer-based resonant super-twisting sliding mode control for grid-connected power converters. IEEE Trans. Ind. Electron. 2020, 68, 5897–5908. [Google Scholar] [CrossRef]
- Söffker, D.; Yu, T.-J.; Müller, C. State estimation of dynamical systems with nonlinearities by using proportional-integral observer. Int. J. Syst. Sci. 1995, 26, 1571–1582. [Google Scholar] [CrossRef]
- Qi, Y.; Zafarani, M.; Gurusamy, V.; Akin, B. Advanced severity monitoring of interturn short circuit faults in PMSMs. IEEE Trans. Transp. Electrif. 2019, 5, 395–404. [Google Scholar] [CrossRef]
- Mukherjee, S.; Chowdhury, V.R.; Shamsi, P.; Ferdowsi, M. Grid Voltage Estimation and Current Control of a Single-Phase Grid-Connected Converter Without Grid Voltage Sensor. IEEE Trans Power Electron. 2018, 33, 4407–4418. [Google Scholar] [CrossRef]
- Dardouri, M.; El Khil, S.K.; Jelassi, K. Sensorless Active Damping of LCL_Filter based on MRAS Estimator for Single-Phase Grid-Connected Inverter. In Proceedings of the 2019 10th International Renewable Energy Congress (IREC), Sousse, Tunisia, 26–28 March 2019; pp. 1–5. [Google Scholar]
- Mehreganfar, M.; Saeedinia, M.H.; Davari, S.A.; Garcia, C.; Rodriguez, J. Sensorless Predictive Control of AFE Rectifier with Robust Adaptive Inductance Estimation. IEEE Trans Ind. Inform. 2019, 15, 3420–3431. [Google Scholar] [CrossRef]












| Description | Symbol | Value |
|---|---|---|
| RMS voltage supply | Vg | 230 V |
| DC-bus voltage | Vdc | 400 VDC |
| Sampling time | Ts | 100 µs |
| Switching frequency | fsw | 10 kHz |
| Line impedance | L, R | 20 mH, 0.2 Ω |
| DC-Link capacitor | C | 1100 µF |
| Rated Load resistance | RL | 100 Ω |
| Description | Symbol | Value |
|---|---|---|
| RMS voltage supply | Vg | 230/48 V |
| DC-Link voltage | Vdc | 80 VDC |
| Sampling time | Ts | 100 µs |
| Switching frequency | fsw | 10 kHz |
| Line impedance | L, R | 20 mH, 0.2 Ω |
| DC-Link capacitor | C | 1100 µF |
| Rated Load resistance | RL | 36 Ω |
| Estimator | Simulations | Experiments | ||
|---|---|---|---|---|
| kp | ki | kp | ki | |
| Vg estimator | 2.5 × 103 | 8 × 106 | 100 | 1 × 105 |
| Vdc estimator | 10 | 1 × 104 | 500 | 5 × 105 |
| ig estimator | 0.7 × 103 | 5 × 102 | 31 | 10 |
| Fault Diagnosis Method | Fault Modes | Single- and Multiple-Sensor Fault Tolerance | Detection Time | Need of Additional Sensor | Algorithm Accuracy | Algorithm Complexity |
|---|---|---|---|---|---|---|
| Luenberger observer [15] | Current and DC-link voltage sensor faults | Single-sensor FTC | <0.02 Tf | Yes | Robust against variations | Medium |
| Open-loop estimator [17] | Current and DC-link voltage sensor faults | Single-sensor FTC | <0.2 Tf | No | Affected by parameters’ variations | Medium |
| Sliding-mode observer [21] | Current and DC-link voltage sensor faults | Single-sensor FTC | ≈0.05 Tf | No | Robust against variations | Medium |
| Fault estimation [30] | Current and DC-link voltage sensor faults | Single-sensor FTC | --- | Yes | Robust against variations | Medium |
| DSOGI estimator [25] | Current and AC voltage sensor faults | Single-sensor FTC | --- | Yes | Robust against variations | Medium |
| State estimator [27] | Current and DC-link voltage sensor faults | Single- and multiple-sensor FTCs | ≈0.05 Tf | Yes | Robust against variations | Medium |
| Reduced-order observer [19] | Current and DC-link voltage sensor faults | Single- and multiple-sensor FTCs | <0.015 Tf | Yes | Robust against variations | Medium |
| Proposed approach | Current, DC-link voltage and AC voltage sensor faults | Single- and multiple-sensor FTCs | ≈0.05 Tf | No | Robust against variations | Medium |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dardouri, M.; Salman, M.; Khojet El Khil, S.; Boccaletti, C.; Jelassi, K. A Multiple-Sensor Fault-Tolerant Control of a Single-Phase Pulse-Width Modulated Rectifier Based on MRAS and GPI Observers. Electronics 2024, 13, 502. https://doi.org/10.3390/electronics13030502
Dardouri M, Salman M, Khojet El Khil S, Boccaletti C, Jelassi K. A Multiple-Sensor Fault-Tolerant Control of a Single-Phase Pulse-Width Modulated Rectifier Based on MRAS and GPI Observers. Electronics. 2024; 13(3):502. https://doi.org/10.3390/electronics13030502
Chicago/Turabian StyleDardouri, M., M. Salman, S. Khojet El Khil, C. Boccaletti, and K. Jelassi. 2024. "A Multiple-Sensor Fault-Tolerant Control of a Single-Phase Pulse-Width Modulated Rectifier Based on MRAS and GPI Observers" Electronics 13, no. 3: 502. https://doi.org/10.3390/electronics13030502






