5G Reconfigurable Intelligent Surface TDOA Localization Algorithm

Abstract

In everyday life, 5G-based localization technology is commonly used, but non-line-of-sight (NLOS) environments can block the propagation of the localization signal, thus preventing localization. In order to solve this problem, this paper proposes a reconfigurable intelligent surface non-line-of-sight time difference of arrival (TDOA) localization (RNTL) algorithm. Firstly, a model of a reflective-surface-based intelligent localization (RBP) system is constructed, which utilizes multiple RISs deployed in the air to reflect signals. Secondly, in order to reduce the localization error, this paper establishes the optimization problem of minimizing the distance between each estimated coordinate and the actual coordinate and solves it via the piecewise linear chaotic map–gray wolf optimization algorithm (PWLCM-GWO). Finally, the simulation results show that the RNTL algorithm significantly outperforms the traditional gray wolf optimization and particle swarm optimization algorithms in different signal-to-noise ratios, and the localization errors are reduced by 46% and 53.5%, respectively.

1. Introduction

With the ongoing advancements in wireless communication, particularly with the continuous evolution of 5G technology, localization has been integrated into people’s lives in all aspects such as car navigation, driverless vehicles, logistics management, medical and health care, industrial IoT, and many other fields [1,2]. To provide better location services, it is necessary to have higher localization accuracy for convenience in navigation, safety and security, resource management optimization, personalized experience, and other aspects of the benefits, thereby significantly improving people’s work efficiency and quality of life [3,4]. It is clear that 5G-based location services have become an indispensable part of people’s lives, and the study of 5G localization technology is of great practical significance [5,6].

Research has been conducted using 5G-based localization techniques, including localization methods for 5G cellular networks. The localization method of the 5G cellular network determines the location of the mobile device through transverse signal propagation and reception of the mobile communication base station. Scholars have conducted extensive research on traditional localization methods and proposed many improved localization methods. In terms of time of arrival (TOA) [7], Zhao et al. [8] proposed a bidirectional TOA localization method based on optimal maximum likelihood, which considers user device mobility to compensate for the error caused by user device motion. The result of the emulation indicates that the localization accurate of this approach is superior to the conventional unidirectional TOA method; however, the TOA localization is limited by the clock synchronization problem. In terms of angle of arrival (AoA) [9,10], Hong et al. [11] proposed a learning-based AoA estimates approach which exploits phase differences to mitigate the AoA estimation error through a multilayer perceptron. The results of simulation indicated that it is significantly superior to the traditional AoA localization method in estimation and location performance. Zhao et al. [12] proposed a method of the joint estimation of AoA and (time of flight) ToF using discrete wavelet transform for the estimation error caused by phase shift and noise interference. It is shown in the simulation results that the presented approach can improve angle estimation accuracies by over 20%. Although the AoA localization method is free from the clock synchronization problem, it is limited by the NLOS environment. In terms of time difference of arrival (TDOA) [13], Zhang et al. [14] derived a weighted least squares localization algorithm based on the linear equality constraint of the time difference of arrival (TDOA), and numerical simulations showed that the localization deviation of the proposed method was significantly reduced. Delcourt et al. [15] proposed a method for two-step TDOA positioning that uses newly created weights and weighted least squares estimation of TDOA measured values obtained from an uncertain origin, and results of the simulations have shown that the approach performs well. Although TDOA solves the problem of clock synchronization of the transmitted signal to the received signal, it is also affected by NLOS. To ameliorate the problem of inability to localize in NLOS environments, the introduction of reconfigurable smart surfaces provides a new approach.

In recent years, reconfigurable intelligent surfaces (RISs) [16,17,18,19] have emerged as a new type of technology that has a significant impact on the development of next-generation wireless communication technologies. An RIS consists of numerous passive reflective elements, and each element has the ability to autonomously adjust the magnitude and phase displacement of the incoming signal, thereby changing the direction of the signal propagation and facilitating its reception by users in different locations [2,20]. In wireless communications, RISs can be deployed as intelligent reflectors on base stations, buildings, vehicles, drones [21], and other objects. When an electromagnetic wave interacts with an RIS, it can adjust the reflected beam direction, change the amplitude and phase of the signal, and even generate a wavefront-shaping effect in real time, thereby achieving dynamic adjustment and optimization of the signal. Thus, an RIS can improve signal coverage, increase the reliability of communication, enhance privacy security, and significantly improve the energy efficiency of wireless communication systems [22].

The localization method of the RIS [23,24] refers to the use of the RIS as a localization device to estimate the location of a mobile device using the phase and amplitude information of the received signal [25,26]. Simultaneously, RIS technology has the potential to address the problem of occlusion. By deploying the RIS in the signal travel route, the signal travel route is adjusted to bypass occlusions or optimize bypass paths, thus reducing signal fading and blocking, and can be used to solve the localization problem in the case of NLOS [27]. Luan et al. [28] developed an extensive structure for RIS-assisted local positioning, which includes RIS phase design and position identification, and demonstrated the proposed modelling framework through numerical results; however, the approach requires accurate a priori information. Zhang et al. [29] used RIS for RSS-based multi-user localization, designed a phase-shift optimization algorithm for the optimization problem of RIS-assisted localization, derived an optimal solution correlation function, and verified its effectiveness through simulation; however, the performance of the algorithm was diminished in the multi-user case. Fascista et al. [30] proposed a joint positioning method based on the optimal demodulation of RIS passive-phase contours and designed the metric as a theoretical position error constraint to achieve the optimization of BS-RIS beamforming, and the simulation results showed that the scheme exhibited better positioning performance. The above literature proves that RISs have a significant effect on solving the problem of large positioning errors in NLOS environments; however, the above studies do not consider the effects of the number of RISs and the RISs’ reflection units on the positioning error at the same time, and they also do not consider the application of RISs in TDOA positioning.

In order to tackle this issue, this study suggests a 5G reconfigurable intelligent surface TDOA localization algorithm that utilizes multiple RISs to assist TDOA localization and derives a more accurate localization result with multiple error-inclusive localization results to enhance localization accuracy further.

This study’s primary contributions include the following:

(1)

A reconfigurable intelligent surface-based localization (RBL) system model (composed of a single-antenna base station, a user to be localized, and multiple RISs) was designed. The system is set up as an NLOS environment for the base station and user to be localized, communicating through the RIS, which effectively solves the problem of poor localization under the NLOS path.

(2)

A reconfigurable intelligent surface non-line-of-sight TDOA localization (RNTL) algorithm is proposed, and the range from RIS to user to be located is solved by adjusting the RIS’s phase shift matrix (PSM). The estimated coordinates of the user to be located are further solved, and an optimal issue is created to minimalize the separation between each of the estimated coordinates and the actual coordinates.

(3)

A PWLCM–gray wolf optimization (PWLCM-GWO) algorithm is suggested to address the optical issue. First, PWLCM chaotic mapping is introduced to address the issue of insufficient diversity of individuals in the traditional GWO algorithm. Second, an improved convergence factor is used to solve the problem of difficulty in balancing the global search and local hunting in the traditional GWO algorithm. Finally, population elimination is induced to lower the computational complexity of the method while maintaining the accuracy of the calculation.

(4)

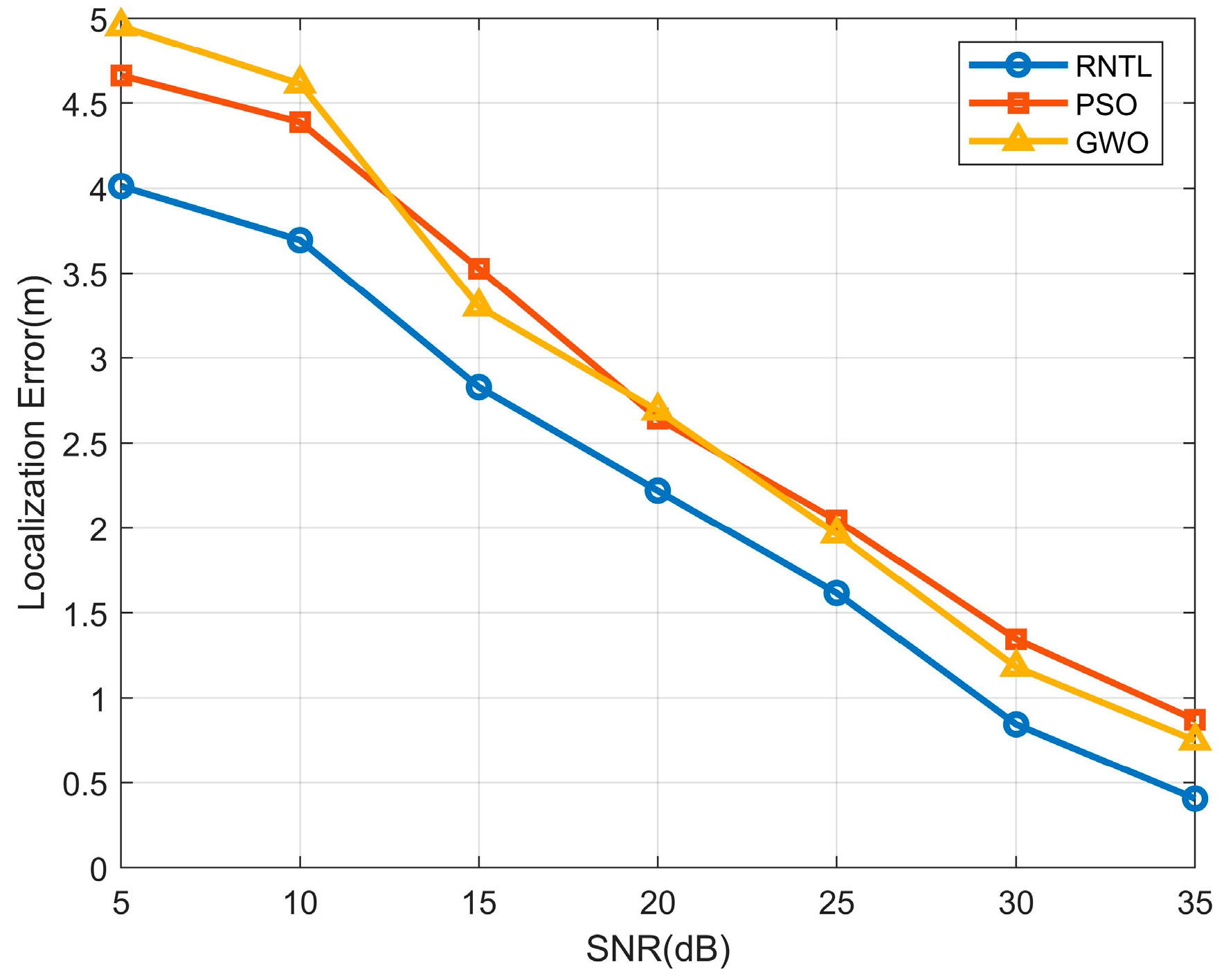
Simulation results indicate that the proposed RNTP algorithm has superior performance to that of the GWO and particle swarm optimization (PSO) algorithms in varying signal-to-noise ratios (SNRs), and the localization error obtained by this algorithm can be reduced by up to 46% and 53.5% compared with the GWO and PSO algorithms, respectively.

2. System Model

The RBL system is shown in Figure 1, which has a single-antenna base station (BS), multiple reconfigurable intelligent surfaces (RIS), and a single-antenna user equipment (UE) to be located. We can assume that the system contains $I(I\ge 4)$ reconfigurable intelligent surfaces denoted as set $RIS=\left\{RI{S}_1,RI{S}_2,\cdots ,RI{S}_i,\cdots ,RI{S}_I\right\},i=1,\cdots ,I$, where $RI{S}_i$ represents the ith reconfigurable intelligent surface. Each RIS consists of N uniformly horizontally linearly arranged reflection units, where the reflection units of $RI{S}_i$ are denoted as set $U=\left\{U_1^i,U_2^i,\cdots ,U_n^i,\cdots ,U_N^i\right\},n=1,\cdots ,N$, among which $U_n^i$ denotes the nth reflection unit of $RI{S}_i$.

In the system model set up in this paper, BS and UE cannot communicate directly. Therefore, when BS wants to communicate with UE, the RIS $I$ first receives the signal transmitted by the BS and adjusts the amplitude and phase shift of the received signal by controlling each reflection unit on the RIS through a circuit to reflect it to the UE. Assuming that the locations of the BS and RIS are fixed and known, the location of the base station will be $\left(x^B,y^B,z^B\right)$, and the location of $U_n^i$ in $RI{S}_i$ will be $\left(x_i^n,y_i^n,z_i^n\right)$. The location of the user to be localized (UE) is unknown and is set to $\left(x,y,z\right)$.

Let the PSM of $RI{S}_i$ be ${\mathit{\Theta }}_i=\mathrm{diag}\left({\gamma }_i^1{e}^{j{\theta }_i^1},\cdots ,{\gamma }_i^n{e}^{j{\theta }_i^n},\cdots ,{\gamma }_i^N{e}^{j{\theta }_i^N}\right)$, where $\mathrm{diag}(.)$ denotes diagonal matrix, ${\theta }_i^n$ denotes the phase shift of $U_n$ on $RI{S}_i$, and ${\theta }_i^n\in [0,2\pi ]$; ${\gamma }_i^n$ denotes the amplitude reflection coefficient of $U_n$ on $RI{S}_i$. Changes to the signal amplitude are not considered in this paper; thus, for ease of computation, setting ${\gamma }_i^n=1$ simplifies the PSM of $RI{S}_i$ to ${\mathit{\Theta }}_i=\mathrm{diag}\left(e^{j{\theta }_i^1},\cdots ,e^{j{\theta }_i^n},\cdots ,e^{j{\theta }_i^N}\right)$.

Let the channel of the nth reflection unit $U_n^i$ from BS to $RI{S}_i$ be

$$h_i^n={\left(D_i^n\right)}^{-\beta /2}{e}^{-j{\phi }_i^n}$$

(1)

where $D_i^n$ denotes the $U_n^i$ wireless communication channel distance from BS to $RI{S}_i$, $\beta$ and ${\phi }_i^n$ denote the path loss exponent and delay phase shift. The wireless communication channels from BS to RIS are ${\mathit{H}}_1$, ${\mathit{H}}_2$,…, ${\mathit{H}}_i$,…, and ${\mathit{H}}_{\mathit{I}}$ can be expressed as

$$\begin{array}{l}{\mathit{H}}_{\mathit{i}}=\left[h_i^1,h_i^2,\cdots ,h_i^n,\cdots ,h_i^N\right]\\ \hspace{1em}=\left[{\left(D_i^1\right)}^{-\beta /2}{e}^{-j{\phi }_i^1},{\left(D_i^2\right)}^{-\beta /2}{e}^{-j{\phi }_i^2},\cdots ,\right.\\ \left.\hspace{1em}\hspace{1em}{\left(D_i^n\right)}^{-\beta /2}{e}^{-j{\phi }_i^n},\cdots {\left(D_i^N\right)}^{-\beta /2}{e}^{-j{\phi }_i^N}\right]\end{array}$$

(2)

Let the nth reflection cell $U_n^i$ from $RI{S}_i$ to the UE channel be

$$g_i^n={\left(d_i^n\right)}^{-\beta /2}{e}^{-j{\varphi }_i^n}$$

(3)

where $d_i^n$ denotes the wireless communication channel range from $U_n^i$ to UE of $RI{S}_i$.

Wireless communication channels between RIS to UE are ${\mathit{G}}_1$, ${\mathit{G}}_2$,…, ${\mathit{G}}_i$,…, and ${\mathit{G}}_{\mathit{I}}$, which can be expressed as

$$\begin{array}{l}{\mathit{G}}_{\mathit{i}}={\left[g_i^1,g_i^2,\cdots ,g_i^n,\cdots ,g_i^N\right]}^T\\ \hspace{1em}=\left[{\left(d_i^1\right)}^{\beta /2}{e}^{-j{\phi }_i^1},{\left(d_i^2\right)}^{\beta /2}{e}^{-j{\phi }_i^2},\cdots ,\right.\\ \hspace{1em} {\left.{\left(d_i^n\right)}^{\beta /2}{e}^{-j{\phi }_i^n},\cdots ,{\left(d_i^N\right)}^{\beta /2}{e}^{-j{\phi }_i^N}\right]}^T\end{array}$$

(4)

Let the channel for sending a signal from BS reach UE through the nth reflection unit $U_n$ of $RI{S}_i$ be

$$h_i^n{\mathit{\Theta }}_i^n{g}_i^n={\left(D_i^n\right)}^{-\beta /2}{e}^{-j{\phi }_i^n}{\gamma }_i^n{e}^{j{\theta }_i^n}{\left(d_i^n\right)}^{-\beta /2}{e}^{-j{\phi }_i^n}$$

(5)

The total channel for communication between $IR{S}_m$ aided UE and BS can be expressed as

$$\begin{array}{c}{\mathit{H}}_i{\mathit{\Theta }}_i{\mathit{G}}_i=\left[h_i^1,h_i^2,\cdots h_i^n\cdots ,h_i^N\right]\mathrm{diag}\left(e^{j{\theta }_i^1},\cdots ,e^{j{\theta }_i^n},\cdots ,e^{j{\theta }_i^N}\right)\\ \cdot {\left[g_i^1,g_i^2,\cdots g_i^n,\cdots g_i^N\right]}^T\end{array}$$

(6)

where ${\mathit{\Theta }}_i$ is a unit matrix, and the left side of Equation (5) is modulo-collapsed:

$$\left|h_i^n{g}_i^n\right|={\left(D_i^n\right)}^{-\beta /2}{\left(d_i^n\right)}^{-\beta /2}$$

(7)

This provides the distance from each cell to the user to be localized.

$$d_i^n=\frac{{\left(\left|h_i^n{g}_i^n\right|\right)}^{-2/\beta }}{D_i^n}$$

(8)

Equation (6) can be further expressed as

$$\left|{\mathit{H}}_{\mathit{i}}{\mathit{G}}_{\mathit{i}}\right|={\displaystyle \sum _{n=1}^N\left|h_i^n{g}_i^n\right|}$$

(9)

When the range from the BS to RIS is large, the difference in distance between each unit is negligible. Therefore, it can be assumed that the distance from each unit to the base station in an RIS is equal. The wireless communication channel distance between $RI{S}_i$ and UE is the average of the distances from each unit in $RI{S}_i$ to the user to be located and is denoted as

$$R_i=\frac{1}{N}{\displaystyle \sum _{n=1}^N{d}_i^n}=\frac{{\left(\frac{\left|{\mathit{H}}_{\mathit{i}}{\mathit{G}}_{\mathit{i}}\right|}{N}\right)}^{-2/\beta }}{\frac{1}{N}{\displaystyle \sum _{n=1}^N{D}_i^n}}$$

(10)

3. RNTL Algorithm

3.1. RNTL Algorithm

When BS transmits a known signal $s$, let $y$ be the sum of all $I$ RIS-reflected signals received by UE, which is represented as

$$y=\left({\mathit{H}}_1{\mathit{\Theta }}_1{\mathit{G}}_1+{\mathit{H}}_2{\mathit{\Theta }}_2{\mathit{G}}_2+\cdots {\mathit{H}}_i{\mathit{\Theta }}_i{\mathit{G}}_i\cdots +{\mathit{H}}_I{\mathit{\Theta }}_I{\mathit{G}}_I\right)s+n$$

(11)

where $n$ denotes the Gaussian white noise of ${\sigma }^2$.

Assuming that the channel coefficients are constant, the distance from $RI{S}_i$ to UE can be obtained by setting PSM of $I$ reconfigurable intelligent surface $m\in M$$\left(M=I\right)$ times.

When $m=1$, the PSM ${\mathit{\Theta }}_1,{\mathit{\Theta }}_2,\cdots {\mathit{\Theta }}_i,\cdots ,{\mathit{\Theta }}_I=\mathit{E}$, where $\mathit{E}$ is the unit matrix, can be obtained as

$${\tilde{y}}_1=\left({\mathit{H}}_1{\mathit{G}}_1+{\mathit{H}}_2{\mathit{G}}_2+\cdots {\mathit{H}}_i{\mathit{G}}_i\cdots +{\mathit{H}}_I{\mathit{G}}_I\right)s+{\mathrm{n}}_1$$

(12)

When $m=2$, let the PSM ${\mathit{\Theta }}_1,{\mathit{\Theta }}_2,\cdots ,{\mathit{\Theta }}_i,\cdots {\mathit{\Theta }}_{I-1},-{\mathit{\Theta }}_I=\mathit{E}$, where the PSM of the first $I-1$ RIS is a unit vector, and the PSM of the last RIS is a negative unitary vector.

$$\begin{array}{c}{\tilde{y}}_2=\left({\mathit{H}}_1{\mathit{G}}_1+{\mathit{H}}_2{\mathit{G}}_2+\cdots +{\mathit{H}}_i{\mathit{G}}_i+\cdots \right.\\ \left.+{\mathit{H}}_{I-1}{\mathit{G}}_{I-1}-{\mathit{H}}_I{\mathit{G}}_I\right)s+n_2\end{array}$$

(13)

Similarly, during $m=(3,\dots ,M-1)$, let the PSM $\left\{\begin{array}{l}{\mathit{\Theta }}_1,{\mathit{\Theta }}_2,\cdots ,{\mathit{\Theta }}_i,\cdots {\mathit{\Theta }}_{I-2},-{\mathit{\Theta }}_{I-1},-{\mathit{\Theta }}_I=\mathit{E}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\Theta }_1,-{\mathit{\Theta }}_2,\cdots ,-{\mathit{\Theta }}_i,\cdots ,-{\mathit{\Theta }}_I=\mathit{E}\end{array}\right.$ be obtained as

$$\left\{\begin{array}{l}{\tilde{y}}_3=\left({\mathit{H}}_1{\mathit{G}}_1+{\mathit{H}}_2{\mathit{G}}_2+\cdots {\mathit{H}}_i{\mathit{G}}_i+\cdots +{\mathit{H}}_{I-2}{\mathit{G}}_{I-2}\right.\\ \left.\hspace{1em}\hspace{1em}-{\mathit{H}}_{I-1}{\mathit{G}}_{I-1}-{\mathit{H}}_I{\mathit{G}}_I\right)s+n_2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\tilde{y}}_{I-1}=\left({\mathit{H}}_1{\mathit{G}}_1-{\mathit{H}}_2{\mathit{G}}_2-\cdots {\mathit{H}}_i{\mathit{G}}_i\cdots -{\mathit{H}}_I{\mathit{G}}_I\right)s+n_I\end{array}\right.$$

(14)

Because there is a case of noise interference in the signal propagation, the multiplication of the channel between BS to RIS and the channel from RIS to UE in the case can be estimated using Equations (7)–(9) as follows:

$$\left\{\begin{array}{l}{\tilde{\mathit{H}}}_1{\tilde{\mathit{G}}}_1=\frac{1}{2s}({\tilde{y}}_1+{\tilde{y}}_I)\\ {\tilde{\mathit{H}}}_2{\tilde{\mathit{G}}}_2=\frac{1}{2s}({\tilde{y}}_{I-1}-{\tilde{y}}_I)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\tilde{\mathit{H}}}_i{\tilde{\mathit{G}}}_i=\frac{1}{2s}({\tilde{y}}_{I-(i-1)}-{\tilde{y}}_{I-(i-2)})\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\tilde{\mathit{H}}}_I{\tilde{\mathit{G}}}_I=\frac{1}{2s}({\tilde{y}}_1-{\tilde{y}}_2)\end{array}\right.$$

(15)

Substituting Equation (15) into Equation (10) yields the value of the wireless communication channel distance from RIS to UE of the user to be localized when containing noise as follows:

$$\begin{array}{l}{\tilde{R}}_1=\left(\frac{{\left|\frac{{\tilde{y}}_1+{\tilde{y}}_I}{2s\times N}\right|}^{-2/\beta }}{\frac{1}{N}{\displaystyle \sum _{n=1}^N{D}_i^n}}\right),\\ {\tilde{R}}_2=\left(\frac{{\left|\frac{{\tilde{y}}_{I-1}-{\tilde{y}}_I}{2s\times N}\right|}^{-2/\beta }}{\frac{1}{N}{\displaystyle \sum _{n=1}^N{D}_i^n}}\right),\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\tilde{R}}_i=\left(\frac{{\left|\frac{{\tilde{y}}_{i-(i-1)}-{\tilde{y}}_{i-(i-2)}}{2s\times N}\right|}^{-2/\beta }}{\frac{1}{N}{\displaystyle \sum _{n=1}^N{D}_i^n}}\right)\end{array}$$

(16)

3.2. PWLCM-GWO

The distance difference containing noise can be expressed as

$$\begin{array}{l}{\tilde{R}}_{i,j}={\tilde{R}}_i-{\tilde{R}}_j\\ \hspace{1em} =\sqrt{{\left(x_i-x\right)}^2+{\left(y_i-y\right)}^2+{\left(z_i-z\right)}^2}-\\ \hspace{1em}\hspace{1em}\sqrt{{\left(x_j-x\right)}^2+{\left(y_j-y\right)}^2+{\left(z_j-z\right)}^2}\end{array}$$

(17)

The coordinates of the estimated points can be solved by selecting three different groups of ${\tilde{R}}_{i,j}$ and associating them through the principle of TDOA; however, there may be some outliers in these estimated points whose coordinates are far beyond the localization range, which can be removed by preprocessing through the quaternion method.

The fitness function $F(x,y,z)$ is designed by calculating the difference between each estimated point and the actual location separately and minimizing the summation as the principle to seek the individual with the best agreement between the actual and estimated values, that is, the optimal solution of the improved gray wolf algorithm $(x,y,z)$. The optimization problem is expressed as

$$F(x,y,z)=\min {\displaystyle \sum _{j=1}^J\sqrt{{(x_j-x)}^2+{(y_j-y)}^2+{(z_j-z)}^2}}$$

(18)

In the phase of generating the initial positions of gray wolf individuals, this study introduces PWLCM chaotic mapping to solve the problem of the lack of diversity of population individuals caused by randomly generating the initial positions of gray wolf individuals, thus enhancing the optimization effect of the algorithm. PWLCM chaotic mapping has non-periodicity and ergodicity, which helps the algorithm avoid local optima and improves the ability of the global search to solve the optimization problem. The PWLCM chaotic mapping is represented by

$$\Gamma (c+1)=\left\{\begin{array}{ll}\Gamma (c)/l& \Gamma (c)\in \left[0,l\right)\\ \left(\Gamma (c)-l\right)/\left(1/2-l\right)& \Gamma (c)\in \left[l,1/2\right)\\ \left(1-l-\Gamma (c)\right)/\left(1/2-l\right)& \Gamma (c)\in [1/2,1-l)\\ \left(1-\Gamma (c)\right)/l& \Gamma (c)\in [1-l,1) \end{array}\right.$$

(19)

where $\Gamma \left(1\right)$ assumes the value of $\left(0,1\right)$ and $l$ is the control parameter taking the value of $\left(0,1/2\right)$.

In this study, the gray wolf population was divided into four parts, where $\mu$ is the optimal individual, $\mathsf{\varpi }$ is the second optimal individual, $\zeta$ is the third optimal individual, and $\vartheta$ is another candidate individual. The distance of the qth individual from the optimal individual in the pth hunt can be expressed as

$$L_q^{p,\mu }=\left|E_q^{p,\mu }\cdot s^{p,\mu }-s_q^p\right|$$

(20)

where $s^{p,\mu }$ denotes the position of the optimal individual in the pth hunt, $s_q^p$ denotes the position of the qth individual in the pth hunt, and $E_q^{p,\mu }$ denotes the swing factor vector, which can be expressed as follows:

$$E_q^{p,\mu }=2r_1$$

(21)

where $r_1$ is a vector of random numbers between $\left[0,1\right]$.

The gray wolf individual position vector consists of three elements corresponding to the $\left(x,y,z\right)$ three-dimensional position coordinates of the location to be localized, the distance of the qth individual from the second-best individual in the pth hunt, and the distance of the third-best individual, which are expressed as

$$\left\{\begin{array}{l}{L}_q^{p,\mathsf{\varpi }}=\left|E_q^{p,\mathsf{\varpi }}\cdot s^{p,\mathsf{\varpi }}-s_q^p\right|\\ L_q^{p,\zeta }=\left|E_q^{p,\zeta }\cdot s^{p,\zeta }-s_q^p\right|\end{array}\right.$$

(22)

where $E_q^{p,\mathsf{\varpi }}=2r_1$ and $E_q^{p,\zeta }=2r_1$ are swing factor vectors and $s^{p,\mathsf{\varpi }}$ and $s^{p,\zeta }$ are the positions of the pth hunt for the second- and third-best individuals, respectively.

The effect of the qth individual on the pth hunt with the best, second best, and third best individuals can be expressed as

$$\left\{\begin{array}{l}{\widehat{s}}_q^{p,\mu }=s^{p,\mu }-a_q^{p,\mu }{L}_q^{p,\mu }\\ {\widehat{s}}_q^{p,\mathsf{\varpi }}=s^{p,\mathsf{\varpi }}-a_q^{p,\mathsf{\varpi }}{L}_q^{p,\mathsf{\varpi }}\\ {\widehat{s}}_q^{p,\zeta }=s^{p,\zeta }-a_q^{p,\zeta }{L}_q^{p,\zeta }\end{array}\right.$$

(23)

where $a_q^{p,\mu }$, $a_q^{p,\mathsf{\varpi }}$, and $a_q^{p,\zeta }$ are convergence factor vectors expressed as follows:

$$a_q^{p,\mu }=2a^p{r}_2-a^p,a_q^{p,\mathsf{\varpi }}=2a^p{r}_2-a^p,a_q^{p,\zeta }=2a^p{r}_2-a^p$$

(24)

where $r_2$ denotes a random number between $\left[0,1\right]$.

When $\left|a_q^{p,\mu }\right|,\left|a_q^{p,\mathsf{\varpi }}\right|,\left|a_q^{p,\zeta }\right|>1$, the wolf pack spreads to search for prey, and when $\left|a_q^{p,\mu }\right|,\left|a_q^{p,\mathsf{\varpi }}\right|,\left|a_q^{p,\zeta }\right|\le 1$, the wolf pack hunts locally. Therefore, the value of the control parameter $a^p$ will significantly affect the stability of the algorithm and the optimization effect. In this study, we adopted the improved nonlinear control parameter $a^p$ to replace the control parameter that is linearly reduced from two to zero in the traditional gray wolf algorithm, which solves the problem of difficulty in the traditional algorithm to achieve a balance between global and local searches. The $a^p$ can be expressed as

$$a^p=2\cdot \left[1-\frac{1}{\mathrm{e}-1}\cdot \left({\mathrm{e}}^{\frac{p}{p_{\max }}}-1\right)\right]$$

(25)

where $p_{\max }$ denotes the maximum number of hunts.

The qth individual’s position in the (p + 1)th hunt is as follows:

$$s_q^{p+1}=\frac{{\widehat{s}}_q^{p,\mu }+{\widehat{s}}_q^{p,\mathsf{\varpi }}+{\widehat{s}}_q^{p,\zeta }}{3}$$

(26)

Meanwhile, this study eliminates some gray wolf individuals during the hunting process to decrease the computational complexity of the algorithm.

$$\left\{\begin{array}{l}V=V_{\max },\hspace{1em}o>o_1\hfill \\ V=V_{\min }{o}^{\left[\lg V_{\max }-\lg V_{\min }\right]/\lg o_1},\hspace{1em}1<o\le o_1\hfill \\ V=V_{\min },\hspace{1em}o\le 1\hfill \end{array}\right.$$

(27)

$$o=\sqrt{{\displaystyle \sum _{d=1}^3{\left(s_d^{p,\mathrm{b}}-s_d^{p,\mathrm{w}}\right)}^2}}$$

(28)

where $V$, $V_{\max }$, and $V_{\min }$ are the number, maximum number, and minimum number of populations. $o$ is the Euclidean distance between the current optimal and worst particles, $o_1$ is the Euclidean distance between the optimal and worst particles at the time of initialization of populations, $d$ is the dimensionality of particles, $s_d^{p,\mathrm{b}}$ is the position of the optimal particles of the pth hunt, and $s_d^{p,\mathrm{w}}$ is the position of the worst particles of the pth hunt.

In summary, the flow of the RNTL algorithm proceeds as follows as shown in Algorithm 1:

Algorithm 1 RNTL Algorithm
Input: maximum population size $U_{\max }$, minimum population size $U_{\min }$, maximum number of hunts $p_{\max }$, the location of BS $\left(x^B,y^B,z^B\right)$, the location of $U_n^i$ in $RI{S}_i$ $\left(x_i^n,y_i^n,z_i^n\right)$, free space loss $\beta$, input signal s;
1.	Find the output when noise is included according to Equation (14);
2.	The distance between $RIS$ and the user to be localized UE is found by Equation (16);
3.	The estimated point coordinates are solved by the TDOA principle, and the anomalies are removed using the quadrature method;
4.	The initial position of the individual is generated according to the PWLCM chaotic mapping in Equation (19);
5.	Calculate the fitness of all individuals according to Equation (18), and find the three individuals with the smallest fitness;
6.	for $p\in \left(1,p_{\max }\right)$ do
7.	for $q\in \left(1,V\right)$ do
8.	Calculate the wiggle factor according to Equation (21);
9.	Calculate the convergence factor according to Equation (24);
10.	Calculate the new position of the individual according to Equations (20), (22), (23) and (26);
11.	Discipline the transgressing individual;
12.	The new fitness of each individual is calculated according to Equation (18);
13.	end
14.	While protecting the better individuals, some of the worse individuals are eliminated according to Equations (27) and (28);
15.	Re-comparison determines the three individuals with the smallest fitness;
16.	end
Output: localize the optimal solution $(x,y,z)$

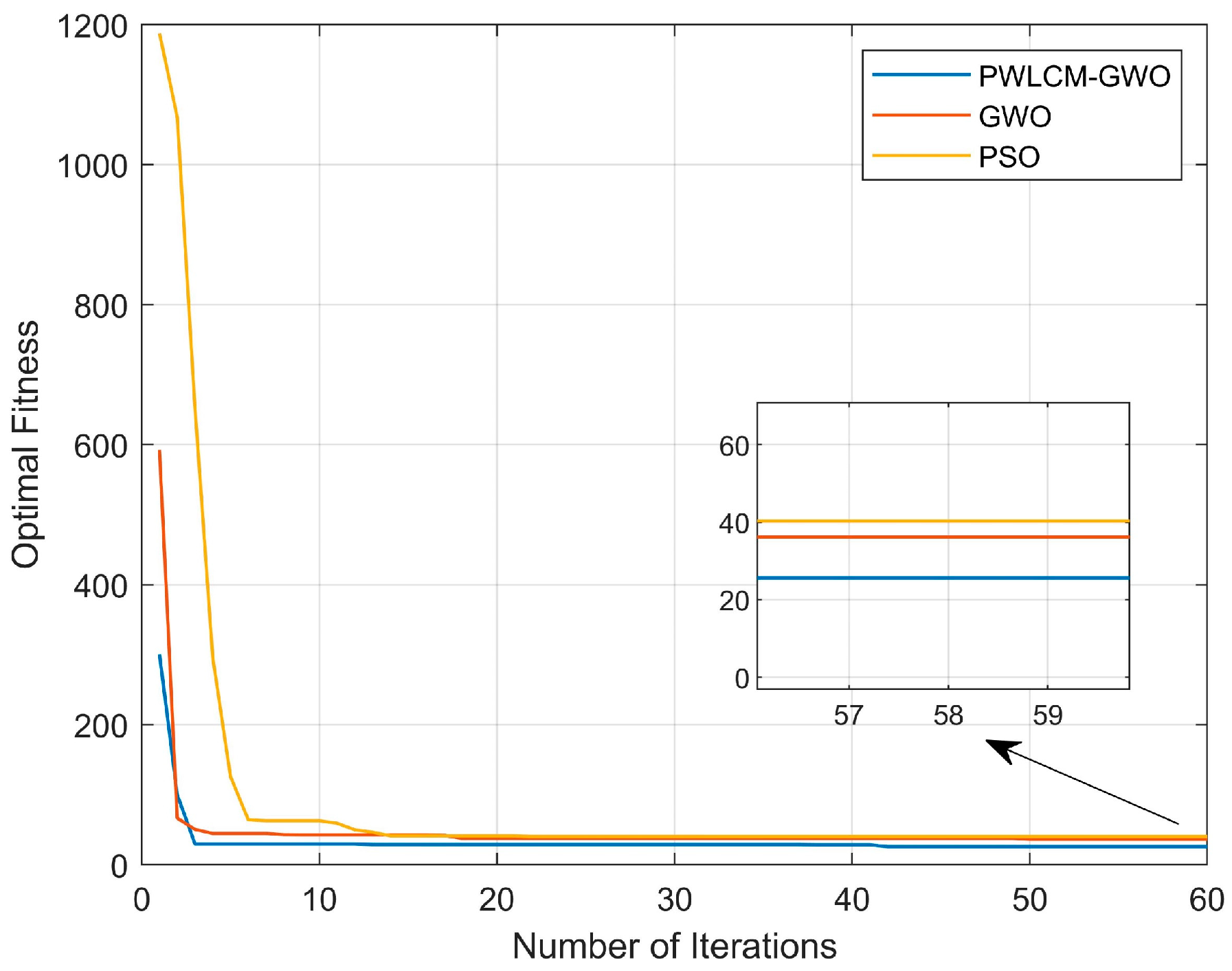
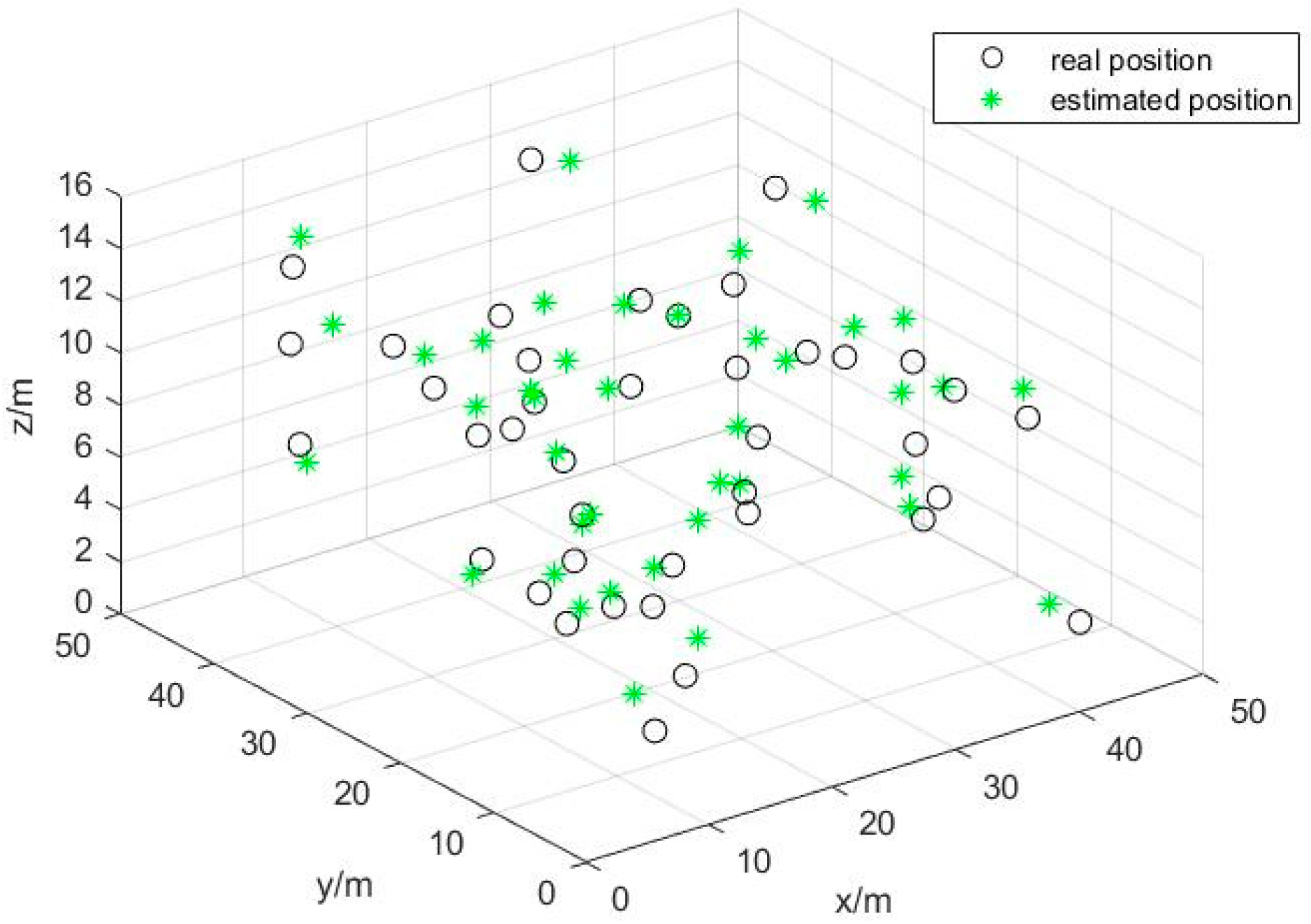
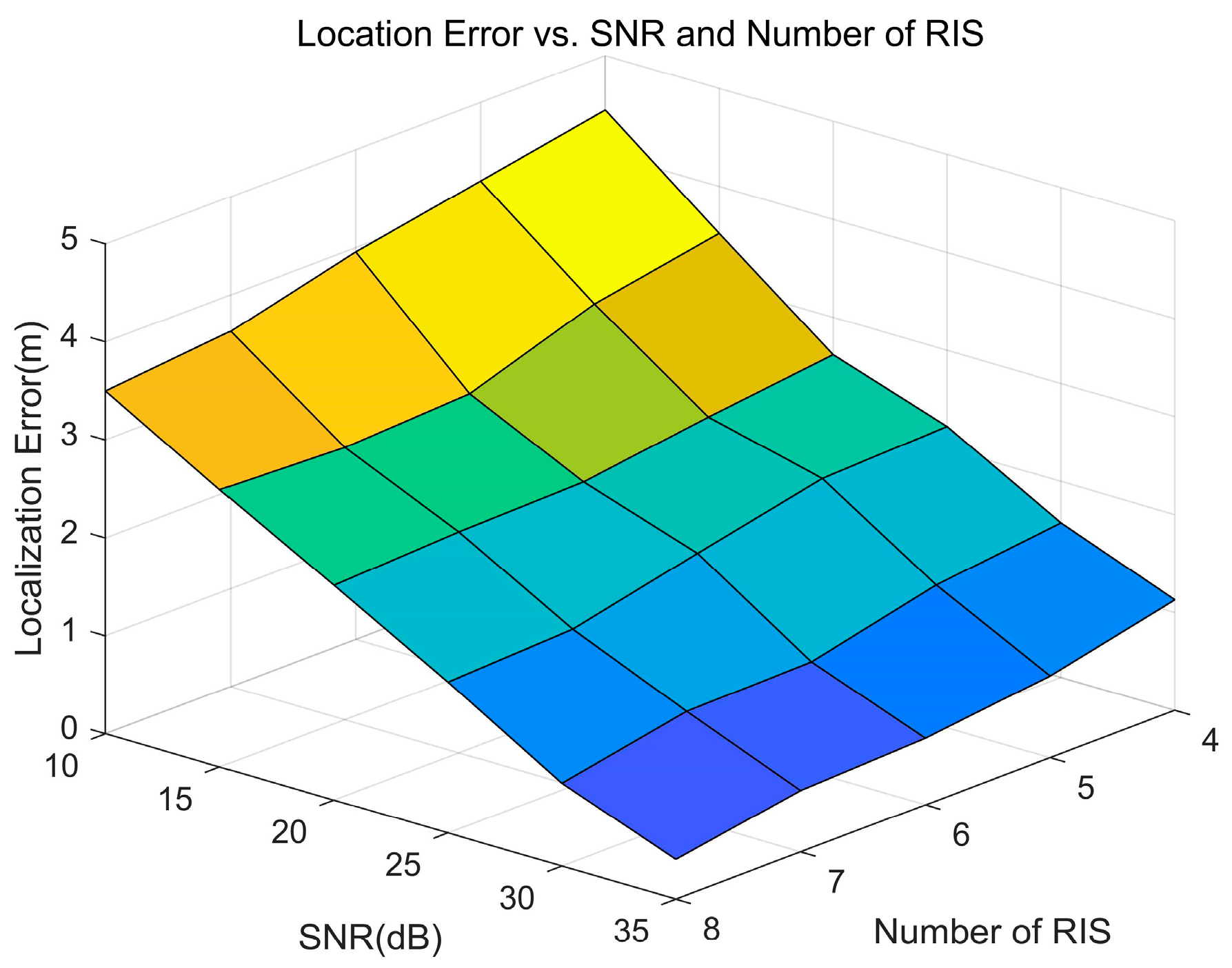
4. Simulation Results and Analysis

In this study, based on the MATLAB simulation platform, a $50 \mathrm{m}\times 50 \mathrm{m}\times 16 \mathrm{m}$ three-dimensional space was established. We set the speed of light $c=3\times {10}^8$, the carrier frequency $f=2 \mathrm{GHz}$, number of RIS is $I=8$, number of units of each RIS $N=4$, and the spacing of each RIS unit at 0.5 m, the path loss exponent $\beta$ = 2, the amplitude reflection coefficient ${\gamma }_i^n=1$, number of population iterations $p_{\max }=100$, and number of populations $v=100$.

A simulation comparing the fitness of different algorithms under various iterations is shown in Figure 2, where the horizontal and vertical axis represent the number of iterations and fitness, the blue curve in the figure represents the RNTL algorithm, the orange and red curves represent the GWO algorithm, and the yellow curve represents the PSO algorithm. The fitness reduces as the iterations increase and eventually converge to a different value. The proposed RNTL algorithm converged with significantly less adaptation than the GWO and PSO algorithms. Compared to the GWO and PSO algorithms, PWLCM-GWO helps to maintain the population diversity by introducing PWLCM, which avoids the neglect of certain regions. By reasonably adjusting the parameters of chaotic mapping, the PWLCM-GWO algorithm is able to accelerate the convergence speed while ensuring the balance of exploration and exploitation.

When the SNR is 18 dB and 50 known nodes are distributed inside the space, the 3D localization results of the RNTL localization algorithm are shown in Figure 3, where “$\circ$” represents the real location of the user to be localized, and the green “$\ast$” in the figure represents the user’s location estimated by the RNTL algorithm. It can be observed from the figure that there is a higher degree of overlap between the location estimated and the real location of the user to be localized, which shows that the algorithm in this study has a higher localization accuracy.

A simulation comparison of different SNRs under the variation rule of the localization error is as in Figure 4, where the horizontal and vertical axis indicate the SNR and localization error, and curves with circles, squares, and triangles in the figure indicate the RNTL, PSO, and GWO algorithms, respectively. It can be observed from the figure that with the increasing SNR, the localization error decreases, which is due to the improvement in the SNR that makes the quality of the communication transmission improve, thus improving the localization accuracy. It is evident that the RNTL algorithm is significantly better than the GWO and PSO algorithm; in addition, we can learn from the figure that when $SNR=35$, the RNTL, GWO, and PSO algorithms have a localization error of 0.405725, 0.75053, and 0.872264, respectively, which can be observed as the paper’s proposed RNTL algorithm obtains a localization error of up to 46% lower than the GWO and PSO algorithms. The PSO algorithm can be reduced by up to 46% and 53.5%, respectively, and the proposed RNTL algorithm is effective. The RNTL algorithm proposed in this paper utilizes PWLCM-GWO, an improved convergence factor, and introduces population elimination, which ensures a balanced global and local search and ensures the localization accuracy. In addition, the larger the signal-to-noise ratio is, the stronger the useful signal in the received signal and the smaller the interference is; conversely, the smaller the signal-to-noise ratio is, the smaller the useful signal received.

The simulation comparing the localization error for different numbers of RIS at different SNRs is shown in Figure 5, where the x-, y-, and z-axis represent the SNR, number of RISs, and localization error, respectively. From the figure, it can be observed that yellow color represents poor localization accuracy and blue color represents high localization accuracy; as the number of RISs and SNRs increases, the localization error of the RNTL algorithm decreases gradually. This is due to the fact that the larger the SNR is, the stronger the useful received signals are and the smaller the interference is; on the contrary, the smaller the SNR is, the smaller the received useful signals are. An increase in the number of RISs allows the system to solve more estimated coordinates by applying the principle of TDOA, so that the RNTP algorithm of this paper obtains better localization accuracy. At $SNR=35$, when the number of RISs is four, the localization error is 1.12836 m, and when the number of RISs is more than four, the localization error is less than 1 m.

5. Conclusions

In this study, we designed an RBL system composed of a single-antenna base station and user to be localized as well as multiple RISs. The system was set up as an NLOS environment for the base station and user to be localized to communicate through the RIS, which effectively solves the problem of poor localization on the NLOS path. An RNTL algorithm was proposed to establish the a solution for minimizing the distance between each estimated coordinate and the actual coordinate. Second, a PWLCM-GWO algorithm was proposed to introduce PWLCM chaotic mapping to address the issue of insufficient diversity of individuals in the traditional GWO algorithm, to use an improved convergence factor to solve the problem of difficulty in achieving a balance between global search and local hunting in the traditional GWO algorithm, and to introduce population elimination to reduce complexity. In the simulation effect, it is indicated that the locating error obtained by the RNTP algorithm suggested in this paper can be reduced up to 46% and 53.5%, respectively, compared to the GWO and PSO algorithms, which showed good performance.