The Quasi-Resonant Structure and Control Strategy of a Photovoltaic Flyback Grid-Connected Microinverter
Abstract
:1. Introduction
2. Materials and Methods
2.1. Topology Structure and Operating Principle
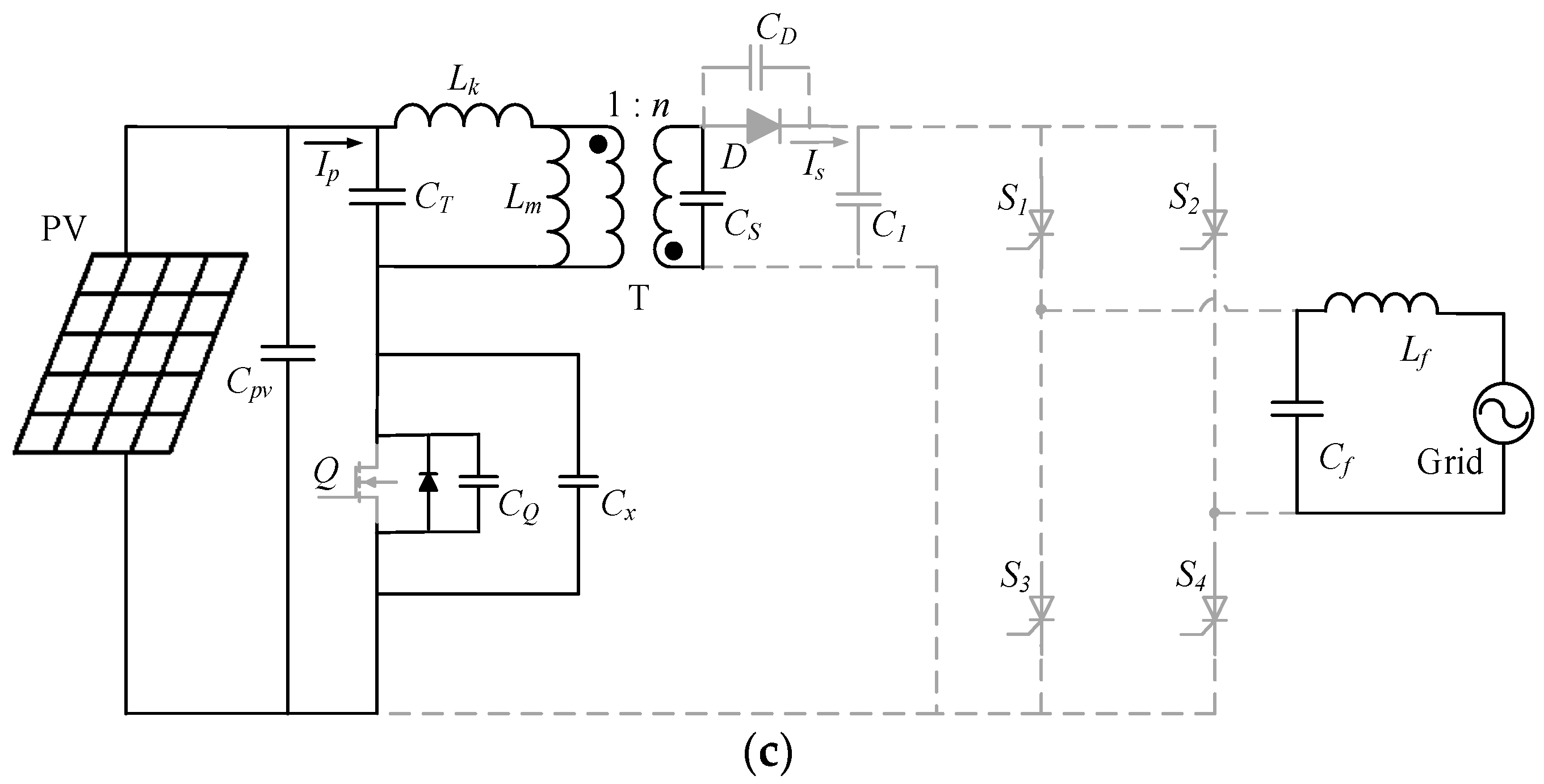
2.1.1. Flyback Inverter Topology
2.1.2. Flyback Inverter Modal Analysis
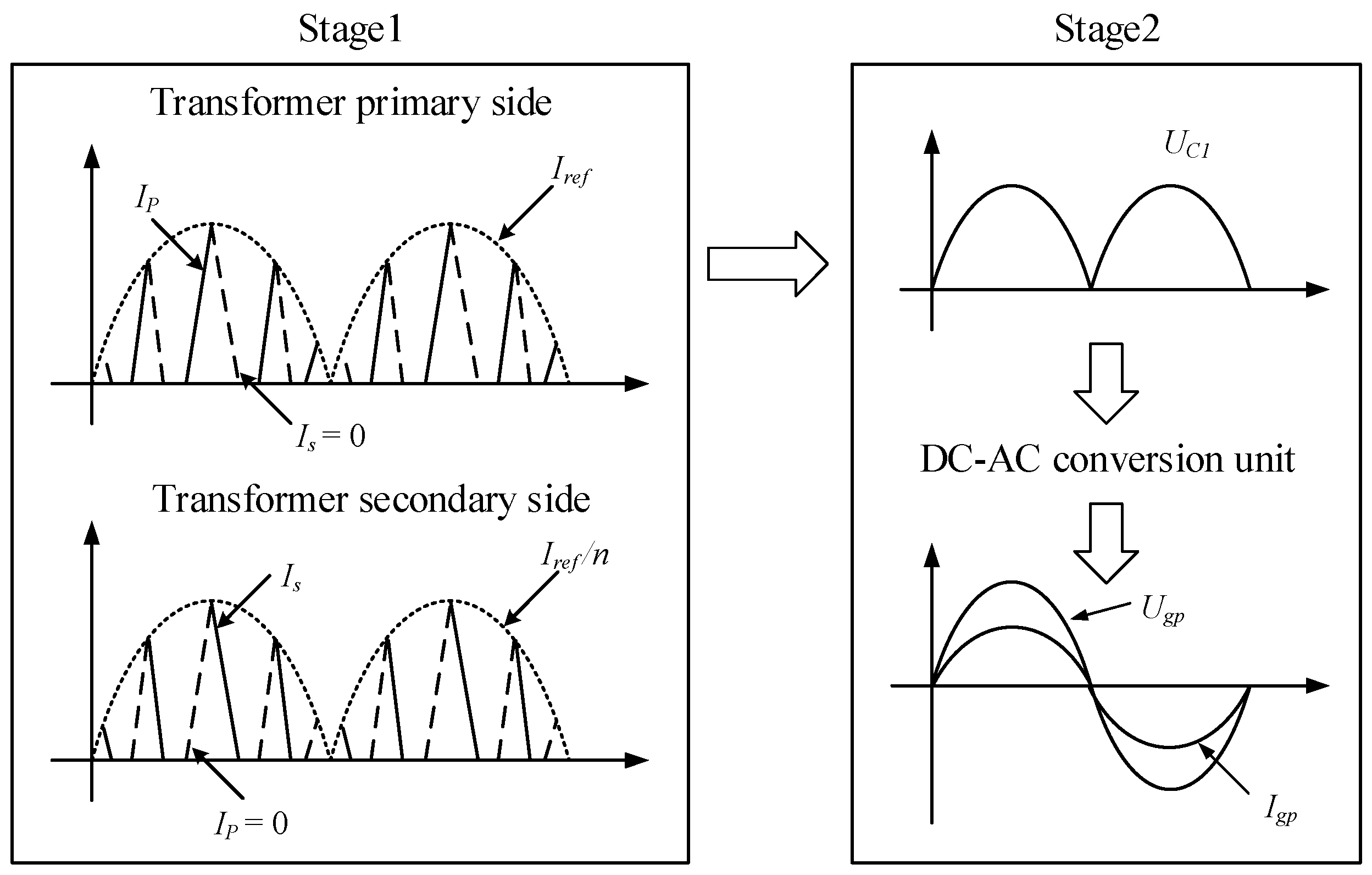
2.2. Multi-Valley Turn-On Control Strategy in the DCM
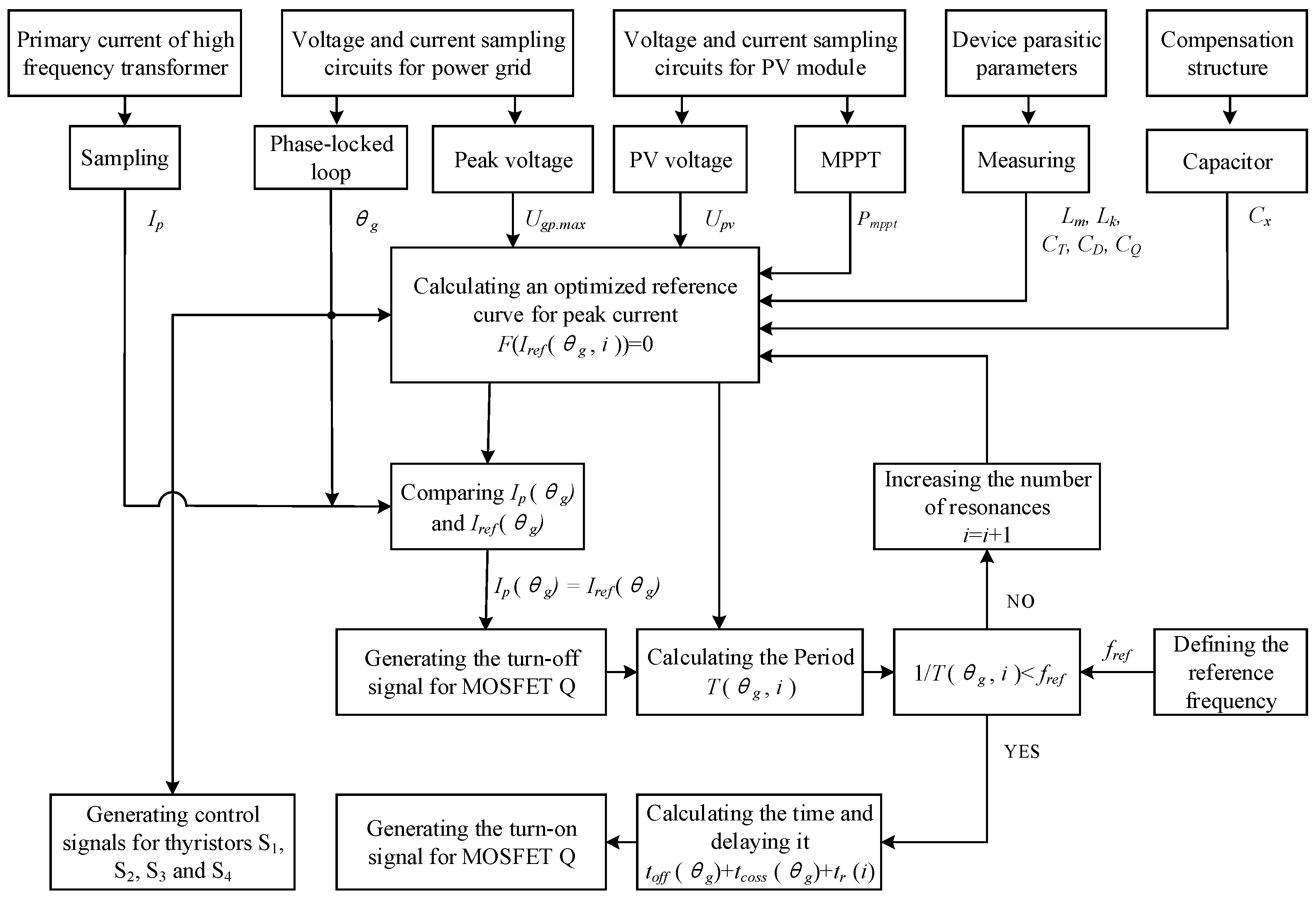
2.2.1. Control Strategy Implementation Process
- Detection and calculation of relevant parameters
- 2.
- The optimised reference current curve for peak current control is calculated through mathematical derivation. The specific derivation process can be found in Section 3.2.
- 3.
- Generation of the turn-off signal for switch tube Q
- 4.
- Generation of the turn-on signal for the switch tube Q
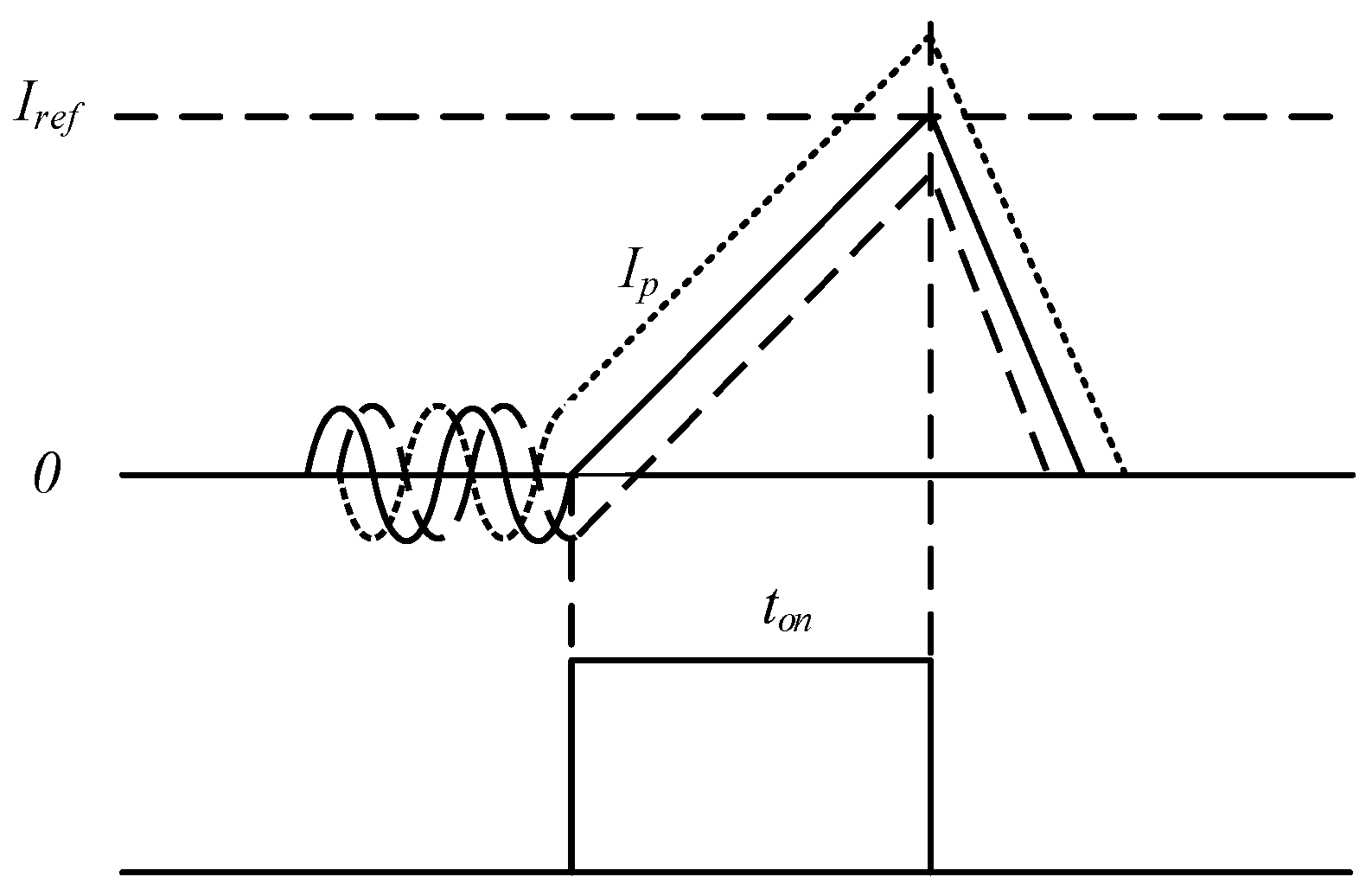
2.2.2. Derivation Process of the Reference Current Curve
2.3. Experimental Platform Construction
3. Results and Discussion
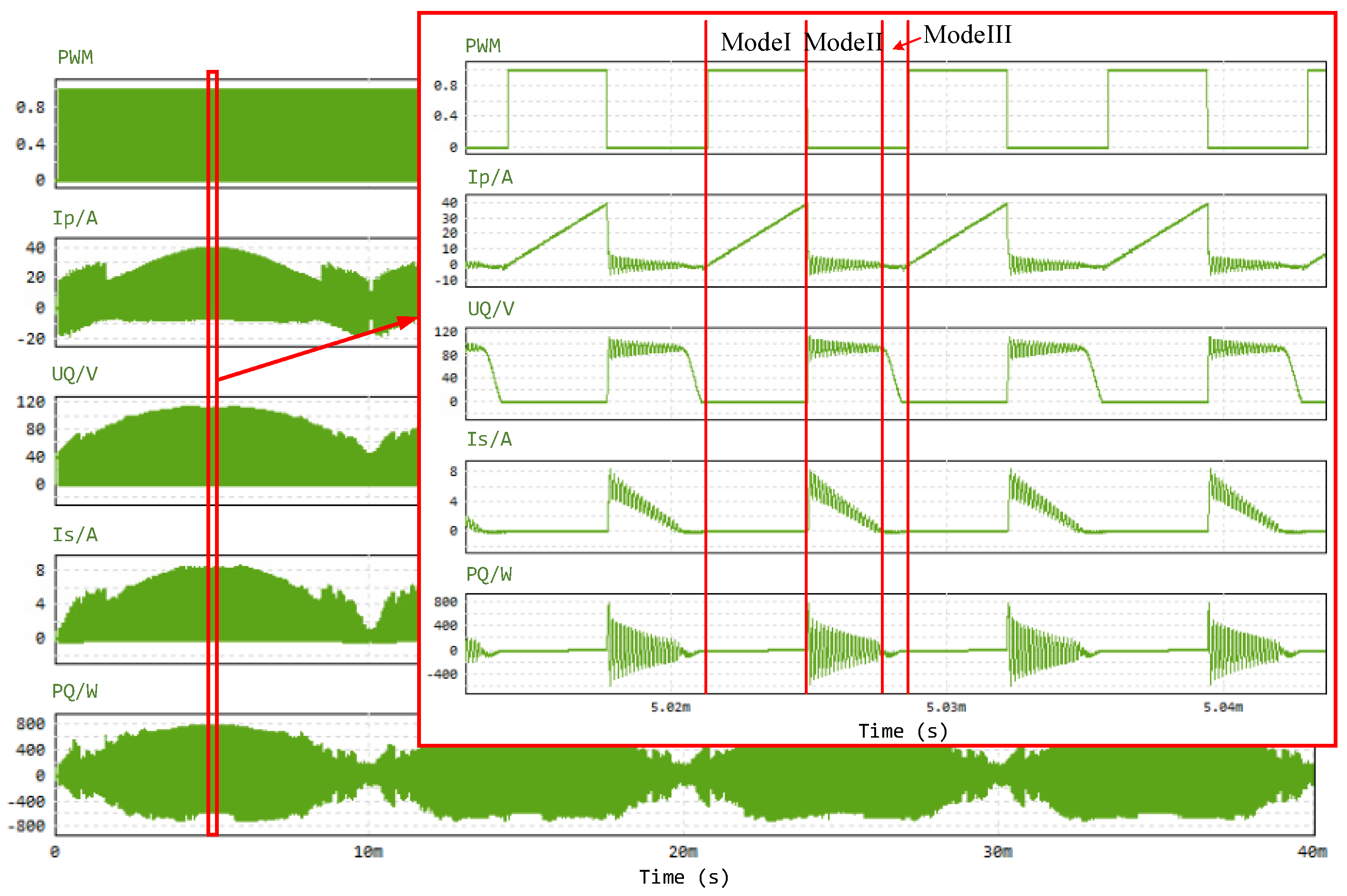
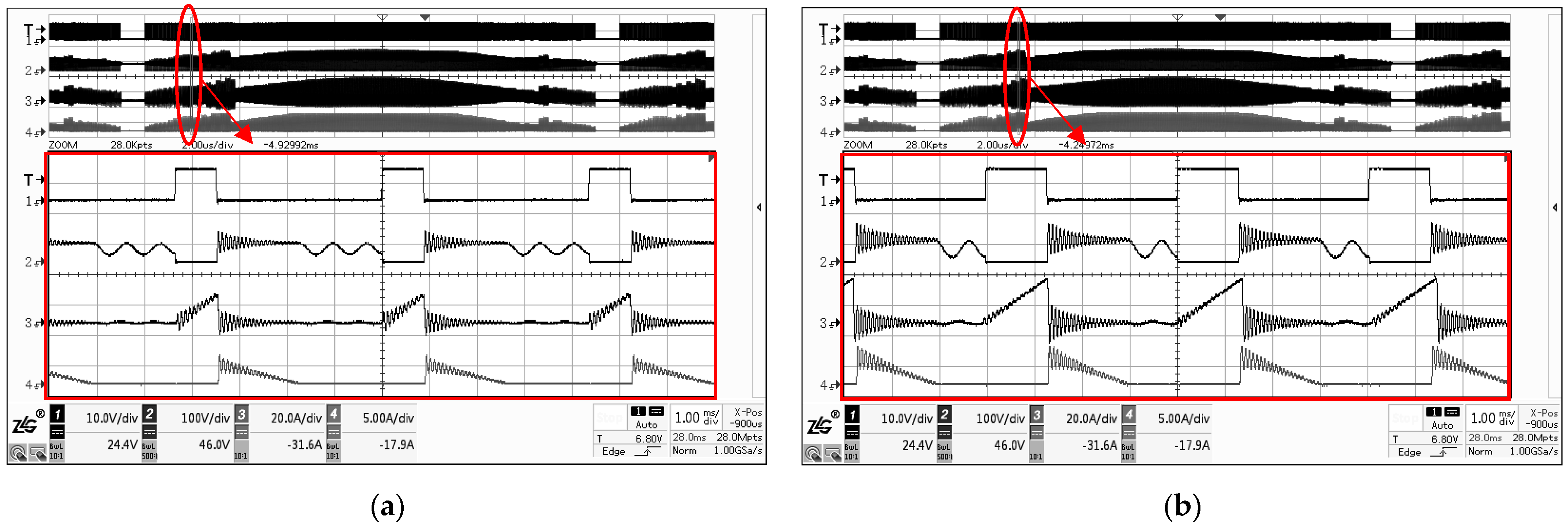
3.1. Simulation Validation
3.1.1. Topology Circuit Verification
3.1.2. Control Strategy Verification
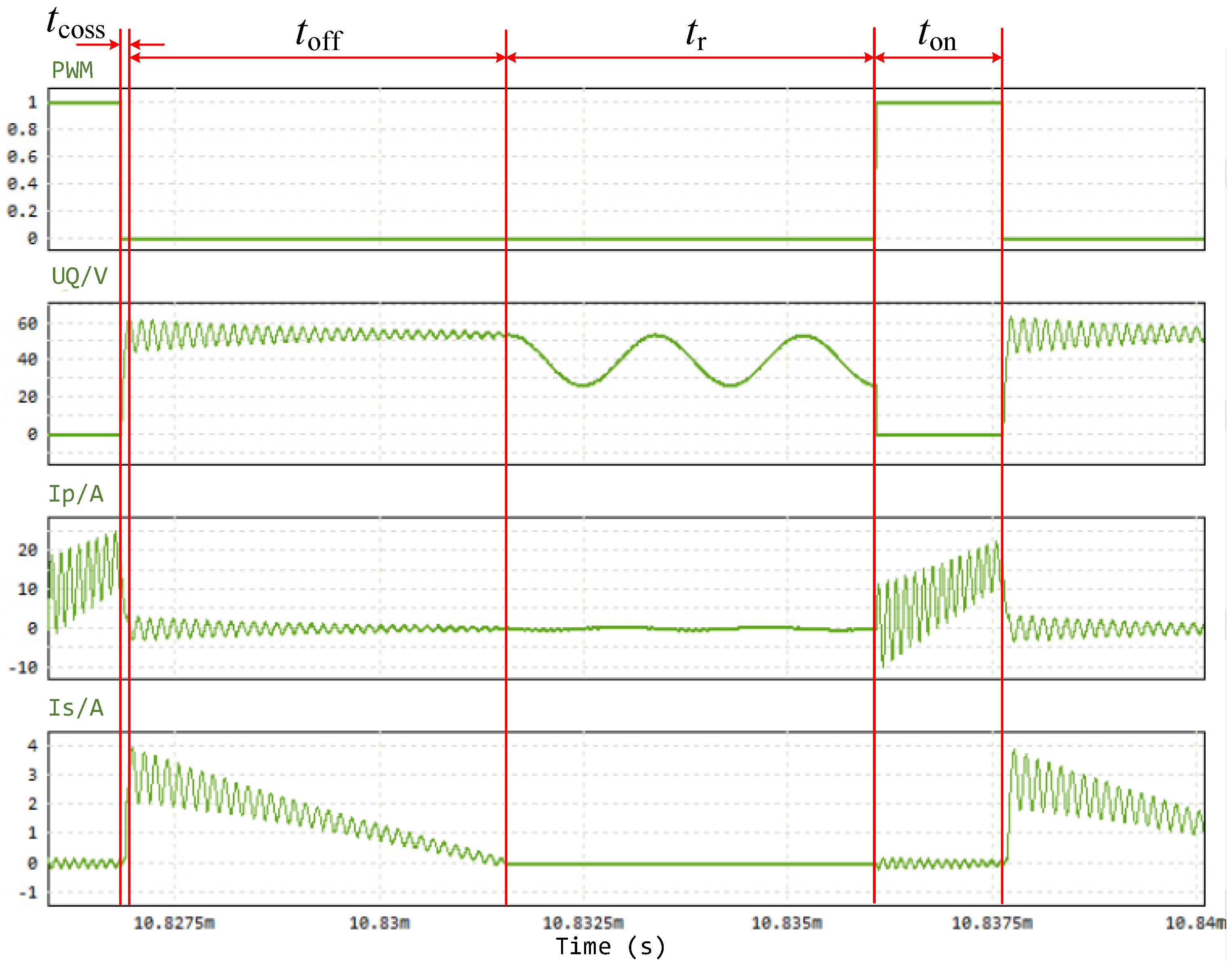
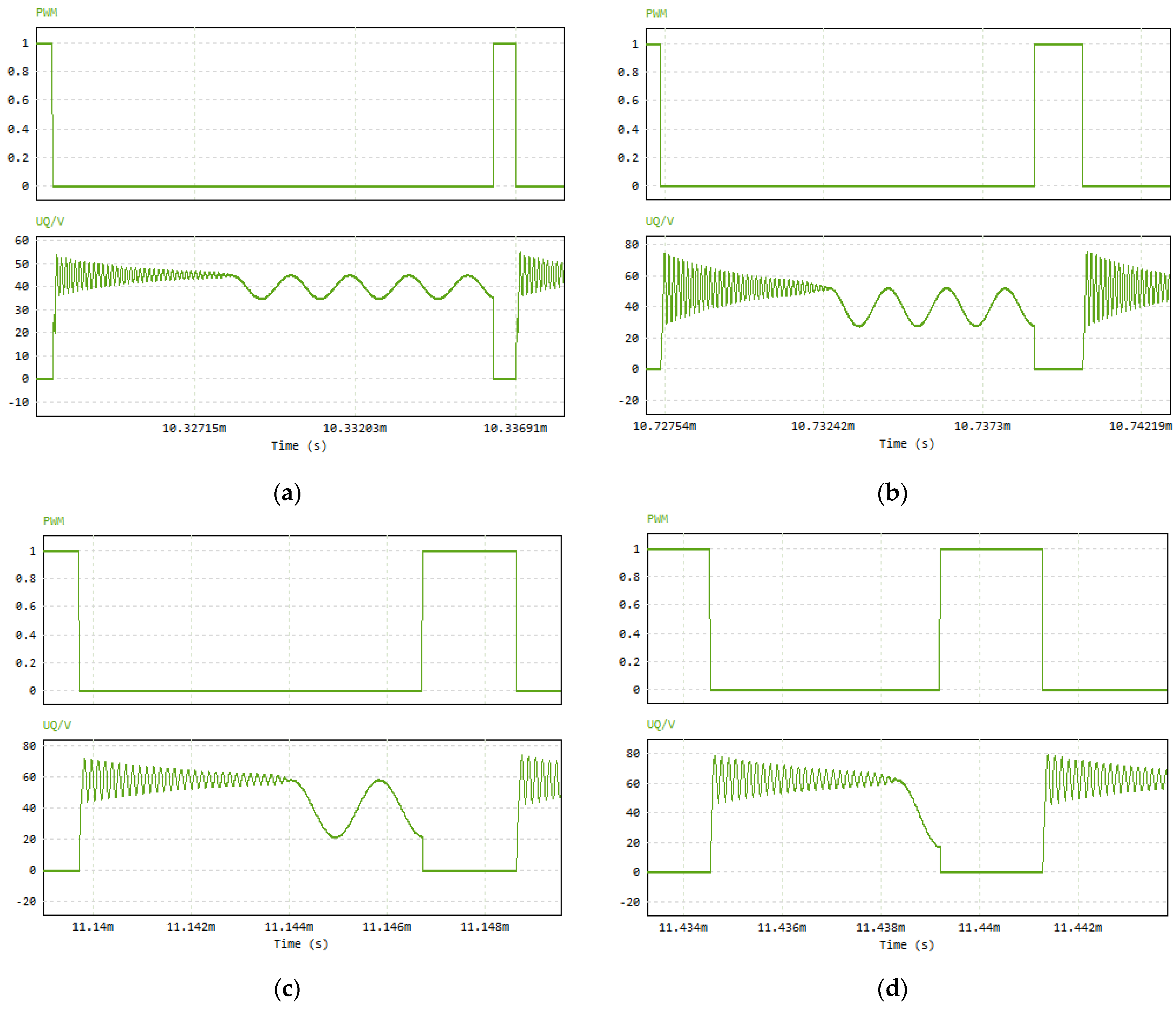
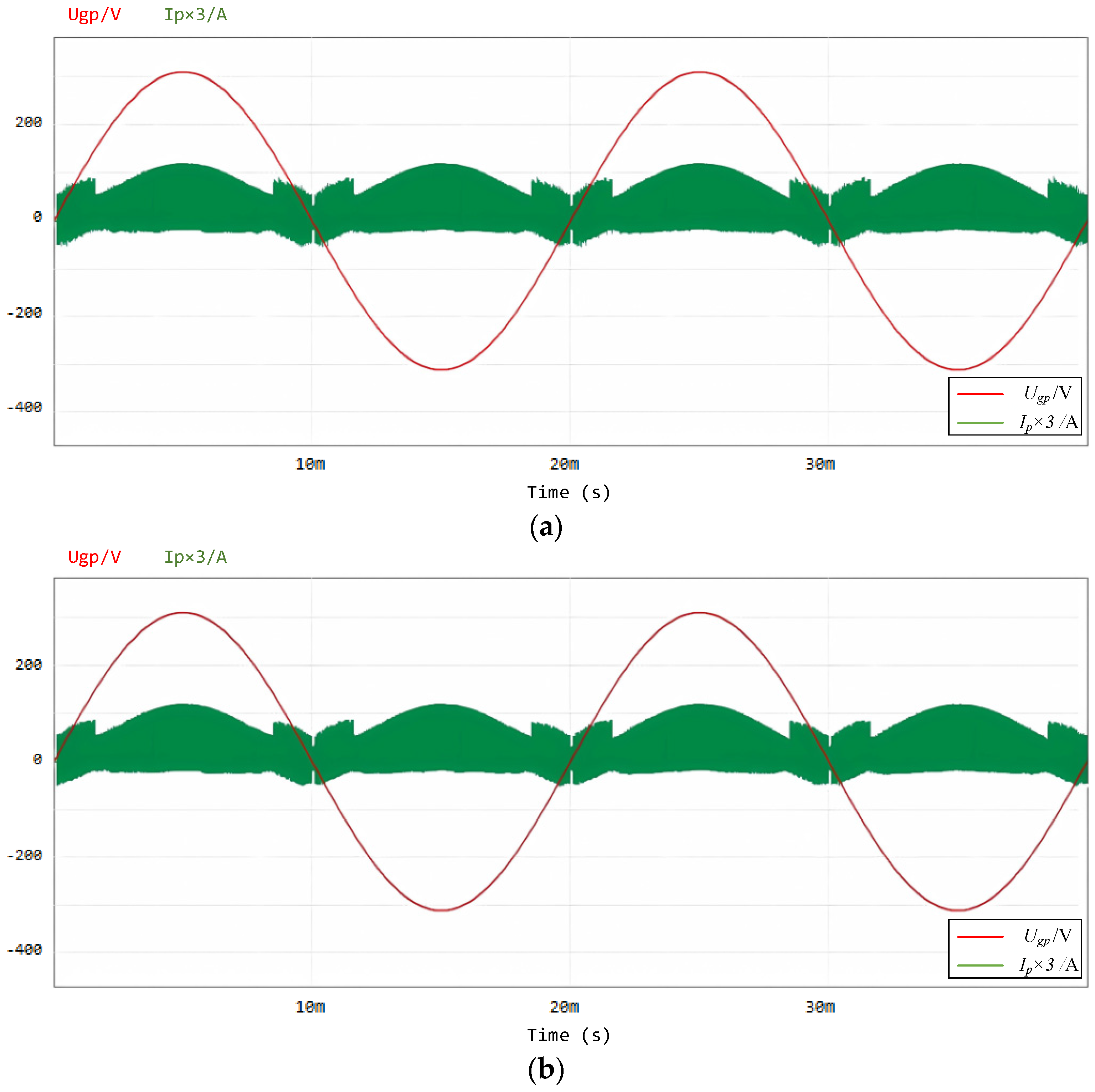
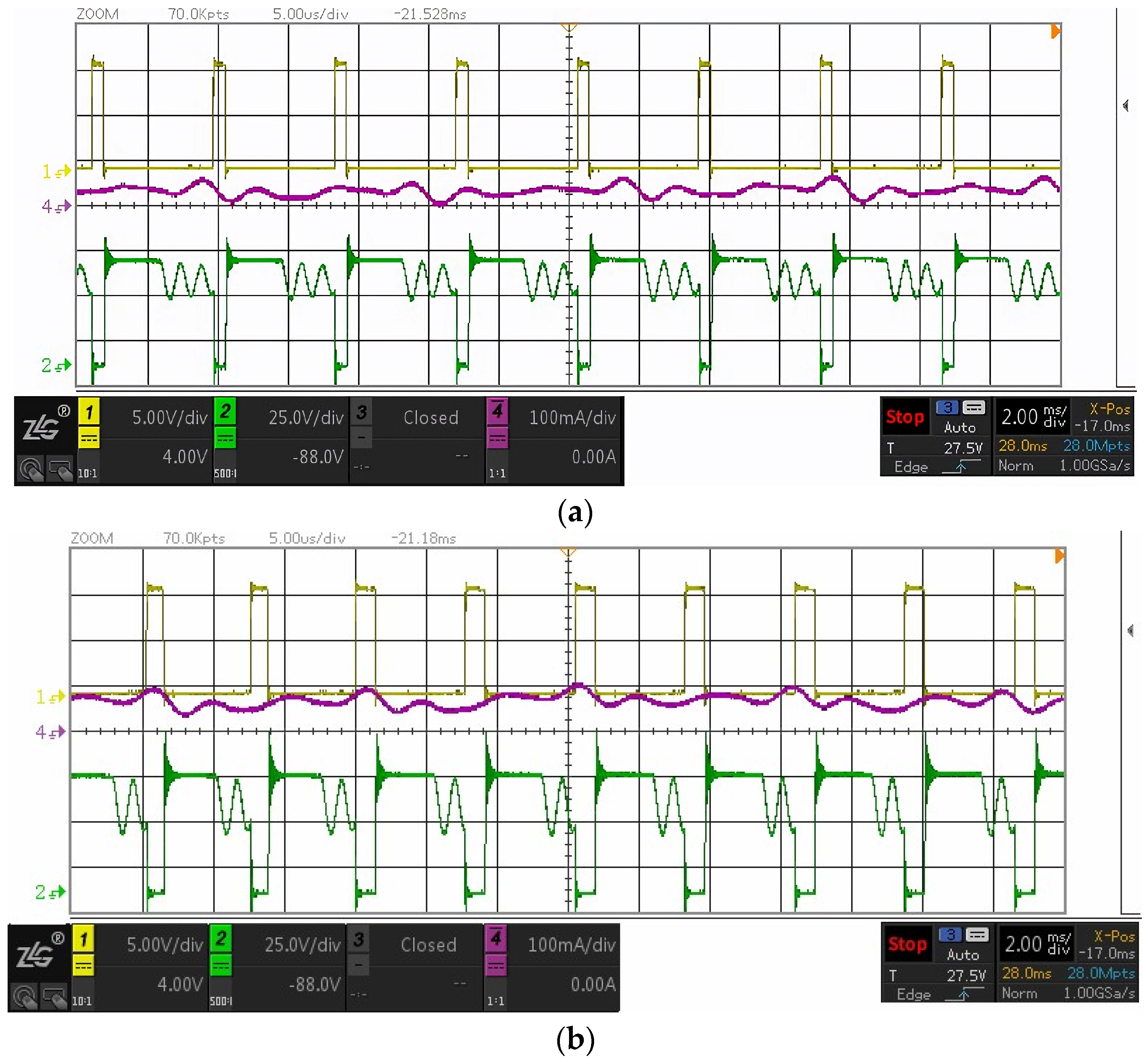
3.2. Experimental Validation
4. Conclusions
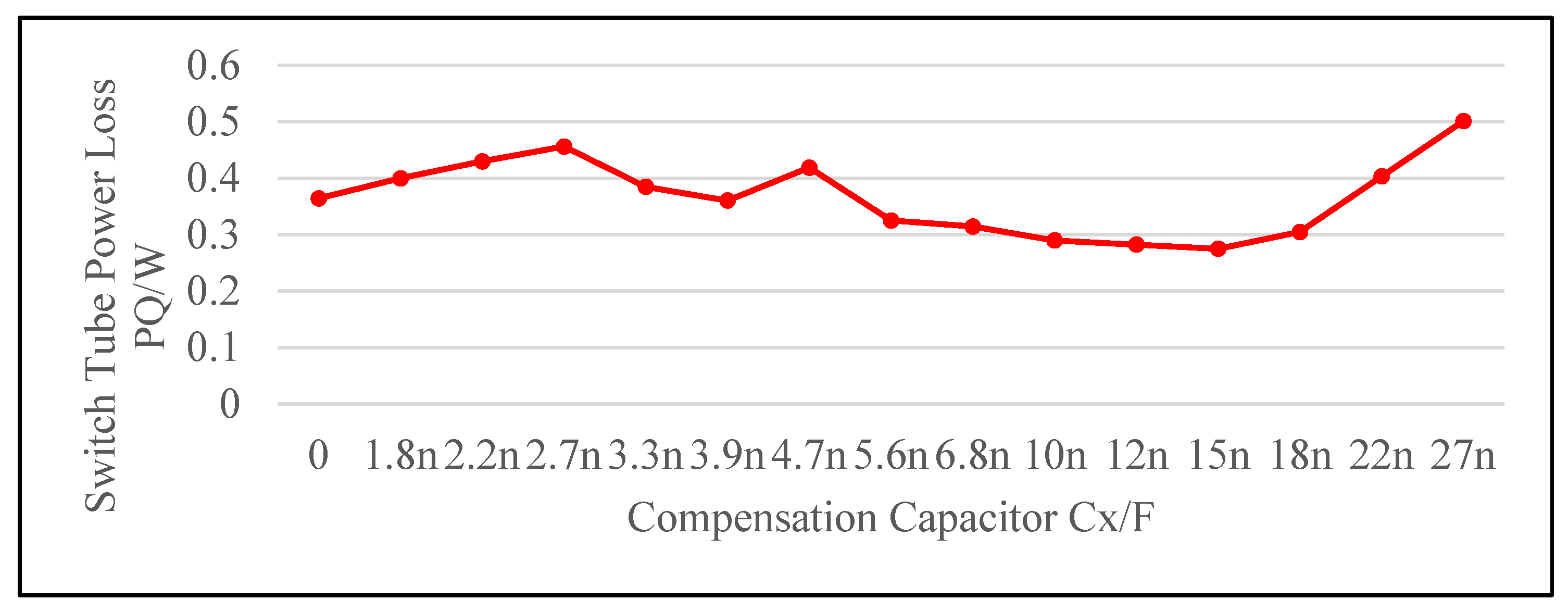
- When the grid phase angle is small, the power is also low, and the switch tube has a very high frequency, which strongly affects the performance of the device, leading to increased device stress and switch losses. This paper introduces a topology structure that incorporates a compensation capacitor to increase the resonance period, addressing the issues of high switching frequency and increased losses.
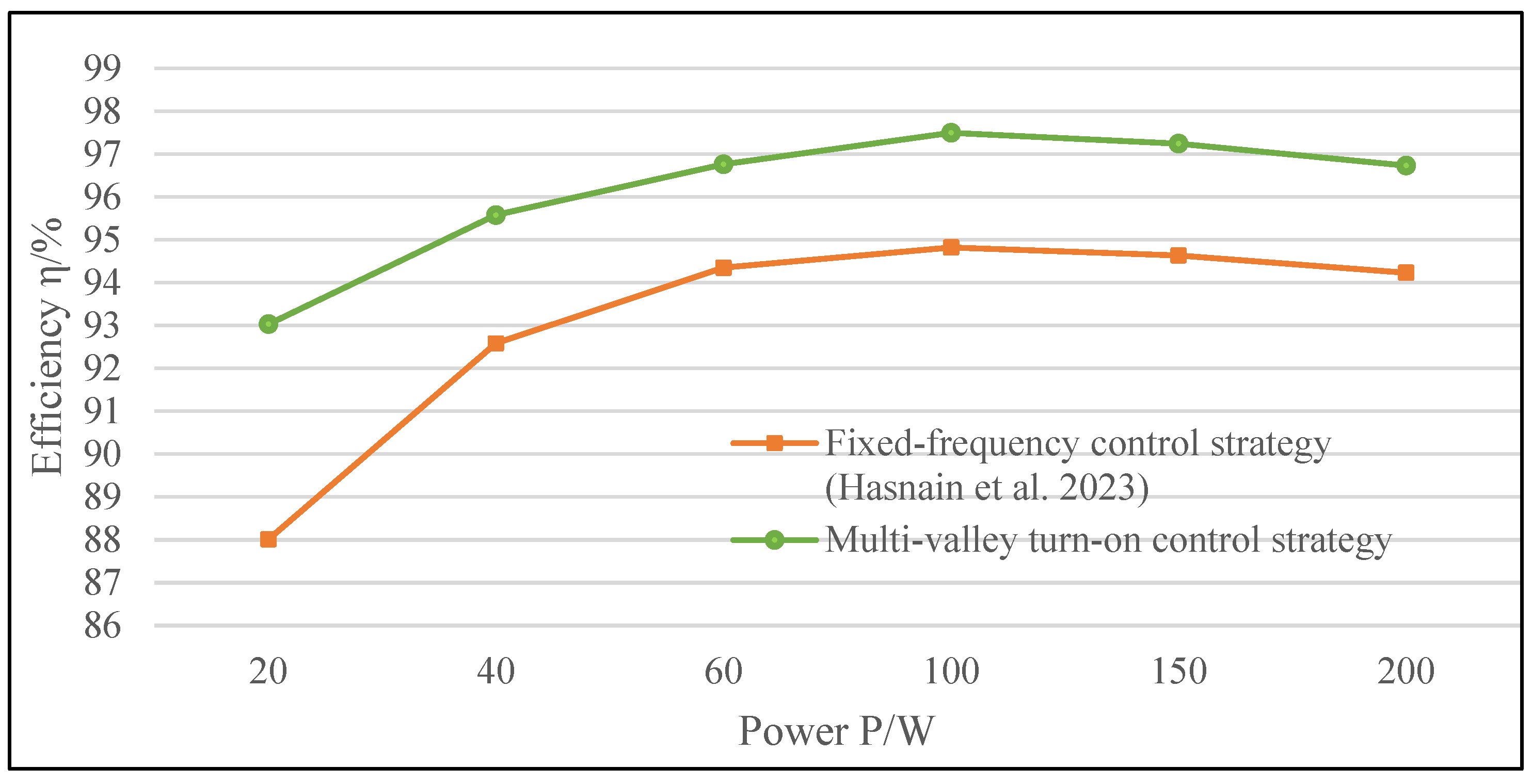
- The reference current curve for conventional peak current control considers only ideal device conditions, which will affect the waveform for circuits with parasitic parameters. This paper proposes an optimised method for calculating the peak current reference curve, which can accurately calculate the reference waveform under actual engineering conditions, ensuring the accuracy of the turn-off signal. At the same time, a multi-valley turn-on method is proposed to reduce device losses and harmonic content of the grid-connected current.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sutikno, T.; Arsadiando, W.; Wangsupphaphol, A.; Yudhana, A.; Facta, M. A Review of Recent Advances on Hybrid Energy Storage System for Solar Photovoltaics Power Generation. IEEE Access 2022, 10, 42346–42364. [Google Scholar] [CrossRef]
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. A review of single-phase grid-connected inverters for photovoltaic modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- Li, Q.; Wolfs, P. A Review of the Single Phase Photovoltaic Module Integrated Converter Topologies with Three Different DC Link Configurations. IEEE Trans. Power Electron. 2008, 23, 1320–1333. [Google Scholar]
- Chiu, H.; Lo, Y.; Yang, C.; Cheng, S.; Huang, C.-M.; Chuang, C.; Kuo, M.; Huang, Y.; Jean, Y.; Huang, Y. A module-integrated isolated solar microinverter. IEEE Trans. Ind. Electron. 2013, 60, 781–788. [Google Scholar] [CrossRef]
- Shafiullah, M.; Ahmed, S.D.; Al-Sulaiman, F.A. Grid Integration Challenges and Solution Strategies for Solar PV Systems: A Review. IEEE Access 2022, 10, 52233–52257. [Google Scholar] [CrossRef]
- Tang, Z.; Yang, Y.; Blaabjerg, F. Power electronics: The enabling technology for renewable energy integration. CSEE J. Power Energy Syst. 2022, 8, 39–52. [Google Scholar]
- Tacca, H.E. Single-switch two-output flyback-forward converter operation. IEEE Trans. Power Electron. 1998, 13, 903–911. [Google Scholar]
- Bidram, A.; Davoudi, A.; Balog, R.S. Control and Circuit Techniques to Mitigate Partial Shading Effects in Photovoltaic Arrays. IEEE J. Photovolt. 2012, 2, 532–546. [Google Scholar]
- Meneses, D.; Blaabjerg, F.; García, Ó.; Cobos, J.A. Review and Comparison of Step-Up Transformerless Topologies for Photovoltaic AC-Module Application. IEEE Trans. Power Electron. 2013, 28, 2649–2663. [Google Scholar] [CrossRef]
- Kouro, S.; Leon, J.I.; Vinnikov, D.; Franquelo, L.G. Grid-Connected Photovoltaic Systems: An Overview of Recent Research and Emerging PV Converter Technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Díaz, M.; Muñoz, J.; Rivera, M.; Rohten, J. A Comprehensive Control Strategy for a Push–Pull Microinverter Connected to the Grid. Energies 2023, 16, 3196. [Google Scholar] [CrossRef]
- Front Matter. In Control of Power Electronic Converters and Systems; Blaabjerg, F. (Ed.) Academic Press: Cambridge, MA, USA, 2018; pp. i–ii. [Google Scholar] [CrossRef]
- Myrzik, J.M.A.; Calais, M. String and module integrated inverters for single-phase grid connected photovoltaic systems—A review. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 2, p. 8. [Google Scholar]
- Scholten, D.M.; Ertugrul, N.; Soong, W.L. Micro-inverters in small scale PV systems: A review and future directions. In Proceedings of the 2013 Australasian Universities Power Engineering Conference (AUPEC), Hobart, Australia, 29 September–3 October 2013; pp. 1–6. [Google Scholar]
- Gong, X.; Josifović, I.; Ferreira, J.A. Modeling and Reduction of Conducted EMI of Inverters with SiC JFETs on Insulated Metal Substrate. IEEE Trans. Power Electron. 2013, 28, 3138–3146. [Google Scholar] [CrossRef]
- Cichowski, A.; Nieznanski, J. Self-tuning dead-time compensation method for voltage-source inverters. IEEE Power Electron. Lett. 2005, 3, 72–75. [Google Scholar] [CrossRef]
- Cheng, H.-C.; Shen, Y.-H.; Chen, W.-H. Parasitic extraction and power loss estimation of power devices. J. Mech. 2021, 37, 134–148. [Google Scholar] [CrossRef]
- Yaqoob, S.J.; Raham, J.K.; Sadiq, H.A. Analysis and Simulation of Current-source Flyback Inverter with Efficient BCM Control Strategy. WSEAS Trans. Electron. 2021, 12, 132–140. [Google Scholar] [CrossRef]
- Trubitsyn, A.; Pierquet, B.J.; Hayman, A.K.; Gamache, G.E.; Sullivan, C.R.; Perreault, D.J. High-efficiency inverter for photovoltaic applications. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 2–16 September 2010; pp. 2803–2810. [Google Scholar]
- Sharma, R.; Ball, J.A.R. Unipolar switched inverter low-frequency harmonics caused by switching delay. IET Power Electron. 2009, 2, 508–516. [Google Scholar] [CrossRef]
- Blahník, V.; Peroutka, Z.; Žák, J.; Talla, J. Elimination of dead-time effect causing current distortion of single-phase power converters. In Proceedings of the 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. DS1e.3-1–DS1e.3-6. [Google Scholar]
- Ma, X. Research on the Control Method of the Inverter Based on Discontinuous Inductor Current Mode. Master’s Thesis, Huazhong University of Science & Technology, Wuhan, China, 2020. [Google Scholar]
- Fantino, R.A.; Christian, S.F.; Balda, J.C. Synchronous-Variable-Frequency Control of Bidirectional DCM Interleaved DC–DC Converter for Wide-Range Enhanced Efficiency. IEEE Trans. Ind. Electron. 2022, 69, 5844–5853. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, J.; Shao, S. A Variable Off-Time Control Method for a Single-Phase DCM Microinverter. IEEE Trans. Power Electron. 2018, 33, 7229–7239. [Google Scholar] [CrossRef]
- Christidis, G.; Nanakos, A.; Tatakis, E. Optimal Design of a Flyback Microinverter Operating under Discontinuous-Boundary Conduction Mode (DBCM). Energies 2021, 14, 7480. [Google Scholar] [CrossRef]
- Pan, M.; Su, X.; Wang, Z. High efficiency solar energy single-stage grid-connected micro-inverter based on flyback topology. J. Mech. Electr. Eng. 2013, 30, 4. [Google Scholar]
- Lang, T.; Du, S.; Yin, H.; Hu, H. Optimizing Method for Light-Load Efficiency of a H-Bridge Inverter Based on Variable Turn-Off Time Discontinuous Current Mode. Trans. China Electrotech. Soc. 2020, 35, 4761–4770. [Google Scholar]
- Hasnain, A.; D’Antonio, M.; Singhabahu, C.; Shen, Y.; Zakzewski, D.; Khaligh, A. Optimal Modulation and DM Filter Design for a High Switching Frequency Single-Stage Microinverter. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; pp. 1483–1488. [Google Scholar]






| Parameter | Value | Unit |
|---|---|---|
| DC input voltage Upv | 25–55 | V |
| Effective value of AC output voltage Ugp | 220 | V |
| Output voltage frequency fgp | 50 | Hz |
| Rated output power P | 200 | W |
| Output filter capacitors C1 | 10n | F |
| Absorption capacitor CS | 220p | F |
| Grid-side capacitors Cf | 330n | F |
| Grid-side inductor Lf | 0.6m | H |
| Maximum switching frequency fmax | 300 | kHz |
| Ratio of transformer n | 2:12 | - |
| Parameter | Value | Unit |
|---|---|---|
| Excitation inductor Lm | 3.4u | H |
| Leakage inductor Lk | 34.2n | H |
| Distributed capacitor CT | 321.5p | F |
| Parasitic capacitor of transistor Q CQ | 321.5p | F |
| Parasitic capacitor of diode D CD | 22p | F |
| Power (W) | 40 | 80 | 120 | 160 | 200 |
|---|---|---|---|---|---|
| Fixed-frequency control strategy | 6.32% | 5.04% | 4.43% | 4.00% | 3.87% |
| Multi-valley turn-on control strategy | 5.11% | 3.87% | 3.19% | 2.67% | 2.39% |
| Literature | Methods | Main findings | Drawbacks | Efficiency | THD |
|---|---|---|---|---|---|
| [18] | BCM control strategy suitable for medium and small power-level inverters | It achieved Zero Voltage Switching (ZVS) of the switch tube. | When operating at light load, the high switching frequency exacerbates turn-off losses. | / | 2.9% |
| [22] | DCM with fixed turn-off time for inductance current | The inverter efficiency under DCM is significantly higher than that under CCM. | When operating at light load, the switching frequency still increases. | 93.2% | 2.5% |
| [23] | Bidirectional DCM constant on-time variable-frequency control strategy | It enhanced the converter efficiency at low-power conditions. | This method is not applicable to the single-phase microinverters studied. | 96.7% | / |
| [24] | Variable turn-off time control method | It was effective in light load efficiency improvement. | It did not mention the issues of switch tube losses and harmonics. | 95.4% | / |
| [25] | Hybrid DBCM operation | It inherited the merits of both DCM and BCM. | It did not take into account the parasitic parameters. | 92.1% | / |
| [27] | Variable turn-off time method in DCM | It improved the quality of light-load current. | It required additional hardware to limit the peak inductance current. | 95.7% | 3.6% |
| This research | Multi--valley turn-on control strategy | Considering parasitic parameters, It minimised switch losses. | / | 95.2% | 2.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Jamali, A.b.; Yassin, A.; Huang, Y. The Quasi-Resonant Structure and Control Strategy of a Photovoltaic Flyback Grid-Connected Microinverter. Electronics 2024, 13, 1903. https://doi.org/10.3390/electronics13101903
Cao Z, Jamali Ab, Yassin A, Huang Y. The Quasi-Resonant Structure and Control Strategy of a Photovoltaic Flyback Grid-Connected Microinverter. Electronics. 2024; 13(10):1903. https://doi.org/10.3390/electronics13101903
Chicago/Turabian StyleCao, Zipei, Annisa binti Jamali, Abdullah Yassin, and Ya Huang. 2024. "The Quasi-Resonant Structure and Control Strategy of a Photovoltaic Flyback Grid-Connected Microinverter" Electronics 13, no. 10: 1903. https://doi.org/10.3390/electronics13101903




