A Critical Review on Channel Modeling: Implementations, Challenges and Applications
Abstract
:1. Introduction
1.1. Motivation and Contributions
- LCX-based Enhanced Channel Performance and Classification: Our intention is to bring earlier research into consideration, classify gaps and directions, and summarize achievements. To assist researchers in determining of a specific study gain in their upcoming research problems regarding wireless communication field, we first review the LCX-based wireless communication incentives by comparing it with the traditional communication techniques. Then, we look into the factors which have greater influence on channel performance such as antenna types, channel modeling schemes, the tunnel or mine geometries, fading characteristics, Doppler effects, wave classification, diffraction, reflection, different challenges to deal with antenna configurations, etc.
- Massive MIMO Channel Modeling and Challenges: To meet the need for service stability and enhancement, we summarize the important aspects of massive MIMO channels and latest developments of channel modeling schemes in V2V and high-speed train (HST) scenarios. After examining the conventional, LCX, and IRS-based mmWave MIMO channels, we move on to discuss how to deal with challenges related to spatial characteristics, channel correlation, channel capacity, etc.
- Specifying Potential and Research Recommendations: In order to specify the potential techniques to lift the performance of massive MIMO systems, we propose suggestions and emerging ideas for future research directions in wireless communication field.
1.2. Article Structure
2. Establishment of Wireless Communications in Underground Environments
2.1. Wireless Communication’s History and Evolution
2.2. Antenna Characteristics
- While the antenna and applied radio signal are resonant at the similar frequency.
- While the feeding point of antenna is paired with the impedance of transmitting power source.
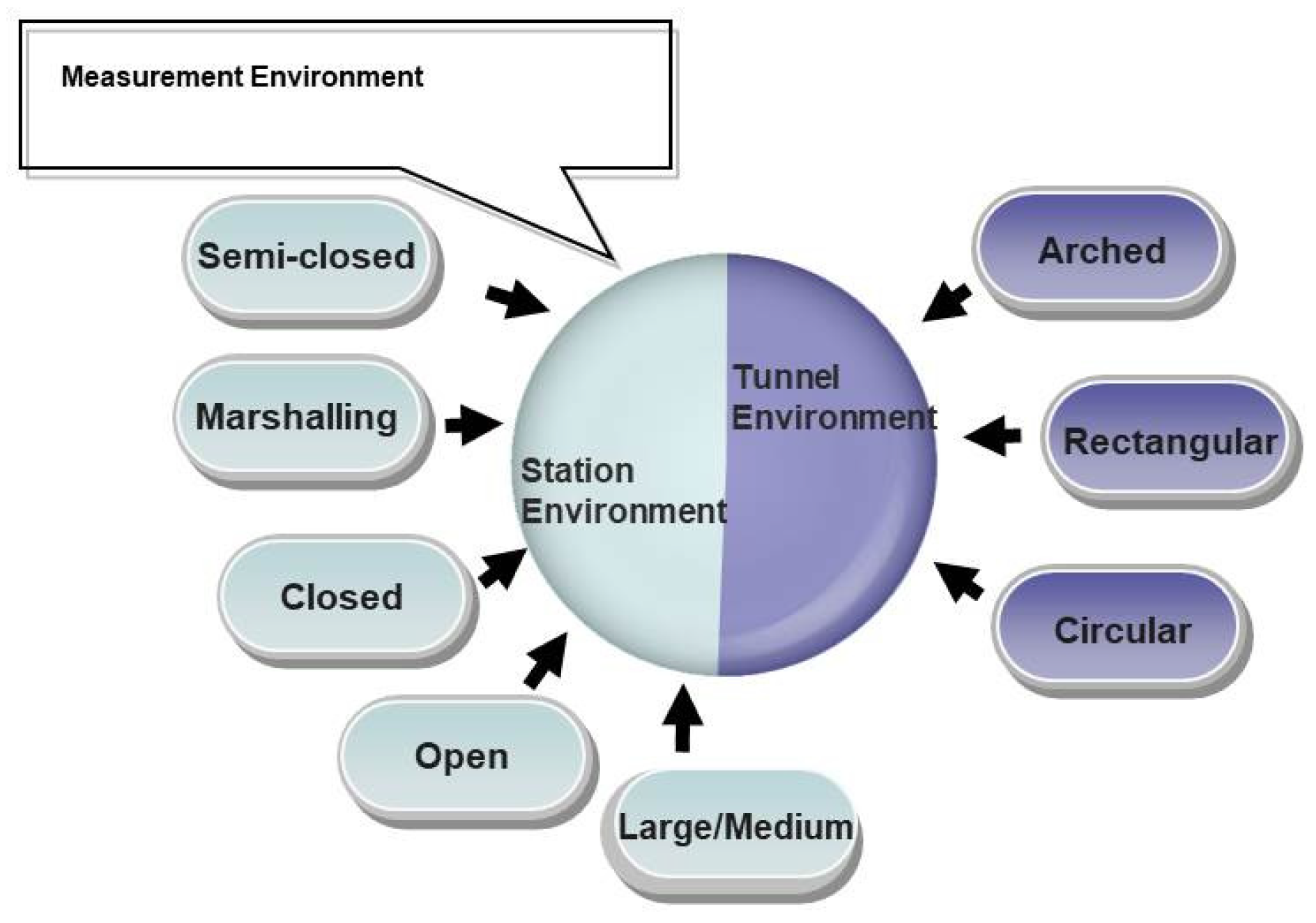
2.3. Channel Measurement Environment
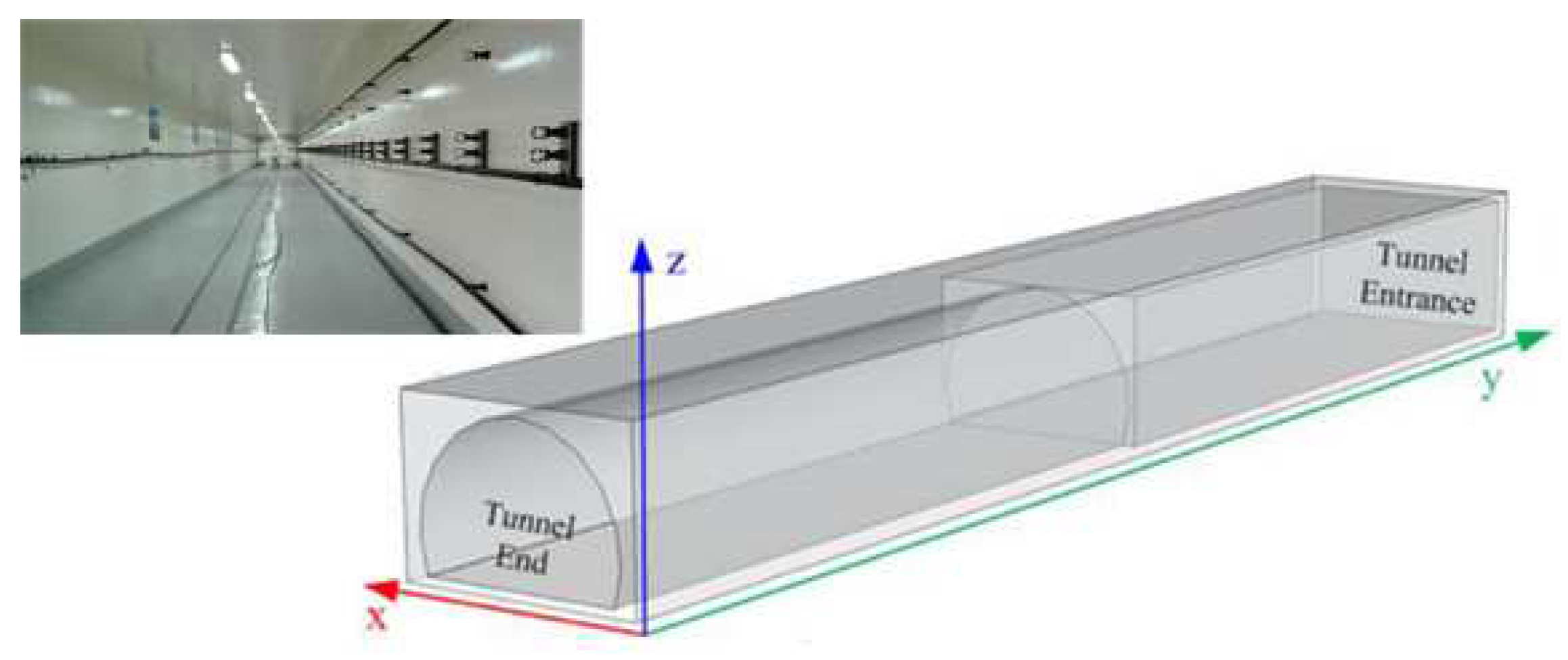
2.3.1. Tunnel Environment
2.3.2. Station Environment
2.3.3. Tunnel Geometry
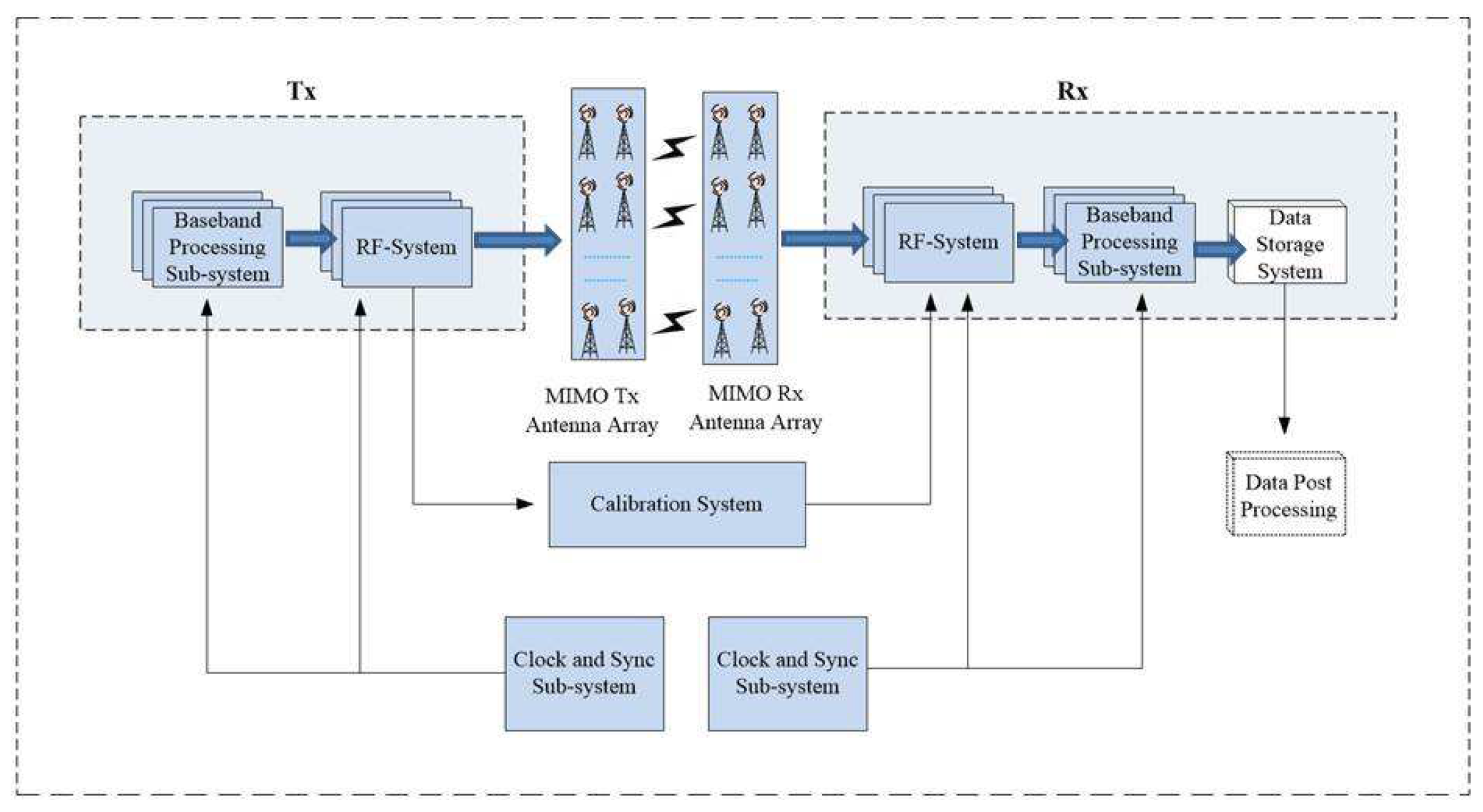
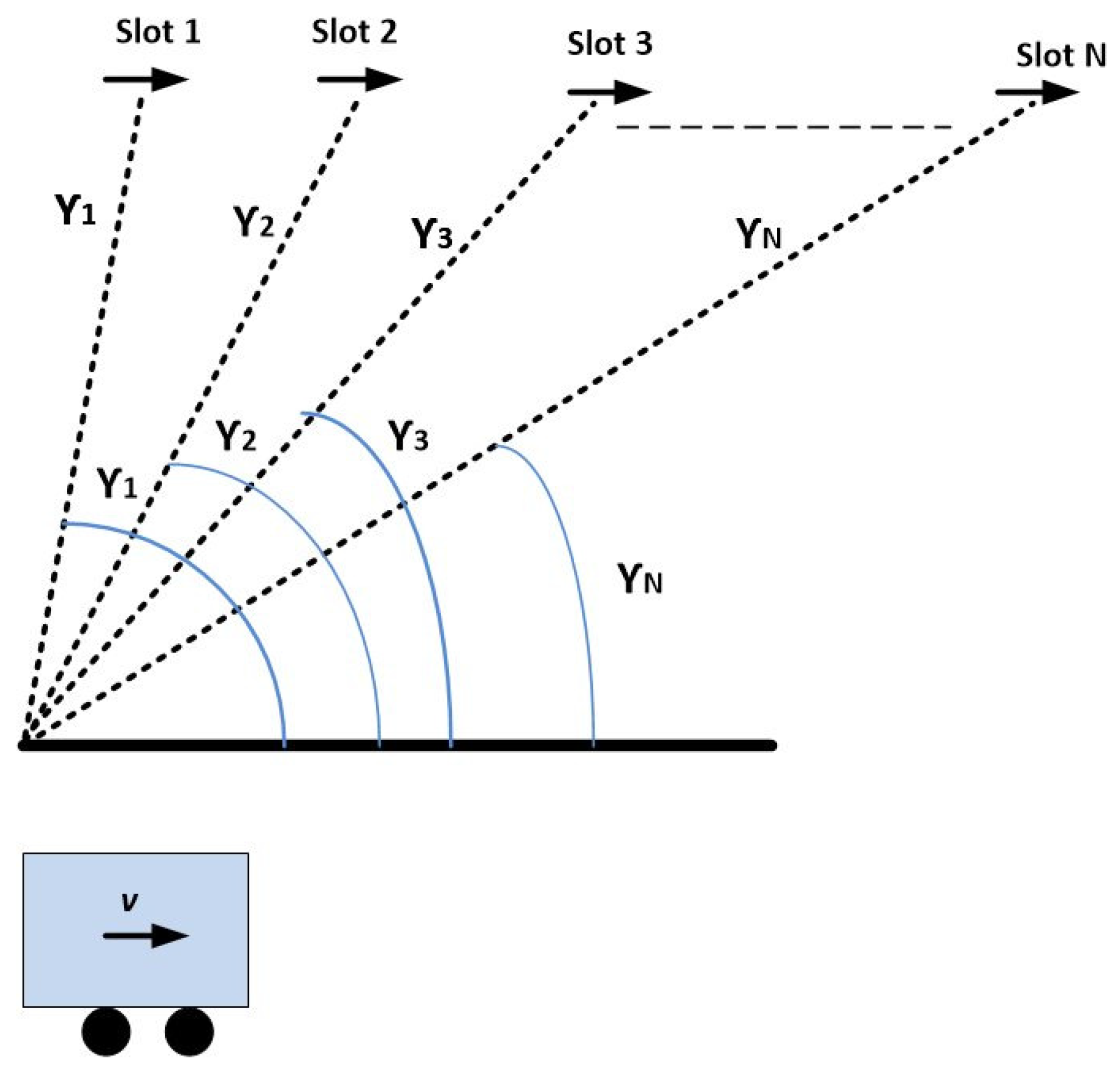
2.4. Channel Sounding
- By considering the time-division-multiplexing (TDM) technique to transmit single element at a given time.
- By utilizing the frequency-division-multiplexing (FDM) technique to transmit signals at different frequencies.
- By using the distinctive code-word for each element, named as code-division multiplexing (CDM).
2.4.1. Fully Switched Channels
2.4.2. Semi-Switched Channels
2.4.3. Fully Parallel Channels
2.4.4. Hybrid Channels
2.5. Bandwidth and Carrier Frequency
3. Parametric Effect of Propagation Characteristics
3.1. Diffraction and Reflection
3.2. Coupling Loss
3.3. Antenna Polarization
3.4. Path Losses
- Two-ray ground model: The two-ray ground model is also recognized as the two-path model, which is usually practiced for the path loss model. In this model, the signals approach the Rx through two different paths, one through an LoS path and the other through an NLoS path. Moreover, the PL (in dB) increases linearly with the increase of distance in mine tunnels.
- Smooth transition model: The smooth transition model is typically the upgrading of the basic power–distance relationship.
- Propagation model: The propagation model is the simplest PL modeln in which a direct-path of signals exist between the Tx and Rx without the consideration of substantial multipath components or atmospheric attenuation.
3.5. Doppler Effect
4. Propagation Channel Models in Tunnel Environments
4.1. Deterministic Channel Modeling
4.1.1. Fdtd-Based Channel Modeling
4.1.2. Full-Wave Channel Modeling
4.1.3. Ray-Tracing Channel Modeling
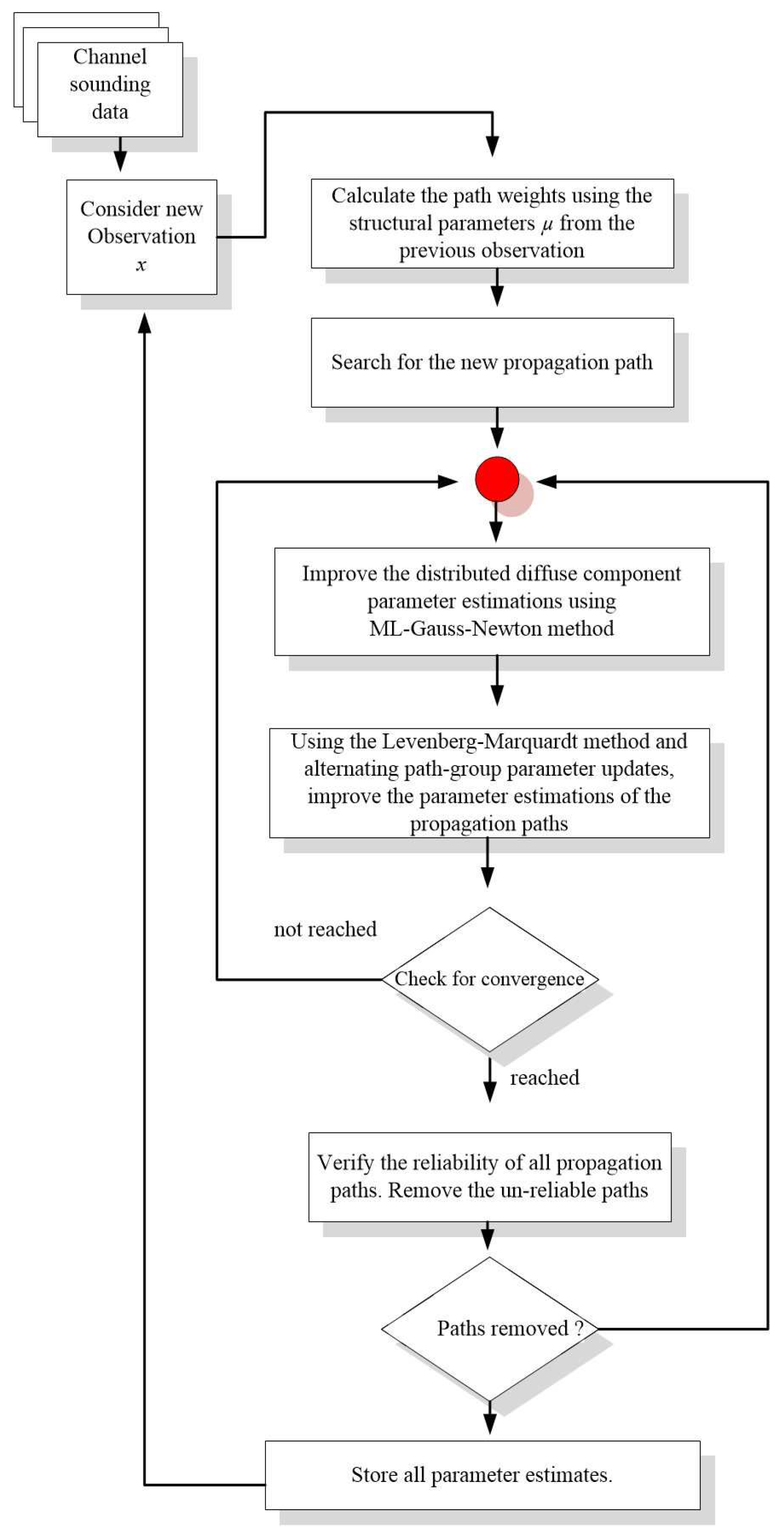
4.2. Stochastic Channel Modeling
4.2.1. Markov Channel Modeling
4.2.2. GBSM Channel Modeling
5. Channel Propagation Characteristics and Fundamentals
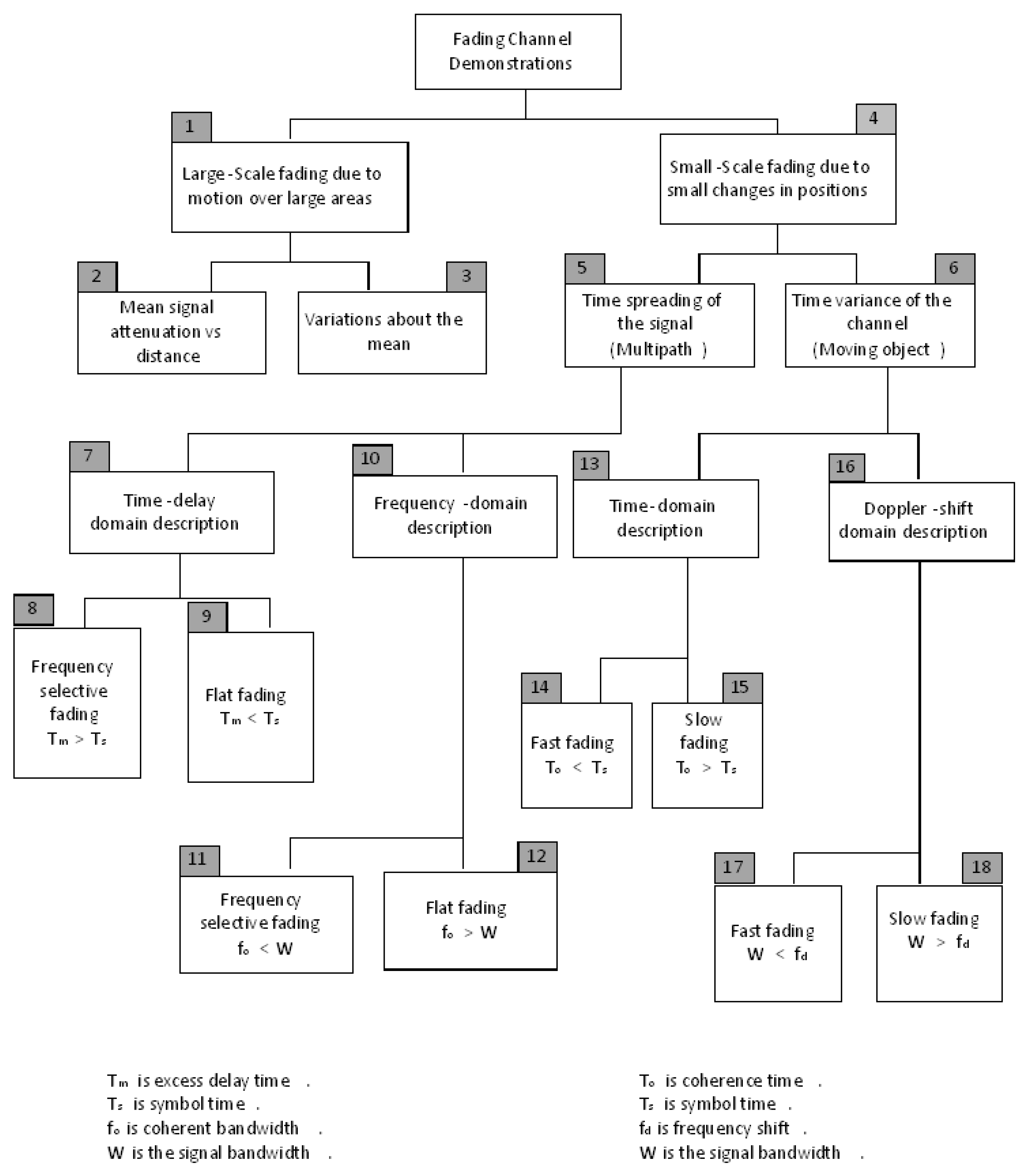
5.1. Channel Fading Characteristics
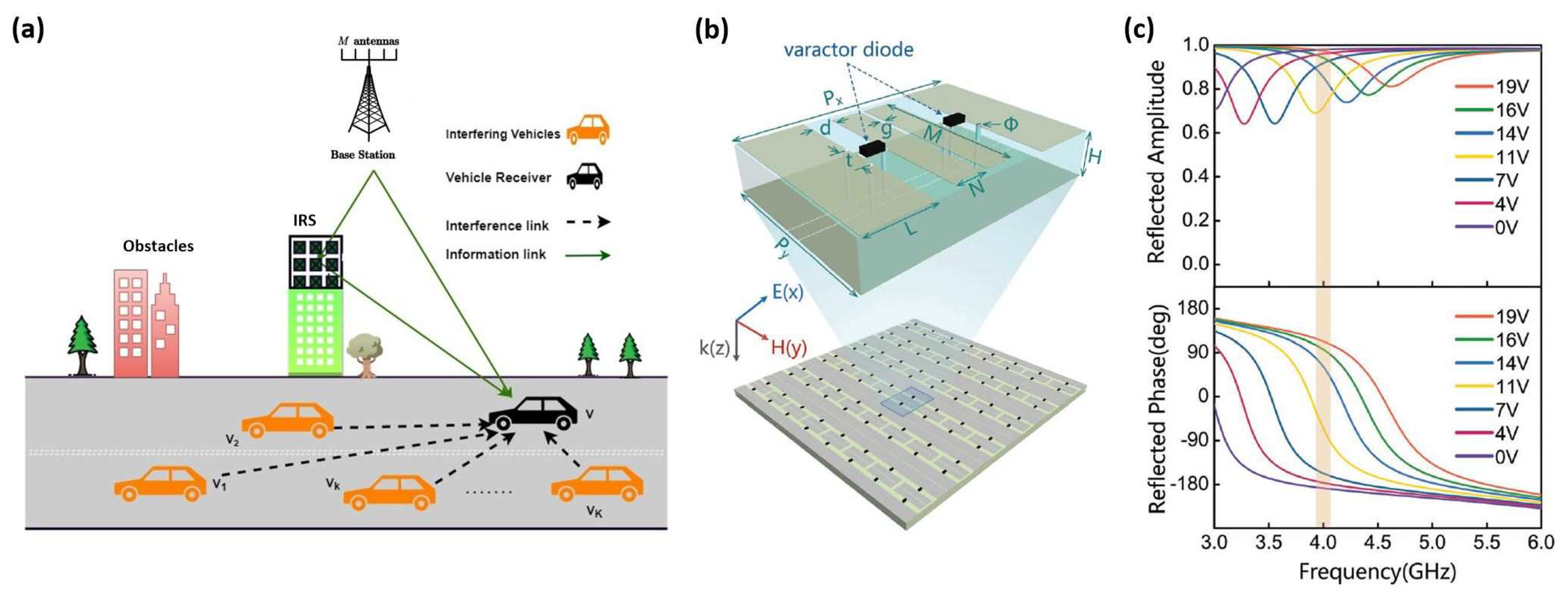
5.2. IRS Channel Characteristics
5.3. HST Channel Characteristics
5.3.1. Cluster Evolution in Stf Channel
5.3.2. Waveguide Effect
5.3.3. Near and Far Regions in the Tunnel
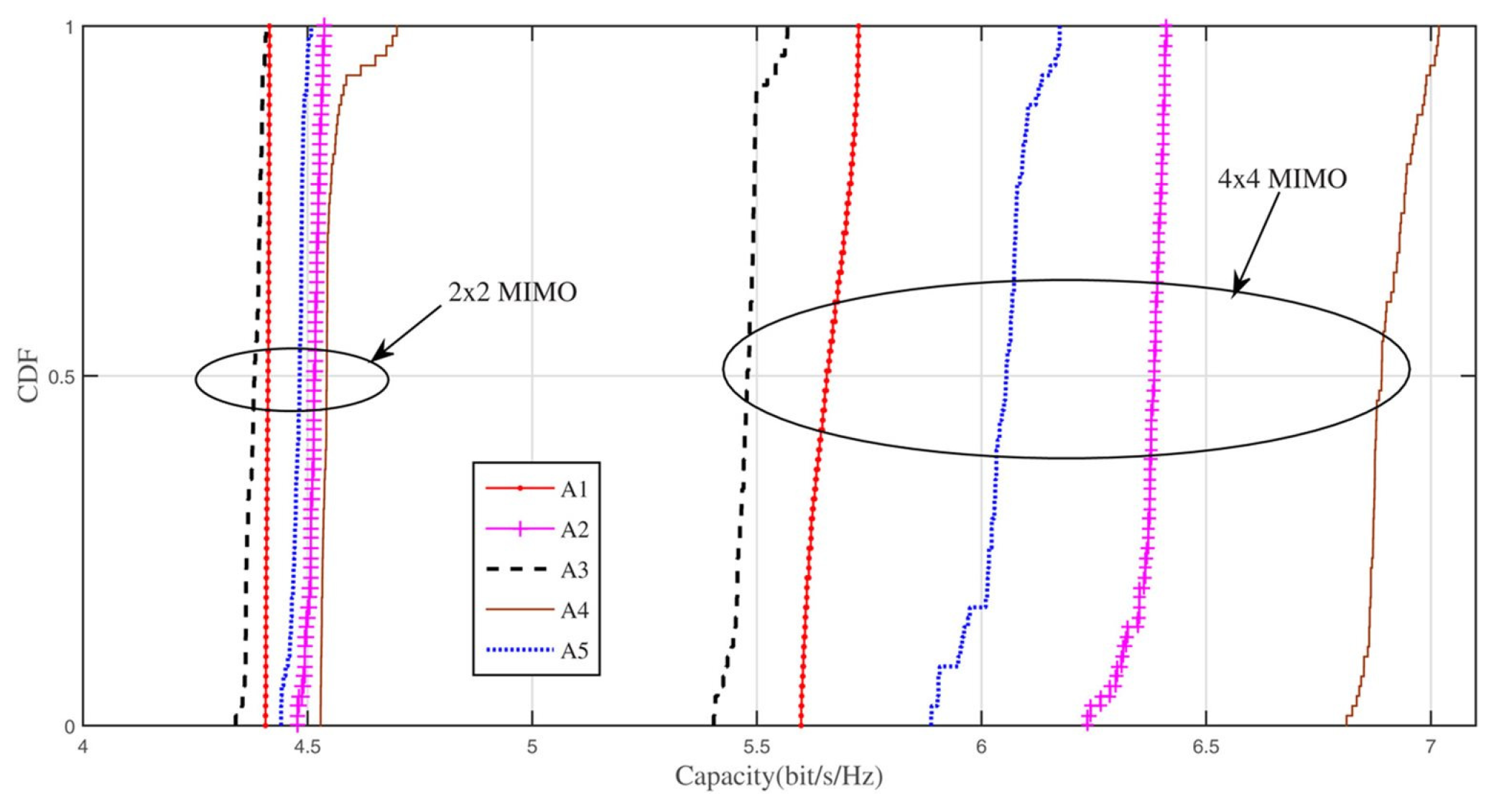
5.4. Millimeter Wave Mimo Channel Characteristics
6. Future Challenges and Trends
- : The SV model is widely used to assess the system performance under the assumption of channel bandwidth when it is quite large (500 MHz). In the SV model, the total numbers of signals are assumed to pursue the Poisson distribution, and the signals with certain delays inside the cluster can be determined due to the large time resolution [190]. The IEEE WPAN has already appraised the SV model in its standards [190,191]. To practice the massive MIMO and mmWave scenarios in 5G systems, the on-going SV model needs to be upgraded. By consuming the large number of antenna arrays along the array axis, the cluster evolution which is established through the birth–death process can be introduced in the SV channel model for the massive MIMO systems [192]. In the meantime, the information of geometrical correspondence of a channel model is also required when the non-stationary characteristics along the time axis are perceived. Consequently, the cluster formation algorithm in [192] needs to be upgraded in order to consider the generation of parameters for signals within different clusters. In addition, the directional antenna systems can be extensively used in the mmWave communication channels to overcome the atmospheric absorption and path loss [193]. As a result, different channels based on directional antennas should be integrated in the given SV model. Moreover, the 3-D channels can be conceived to model new clusters against their vertical planes [194].
- : The GBSM and METIS projects have proposed a new modeling technique for the massive MIMO networks known as map-based channel modeling (MBCM) [195]. The METIS-based MBCM model is demonstrated based on an RT approach. It is focusing at the tracking of each ray approaching from transmitting antenna to receiving antenna. Moreover, the interactions between signals and the scattering/shadowing objects, i.e., blocking, diffraction, diffuse scattering, and specular reflection, have been carefully deliberated in few studies. These scattering/shadowing objects need to be introduced randomly in given scenarios. Since each signal is tracked through the MBCM, therefore the massive MIMO system properties, i.e., non-stationary characteristics of different clusters and spherical wavefronts are incorporated in this model. By considering the Doppler effects at both the transmitting and receiving antenna sides, the METIS-based MBCM is capable to facilitate such environments where M2M communications for massive MIMO channels are required. However, the RT nature of the MBCM causes for a quite high complexity in channel modeling [195]. The practicability of MBCM needs to be explored further.
- : It was demonstrated in [196] that machine-to-machine communications can play a vital role in future 5G communication networks, where the devices are all interlinked. Different channel models for the M2M communications along conventional MIMO systems can be found in [197], where Doppler effect was considered at both the transmitting and receiving antennas. Having the capability to boost the channel performance, the M2M and massive MIMO systems need to be integrated. The evolving applications of HST channel in 5G communication systems appeal to researchers to consider the HST channels in their future research [198]. Massive MIMO channels can be anticipated to enhance the system performance if they are equipped at the HST or at the base station. Conversely, the high velocity of HST communication channels introduces different challenges in channel modeling. Therefore, the channel can be considered as a non-stationary. In [192], the array-time algorithm has been proposed and can be possibly extended to justify the HST massive MIMO channel. To collectively model the massive MIMO system characteristics for other advanced 5G scenarios (HST or M2M), a general channel model would be constructive if it includes the array-time evolution and Doppler effects at both the transmitting and receiving antenna arrays. These can be acquired through a GBSM framework introduced in [199] by incorporating the SV and WINNER II models. Additionally, the polarized arrays and the 3-D features can be further investigated. Finally, it can be proved that each signal has its own complex gain and delay in the GBSM framework due to the involvement of the SV model [199].
- : The spectrum of THz communications, ranging between 0.3 and 10 THz, stands between the infrared lightwave and mmWave in the electromagnetic spectrums. The THz spectrum can be regarded as the novel spectrum resource and has been not completely explored so far [200]. However, due to the growing demands of wireless access in HST and the evolution of different semiconductor devices, the THz communication networks have gained the considerable attentions of researchers. Because of the vast bandwidth, the THz communications are expected to deliver improve data rates (100 Gbps or even more) [201]. On the other hand, because of the higher frequency bands, the signals at THz band encounter atmospheric attenuation and much higher free space PL than those working at the microwave frequency band [202]. Thus, the THz communications are most likely to be useful in confined scenarios combined with the beam-steering systems. The channel modeling of THz communications is yet in its initial phase and quite a few models of THz communications have been investigated so far. The authors in [203] aimed at a GBSM model for THz communications which can be used to estimate the system-level throughput and to explore the THz channel physical characteristics. In [204], the multi-ray THz communication channel model using an RT technique has been considered to explore the diffracted, scattered, LoS, and NLoS component interactions. Intelligent reconfigurable surface (IRS) and THz are two promising candidate technologies for fulfilling the aforesaid requirements. THz communication can achieve exceptionally high transmission rates by providing ultra-wide bandwidth. However, due to diffraction and high path loss issues, THz signal coverage is limited. To accomplish this, an IRS made up of a high number of reconfigurable passive elements can be utilized to change the signal strength and propagation direction by modifying the amplitude or phase of the IRS elements, hence increasing THz signal coverage [205]. IRS is capable of dynamically modifying wireless channels to improve communication performance by smartly tuning signal reflection via a large number of low-cost passive reflecting devices. As a result, the new IRS-assisted hybrid wireless network, which includes both passive and active components, is predicted to be highly promising in terms of capacity and cost reduction in future.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kadakolmath, L.; Ramu, U. A Survey on Formal Specification and Verification of Smart Mass Transit Railway Interlocking System. Int. J. Saf. Secur. Eng. IIETA 2021, 11, 671–682. [Google Scholar] [CrossRef]
- Zhang, K.; Zheng, G.; Wang, H.; Zhang, C.; Yu, X. Channel Model and Performance Analysis for MIMO Systems with Single Leaky Coaxial Cable in Tunnel Scenarios. Sensors 2022, 22, 5776. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Wang, H.; Wen, H.; Guo, J. Propagation Characteristics of Electromagnetic Waves in Mine Roadways. J. Appl. Geophys. 2020, 173, 1–7. [Google Scholar] [CrossRef]
- Jakes, W.C.; Cox, D.C. Microwave Mobile Communications; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Wang, Z.; Xu, D. Online optimization of Intelligent Reflecting Surface-aided Energy-Efficient IoT-Edge Computingy. Future Gener. Comput. Syst. 2023, 141, 611–625. [Google Scholar] [CrossRef]
- Pan, C.; Ren, H.; Wang, K.; Elkashlan, M.; Nallanathan, A.; Wang, J.; Hanzo, L. Intelligent Reflecting Surface Aided MIMO Broadcasting for Simultaneous Wireless Information and Power Transfer. IEEE J. Sel. Areas Commun. 2020, 38, 1719–1734. [Google Scholar] [CrossRef]
- Tasgaonkar, P.P.; Garg, R.D.; Garg, P.K. Vehicle Detection and Traffic Estimation with Sensors Technologies for Intelligent Transportation Systems. Sens Imaging 2020, 21, 1–28. [Google Scholar] [CrossRef]
- Srikanth, B.; Kumar, H.; Rao, K. A Robust Approach for WSN Localization for Underground Coal Mine Monitoring using Improved RSSI Technique. Math. Model. Eng. Probl. IIETA 2018, 5, 225–231. [Google Scholar] [CrossRef]
- Ahmad, S.; Spiryagin, M.; Cole, C.; Wu, Q.; Wolfs, P.; Bosomworth, C. Analysis of Positioning of Wayside Charging Stations for Hybrid Locomotive Consists in Heavy Haul Train Operations. Railw. Eng. Sci. 2021, 29, 285–298. [Google Scholar] [CrossRef]
- Vedenkin, D.; Morozov, O.; Sedelnikov, Y.; Agliullin, T.; Nasybullin, A. Increasing the Accuracy Characteristics of Focused Electromagnetic Devices for Non-Destructive Testing and Technical Diagnostics by Implementing Sum–CDifference Signal Processing. Electronics 2023, 12, 436. [Google Scholar] [CrossRef]
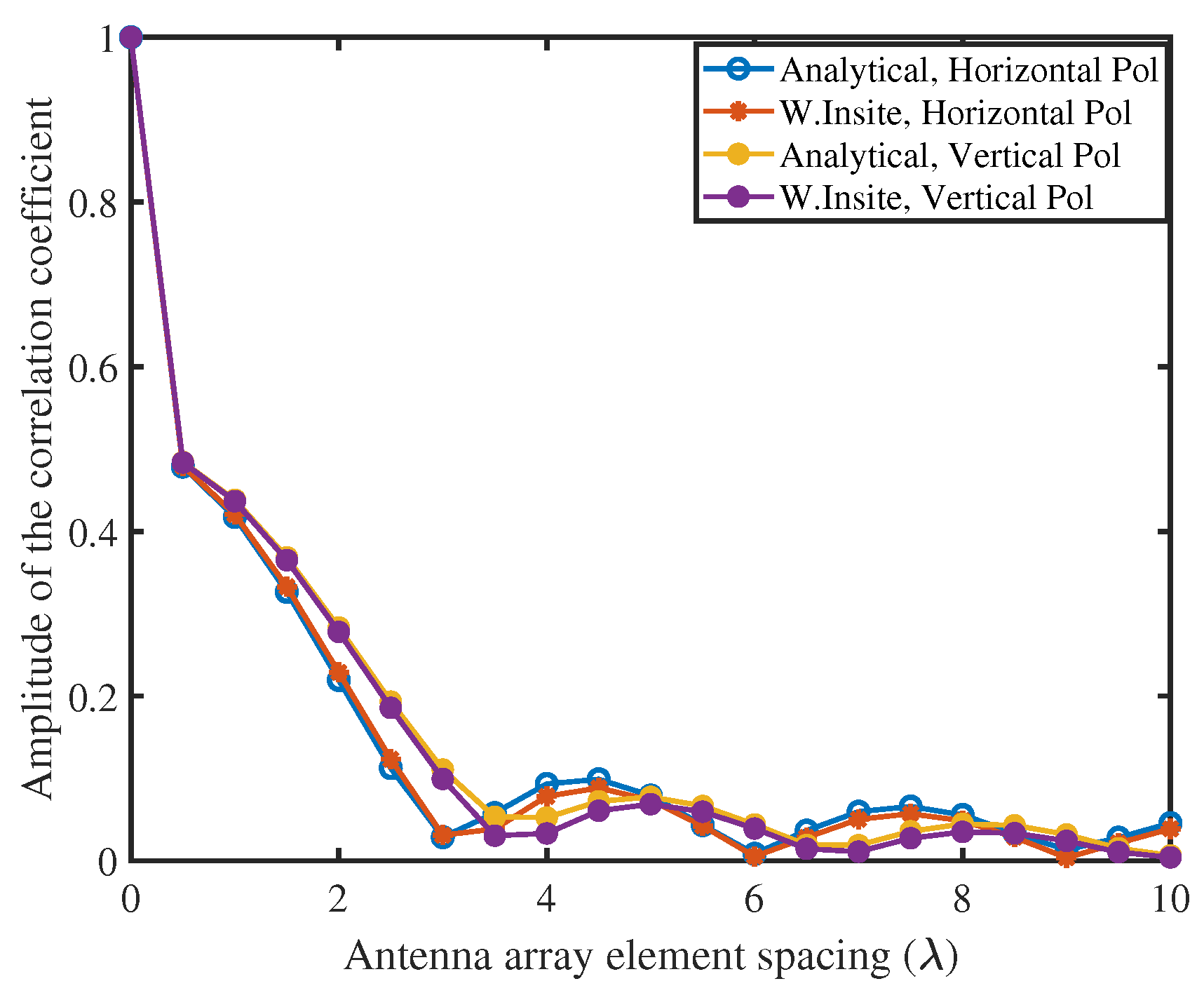
- Saleem, A.; Cui, H.; He, Y.; Boag, A. Channel Propagation Characteristics for Massive Multiple-Input/Multiple-Output Systems in a Tunnel Environment [Measurements Corner]. IEEE Antennas Propag. Mag. 2022, 64, 126–142. [Google Scholar] [CrossRef]
- Martin, D.J. Leaky-Feeder Radio Communication: A Historical Review. In Proceedings of the 34th IEEE Vehicular Technology Conference (VTC), Pittsburgh, PA, USA, 21–23 May 1984; Volume 34, pp. 25–30. [Google Scholar]
- Siddiqui, Z.; Sonkki, M.; Tuhkala, M.; Myllymäki, S. Periodically Slotted Coupled Mode Leaky Coaxial Cable with Enhanced Radiation Performance. IEEE Trans. Antennas Propag. 2020, 68, 7595–7600. [Google Scholar] [CrossRef]
- Hou, Y.; Zhu, J.; Denno, S.; Okada, M. Capacity of 4-by-4 MIMO Channel Using One Composite Leaky Coaxial Cable With User Position Information. IEEE Trans. Veh. Technol. 2019, 68, 11042–11051. [Google Scholar] [CrossRef]
- Malhotra, M.; Aulakh, I.K. Next-Generation Communication Networks: Wired or Wireless-A Big Question! In ICT Analysis and Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 227–234. [Google Scholar]
- Michelson, D.G.; Ghassemzadeh, S.S. Measurement and Modeling of Wireless Channels. In New Directions in Wireless Communications Research; Springer: Boston, MA, USA, 2009; pp. 1–27. [Google Scholar]
- Pittman, B.W.E., Jr.; Church, R.H.; McLendon, J.T. Through-the-Earth Electromagnetic Trapped Miner Location Systems: A Review; US Department of the Interior, Bureau of Mines: Pittsburgh, PA, USA, 1985. [Google Scholar]
- Delogne, P. EM Propagation in Tunnels. IEEE Trans. Antennasand Propag. 1991, 39, 401–406. [Google Scholar] [CrossRef]
- Large, D.; Ball, L.; Farstad, A. Radio Transmission to and from Underground Coal Mines-Theory and Measurement. IEEE Trans. Commun. 1973, 21, 194–202. [Google Scholar] [CrossRef]
- Durkin, J. Apparent Earth Conductivity over Coal Mines as Estimated from through-the-Earth Electromagnetic Transmission Tests; US Department of the Interior, Bureau of Mines: Pittsburgh, PA, USA, 1984; p. 8869. [Google Scholar]
- Hill, D.A.; Wait, J.R. Theoretical Noise and Propogation Models for through-the-Earth Communication; US Department of the Interior, Bureau of Mines: Pittsburgh, PA, USA, 1982. [Google Scholar]
- Patri, A.; Nayak, A.; Jayanthu, S. Wireless Communication Systems for Underground Mines–A Critical Appraisal. Int. J. Eng. Trends Technol. 2013, 4, 3149–3153. [Google Scholar]
- Liénard, M.; Degauque, P. Natural Wave Propagation in Mine Environments. IEEE Trans. Antennas Propag. 2000, 48, 1326–1339. [Google Scholar] [CrossRef]
- Frielos, D. Xstrata Mines RFIDS Benefits. RFID J. 2007, 7, 1–2. [Google Scholar]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.; Zhang, J.C. What will 5G be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Mohsan, S.; Amjad, H. A Comprehensive Survey on Hybrid Wireless Networks: Practical Considerations, Challenges, Applications and Research Directions. Opt. Quantum Electron. 2021, 53, 1–56. [Google Scholar]
- Zhai, Y.; Bao, T.; Zhu, L.; Shen, M.; Du, X.; Guizani, M. Toward Reinforcement-Learning-based Service Deployment of 5G Mobile Edge Computing with Request-Aware Scheduling. IEEE Wirel. Commun. 2020, 27, 84–91. [Google Scholar] [CrossRef]
- Hayat, O.; Ngah, R.; Hashim, S.Z.M. Performance Analysis of Device Discovery Algorithms for D2D Communication. Arab. J. Sci. Eng. 2020, 45, 1457–1471. [Google Scholar] [CrossRef]
- Garrocho, C.T.; da Silva, M.J.; Oliveira, R.A. D2d Pervasive Communication System with Out-of-Band Control Autonomous to 5G Networks. Wirel. Netw. 2020, 26, 373–386. [Google Scholar] [CrossRef]
- Wang, K.; Liu, L.; Zhang, J.; Zhou, T. Channel Characterization for Hyperloops Using the Nonstationary Geometry-Based Model. J. Circuits Syst. Comput. 2022, 32, 2350012. [Google Scholar] [CrossRef]
- Sang, T.; Su, C.; Mi, X. Research on the Influence of Vacuum Pipe Blocking Ratio on the Aerodynamic Characteristics of Super High Speed Train. In Proceedings of the IEEE 24th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Dalian, China, 5–7 May 2021; pp. 931–935. [Google Scholar]
- Hasegawa, F.; Taira, A.; Noh, G.; Hui, B.; Nishimoto, H.; Okazaki, A.; Okamura, A.; Kim, I. High-Speed Train Communications Standardization in 3GPP 5G NR. IEEE Commun. Stand. Mag. 2018, 2, 44–52. [Google Scholar] [CrossRef]
- Zhou, T.; Tao, C.; Salous, S.; Liu, L. Geometry-based Multi-Link Channel Modeling for High-Speed Train Communication Networks. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1229–1238. [Google Scholar] [CrossRef]
- Hu, Z.; Ji, W.; Zhao, H.; Zhai, X.; Saleem, A.; Zheng, G. Channel Measurement for Multiple Frequency Bands in Subway Tunnel Scenario. Int. J. Antennas Propag. 2021, 2021, 92–99. [Google Scholar] [CrossRef]
- Masson, É.; Berbineau, M. Broadband Wireless Communications for Railway Applications; Springer: New York, NY, USA, 2017. [Google Scholar]
- Zhou, T.; Tao, C.; Salous, S.; Liu, L. Measurements and Analysis of Short-Term Fading Behavior in High-Speed Railway Communication Networks. IEEE Trans. Veh. Technol. 2018, 68, 101–112. [Google Scholar] [CrossRef]
- Mistry, K.; Lazaridis, P.; Zaharis, Z.D.; Akinsolu, M.; Liu, B.; Lo, T.H. Accurate Antenna Gain Estimation Using the Two-Antenna Method. In Proceedings of the IET’s Antennas and Propagation Conference (APC), Birmingham, UK, 11–12 November 2019. [Google Scholar]
- Liu, X.; Yin, X.; Zheng, G. Experimental Investigation of Millimeter-Wave MIMO Channel Characteristics in Tunnel. IEEE Access 2019, 7, 108395–108399. [Google Scholar] [CrossRef]
- Saleem, A.; Wang, M.; Zheng, G. Scattering of Electric Field from Leaky Coaxial Cable in Confined Area. Int. J. Antennas Propag. 2017, 2017, 2894397. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, F.; Zheng, C.G.; Cang, L. Three-Dimensional MIMO Channel Model with High-Mobility Wireless Communication Systems Using Leaky Coaxial Cable in Rectangular Tunnel. Int. J. Antennas Propag. 2021, 2021, 6622135. [Google Scholar] [CrossRef]
- Bian, J.; Wang, C.; Gao, X.; You, X.; Zhang, M. A General 3D Non-Stationary Wireless Channel Model for 5G and Beyond. IEEE Trans. Wirel. Commun. 2021, 20, 3211–3224. [Google Scholar] [CrossRef]
- Guan, K.; Zhong, Z.; Ai, B. Statistic Modeling for Propagation in Tunnels based on Distributed Antenna Systems. In Proceedings of the IEEE 2013 IEEE Antennas and Propagation Society International Symposium (APSURSI’13), Orlando, FL, USA, 7–13 July 2013; pp. 1920–1921. [Google Scholar]
- Guan, K.; Zhong, Z.; Ai, B.; Kürner, T. Propagation Measurements and Analysis for Train Stations of High-Speed Railway at 930 MHz. IEEE Trans. Veh. Technol. 2014, 63, 3349–3516. [Google Scholar] [CrossRef]
- Tami, D.; Rego, C.G.; Guevara, D.; Navarro, A.; Moreira, F.J.; Giménez, J.; Triana, H.G. Analysis of Heuristic Uniform Theory of Diffraction Coefficients for Electromagnetic Scattering Prediction. Int. Antennas Propag. 2018, 2018, 3029152. [Google Scholar] [CrossRef]
- Saleem, A.; Zhang, F.; Wang, M.; Yin, X.; Zheng, G. Proficiency of Leaky Coaxial Cable-based MIMO System using Radiated Field Distribution. Int. J. Antennas Propag. 2018, 2018, 5016847. [Google Scholar] [CrossRef]
- Sun, R.; Matolak, D.W.; Tao, C.; Liu, L.; Tan, Z.; Zhou, T. Investigation of MIMO Channel Characteristics in a Two-Section Tunnel at 1.4725 GHz. Int. J. Antennas Propag. 2017, 2017, 3693149. [Google Scholar] [CrossRef]
- Kivinen, J.; Korhonen, T.O.; Aikio, P.; Gruber, R.; Vainikainen, P.; Haggman, S.G. Wideband Radio Channel Measurement System at 2GHz. IEEE Trans. Instrum. Meas. 1999, 48, 39–44. [Google Scholar] [CrossRef]
- Salous, S.; Lewenz, R.; Hawkins, I.; Razavi-Ghods, N. Parallel Receiver Channel Sounder for Spatial and MIMO Characterisation of the Mobile Radio Channel. IEE Proc. Commun. 2005, 152, 912–918. [Google Scholar] [CrossRef]
- Safer, H.; Berger, G.; Seifert, F. Wideband Propagation Measurements of the VHF-Mobile Radio Channel in Different Areas of Austria. In Proceedings of the IEEE 5th International Symposium on Spread Spectrum Techniques and Applications, Sun City, South Africa, 4 September 1998; pp. 502–506. [Google Scholar]
- Takada, J.; Sakaguchi, K.; Araki, K. Development of High Resolution MIMO Channel Sounder for the Advanced Modeling of Wireless Channels. In Proceedings of the Asia-Pacific Microwave Conference, APMC2001, Taipei, Taiwan, 3–6 December 2001; pp. 563–568. [Google Scholar]
- Nielsen, O.J.; Andersen, J.; Eggers, P.; Pedersen, G.F.; Olesen, K.; Suda, H. Measurements of Indoor 16*2 Wideband MIMO Channels at 5.8 GHz. In Proceedings of the International Symposium on Spread Spectrum Techniques and Applications, Sydney, Australia, 30 August 2004–2 September 2004; pp. 864–868. [Google Scholar]
- He, R.; Molisch, A.F.; Zhong, Z.; Ai, B.; Ding, J.; Chen, R.; Li, Z. Measurement based Channel Modeling with Directional Antennas for High-Speed Railways. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2932–2936. [Google Scholar]
- He, R.; Zhong, Z.; Ai, B.; Xiong, L.; Wei, H. A Novel Path Loss Model for High-Speed Railway Viaduct Scenaios. In Proceedings of the IEEE 7th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM), Wuhan, China, 23–25 September 2011; pp. 1–5. [Google Scholar]
- Kita, N.; Ito, T.; Yokoyama, S.; Tseng, M.C.; Sagawa, Y. Experimental Study of Propagation Characteristics for Wireless Communications in High-Speed Train Cars. In Proceedings of the 3rd European Conference on Antennas and Propagation (EuCAP), Berlin, Germany, 23–27 March 2009; pp. 897–901. [Google Scholar]
- Liu, L.; Tao, C.; Qiu, J.; Chen, H.; Yu, L.; Dong, W.; Yuan, Y. Position-based Modeling for Wireless Channel on High Speed Railway under a Viaduct at 2.35 GHz. IEEE J. Sel. Areas Commun. 2012, 30, 834–845. [Google Scholar] [CrossRef]
- Kusayakin, O.; Melezhik, N.; Poyedinchuk, A.Y.; Troschylo, O.S. Absorbing Properties of a Negative Permittivity Layer Placed on a Reflecting Grating. Prog. Electromagn. Res. 2006, 64, 135–148. [Google Scholar] [CrossRef]
- Delogne, P.; Deryck, L. Underground Use of a Coaxial Cable with Leaky Sections. IEEE Trans. Antennas Propag. 1980, 28, 875–883. [Google Scholar] [CrossRef]
- "Okada, S.; Kishimoto, T.; Akagawa, K.; Nakahara, Y.; Mikoshiba, K.; Horiguchi, F.; Okamoto, K. Leaky Coaxial Cable for Communication in High Speed Railway Transportation. Radio Electron. Eng. 1975, 45, 224–228. [Google Scholar]
- Saleem, A.; Wang, M.; Zheng, G.; Yin, X. Spatial Characteristics of Wideband Channels using Leaky Coaxial Cables in Tunnel Scenario. Int. J. Antennas Propag. 2019, 2019, 9374905. [Google Scholar] [CrossRef]
- Owyang, G.H. Foundations for Microwave Circuits; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Bouhaj, M.; Von Estorff, O.; Peiffer, A. An Approach for the Assessment of the Statistical Aspects of the Sea Coupling Loss Factors and the Vibrational Energy Transmission in Complex Aircraft Structures: Experimental Investigation and Methods Benchmark. J. Sound Vib. 2017, 403, 152–172. [Google Scholar] [CrossRef]
- Pan, Y.; Zheng, G.; Oestges, C. Characterization of Polarized Radio Channel with Leaky Coaxial Cable in a Tunnel-Like Environment. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2803–2807. [Google Scholar] [CrossRef]
- Buendia, V.; Podilchak, S.; Goussetis, G.; Masotti, D.; Costanzo, A.; Nicole, P. A Smart Cable Offering Selective and Distributed Antenna Radiation Using RF Switches and Non-Conventional Hybrid Couplers. IEEE Trans. Antennas Propag. 2018, 66, 6346–6351. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, X.; Fan, X. Design and Simulation Analysis of the Graded LCX. In Proceedings of the International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 22–24 March 2017; pp. 675–678. [Google Scholar]
- Zainud-Deen, S.; Malhat, H. Circularly Polarized SIW DRA Fed by Ridge Gap Waveguide for 60 GHz Communications. Wireless Personal Communications. Wirel. Pers. Commun. 2020, 114, 113–122. [Google Scholar] [CrossRef]
- Wu, Y.; Zheng, G.; Saleem, A.; Zhang, Y. An Experimental Study of MIMO Performance using Leaky Coaxial Cables in a Tunnel. IEEE Antennas And Wireless Propag. Lett. 2017, 16, 1663–1666. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications–Principles and Practice, (The Book End). Microw. J. 2002, 45, 128–129. [Google Scholar]
- HUAWEI. Elte Rapid Deployment Broadband Trunking System. Available online: http://e.huawei.com/za/products/wireless/elte-trunking/rapiddeployment/ (accessed on 5 April 2020).
- Benzakour, A.; Affes, S.; Despins, C.; Tardif, P.-M. Wideband Measurements of Channel Characteristics at 2.4 and 5.8 GHz in Underground Mining Environments. In Proceedings of the IEEE 60th Vehicular Technology Conference (VTC-Fall), Los Angeles, CA, USA, 26–29 September 2004; Volume 5, pp. 3595–3599. [Google Scholar]
- Boutin, M.; Benzakour, A.; Despins, C.L.; Affes, S. Radio Wave Characterization and Modeling in Underground Mine Tunnels. IEEE Trans. Antennas Propag. 2008, 56, 540–549. [Google Scholar] [CrossRef]
- Nerguizian, C.; Despins, C.L.; Affès, S.; Djadel, M. Radio-Channel Characterization of an Underground Mine at 2.4 GHz. IEEE Trans. Wirel. Commun. 2005, 4, 2441–2453. [Google Scholar] [CrossRef]
- El Khaled, M.; Fortier, P.; Ammari, M.L. A Performance Study of Line-of-Sight Millimeter-Wave Underground Mine Channel. IEEE Antennas And Wirel. Propag. Lett. 2014, 13, 1148–1151. [Google Scholar] [CrossRef]
- Rissafi, Y.; Talbi, L.; Ghaddar, M. Experimental Characterization of an UWB Propagation Channel in Underground Mines. IEEE Trans. Antennas Propag. 2011, 60, 240–246. [Google Scholar] [CrossRef]
- Mabrouk, I.B.; Hautcoeur, J.; Talbi, L.; Nedil, M.; Hettak, K. Feasibility of a Millimeter-Wave MIMO System for Short-Range Wireless Communications in an Underground Gold Mine. IEEE Trans. Antennas Propag. 2013, 61, 4296–4305. [Google Scholar] [CrossRef]
- Mnasri, B.; Nedil, M.; Kandil, N.; Talbi, L.; Mabrouk, I.B. Experimental Characterization of Wireless MIMO Channel at 5.8 GHz in Underground Gold Mine. Prog. Electromagn. Res. 2013, 36, 169–180. [Google Scholar] [CrossRef]
- Ghaddar, M.; Nedil, M.; Mabrouk, I.B.; Talbi, L. Multiple-input Multiple-output Beam-Space for High-Speed Wireless Communication in Underground Mine. IET Microw. Antennas Propag. 2016, 10, 8–15. [Google Scholar] [CrossRef]
- Li, C.; Liu, L.; Xie, J. Finite-State Markov Wireless Channel Modeling for Railway Tunnel Environments. China Commun. IEEE 2020, 17, 30–39. [Google Scholar] [CrossRef]
- Li, M.; Zhu, Z.; Deng, T.; Sheng, X. An Investigation into High-Speed Train Interior Noise with Operational Transfer Path Analysis Method. Railw. Eng. Sci. 2021, 29, 1–14. [Google Scholar] [CrossRef]
- Zhou, L.; Ma, H.; Yang, Z.; Zhou, S.; Zhang, W. Unmanned Aerial Vehicle Communications: Path-Loss Modeling and Evaluation. IEEE Veh. Mag. 2020, 15, 121–128. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, B.; Cheng, Z.; Chen, C.; Huang, L. Marine Mobile Wireless Channel Modeling based on Improved Spatial Partitioning Ray Tracing. China Commun. 2020, 17, 1–11. [Google Scholar] [CrossRef]
- Fong, S.; Dey, N.; Joshi, A. ICT Analysis and Applications: Proceedings of ICT4SD 2019, Volume 2. 2020. Available online: https://link.springer.com/book/10.1007/978-981-15-0630-7 (accessed on 8 March 2023).
- Pandit, P. Review on Characteristics of Wireless Communication Systems. Int. Res. J. Eng. Technol. 2019, 6, 1036–1041. [Google Scholar]
- Yang, H.-C.; Alouini, M.-S. Advanced Wireless Transmission Technologies: Analysis and Design; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Bian, J.; Wang, C.-X.; Zhang, M.; Ge, X.; Gao, X. A 3-D Non-Stationary Wideband MIMO Channel Model Allowing for Velocity Variations of the Mobile Station. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Zheng, X.; Jiang, T.; Xue, W. Improving Passive Radar Target Recognition using a Convolution Composite WiFi Preamble. IEEE Sens. J. 2020, 20, 6470–6477. [Google Scholar] [CrossRef]
- Hou, W.; Zhang, X.; Wang, J.; Sarris, C. Hybrid Numerical Modeling of Electromagnetic Interference in Train Communication Systems. IEEE Trans. Electromagn. Compat. 2019, 62, 715–724. [Google Scholar] [CrossRef]
- Rana, M.M.; Mohan, A.S. Segmented-Locally-One-Dimensional-FDTD Method for EM Propagation Inside Large Complex Tunnel Environments. IEEE Trans. Magn. 2012, 48, 223–226. [Google Scholar] [CrossRef]
- Yang, M.; Fang, H.; Chen, D.; Du, X.; Wang, F. The Conformal Finite-Difference Time-Domain Simulation of GPR Wave Propagation in Complex Geoelectric Structures. Geofluids 2020, 2020, 3069372. [Google Scholar] [CrossRef]
- Yu, L.; Cyue, Z.; Su, G.-D.J. Three-Stage Full-Wave Simulation Architecture for In-Depth Analysis of Microspheres in Microscopy. Opt. Express 2020, 28, 8862–8877. [Google Scholar] [CrossRef] [PubMed]
- Hrovat, A.; Kandus, G.; Javornik, T. A Survey of Radio Propagation Modeling for Tunnels. IEEE Commun. Surv. Tutor. 2013, 16, 658–669. [Google Scholar] [CrossRef]
- Niu, K.; Huang, Z.; Ren, X.; Li, M.; Wu, B.; Wu, X. An Optimized 3-D HIE-FDTD Method with Reduced Numerical Dispersion. IEEE Trans. Antennas Propag. 2018, 66, 6435–6440. [Google Scholar] [CrossRef]
- Rafiee, M.; Ahmed, H.; Chandra, S.; Loughlin, C.M.; Glenn, A.; McCormack, S. Towards Reducing Computational Costs of Finite Difference Time Domain Algorithm in Plasmonic Optical Properties Modelling of Metal Nanoparticles. In Materials Science Forum; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2020; Volume 995, pp. 203–208. [Google Scholar]
- Halder, A.; Chakravarty, D. Investigation of Wireless Tracking Performance in the Tunnel-like Environment with Particle Filter. Math. Model. Eng. Probl. IIETA 2018, 5, 93–101. [Google Scholar] [CrossRef]
- Jijo, B.; Zeebaree, S.; Zebari, R.; Sadeeq, M.A.; Sallow, A.B.; Mohsin, S.; Ageed, Z.S. A Comprehensive Survey of 5G mm-Wave Technology Design Challenges. Asian J. Res. Comput. Sci. 2021, 2021, 1–20. [Google Scholar] [CrossRef]
- Guan, K.; He, D.; Ai, B.; Matolak, D.W.; Wang, Q.; Zhong, Z.; Kürner, T. 5-GHz Obstructed Vehicle-to-Vehicle Channel Characterization for Internet of Intelligent Vehicles. IEEE Internet Things J. 2018, 6, 100–110. [Google Scholar] [CrossRef]
- Kwon, C.; Kim, H.; Lee, H.; Choi, H.H.; Byun, W.-J.; Kim, K. A Temporal Millimeter Wave Propagation Model for Tunnels using Ray Frustum Techniques and FFT. Int. J. Antennas Propag. 2014, 2014, 172924. [Google Scholar] [CrossRef]
- Li, G.; Ai, B.; He, D.; Zhong, Z.; Hui, B.; Kim, J. On the Feasibility of High Speed Railway mmWave Channels in Tunnel Scenario. Wirel. Commun. Mob. Comput. 2017, 2017, 7135896. [Google Scholar] [CrossRef]
- Guan, K.; Ai, B.; Peng, B.; He, D.; Li, G.; Yang, J.; Zhong, Z.; Kürner, T. Towards Realistic High-Speed Train Channels at 5G Millimeter-Wave Band-Part II: Case Study for Paradigm Implementation. IEEE Trans. OnVehicular Technol. 2018, 67, 9129–9144. [Google Scholar] [CrossRef]
- Guan, K.; Ai, B.; Peng, B.; He, D.; Li, G.; Kürner, T. Towards Realistic High-Speed Train Channels at 5G Millimeter-Wave Band-Part I: Paradigm, Significance Analysis, and Scenario Reconstruction. IEEE Trans. Veh. Technol. 2018, 67, 9112–9128. [Google Scholar] [CrossRef]
- Hrovat, A.; Guan, K.; Javornik, T. Traffic Impact on Radio Wave Propagation at Millimeter-Wave Band in Tunnels for 5G Communications. In Proceedings of the 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 2903–2906. [Google Scholar]
- Hrovat, A.; Javornik, T.; Guan, K. Analysis of Radio Wave Propagation at Millimeter-Wave Band in Tunnels for 5G Communications. In Proceedings of the 22nd International Conference on Applied Electromagnetics and Communications (ICECOM), Dubrovnik, Croatia, 19–21 September 2016; pp. 1–5. [Google Scholar]
- Wei, H.; Zheng, G.; Jia, M. The Measurements and Simulations of Millimeter Wave Propagation at 38 GHz in Circular Subway tunnels. In Proceedings of the China-Japan Joint Microwave Conference (CJMW), Shanghai, China, 10–12 September 2008; pp. 51–54. [Google Scholar]
- Jia, M.; Zhao, J. A Novel Method to Predict the Wideband Characteristics of MMW Propagation in Tunnels. In Proceedings of the 7th International Conference on Wireless Communications, Networking and Mobile Computing. (WiCom), Washington, DC, USA, 23–25 September 2011; pp. 1–4. [Google Scholar]
- Fono, V.; Talbi, L.; Hakem, N. Propagation Modeling in Complex Rough Environment based on Ray Tracing. In Proceedings of the IEEE Antennas and Propagation Society International Symposium (APSURSI), Orlando, FL, USA, 7–13 July 2013; pp. 1924–1925. [Google Scholar]
- Mani, F.; Quitin, F.; Oestges, C. Directional Spreads of Dense Multipath Components in Indoor Environments: Experimental Validation of a Ray-Tracing Approach. IEEE Trans. Antennas Propag. 2012, 60, 3389–3396. [Google Scholar] [CrossRef]
- Jimenez, M.J.C.; Arana, K.; Arias, M.R. Outdoor-to-Indoor Propagation Mechanisms in Multistorey Building for 0.85 GHz and 1.9 GHz Bands. In Proceedings of the IEEE 37th Central America and Panama Convention, (CONCAPAN XXXVII), Managua, Nicaragua, 15–17 November 2017; pp. 1–6. [Google Scholar]
- He, D.; Ai, B.; Guan, K.; Zhong, Z.; Hui, B.; Kim, J.; Chung, H.; Kim, I. Channel Measurement, Simulation, and Analysis for High-Speed Railway Communications in 5G Millimeter-Wave bBand. IEEE Trans. Intell. Transp. Syst. 2017, 19, 3144–3158. [Google Scholar] [CrossRef]
- Lin, S.; Kong, L.; He, L.; Guan, K.; Ai, B.; Zhong, Z.; Briso-Rodríguez, C. Finite-State Markov Modeling for High-Speed Railway Fading Channels. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 954–957. [Google Scholar] [CrossRef]
- Zhou, T.; Tao, C.; Salous, S.; Tan, Z.; Liu, L.; Tian, L. Graph-based Stochastic Model for High-Speed Railway Cutting Scenarios. IET Microw. Antennas Propag. 2015, 9, 1691–1697. [Google Scholar] [CrossRef]
- Jiang, S.; Wang, W.; Miao, Y.; Fan, W.; Molisch, A.F. A Survey of Dense Multipath and Its Impact on Wireless Systems. IEEE Open J. Antennas Propag. 2022, 3, 435–460. [Google Scholar] [CrossRef]
- Kshetri, S.; Tanghe, E.; Gaillot, D.; Lienard, M.; Martens, L.; Joseph, W. Polarimetrie Properties of Indoor MIMO Channels for Different Floor Levels in a Residential House. In Proceedings of the European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 12463–12467. [Google Scholar]
- Forooshani, A.E.; Bashir, S.; Michelson, D.G.; Noghanian, S. A Survey of Wireless Communications and Propagation Modeling in Underground Mines. IEEE Commun. Surv. Tutor. 2013, 15, 1524–1545. [Google Scholar] [CrossRef]
- Chenhao, Q.; Ci, W.; Zhang, J.; You, X. Hybrid Beamforming for Millimeter Wave MIMO Integrated Sensing and Communications. IEEE Commun. Lett. 2022, 26, 1136–1140. [Google Scholar]
- Wu, S.; Wang, C.-X.; Alwakeel, M.M.; You, X. A General 3-D Non-Stationary 5G Wireless Channel Model. IEEE Trans. Commun. 2017, 66, 3065–3078. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, F.; Zheng, G.; Saleem, A.; Guan, K. A 3D Non-Stationary Channel Model with Moving Mobile Station in Rectangular Tunnel. Int. J. Antennas Propag. 2019, 2019, 6750153. [Google Scholar] [CrossRef]
- Avazov, N.; Pätzold, M. A Novel Wideband MIMO Car-to-Car Channel Model based on a Geometrical Semi-Circular Tunnel Scattering Model. IEEE Trans. Veh. Technol. 2015, 65, 1070–1082. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, C.-X.; Lopez, C.; Ge, X. 3D Non-Stationary Wideband Circular Tunnel Channel Models for High-Speed Train Wireless Communication Systems. Sci. China Inf. Sci. 2017, 60, 082304. [Google Scholar] [CrossRef]
- Dorf, R.C. The Electrical Engineering Handbook-Six Volume Set; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Yu, J.; Chen, W.; Yang, K.; Li, C.; Li, F.; Shui, Y. Path Loss Channel Model for Inland River Radio Propagation at 1.4 GHz. Int J Antennas Propag. 2017, 2017, 5853724. [Google Scholar] [CrossRef]
- Wang, H.; Ning, B.; Jiang, H. An Experimental Study of 2.4 GHz Frequency Band Leaky Coaxial Cable in CBTC Train Ground Communication. In Proceedings of the IEEE 73rd Vehicular Technology Conference (VTC Spring), Budapest, Hungary, 15–18 May 2011; pp. 1–5. [Google Scholar]
- Chehri, A.; Mouftah, H. Radio Channel Characterization Through Leaky Feeder for Different Frequency Bands. In Proceedings of the 21st Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Istanbul, Turkey, 26–30 September 2010; pp. 347–351. [Google Scholar]
- Zhang, Y. Indoor Radiated-Mode Leaky Feeder Propagation at 2.0 GHz. IEEE Trans. Veh. Technol. 2001, 50, 536–545. [Google Scholar] [CrossRef]
- Coaxial Communication Cables-Part 4 Sectional Specification for Radiating Cables. 2004. Available online: https://standards.iteh.ai/catalog/standards/iec/79d5f0b8-f401-4562-9d12-6087e52a547b/iec-61196-4-2015 (accessed on 8 March 2023).
- Han, Y.; Tang, W.; Jin, S.; Wen, C.; Ma, X. Large Intelligent Surface Assisted Wireless Communication Exploiting Statistical CSI. IEEE Trans. Veh. Technol. 2019, 68, 8238–8242. [Google Scholar] [CrossRef]
- Dai, J.; Tang, W.; Zhao, J.; Li, X.; Cheng, Q.; Ke, J.; Chen, M.; Jin, S.; Cui, T. Wireless Communications Through a Simplified Architecture based on Time-Domain Digital Coding Metasurface. Adv. Mater. Technol. 2019, 4, 1900044. [Google Scholar] [CrossRef]
- He, X.; Huang, L.; Wang, J. Novel Relax-and-Retract Algorithm for Intelligent Reflecting Surface Design. IEEE Trans. Veh. Technol. 2021, 70, 1995–2000. [Google Scholar] [CrossRef]
- Huang, C.; Zappone, A.; Alexandropoulos, G.C.; Debbah, M.; Yuen, C. Reconfigurable Intelligent Surfaces for Energy Efficiency in Wireless Communication. IEEE Trans. Wirel. Commun. 2019, 18, 4157–4170. [Google Scholar] [CrossRef]
- Tang, W.; Chen, M.Z.; Chen, X.; Dai, J.Y.; Han, Y.; Di Renzo, M.; Zeng, Y.; Jin, S.; Cheng, Q.; Cui, T.J. Wireless Communications with Reconfigurable Intelligent Surface: Path Loss Modeling and Experimental Measurement. IEEE Trans. Wirel. Commun. 2021, 20, 421–439. [Google Scholar] [CrossRef]
- Chen, W.; Chen, Z.; Ma, X.; Chi, Y.; Li, Z. Spectral Efficiency Optimization for Intelligent Reflecting Surface aided Multi-input Multi-output Terahertz System. Microw. Opt. Technol. Lett. 2020, 62, 2754–2759. [Google Scholar] [CrossRef]
- Zhao, D.; Lu, H.; Wang, Y.; Sun, H.; Gui, Y. Joint Power Allocation and User Association Optimization for IRS-assisted mmWave Systems. IEEE Trans. Wirel. Commun. 2022, 21, 577–590. [Google Scholar] [CrossRef]
- Li, Z.; Wu, C.; Wagner, S.; Sturm, J.C.; Verma, N.; Jamieson, K. REITS: Reflective Surface for Intelligent Transportation Systems. In Proceedings of the 22nd International Workshop on Mobile Computing Systems and Applications, Virtual, UK, 24–26 February 2021; pp. 78–84. [Google Scholar]
- Shen, H.; Xu, W.; Gong, S.; He, Z.; Zhao, C. Secrecy Rate Maximization for Intelligent Reflecting Surface assisted Multi-Antenna Communications. IEEE Commun. Lett. 2019, 23, 1488–1492. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Zhang, J.; Renzo, M.D. QoS-Driven Spectrum Sharing for Reconfigurable Intelligent Surfaces (RISs) aided Vehicular Networks. IEEE Trans. Wirel. Commun. 2021, 20, 5969–5985. [Google Scholar] [CrossRef]
- Joo, J.; Park, M.C.; Han, D.S.; Pejovic, V. Deep Learning-based Channel Prediction in Realistic Vehicular Communications. IEEE Access 2019, 7, 27846–27858. [Google Scholar] [CrossRef]
- Wei, Z.; Cai, Y.; Sun, Z.; Ng, D.W.K.; Yuan, J.; Zhou, M.; Sun, L. Sum-Rate Maximization for IRS-assisted UAV OFDMA Communication Systems. IEEE Trans. Wirel. Commun. 2021, 20, 2530–2550. [Google Scholar] [CrossRef]
- Gao, X. Reconfigurable Intelligent Surfaces-Assisted Multiuser MIMO Uplink Transmission with Partial CSI. IEEE Trans. Veh. Technol. 2020, 20, 5613–5627. [Google Scholar]
- Fokum, D.T.; Frost, V.S. A Survey on Methods for Broadband Internet Access on Trains. IEEE Commun. Surv. Tutor. 2010, 12, 171–185. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, H.; He, Z.; Guo, X.; Pan, W. A Power-Quality Monitoring and Assessment System for High-Speed Railways based on Train-Network-Data Center Integration. Railw. Eng. Sci. 2021, 29, 30–41. [Google Scholar] [CrossRef]
- Ai, B.; He, R.; Zhong, Z.; Guan, K.; Chen, B.; Liu, P.; Li, Y. Radio Wave Propagation Scene Partitioning for High-Speed Rails. Int. Antennas Propag. 2012, 2012, 815232. [Google Scholar] [CrossRef]
- Sun, Z.; Akyildiz, I.F. Channel Modeling and Analysis for Wireless Networks in Underground Mines and Road Tunnels. IEEE Trans. Commun. 2010, 58, 1758–1768. [Google Scholar] [CrossRef]
- Zheng, H.-d.; Nie, X.-y. GBSB Model for MIMO Channel and its Space-Time Correlation Analysis in Tunnel. In Proceedings of the IEEE International Symposium on Knowledge Acquisition and Modeling Worksho (KAM), Wuhan, China, 21–22 December 2008; pp. 221–224. [Google Scholar]
- Li, J.; Zhao, Y.; Zhang, J.; Jiang, R.; Tao, C.; Tan, Z. Radio Channel Measurements and Analysis at 2.4/5 GHz in Subway Tunnels. China Commun. 2015, 12, 36–45. [Google Scholar] [CrossRef]
- Hairoud, S.; Combeau, P.; Pousset, Y.; Cocheril, Y.; Berbineau, M. WINNER Model for Subway Tunnel at 5.8 GHz. In Proceedings of the 12th International Conference on ITS Telecommunications (ITST), Taipei, Taiwan, 5–8 November 2012; pp. 743–747. [Google Scholar]
- Zhou, C. Physics-based Ultra-Wideband Channel Modeling for Tunnel/Mining Environments. In Proceedings of the IEEE Radio and Wireless Symposium (RWS), San Diego, CA, USA, 25–28 January 2015; pp. 92–94. [Google Scholar]
- Forooshani, A.E.; Noghanian, S.; Michelson, D.G. Characterization of Angular Spread in Underground Tunnels based on the Multimode Waveguide Model. IEEE Trans. Commun. 2014, 62, 4126–4133. [Google Scholar] [CrossRef]
- Zhang, J.; Tao, C.; Liu, L.; Sun, R. A Study on Channel Modeling in Tunnel Scenario based on Propagation-Graph Theory. In Proceedings of the IEEE 83rd Vehicular Technology Conference (VTC-Spring), Nanjing, China, 15–18 May 2016; pp. 1–5. [Google Scholar]
- Liu, C.; Chen, Q.; Zhang, E.; Yang, G. A Calculation Model and Characteristics Analysis of Radio Wave Propagation in Rectangular Shed Tunnel. In Proceedings of the 10th International Symposium on Antennas, Propagation, and EM Theory (ISAPE), Xian, China, 22–26 October 2012; pp. 535–539. [Google Scholar]
- Wang, H.; Yu, F.R.; Zhu, L.; Tang, T.; Ning, B. Finite-State Markov Modeling for Wireless Channels in Tunnel Communication-Based Train Control Systems. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1083–1090. [Google Scholar] [CrossRef]
- Guan, K.; Zhong, Z.; Alonso, J.I.; Briso-Rodríguez, C. Measurement of Distributed Antenna Systems at 2.4 GHz in a Realistic Subway Tunnel Environment. IEEE Trans. Veh. Technol. 2011, 61, 834–837. [Google Scholar] [CrossRef]
- Saleem, A.; He, Y. Investigation of Massive MIMO Channel Spatial Characteristics for Indoor Subway Tunnel Environment. In Proceedings of the Computing, Communications and IoT Applications (ComComAp), Shenzhen, China, 26–28 November 2021; pp. 162–167. [Google Scholar]
- Bashir, S. Effect of Antenna Position and Polarization on UWB Propagation Channel in Underground Mines and Tunnels. IEEE Trans. Antennas Propag. 2014, 62, 4771–4779. [Google Scholar] [CrossRef]
- Yu, D.; Yue, G.; Wei, N.; Yang, L.; Tan, H.; Liang, D.; Gong, Y. Empirical Study on Directional Millimeter-Wave Propagation in Railway Communications between Train and Trackside. IEEE J. Sel. Areas Commun. 2020, 38, 2931–2945. [Google Scholar] [CrossRef]
- Ahmed, N.; Hua, B.; Zhu, Q.; Mao, K.; Bao, J. Novel GBSM for Non-Stationary V2V Channels Allowing 3D Velocity Variations. Sensors 2021, 21, 3271. [Google Scholar] [CrossRef]
- Jembre, Z.; Jung, Y.W.-y.; Attique, M.; Paul, R.; Kim, B. Mobile Broadband Performance Evaluation: Analysis of National Reports. Electronics 2022, 11, 3. [Google Scholar]
- Wenxuan, L.; Liu, Y.; Li, X.; Shen, Y. Three-dimensional cooperative localization via space-air-ground integrated networks. China Commun. 2022, 19, 253–263. [Google Scholar]
- Ghazal, A.; Yuan, Y.; Wang, C.-X.; Zhang, Y.; Yao, Q.; Zhou, H.; Duan, W. A Non-Stationary IMT-Advanced MIMO Channel Model for High-Mobility Wireless Communication Systems. IEEE Trans. Wirel. Commun. 2016, 16, 2057–2068. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.X.; Huang, J.; Wang, H.; Gao, X. A General 3D Space-Time-Frequency Non-Stationary THz Channel Model for 6G Ultra-Massive MIMO Wireless Communication Systems. IEEE J. Sel. Areas Commun. 2021, 39, 1576–1589. [Google Scholar] [CrossRef]
- Ziwei, H.; Cheng, X.; Yin, X. A General 3D Non-Stationary 6G Channel Model with Time-Space Consistency. IEEE Trans. Commun. 2022, 70, 3436–3450. [Google Scholar]
- Liu, Y.; Wang, C.-X.; Huang, J.; Sun, J.; Zhang, W. Novel 3-D Nonstationary mmWave Massive MIMO Channel Models for 5G High-Speed Train Wireless Communications. IEEE Trans. Veh. Technol. 2018, 68, 2077–2086. [Google Scholar] [CrossRef]
- Saleem, A.; He, Y.; Xu, Y.; Chen, Z.N. A Non-Stationary 3D-GBSM V2V Channel Model for Wideband Massive MIMO Systems. IEEE Commun. Lett. 2023, 27, 19–23. [Google Scholar] [CrossRef]
- Wang, C.-X.; Ghazal, A.; Ai, B.; Liu, Y.; Fan, P. Channel Measurements and Models for High-Speed Train Communication Systems: A Survey. IEEE Commun. Surv. Tutor. 2015, 18, 974–987. [Google Scholar] [CrossRef]
- Bian, J.; Sun, J.; Wang, C.-X.; Feng, R.; Huang, J.; Yang, Y.; Zhang, M. A WINNER+ based 3-D Non-Stationary Wideband MIMO Channel Model. IEEE Trans. Wirel. Commun. 2017, 17, 1755–1767. [Google Scholar] [CrossRef]
- Ranjan, A.; Sahu, H.; Misra, P. Modeling and Measurements for Wireless Communication Networks in Underground Mine Environments. Measurement 2020, 149, 106980. [Google Scholar] [CrossRef]
- Rizzo, C.; Lera, F.; Villarroel, J.L. 3-D Fadings Structure Analysis in Straight Tunnels Toward Communication, Localization, and Navigation. IEEE Trans. Antennas Propag. 2019, 67, 6123–6137. [Google Scholar] [CrossRef]
- Kalyankar, S.K.; Lee, Y.H.; Meng, Y.S. Two-Slope Path Loss Model for Curved-Tunnel Environment with Concept of Break Point. IEEE Intell. Transp. Syst 2020, 22, 7850–7859. [Google Scholar] [CrossRef]
- Celaya-Echarri, M.; Azpilicueta, L.; Lopez-Iturri, P.; Picallo, I.; Aguirre, E.; Astrain, J.J.; Villadangos, J.; Falcone, F. Wireless Channel Characterization and System Analysis of Complex Utility Tunnel Environments. Proceedings 2019, 42, 53. [Google Scholar]
- Saleem, A.; Xu, Y.; Khan, R.; Rasheed, I.; Jaffri, Z.; Layek, M. Statistical Characteristics of 3D MIMO Channel Model for Vehicle-to-Vehicle Communications. Wirel. Commun. Mob. Comput. 2022, 22, 9090494. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Z.; Wu, L.; Dang, J.; Gui, G. A 3-D Non-Stationary Wideband Geometry-Based Channel Model for MIMO Vehicle-to-Vehicle Communications in Tunnel Environments. IEEE Trans. Veh. Technol. 2019, 68, 6257–6271. [Google Scholar] [CrossRef]
- CWang, X.; Wu, S.; Bai, L.; You, X.; Wang, J.; Chih-Lin, I. Recent Advances and Future Challenges for Massive MIMO Channel Measurements and Models. Sci. China Inf. Sci. 2016, 59, 1–16. [Google Scholar]
- Rottenberg, F.; Choi, T.; Luo, P.; Zhang, C.J.; Molisch, A.F. Performance Analysis of Channel Extrapolation in fDD Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2020, 19, 2728–2741. [Google Scholar] [CrossRef]
- Kristem, V.; Sangodoyin, S.; Bas, C.U.; Käske, M.; Lee, J.; Schneider, C.; Zhang, C.J.; Thomä, R.S.; Molisch, A.F. 3D MIMO Outdoor-to-Indoor Propagation Channel Measurement. IEEE Trans. Wirel. Commun. 2017, 16, 4600–4613. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Yu, Y.; Xu, R.; Zheng, Q.; Zhang, P. 3-D MIMO: How much does it meet our expectations observed from channel measurements? IEEE J. Sel. Areas Commun. 2017, 35, 1887–1903. [Google Scholar] [CrossRef]
- Gao, X.; Edfors, O.; Rusek, F.; Tufvesson, F. Massive MIMO Performance Evaluation based on Measured Propagation Data. IEEE Trans. Wirel. Commun. 2015, 14, 3899–3911. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Z.; Zhang, Y.; Xi, J.; Zhao, X.; Gui, G. 3D MIMO for 5G NR: Several Observations from 32 to Massive 256 Antennas based on Channel Measurement. IEEE Commun. Mag. 2018, 56, 62–70. [Google Scholar] [CrossRef]
- Huang, J.; Wang, C.-X.; Feng, R.; Sun, J.; Zhang, W.; Yang, Y. Multi-Frequency mmWave Massive MIMO Channel Measurements and Characterization for 5G Wireless Communication Systems. IEEE J. Sel. Areas Commun. 2017, 35, 1591–1605. [Google Scholar] [CrossRef]
- Payami, S.; Tufvesson, F. Channel Measurements and Analysis for very Large Array Systems at 2.6 GHz. In Proceedings of the 6th European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 2012; pp. 433–437. [Google Scholar]
- Yin, X.; Wang, S.; Zhang, N.; Ai, B. Scatterer Localization using Large-Scale Antenna Arrays based on a Spherical Wave-Front Parametric Model. IEEE Trans. Wirel. Commun. 2017, 10, 6543–6556. [Google Scholar] [CrossRef]
- Liu, L.; Matolak, D.W.; Tao, C.; Lu, Y.; Ai, B.; Chen, H. Geometry based Large Scale Attenuation over Linear Massive MIMO Systems. In Proceedings of the 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–5. [Google Scholar]
- Chen, J.; Yin, X.; Cai, X.; Wang, S. Measurement-based Massive MIMO Channel Modeling for Outdoor LoS and NLoS Environments. IEEE Access 2017, 5, 2126–2140. [Google Scholar] [CrossRef]
- Jiang, Y.; Zheng, G.; Yin, X.; Saleem, A.; Ai, B. Performance Study of Millimetre-Wave MIMO Channel in Subway Tunnel using Directional Antennas. IET Microw. Antennas Propag. 2017, 12, 833–839. [Google Scholar] [CrossRef]
- Briso-Rodríguez, C.; Guan, K.; Matolak, D.W.; Berbineau, M. Guest Editorial Special Section on Smart Rail Mobility: Communications, Signaling, and Emerging Technologies. IEEE Trans. Veh. 2019, 68, 2021–2023. [Google Scholar]
- Wang, K.; Liu, L.; Zhang, J.; Liu, M. Channel Fading Characteristics of Hyperloop Scenarios Based on Ray-Tracing Model. Symmetry 2023, 15, 567. [Google Scholar] [CrossRef]
- Pi, Z.; Khan, F. An Introduction to Millimeter-Wave Mobile Broadband Systems. IEEE Commun. Mag. 2011, 49, 6. [Google Scholar] [CrossRef]
- Perahia, E.; Cordeiro, C.; Park, M.; Yang, L.L. IEEE 802.11 ad: Defining the Next Generation Multi-GBPS Wi-Fi. In Proceedings of the 7th Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2010; pp. 1–5. [Google Scholar]
- Elkholy, K.; Lichtblau, J.; Reissland, T.; Weigel, R.; Koelpin, A. Channel Measurements for the Evaluation of Evolving Next Generation Wireless Railway Communication Applications. In Proceedings of the German Microwave Conference (GeMiC), Cottbus, Germany, 9–11 March 2020; pp. 120–123. [Google Scholar]
- Shay, W.-T.; Shen, K.-J.; Chen, Y.-R.; Lin, Y.-Y.; Tsai, Z.-M.; Tarng, J.-H. Millimeter-Wave Channel Modelling and Ray-Tracing Method Validation. In Proceedings of the Photonics Electromagnetics Research Symposium (PIERS-Fall), Xiamen, China, 17–20 December 2019; pp. 2612–2620. [Google Scholar]
- Ai, B.; Molisch, A.F.; Rupp, M.; Zhong, Z.-D. 5G Key Technologies for Smart Railways. Proc. IEEE 2020, 108, 856–893. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, X.; Chen, J.; Huang, Y. A Survey of Testing for 5G: Solutions, Opportunities, and Challenges. China Commun. 2019, 16, 69–85. [Google Scholar]
- Ma, W.; Qi, C.; Zhang, Z.; Cheng, J. Sparse Channel Estimation and Hybrid Precoding using Deep Learning for Millimeter Wave Massive MIMO. IEEE Trans. Commun. 2020, 68, 2838–2849. [Google Scholar] [CrossRef]
- Roy, M.; Paquelet, S.; Crussière, M. Degrees of Freedom of Ray-based Models for mm-Wave Wideband MIMO-OFDM. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Taipei, Taiwan, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Agrawal, A.; Misha, V.K.; Gupta, A.; Bansal, B. Performance Analysis of Beamforming Aided Uncorrelated mm-Wave MIMO System for IEEE 802.15. 3C Standard. Phys. Commun. 2020, 41, 101114. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, C.-X.; Lopez, C.F.; Goussetis, G.; Yang, Y.; Karagiannidis, G.K. 3D Non-Stationary Wideband Tunnel Channel Models for 5G High-Speed Train Wireless Communications. IEEE Trans. Intell. Transp. Syst. 2019, 21, 259–272. [Google Scholar] [CrossRef]
- MacCartney, G.R.; Rappaport, T.S. Millimeter-Wave Base Station Diversity for 5G Coordinated Multipoint (CoMP) Applications. IEEE Trans. Wirel. Commun. 2019, 18, 3395–3410. [Google Scholar] [CrossRef]
- Kammoun, A.; Alouini, M.-S. Elevation Beamforming with Full Dimension MIMO Architectures in 5G Systems: A Tutorial. IEEE Commun. Surv. Tutor. 2019, 21, 3238–3273. [Google Scholar]
- Fu, Z.; Cui, H.; Geng, S.; Zhao, X. 5G Millimeter Wave Channel Modeling and Simulations for a High-Voltage Substation. In Proceedings of the IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 1822–1826. [Google Scholar]
- Zhou, Z.; Chen, X.; Zhang, Y.; Mumtaz, S. Blockchain-Empowered Secure Spectrum Sharing for 5G Heterogeneous Networks. IEEE Netw. 2020, 34, 24–31. [Google Scholar] [CrossRef]
- Ma, Z.; Ai, B.; He, R.; Wang, G.; Niu, Y.; Zhong, Z. A Wideband Non-Stationary Air-to-Air Channel Model for UAV Communications. IEEE Trans. Veh. Technol. 2019, 69, 1214–1226. [Google Scholar] [CrossRef]
- Jiang, H.; Gui, G. Channel Modeling in 5G Wireless Communication Systems; Springer: New York, NY, USA, 2020. [Google Scholar]
- Wu, S.; Wang, C.-X.; Aggoune, E.-H.M.; Alwakeel, M.M. A Novel Kronecker-Based Stochastic Model for Massive MIMO Channels. In Proceedings of the IEEE/CIC International Conference on Communications in China. (ICCC), Shenzhen, China, 2–4 November 2015; pp. 1–6. [Google Scholar]
- Peng, B.; Guan, K.; Kuter, A.; Rey, S.; Patzold, M.; Kuerner, T. Channel Modeling and System Concepts for Future Terahertz Communications: Getting Ready for Advances Beyond 5G. IEEE Veh. Technol. Mag. 2020, 15, 136–143. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, X.; Zhang, B.; Zhang, Y.; Niu, Z.; Kuang, N.; Chen, W.; Li, L.; Li, S. A Survey on Terahertz Communications. China Commun. 2019, 16, 1–35. [Google Scholar] [CrossRef]
- Juyal, J.F.; Zajić, A. THz Channel Characterization of Chip-to-Chip Communication in Desktop Size Metal Enclosure. IEEE Trans. Antennas Propag. 2019, 67, 7550–7560. [Google Scholar]
- Choi, Y.; Choi, J.-W.; Cioffi, J.M. A Geometric-Statistic Channel Model for THz Indoor communications. J. Infrared Millim. Terahertz Waves 2013, 34, 456–467. [Google Scholar] [CrossRef]
- Han, C.; Bicen, A.O.; Akyildiz, I.F. Multi-Ray Channel Modeling and Wideband Characterization for Wireless Communications in the Terahertz Band. IEEE Trans. Wirel. Commun. 2014, 14, 2402–2412. [Google Scholar] [CrossRef]
- Piao, Z.; Qiao, D.; Wu, Q.; Wu, Y. Throughput Maximization for Active Intelligent Reflecting Surface Aided Wireless Powered Communications. IEEE Wirel. Commun. Lett. 2022, 11, 992–996. [Google Scholar]
- Ravi, J.; Koch, T. Capacity per Unit-Energy of Gaussian Many-Access Channels. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 2763–2767. [Google Scholar]
- Ali, M.S.; Li, Y.; Chen, S.; Lin, F. On Improved DFT-based Low-Complexity Channel Estimation Algorithms for LTE-based Uplink NB-IoT Systems. Comput. Commun. 2020, 149, 214–224. [Google Scholar] [CrossRef]





| Sr. No | Acronym | Full Name |
|---|---|---|
| 1 | AAoA | Azimuth Angle of Arrival |
| 2 | AAoD | Azimuth Angle of Departure |
| 3 | CBTC | Communication-Based Train Control |
| 4 | CL | Coupling Loss |
| 5 | CPML | Convolutional Perfectly Matched Layer |
| 6 | CDM | Code-Division Multiplexing |
| 7 | CSI | Channel Status Information |
| 8 | CFL | Courant–Friedrichs–Lewy |
| 9 | CAPEX | Capital Expenditure |
| 10 | DAS | Distributed Antenna System |
| 11 | DMCs | Dense Multipath Components |
| 12 | DPA | Dual Polarized Antenna |
| 13 | D2D | Device-to-Device |
| 14 | DSPN | Deterministic and Stochastic Petri Net |
| 15 | EAoA | Elevation Angle of Arrival |
| 16 | EAoD | Elevation Angle of Departure |
| 17 | ELF | Extremely Low Frequency |
| 18 | EoD | Elevation of Departure |
| 19 | ERTMS | European Railway Traffic Management System |
| 20 | EP | Equal Power |
| 21 | FDTD | Finite Difference Time Domain |
| 22 | FDM | Frequency-Division Multiplexing |
| 23 | FM | Frequency Modulation |
| 24 | GBSB | Geometrically-Based Single-Bounce |
| 25 | HSR | High-Speed Railway |
| 26 | HFSS | High-Frequency Structure Simulator |
| 27 | ISM | Industrial, Scientific, and Medical |
| 28 | IRS | Intelligent Reconfigurable Surface |
| 29 | LTE-M | Long-Term Evolution for Metro |
| 30 | LCX | Leaky Coaxial Cable |
| 31 | LAS | Likelihood Ascent Search |
| 32 | LSF | Large Scale Fading |
| 33 | LoS | Line of Sight |
| 34 | MIMO | Multi-Input Multi-Output |
| 35 | MMSE | Minimum Mean Squared Error |
| 36 | mmWave | MillimeterWave |
| 37 | NLoS | Non-Line of Sight |
| 38 | NFV | Network Function Virtualization |
| 39 | ODA | Omnidirectional Array |
| 40 | OPEX | Operational Expenditure |
| 41 | OFDM | Orthogonal Frequency-Division Multiplexing |
| 42 | PL | Path Loss |
| 43 | PAS | Power Azimuth Spectrum |
| 44 | PAP | Power Angular Profile |
| 45 | PDP | Power Delay Profile |
| 46 | PED | Personal Emergency Device |
| 47 | QoS | Quality of Service |
| 48 | RAT | Radio Access Technology |
| 49 | RF | Radio Frequency |
| 50 | SISO | Single-Input Single-Output |
| 51 | SD | Sphere Decoding |
| 52 | SIC | Soft Interference Cancellation |
| 53 | SMCs | Specular Multipath Components |
| 54 | STF | Space–Time Frequency |
| 55 | SDN | Software Defined Networking |
| 56 | TDM | Time-Division-Multiplexing |
| 57 | TTA | Through-the-Air |
| 58 | TTE | Through-the-Earth |
| 59 | TTW | Through-the-Wire |
| 60 | TS | Tabu Search |
| 61 | TCF | Temporal Correlation Function |
| 62 | UAV | Unmanned Aerial Vehicle |
| 63 | UCA | Uniform Cylindrical Array |
| 64 | ULA | Uniform Linear Array |
| 65 | UHF | Ultra-High Frequency |
| 66 | UPA | Uniform-Planar Array |
| 67 | VHF | Very High Frequency |
| 68 | VHFFM | Very High Frequency-Frequency Modulation |
| 69 | VPE | Vector Parabolic Equation |
| 70 | WLAN | Wireless Local Area Network |
| 71 | WSN | Wireless Sensor Network |
| 72 | WPAN | Wireless Personal Area Network |
| 73 | XPD | Cross-Polarization Discrimination |
| Environment Dimensions in Meter | Measurement Frequency | Antenna Polarization | Antenna Configuration | Antenna Bandwidth | Scenarios | Path Loss Exponent | Ref. | ||
|---|---|---|---|---|---|---|---|---|---|
| Free Space | — | — | — | — | — | 2 | [67] | ||
| In Building, LoS | 1.6–1.8 | ||||||||
| In Building, Obstructed | 4–6 | ||||||||
| Straight Tunnel | 7.5 × 4 × 2000 | 900 MHz | Linear | SISO | Omni-directional | LoS | 3.87–4.44 | [68] | |
| 7 × 3.7 × 120 | 2.9–3.7 | ||||||||
| 4.2 × 3 × 10,000 | 1.87–2.37 | ||||||||
| Straight Tunnel (3.34 × 2.6 × 259) | 900 MHz | Linear | SISO | Omni-directional | LoS | 4.2–4.49 | [68] | ||
| 1.8 GHz | 2.12–2.46 | ||||||||
| CANMET Level 70 m (2.5 × 4 × 70) | 2.3–2.5 GHz | Linear | SISO | Omni-directional | LoS | 2.03 | [69,70] | ||
| NLoS | 4.62 | ||||||||
| 5.7–5.9 GHz | LoS | 2.22 | |||||||
| NLoS | 3.52 | ||||||||
| CANMET Level 40 m (5 × 5 × 75) | 2.3–2.5 GHz | Linear | SISO | Omni-directional | LoS | 2.13–2.33 | [71] | ||
| NLoS | |||||||||
| CANMET Level 40 m (4 × 5 × 8) | 57.24–59.4 GHz | Linear | SISO | Horn–Horn | Omni-directional and Horn | LoS | 1.82 | [72] | |
| Omni–Horn | 1.28 | ||||||||
| CANMET Level 70 m (2.5 × 4 × 8) | Horn–Horn | 1.45 | |||||||
| Omni–Horn | 1.41 | ||||||||
| CANMET Level 70 m (2.5 × 4 × 10) | 3–10 GHz | Linear | SISO | Omni-directional | LoS | 2.11 | [73] | ||
| NLoS | 3.00 | ||||||||
| Directional | LoS | 2.01 | |||||||
| NLoS | 6.16 | ||||||||
| CANMET Level 40 m (5 × 5 × 25) | 2.3–2.5 GHz | Linear | 2 × 2 MIMO | Directional Patch | LoS | 1.73 | [73] | ||
| NLoS | 3.03 | ||||||||
| CANMET Level 4 m (5 × 5 × 10) | 57–64 GHz | Linear | 2 × 2 MIMO Patch | Directional | LoS | 1.48 | [74] | ||
| NLoS | 2.40 | ||||||||
| CANMET Level 70 m (2.5 × 4 × 10) | 5.7–5.9 GHz | Linear | 2 × 2 MIMO | Vivaldi | LoS | 2.1 | [75] | ||
| CANMET Level 40 m (3.4 × 4.6 × 30) | 2.35–2.55 GHz | Linear | 4 × 4 MIMO CMPA | Directional | LoS | 1.18 | [76] | ||
| NLoS | 2.56 | ||||||||
| 4 × 4 MIMO PMPA | LoS | 1.29 | |||||||
| NLoS | 3.8 | ||||||||
| Carrier Frequency | Tunnel Type | Research Method | Main Content | Ref. |
|---|---|---|---|---|
| 400 MHz | Rectangular concrete subway tunnel | Ray Tracing | FDTD method was used to estimate the path gain | [96] |
| 900 MHz | Straight rectangular tunnel | Ray Tracing | RMS-DS for vertically and horizontally receiving antennas | [97] |
| 28 GHz | Nantong subway tunnel | Ray Tracing | MIMO system performance under LoS condition | [98] |
| 25 GHz | Subway tunnel, Line 8 in Seoul, Korea | Use of ray tracing after comparing with measurement results | Study the millimeter wave, propagation characteristics of straight tunnels and curved tunnels, like PL, AoA, AoD by ray tracing | [99,100] |
| 32.5 GHz | Subway tunnel in Korea | Ray Tracing | Study the PL and Shadowing fading under arched tunnel environment by ray tracing | [101] |
| 24 GHz | Subway tunnel | Ray Tracing | Study the effect of tunnel structure and roughness on millimeter wave propagation | [102] |
| 32.5 GHz | High-speed train tunnel | Ray Tracing | Study the propagation characteristics under arched tunnel environment by ray tracing | [62,103] |
| 60 GHz | Highway tunnel | Ray Tracing | Study the effect of vehicles of on millimeter wave propagation by ray tracing | [104] |
| 75 GHz | Railway tunnel | Ray Tracing | PL and RMS-DS | [101] |
| 38 GHz | Shanghai subway tunnel, Line 9 | Ray Tracing | PL, RMS-DS of straight and curved tunnels | [105,106] |
| Communication Networks | Design Parameters | Aims | Applications | Limitations | Ref. |
|---|---|---|---|---|---|
| Multi-Stream MIMO | IRS elements and the transmitted signal’s covariance matrix | Improvement in feasible rate | Gradient Method | Smaller IRS unit cells and indoor communications | [126] |
| MISO | Beamforming at ITS and BS | Minimize transmitted power | Particle swarm optimization algorithm | Improve SNR without CSI knowledge | [127] |
| Single-User MIMO | Optimization of IRS elements | Rank improvement | Water-filling algorithm | Power allocation and LoS scenario | [128] |
| Downlink THz-MIMO | Pre-coded and phase shift matrix of IRS | Spectral efficiency | Cross entropy, water filling, and SVD models | Substantial transmission loss | [129] |
| Downlink multi-user MISO-mmWave | Phase shift matrix of IRS and transmitted power | Improve energy efficiency and sum-rate | Sequential fractional programming | Smaller outage and coverage probability | [130] |
| IRS-based ITS | Array reflector of the Van-Atta type | QoS and RF sensing | REITS method | Increased mobility | [131] |
| Multi-antenna system | Spectral phase shift and source transmitted covariance | Strengthen secrecy | Optimization at the variable-level | Source transmitted power | [132] |
| IRS-based vehicular | IRS-based resources allocation | Probability of secrecy outage | IRS as receiving antenna in V2I and relay for V2V scenario | High number of IRS elements | [133] |
| Vehicular network | IEEE 802.11p transmission samples | Received signal power and channel prediction | Deep learning method | Various environments | [134] |
| IRS for communications with UAVs | OFDMA networks | Optimized sum-rate | Variable-level optimization | Phase shift of IRS | [135] |
| Channel Model | Operating Frequency | Antenna Configuration | Scenario | Channel Characteristics | Ref. |
|---|---|---|---|---|---|
| Multimode model | 450 MHz, 900 MHz | SISO | Rectangular subway tunnel | PDP, Field distribution | [140] |
| GBSB model | 900 MHz | MIMO | Rectangular tunnel | Rice factor, PDP, Correlation function of space-time | [141] |
| Path loss model | 2.4 GHz, 5 GHz | SISO | Subway tunnel | RMS-DS, PL, Channel capacity, Channel stationarity | [142] |
| WINNER model | 5.8 GHz | MIMO | Subway tunnel | AoA, AoD, PL, Delays, Fast fading | [143] |
| Deterministic Physics-based UWB | 5.8 GHz | SISO | Rectangular tunnel | CIR, RMS-DS, Received power | [144] |
| Multimode waveguide | 2.4 GHz | MIMO | Underground mine, Subway tunnel | PAS, Correlation, Angular properties | [145] |
| Theory of propagation-graph | 1.8 GHz | MIMO | Arched tunnel | Channel capacity, Correlation coefficient, CIR, Channel coefficients | [146] |
| Geometrical optics model | 900 MHz | SISO | Underground mine | SSF,LSF | [147] |
| FSMM | 2.412 GHz | SISO | Subway tunnel | SNR, Distance interval, States number | [148] |
| Propagation model | 2.4 GHz | SISO | Subway tunnel | Fast fading, PL, SF, AFD, LCF | [149] |
| Bartlett model | 3.5 GHz | MIMO | Subway tunnel | PDP. Angular spread, Condition number | [150] |
| Path loss model | 2.49–4 GHz | MIMO | Rectangular tunnel | Delay spread, PL | [151] |
| Channel Sounder | Scenario | Antenna Array Configuration | Carrier Frequency | Channel Characteristics | Ref. |
|---|---|---|---|---|---|
| RUSK-Hyeff | O2I | Tx ULA/Rx DPA (16 × 24)Tx ULA/Rx DPA(16 × 24) Tx ULA/Rx DPA (16 × 24) | 2.53 GHz | Capacity, elevations, angles, AS Capacity, elevations, angles, AS Capacity, elevations, angles, AS | [171] |
| PropSound CS | O2I, outdoor | Tx UPA/Rx ODA (32 × 56) Tx UPA/Rx ODA(32 × 56) Tx UPA/Rx ODA (32 × 56) | 3.5 GHz | Capacity, spatial correlation, eigenvalues, AS, PAS | [172] |
| 1lVNA and RUSK-LUND | Outdoor | Tx UCA and ULA (64 and 128) Tx UCA and ULA(64 and 128) Tx UCA and ULA (64 and 128) | 2.6 GHz | Capacity, SVS | [173] |
| PropSound CS | O2I, outdoor | Tx UPA/Rx ODA (256 × 16) Tx UPA/Rx ODA(256 × 16) Tx UPA/Rx ODA (256 × 16) | 3.5, 6 GHz | PDP, AS, PAS, eigenvalue spread, capacity | [174] |
| VNA | Indoor | Tx Horn /Rx Biconical (51 × 51, 76 × 76, 91 × 91, 121 × 121) | 11, 16, 28, 38 GHz | DS, Power, AS, AoA, EoA, spatial correlation | [175] |
| VNA | Outdoor | Tx ULA (128) | 2.6 GHz | K-factor, spatial correlation, power, PAS, eigenvalue | [176] |
| 1lMedav sliding-correlator | Indoor | Tx ODA/Rx UPA (1 × 121) Tx ODA/Rx UPA(1 × 121) Tx ODA/Rx UPA (1 × 121) | 9.5 GHz | AoD, AoA, EoA, EoD | [177] |
| Constructed | Outdoor | Tx ULA/Rx ULA (144 × 144) Tx ULA/Rx ULA(144 × 144) Tx ULA/Rx ULA (144 × 144) | 1.4725 GHz | Path loss, PAS | [178] |
| VNA | Indoor | Tx ODA/Rx UPA (1 × 1600) Tx ODA/Rx UPA(1 × 1600) Tx ODA/Rx UPA (1 × 1600) | 15 GHz | K-factor, AOA, power, AS, cluster number, EoA | [179] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleem, A.; Zhang, X.; Xu, Y.; Albalawi, U.A.; Younes, O.S. A Critical Review on Channel Modeling: Implementations, Challenges and Applications. Electronics 2023, 12, 2014. https://doi.org/10.3390/electronics12092014
Saleem A, Zhang X, Xu Y, Albalawi UA, Younes OS. A Critical Review on Channel Modeling: Implementations, Challenges and Applications. Electronics. 2023; 12(9):2014. https://doi.org/10.3390/electronics12092014
Chicago/Turabian StyleSaleem, Asad, Xingqi Zhang, Yan Xu, Umar A. Albalawi, and Osama S. Younes. 2023. "A Critical Review on Channel Modeling: Implementations, Challenges and Applications" Electronics 12, no. 9: 2014. https://doi.org/10.3390/electronics12092014






