Inversion of Target Magnetic Moments Based on Scalar Magnetic Anomaly Signals
Abstract
:1. Introduction
2. Principles and Methods
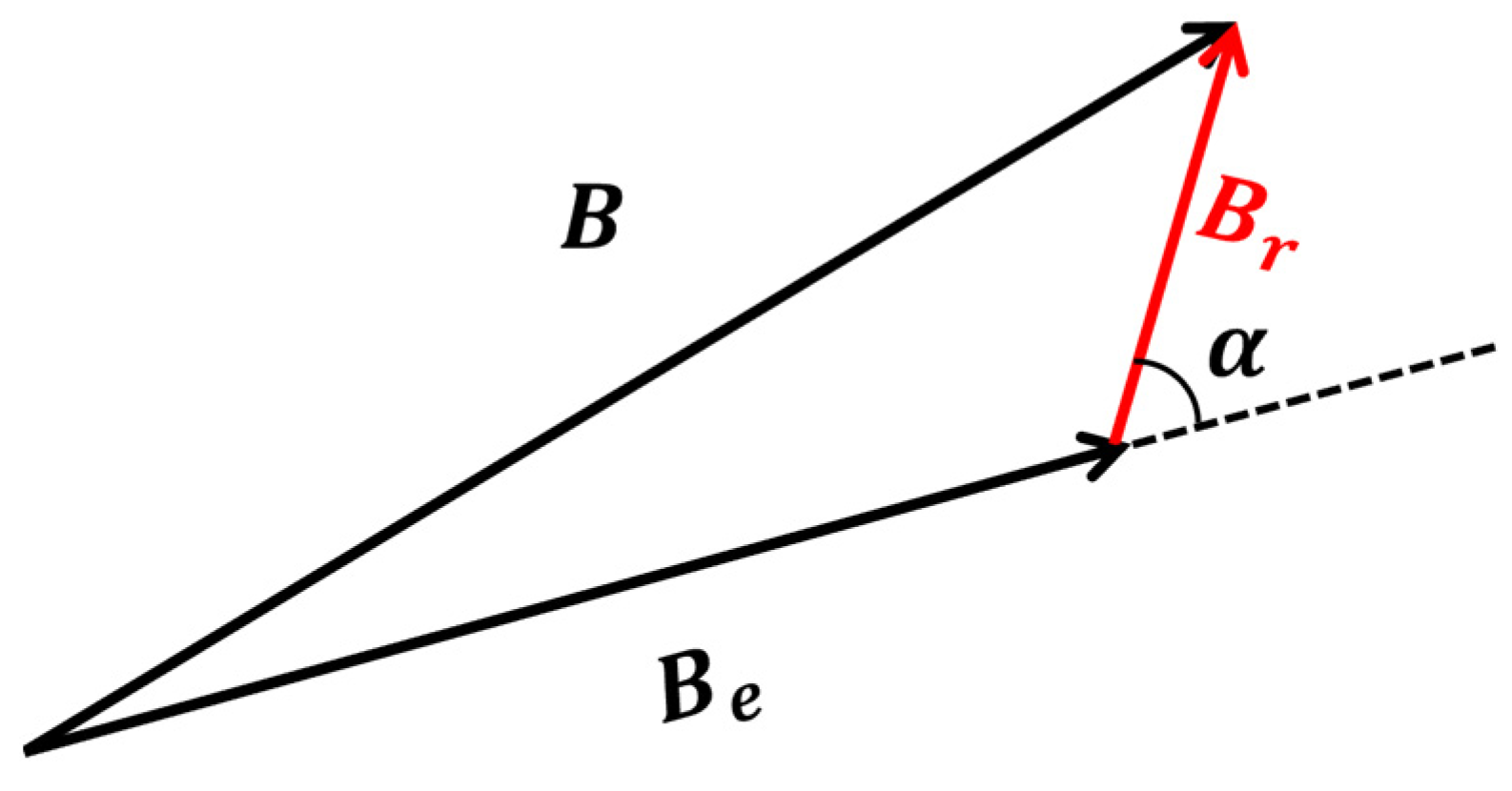
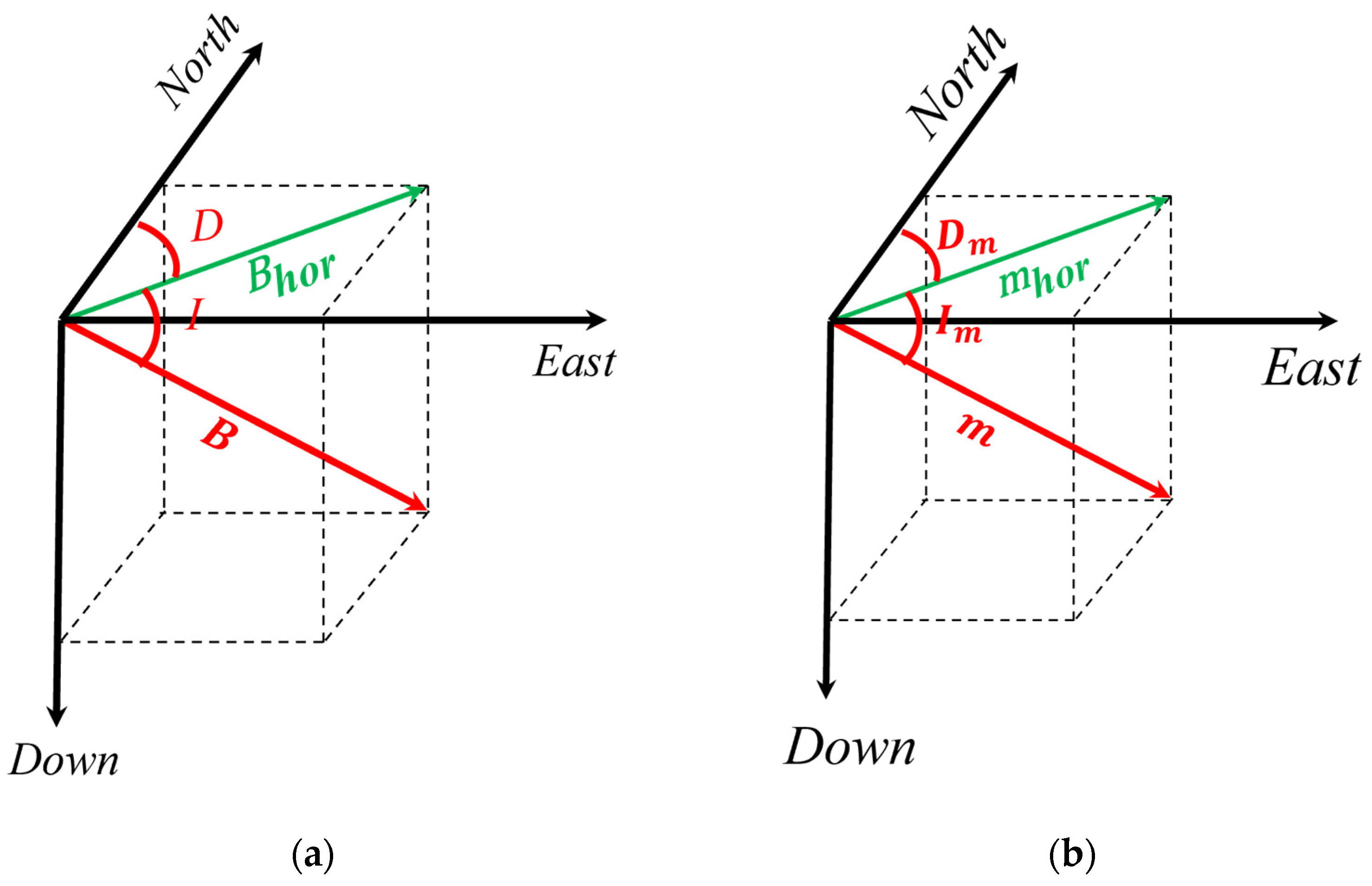
2.1. Magnetic Field Distribution of Magnetic Dipoles
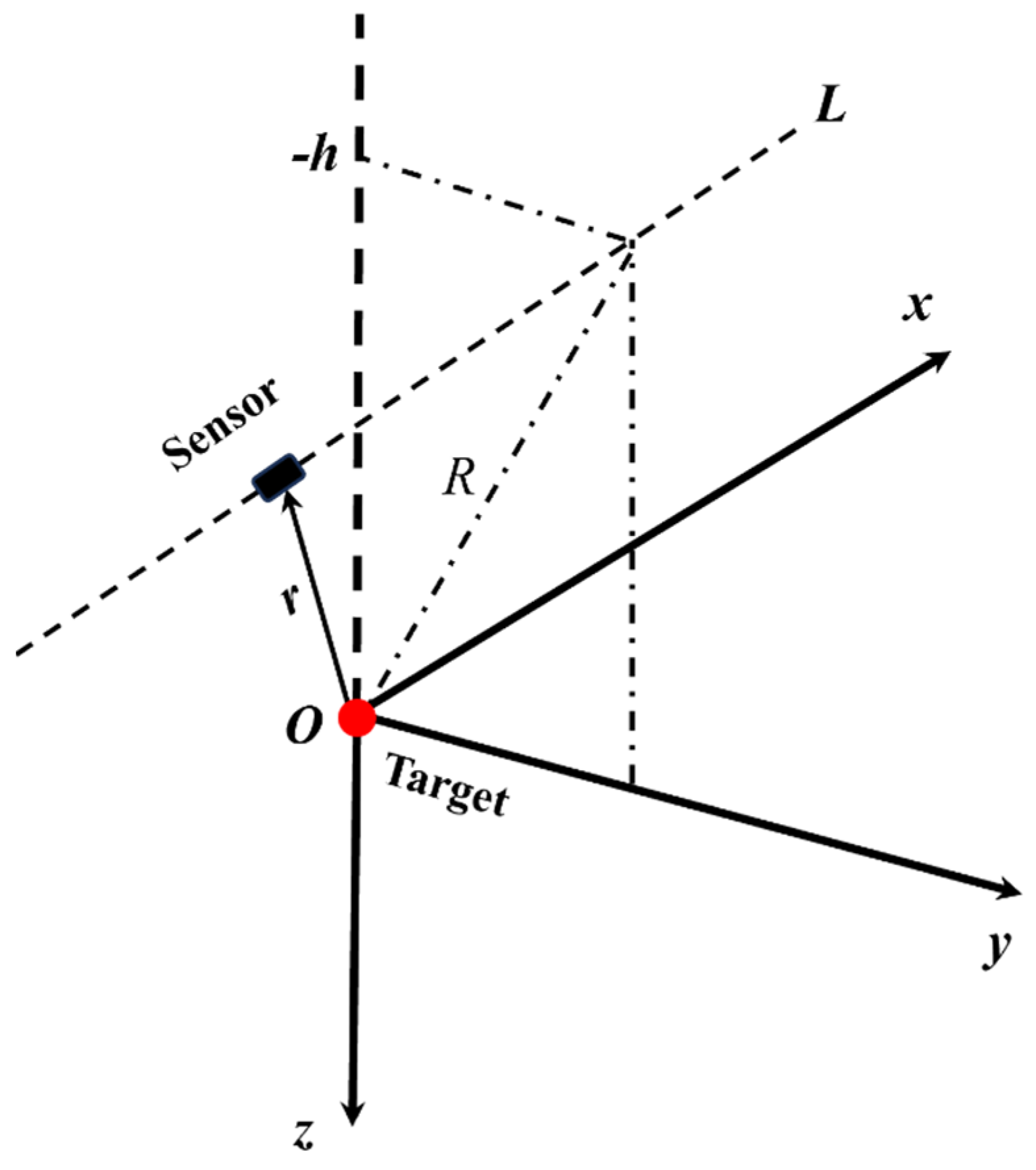
2.2. Principle of Aeromagnetic Anomaly Detection
2.3. Proposed Method
3. Results
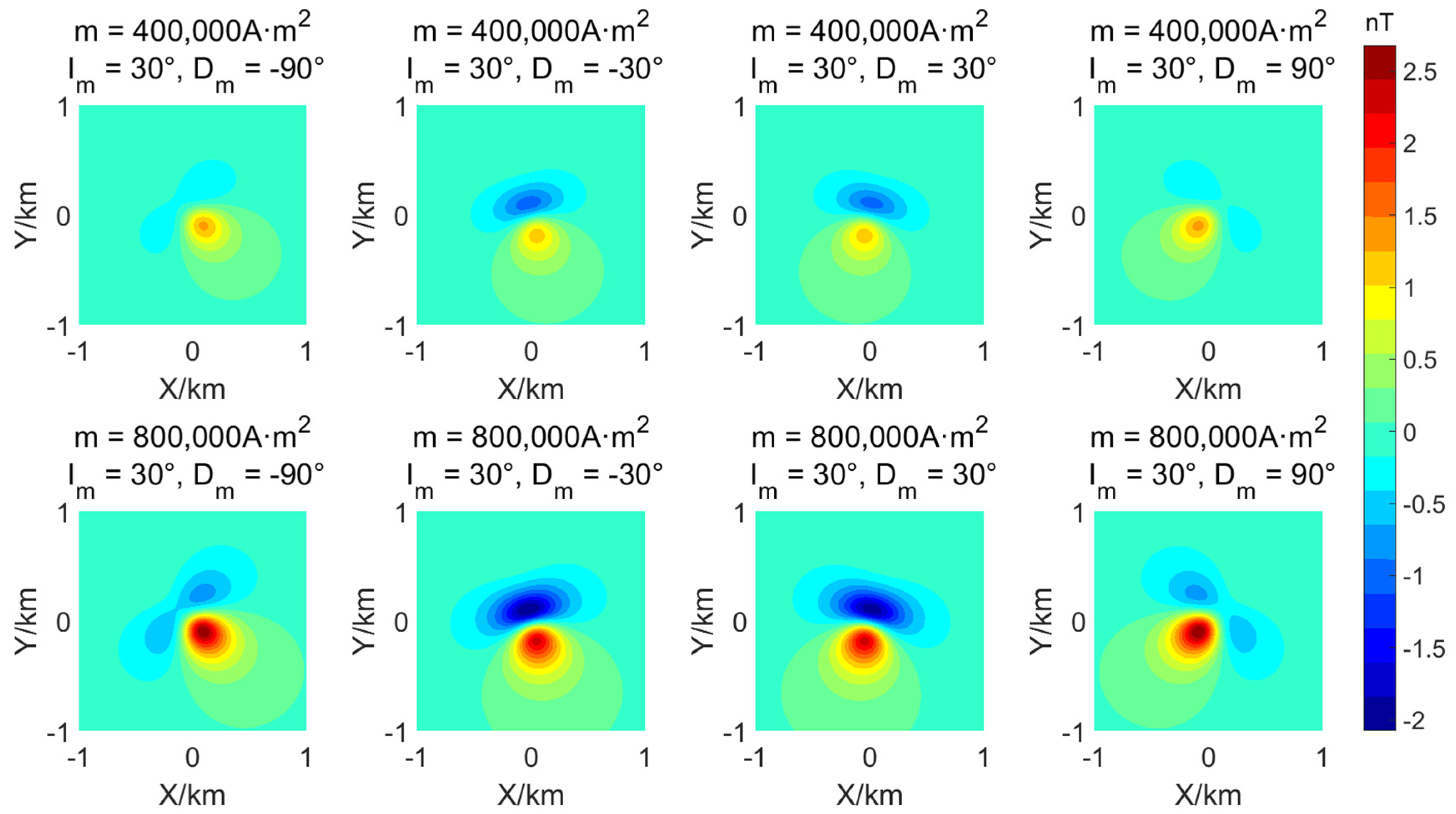
3.1. Analysis of Magnetic Moment Inversion Error
3.2. Magnetic Moment Inversion Experiment
- 1.
- The geomagnetic field is constant;
- 2.
- The airplane flies strictly on a straight course;
- 3.
- The magnetic anomaly signal is not affected by noise.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, C. Some problems concerning the magnetic anomaly detection (MAD). Chin. J. Eng. Geophys. 2007, 4, 549–553. [Google Scholar]
- Sheinker, A.; Ginzburg, B.; Salomonski, N.; Dickstein, P.A.; Frumkis, L.; Kaplan, B.-Z. Magnetic anomaly detection using high-order crossing method. IEEE Trans. Geosci. Remote Sens. 2011, 50, 1095–1103. [Google Scholar] [CrossRef]
- Gunn, P.; Dentith, M. Magnetic responses associated with mineral deposits. AGSO J. Aust. Geol. Geophys. 1997, 17, 145–158. [Google Scholar]
- Hirota, M.; Furuse, T.; Ebana, K.; Kubo, H.; Tsushima, K.; Inaba, T.; Shima, A.; Fujinuma, M.; Tojyo, N. Magnetic detection of a surface ship by an airborne LTS SQUID MAD. IEEE Trans. Appl. Supercond. 2001, 11, 884–887. [Google Scholar] [CrossRef]
- Paoletti, V.; Buggi, A.; Pašteka, R. UXO detection by multiscale potential field methods. Pure Appl. Geophys. 2019, 176, 4363–4381. [Google Scholar] [CrossRef]
- Wigh, M.D.; Hansen, T.M.; Døssing, A. Inference of unexploded ordnance (UXO) by probabilistic inversion of magnetic data. Geophys. J. Int. 2020, 220, 37–58. [Google Scholar] [CrossRef]
- Hood, P. History of aeromagnetic surveying in Canada. Lead. Edge 2007, 26, 1384–1392. [Google Scholar] [CrossRef]
- Reford, M.; Sumner, J. Aeromagnetics. Geophysics 1964, 29, 482–516. [Google Scholar] [CrossRef]
- Wynn, W.; Frahm, C.; Carroll, P.; Clark, R.; Wellhoner, J.; Wynn, M. Advanced superconducting gradiometer/magnetometer arrays and a novel signal processing technique. IEEE Trans. Magn. 1975, 11, 701–707. [Google Scholar] [CrossRef]
- Nara, T.; Suzuki, S.; Ando, S. A closed-form formula for magnetic dipole localization by measurement of its magnetic field and spatial gradients. IEEE Trans. Magn. 2006, 42, 3291–3293. [Google Scholar] [CrossRef]
- Wiegert, R.; Oeschger, J.; Tuovila, E. Demonstration of a novel man-portable magnetic STAR technology for real time localization of unexploded ordnance. In Proceedings of the OCEANS 2007, Vancouver, BC, Canada, 29 September–4 October 2007; pp. 1–7. [Google Scholar]
- Yang, Z.; Yan, S.; Chen, L.; Li, B. Ferromagnetic Object Localization Based on Improved Triangulating and Ranging. IEEE Magn. Lett. 2019, 10, 1–5. [Google Scholar] [CrossRef]
- Yin, G.; Li, P.; Wei, Z.; Liu, G.; Yang, Z.; Zhao, L. Magnetic dipole localization and magnetic moment estimation method based on normalized source strength. J. Magn. Magn. Mater. 2020, 502, 166450. [Google Scholar] [CrossRef]
- Yin, G.; Zhang, L.; Jiang, H.; Wei, Z.; Xie, Y. A closed-form formula for magnetic dipole localization by measurement of its magnetic field vector and magnetic gradient tensor. J. Magn. Magn. Mater. 2020, 499, 166274. [Google Scholar] [CrossRef]
- Xu, L.; Gu, H.; Chang, M.; Fang, L.; Lin, P.; Lin, C. Magnetic target linear location method using two-point gradient full tensor. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]
- Wiegert, R.; Oeschger, J. Generalized magnetic gradient contraction based method for detection, localization and discrimination of underwater mines and unexploded ordnance. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005; pp. 1325–1332. [Google Scholar]
- Sheinker, A.; Salomonski, N.; Ginzburg, B.; Frumkis, L.; Kaplan, B.-Z. Remote sensing of a magnetic target utilizing population based incremental learning. Sens. Actuators A Phys. 2008, 143, 215–223. [Google Scholar] [CrossRef]
- Shao, G.; Tang, Y.; Tang, L.; Dai, Q.; Guo, Y.-X. A Novel Passive Magnetic Localization Wearable System for Wireless Capsule Endoscopy. IEEE Sens. J. 2019, 19, 3462–3472. [Google Scholar] [CrossRef]
- Wang, J.; Shen, Y.; Zhao, R.; Zhou, C.; Gao, J. Estimation of dipole magnetic moment orientation based on magnetic signature waveform analysis by a magnetic sensor. J. Magn. Magn. Mater. 2020, 505, 166761. [Google Scholar] [CrossRef]
- Qin, Y.; Li, M.; Li, K.; Pan, Y.; Yang, X.; Ouyang, J. Target magnetic moment orientation estimation method based on full magnetic gradient orthonormal basis function. AIP Advances. 2022, 12. [Google Scholar] [CrossRef]
- Lemercier, D.; Salvi, A. Method and Device for Determining the Depth of a Magnetic Anomaly. U.S. Patent 3,808,519, 30 April 1974. [Google Scholar]
- Mooney, H.M. Interpretation Theory in Applied Geophysics. Science 1966, 152, 339–340. [Google Scholar] [CrossRef]
- Munschy, M.; Boulanger, D.; Ulrich, P.; Bouiflane, M. Magnetic mapping for the detection and characterization of UXO: Use of multi-sensor fluxgate 3-axis magnetometers and methods of interpretation. J. Appl. Geophys. 2007, 61, 168–183. [Google Scholar] [CrossRef]
- Tantum, S.L.; Yu, Y.; Collins, L.M. Bayesian Mitigation of Sensor Position Errors to Improve Unexploded Ordnance Detection. IEEE Geosci. Remote Sens. Lett. 2008, 5, 103–107. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Pang, H.F.; Pan, M.C.; Wan, C.B. Calibration and Compensation of Geomagnetic Vector Measurement System and Improvement of Magnetic Anomaly Detection. IEEE Geosci. Remote Sens. Lett. 2016, 13, 447–451. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 2nd ed.; Wiley: Hoboken, NJ, USA, 1975. [Google Scholar]
- Wan, C. Investigations on the Theory and Method of Magnetic Anomaly Detection. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2018. [Google Scholar]
- Tolles, W.E.; Lawson, J. Magnetic Compensation of MAD Equipped Aircraft; Airborne Instrum. Lab. Inc., Mineola NY Rept: Georgetown, TX, USA, 1950; p. 201. [Google Scholar]


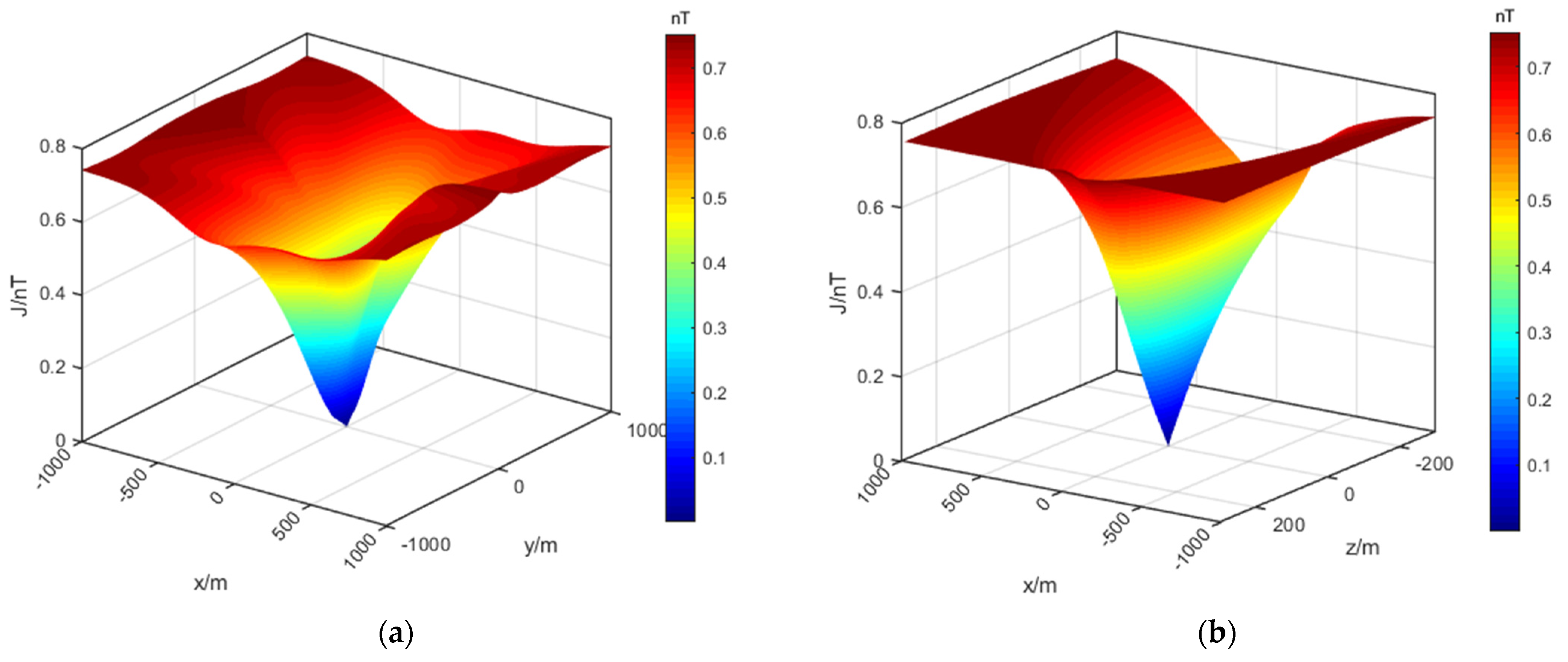
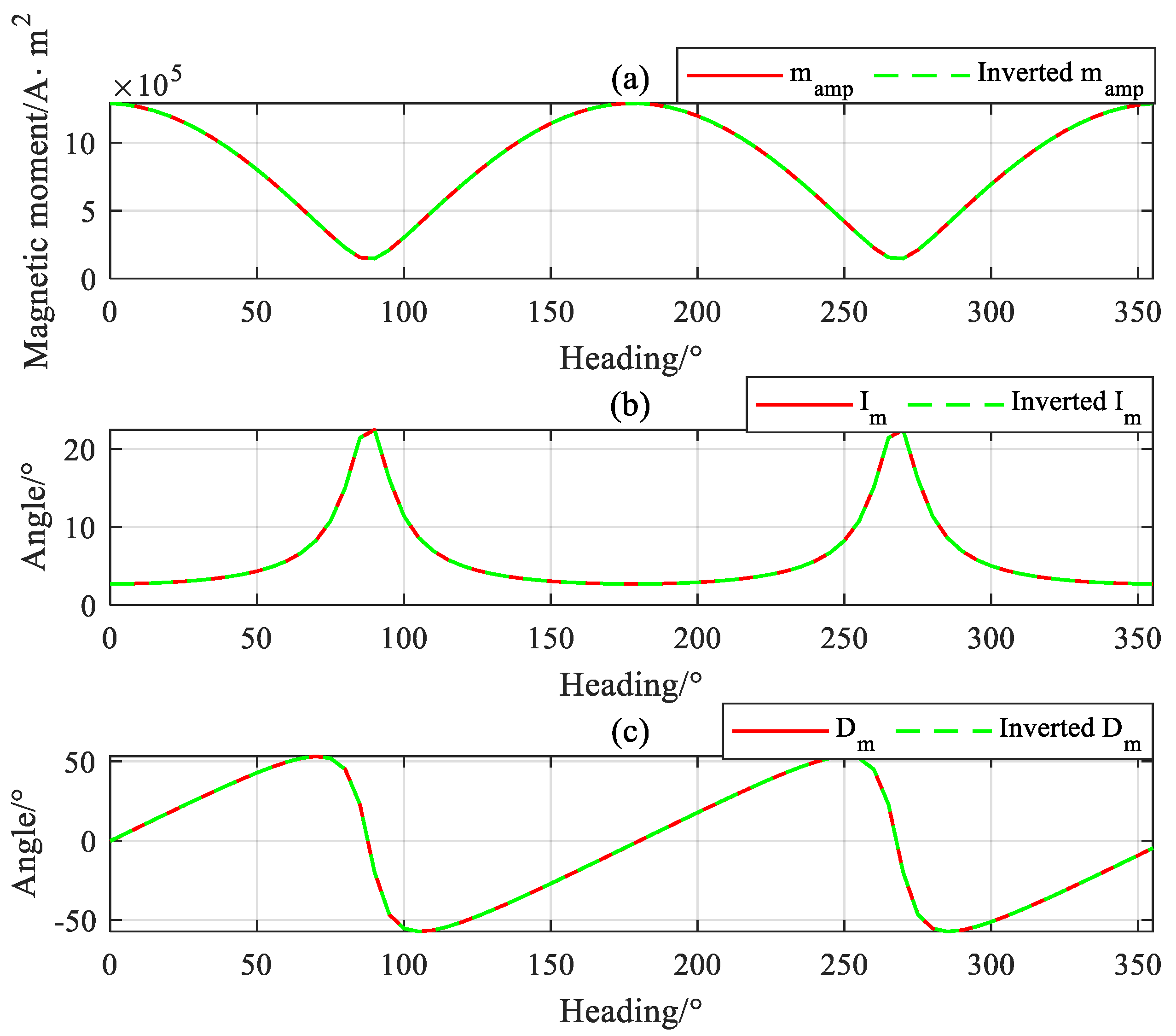
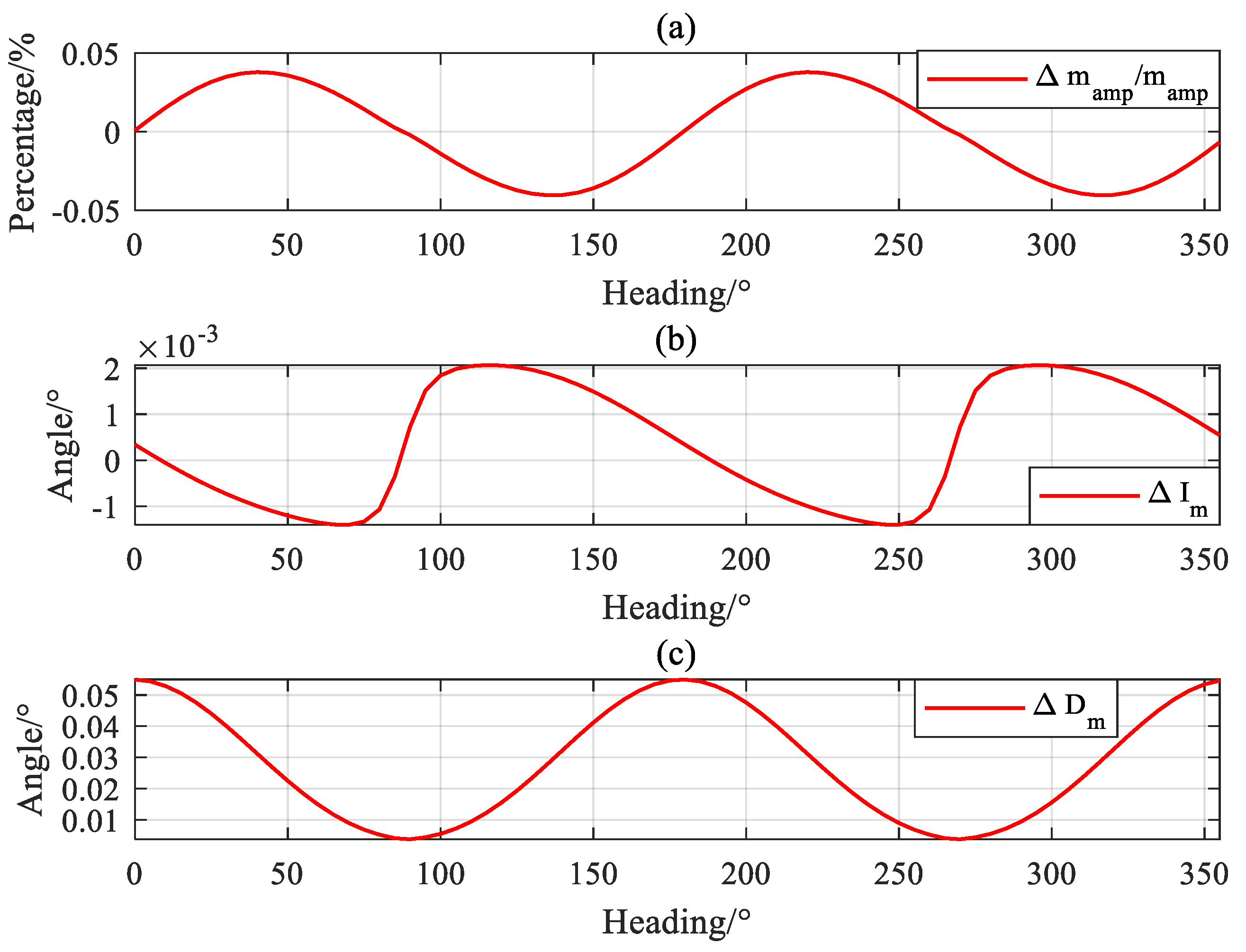


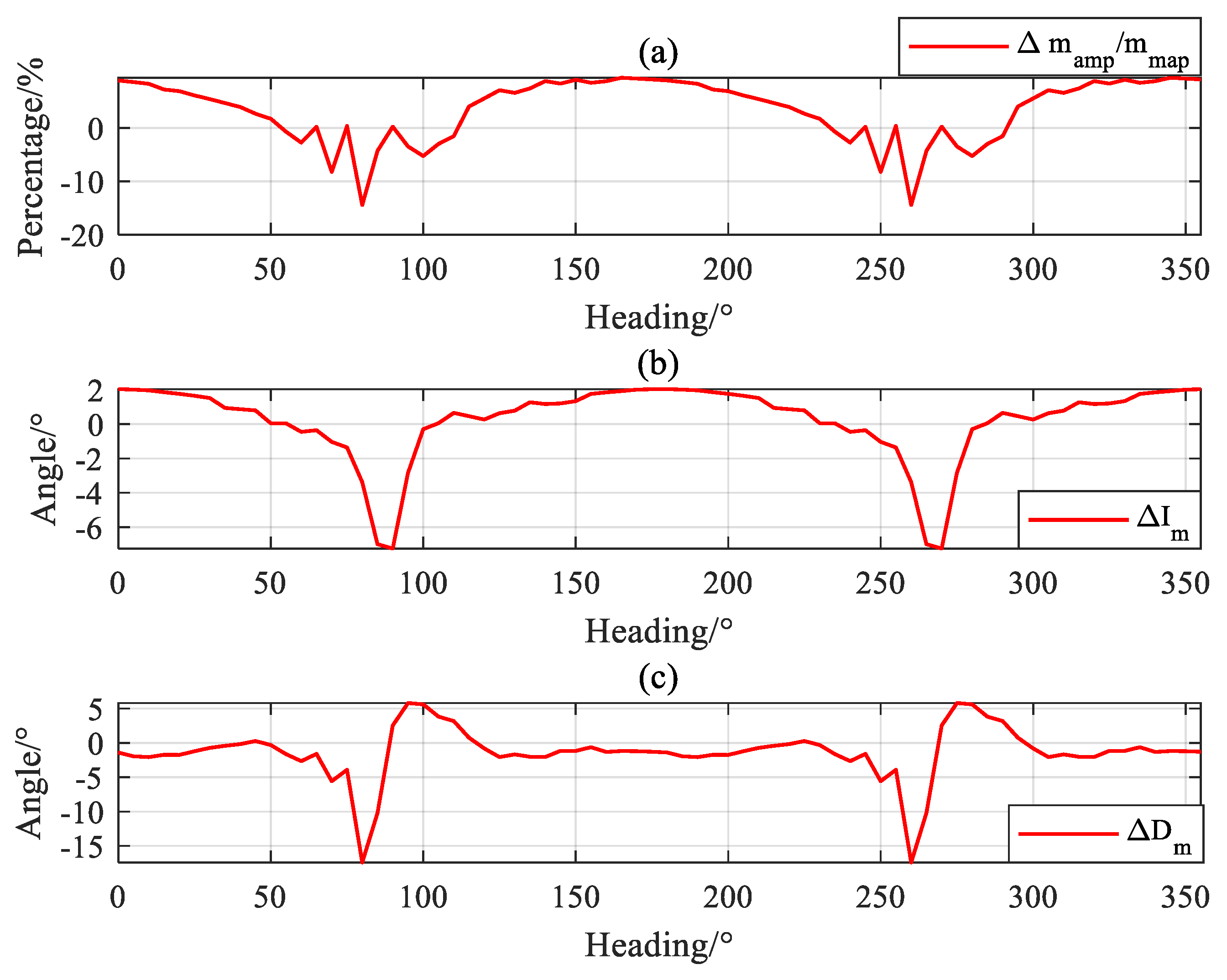
| Inversion Errors | Value |
|---|---|
| Amplitude error | 0.025% |
| Inclination error | 0.0012° |
| Deflection error | 0.0284° |
| Technical Indicators | Parameters | |
|---|---|---|
| Magnetic Sensors | Fluxgate Magnetometer | Optical Pump Magnetometer |
| Measuring range | ±10,000 nT | 15,000 nT~105,000 nT |
| Noise level | ||
| Orthogonality error | 0.5° | \ |
| Absolute accuracy | 10 nT | 2.5 nT |
| Inversion Errors | Value |
|---|---|
| Amplitude error | 5.85% |
| Inclination error | 1.58° |
| Deflection error | 2.79° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; You, X.; Liu, X.; Liu, J.; Zhu, W. Inversion of Target Magnetic Moments Based on Scalar Magnetic Anomaly Signals. Electronics 2023, 12, 4900. https://doi.org/10.3390/electronics12244900
Zhang K, You X, Liu X, Liu J, Zhu W. Inversion of Target Magnetic Moments Based on Scalar Magnetic Anomaly Signals. Electronics. 2023; 12(24):4900. https://doi.org/10.3390/electronics12244900
Chicago/Turabian StyleZhang, Ke, Xiuzhi You, Xiaodong Liu, Jiarui Liu, and Wanhua Zhu. 2023. "Inversion of Target Magnetic Moments Based on Scalar Magnetic Anomaly Signals" Electronics 12, no. 24: 4900. https://doi.org/10.3390/electronics12244900





