Short-Block-Length Low-Density Parity-Check Codes-Based Underwater Acoustic Spread-Spectrum Communication System
Abstract
:1. Introduction
2. LDPC Codes
2.1. CCSDS Code
2.2. LDPC Decoding Algorithm
3. Spread-Spectrum Technology
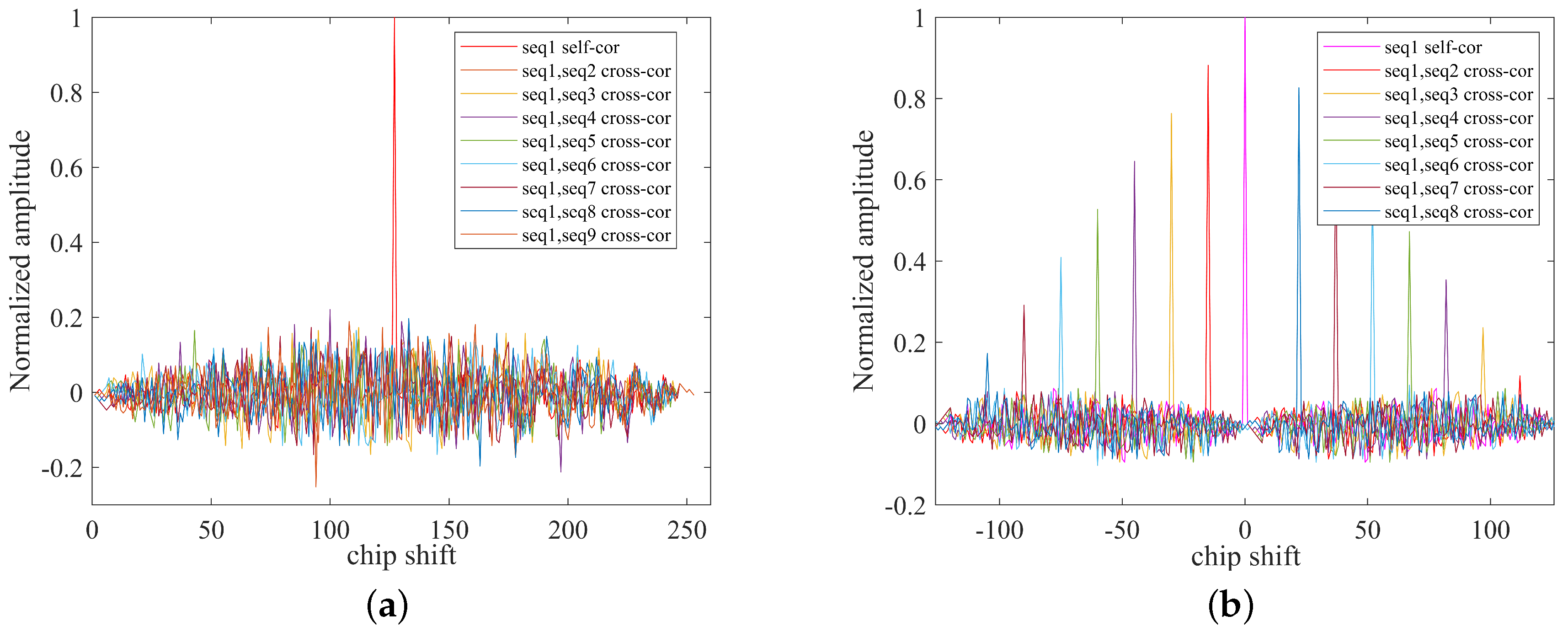
3.1. Direct-Sequence Spread-Spectrum
3.2. M-ary Spread-Spectrum
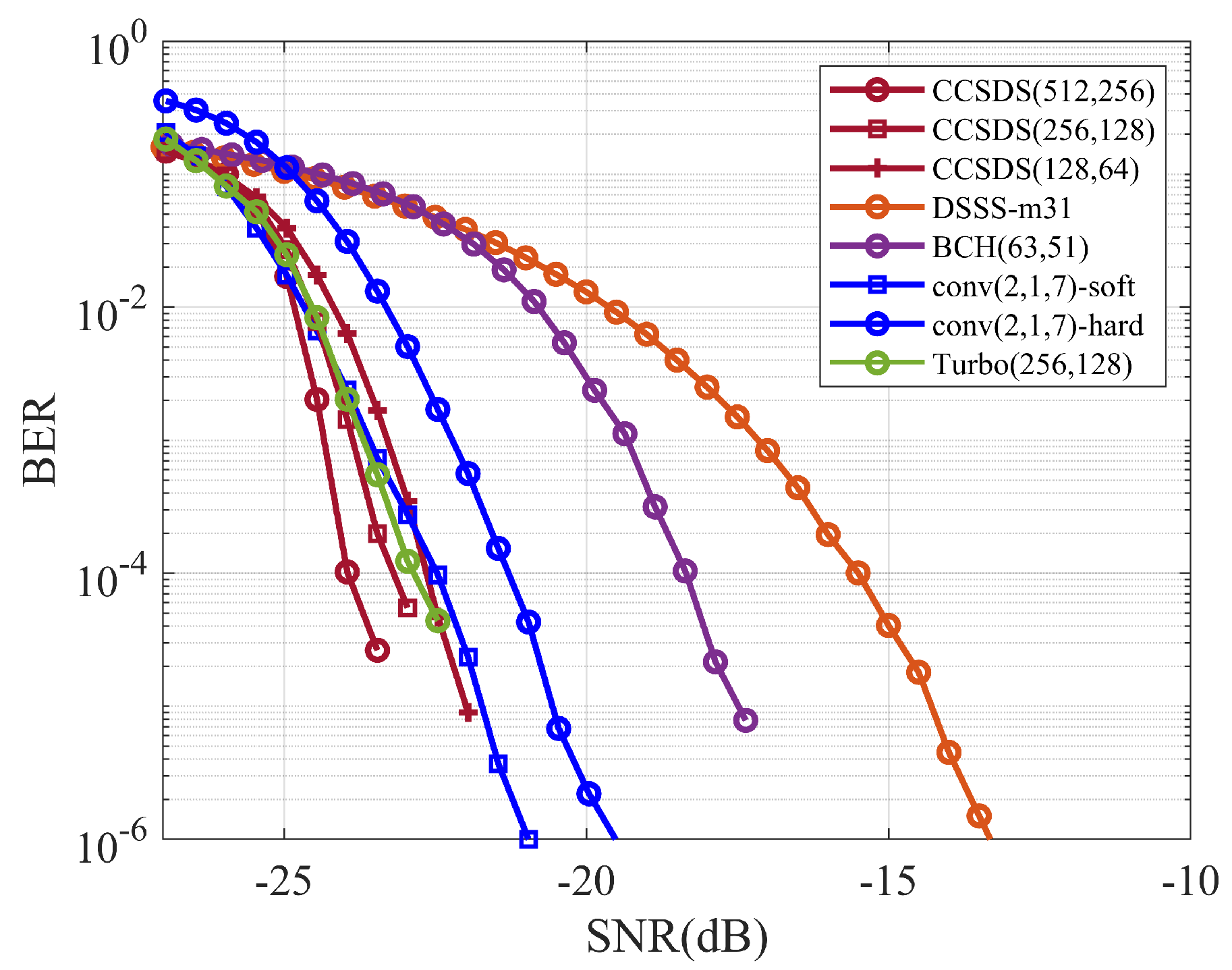
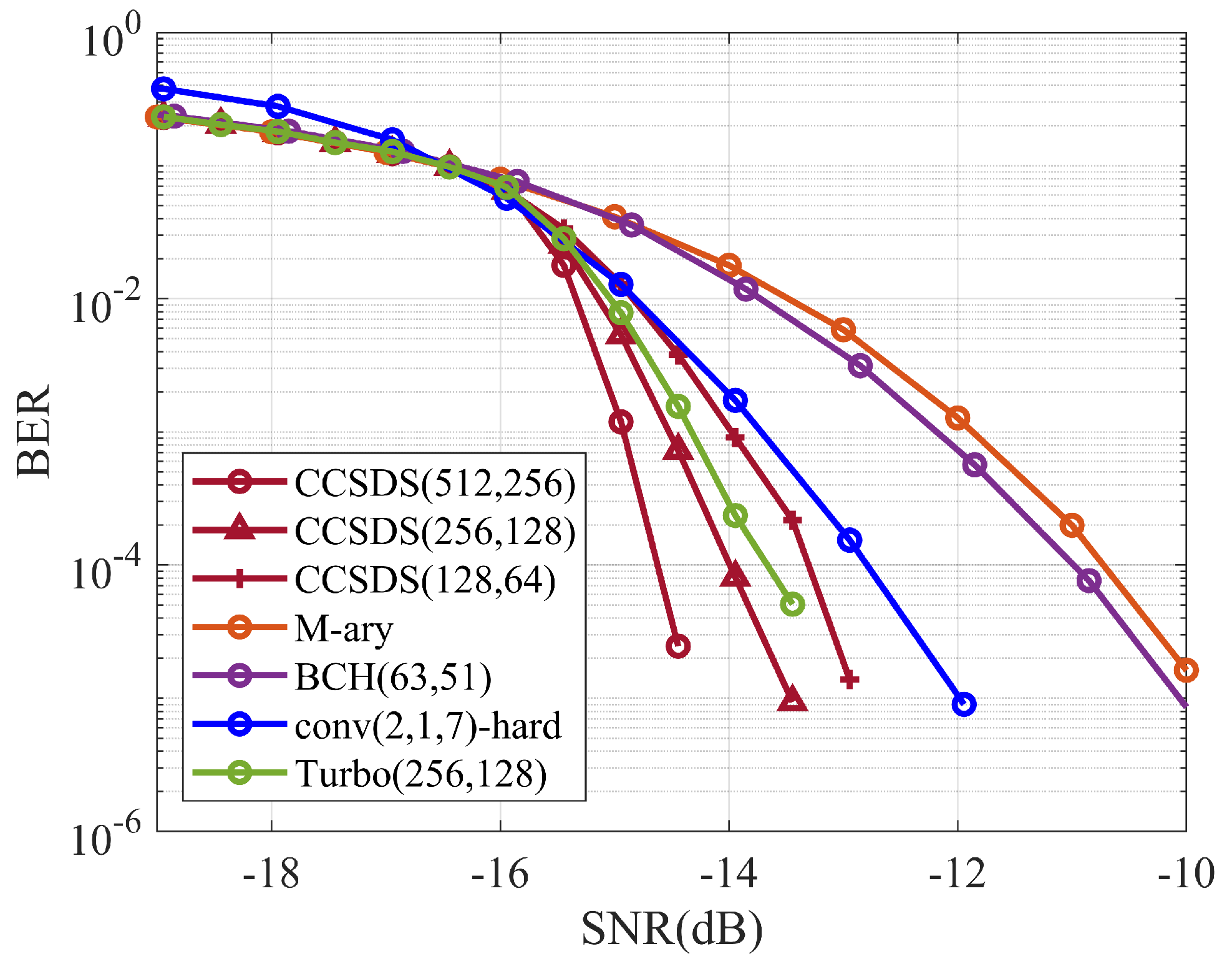
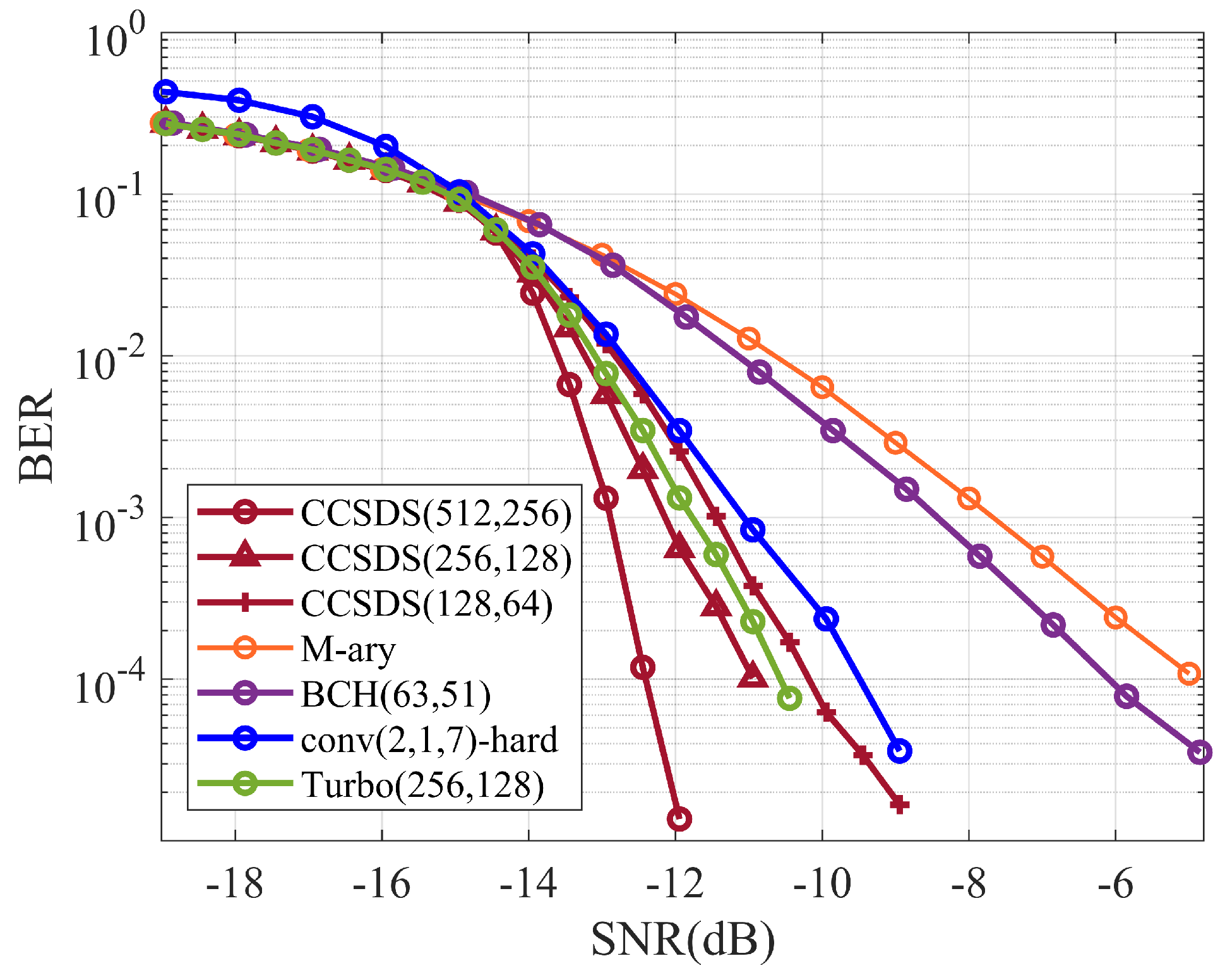
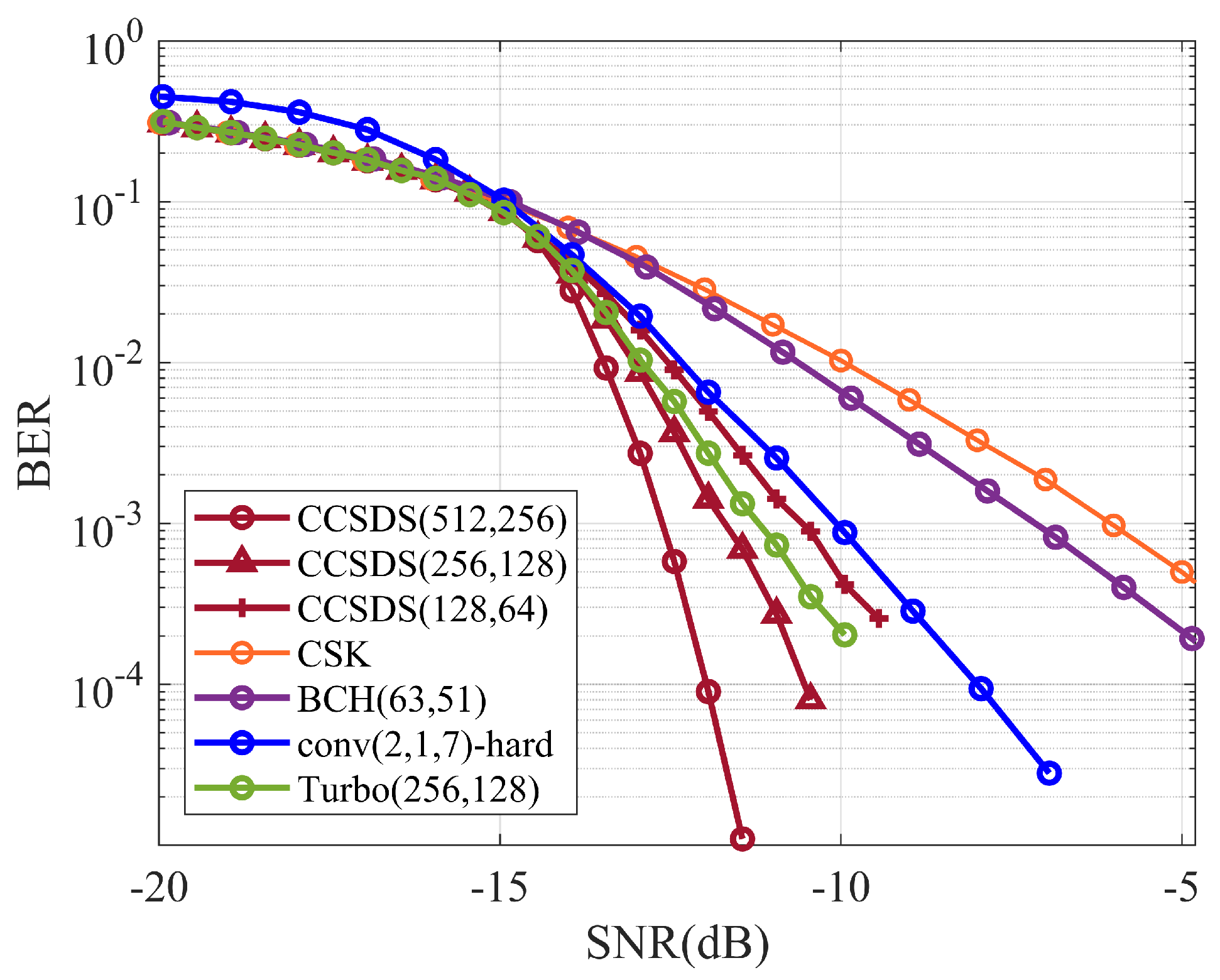
4. Simulations and Results
4.1. Overview of Spread-Spectrum Coding Systems
4.2. Simulation Analysis
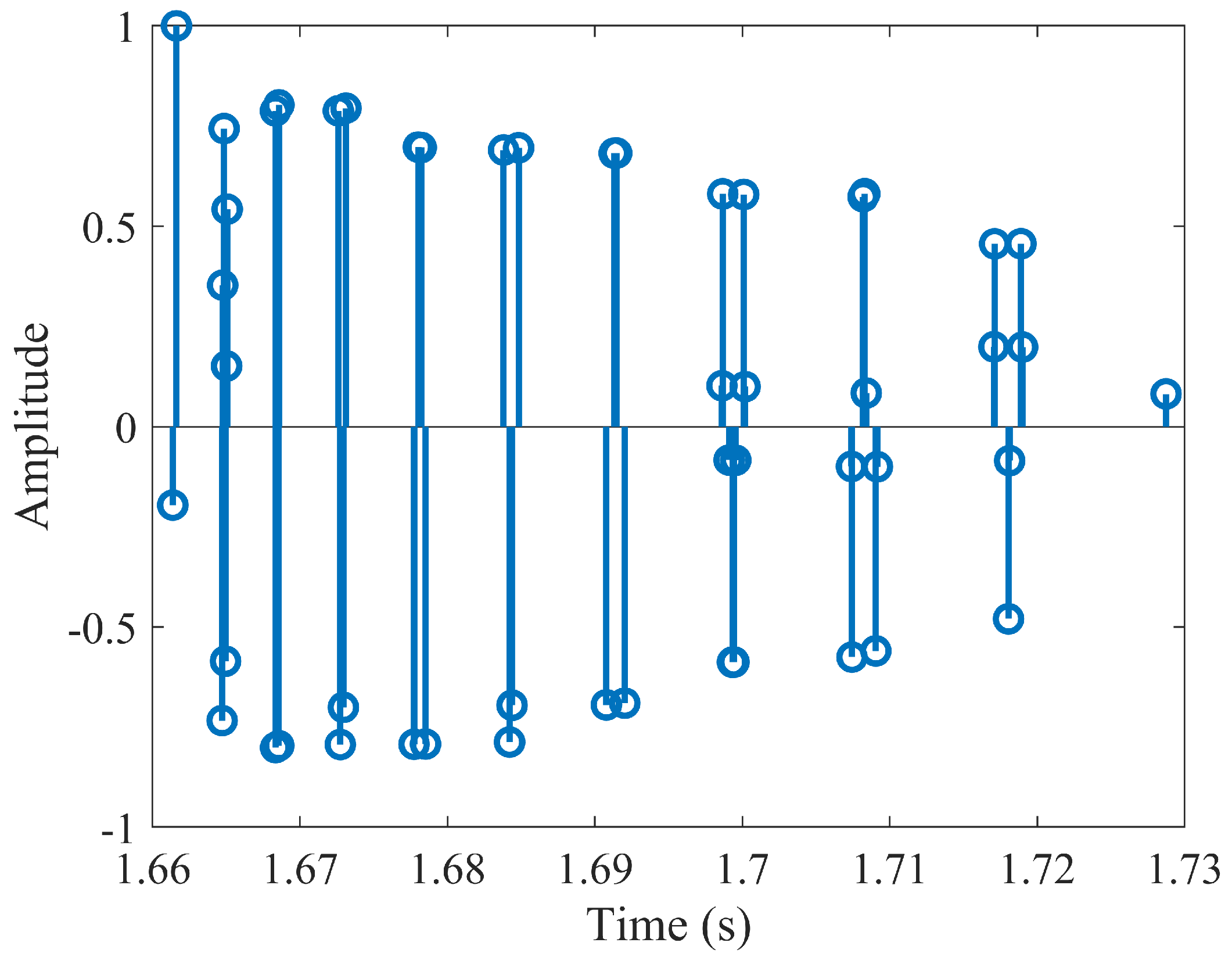
4.2.1. Channel Description
4.2.2. Simulation of Direct Spread-Spectrum Coding Systems
4.2.3. M-ary Spread-Spectrum Coding System Simulation
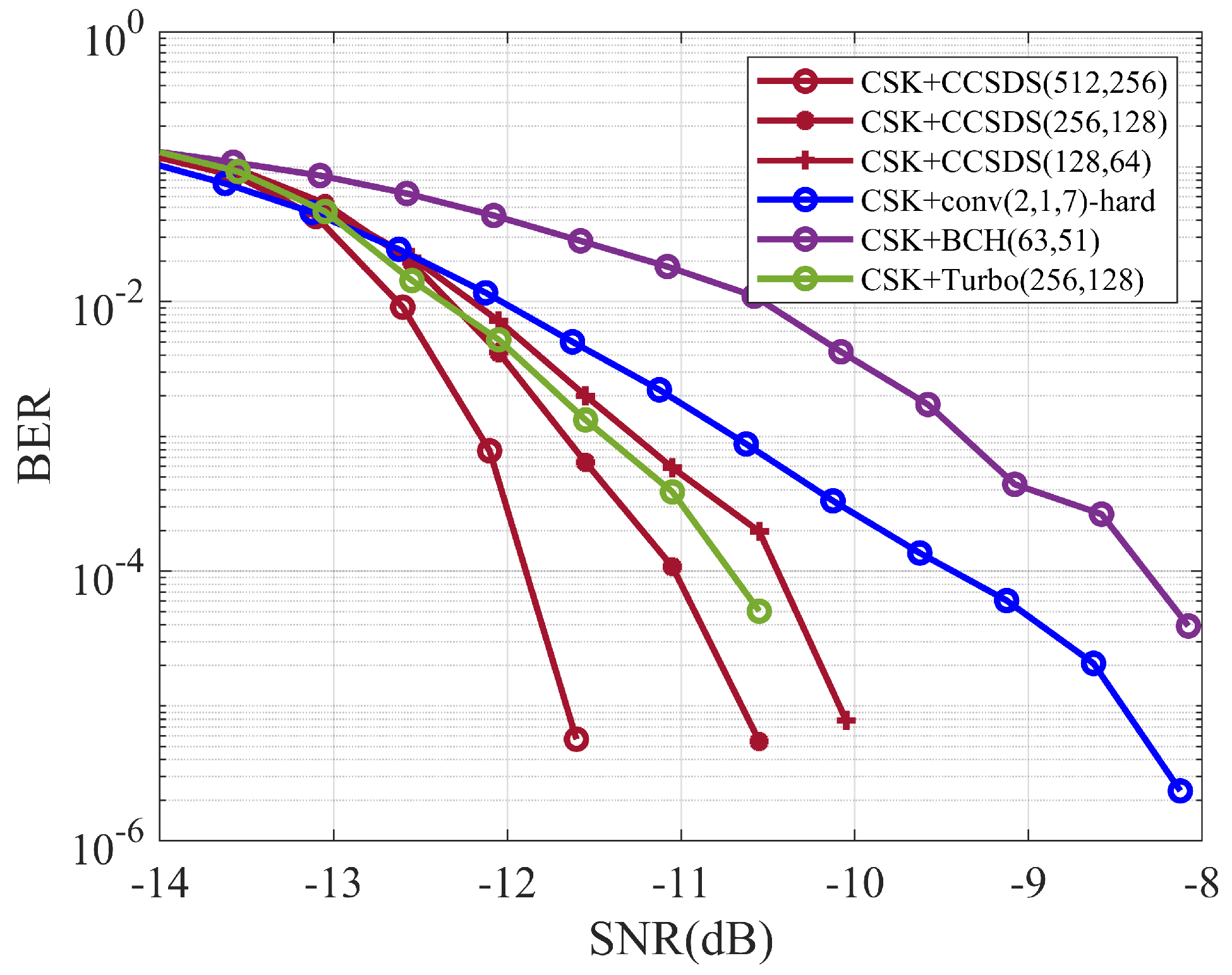
4.2.4. CSK Spread-Spectrum Coding System Simulation
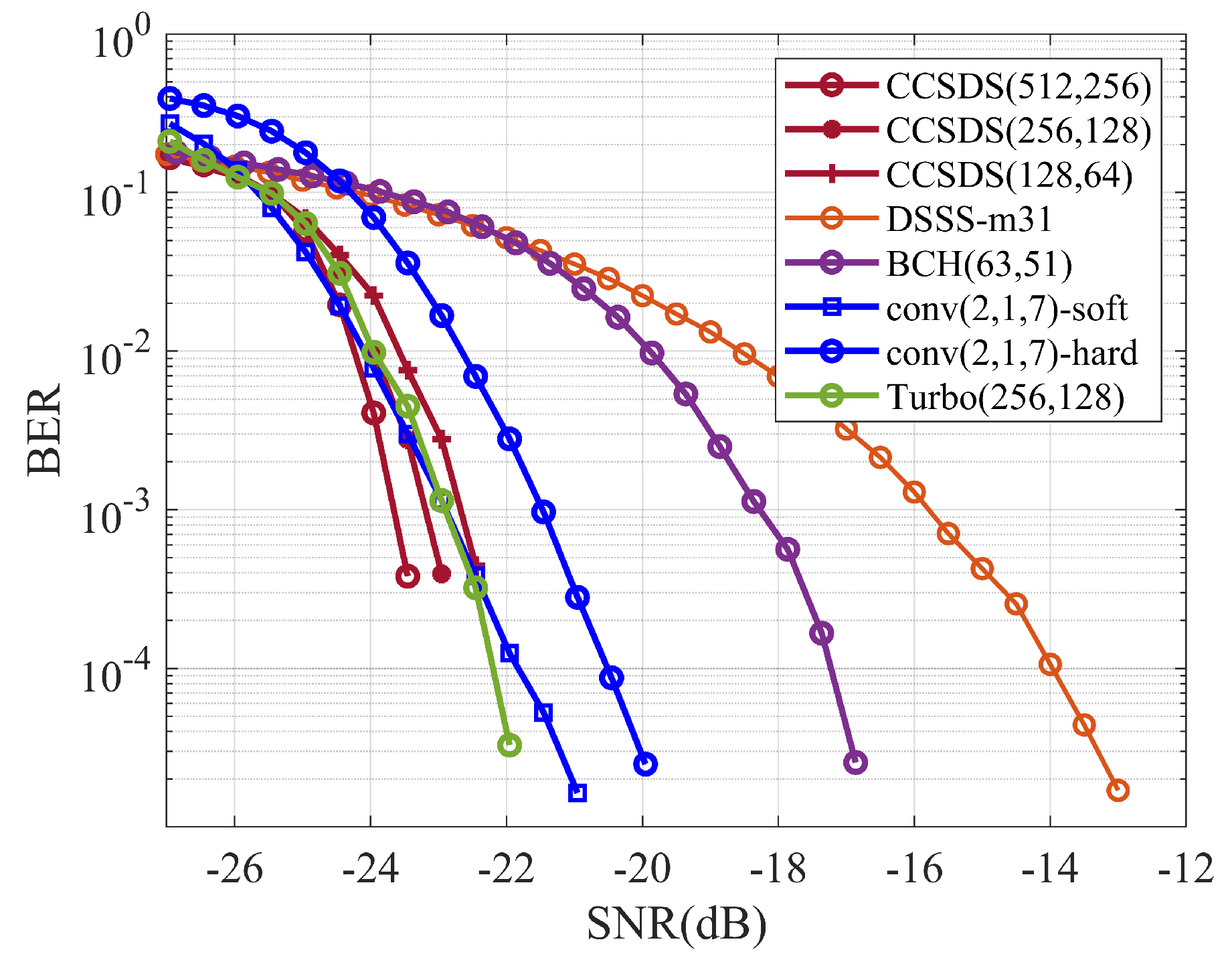
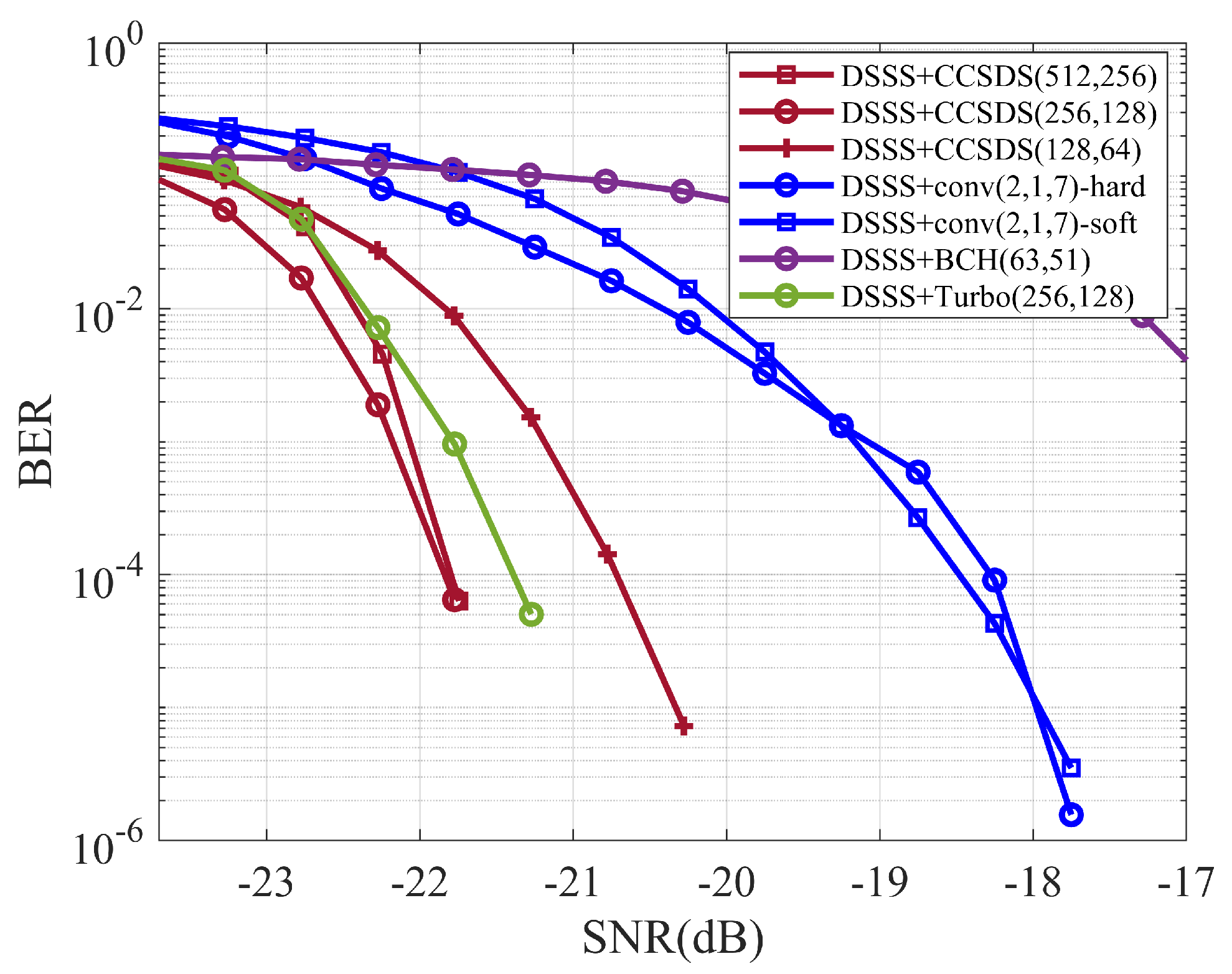
5. Water Pool Experiment
5.1. Experimental Conditions and Parameter Settings
5.2. Analysis of Experimental Results
5.2.1. Direct Spread-Spectrum Coding System
5.2.2. M-ary Spread-Spectrum Coding System
5.2.3. CSK Spread-Spectrum Coding System
6. Discussion
6.1. Significance of the Proposed Method
6.2. Limitations of the Proposed Method
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, M.R.; Das, B.; Pati, B.B. Channel estimation strategies for underwater acoustic (UWA) communication: An overview. J. Frankl. Inst. 2020, 357, 7229–7265. [Google Scholar] [CrossRef]
- Zhang, Y.; Venkatesan, R.; Dobre, O.A.; Li, C. Efficient estimation and prediction for sparse time-varying underwater acoustic channels. IEEE J. Ocean. Eng. 2019, 45, 1112–1125. [Google Scholar] [CrossRef]
- Boluda-Ruiz, R.; Rico-Pinazo, P.; Castillo-Vázquez, B.; Zambrana, A.; Qaraqe, K. Impulse response modeling of underwater optical scattering channels for wireless communication. IEEE Photonics J. 2020, 12, 1–14. [Google Scholar] [CrossRef]
- Yang, G.; Zhou, F.; Lou, Y.; Qiao, G.; Ahmed, N.; He, Y. Double-differential coded M-ary direct sequence spread spectrum for mobile underwater acoustic communication system. Appl. Acoust. 2021, 183, 108303. [Google Scholar] [CrossRef]
- Yang, G.; Zhou, F.; Qiao, G.; Zhao, Y.; Liu, Y.; Lu, Y.; He, Y. Optimized Doppler Estimation and Symbol Synchronization for Mobile M-ary Spread Spectrum Underwater Acoustic Communication. J. Mar. Sci. Eng. 2021, 9, 1001. [Google Scholar] [CrossRef]
- Lyu, W.C.; Zhao, M.M.; Chen, X.; Yang, X.; Qiu, Y.; Hu, J. Experimental demonstration of an underwater wireless optical communication employing spread spectrum technology. Opt. Express 2020, 28, 10027–10038. [Google Scholar] [CrossRef] [PubMed]
- Danish, M.N.; Pasha, S.A.; Hashmi, A.J. Quasi-cyclic LDPC codes for short block-lengths. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021; pp. 1–8. [Google Scholar]
- Medova, L.R.; Rybin, P.S.; Filatov, I.V. Short length LDPC code-candidate for satellite control channel. In Proceedings of the 2018 Engineering and Telecommunication (EnT-MIPT), Moscow, Russia, 15–16 November 2018; pp. 163–166. [Google Scholar]
- Ranganathan SV, S.; Divsalar, D.; Wesel, R.D. Quasi-cyclic protograph-based raptor-like LDPC codes for short block-lengths. IEEE Trans. Inf. Theory 2019, 65, 3758–3777. [Google Scholar] [CrossRef]
- Abdu-Aguye, U.F.; Ambroze, M.A.; Tomlinson, M. Improved minimum weight, girth, and ACE distributions in ensembles of short block length irregular LDPC codes constructed using PEG and cyclic PEG (CPEG) algorithms. In Proceedings of the 2016 9th International Symposium on Turbo Codes and Iterative Information Processing (ISTC), Brest, France, 5–9 September 2016; pp. 186–190. [Google Scholar]
- Rahman, M.R.; Bojja-Venkatakrishnan, S.; Alwan, E.A.; Volakis, J.L. Spread Spectrum Techniques with Channel Coding for Wideband Secured Communication Links. In Proceedings of the 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting, Montreal, QC, Canada, 5–10 July 2020; pp. 1783–1784. [Google Scholar]
- Qiu, M.; Wu, X.; i Amat, A.G.; Yuan, J. Analysis and design of partially information-and partially parity-coupled Turbo codes. IEEE Trans. Commun. 2021, 69, 2107–2122. [Google Scholar] [CrossRef]
- He, Y.; Zhang, J.; Jin, S.; Li, G.; Wen, C. Model-driven DNN decoder for Turbo codes: Design, simulation, and experimental results. IEEE Trans. Commun. 2020, 68, 6127–6140. [Google Scholar] [CrossRef]
- Spasov, D. Decoding of LTE Turbo Codes Initialized with the Two Recursive Convolutional Codes. In Proceedings of the 2020 43rd International Convention on Information, Communication and Electronic Technology (MIPRO), Opatija, Croatia, 28 September–2 October 2020; pp. 393–396. [Google Scholar]
- Mostari, L.; Taleb-Ahmed, A. High performance short-block binary regular LDPC codes. Alex. Eng. J. 2018, 57, 2633–2639. [Google Scholar] [CrossRef]
- Ranganathan, S.V.S.; Divsalar, D.; Wesel, R.D. Design of improved quasi-cyclic protograph-based Raptor-like LDPC codes for short block-lengths. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1207–1211. [Google Scholar]
- Li, W.; Zhang, W.; Li, L.; Zhou, H.; Yu, N. Designing near-optimal steganographic codes in practice based on polar codes. IEEE Trans. Commun. 2020, 68, 3948–3962. [Google Scholar] [CrossRef]
- Geiselhart, M.; Elkelesh, A.; Ebada, M.; Liu, M. CRC-aided belief propagation list decoding of polar codes. In Proceedings of the 2020 IEEE International Symposium on Information Theory (ISIT), Shenzhen, China, 13–15 November 2020; pp. 395–400. [Google Scholar]
- Liao, Y.; Hashemi, S.A.; Cioffi, J.M.; Goldsmith, A. Construction of polar codes with reinforcement learning. IEEE Trans. Commun. 2021, 70, 185–198. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, D.; Yang, F. Performance Analysis of LDPC in Ultraviolet Communication System. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 27–29 June 2020; pp. 292–295. [Google Scholar]
- Wei, X.F.; Chen, J. Performance Simulation of Underwater Acoustic Spread Spectrum Communication Based on LDPC Code. J. Phys. Conf. Ser. 2021, 1873, 012018. [Google Scholar] [CrossRef]
- Sun, D.; Hong, X.; Cui, H.; Liu, L. A symbol-based passband Doppler tracking and compensation algorithm for underwater acoustic DSSS communications. J. Commun. Inf. Netw. 2020, 5, 168–176. [Google Scholar] [CrossRef]
- Sozer, E.M.; Proakis, J.G.; Stojanovic, R.; Liu, L. Direct sequence spread spectrum based modem for under water acoustic communication and channel measurements. In Proceedings of the Oceans’ 99, MTS/IEEE, Riding the Crest into the 21st Century, Conference and Exhibition (IEEE Cat. No. 99CH37008), Seattle, WA, USA, 13–16 September 1999; Volume 1, pp. 228–233. [Google Scholar]
- Stojanovic, M.; Freitag, L. Hypothesis-feedback equalization for direct-sequence spread-spectrum underwater communications. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition (Cat. No. 00CH37158), Providence, RI, USA, 11–14 September 2000; Volume 1, pp. 123–129. [Google Scholar]
- Xiaomei, X.; Yougan, C.; Lan, Z.; Liu, L. Comparison of the performance of LDPC codes over different underwater acoustic channels. In Proceedings of the 2010 IEEE 12th International Conference on Communication Technology, Nanjing, China, 11–14 November 2010; pp. 155–158. [Google Scholar]
- Padala, S.K.; D’Souza, J. Performance of spatially coupled LDPC codes over underwater acoustic communication channel. In Proceedings of the 2020 National Conference on Communications (NCC), Kharagpur, India, 21–23 February 2020; pp. 1–5. [Google Scholar]










| Spectrum | Spreading Mode | Codes|Modulation |
|---|---|---|
| DSSS | CCSDS(512,256) | BPSK |
| CCSDS(256,128) | ||
| CCSDS(128,64) | ||
| M-ary SS | CCSDS(512,256) | BPSK |
| CCSDS(256,128) | ||
| CCSDS(128,64) | ||
| CSK SS | CCSDS(512,256) | BPSK |
| CCSDS(256,128) | ||
| CCSDS(128,64) |
| System bandwidth | 2 kHz |
| Carrier frequency | 2 kHz |
| Modulation | BPSK |
| Spread-spectrum system | DSSS/M-ary SS(16ary)/CSK SS(16ary) |
| Roll-off factor | 0.5 |
| Frame synchronization | LFM |
| Encoding | CCSDS(512,256)/(256,128)/(128,64) |
| Decoding | Normalized-MSA |
| Spreading sequence | 5-step M-sequence (DSSS) |
| 5-step Gold sequence (M-ary SS) | |
| 5-step M-sequence cyclic shift (CSK SS) | |
| Bit rate | 32.3 bps (DSSS) |
| 129.0 bps (M-ary) | |
| 129.0 bps (CSK) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Sun, Z. Short-Block-Length Low-Density Parity-Check Codes-Based Underwater Acoustic Spread-Spectrum Communication System. Electronics 2023, 12, 3884. https://doi.org/10.3390/electronics12183884
Zhao Z, Sun Z. Short-Block-Length Low-Density Parity-Check Codes-Based Underwater Acoustic Spread-Spectrum Communication System. Electronics. 2023; 12(18):3884. https://doi.org/10.3390/electronics12183884
Chicago/Turabian StyleZhao, Zichen, and Zongxin Sun. 2023. "Short-Block-Length Low-Density Parity-Check Codes-Based Underwater Acoustic Spread-Spectrum Communication System" Electronics 12, no. 18: 3884. https://doi.org/10.3390/electronics12183884






