Energy-Based MRI Semantic Augmented Segmentation for Unpaired CT Images
Abstract
1. Introduction
- -
- The proposed ESAS, which leverages the latent semantic features’ energy of the support modality to generate semantic comparative modality information, is a novel and general method that can be applied to most unpaired multimodal image-learning tasks;
- -
- Instead of generating a whole image, this work only transforms the semantic features, making the approach lightweight and efficient;
- -
- Extensive experiments on the MM-WHS 2017 challenge dataset [2] demonstrate the effectiveness of the proposed method, ESAS, which outperforms the state-of-the-art methods.
2. Materials and Methods
2.1. Pre-Trained Model with Shared Parameters
- : the loss measures the difference between the full-sized segmentation results of the U-shaped network and the ground truth.
- : the loss measures the difference between the low-resolution inference results of the simple decoders and the downsampled ground truth.
2.2. Energy-Based Modal
3. Experiments and Results
3.1. Dataset and Implementation Details
3.2. Comparison with Other Methods
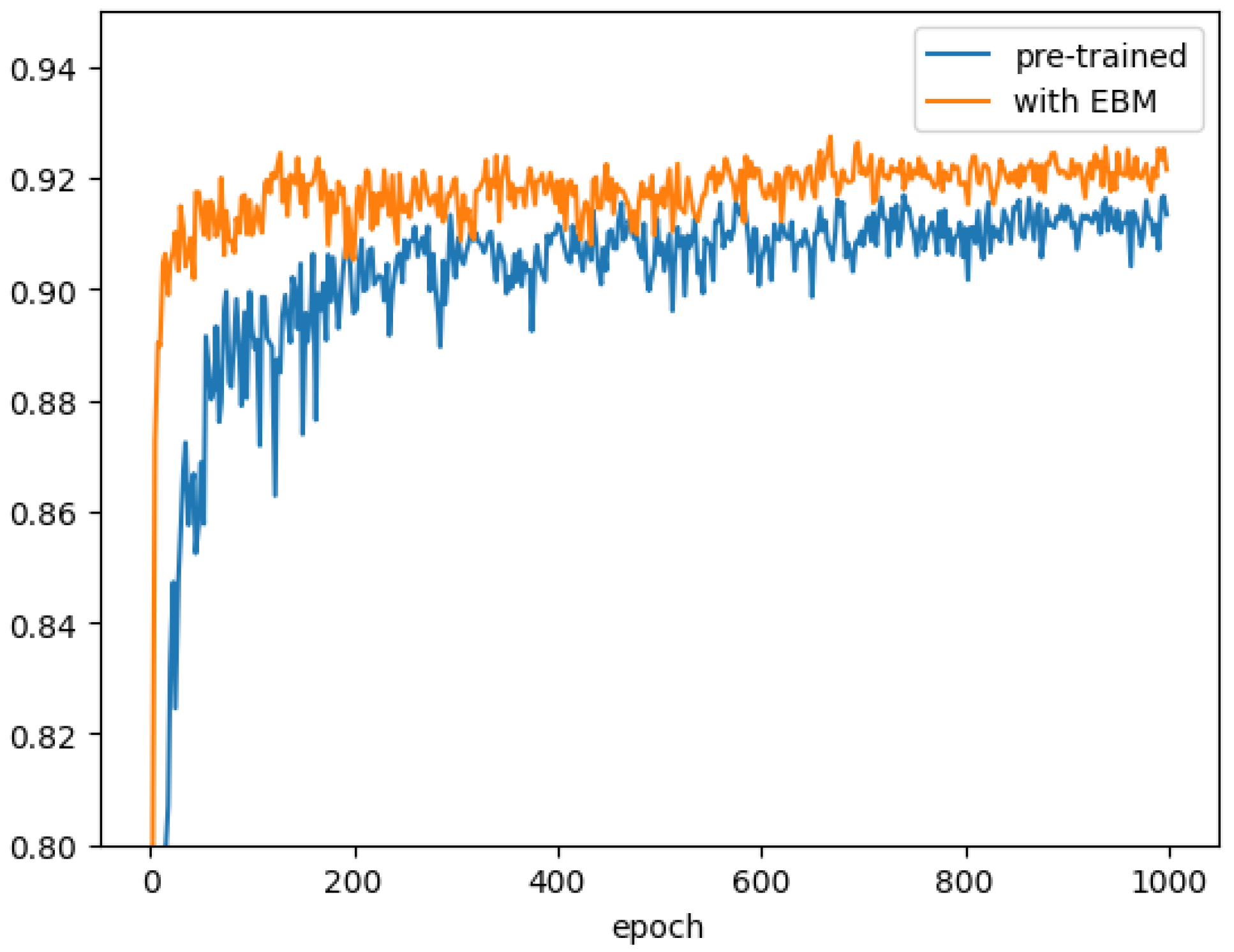
3.3. Ablation Study of Key Components
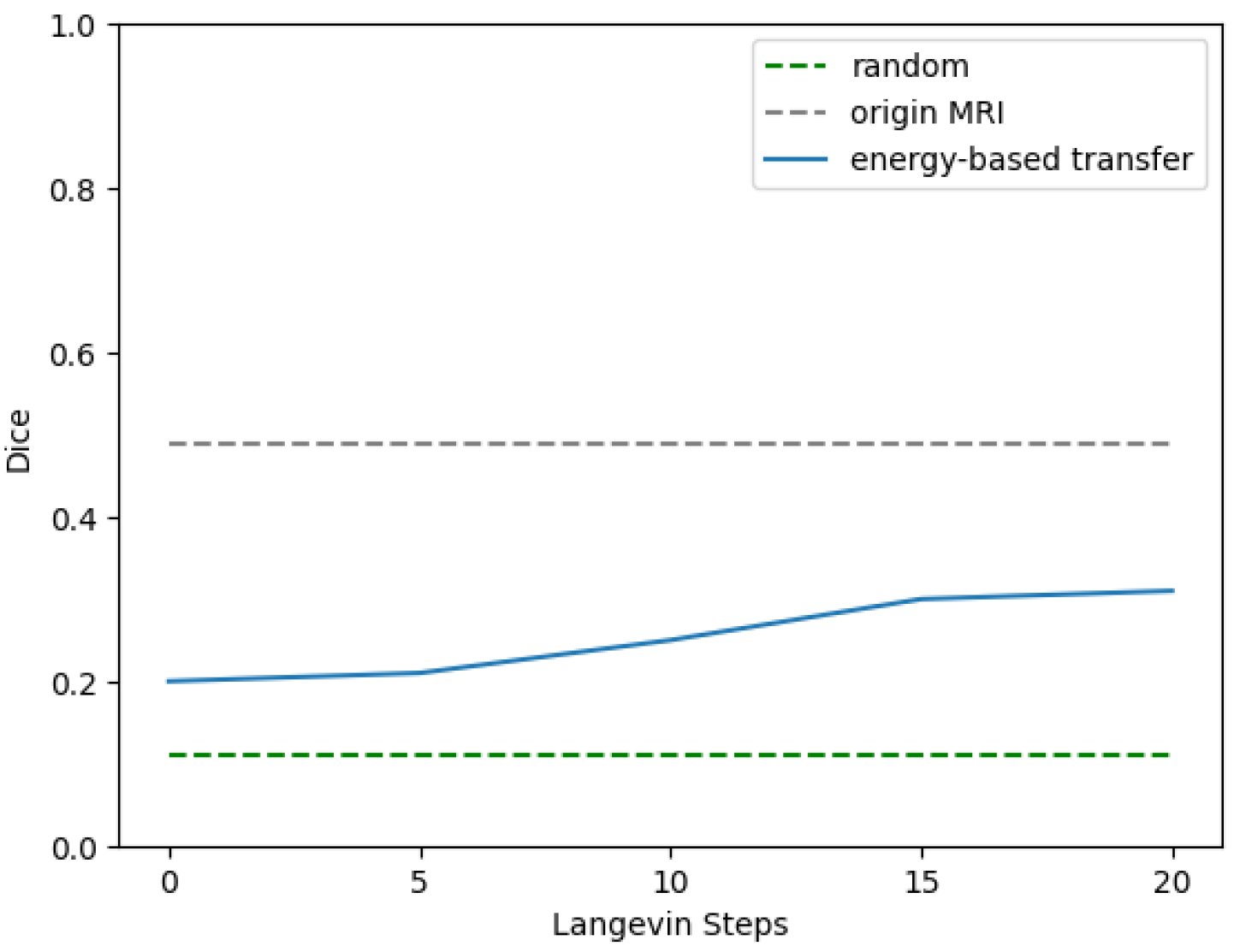
3.4. Proof-of-Concept Verification of the EBM
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, X.; Yang, J.; Gao, Y.; Guo, Y.; Wu, G.; Shen, D. Dual-core steered non-rigid registration for multi-modal images via bi-directional image synthesis. Med. Image Anal 2017, 41, 18–31. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, X.; Li, L.; Payer, C.; Štern, D.; Urschler, M.; Heinrich, M.P.; Oster, J.; Wang, C.; Smedby, Ö.; Bian, C.; et al. Evaluation of algorithms for multi-modality whole heart segmentation: An open-access grand challenge. Med. Image Anal. 2019, 58, 101537. [Google Scholar] [CrossRef]
- Liu, X.; Guo, S.; Yang, B.; Ma, S.; Zhang, H.; Li, J.; Sun, C.; Jin, L.; Li, X.; Yang, Q.; et al. Automatic organ segmentation for CT scans based on super-pixel and convolutional neural networks. J. Digital Imaging 2018, 31, 748–760. [Google Scholar] [CrossRef] [PubMed]
- Moltz, J.H.; Bornemann, L.; Dicken, V.; Peitgen, H. Segmentation of liver metastases in CT scans by adaptive thresholding and morphological processing. In Proceedings of the MICCAI workshop, New York, NY, USA, 6 September 2008; Volume 41, p. 195. [Google Scholar]
- Chang, Y.L.; Li, X. Adaptive image region-growing. IEEE Trans. Med. Imaging 1994, 3, 868–872. [Google Scholar] [CrossRef] [PubMed]
- Pohle, R.; Toennies, K.D. Segmentation of medical images using adaptive region growing. In Proceedings of the Medical Imaging 2001: Image Processing, Davis, CA, USA, 18–22 June 2001; Volume 4322, pp. 1337–1346. [Google Scholar]
- Luo, S. Review on the methods of automatic liver segmentation from abdominal images. J. Comput. Commun. 2014, 2, 1. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Van Der Laak, J.A.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Alqazzaz, S.; Sun, X.; Yang, X.; Nokes, L. Automated brain tumor segmentation on multi-modal MR image using SegNet. Comput. Vis. Media 2019, 5, 209–219. [Google Scholar] [CrossRef]
- Han, Z.; Chen, Q.; Zhang, L.; Mo, X.; You, J.; Chen, L.; Fang, J.; Wang, F.; Jin, Z.; Zhang, S.; et al. Radiogenomic association between the t2-flair mismatch sign and idh mutation status in adult patients with lower-grade gliomas: An updated systematic review and meta-analysis. European Radiol. 2022, 32, 5339–5352. [Google Scholar] [CrossRef] [PubMed]
- Kamnitsas, K.; Ledig, C.; Newcombe, V.F.; Simpson, J.P.; Kane, A.D.; Menon, D.K.; Rueckert, D.; Glocker, B. Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation. Med. Image Anal. 2017, 36, 61–78. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Ding, C.; Lu, Z.; Wang, X.; Tao, D. One-pass multi-task convolutional neural networks for efficient brain tumor segmentation. In Part III 11, Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2018: 21st International Conference, Granada, Spain, 16–20 September 2018; Proceedings, Part III 11. Springer: Berlin/Heidelberg, Germany, 2018; pp. 637–645. [Google Scholar]
- Pereira, S.; Pinto, A.; Alves, V.; Silva, C.A. Brain tumor segmentation using convolutional neural networks in MRI images. IEEE Trans. Med. Imaging 2016, 35, 1240–1251. [Google Scholar] [CrossRef] [PubMed]
- Tseng, K.L.; Lin, Y.L.; Hsu, W.; Huang, C.Y. Joint sequence learning and cross-modality convolution for 3D biomedical segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6393–6400. [Google Scholar]
- Dolz, J.; Gopinath, K.; Yuan, J.; Lombaert, H.; Desrosiers, C.; Ayed, I.B. HyperDense-Net: A hyper-densely connected CNN for multi-modal image segmentation. IEEE Trans. Med. Imaging 2018, 38, 1116–1126. [Google Scholar] [CrossRef] [PubMed]
- Nie, D.; Wang, L.; Gao, Y.; Shen, D. Fully convolutional networks for multi-modality isointense infant brain image segmentation. In Proceedings of the 2016 IEEE 13Th international symposium on biomedical imaging (ISBI), Prague, Czech Republic, 13–16 April 2016; pp. 1342–1345. [Google Scholar]
- Valindria, V.V.; Pawlowski, N.; Rajchl, M.; Lavdas, I.; Aboagye, E.O.; Rockall, A.G.; Rueckert, D.; Glocker, B. Multi-modal learning from unpaired images: Application to multi-organ segmentation in CT and MRI. In Proceedings of the 2018 IEEE winter conference on applications of computer vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 547–556. [Google Scholar]
- Jiang, J.; Hu, Y.C.; Tyagi, N.; Zhang, P.; Rimner, A.; Mageras, G.S.; Deasy, J.O.; Veeraraghavan, H. Tumor-aware, adversarial domain adaptation from CT to MRI for lung cancer segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2018: 21st International Conference, Granada, Spain, 16–20 September 2018; Proceedings, Part III 11. Springer: Berlin/Heidelberg, Germany, 2018; pp. 777–785. [Google Scholar]
- Zhang, Z.; Yang, L.; Zheng, Y. Translating and segmenting multimodal medical volumes with cycle-and shape-consistency generative adversarial network. In Proceedings of the IEEE conference on computer vision and pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9242–9251. [Google Scholar]
- Vesal, S.; Gu, M.; Kosti, R.; Maier, A.; Ravikumar, N. Adapt everywhere: Unsupervised adaptation of point-clouds and entropy minimization for multi-modal cardiac image segmentation. IEEE Trans. Med. Imaging 2021, 40, 1838–1851. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Zhou, F.; Xu, K.; Zeng, Z.; Guan, C.; Zhou, K. LE-UDA: Label-efficient unsupervised domain adaptation for medical image segmentation. IEEE Trans. Med. Imaging 2022, 42, 633–646. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Yu, L.; Wang, S.; Heng, P.A. Towards cross-modality medical image segmentation with online mutual knowledge distillation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 775–783. [Google Scholar]
- Dou, Q.; Liu, Q.; Heng, P.A.; Glocker, B. Unpaired multi-modal segmentation via knowledge distillation. IEEE Trans. Med. Imaging 2020, 39, 2415–2425. [Google Scholar] [CrossRef] [PubMed]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning. PMLR, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Instance normalization: The missing ingredient for fast stylization. arXiv 2016, arXiv:1607.08022. [Google Scholar]
- Wu, Y.; He, K. Group normalization. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Kingma, D.P. How to train your energy-based models. arXiv 2021, arXiv:2101.03288. [Google Scholar]
- Welling, M.; Teh, Y.W. Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, DC, USA, 28 June–2 July 2011; pp. 681–688. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. Conference Track Proceedings. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, 2–4 May 2016. Conference Track Proceedings. [Google Scholar]
- Zeiler, M.D.; Krishnan, D.; Taylor, G.W.; Fergus, R. Deconvolutional networks. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2528–2535. [Google Scholar]


| Architecture | Modules | Operators | Input Size | Output Size | Kernel Size |
|---|---|---|---|---|---|
| Encoder | Down1 | Conv3D + Batch Norm + LeakyReLU | |||
| Dilated Conv3D + Batch Norm + LeakyReLU | |||||
| Down2 | Conv3D + Batch Norm + LeakyReLU | C | |||
| Dilated Conv3D + Batch Norm + LeakyReLU | |||||
| Encoder | Down3 | Conv3D + Batch Norm + LeakyReLU | |||
| Dilated Conv3D + Batch Norm + LeakyReLU | |||||
| Down4 | Conv3D + Batch Norm + LeakyReLU | ||||
| Dilated Conv3D + Batch Norm + LeakyReLU | |||||
| Residual | Conv0 | Conv3D | |||
| Decoder | Up1 | ConvTranspose3D + Batch Norm + LeakyReLU | (P/16)16C | (P/8)8C | |
| Conv3D + Batch Norm + LeakyReLU | |||||
| Up2 | ConvTranspose3D + Batch Norm + LeakyReLU | ||||
| Conv3D + Batch Norm + LeakyReLU | |||||
| Up3 | ConvTranspose3D + Batch Norm + LeakyReLU | ||||
| Conv3D + Batch Norm + LeakyReLU | |||||
| Up4 | ConvTranspose3D + Batch Norm + LeakyReLU | (P/2) | |||
| Conv3D + Batch Norm + LeakyReLU | |||||
| Output | Conv3D | ||||
| EBM | Conv1 | Conv3D + Batch Norm + LeakyReLU | |||
| Conv2 | Conv3D + Batch Norm + LeakyReLU | ||||
| Conv3 | Conv3D | (P/16) |
| Method | Mean Dice | Dice of Substructure of Heart | ||||||
|---|---|---|---|---|---|---|---|---|
| MYO | LA | LV | RA | RV | AA | PA | ||
| Baseline | 0.8706 | 0.8702 | 0.8922 | 0.9086 | 0.8386 | 0.8460 | 0.9252 | 0.8134 |
| Fine-tune | 0.8769 | 0.8716 | 0.9040 | 0.9079 | 0.8443 | 0.8526 | 0.9274 | 0.8305 |
| Joint-training | 0.8743 | 0.8665 | 0.9076 | 0.9123 | 0.8278 | 0.8492 | 0.9302 | 0.8266 |
| X-Shape [19] | 0.8767 | 0.8719 | 0.8979 | 0.9094 | 0.8551 | 0.8444 | 0.9343 | 0.8240 |
| Jiang et al. [20] | 0.8765 | 0.8723 | 0.9054 | 0.9073 | 0.8338 | 0.8525 | 0.9484 | 0.8156 |
| Zhang et al. [21] | 0.8850 | 0.8781 | 0.9112 | 0.9134 | 0.8514 | 0.8631 | 0.9430 | 0.8342 |
| Ours | 0.8945 | 0.8961 | 0.9230 | 0.9045 | 0.8661 | 0.8685 | 0.9492 | 0.8539 |
| Ours (patch-based) | 0.9267 | 0.9183 | 0.9405 | 0.9411 | 0.9323 | 0.9343 | 0.9530 | 0.8669 |
| MR | Simple Decoder | EBM | Mean Dice | Dice of Substructure of Heart | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MYO | LA | LV | RA | RV | AA | PA | ||||
| 0.9245 | 0.9126 | 0.9368 | 0.9371 | 0.9287 | 0.9343 | 0.9503 | 0.8718 | |||
| ✓ | 0.9247 | 0.9130 | 0.9381 | 0.9387 | 0.9312 | 0.9357 | 0.9513 | 0.8651 | ||
| ✓ | ✓ | 0.9250 | 0.9163 | 0.9375 | 0.9395 | 0.9312 | 0.9361 | 0.9512 | 0.8635 | |
| ✓ | ✓ | ✓ | 0.9267 | 0.9183 | 0.9405 | 0.9411 | 0.9323 | 0.9343 | 0.9530 | 0.8669 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, S.; Shen, C.; Wang, X. Energy-Based MRI Semantic Augmented Segmentation for Unpaired CT Images. Electronics 2023, 12, 2174. https://doi.org/10.3390/electronics12102174
Cai S, Shen C, Wang X. Energy-Based MRI Semantic Augmented Segmentation for Unpaired CT Images. Electronics. 2023; 12(10):2174. https://doi.org/10.3390/electronics12102174
Chicago/Turabian StyleCai, Shengliang, Chuyun Shen, and Xiangfeng Wang. 2023. "Energy-Based MRI Semantic Augmented Segmentation for Unpaired CT Images" Electronics 12, no. 10: 2174. https://doi.org/10.3390/electronics12102174
APA StyleCai, S., Shen, C., & Wang, X. (2023). Energy-Based MRI Semantic Augmented Segmentation for Unpaired CT Images. Electronics, 12(10), 2174. https://doi.org/10.3390/electronics12102174






