Experimental Evaluation of Predictive Torque Control of IPMSM under Speed Sensor and Sensorless Extended EMF Method
Abstract
:1. Introduction
2. Mathematical Model of IPMSM
3. Proposed Sensorless EEMF-PTC
3.1. Impact of Speed on the Torque Variation
3.2. Extended EMF Method
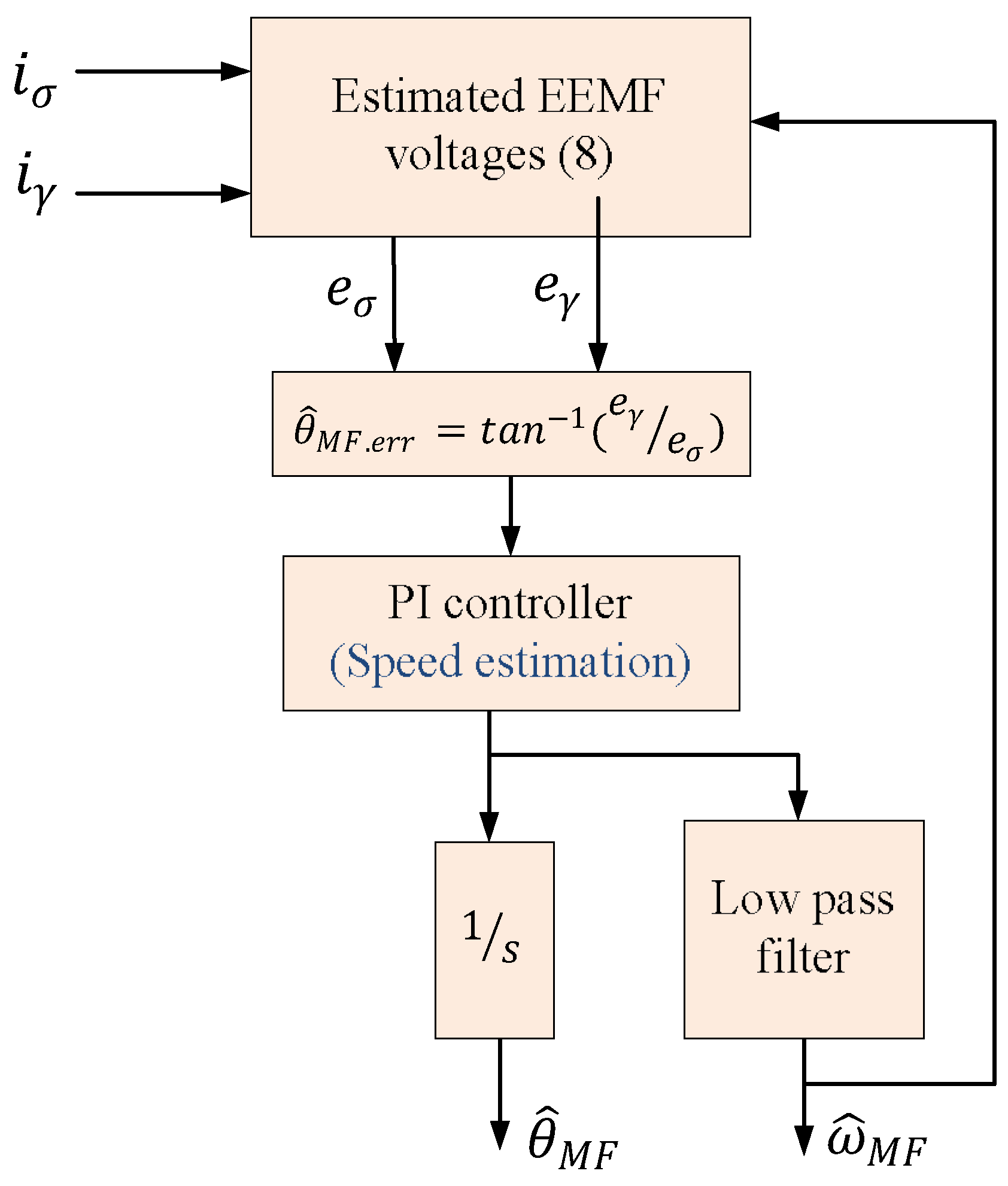
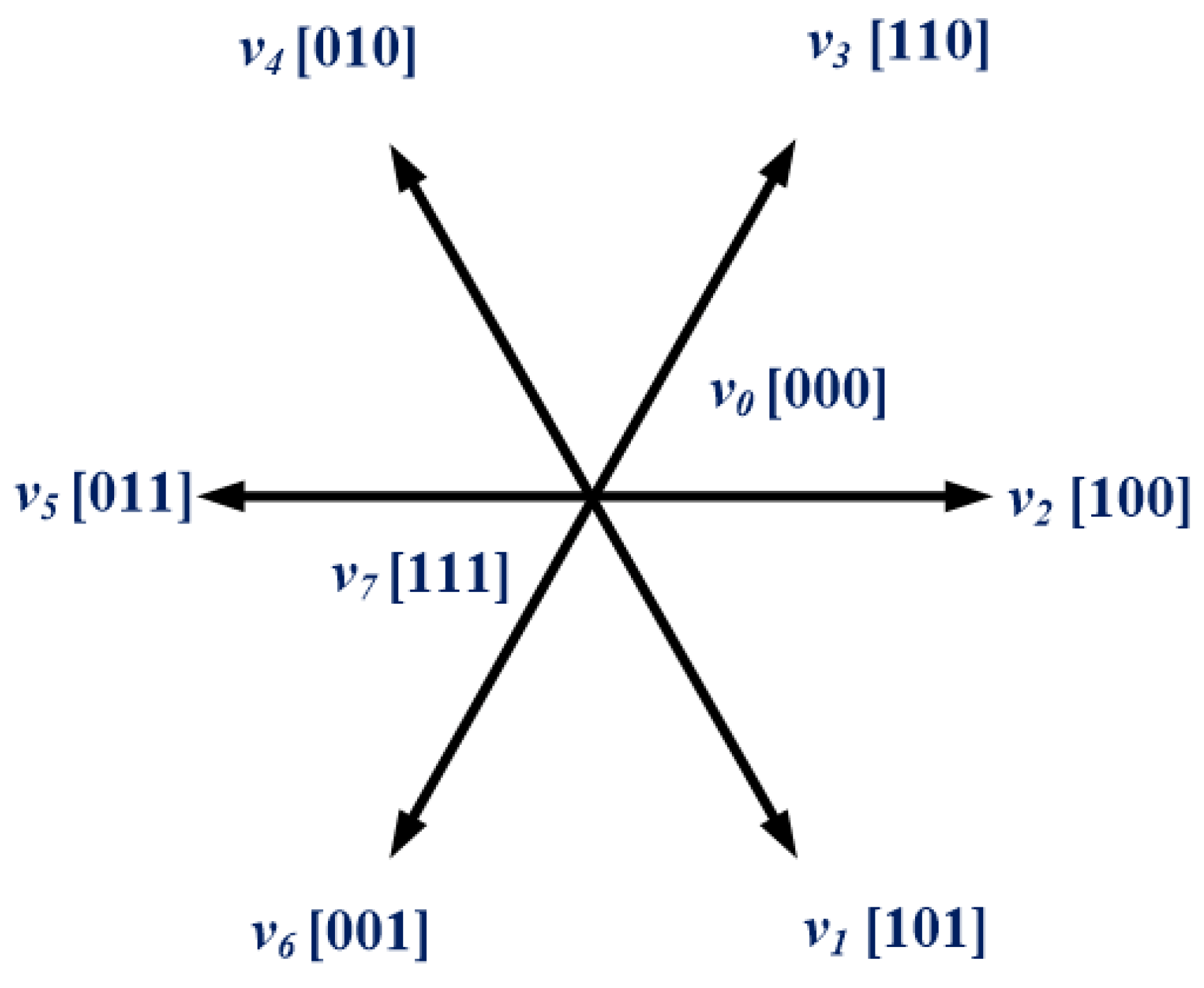
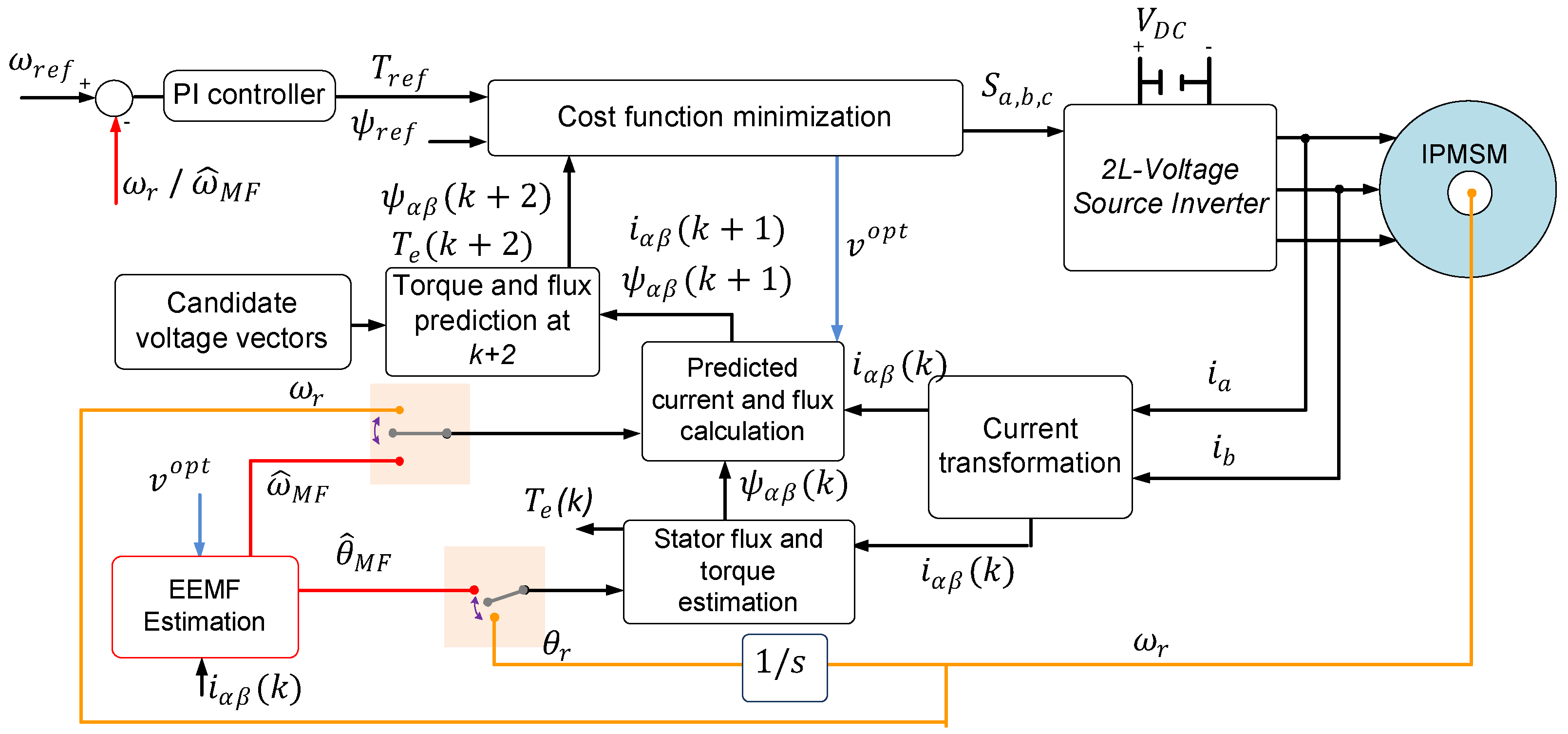
3.3. Sensorless EEMF-PTC Method
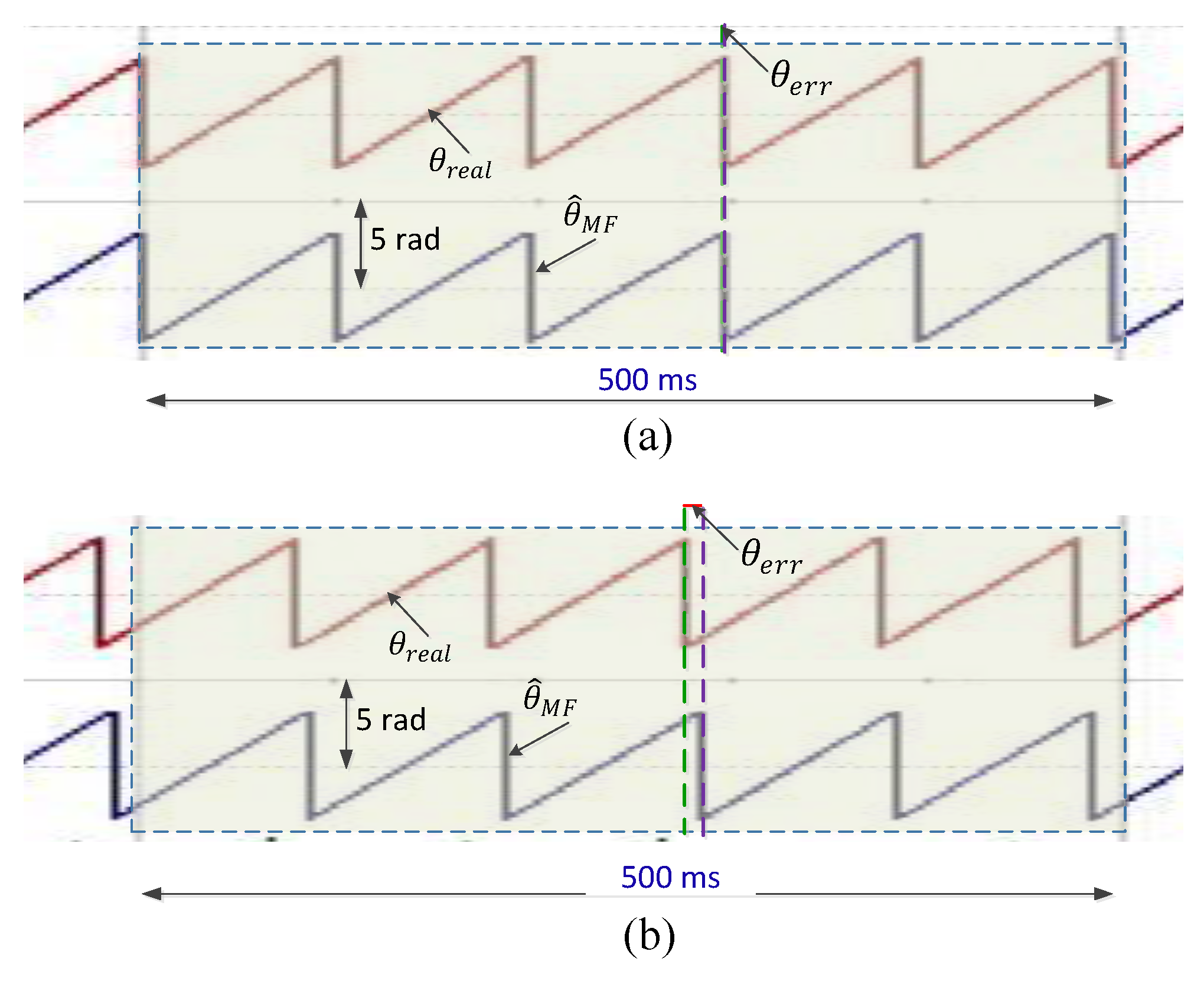
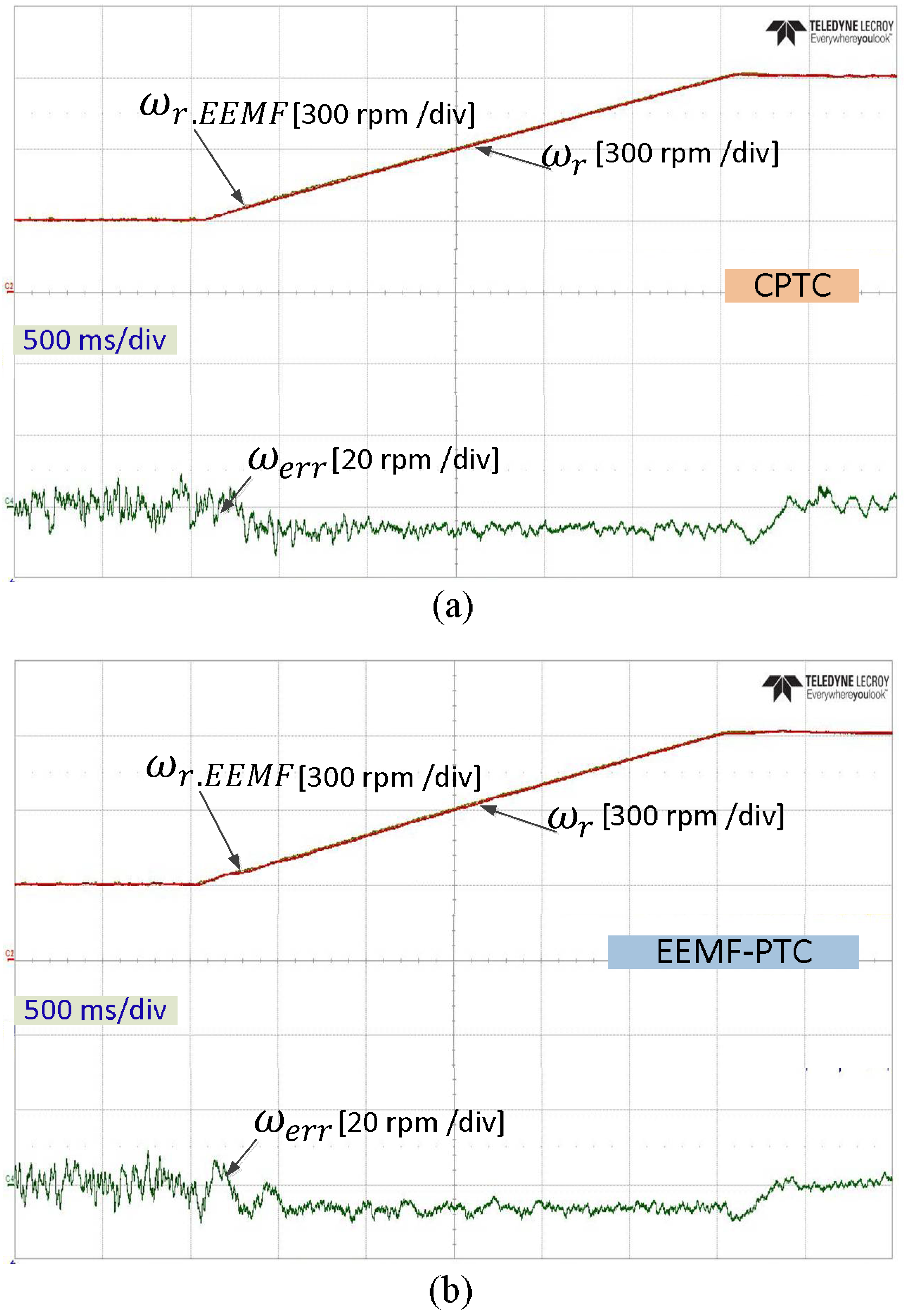
4. Implementation and Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alsofyani, I.M.; Lee, K.-B. Predictive Torque Control Based on Discrete Space Vector Modulation of PMSM without Flux Error-Sign and Voltage-Vector Lookup Table. Electronics 2020, 9, 1542. [Google Scholar] [CrossRef]
- Seo, D.-W.; Bak, Y.; Lee, K.-B. An improved rotating restart method for a sensorless permanent magnet synchronous motor drive system using repetitive zero voltage vectors. IEEE Trans. Ind. Electron. 2020, 67, 3496–3504. [Google Scholar] [CrossRef]
- Cho, Y.; Lee, K.-B.; Song, J.-H.; Lee, Y.I. Torque-ripple minimization and fast dynamic scheme for torque predictive control of permanent-magnet synchronous motors. IEEE Trans. Power Electron. 2015, 30, 2182–2190. [Google Scholar] [CrossRef]
- Bak, Y.; Lee, K.-B. Constant speed control of a permanent-magnet synchronous motor using a reverse matrix converter under variable generator input conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 315–326. [Google Scholar] [CrossRef]
- Zhu, Y.; Tao, B.; Xiao, M.; Yang, G.; Zhang, X.; Lu, K. Luenberger Position Observer Based on Deadbeat-Current Predictive Control for Sensorless PMSM. Electronics 2020, 9, 1325. [Google Scholar] [CrossRef]
- Elgbaily, M.; Anayi, F.; Alshbib, M.M. A Combined Control Scheme of Direct Torque Control and Field-Oriented Control Algorithms for Three-Phase Induction Motor: Experimental Validation. Mathematics 2022, 10, 3842. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Lee, K. Enhanced Performance of Constant Frequency Torque Controller–Based Direct Torque Control of Induction Machines with Increased Torque-Loop Bandwidth. IEEE Trans. Ind. Electron. 2020, 67, 10168–10179. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef] [Green Version]
- Alsofyani, I.M.; Lee, K.B. A Uni-Directional Voltage Vector Preselection Strategy for Optimizing Model Predictive Torque Control with Discrete Space Vector Modulation of IPMSM. IEEE Trans. Ind. Electron. 2022, 69, 12305–12315. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, Y.; Hou, Y. Multi-step model predictive current control of permanent-magnet synchronous motor. J. Power Electron. 2020, 20, 176–187. [Google Scholar] [CrossRef]
- Fan, S.; Tong, C. Model predictive current control method for PMSM drives based on an improved prediction model. J. Power Electron. 2020, 20, 1456–1466. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model predictive control: A review of its applications in power electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Cortes, P.; Kouro, S.; La Rocca, B.; Vargas, R.; Rodriguez, J.; Leon, J.I.; Vazquez, S.; Franquelo, L.G. Guidelines for weighting factors design in model predictive control of power converters and drives. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Churchill, Australia, 10–13 February 2009; pp. 1–7. [Google Scholar]
- Shadmand, M.B.; Balog, R.S.; Rub, H.A. Auto-tuning the cost function weight factors in a model predictive controller for a matrix converter VAR compensator. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 20–24 September 2015; pp. 3807–3814. [Google Scholar]
- Fretes, H.; Rodas, J.; Doval-Gandoy, J.; Gomez, V.; Gomez, N.; Novak, M.; Rodriguez, J.; Dragičević, T. Pareto Optimal Weighting Factor Design of Predictive Current Controller of a Six-Phase Induction Machine Based on Particle Swarm Optimization Algorithm. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 207–219. [Google Scholar] [CrossRef]
- Norambuena, M.; Rodriguez, J.; Zhang, Z.; Wang, F.; Garcia, C.; Kennel, R. A very simple strategy for high-quality performance of AC machines using model predictive control. IEEE Trans. Power Electron. 2019, 34, 794–800. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Bak, Y.; Lee, K.-B. Improved Finite Set-Predictive Torque Control of PMSM Fed by Indirect Matrix Converter with Discrete Space Vector Modulation. Electronics 2020, 9, 2133. [Google Scholar] [CrossRef]
- Zouari, W.; El Badsi, I.N.; El Badsi, B.; Masmoudi, A. Three-Level NPC Inverter-Fed IM Drives under PTC, Minimizing the Involved Voltage Vectors and Balancing the DC Bus Capacitor Voltages. Sustainability 2022, 14, 13522. [Google Scholar] [CrossRef]
- Alaei, A.; Lee, D.-H.; Ahn, J.-W.; Nejad, S.M.S. Sensorless control of IPMSM with a simplified high- frequency square wave injection method. J. Electr. Eng. Technol. 2018, 13, 1515–1527. [Google Scholar]
- Motor Control: Efficient, Flexible and Secure. Available online: https://www.nxp.com/applications/enabling-technologies/motor-control:MOTOR-CONTROL (accessed on 12 December 2022).
- Yongsoon, P.; Seung-Ki, S. Sensorless control method for PMSM based on frequency-adaptive disturbance observer. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 143–151. [Google Scholar] [CrossRef]
- Teja, A.V.R.; Chakraborty, C.; Maiti, S.; Hori, Y. A new model reference adaptive controller for four quadrant vector controlled induction motor drives. IEEE Trans. Ind. Electron. 2012, 59, 3757–3767. [Google Scholar] [CrossRef]
- Yin, Z.G.; Zhao, C.; Zhong, Y.R.; Liu, J. Research on robust performance of speed-sensorless vector control for the induction motor using an interfacing multiple-model extended Kalman filter. IEEE Trans. Power Electron. 2014, 29, 3011–3019. [Google Scholar] [CrossRef]
- Han, D.-Y.; Cho, Y.; Lee, K.-B. Simple sensorless control of interior permanent magnet synchronous motor using PLL based on extended EMF. J. Electr. Eng. Technol. 2017, 12, 711–717. [Google Scholar] [CrossRef]
- Chi, S.; Zhang, Z.; Xu, L. Sliding-mode sensorless control of directdrive PM synchronous motors for washing machine applications. IEEE Trans. Ind. Appl. 2009, 45, 582–590. [Google Scholar] [CrossRef]
- Woldegiorgis, A.T.; Ge, X.; Wang, H.; Hassan, M. A New Frequency Adaptive Second-Order Disturbance Observer for Sensorless Vector Control of Interior Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2021, 68, 11847–11857. [Google Scholar] [CrossRef]
- Özkurt, G.; Zerdali, E. Design and Implementation of Hybrid Adaptive Extended Kalman Filter for State Estimation of Induction Motor. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Wang, G.; Valla, M.; Solsona, J. Position sensorless permanent magnet synchronous machine drives—A review. IEEE Trans. Ind. Electron. 2020, 67, 5830–5842. [Google Scholar] [CrossRef]
- Wang, S.; Yang, K.; Chen, K. An improved position-sensorless control method at low speed for PMSM based on high-frequency signal injection into a rotating reference frame. IEEE Access 2019, 7, 86510–86521. [Google Scholar] [CrossRef]
- Yoon, T.-M.; Lee, J.-S.; Lee, K.-B. Rotor position estimation method of IPMSM using HF signal injection and sliding-mode controller. IEEJ Trans. Electr. Electron. Eng. 2014, 9, S56–S63. [Google Scholar] [CrossRef]
- Kim, S.; Ha, J.-I.; Sul, S.-K. PWM switching frequency signal injection sensorless method in IPMSM. IEEE Trans. Ind. Appl. 2012, 48, 1576–1587. [Google Scholar] [CrossRef]
- Wang, G.; Li, Z.; Zhang, G.; Yu, Y.; Xu, D. Quadrature PLL-based highorder sliding–mode observer for IPMSM sensorless control with online MTPA control strategy. IEEE Trans. Energy Convers. 2013, 28, 214–224. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, L.; Cheng, M.; Chau, K.T. Sensorless SVPWMFADTC of a new flux-modulated permanent-magnet wheel motor based on a wide-speed sliding mode observer. IEEE Trans. Ind. Electron. 2015, 62, 3143–3151. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.M.; Zhu, Z.Q. Improved sensorless control of permanent magnet synchronous machine based on third-harmonic back EMF. IEEE Trans. Ind. Appl. 2014, 50, 1861–1870. [Google Scholar] [CrossRef]
- Smith, A.; Gadoue, S.; Finch, J. Improved rotor flux estimation at low speeds for torque MRAS-based sensorless induction motor drives. IEEE Trans. Energy Convers. 2016, 31, 270–282. [Google Scholar] [CrossRef] [Green Version]
- Zerdali, E. Adaptive Extended Kalman Filter for Speed-Sensorless Control of Induction Motors. IEEE Trans. Energy Convers. 2019, 34, 789–800. [Google Scholar] [CrossRef]
- Zhong, Z.; Zhou, S.; Shao, Z. Multiple reference frame-based current harmonic control for interior PMSMs considering motional EMF. J. Power Electron. 2021, 21, 921–931. [Google Scholar] [CrossRef]
- Lee, H.; Cho, D.; Lee, K. Rotor position estimation over entire speed range of interior permanent magnet synchronous motors. J. Power Electron. 2021, 21, 693–702. [Google Scholar] [CrossRef]
- Morimoto, S.; Kawamoto, K.; Sanada, M.; Takeda, Y. Sensorless control strategy for salient-pole PMSM based on extended EMF in rotating reference frame. IEEE Trans. Ind. Appl. 2002, 38, 1054–1061. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Torque rating, Te.rat | 60 Nm |
| Power rating, P.rat | 11 kW |
| Current rating, I.rat | 19.9 A |
| Speed rating, | 1750 rpm |
| Permanent magnet flux, | 0.554 Wb |
| Number of pole pairs, Pn | 3 |
| Stator resistance, Rs | 0.349 Ω |
| Stator resistance, Ls | 15.6 mH |
| Operating Condition | Method | Torque Ripple (Nm) | THD (%) | |
|---|---|---|---|---|
| Speed | Torque | |||
| 200 RPM | 0 Nm | CPTC | 2.107 | 33.5 |
| EEMF-PTC | 1.789 | 32.7 | ||
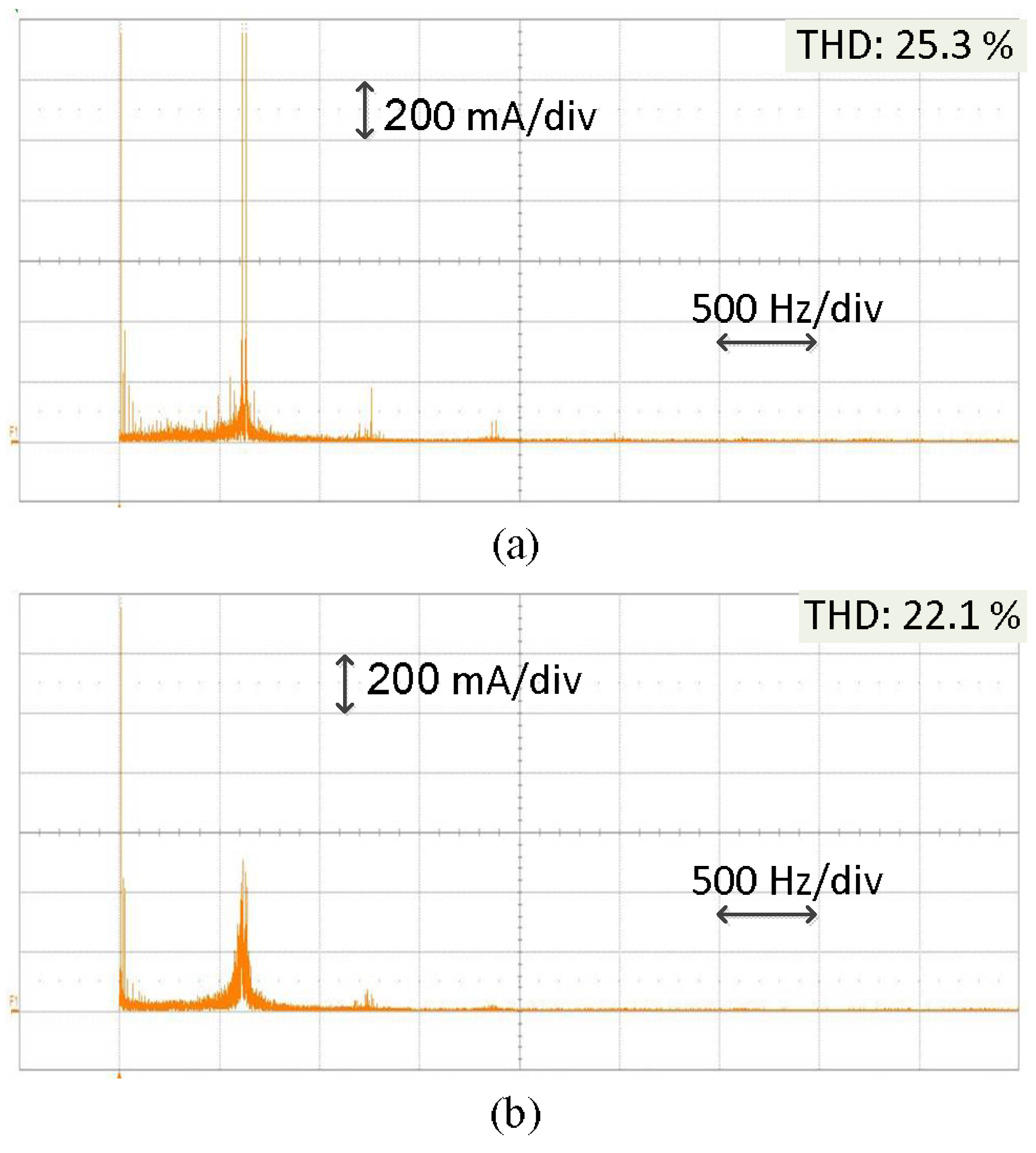
| 200 RPM | 20 Nm | CPTC | 3.88 | 25.3 |
| EEMF-PTC | 2.46 | 22.1 | ||
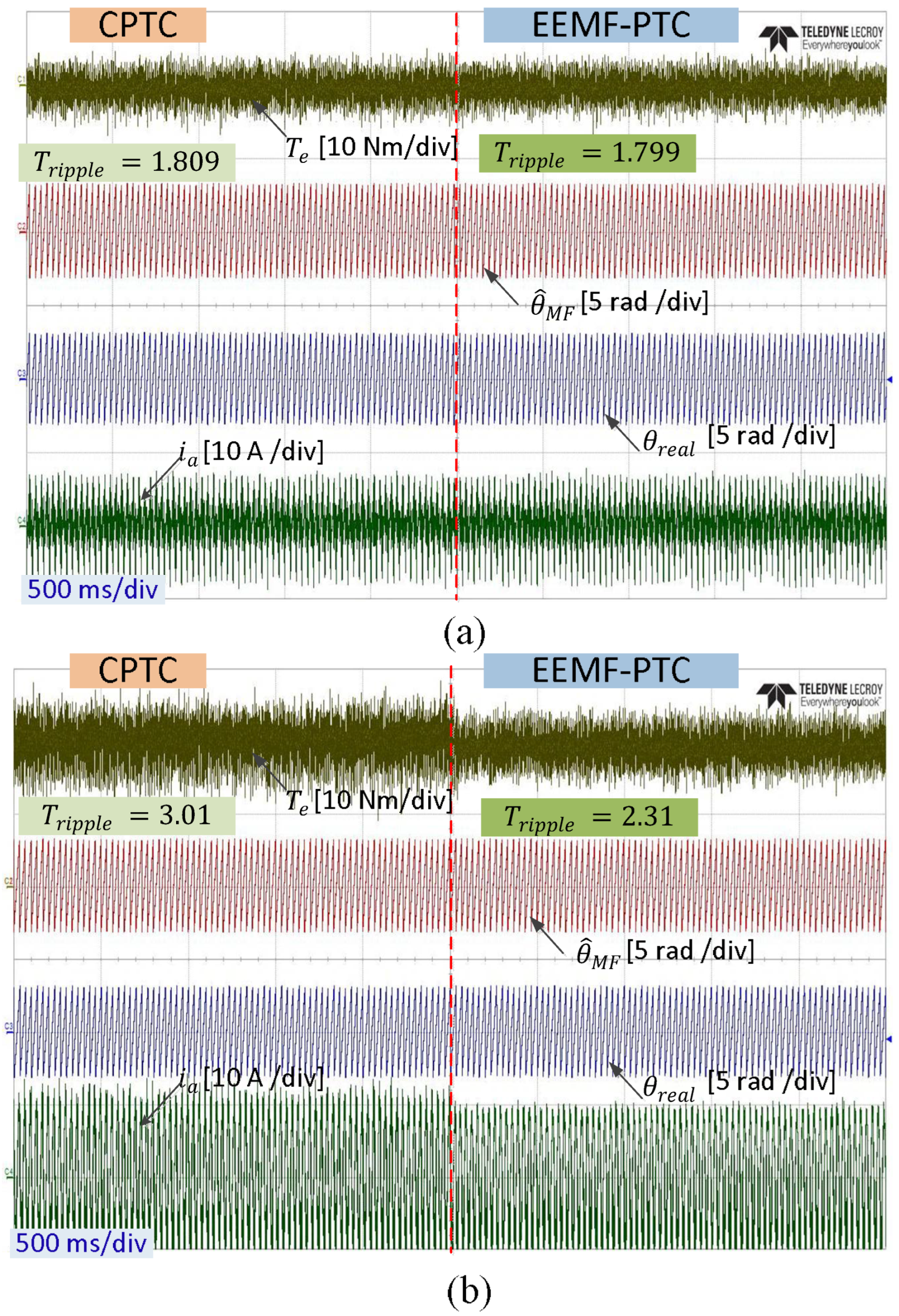
| 600 RPM | 0 Nm | CPTC | 1.809 | 29.8 |
| EEMF-PTC | 1.799 | 29.3 | ||
| 600 RPM | 20 Nm | CPTC | 3.01 | 28.4 |
| EEMF-PTC | 2.31 | 23.6 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsofyani, I.M.; Mohammed, S.A.Q. Experimental Evaluation of Predictive Torque Control of IPMSM under Speed Sensor and Sensorless Extended EMF Method. Electronics 2023, 12, 68. https://doi.org/10.3390/electronics12010068
Alsofyani IM, Mohammed SAQ. Experimental Evaluation of Predictive Torque Control of IPMSM under Speed Sensor and Sensorless Extended EMF Method. Electronics. 2023; 12(1):68. https://doi.org/10.3390/electronics12010068
Chicago/Turabian StyleAlsofyani, Ibrahim Mohd, and Sadeq Ali Qasem Mohammed. 2023. "Experimental Evaluation of Predictive Torque Control of IPMSM under Speed Sensor and Sensorless Extended EMF Method" Electronics 12, no. 1: 68. https://doi.org/10.3390/electronics12010068





