Optimal 3D Placement of UAV-BS for Maximum Coverage Subject to User Priorities and Distributions
Abstract
:1. Introduction
- We consider a practical scenario where a UAV serves as a BS for two groups of GNs with different priorities and location distributions, i.e., the high-priority GNs are uniformly distributed in the network area while the low-priority GNs gather into several clusters.
- We further develop the work of [11] in another aspect. Specifically, we propose an optimal algorithm that returns the best 3D locations of the UAV-BS so that it can cover the maximum number of high-priorities GNs. We use the MOSEK solver [20] to deal with the mixed-integer second-order cone problem (MISOCP). The performance of the proposed algorithm is compared with that of [11] (i.e., the conventional algorithm) in different urban environments and user’s location distributions.
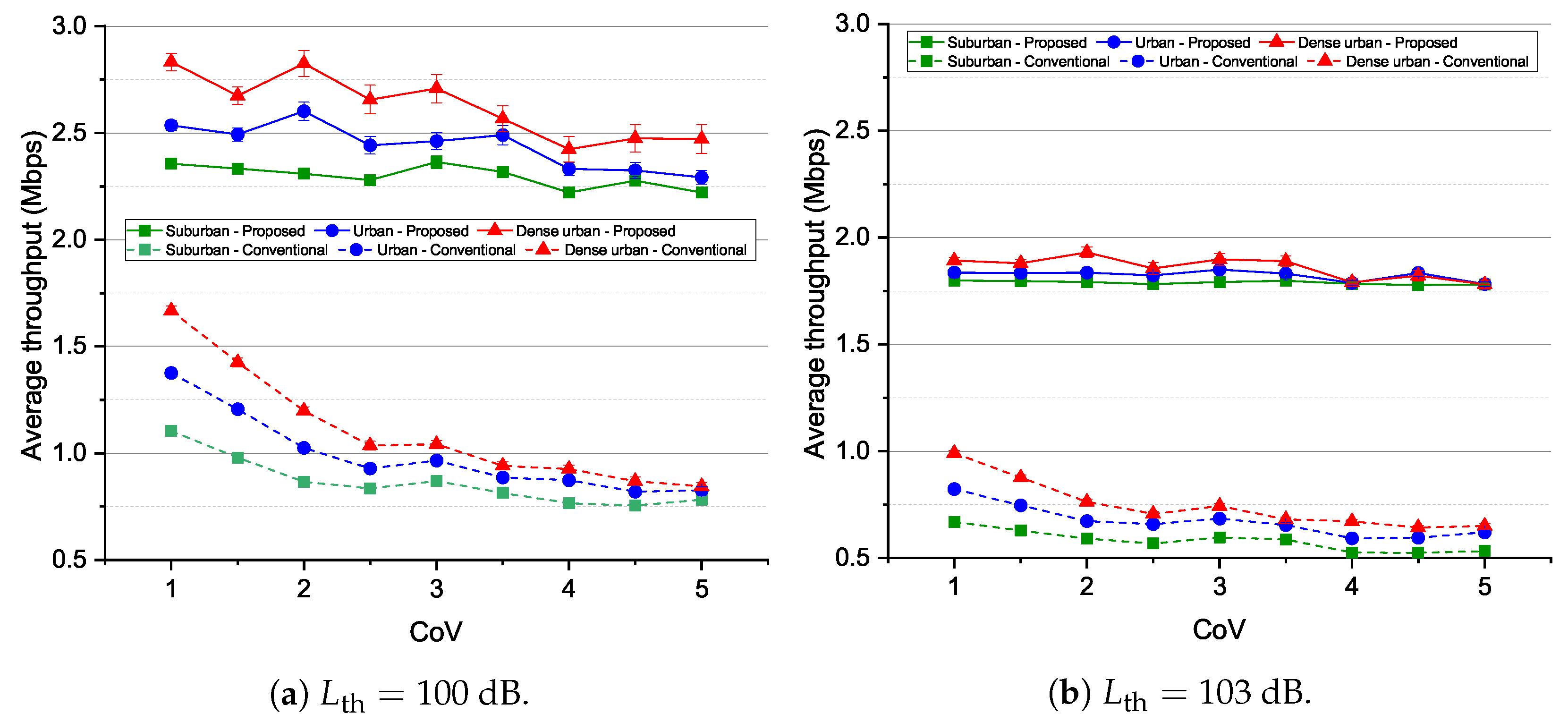
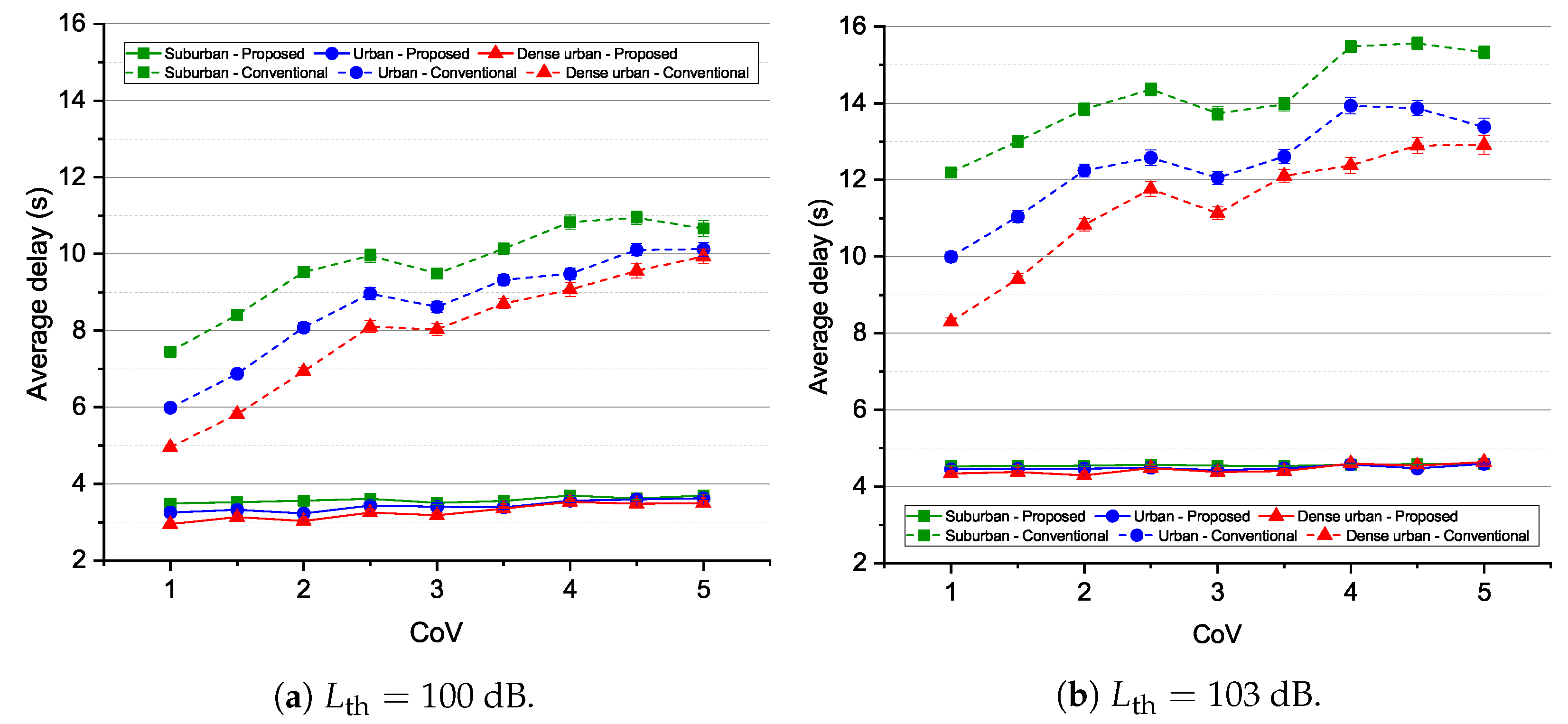
- We show that the proposed algorithm can cover high-priority GNs more efficiently compared to the conventional algorithm, which focuses on maximizing the number of GNs regardless of their priorities. As a result, the proposed algorithm maintains significantly higher average throughput and lower average delay for different location distributions and urban environments.
2. System Model
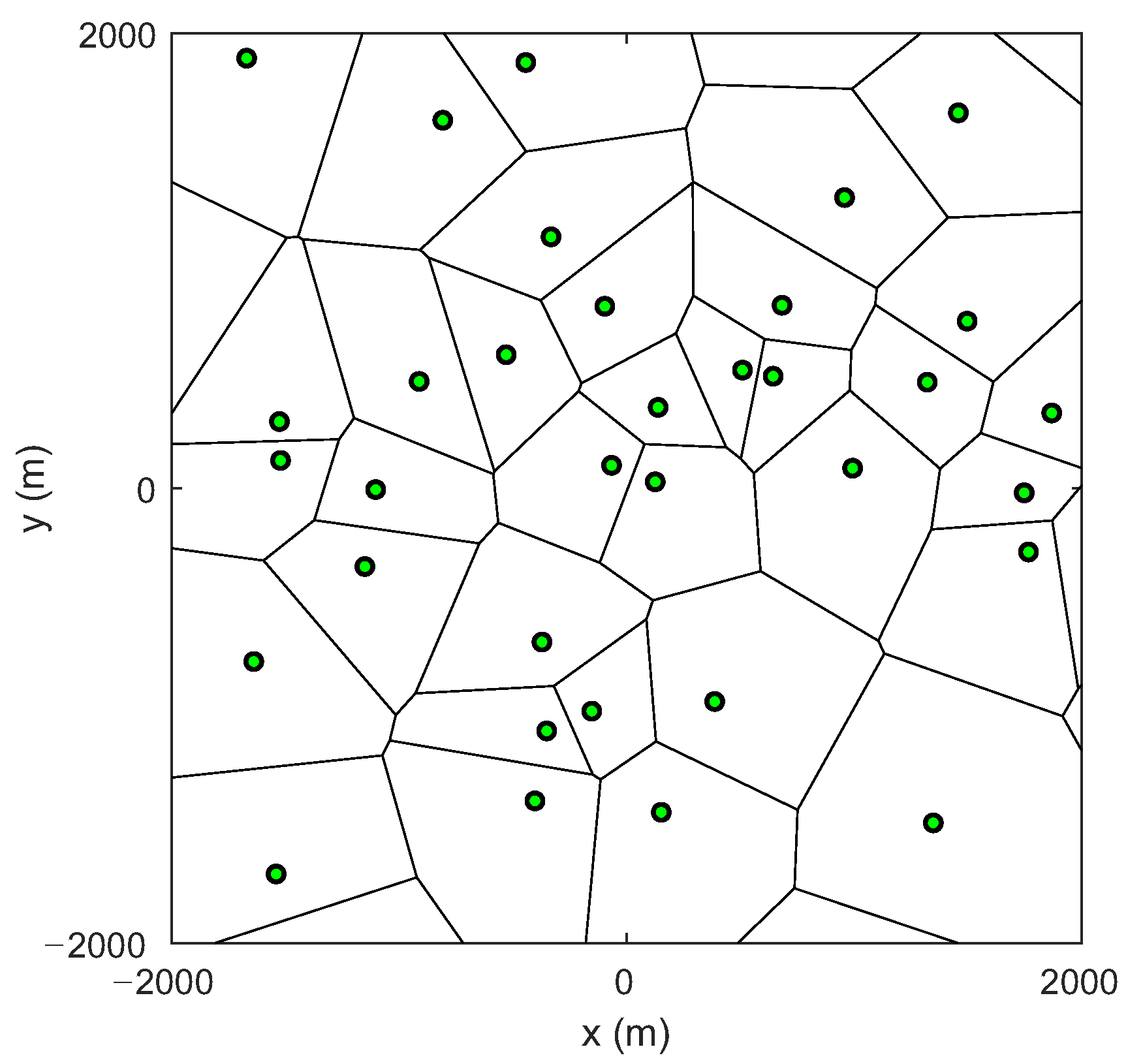
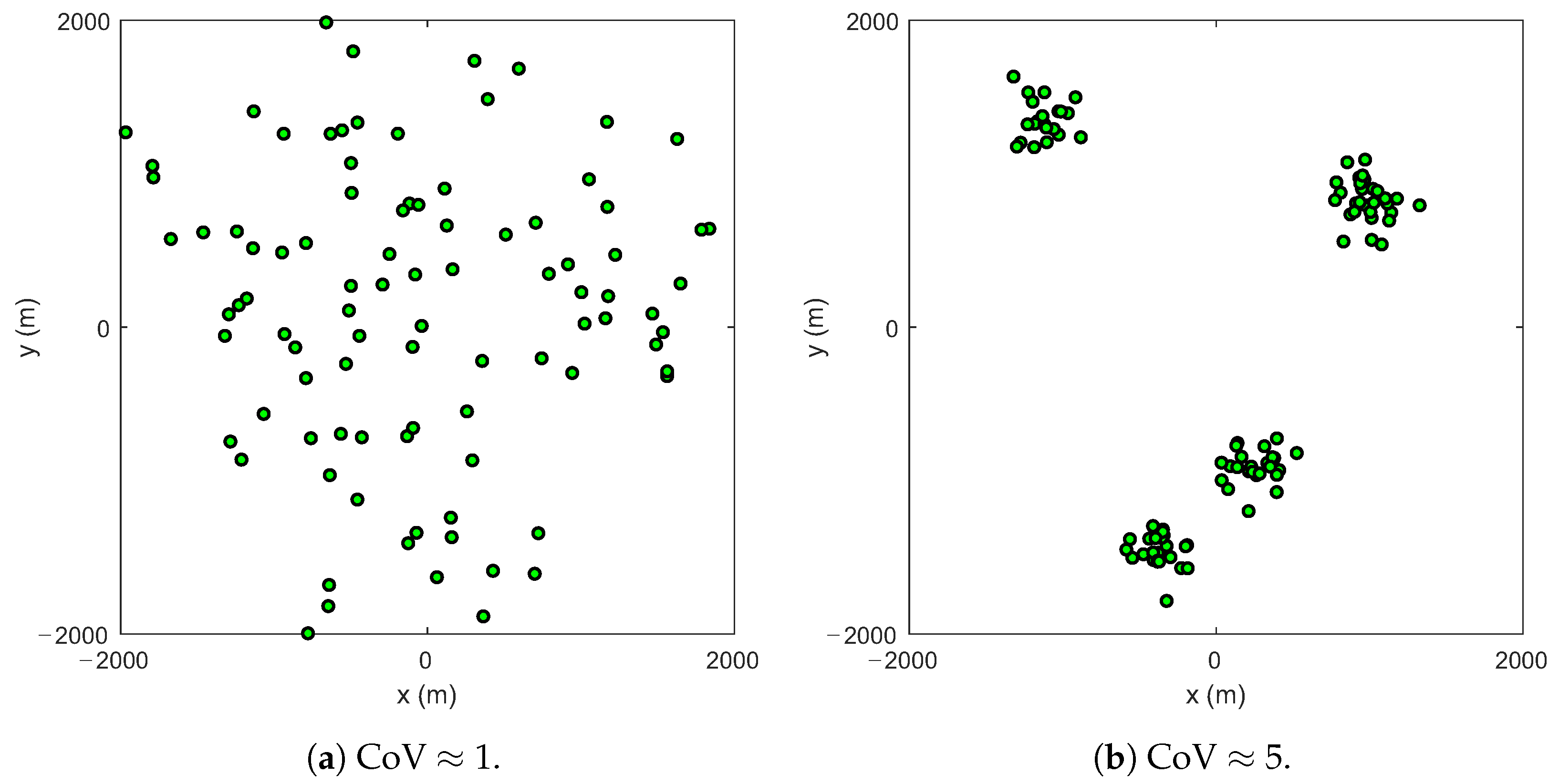
2.1. Node Distribution
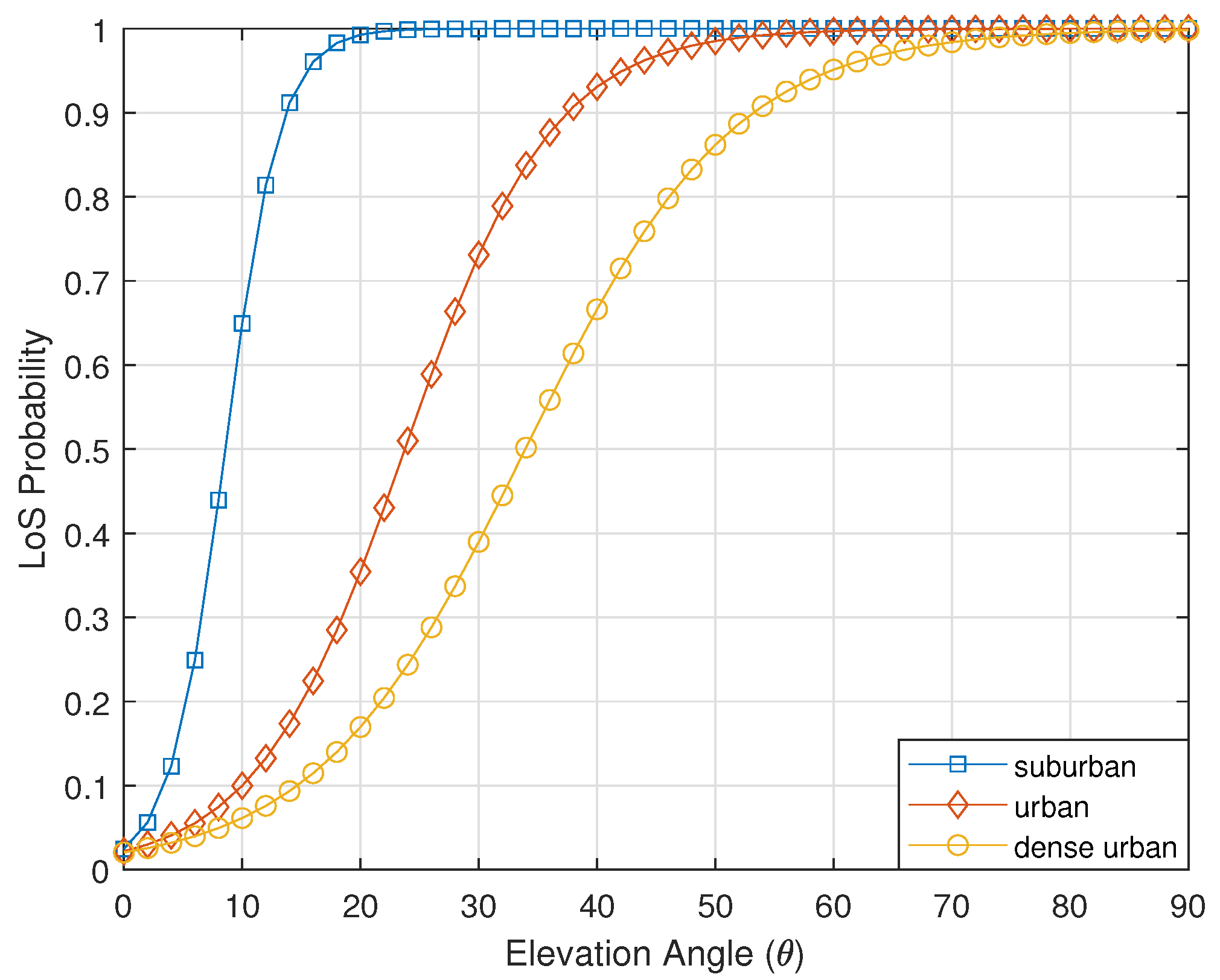
2.2. Wireless Channel
3. Deployment of the UAV for Maximizing Covered Users Subject to GN Priorities
3.1. Finding Optimal Altitude for Maximal Coverage Area
3.2. Finding Optimal Position of the UAV Subject to GN Priorities
| Algorithm 1: Obtain optimal 3D position of the UAV. |
| Input: Output: , numbers of low-priority and high-priority nodes Obtain by solving (9) Obtain UAV’s coverage radius R by solving (11) Obtain by solving (12) Solve the problem: Obtain and numbers of high-priority and low-priority GNs by solving (16) |
4. Performance Evaluation
4.1. Evaluation Metrics
4.2. Parameter Settings
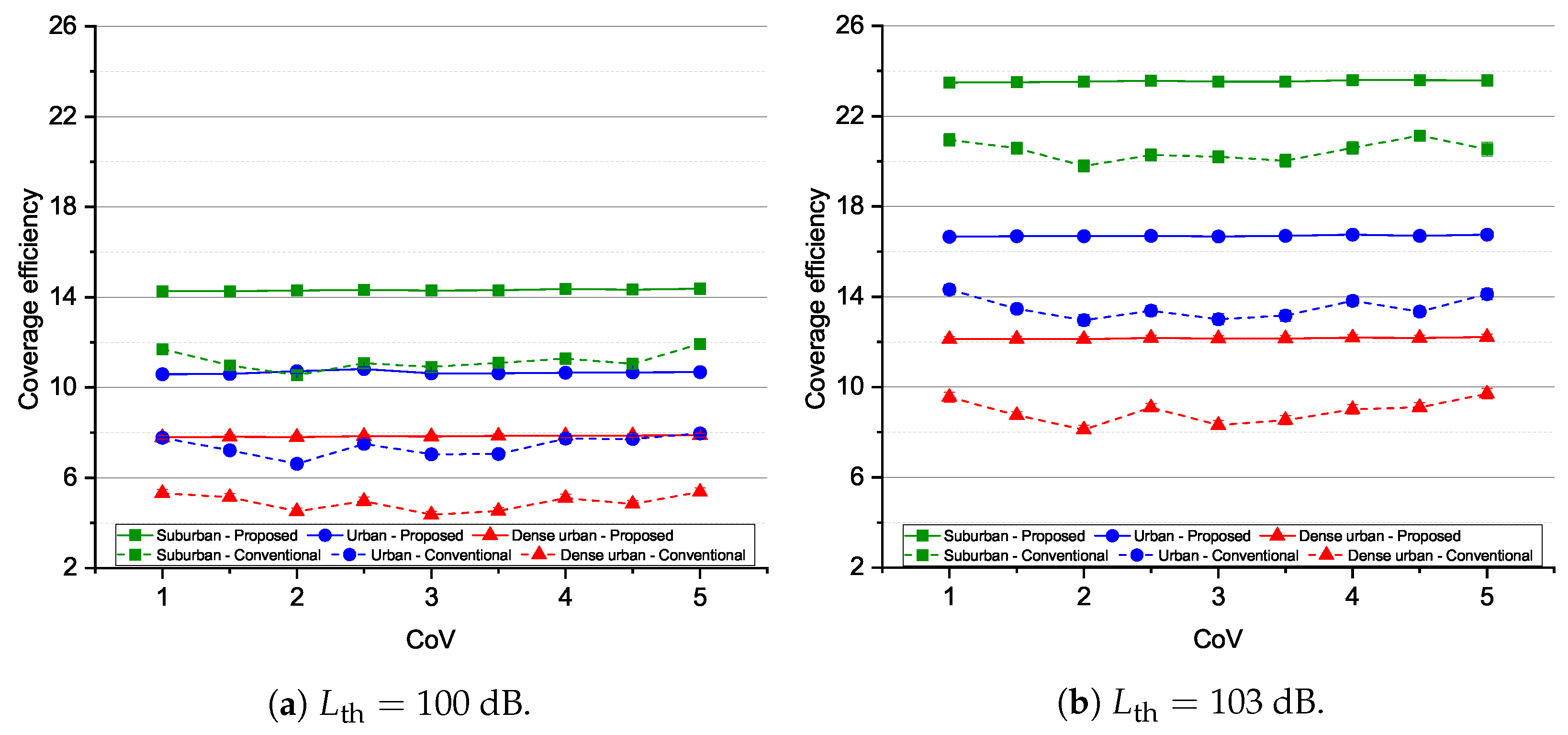
4.3. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.H.; Debbah, M. A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef] [Green Version]
- Gupta, L.; Jain, R.; Vaszkun, G. Survey of Important Issues in UAV Communication Networks. IEEE Commun. Surv. Tutor. 2016, 18, 1123–1152. [Google Scholar] [CrossRef] [Green Version]
- Alsamhi, S.H.; Ma, O.; Ansari, M.S. Predictive Estimation of the Optimal Signal Strength from Unmanned Aerial Vehicle over Internet of Things Using ANN. arXiv 2018, arXiv:1805.07614. [Google Scholar]
- Saif, A.; Dimyati, K.; Noordin, K.; Shah, N.; Alsamhi, S.; Abdullah, Q. Energy-Efficient Tethered UAV Deployment in B5G for Smart Environments and Disaster Recovery. In Proceedings of the 1st International Conference on Emerging Smart Technologies and Applications (eSmarTA), Sana’a, Yemen, 10–12 August 2021; pp. 1–6. [Google Scholar]
- Al-Hourani, A.; Kandeepan, S.; Jamalipour, A. Modeling air-to-ground path loss for low altitude platforms in urban environments. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 2898–2904. [Google Scholar]
- Khuwaja, A.A.; Chen, Y.; Zhao, N.; Alouini, M.S.; Dobbins, P. A Survey of Channel Modeling for UAV Communications. IEEE Commun. Surv. Tutor. 2018, 20, 2804–2821. [Google Scholar] [CrossRef] [Green Version]
- Gapeyenko, M.; Moltchanov, D.; Andreev, R.W.H.S. Line-of-Sight Probability for mmWave-Based UAV Communications in 3D Urban Grid Deployments. IEEE Trans. Wirel. Commun. 2021, 20, 6566–6579. [Google Scholar] [CrossRef]
- Huang, Y.; Cui, M.; Zhang, G.; Chen, W. Bandwidth, Power and Trajectory Optimization for UAV Base Station Networks With Backhaul and User QoS Constraints. IEEE Access 2020, 8, 67625–67634. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Afghah, F.; Sahal, R.; Hawbani, A.; Al-qaness, M.A.; Lee, B.; Guizani, M. Green internet of things using UAVs in B5G networks: A review of applications and strategies. Ad Hoc Netw. 2021, 117, 1–16. [Google Scholar] [CrossRef]
- Alzenad, M.; El-Keyi, A.; Lagum, F.; Yanikomeroglu, H. 3-D Placement of an Unmanned Aerial Vehicle Base Station (UAV-BS) for Energy-Efficient Maximal Coverage. IEEE Wirel. Commun. Lett. 2017, 6, 434–437. [Google Scholar] [CrossRef] [Green Version]
- Alzenad, M.; El-Keyi, A.; Yanikomeroglu, H. 3-D Placement of an Unmanned Aerial Vehicle Base Station for Maximum Coverage of Users With Different QoS Requirements. IEEE Wirel. Commun. Lett. 2018, 7, 38–41. [Google Scholar] [CrossRef] [Green Version]
- Bor-Yaliniz, R.I.; El-Keyi, A.; Yanikomeroglu, H. Efficient 3-D placement of an aerial base station in next generation cellular networks. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–5. [Google Scholar]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP Altitude for Maximum Coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef] [Green Version]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Drone Small Cells in the Clouds: Design, Deployment and Performance Analysis. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Chen, Y.; Feng, W.; Zheng, G. Optimum Placement of UAV as Relays. IEEE Commun. Lett. 2018, 22, 248–251. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Chang, T.H.; Cai, S. UAV Positioning and Power Control for Two-Way Wireless Relaying. IEEE Trans. Wirel. Commun. 2020, 19, 1008–1024. [Google Scholar] [CrossRef] [Green Version]
- Bushnaq, O.; Kishk, M.; Celik, A.; Alouini, M.S.; Al-Naffouri, T. Optimal Deployment of Tethered Drones for Maximum Cellular Coverage in User Clusters. IEEE Trans. Wirel. Commun. 2020, 20, 2092–2108. [Google Scholar] [CrossRef]
- Chen, Q. Joint Position and Resource Optimization for Multi-UAV-Aided Relaying Systems. IEEE Access 2020, 8, 10403–10415. [Google Scholar] [CrossRef]
- ApS, M. MOSEK Optimization Toolbox for MATLAB. Release 9.2.44; Mosek: Copenhagen, Denmark, 2021. [Google Scholar]
- Mirahsan, M.; Schoenen, R.; Yanikomeroglu, H. HetHetNets: Heterogeneous Traffic Distribution in Heterogeneous Wireless Cellular Networks. IEEE J. Sel. Areas Commun. 2015, 33, 2252–2265. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Liu, Y.; Chen, Y. Deployment and Movement for Multiple Aerial Base Stations by Reinforcement Learning. In Proceedings of the 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Rugelj, M.; Sedlar, U.; Volk, M.; Sterle, J.; Hajdinjak, M.; Kos, A. Novel Cross-Layer QoE-Aware Radio Resource Allocation Algorithms in Multiuser OFDMA Systems. IEEE Trans. Commun. 2014, 62, 3196–3208. [Google Scholar] [CrossRef]


| Ref. | System Model and Contribution | Optimal Altitude | Optimal Trajectory | Different Priorities for GNs |
|---|---|---|---|---|
| [8] (2021) | UAV communicate with GN; deriving the closed-form LoS and non-LoS probabilities | yes | no | no |
| [11] (2017) | UAV server GNs; finding the altitude and trajectory for maximum coverage region | yes | yes | no |
| [12] (2018) | UAV server GNs; finding the altitude and trajectory for maximizes the number of covered users with different quality-of-service requirements | yes | yes | no |
| [16] (2018) | UAV communicate with GN; deriving the closed-form expression of outage probability | yes | fixed | no |
| [18] (2021) | UAV communicate with GN; deriving the closed-form coverage probability at GNs. | no | yes | no |
| Our work | UAV server GNs; finding the altitude and trajectory for maximum coverage region for both clusters (high-priority GNs and low-priority GNs) | yes | yes | yes |
| Notation | Description |
|---|---|
| , | Locations of low-priority node and high-priority nodes |
| The elevation angle between horizontal plane and the line from ith ground node to UAV | |
| R | The radius of the coverage area of the UAV |
| f | Carrier frequency |
| Path loss of ith ground node | |
| Path loss threshold |
| Environment | (a, b) |
|---|---|
| Suburban | (4.88, 0.43) |
| Urban | (9.61, 0.16) |
| Dense urban | (12.08, 0.114) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, I.; Dung, L.T.; Kim, T. Optimal 3D Placement of UAV-BS for Maximum Coverage Subject to User Priorities and Distributions. Electronics 2022, 11, 1036. https://doi.org/10.3390/electronics11071036
Moon I, Dung LT, Kim T. Optimal 3D Placement of UAV-BS for Maximum Coverage Subject to User Priorities and Distributions. Electronics. 2022; 11(7):1036. https://doi.org/10.3390/electronics11071036
Chicago/Turabian StyleMoon, Inseok, Le The Dung, and Taejoon Kim. 2022. "Optimal 3D Placement of UAV-BS for Maximum Coverage Subject to User Priorities and Distributions" Electronics 11, no. 7: 1036. https://doi.org/10.3390/electronics11071036







