A Comparative Analysis of S-S and LCCL-S Compensation for Wireless Power Transfer with a Wide Range Load Variation

Abstract

Wireless power transmission (WPT) has great potential for charging electric vehicles. Constant voltage (CV) and constant current (CC) are two major types of battery charging modes. In this paper, we analyze the output characteristics of series-series (S-S) topology and double capacitances and inductances-series (LCCL-S) topology. Voltage gain variation is achieved in the LCCL-S compensation structure without additional components, and the system is still kept in resonant condition. A WPT experimental platform was also built and tested based on the theoretical analysis. When the load resistance is 300 Ω, a voltage gain of 0.7 or 2.22 is achieved for the LCCL-S with a compensating inductor of 100 μH or 33 μH, respectively. The experimental results fit the theoretical analysis. The CC/CV output characteristics and efficiencies of S-S and LCCL-S topologies in a wide load resistance range are also demonstrated. Moreover, zero voltage switch (ZVS) is also implemented in both two systems.

1. Introduction

With the growth of the electric vehicle industry in recent years and the limitations of battery capacity, a flexible, safe, and efficient charging method is required [1]. Compared to traditional plug-in wired charging, wireless power transmission (WPT) eliminates the need for charging cables and plugs. Meanwhile, the potential risk of electric shock is also reduced. Furthermore, the charging device can be designed to be more hermetically sealed, which allows it to be more suitable for extreme operating condition, such as rain, snow, and typhoons [2].

To increase the efficiency and reduce the reactive power of the WPT system, it is necessary to achieve the resonant condition for both transmitter and receiver sides [3]. There are four types of traditional resonant topologies using a capacitor compensated coil on one side as series-series (S-S), Series-Parallel (S-P), Parallel-Series (P-S), Parallel-Parallel (P-P) [4]. Aubakirov [5] from the National Research University of Electronic Technology optimizes the S-S and S-P topology, while the S-P topology is limited by load variations.

These traditional topologies are strongly influenced by the loosely coupled transformer (LCT) parameters [6]. Therefore, researchers proposed higher-order compensation networks to increase the system design freedom such as LCL, LCCL. Yao et al. [6] used the double side-LCL (DS-LCL) topology with conventional compensation and improved compensation with parameter tuning to achieve 200 W output and reduce harmonics in the system. Kavimandan et al. [7] compared the tolerance of LCCL-S with LCCL-P for the case where the coils are aligned. It was found that LCCL-P possesses better resistance to offsets, while the LCCL-S topology is used to reduce the reactive power. Chen et al. [8] investigated the output characteristics of the S-S and LCCL-S topologies under detuned condition. The results demonstrate that the S-S topology has better performance to high power levels condition, while the LCCL-S topology can achieve higher efficiency at lower power levels. Moreover, due to the charging characteristics of Li-ion batteries, the constant voltage (CV) or constant current (CC) output of the topology needs to be addressed [9]. Li et al. [10] proposed a parameter tuning method for the DS-LCC topology. This method can be used to achieve CC output and to realize zero phase angle, which improves the power factor of the system. Chen et al. [11] propose an asymmetric parameter tuning method that varies the values of the two compensating inductors of the LCC-LCC topology. The efficiency of the system is improved without changing the system CC output. However, too many passive components will cause extra loss [12]. Li et al. [13] also demonstrated that the S-S topology possesses higher efficiency than the LCL-S topology. In addition, wide band semiconductor devices are used to improve the efficiency of WPT systems due to their excellent performance [14]. Qian et al. verified that cascade GaN HEMTs have efficiency advantages for Si MOS over the wide load range in WPT system [15]. As mentioned by Hu et al. [16] and Vitols et al. [17], the required voltage levels are specified for different loads. Electric vehicles have DC voltages from a few volts to several hundred volts depending on the battery packs, while the electric scooter only requires a low voltage level of 24–72 V. Laha et al. [18] utilized a cascade converter to vary the output voltage at the secondary side by an external control system. However, this method causes additional power losses and raises costs. Thus, to investigate the tuning of topological parameters to produce different voltage gains for the same coil is necessary.

In this paper, the main purpose is to investigate the implementation of the LCCL-S topology with varying voltage gain, without adding additional components and ensuring a resonant state. The equivalent circuit models of two topologies, S-S and LCCL-S, are analyzed. The S-S is utilized for the CC model, and two sets of LCCL-S topologies for the CV model with different voltage gains are designed. A WPT experimental platform was built to demonstrate the output implementation of two optimized LCCL-S topologies and the S-S topology over a wide range of load variations.

2. S-S and LCCL-S WPT System Modeling Analysis

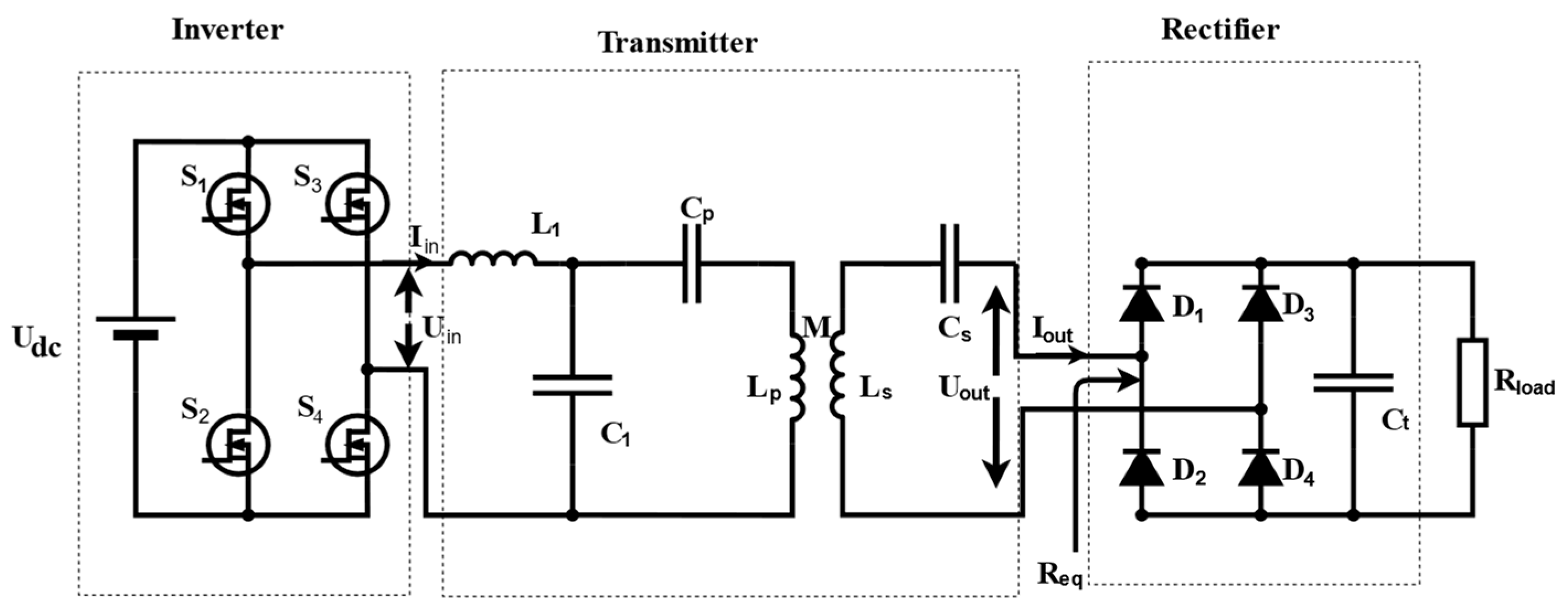
2.1. WPT System Structure

The WPT system diagram used in this paper is shown in Figure 1. It mainly contains four components: full bridge inverter (FBI), transmitter, rectifier circuit, and load resistance. For the transmitter part, there is a transmitting coil and a receiving coil with correspondent resonant compensation circuits. U_dc is the DC supply voltage. S₁–S₄ are the four transistors used in the FBI. U_in and U_out are the input and output voltages of the resonant network, respectively. I_in and I_out are the input and output current of the resonant network, respectively. L₁ is the inductance in the LCCL-S topology. C₁, C_p, and C_s are the capacitances in this topology. L_p and L_s represent the self-inductance of the transmitter-receiver coils. M represents the mutual inductance between the coils. R_eq is the equivalent load on the secondary side. D₁–D₄ are the four diodes used in the rectifier. C_t is the rectifier filter capacitor. R_load is the load resistor.

On the primary side, the DC source U_dc is converted to a square wave voltage U_in through the FBI and then flow into the resonance compensation topology. On the secondary side, a full bridge rectifier filter is utilized for converting the transferred AC voltage into DC voltage to load resistance.

T-type model is widely used to analyze WPT charging systems [19,20]. The model of a T-type circuit is shown in Figure 2. Z₁, Z₂, and Z₃ are the impedance values on each branch of the T-type circuit and Z_L-T is the load impedance of the T-type circuit. When Z₁ = Z₂ = Z₃ = jX, the topology achieves conversion from a constant current supply to a constant voltage supply, or from constant voltage input to constant current output [21]. X represents the value of reactance, and the unit imaginary number is represented by j. While achieving these functions, the T-type circuit can also achieve zero phase angle (ZPA) if the load is purely resistive.

The equation for the conversion of a CV source to a CC source is:

$$I_{out-T}=\frac{U_{in-T}}{jX}$$

(1)

$U_{in-T}$ is the input voltage of the T-type circuit. $I_{out-T}$ is the output current of this circuit.

The equation for the conversion of a CC source to a CV source is:

$$U_{out-T}=jX{I}_{in-T}$$

(2)

$I_{in-T}$ is the input current of the T-type circuit. $U_{out-T}$ is the output voltage of this circuit.

Input impedance is set to Z_in-T. Its input impedance is:

$$Z_{in-T}=\frac{X^2}{Z_{L-T}}$$

(3)

Z_L-T is the load impedance.

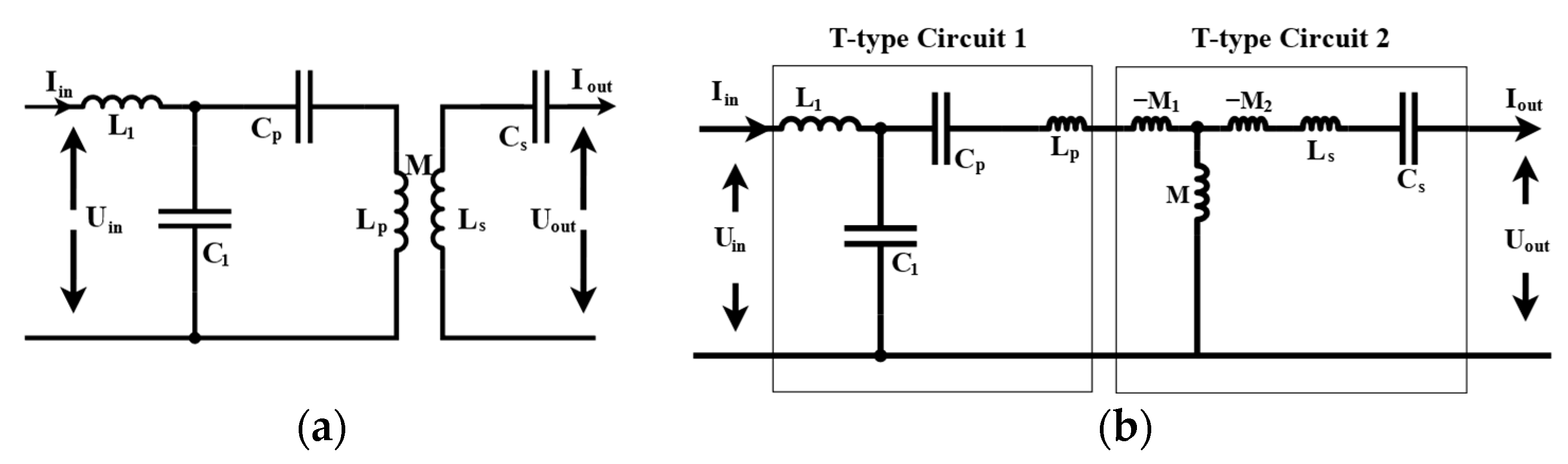
2.2. S-S Resonant Topology

The S-S resonant compensation topology model is depicted in Figure 3a, where the inductance of the coil is directly compensated by the capacitance which is connected in series with it [4]. C_p represents the primary side compensated capacitor and C_s represent the secondary side compensated capacitor. As shown in Figure 3b, the mutual inductance M of the symmetrical coil can be equated to a T-type circuit [22].

The relationship between its compensation capacitance and coil inductance is as follows.

$${\omega }_0{L}_s=\frac{1}{{\omega }_0{C}_s}$$

(4)

$${\omega }_0{L}_p=\frac{1}{{\omega }_0{C}_p}$$

(5)

${\omega }_0$ is the angular frequency of the system at resonance.

In Figure 3b, the impedances of C_p, L_p, and −M₁ are equivalent to Z₁ of the T-type circuit model. The impedance of −M₂, L_s, and C_s are equivalent to Z₂. The impedance of M is equivalent to Z₃. As the S-S topology is equated to a T-type circuit at resonance, the topology functions as such, converting constant voltage input into constant current output.

According to Equation (1), CC output is:

$$I_{out0\left(S-S\right)}=\frac{U_{in}}{j{\omega }_{0}M}$$

(6)

I_out0(S-S) is the output current of the topology at resonance.

The equivalent impedance at resonance:

$$Z_{in0\left(S-S\right)}=\frac{{{\omega }_0}^2{M}^2}{R_{eq}}$$

(7)

Z_in0(S-S) is the input impedance.

2.3. LCCL-S Resonant Topology

The structure of the LCCL-S topology is shown in Figure 4a [23], and the equivalent circuit diagram for the LCCL-S topology could be found in Figure 4b. The coil is connected in series with the capacitor C_p, which equates to Z₃ in a T-type circuit; this combination forms a T-type equivalent circuit with L₁ and C₁. The mutual inductance of the symmetrical coils is also equivalent to a T-type circuit. Therefore, the LCCL-S circuit would be equated to a cascade of two T-type circuits. The parameters of the T-type circuit equivalent of the mutual inductor cannot be changed, while the T-type circuit parameters of L₁ can be freely designed.

The relationship between its compensation capacitance and coil inductance in LCCL-S topology is as follows.

$${\omega }_0{L}_1=\frac{1}{{\omega }_0{C}_1}={\omega }_0{L}_P-\frac{1}{{\omega }_0{C}_P}$$

(8)

$$\frac{1}{{\omega }_0{C}_s}={\omega }_0{L}_s$$

(9)

In T-type circuit 1, shown in Figure 4b, the impedance of L₁ is equivalent to Z₁ of the T-type circuit model, the impedance of L_p and C_p is equivalent to Z₂, and the impedance of C₁ is equivalent to Z₃. In T-type circuit 2, the −M₁ impedance is equivalent to Z₁; the impedances of −M₂, L_s, and C_s are equivalent to Z₂ of the T-type circuit; and the impedance of M is equivalent to Z₃. The LCCL-S topology is equated to two T-type circuits cascaded. Thus, T-type circuit 1 converts the CV input into a CC output, and T-type circuit 2 converts this CC output into a CV output again. According to Equations (1) and (2), the topology achieves a constant voltage output independent of the load.

For the CV output:

$$U_{out0\left(LCCL-S\right)}=\frac{U_{in}M}{L_1}$$

(10)

The relative positions between the transmitter coil and receiver coil are assumed to be unchanged in the transmitting process. Therefore, the mutual inductor M is a constant value. Thus, according to Equation (10), the gain of the output voltage U_{out0 (LCCL-S)} with respect to U_in can be varied by the parameters of T-type circuit 1 configured based on the value of L₁. The equivalent impedance at resonance.

$$Z_{in0\left(LCCL-S\right)}=\frac{L_1^2}{M^2}{R}_{eq}$$

(11)

U_out0(LCCL-S) is the output current of the topology at resonance. Z_in0(LCCL-S) is the input impedance.

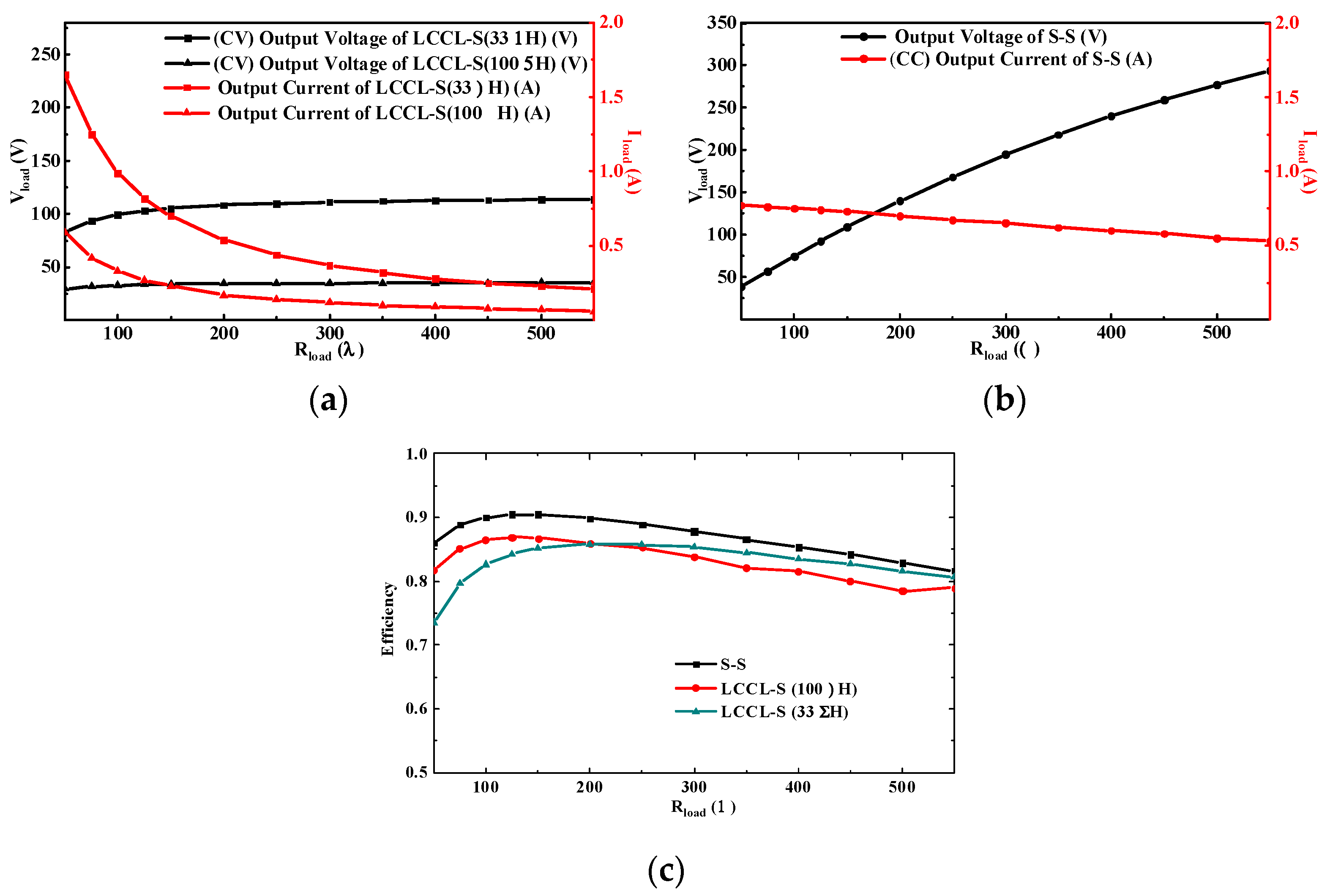
3. Experiment Verification

It is necessary to verify the feasibility of the WPT charging systems. Figure 5 shows the WPT prototype platform and cascade GaN-based FBI. The DC input sources (ITECH IT6526D) is used to supply high-level DC power to the WPT system. Auxiliary power supply (ITECH IT6721) is utilized to support DSP (TMS320F28335) and FBI. The DSP controller requires the input voltage to be 5 V and the FBI requires the constant voltage supply level to be 12 V. The programmable resistors choose ITECH DC electric load IT8816B to provide variable load resistors. The voltage and current measurements are used a current probe (Tektronix P5200A) and a differential voltage probe (Tektronix TCP2020) with an oscilloscope (Agilent DSOX2024A). FBI was formed by four Cascade GaN HEMT(TPH3206PS) and Silicon Carbide Schottky Diode (C3D08060A) are utilized to build the rectifier. The transmitter and receiver coil have the same size with outer diameter of 45 cm and an inner diameter of 30 cm formed with litz wire. The spacing between two coils is 12.5 cm. According to the model equation and experiment measurement result, the parameters of S-S and LCCL-S resonant compensation are shown in

Table 1. Parameters of S-S and LCCL-S resonant compensation.

Parameters	S-S	LCCL-S (L1 = 33 μH)	LCCL-S (L1 = 100 μH)
System Frequency f0	100 kHz	100 kHz	100 kHz
Coil self-inductances Lp, Ls	385 μH	385 μH	385 μH
Coil mutual-inductances M	80 μH	80 μH	80 μH
Primary compensation inductance L1	\	33 μH	100 μH
Primary parallel capacitance C1	\	76 nF	25.33 nF
Primary series capacitance Cp	6.6 nF	7.19 nF	8.89 nF
Secondary series capacitance Cs	6.6 nF	6.6 nF	6.6 nF

. To verify the relationship between the parameters of the resonant compensating inductor L₁ and the voltage gain, the LCCL-S resonant topology with two set of parameters is designed.

To reduce the switching losses of the WPT system on the inverter, the I_in needs to lag behind the U_in by a small angle. In this way, the zero voltage switching (ZVS) is also realized [24]. Figure 6a–c show the output voltage (U_in) phase leads output current (I_in) of the FBI. Figure 6d–f show the V_ds and V_gs for transistor S₄ in FBI, demonstrating that V_ds has dropped to zero before V_gs rises.

The DC supply voltage is used to 50 V and the load resistance is varied from 50 Ω to 550 Ω by a programmable load. Experimental data for CC and CV models with different resonant compensation topologies are shown in part a and part b of Figure 7. Simultaneously, the efficiency of the WPT system with different topologies is shown in part c of Figure 7. S-S topology is used to implement CC Mode and LCCL-S is used to implement CC Mode. For the LCCL-S structure, the experimental results demonstrate the relationship between the magnitude of L₁ and the system mutual inductance M allows the output voltage to be achieved above or below the input voltage. When L₁ is greater than the mutual inductance M, the voltage gain will be less than 1; when L₁ is less than the M, the voltage gain will be greater than 1. According to Equation (10), the output voltage of the LCCL-S (33 μH) is 121 V for a DC input voltage of 50 V, which is approximately 113 V in the actual test. The output voltage of the LCCL-S (100 μH) is 40 V, which is approximately 35 V in the experimental result.

Figure 6a,b shows the output voltage and current for two LCCL-S topologies with different compensated inductors L₁ as well as for the S-S topology. For example, the output voltage and current for the two LCCL-S topologies are 35.05 V, 0.12 A (100 μH), and 112.16 V, 0.37 A (33 μH) and the S-S topology voltage and current are 194.79 V, 0.65 A, for a load resistance equal to 300 Ω. As can be seen in Figure 7a, the output voltage variation rates for the two LCCL-S topologies are 2.6% (100 μH) and 4.8% (33 μH) for load resistances greater than 200 Ω, giving a good constant voltage output performance. Figure 7b shows that the S-S topology has a current variation of 7.9% at loads of 75–200 Ω. At loads above 200 Ω, the constant current performance deteriorates, and the output voltage is extremely high. This can cause damage to devices such as rectifier diodes. Figure 7c shows the variation in efficiency of the three topologies over a wide load range. The topology efficiency rises and then falls as the load resistance changes, with the S-S topology reaching a maximum efficiency of 90.46% at 150 Ω. The LCCL-S (100 μH) reaches a maximum efficiency of 86.92% at 125 Ω. The LCCL-S (33 μH) reaches a maximum efficiency of 85.79% at 200 Ω. However, the LCCL-S topology is the better choice for load ranges above 200 Ω and where a constant voltage output is required. It can also be seen from Figure 7c that the LCCL-S topology with a small compensating inductor is slightly more efficient for load resistances above 200 Ω.

Both the S-S and LCCL-S topologies maintain a high level of efficiency over a wide range of load variations. The overall efficiency of the LCCL-S topology is lower than that of the S-S topology as the LCCL-S topology has more passive components than the S-S topology. For the LCCL-S structure, two group parameters are necessary to be compared. An LCCL-S system with an L₁ value of 100 μH will have a higher efficiency than a system with an L₁ value of 33 μH for a load range of less than 200 Ω. At larger loads, the topology with an L₁ value of 33 μH generates a larger current on the primary side coil, causing larger losses. In a load range greater than 200 Ω, the efficiency of an LCCL-S WPT system with an L₁ value of 100 μH will be lower than an LCCL-S WPT system with an L₁ value of 33 μH. The possible reason for this analysis is that the losses generated by the rectifier account for a larger proportion of the overall losses due to the smaller voltage gain of the topology with an L₁ value of 100 μH.

4. Conclusions

In this paper, equivalent circuit models for the S-S and LCCL-S topology are analyzed. The expressions for the output voltage, current and input impedance are derived. The relationship between the output voltage and inductor L₁ is investigated for the LCCL-S topology. The parameters of the S-S and the LCCL-S topology are specified for the ZVS based on the parameters of the transmission coil and the implementation condition. Two different LCCL-S systems are also developed to verify the relationship between the L₁ inductance value and the mutual inductance M. Under a DC voltage input of 50 V, both topologies achieve ZVS. In the S-S topology, with the load range of 75–200 Ω, it achieves a maximum efficiency of 90.45%. In the LCCL-S topology (100 μH), with the load range of 200–550 Ω, it achieves a maximum efficiency of 85.94%. In the LCCL-S topology (33 μH), with the range of 200–550 Ω, it achieves a maximum efficiency of 85.79%. The output voltage and current also demonstrate that the different topologies accomplish the corresponding CC and CV functions. With a load resistance of 75–200 Ω, the S-S current varies by 7.9%. With a load resistance greater than 200 Ω, the voltage variation is 4.8% for the LCCL-S with a compensating inductor L₁ of 100 μH and 2.6% for the L₁ equal to 33 μH. Two sets of LCCL-S WPT systems obtained special voltage gain. Therefore, the parameter optimization of the LCCL-S WPT system would achieve different voltage gains for same transmitter coil and it is suitable for wide load variation. When the load resistance is equal to 300 Ω, the voltage gain is 0.7 for the LCCL-S with a compensating inductor of 100 μH and 2.22 for the LCCL-S with a compensating inductor of 33 μH.