Optimal Field Sampling of Arc Sources via Asymptotic Study of the Radiation Operator
Abstract
:1. Introduction
1.1. Literature Review
1.2. Goal of the Paper
2. Geometry of the Problem
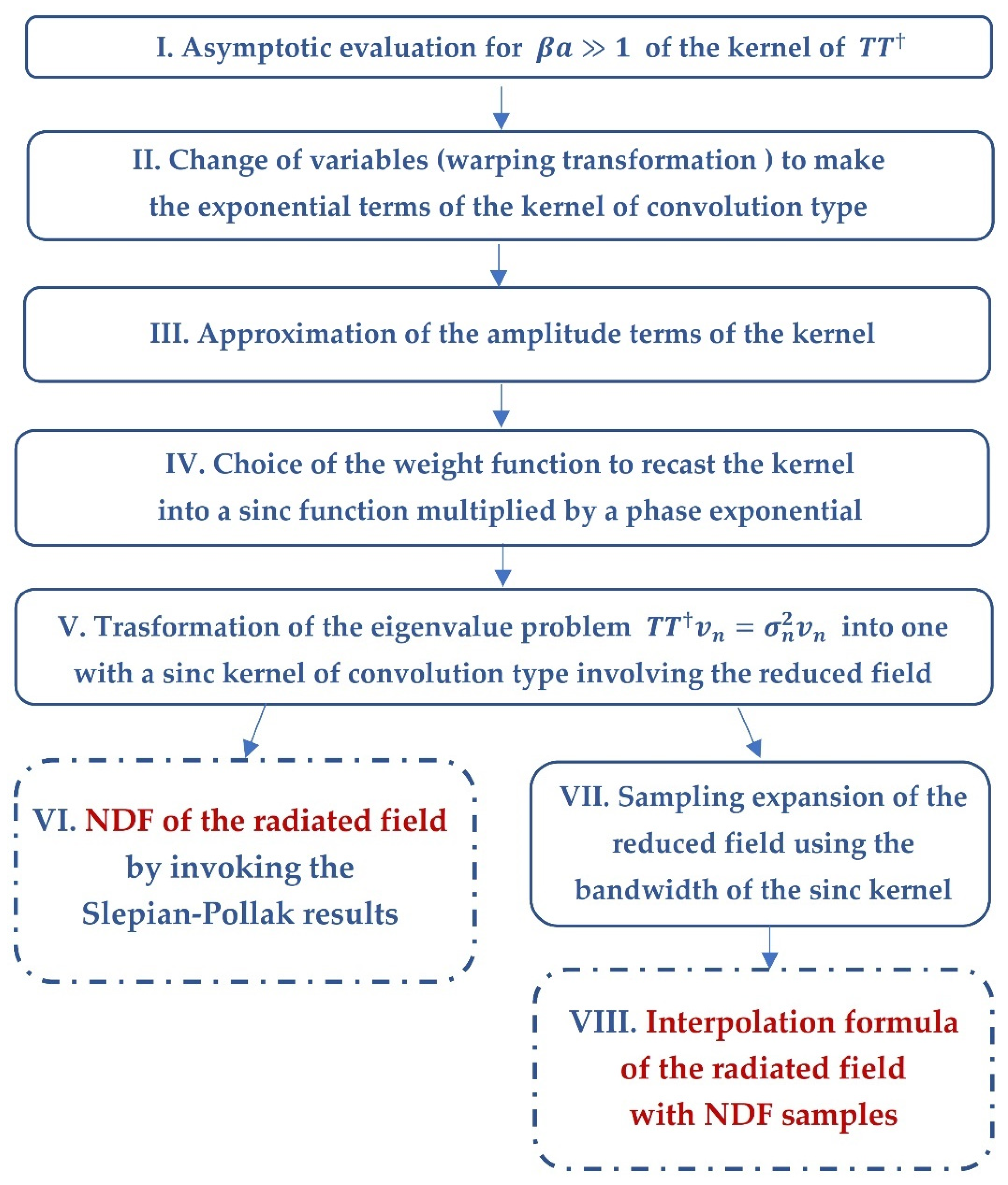
3. Outline of the Sampling Strategy
4. Optimal Sampling of the Far-Field
4.1. Asymptotic Study of the Operator in Far Zone
4.2. NDF Evaluation and Interpolation of the Far Field
- ;
- is the set containing all those indexes such that .
5. Optimal Sampling of the near Field
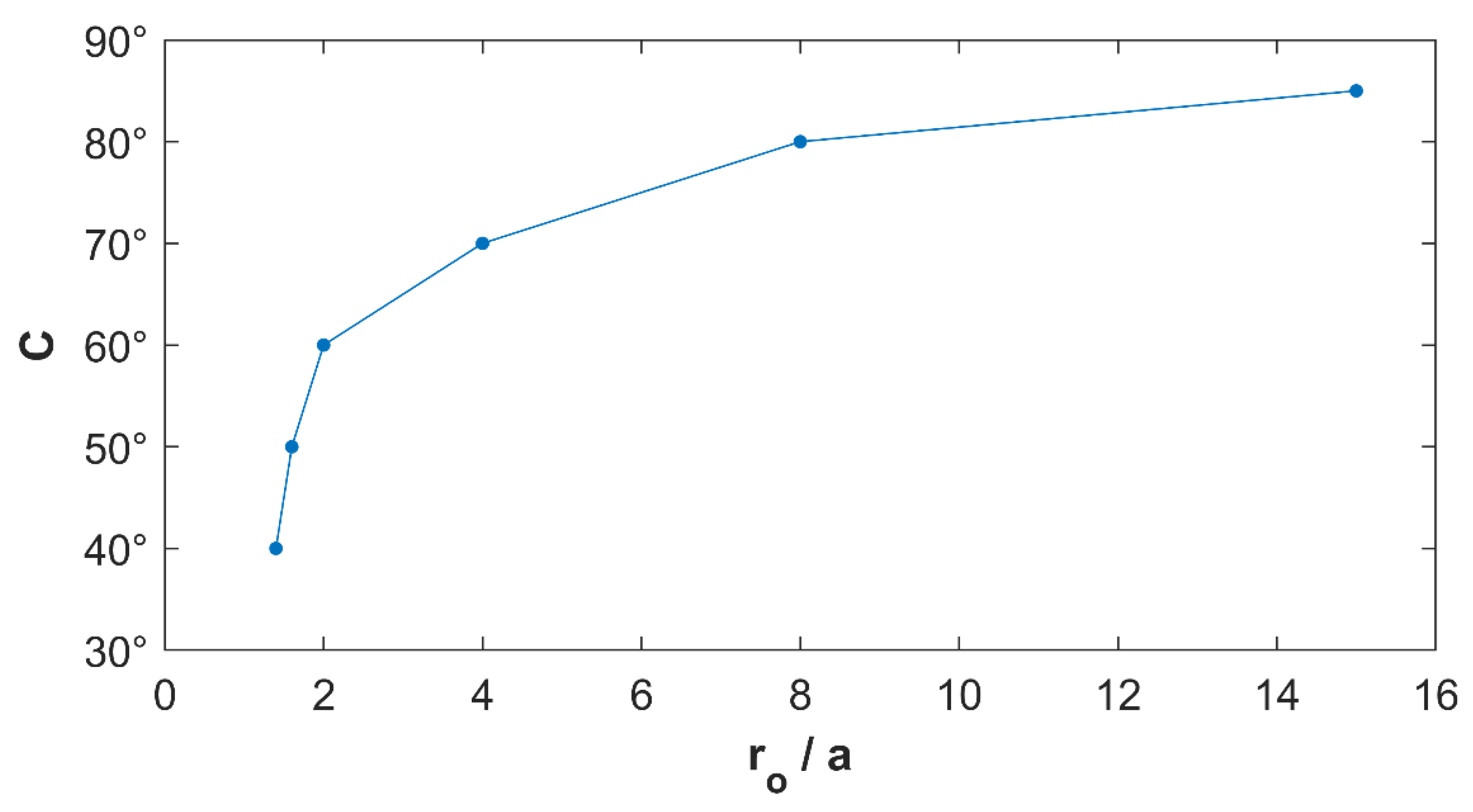
5.1. Asymptotic Study of the of the Operator in Near Zone
- ,
- .
- fixing the source angle , the interval for which no stationary points appear on the source increases with the ratio .
- fixing the ratio , the interval for which no stationary points appear on the source decreases with the source angle .
5.2. NDF Estimation and Interpolation of the near Field
- ;
- is the set containing all those index such that .
6. Comparison between Non-Uniform and Uniform Sampling
- is the Dirichlet function
- are the sampling points uniformly spaced over the observation arc, hence, with and .
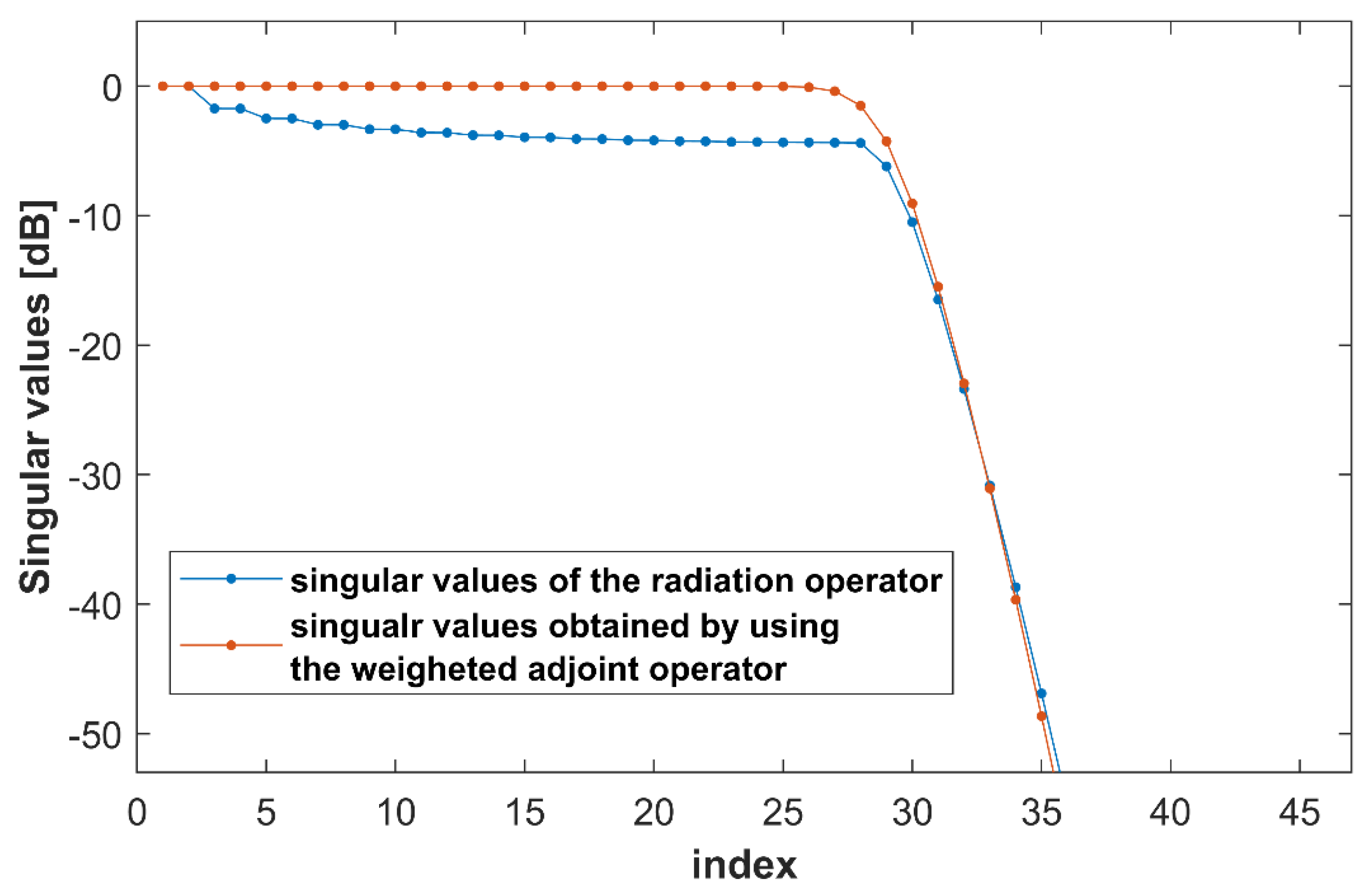
7. Numerical Validation
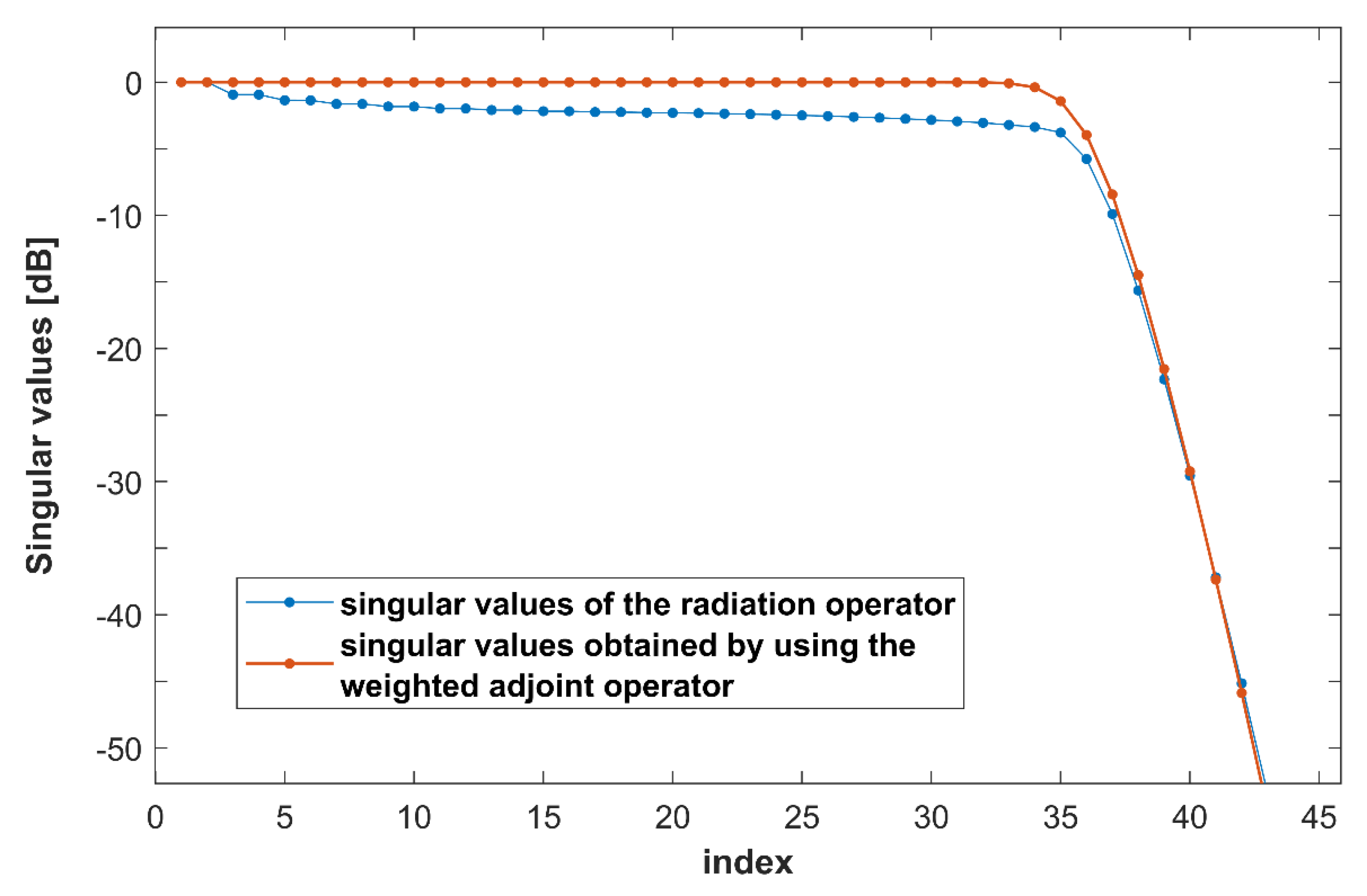
7.1. Far-Field Sampling Validation
7.2. Near-Field Sampling Validation
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Maximum Value of Such That no Stationary Points Appear in | |
|---|---|
| ) | |
| ) |
| Maximum Value of Such That no Stationary Points Appear in | |
|---|---|
| Maximum Value of Such That no Stationary Points Appear in | |
|---|---|
| 1.6 | |
| 2 | |
| 4 | |
| 8 | |
| 15 |
References
- Rahmat-Samii, Y.; Cheung, R. Non-uniform sampling techniques for antenna applications. IEEE Trans. Antennas Propag. 1987, 35, 268–279. [Google Scholar] [CrossRef]
- Wang, J.; Yarovoy, A. Sampling design of synthetic volume arrays for three-dimensional microwave imaging. IEEE Trans. Comp. Imag. 2018, 4, 648–660. [Google Scholar] [CrossRef]
- Mézières, N.; Fuchs, B.; Le Coq, L.; Lerat, J.M.; Contreres, R.; Le Fur, G. On the Antenna Position to Improve the Radiation Pattern Characterization. IEEE Trans. Antennas Propag. 2021, 69, 5335–5344. [Google Scholar] [CrossRef]
- Migliore, M.D. Near field antenna measurement sampling strategies: From linear to nonlinear interpolation. Electronics 2018, 7, 257. [Google Scholar] [CrossRef] [Green Version]
- Foged, L.J.; Saccardi, F.; Mioc, F.; Iversen, P.O. Spherical Near Field Offset Measurements using Downsampled Acquisition and Advanced NF/FF Transformation Algorithm. In Proceedings of the 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016. [Google Scholar]
- D′Agostino, F.; Ferrara, F.; Gennarelli, C.; Guerriero, R.; Migliozzi, M. Fast and Accurate Far-Field Prediction by Using a Reduced Number of Bipolar Measurements. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2939–2942. [Google Scholar]
- Hofmann, B.; Neitz, O.; Eibert, T. On the minimum number of samples for sparse recovery in spherical antenna near-field measurements. IEEE Trans. Antennas Propag. 2019, 67, 7597–7610. [Google Scholar] [CrossRef]
- Kim, Y.H. Greedy sensor selection based on QR factorization. EURASIP J. Adv. Signal Process. 2021, 1, 1–13. [Google Scholar] [CrossRef]
- Behjoo, H.R.; Pirhadi, A.; Asvadi, R. Optimal Sampling in Spherical Near-Field Antenna Measurements by Utilizing the Information Content of Spherical Wave Harmonics. IEEE Trans. Antennas Propag. 2021, 1. [Google Scholar] [CrossRef]
- Leone, G.; Maisto, M.A.; Pierri, R. Inverse Source of Circumference Geometries: SVD Investigation Based on Fourier Analysis. Progr. Electromagn. Res. M 2018, 76, 217–230. [Google Scholar] [CrossRef] [Green Version]
- Solimene, R.; Brancaccio, A.; Romano, J.; Pierri, R. Localizing Thin Metallic Cylinders by a 2.5-D Linear Distributional Approach: Experimental Results. IEEE Trans. Antennas Propag. 2008, 56, 2630–2637. [Google Scholar] [CrossRef]
- Joy, E.; Paris, D. Spatial sampling and filtering in near-field measurements. IEEE Trans. Antennas Propag. 1972, 20, 253–261. [Google Scholar] [CrossRef]
- Leach, W.; Paris, D. Probe compensated near-field measurements on a cylinder. IEEE Trans. Antennas Propag. 1973, 21, 435–445. [Google Scholar] [CrossRef]
- Bucci, O.M.; Gennarelli, C.; Saverese, C. Optimal Interpolation of radiated fields over a sphere. IEEE Trans. Antennas Propag. 1991, 39, 1633–1643. [Google Scholar] [CrossRef]
- Piestun, R.; Miller, D.A.B. Electromagnetic degrees of freedom of an optical system. J. Opt. Soc. Amer. A 2000, 17, 892–902. [Google Scholar] [CrossRef] [PubMed]
- Pierri, R.; Moretta, R. NDF of the near-zone field on a line perpendicular to the source. IEEE Access 2021, 9, 91649–91660. [Google Scholar] [CrossRef]
- Qureshi, M.A.; Schmidt, C.H.; Eibert, T.F. Adaptive Sampling in Spherical and Cylindrical Near-Field Antenna Measurements. IEEE Antennas Propag. Mag. 2013, 55, 243–249. [Google Scholar] [CrossRef]
- Bucci, O.M.; Gennarelli, C.; Savarese, C. Representation of Electromagnetic Fields over Arbitrary Surfaces by a Finite and Nonredundant Number of Samples. IEEE Trans. Antennas Propag. 1998, 46, 351–359. [Google Scholar] [CrossRef]
- Leone, G.; Munno, F.; Solimene, R.; Pierri, R. A PSF Approach to Far Field Discretization for Conformal Sources. IEEE Trans. Comp. Imag. 2022. Available online: https://www.techrxiv.org/articles/preprint/A_PSF_Approach_to_Far_Field_Discretization_for_Conformal_Sources/17708579 (accessed on 12 December 2021).
- Capozzoli, A.; Curcio, C.; Liseno, A. Different Metrics for Singular Value Optimization in Near-Field Antenna Characterization. Sensors 2021, 21, 2122. [Google Scholar] [CrossRef]
- Joshi, S.; Boyd, S. Sensor selection via convex optimization. IEEE Trans. Signal Process. 2008, 57, 451–462. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Soh, Y.; Li, H. Sensor placement by maximal projection on minimum eigenspace for linear inverse problems. IEEE Trans. Signal Process. 2016, 64, 5595–5610. [Google Scholar] [CrossRef] [Green Version]
- Solimene, R.; Maisto, M.A.; Pierri, R. Sampling approach for singular system computation of a radiation operator. JOSA A 2019, 36, 353–361. [Google Scholar] [CrossRef] [PubMed]
- Maisto, M.A.; Pierri, R.; Solimene, R. Near-Field Warping Sampling Scheme for Broad-Side Antenna Characterization. Electronics 2020, 9, 1047. [Google Scholar] [CrossRef]
- Pierri, R.; Moretta, R. Asymptotic Study of the Radiation Operator for the Strip Current in Near Zone. Electronics 2020, 9, 911. [Google Scholar] [CrossRef]
- Bleistein, N.; Handelsman, R.A. Asymptotic Expansions of Integrals; Dover: New York, NY, USA, 1986. [Google Scholar]
- Slepian, D.; Pollack, H.O. Prolate spheroidal wave functions, Fourier analysis, and uncertainty—I. Bell Syst. Tech. J. 1961, 40, 43. [Google Scholar] [CrossRef]
- Khare, K.; George, N. Sampling theory approach to prolate spheroidal wavefunctions. J. Phys. A Math. Gen. 2003, 36, 10011. [Google Scholar] [CrossRef]
- Devaney, A. Mathematical Foundations of Imaging, Tomography and Wavefield Inversion; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Pierri, R.; Leone, G.; Moretta, R. The Dimension of Phaseless Near-Field Data by Asymptotic Investigation of the Lifting Operator. Electronics 2021, 10, 1658. [Google Scholar] [CrossRef]
- Pierri, R.; Moretta, R. On the Sampling of the Fresnel Field Intensity over a Full Angular Sector. Electronics 2021, 10, 832. [Google Scholar] [CrossRef]
- Rodríguez Varela, F.; Fernandez Álvarez, J.; Galocha Iragüen, B.; Sierra Castañer, M.; Breinbjerg, O. Numerical and Experimental Investigation of Phaseless Spherical Near-Field Antenna Measurements. IEEE Trans. Antennas Propag. 2021, 69, 8830–8841. [Google Scholar] [CrossRef]






| 1.05 | |
| 1.22 | |
| 1.40 | |
| 1.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moretta, R.; Leone, G.; Munno, F.; Pierri, R. Optimal Field Sampling of Arc Sources via Asymptotic Study of the Radiation Operator. Electronics 2022, 11, 270. https://doi.org/10.3390/electronics11020270
Moretta R, Leone G, Munno F, Pierri R. Optimal Field Sampling of Arc Sources via Asymptotic Study of the Radiation Operator. Electronics. 2022; 11(2):270. https://doi.org/10.3390/electronics11020270
Chicago/Turabian StyleMoretta, Raffaele, Giovanni Leone, Fortuna Munno, and Rocco Pierri. 2022. "Optimal Field Sampling of Arc Sources via Asymptotic Study of the Radiation Operator" Electronics 11, no. 2: 270. https://doi.org/10.3390/electronics11020270







