Rapid Extraction of the Fundamental Components for Non-Ideal Three-Phase Grid Based on an Improved Sliding Discrete Fourier Transform
Abstract
:1. Introduction
2. Characteristics of the Non-Ideal Grid
3. Signals Extraction
3.1. Traditional SDFT
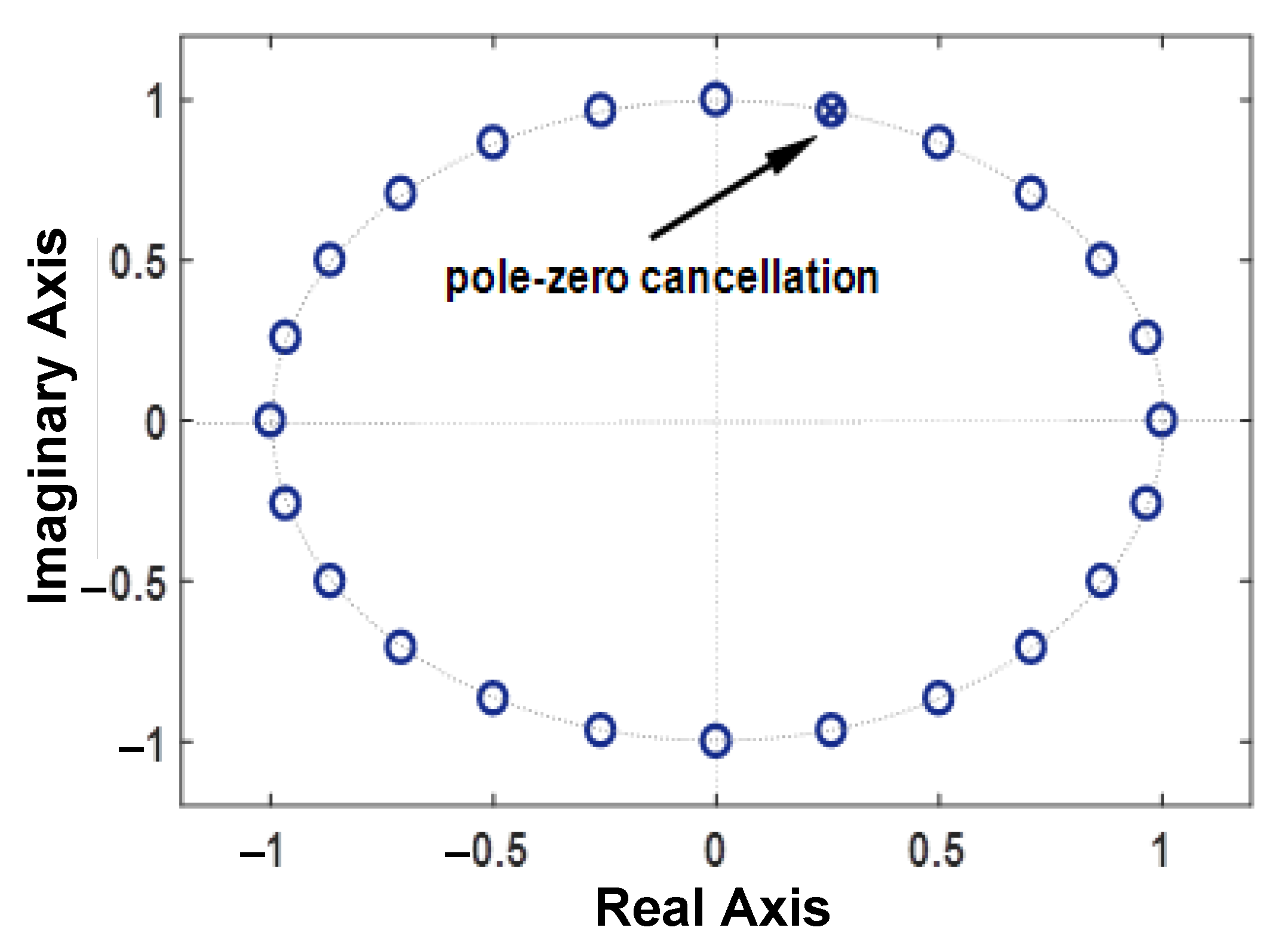
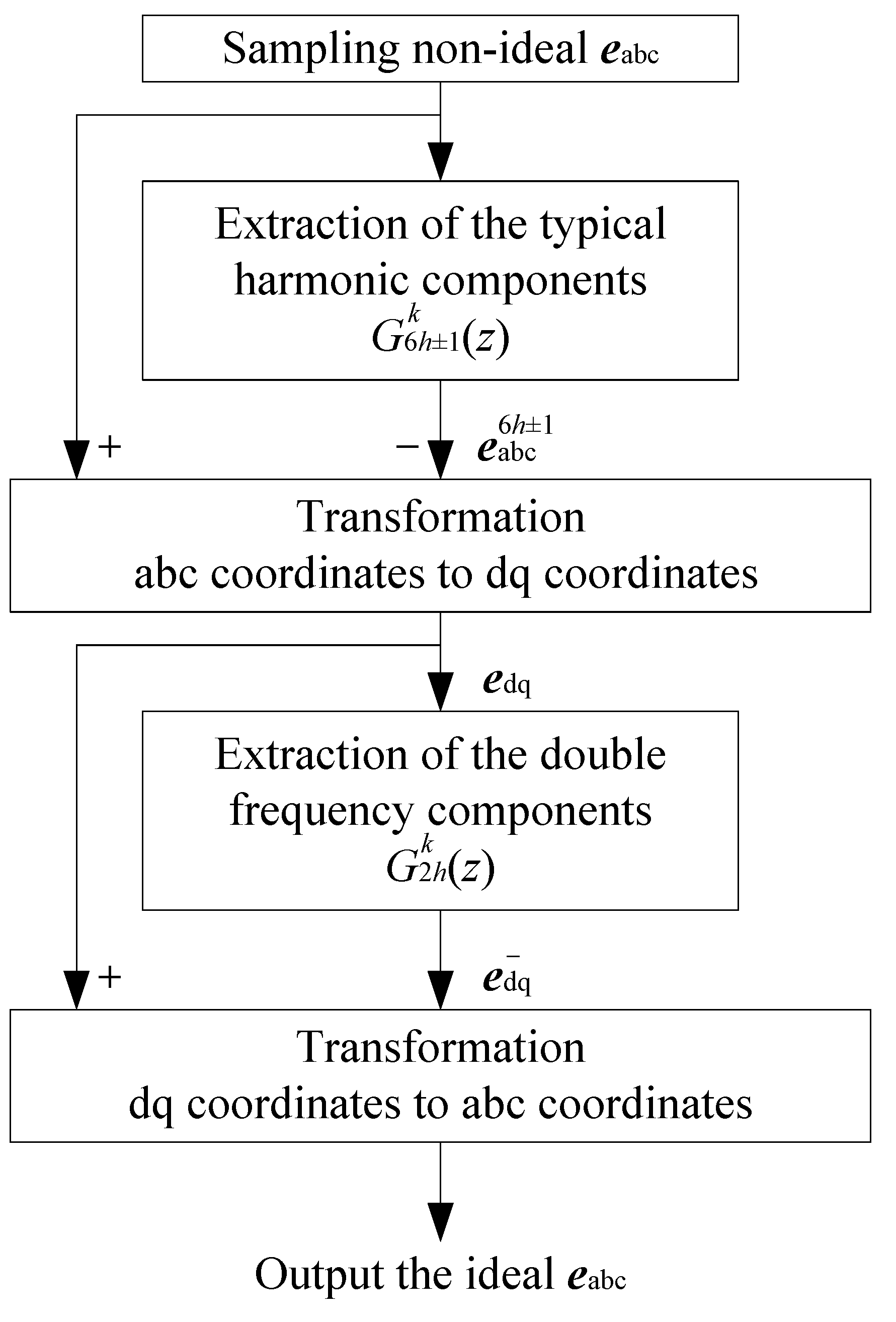
3.2. Proposed ISDFT
4. Experimental Results
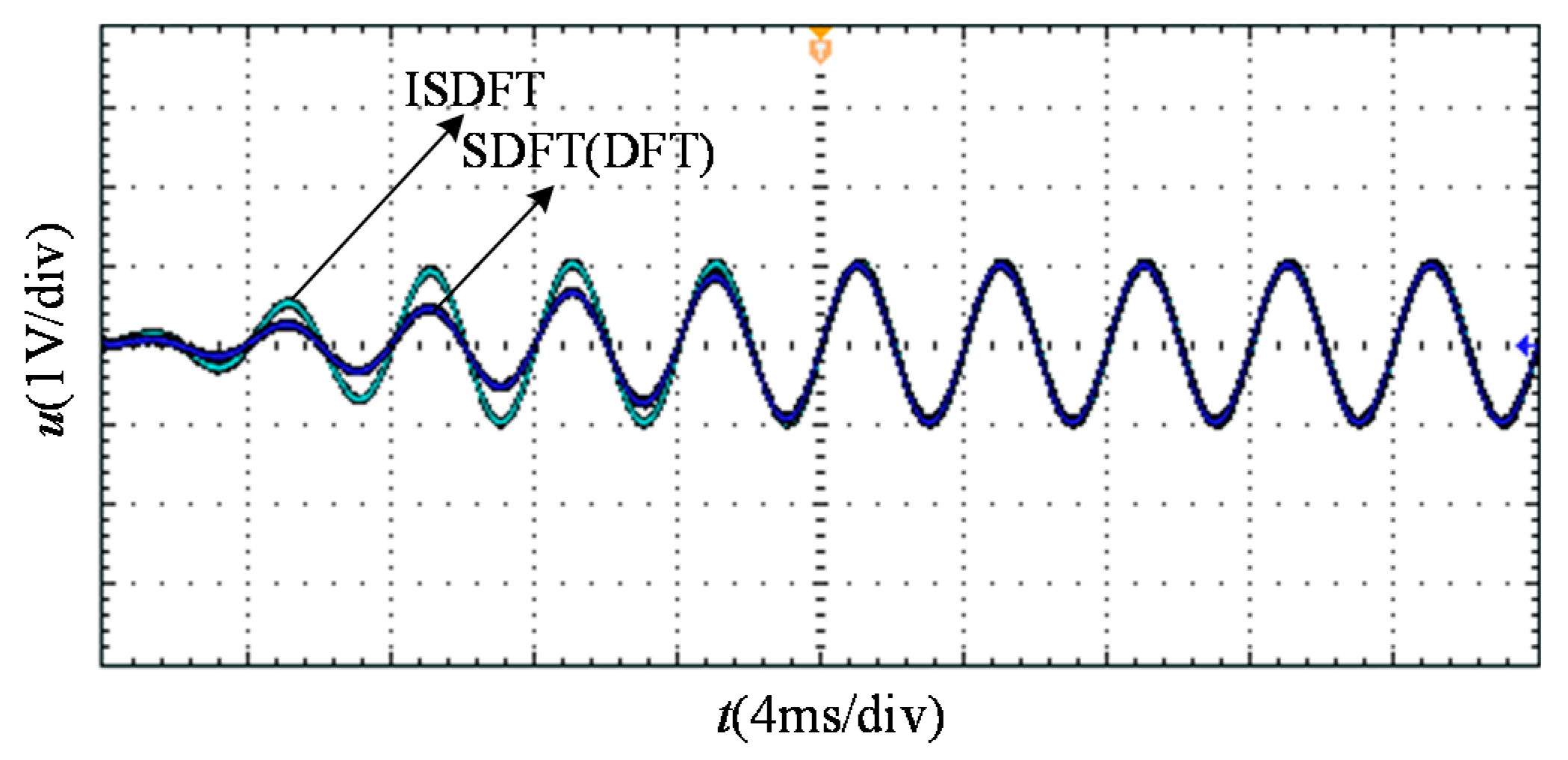
4.1. Signal Tracking Performance
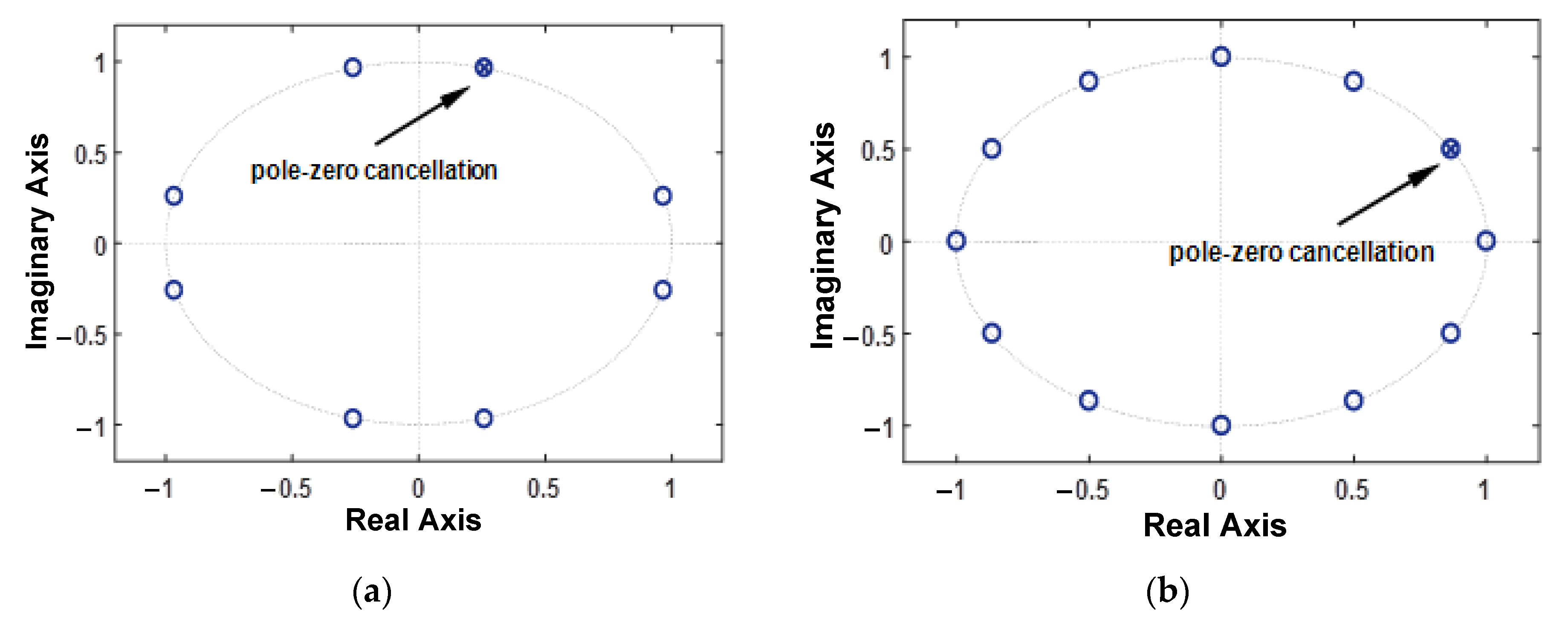
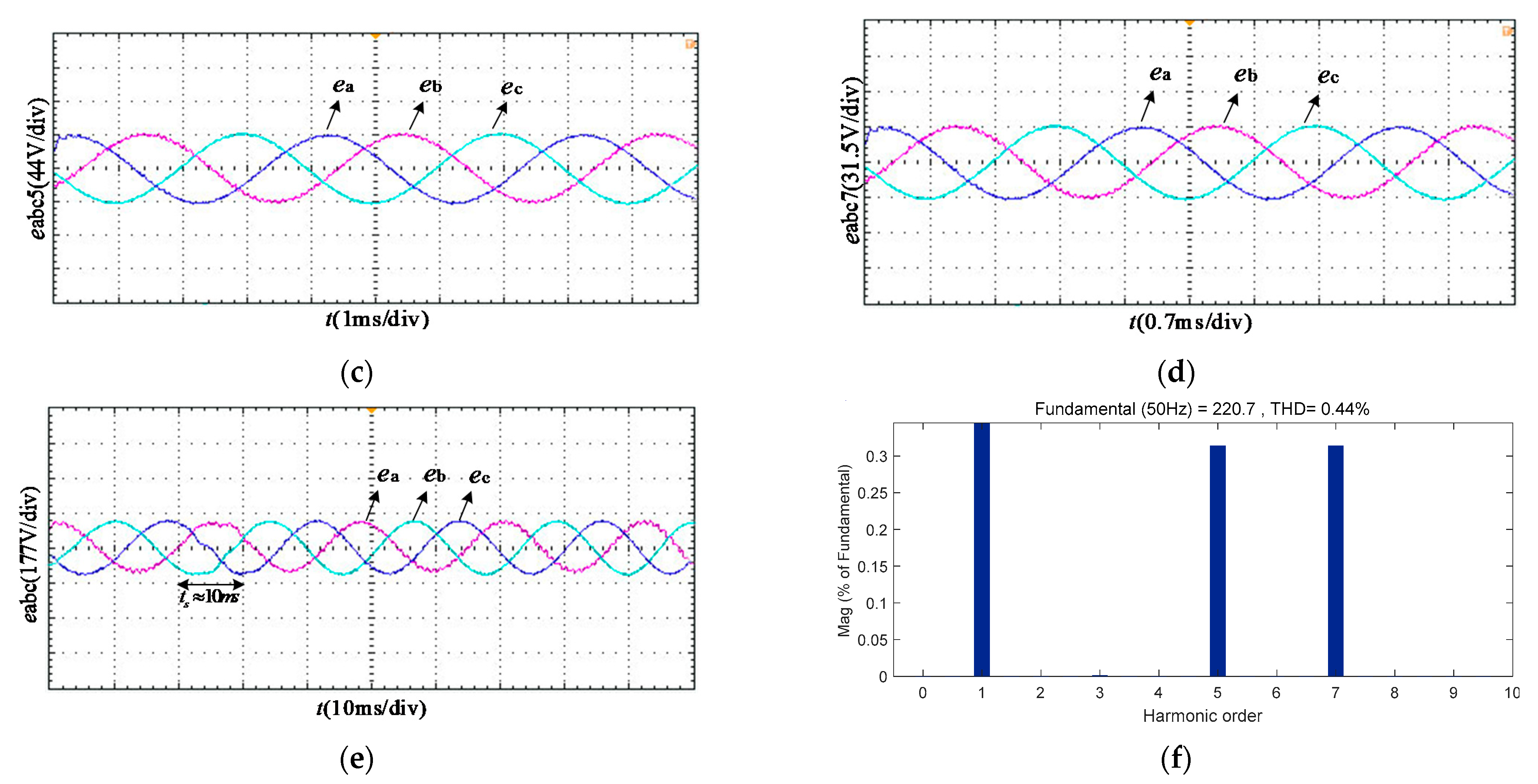
4.2. Harmonic Extraction
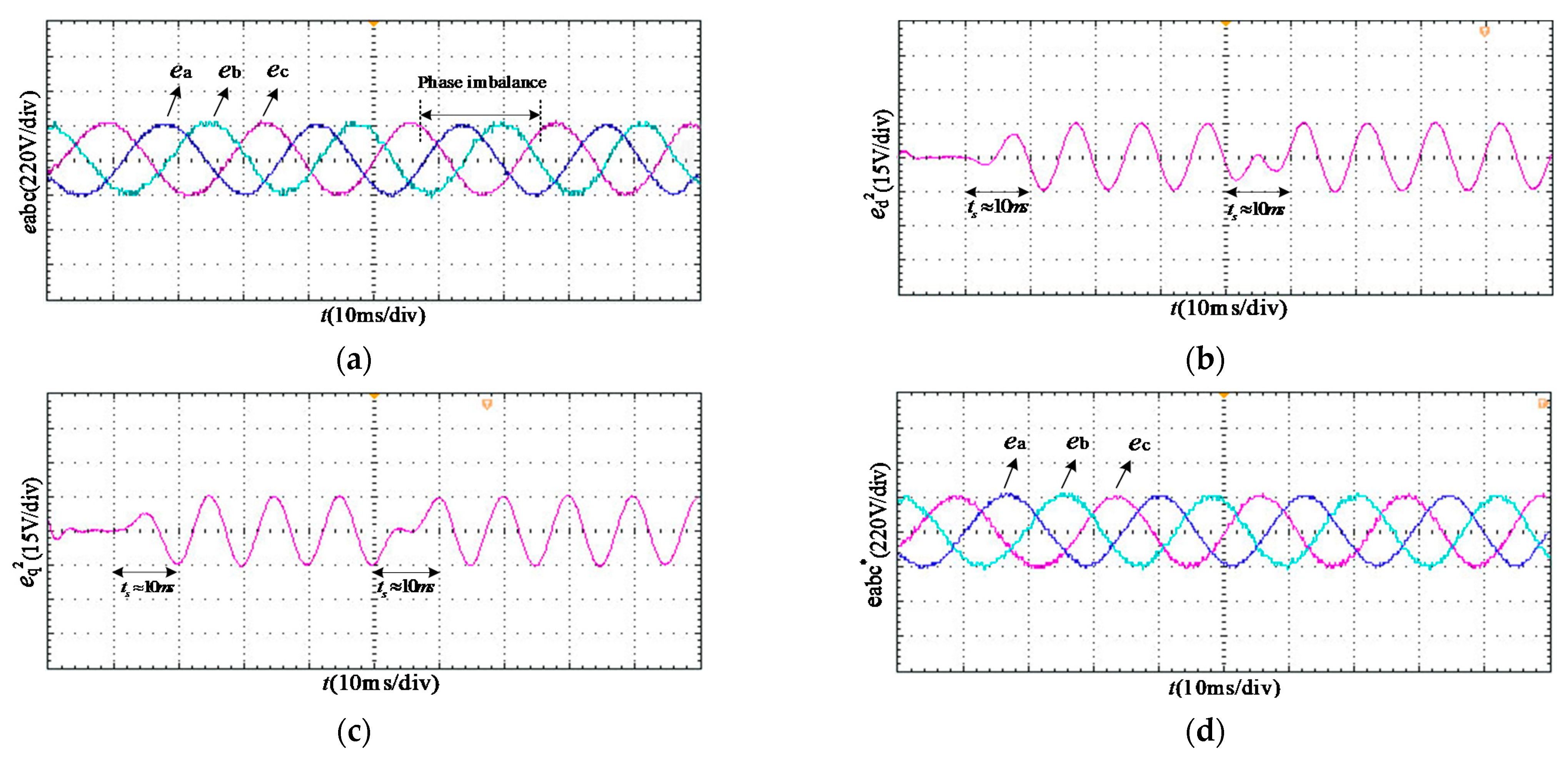
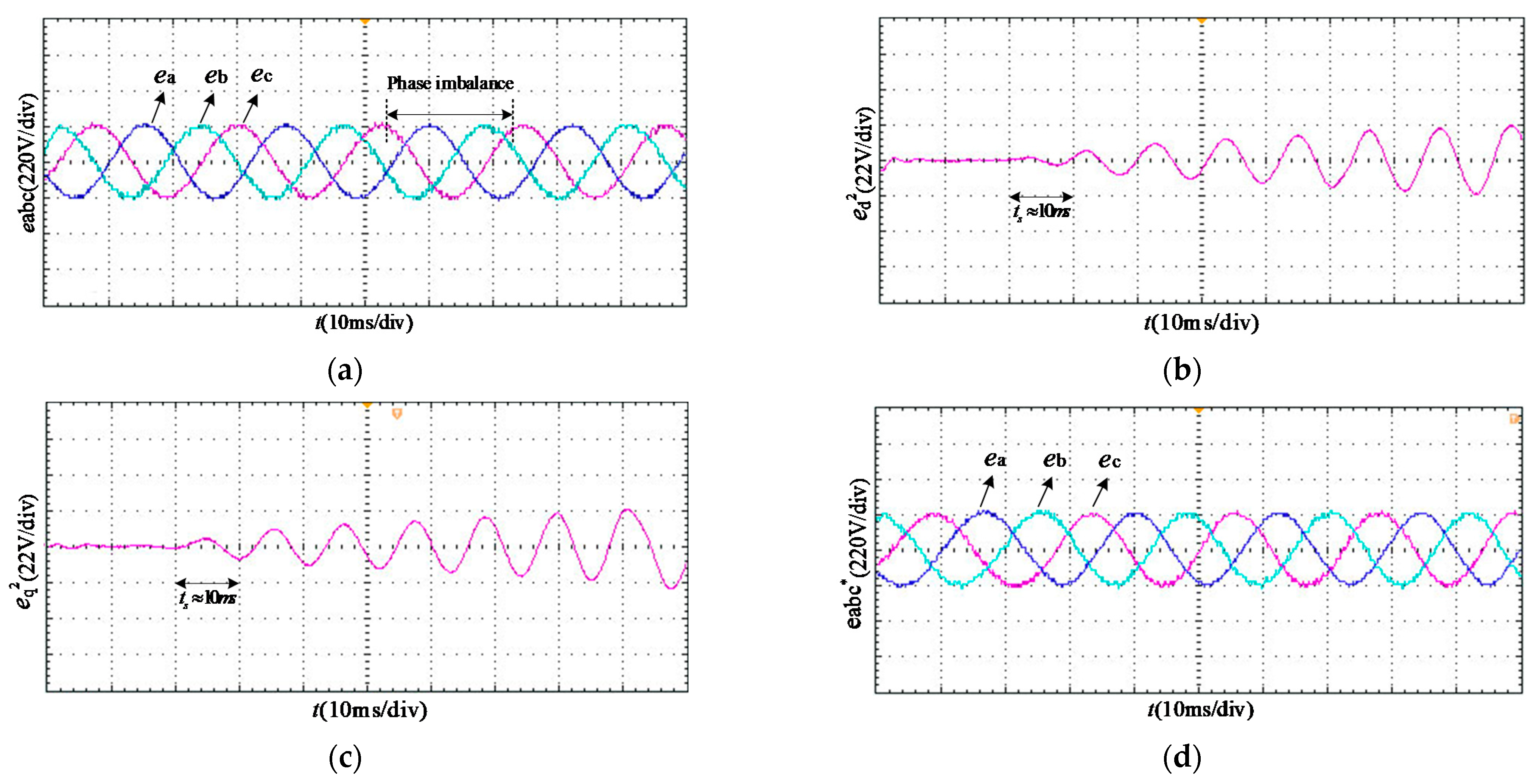
4.3. Other Non-Ideal Signals Extraction
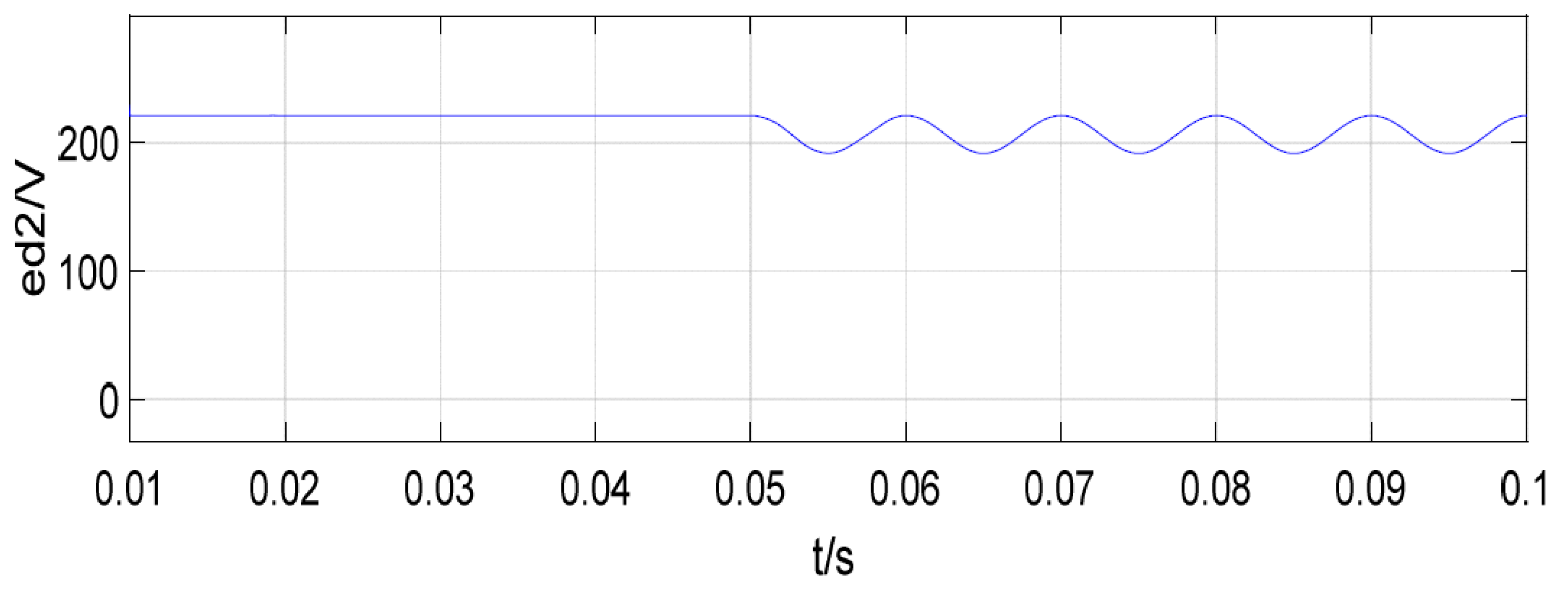
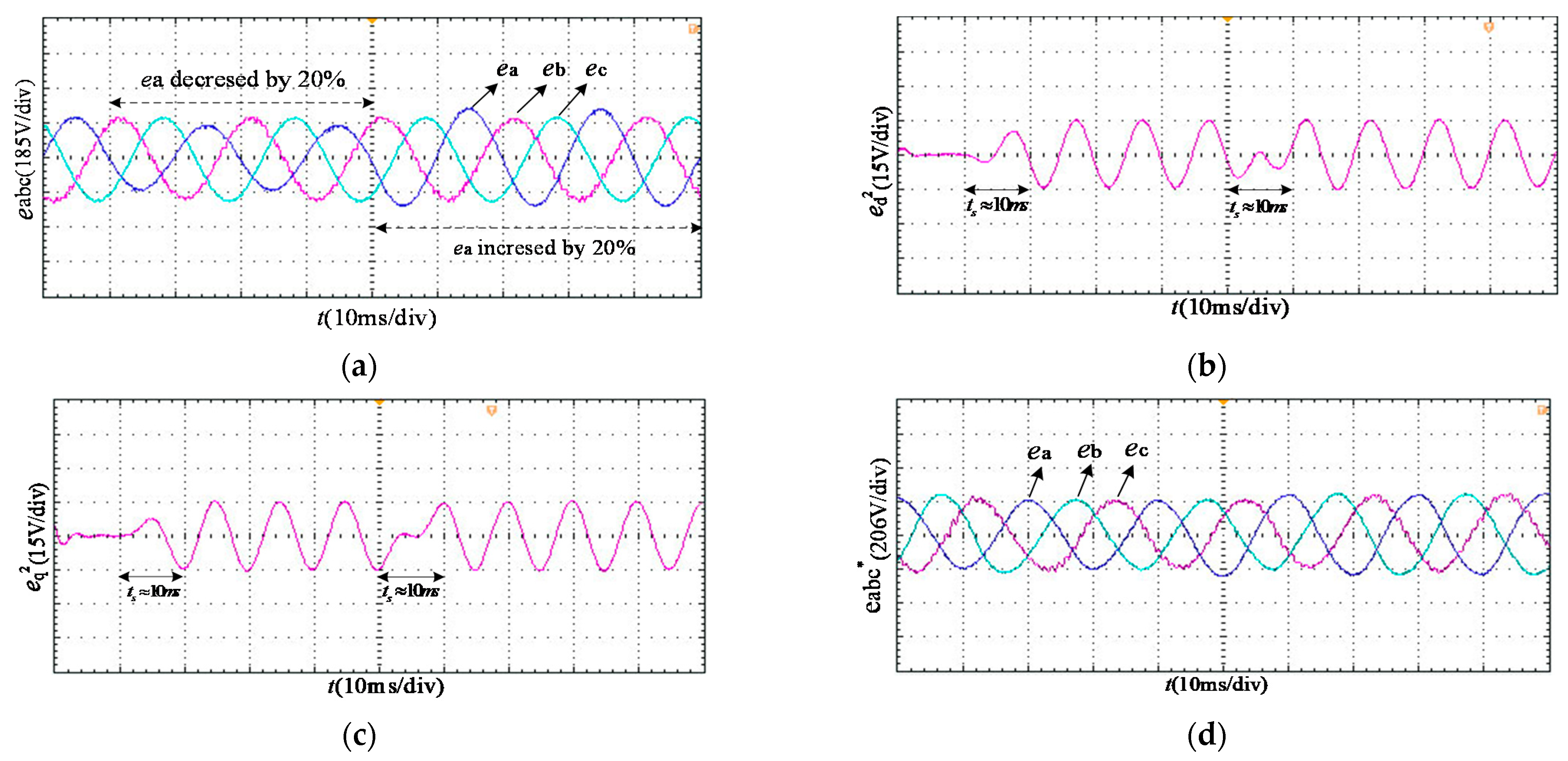
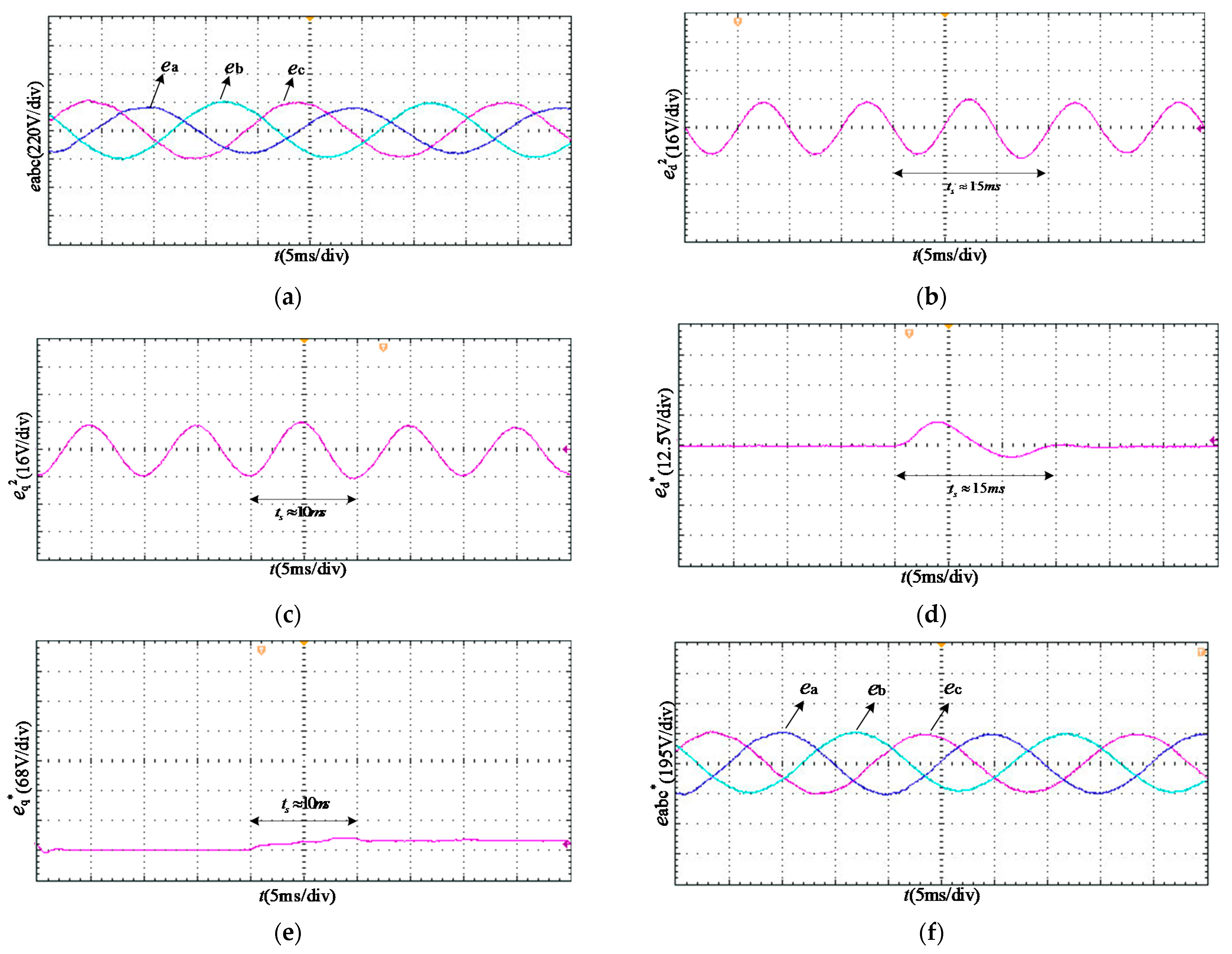
4.4. Non-Ideal Signals Extraction Considering Load Changes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Subramanian, C.; Kanagaraj, R. Rapid tracking of grid variables using prefiltered synchronous reference frame PLL. IEEE Trans. Instrum. Meas. 2015, 64, 1826–1836. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Blaabjerg, F.; Hansen, S. Detection is key—Harmonic detection methods for active power filter applications. IEEE Ind. Appl. Mag. 2007, 13, 22–33. [Google Scholar] [CrossRef]
- Li, Y.W.; He, J. Distribution system harmonic compensation method: An overview of DG-interfacing inverters. IEEE Ind. Electron. Mag. 2014, 8, 18–31. [Google Scholar] [CrossRef]
- Peng, C.; Hu, S.L.; Hao, X.H. An improved detection algorithm of three-phase unbalanced voltage sag detection method for improving power supply reliability. In Proceedings of the 10th International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), Xi’an, China, 8–11 October 2020. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, S.N. Fast harmonic estimation of stationary and time-varying signals using EA-AWNN. IEEE Trans. Instrum. Meas. 2013, 62, 335–343. [Google Scholar] [CrossRef]
- Yan, H.; Wang, X.; Rui, S. Non-Ideal Power Grid Multi-Target Current Reference Instruction Calculating Method, Involves Suppressing Active Power Pulsation and Current Reference Instruction under Three Control Targets of Power Pulsation Based on Instantaneous Theory. China Patent No. CN110676878-A, 10 January 2020. [Google Scholar]
- Liu, H.; Hu, H.; Chen, H.; Zhang, L.; Xing, Y. Fast and flexible selective harmonic extraction methods based on generalized discrete Fourier Transform. IEEE Trans. Power Electron. 2018, 33, 3484–3496. [Google Scholar] [CrossRef]
- Ferrero, R.; Pegoraro, P.A.; Toscani, S. Three-phase synchrophasor estimation through Taylor extended Kalman filtering. In Proceedings of the 10th IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 25–27 September 2019. [Google Scholar] [CrossRef]
- Yu, K.K.C.; Watson, N.R.; Arrillaga, J. An adaptive Kalman filter for dynamic harmonic state estimation and harmonic injection tracking. IEEE Trans. Power Deliv. 2005, 20, 1577–1584. [Google Scholar] [CrossRef]
- Sohn, S.-W.; Lim, Y.-B.; Yun, J.-J.; Choi, H.; Bae, H.-D. A filter bank and a self-tuning adaptive filter for the harmonic and interharmonic estimation in power signals. IEEE Trans. Instrum. Meas. 2012, 61, 64–73. [Google Scholar] [CrossRef]
- Maldonado, J.R. Total harmonic distortion estimation, minimization inter harmonic amplitude and expanding bands rejection in TKF filters. IEEE Lat. Am. Trans. 2016, 14, 652–656. [Google Scholar] [CrossRef]
- Jacobsen, E.; Lyons, R. The sliding DFT. IEEE Signal Processing Mag. 2003, 20, 74–80. [Google Scholar] [CrossRef] [Green Version]
- Jacobsen, E.; Lyons, R. An update to sliding DFT. IEEE Signal Process. Mag. 2004, 21, 110–111. [Google Scholar] [CrossRef]
- Sumathi, P. A frequency demodulation technique based on sliding DFT phase locking scheme for large variation FM signals. IEEE Commun. Lett. 2012, 16, 1864–1867. [Google Scholar] [CrossRef]
- Li, K.; Zheng, W.; Li, K. A fast algorithm with less Operations for length-N = q × 2m DFTs. IEEE Trans. Signal Process. 2015, 63, 673–683. [Google Scholar] [CrossRef]
- Chen, D. An improved harmonics detection method based on sliding discrete Fourier transform for three-phase grid-tie inverter system. IEICE Electron. Express 2019, 16, 20181074. [Google Scholar] [CrossRef] [Green Version]
- Tan, G.; Fu, Q.; Xia, T.; Zhang, X. Development of frequency fixed sliding discrete Fourier transform filter based single-phase phase-locked loop. IEEE Access 2021, 9, 110573–110581. [Google Scholar] [CrossRef]
- Xu, M.; Sang, Z.; Li, X.; You, Y.; Dai, D. An observer-based harmonic extraction method with front SOGI. Machines 2022, 10, 95. [Google Scholar] [CrossRef]
- Reza, M.S.; Sadeque, F.; Hossain, M.M.; Ghias, A.M.Y.M.; Agelidis, V.G. Three-phase PLL for grid-connected power converters under both amplitude and phase unbalanced conditions. IEEE Trans. Ind. Electron. 2019, 66, 8881–8891. [Google Scholar] [CrossRef]
- Lyons, R.; Howard, C. Improvements to the sliding discrete Fourier transform algorithm. IEEE Signal Process. Mag. 2021, 38, 119–127. [Google Scholar] [CrossRef]
- Sumathi, P.; Janakiraman, P.A. Integrated phase-locking scheme for SDFT-based harmonic analysis of periodic signals. IEEE Trans. Circuits Syst. II Express Briefs 2008, 55, 51–55. [Google Scholar] [CrossRef]
- Sumathi, P.; Janakiraman, P.A. Phase locking scheme based on look-up-table-assisted sliding discrete Fourier transform for low-frequency power and acoustic signals. IET Circuits Devices Syst. 2011, 5, 494–504. [Google Scholar] [CrossRef]
- Shen, T.; Chen, L.; Guan, J.; Duan, J. A new sliding frequency Fourier transform phase difference measurement method for extreme frequency signals. Rev. Sci. Instrum. 2020, 91, 015103. [Google Scholar] [CrossRef]
- Tyagi, T.; Sumathi, P. Comprehensive performance evaluation of computationally efficient discrete Fourier transforms for frequency estimation. IEEE Trans. Instrum. Meas. 2019, 69, 2155–2163. [Google Scholar] [CrossRef]






| Harmonic Extraction Method | 5th Harmonic Extraction Time (μs) | 7th Harmonic Extraction Time (μs) |
|---|---|---|
| DFT | 251.41 | 228.93 |
| SDFT | 157.28 | 143.22 |
| ISDFT | 87.19 | 78.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Nai, W. Rapid Extraction of the Fundamental Components for Non-Ideal Three-Phase Grid Based on an Improved Sliding Discrete Fourier Transform. Electronics 2022, 11, 1915. https://doi.org/10.3390/electronics11121915
Li K, Nai W. Rapid Extraction of the Fundamental Components for Non-Ideal Three-Phase Grid Based on an Improved Sliding Discrete Fourier Transform. Electronics. 2022; 11(12):1915. https://doi.org/10.3390/electronics11121915
Chicago/Turabian StyleLi, Kai, and Wei Nai. 2022. "Rapid Extraction of the Fundamental Components for Non-Ideal Three-Phase Grid Based on an Improved Sliding Discrete Fourier Transform" Electronics 11, no. 12: 1915. https://doi.org/10.3390/electronics11121915






