An Area- and Energy-Efficient 16-Channel, AC-Coupled Neural Recording Analog Frontend for High-Density Multichannel Neural Recordings
Abstract
:1. Introduction
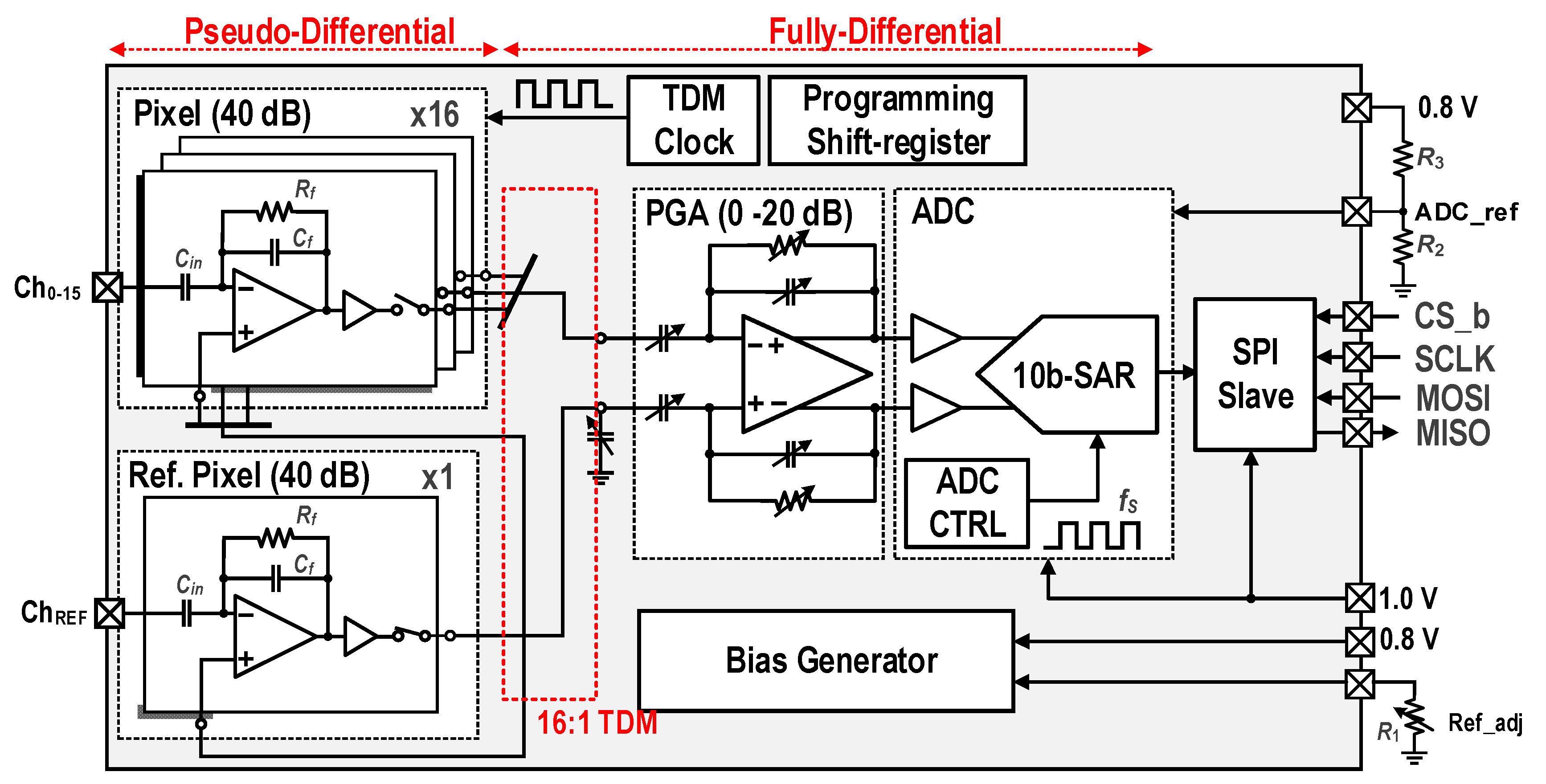
2. A 16-Channel, AC-Coupled Analog Frontend
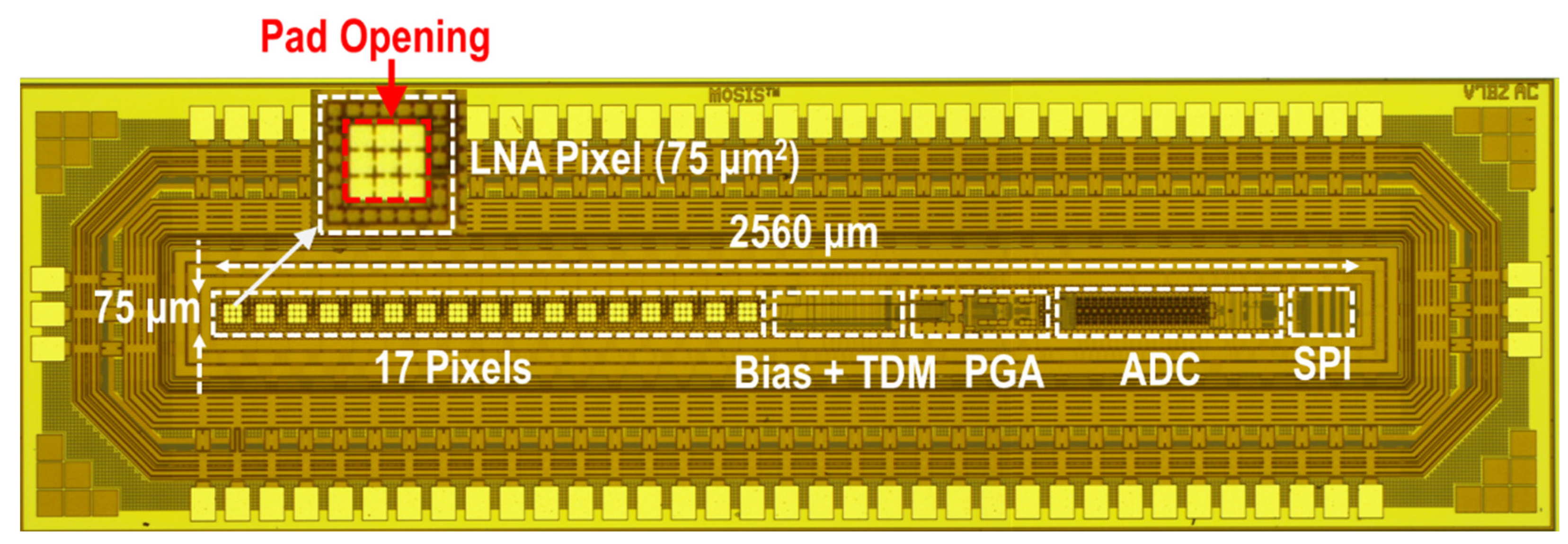
2.1. Integrated Circuit Architecture
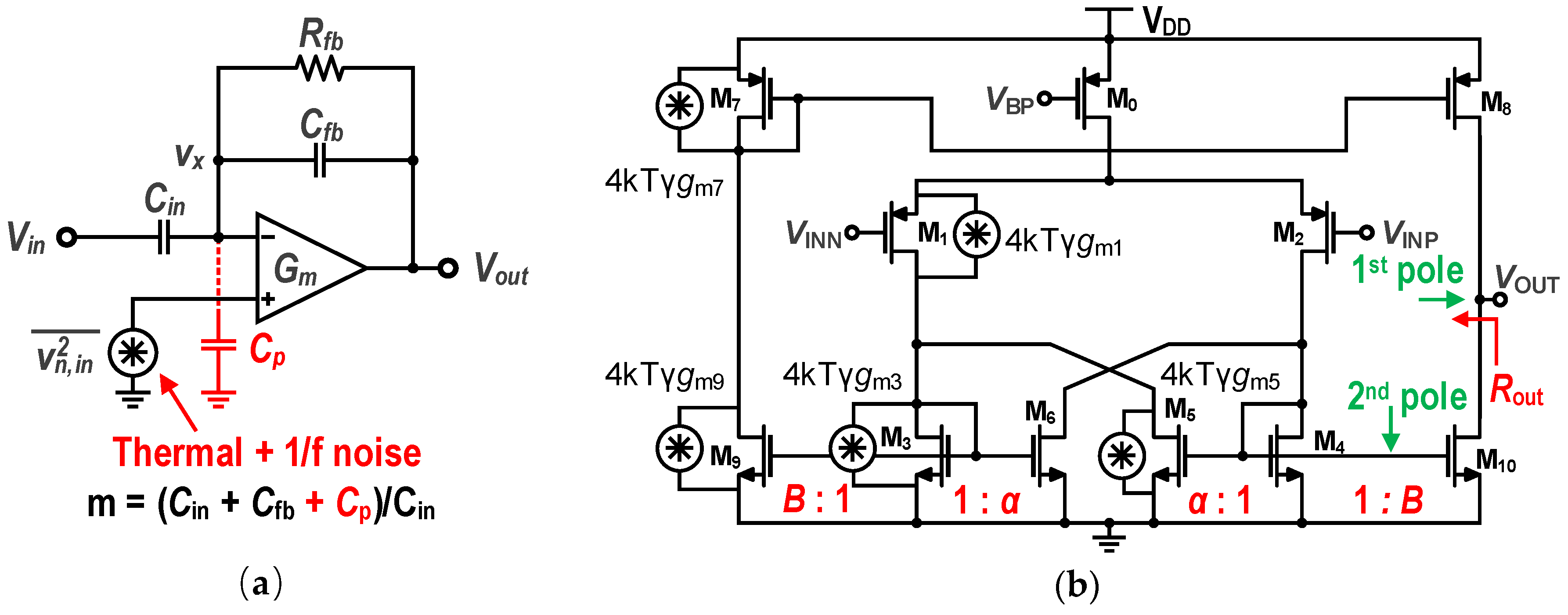
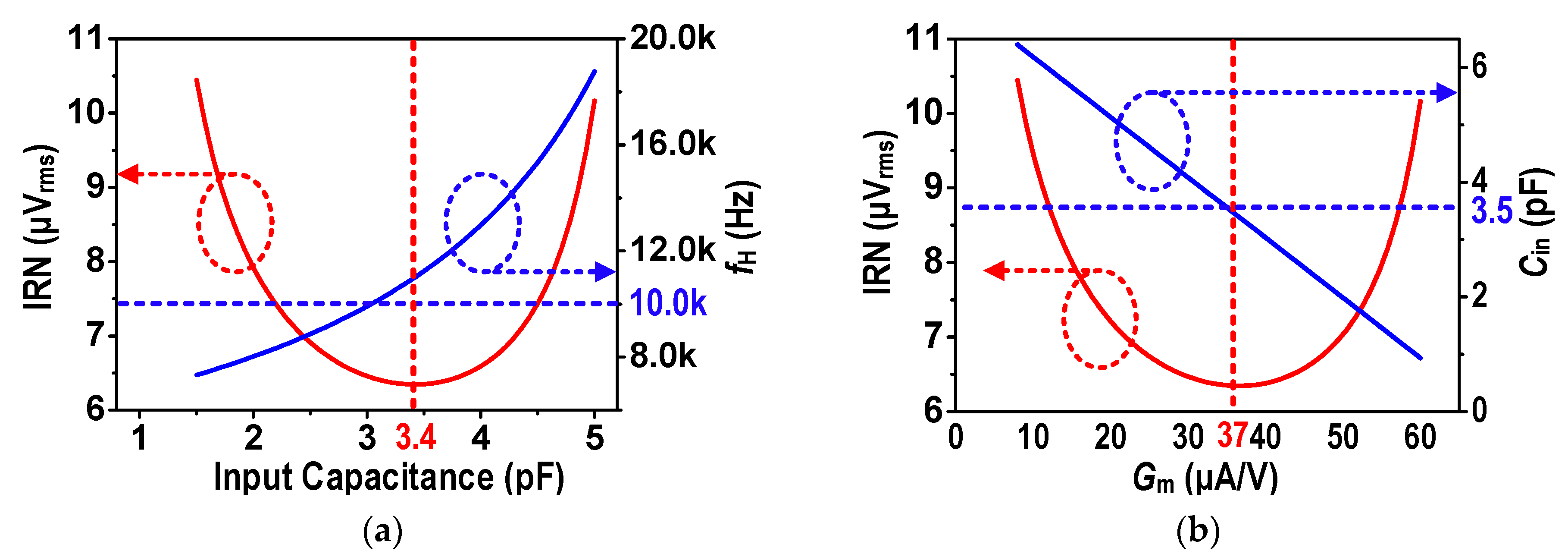
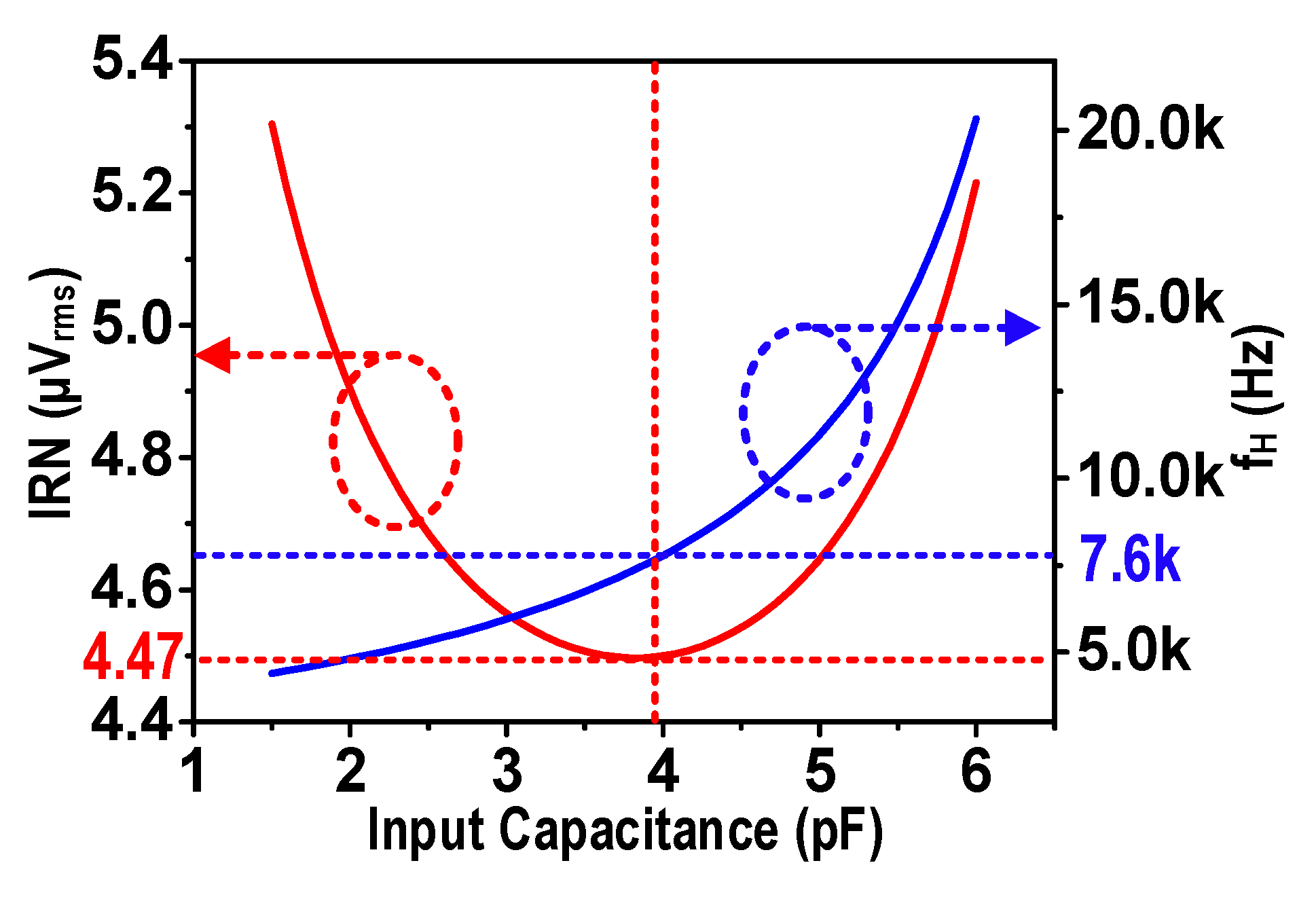
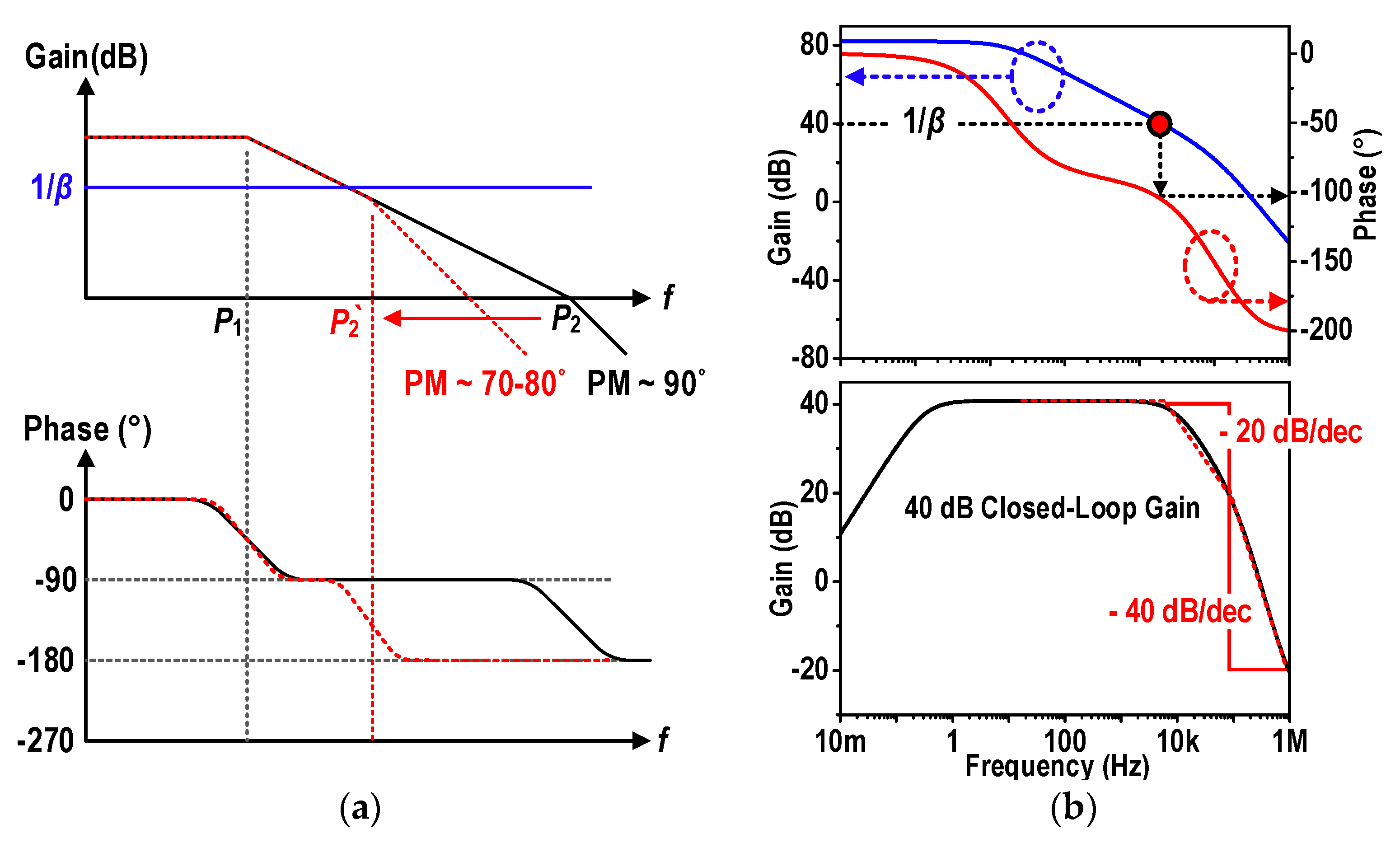
2.2. Area-Aware Design in Low Noise Amplifier
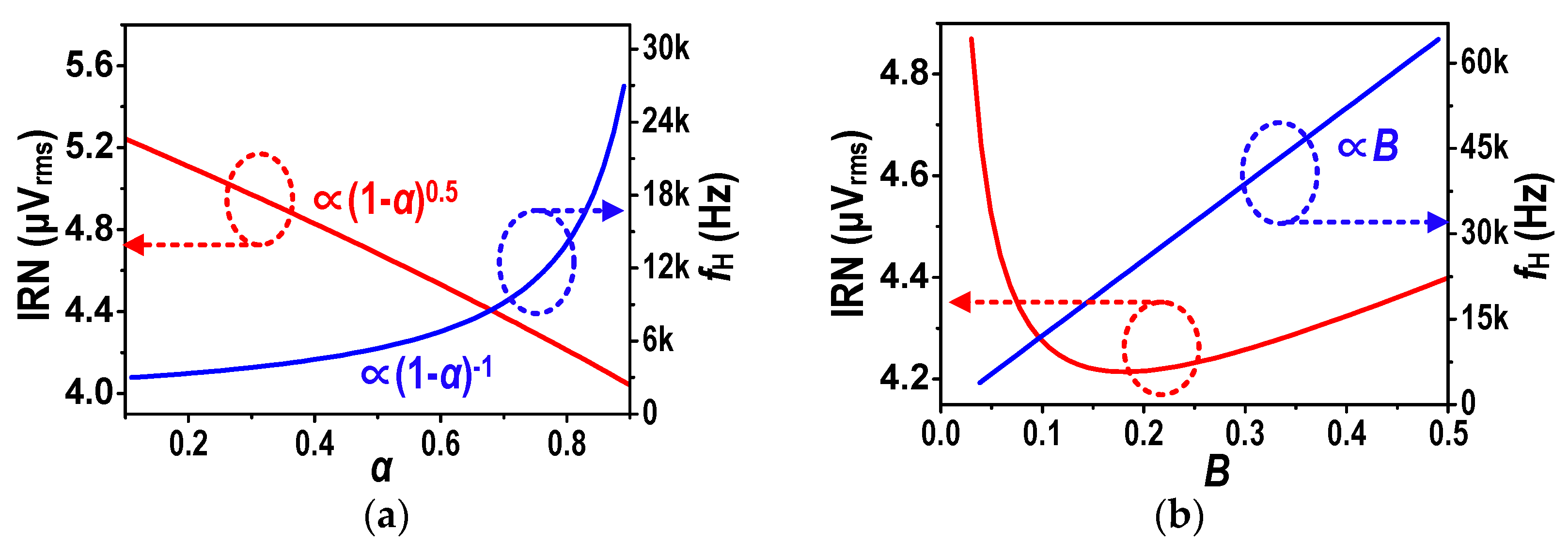
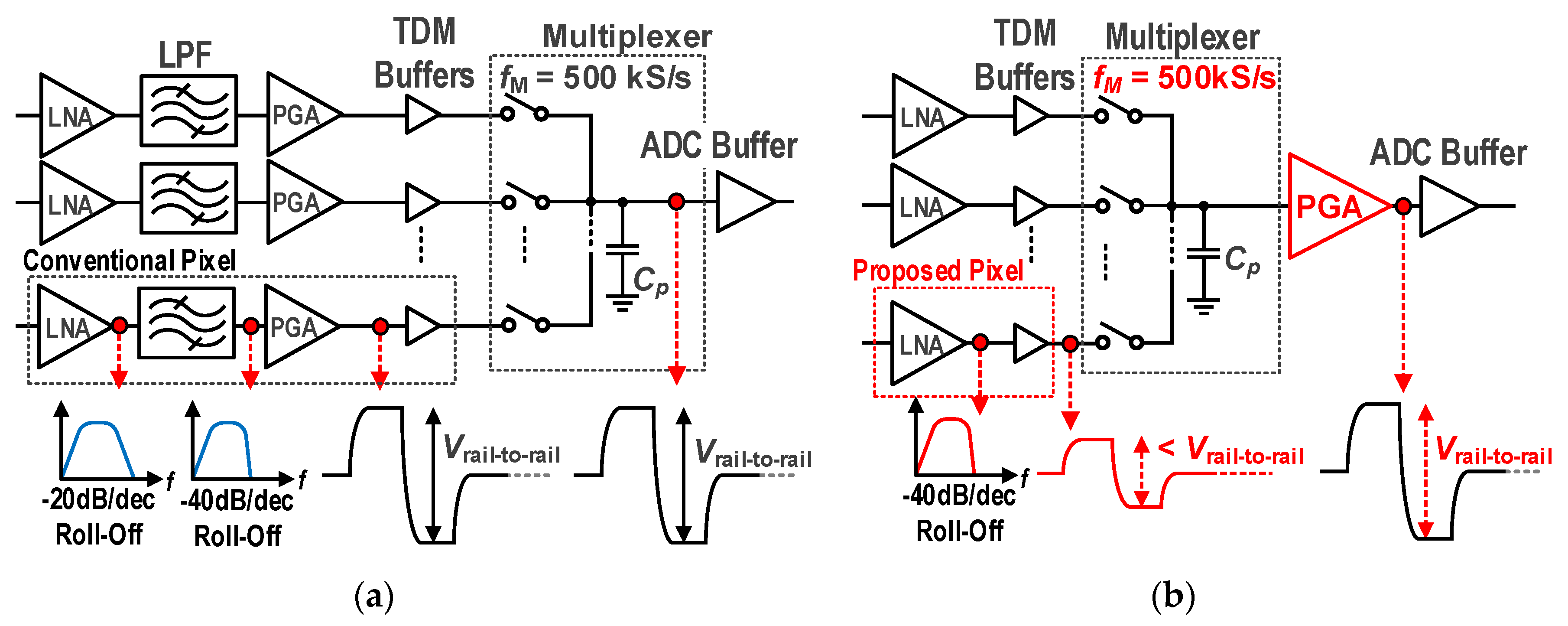
2.3. Improvement in Pixel Structure
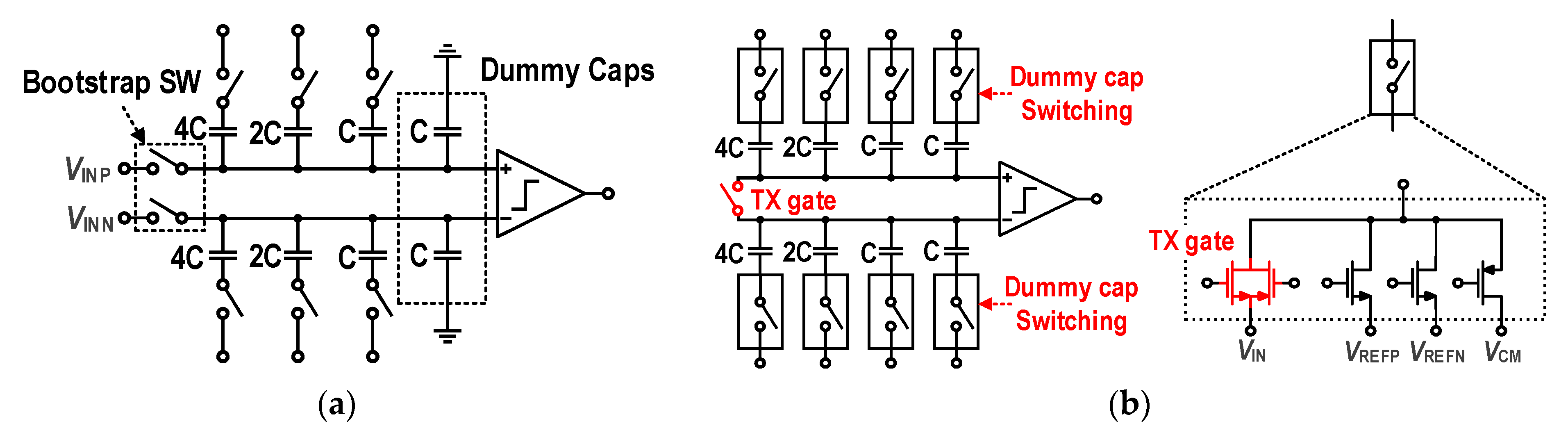
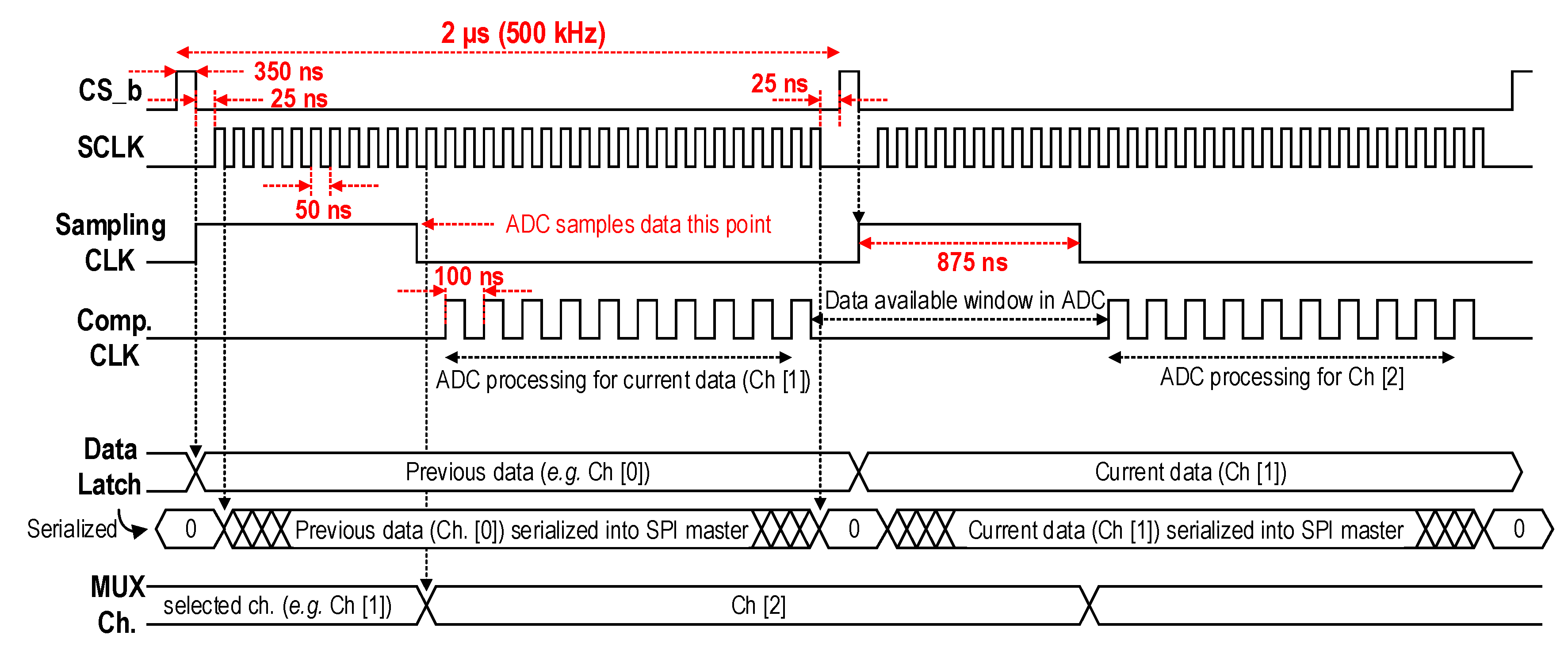
2.4. Analog-to-Digital Converter and Serial Peripheral Interface
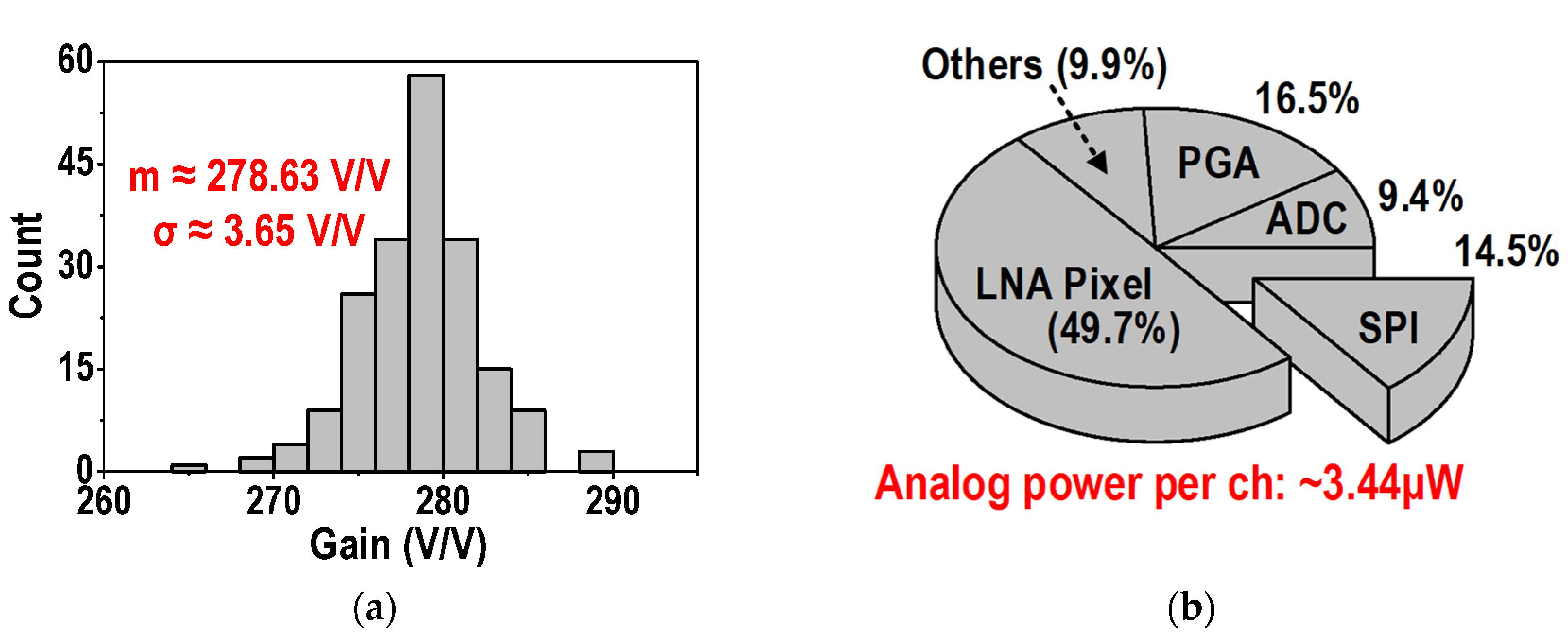
3. Experimental Results
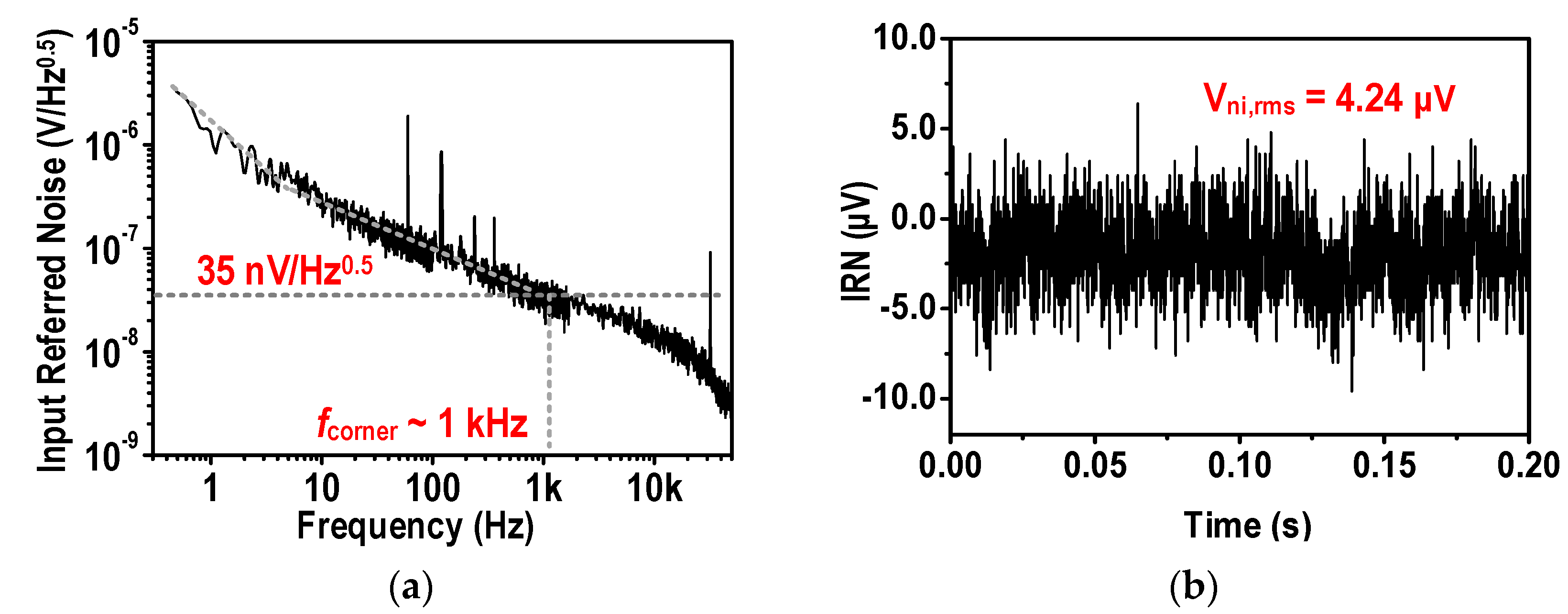
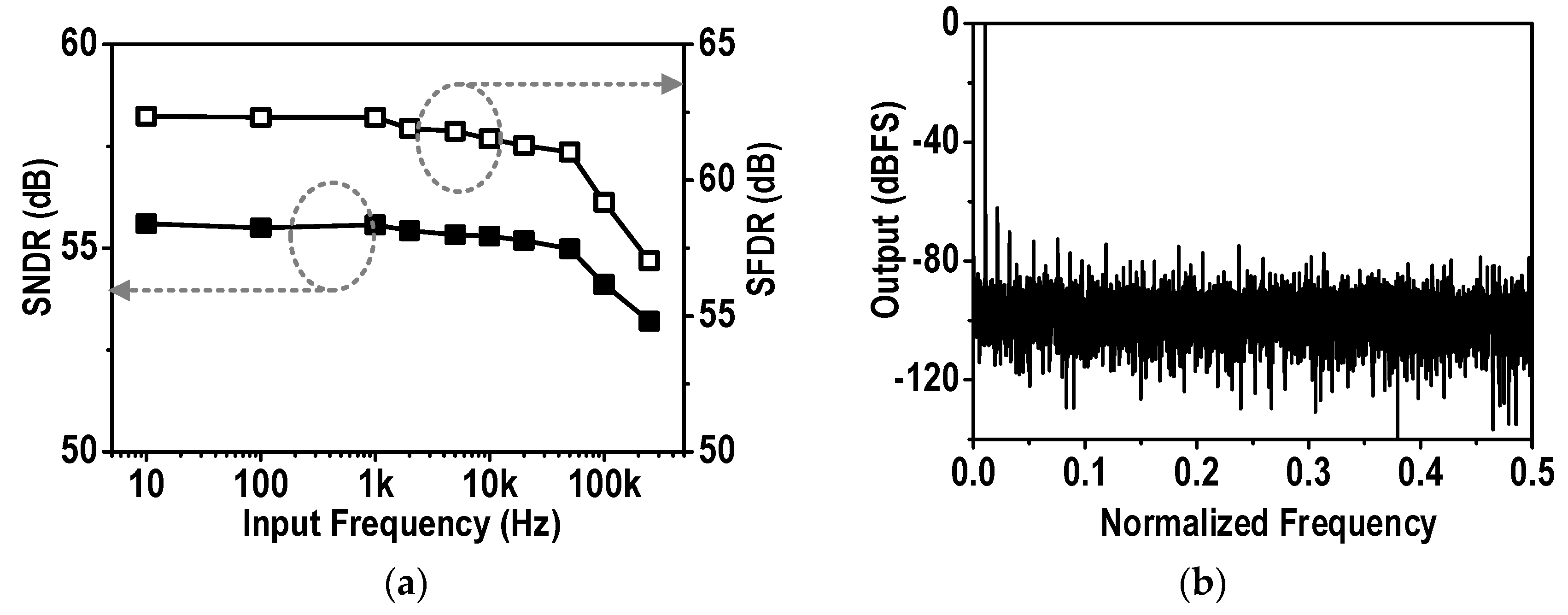
3.1. Benchtop Characterization
3.2. In Vitro Characterization and Performance Comparison
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Buzsáki, G. Large-Scale Recording of Neuronal Ensembles. Nat. Neurosci. 2004, 7, 446–451. [Google Scholar] [CrossRef]
- Buzsáki, G.; Stark, E.; Berényi, A.; Khodagholy, D.; Kipke, D.R.; Yoon, E.; Wise, K.D. Tools for Probing Local Circuits: High-Density Silicon Probes Combined with Optogenetics. Neuron 2015, 86, 92–105. [Google Scholar] [CrossRef] [Green Version]
- Seymour, J.P.; Wu, F.; Wise, K.D.; Yoon, E. State-of-the-art MEMS and microsystem tools for brain research. Microsyst. Nanoeng. 2016, 3, 16066. [Google Scholar] [CrossRef]
- Park, S.-Y.; Cho, J.; Lee, K.; Yoon, E. Dynamic Power Reduction in Scalable Neural Recording Interface Using Spatiotemporal Correlation and Temporal Sparsity of Neural Signals. IEEE J. Solid State Circuits 2018, 53, 1102–1114. [Google Scholar] [CrossRef]
- Razavi, B. Chapter 1 Introduction to Analog Design, Design of Analog CMOS Integrated Circuits, 2nd ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Harrison, R.R.; Charles, C. A Low-Power Low-Noise CMOS Amplifier for Neural Recording Applications. IEEE J. Solid State Circuits 2003, 38, 958–965. [Google Scholar] [CrossRef]
- Wattanapanitch, W.; Sarpeshkar, R. A low-power 32-channel digitally programmable neural recording integrated circuit. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 592–602. [Google Scholar] [CrossRef] [PubMed]
- Muller, R.; Le, H.-P.; Li, W.; Ledochowitsch, P.; Gambini, S.; Bjorninen, T.; Koralek, A.; Carmena, J.M.; Maharbiz, M.M.; Alon, E.; et al. A Minimally Invasive 64-Channel Wireless µECoG Implant. IEEE J. Solid State Circuits 2015, 50, 344–359. [Google Scholar] [CrossRef]
- Park, S.-Y.; Cho, J.; Na, K.; Yoon, E. Toward 1024-Channel Parallel Neural Recording: Modular Δ-ΔΣ Analog Front-End Architecture with 4.84fJ/C-s·mm2 Energy-Area Product. In Proceedings of the 2015 Symposium on VLSI Circuits (VLSI Circuits), Kyoto, Japan, 17–19 June 2015; pp. C112–C113. [Google Scholar] [CrossRef]
- Park, S.-Y.; Cho, J.; Na, K.; Yoon, E. Modular 128-Channel Δ-ΔΣ Analog Front-End Architecture Using Spectrum Equalization Scheme for 1024-Channel 3-D Neural Recording Microsystems. IEEE J. Solid State Circuits 2018, 53, 501–514. [Google Scholar] [CrossRef]
- Uran, A.; Leblebici, Y.; Emami, A.; Cevher, V. An AC-Coupled Wideband Neural Recording Front-End with Sub-1 mm2×fJ/conv-step Efficiency and 0.97 NEF. IEEE Solid State Circuits Lett. 2020, 3, 258–261. [Google Scholar] [CrossRef]
- Denison, T.; Consoer, K.; Santa, W.; Molnar, G.; Mieser, K. A 2 μW, 95nV/√Hz, chopper-stabilized instrumentation amplifier for chronic measurement of bio-potentials. IEEE J. Solid State Circuits 2007, 42, 1–6. [Google Scholar] [CrossRef]
- Zou, X.; Xu, X.; Yao, L.; Lian, Y. A 1-V 450-nW Fully Integrated Programmable Biomedical Sensor Interface Chip. IEEE J. Solid State Circuits 2009, 44, 1067–1077. [Google Scholar] [CrossRef]
- Liu, L.; Zou, X.; Goh, W.L.; Ramamoorthy, R.; Dawe, G.; Je, M. 800 nW 43 nV/√Hz Neural Recording Amplifier with Enhanced Noise Efficiency Factor. Electron. Lett. 2012, 48, 479. [Google Scholar] [CrossRef]
- Han, D.; Zheng, Y.; Rajkumar, R.; Dawe, G.S.; Je, M. A 0.45 V 100-Channel Neural-Recording IC With Sub-μW/Channel Consumption in 0.18 μm CMOS. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 735–746. [Google Scholar] [CrossRef] [PubMed]
- Lopez, C.M.; Andrei, A.; Mitra, S.; Welkenhuysen, M.; Eberle, W.; Bartic, C.; Puers, R.; Yazicioglu, R.F.; Gielen, G.G.E. An Implantable 455-Active-Electrode 52-Channel CMOS Neural Probe. IEEE J. Solid State Circuits 2014, 49, 248–261. [Google Scholar] [CrossRef]
- Chandrakumar, H.; Markovic, D. A 15.2-ENOB 5-kHz BW 4.5-μW Chopped CT ΔΣ-ADC for artifact-tolerant neural recording front ends. IEEE J. Solid State Circuits 2018, 53, 3470–3483. [Google Scholar] [CrossRef]
- Kim, S.J.; Han, S.-H.; Cha, J.-H.; Liu, L.; Yao, L.; Gao, Y.; Je, M. Sub-µW/Ch Analog Front-End for Δ-Neural Recording with Spike-Driven Data Compression. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Muller, R.; Gambini, S.; Rabaey, J.M. A 0.013 mm2, 5 μW, DC-Coupled Neural Signal Acquisition IC with 0.5 V Supply. IEEE J. Solid State Circuits 2012, 47, 1–12. [Google Scholar] [CrossRef]
- Noshahr, F.H.; Nabavi, M. Multi-Channel Neural Recording Implants: A Review. Sensors 2020, 20, 904. [Google Scholar] [CrossRef] [Green Version]
- Tasneem, N.T.; Mahbub, I. A 2.53 NEF 8-bit 10 kS/s 0.5 µm CMOS Neural Recording Read-Out Circuit with High Linearity for Neuromodulation Implants. Electronics 2021, 10, 590. [Google Scholar] [CrossRef]
- Mendrela, A.E.; Park, S.-Y.; Vöröslakos, M.; Flynn, M.P.; Yoon, E. A Battery-Powered Opto-Electrophysiology Neural Interface with Artifact-Preventing Optical Pulse Shaping. In Proceedings of the 2018 IEEE Symposium on VLSI Circuits, Honolulu, HI, USA, 18–22 June 2018; pp. 125–126. [Google Scholar] [CrossRef]
- Park, S.-Y.; Na, K.; Vöröslakos, M.; Song, H.; Slager, N.; Oh, S.; Seymour, J.P.; Buzsáki, G.; Yoon, E. A Miniaturized 256-Channel Neural Recording Interface with Area-Efficient Hybrid Integration of Flexible Probes and CMOS Integrated Circuits. IEEE Trans. Biomed. Eng. 2021. [Google Scholar] [CrossRef]
- Wattanapanitch, W.; Fee, M.; Sarpeshkar, R. An Energy-Efficient Micropower Neural Recording Amplifier. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 136–147. [Google Scholar] [CrossRef]
- Ng, K.A.; Xu, Y.P. A Compact, Low Input Capacitance Neural Recording Amplifier. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 610–662. [Google Scholar] [CrossRef] [PubMed]
- Holleman, J.; Otis, B. A Sub-Microwatt Low-Noise Amplifier for Neural Recording. IEEE Eng. Med. Biol. Soc. 2007, 3930–3933. [Google Scholar] [CrossRef]
- Ng, K.A.; Xu, Y.P. A Multi-Channel Neural-Recording Amplifier System with 90dB CMRR Employing CMOS-Inverter-Based OTAs with CMFB Through Supply Rails in 65 nm CMOS. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 22–26 February 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Xu, J.; Nguyen, A.T.; Luu, D.K.; Drealan, M.; Yang, Z. Noise Optimization Techniques for Switched-Capacitor Based Neural Interfaces. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 1024–1035. [Google Scholar] [CrossRef] [PubMed]
- Pazhouhandeh, M.R.; Kassiri, H.; Shoukry, A.; Wesspapir, I.; Carlen, P.; Genov, R. Artifact-Tolerant Opamp-less Delta-Modulated Bidirectional Neuro-Interface. In Proceedings of the IEEE Symposium on VLSI Circuits, Honolulu, HI, USA, 18–22 June 2018; pp. C127–C128. [Google Scholar] [CrossRef]
- Harrison, R.R. The Design of Integrated Circuits to Observe Brain Activity. Proc. IEEE 2008, 96, 1203–1216. [Google Scholar] [CrossRef]
- Kwak, J.Y.; Park, S.-Y. Compact Continuous Time Common-Mode Feedback Circuit for Low-Power, Area-Constrained Neural Recording Amplifiers. Electronics 2021, 10, 145. [Google Scholar] [CrossRef]
- Roh, J.; Byun, S.; Choi, Y.; Roh, H.; Kim, Y.-G.; Kwon, J.-K. A 0.9-V 60-µW 1-Bit Fourth-Order Delta-Sigma Modulator With 83-dB Dynamic Range. IEEE J. Solid State Circuits 2008, 43, 361–370. [Google Scholar] [CrossRef]
- Chae, M.S.; Liu, W.; Sivaprakasam, M. Design Optimization for Integrated Neural Recording Systems. IEEE J. Solid State Circuits 2008, 43, 1931–1939. [Google Scholar] [CrossRef]
- Chae, M.S.; Yang, Z.; Yuce, M.R.; Hoang, L.; Liu, W. A 128-Channel 6 mW Wireless Neural Recording IC With Spike Feature Extraction and UWB Transmitter. IEEE Trans. Neural Syst. Rehabil. Eng. 2009, 17, 312–321. [Google Scholar] [CrossRef]
- Biderman, W.; Yeager, D.J.; Narevsky, N.; Leverett, J.; Neely, R.; Carmena, J.M.; Alon, E.; Rabaey, J.M. A 4.78 mm2 Fully-Integrated Neuromodulation SoC Combining 64 Acquisition Channels With Digital Compression and Simultaneous Dual Stimulation. IEEE J. Solid State Circuits 2015, 50, 1038–1047. [Google Scholar] [CrossRef]
- Du, J.; Blanche, T.J.; Harrison, R.R.; Lester, H.A.; Masmanidis, S.C. Multiplexed, high density electrophysiology with nanofabricated neural probes. PLoS ONE 2011, 6, e26204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, Z.; Xiao, Y.; Song, X. VCM-based monotonic capacitor switching scheme for SAR ADC. Electron. Lett. 2013, 49, 327–329. [Google Scholar] [CrossRef]



| [6] | [8] | [10] | [11] | [23] | [35] | This Work | |
|---|---|---|---|---|---|---|---|
| Bandwidth (Hz) | 7.5 k | 10–10 k | 0.4–10.9 k | 0.05–10 k | 1.7–17.5 k | 10–8 k | 0.1–7.4 k |
| Sampling Freq. (kS/s) | N/A | 20 | 25 | 20 | 31.25 | 20 | 31.25 |
| IRN (μVrms) | 2.2 | 4.9 | 3.32 | 3.1 | 6.3 | 7.5 | 4.27 |
| NEF/PEF | 4.0/80 1 | 5.99/17.97 | 3.02/4.56 | 0.97/0.94 | 4.96/29.52 | 4.45/12.9 | 3.06/7.49 |
| Multiplexing | N/A | No | No | No | Yes | Yes | Yes |
| Coupling | AC | DC | AC | AC | AC | AC | AC |
| Area/Ch. (mm2) | 0.16 | 0.013 | 0.058 | 0.00656 | 0.0161 | 0.0258 | 2 0.012 |
| Power/Ch. (μW) | 80 | 5.04 | 3.05 | 0.65 | 27.56 | 1.84 | 3.44 |
| Power Supply | ±2.5 | 0.5 | 0.5/1.0 | 1.0 | 1.2/1.8 | 1.0 | 0.8/1.0 |
| Resolution (ENOB) | N/A | 7.2 | 10.3 | 8.1 | 8.99 | 8.2 | 8.98 |
| Channel FoM (fJ/c-s) | N/A | 1713.9 | 108.32 | 118.5 | 1734.5 | 312.86 | 147.87 |
| E-A FoM (fJ/c-s∙mm2) | N/A | 22.28 | 6.34 | 0.78 | 27.93 | 8.07 | 1.774 |
| Technology | 1500 nm | 65 nm | 65 nm | 65 nm | 180 nm | 65 nm | 180 nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.-J.; Park, Y.; Eom, K.; Park, S.-Y. An Area- and Energy-Efficient 16-Channel, AC-Coupled Neural Recording Analog Frontend for High-Density Multichannel Neural Recordings. Electronics 2021, 10, 1972. https://doi.org/10.3390/electronics10161972
Kim H-J, Park Y, Eom K, Park S-Y. An Area- and Energy-Efficient 16-Channel, AC-Coupled Neural Recording Analog Frontend for High-Density Multichannel Neural Recordings. Electronics. 2021; 10(16):1972. https://doi.org/10.3390/electronics10161972
Chicago/Turabian StyleKim, Hyeon-June, Younghoon Park, Kyungsik Eom, and Sung-Yun Park. 2021. "An Area- and Energy-Efficient 16-Channel, AC-Coupled Neural Recording Analog Frontend for High-Density Multichannel Neural Recordings" Electronics 10, no. 16: 1972. https://doi.org/10.3390/electronics10161972






