Improving Decision Making about Natural Disaster Mitigation Funding in Australia—A Framework
Abstract
:1. Introduction
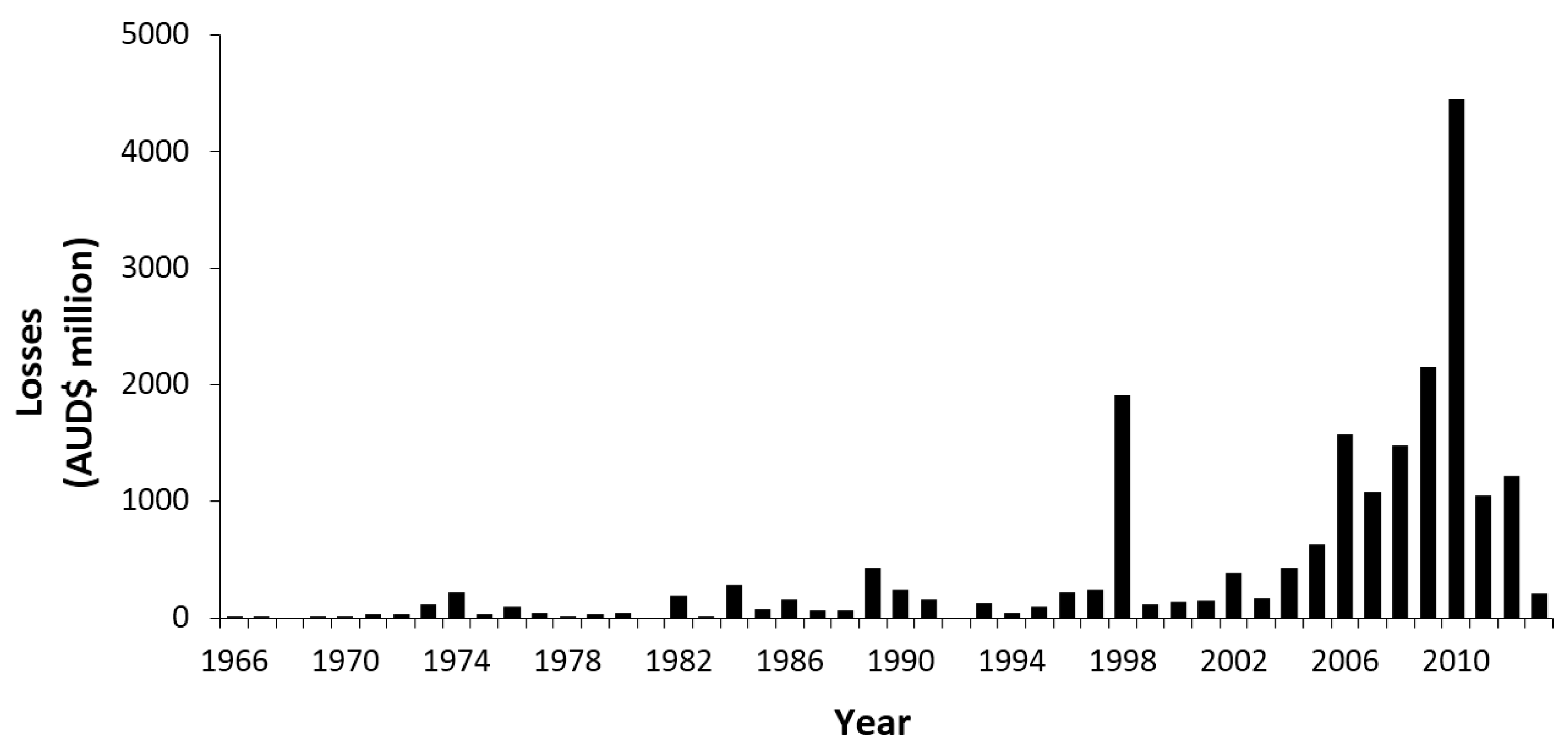
2. Natural Hazard Losses in Australia
2.1. Economic Losses from Natural Disasters
2.2. Natural Disaster Fatalities
3. The Productivity Commission Inquiry: Impetus for a Decision Framework
“Governments overinvest in post‑disaster reconstruction, and underinvest in mitigation that would limit the impact of natural disasters in the first place. As such, natural disaster costs have become a growing, unfunded liability for governments”[8]
4. Decision Making Regarding Disaster Risk Mitigation
5. A Decision Model
5.1. The Project Objective and Key Decision Criteria
“Produce a framework to consistently and reliably evaluate, compare and choose between potentially suitable alternative options for developing safer, healthier and more resilient communities, in the face of limited financial resources.”
5.2. A Hierarchy of Objectives
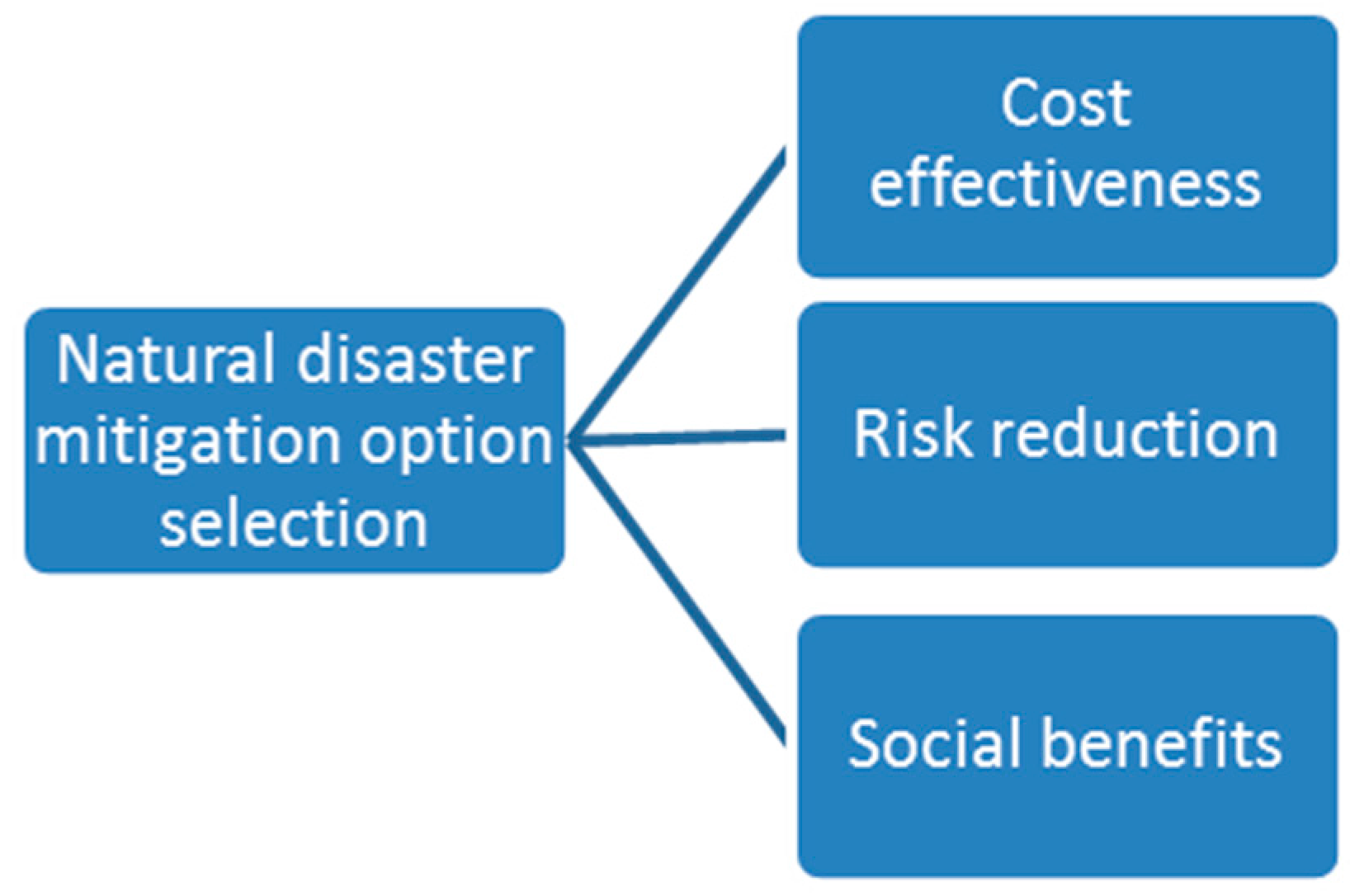
5.2.1. Decision Criteria
- Reduction of risk to the community (“safer”);
- Other social benefits (“healthier and more resilient”);
- Cost effectiveness (“in the face of limited financial resources”).
Cost Effectiveness
- t = year
- n = time horizon (50 years, say; typically the expected lifetime of the mitigation project)
- r = discount rate
- bt = reduction in economic activity losses in year t
- ct = reduction in asset losses in year t
- costst = capital and operational costs of the project in year t
Risk Reduction
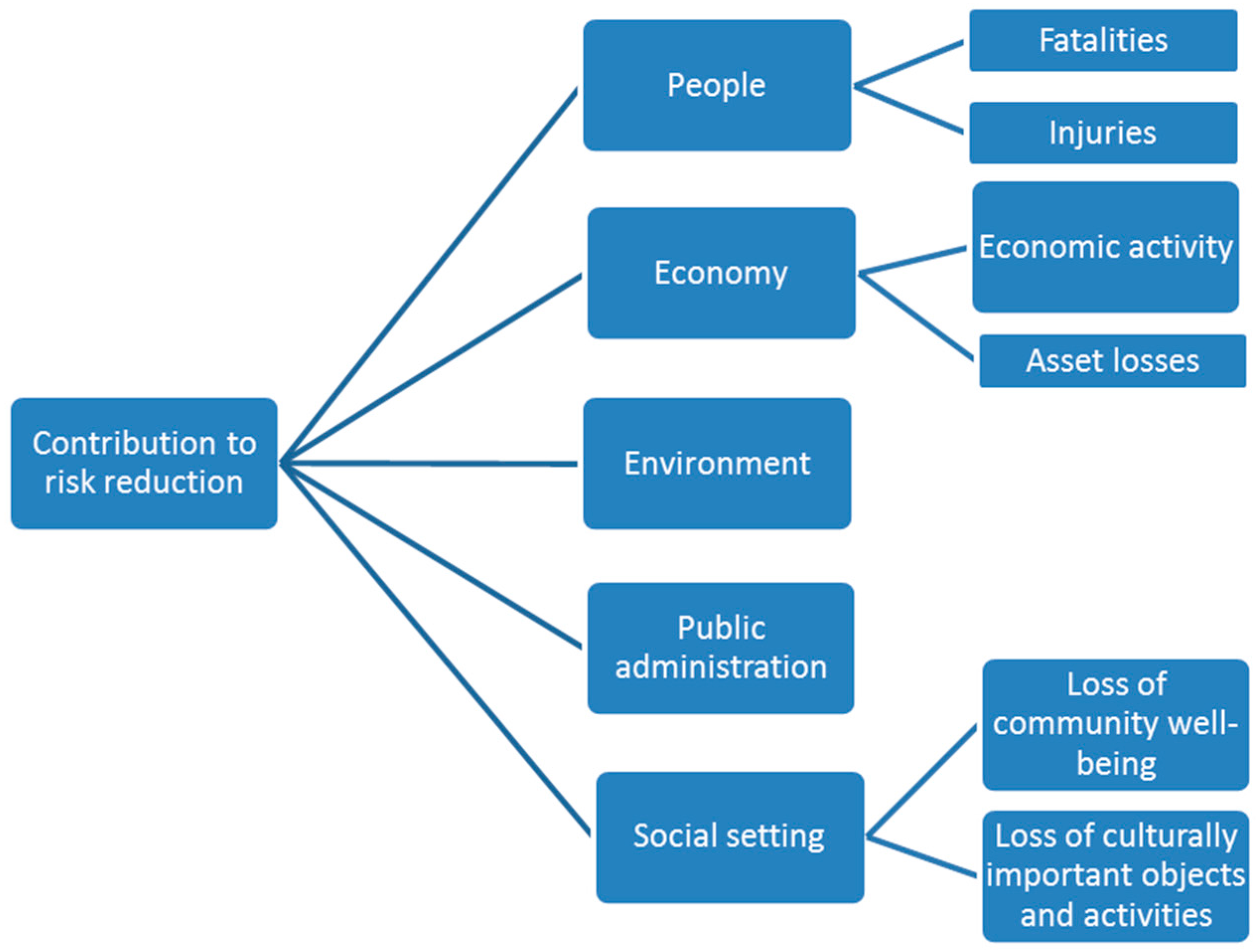
- Human fatalities and injuries ([9] (Table 3, p. 56, people consequences));
- Property, infrastructure or other economic losses ([9] (Table 5, p. 59, economic consequences));
- Critical ecosystem or species loss ([9] (Table 6, pp. 62–63, environmental consequences));
- Impairment of public administration ([9] (Table 7, p. 67, public administration consequences));
- Loss or destruction of community well-being or culturally-important objects or activities ([9] (Table 8, p. 69, social setting consequences)).
- Environment (critical ecosystem and/or species loss);
- Impairment of public administration;
- Social setting (loss or destruction of community well-being or culturally-important objects or activities).
Social Benefits
- Allocating a set amount of mitigation resources (a “mitigation fund”), where a ranking of proposals is required due to proposal values exceeding the available funds;
- Determining options for treating one or more specified hazard risks, where the total funding pool is not specified and will lead to future proposals for funding.
5.2.2. Relative Weighting of Decision Criteria
- Weights for fatalities and injuries should equal one;
- Weights for the five NERAG consequence criteria (five weights) should add up to one.
5.3. Value Functions for the Decision Criteria
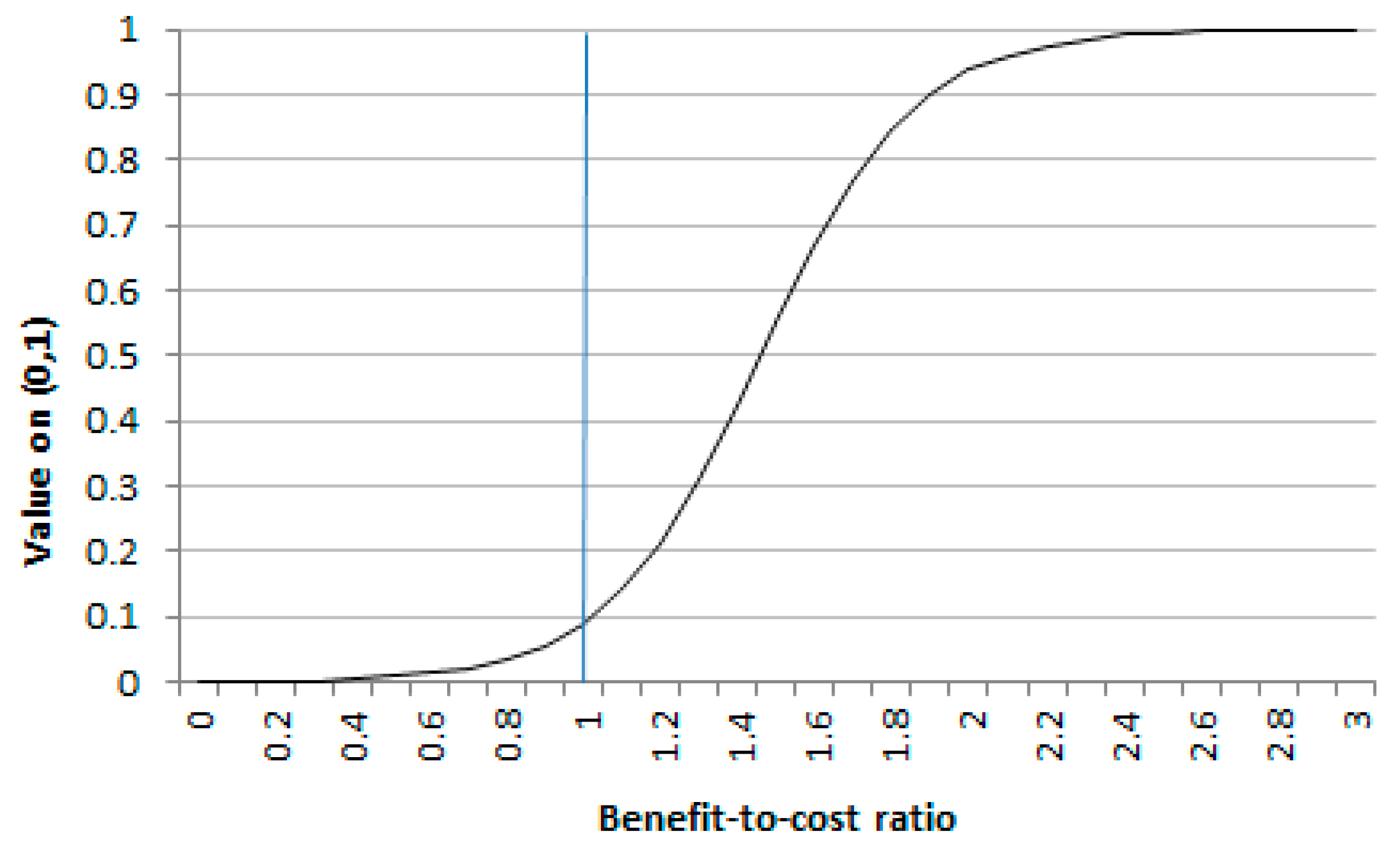
5.3.1. A Value Function for Cost Effectiveness
5.3.2. Value Functions for Risk Reduction Criteria
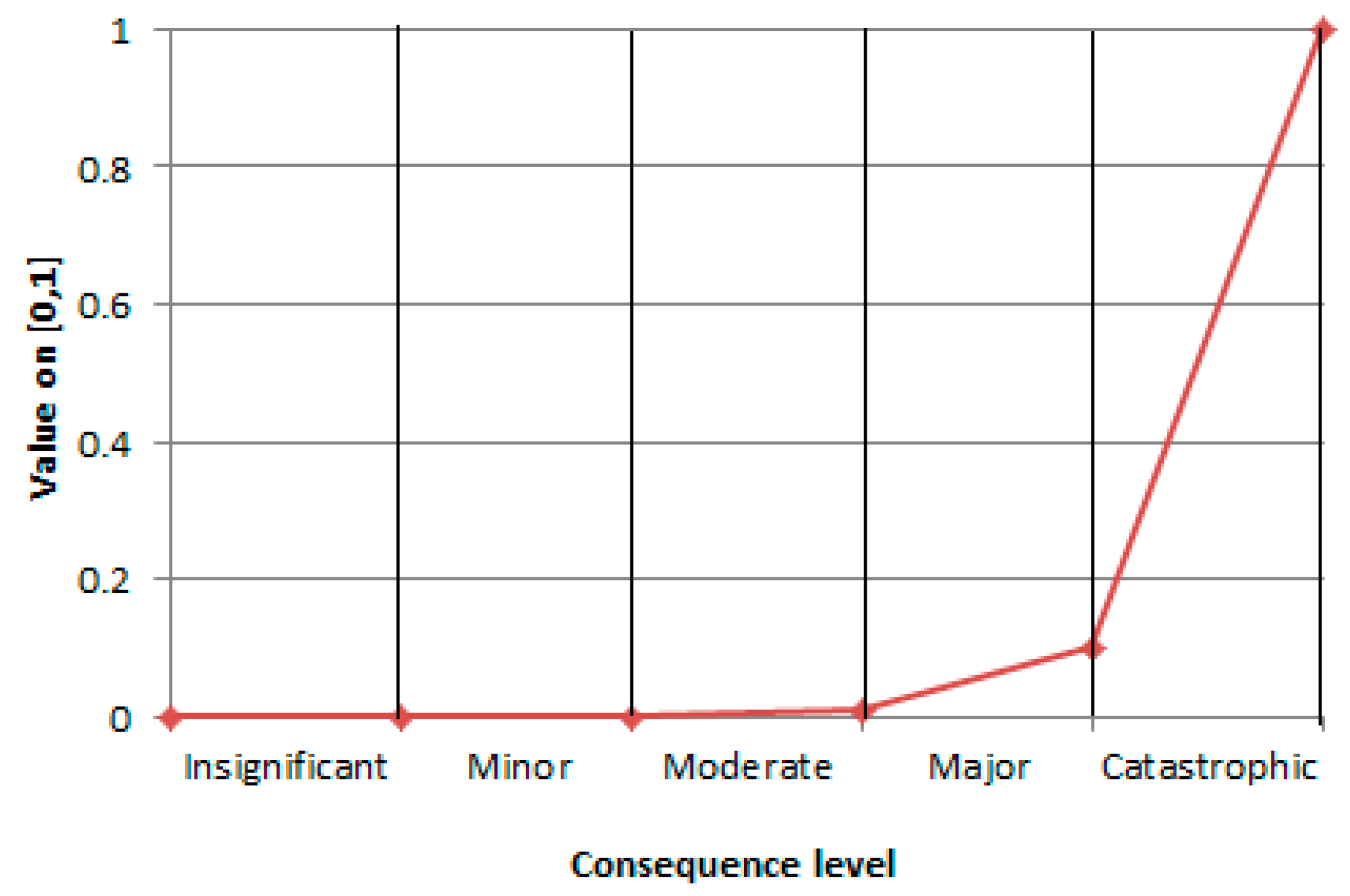
A Value Function for Consequences to People and the Economy
- The lower gradation of the lowest consequence level (“Insignificant”) be allocated a value of zero;
- Successive gradations increase in multiples of 10 due to the exponential scale used in the NERAG consequence tables for these criteria;
- The successive gradations are mapped onto values that are increasing multiples of 10, from 10−4, to cover the range from 0 to 1.
5.3.3. Value Functions for Social Benefit Criteria
5.4. Quantifying Risk Reducing Mitigation Benefits
5.4.1. Quantitative Risk Reduction Criteria
- The likelihood is measured by the annual exceedance probability (AEP). This is the probability of the event occurring exactly once in a year and is expressed as a number in the range 0–1. Another way of expressing this is the average recurrence interval (ARI) or average return period, which measures the average time between successive events of that magnitude.
- The consequence is measured as the weighted total of the consequence “values” (a dimensionless number in the range from 0 to 1), described above.
- the value of the reduction in consequences (if any) × the likelihood of the event (if consequences are reduced)
- the value of the consequences (if any) × the reduction in the likelihood of the event (if likelihood is reduced).
5.4.2. Qualitative Risk Reduction Criteria
5.5. Aggregation of Weights and Values
- RV(a) = overall risk value of mitigation option a (pre- or post-mitigation)
- RVi(a) = value score reflecting potential mitigation option a’s risk level under (sub-)criterion i
- wi = weight assigned to reflect the importance of (sub-)criterion i.
5.6. Calculating Risk Reduction over Natural Disaster Events of All Possible Magnitudes
5.7. The Overall Value of a Mitigation Option: Considering BCR and Risk Reduction
6. Simulation of Design Events Based on Historical Data
7. Project Portfolio Selection through Cost-Effectiveness Analysis
7.1. A Portfolio Decision Analysis Model for Mitigation Project Selection
- Step 0
- Let the overall mitigation project budget be $B.
- Step 1
- Of the available projects, select the one with the highest cost-effectiveness ratio (cost effectiveness ratio = CER = , where the project value is the score determined from the multicriteria model, scaled onto [0, 1]; this ratio allows a comparison of projects; those that offer greater value per dollar spent are preferred) (CER).
- Step 2
- Check that the cost of this project is lower than $B.
- There are a limited number of alternative projects
- The projects are independent of each other
- There are no constraints on the selection process.
- (1)
- Budget considerations will make it unlikely that every potential project will be able to be funded.
- (2)
- A selection panel is likely to impose an upper bound on the funds available for any single project.
- (3)
- The selection panel is likely to want to fund multiple projects. This will have several advantages:
- (i)
- Multiple projects means diversification of project impacts, both geographical and across domains
- (ii)
- Diversification will necessarily reduce the overall portfolio risk.
- a total funding budget of B dollars is available
- the cost of project i is ci dollars
- the value score of project i is vi units on [0, 1]
- at least s projects must be selected (for diversification)
- at most t projects must be selected
- at most r dollars can be spent on any one project.
| c1Y1 + c2Y2 + c3Y3 + … + cnYn ≤ B | (total cost of all projects in the portfolio less than $B) |
| ci Yi ≤ r for all projects i = 1, 2, … , n | (at most r dollars can be spent on any one project) |
| Y1 + Y2 + Y3 + … + Yn ≥ s | (at least s projects selected, for diversification) |
| Y1 + Y2 + Y3 + … + Yn ≤ t | (at most t projects selected) |
| Yi = 0 or 1 | for all projects i = 1, 2, …, n |
7.2. An Illustrative Example: Choosing a Portfolio of Mitigation Projects
- Choose the most cost-effective project. This is Project 5 (CER is largest: 20.00). The cost of this project is $2 million, leaving $43 million available for other projects.
- Of the remaining projects, Project 2 has the largest cost effectiveness ratio (CER: 12.25). As the cost of this project is $4 million, it is added to the portfolio. The available budget is now $39 million.
- Projects 9 (CER = 6.40, cost = $10 million), 6 (CER = 5.67, cost = $6 million), 8 (CER = 4.43, cost = $7 million) and 3 (CER = 3.00, cost = $15 million) are then added iteratively, reducing the available budget to $29 million, $23 million, $16 million and $1 million at successive iterations. No further project can be added to the portfolio due to the budget constraint.
- A total funding budget of $45 million dollars is available.
- At least three projects must be selected (to ensure diversification).
- At most $30 million dollars can be spent on any one project.
- Projects 6 and 8 are selected in every portfolio
- Projects 5 and 9 are included in five of the six portfolios: Project 5 is included when the budget is lower, and Project 9 is included when the budget is higher
- Project 2 is included in four portfolios, mostly when the budget is low
- Projects 1, 3 and 7 are only included in half of the portfolios and only when the budget is high
- Project 4 is never included in any portfolio, as it is by far the costliest project and, thus, offers the lowest value for the money.
8. Conclusions and Limitations
8.1. Practical Utility of the Framework
8.2. Limitations
8.3. Further Work
Acknowledgments
Conflicts of Interest
References
- Insurance Council of Australia. Catastrophe Events and the Community. Available online: http://www.insurancecouncil.com.au/issue-submissions/issues/catastrophe-events (accessed on 28 May 2016).
- Van den Honert, R.C.; Coates, L.; Haynes, K.; Crompton, R. A Century of Natural Disasters—What Are the Costs? Available online: https://issuu.com/afaclimited/docs/fire_summer14-15__01-52_/2 (accessed on 13 September 2016).
- Business Insider Australia. The Exploding Cost of Natural Disasters. Available online: http://www.businessinsider.com.au/chart-natural-disaster-costs-2012-12 (accessed on 28 May 2016).
- Insurance Council of Australia. The Non-Insured: Who, Why and Trends. Available online: http://www.insurancecouncil.com.au/assets/report/the%20non%20insured%20-%20report.pdf (accessed on 1 September 2016).
- Commonwealth of Australia, Department of Finance and Deregulation. Review of the Insurance Arrangements of State and Territory Governments under the Natural Disaster Relief and Recovery Arrangements Determination 2011. Available online: https://www.finance.gov.au/sites/default/files/ndrra-finance-phase-2-report-sep-2012_0.pdf (accessed on 1 September 2016).
- International Federation of Red Cross and Red Crescent Societies. World Disasters Report 2014. Available online: http://www.ifrc.org/en/publications-and-reports/world-disasters-report/world-disasters-report-2014/world-disasters-report-2014---data/ (accessed on 28 May 2016).
- Commonwealth of Australia (n.d.). Productivity Commission—About the Commission. Available online: http://www.pc.gov.au/about (accessed on 28 May 2016).
- Commonwealth of Australia. Productivity Commission—Natural Disaster Funding: Inquiry Report. Available online: http://www.pc.gov.au/inquiries/completed/disaster-funding/report (accessed on 28 May 2016).
- Commonwealth of Australia. National Emergency Risk Assessment Guidelines, 2nd ed.Australian Government Attorney-General’s Department: Canberra, Australia, 2014; p. 136.
- ISO 31000:2009 Risk Management—Principles and Guidelines. Available online: https://www.iso.org/obp/ui/#iso:std:43170:en (accessed on 28 May 2016).
- Penman, T.D.; Eriksen, C.D.; Horsey, B.; Bradstock, R.A. How much does it cost residents to prepare their property for wildfire? Int. J. Disaster Risk Reduct. 2016, 16, 88–98. [Google Scholar] [CrossRef]
- Tamura, H.; Yamamoto, K.; Tomiyama, S.; Hatono, I. Modeling and analysis of decision making problem for mitigating natural disaster risks. Eur. J. Oper. Res. 2000, 122, 461–468. [Google Scholar] [CrossRef]
- Benson, C.; Twigg, J. Methodologies for Assessing Natural Hazard. Risks and the Net Benefits of Mitigation—A Scoping Study; ProVention Consortium for the International Federation of Red Cross and Red Crescent Societies: Geneva, Switzerland, 2004. [Google Scholar]
- Sarin, R.K. A social decision analysis of the earthquake safety problem: The case of existing Los Angeles buildings. Risk Anal. 1983, 3, 35–50. [Google Scholar] [CrossRef]
- Burby, R. Hurricane Katrina and the paradoxes of government disaster policy: Bringing about wise governmental decisions for hazardous areas. Ann. Am. Acad. Political Soc. Sci. 2006, 604, 171–191. [Google Scholar] [CrossRef]
- Kunreuther, H. Disaster mitigation and insurance: Learning from Katrina. Ann. Am. Acad. Political Soc. Sci. 2006, 604, 208–227. [Google Scholar] [CrossRef]
- Ganderton, P.T. Benefit-cost analysis of disaster mitigation: Application as a policy and decision-making tool. Mitig. Adapt. Strateg. Glob. Chang. 2005, 10, 445–465. [Google Scholar] [CrossRef]
- Cardona, O.D. The Need for Rethinking the Concepts of Vulnerability and Risk from a Holistic Perspective: A Necessary review and Criticism for Effective Risk Management. In Mapping Vulnerability: Disasters, Development and People; Bankhoff, G., Frerks, G., Hilhorst, D., Eds.; Earthscan Publishers: London, UK, 2004; pp. 37–51. [Google Scholar]
- Cardona, O.D. Environmental Management and Disaster Prevention: Holistic Risk Assessment and Management. In Natural Disaster Management; Ingleton, J., Ed.; Tudor Rose: London, UK, 1999. [Google Scholar]
- Kiker, G.A.; Bridges, T.S.; Varghese, A.; Seager, T.P.; Linkov, I. Application of multicriteria decision analysis in environmental decision making. Integr. Environ. Assess. Manag. 2005, 1, 95–108. [Google Scholar] [CrossRef] [PubMed]
- Hämäläinen, R.P.; Lindstedt, M.; Sinkko, K. Multi-attribute risk analysis in nuclear emergency management. Risk Anal. 2000, 20, 455–468. [Google Scholar] [CrossRef] [PubMed]
- Janssen, R. On the use of multi-criteria analysis in environmental impact assessment in the Netherlands. J. Multi Criteria Decis. Anal. 2001, 10, 101–109. [Google Scholar] [CrossRef]
- Linares, P. Multiple criteria decision making and risk analysis as risk management tools for power systems planning. IEEE Trans. Power Syst. 2002, 17, 895–900. [Google Scholar] [CrossRef]
- Raaijmakers, R.; Krywkow, J.; Van der Veen, A. Flood risk perceptions and spatial multi-criteria analysis: An exploratory research for hazard mitigation. Nat. Hazards 2008, 46, 307–322. [Google Scholar] [CrossRef]
- Jactel, H.; Branco, M.; Duncker, P.; Gardiner, B.; Grodzki, W.; Langstrom, B.; Moreira, F.; Netherer, S.; Nicoll, B.; Orazio, C.; et al. A multicriteria risk analysis to evaluate impacts of forest management alternatives on forest health in Europe. Ecol. Soc. 2012, 17. [Google Scholar] [CrossRef]
- Molino Stewart, Hawkesbury-Nepean Flood Damages Assessment: Final Report. Report to Infrastructure NSW. Available online: http://www.infrastructure.nsw.gov.au/media/16727/molino_stewart_hn_flood_damages_report_final.pdf (accessed on 28 May 2016).
- Risk Frontiers. Liabilities for Launceston City Council in Respect of Flooding in Invermay: Technical Report on Risk Frontiers’ Probabilistic Flood Loss Modeling; Risk Frontiers, Macquarie University: Sydney, Australia, 2004. [Google Scholar]
- Walker, G.R.; Crompton, R.P.; Mason, M.S.; Musulin, R.T. Application of insurance modelling tools to climate change adaptation decision making relating to the built environment. Struct. Infrastruct. Eng. 2015. [Google Scholar] [CrossRef]
- Risk Frontiers. A Critical Review of the Suitability of Methodologies for the Evaluation and Comparison of Natural Hazard Mitigation Options; Report to SAFECOM, under the auspices of Risk Assessment, Measurement and Mitigation Sub-Committee of ANZEMC: Adelaide, Australia, 2014. [Google Scholar]
- Belton, V.; Stewart, T.J. Multiple Criteria Decision Analysis: An Integrated Approach; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002; p. 372. [Google Scholar]
- Mustajoki, J.; Hämäläinen, R.P.; Lindstedt, M.R.K. Using intervals for global sensitivity and worst-case analyses in multi-attribute value trees. Eur. J. Oper. Res. 2006, 174, 278–292. [Google Scholar] [CrossRef]
- Van den Honert, R.C. Stochastic group preference modelling in the multiplicative AHP: A model of group consensus. Eur. J. Oper. Res. 1998, 110, 99–111. [Google Scholar] [CrossRef]
- Salo, A.; Keisler, J.; Morton, A. Portfolio Decision Analysis: Improved Methods for Resource Allocation; Springer International Series in Operations Research & Management Science; Springer: New York, NY, USA, 2011; p. 409. [Google Scholar]
- Markowitz, H.M. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar] [CrossRef]



| Rank | Event | Peril Type | Year | Actual Insured Cost (A$bn) | Normalised Insured Cost (2011 A$bn) |
|---|---|---|---|---|---|
| 1 | Sydney hailstorm | Hail | 1999 | 1.700 | 4.296 |
| 2 | TC Tracy | Tropical cyclone | 1974 | 0.200 | 4.090 |
| 3 | Newcastle earthquake | Earthquake | 1989 | 0.862 | 3.240 |
| 4 | Brisbane flood | Flood | 1974 | 0.068 | 2.645 |
| 5 | Queensland floods | Flood | 2011 | 2.400 | 2.500 |
| 6 | Brisbane hailstorm | Hail | 1985 | 0.180 | 2.063 |
| 7 | Newcastle East Coast Low storm | Severe storm | 2007 | 1.480 | 1.742 |
| 8 | TC Madge | Tropical cyclone | 1973 | 0.030 | 1.492 |
| 9 | Ash Wednesday bushfires | Bushfire | 1983 | 0.138 | 1.489 |
| 10 | TC Yasi | Tropical cyclone | 2011 | 1.300 | 1.352 |
| Level | Death | Injury and Illness |
|---|---|---|
| Catastrophic | Deaths directly from emergency greater than 1 in 10,000 people for the population of interest | Critical injuries with long-term or permanent incapacitation greater than 1 in 10,000 people for the population of interest |
| Major | Deaths directly from emergency greater than 1 in 100,000 people for the population of interest | Critical injuries with long-term or permanent incapacitation greater than 1 in 100,000 people for the population of interest or Serious injuries greater than 1 in 10,000 people for the population of interest |
| Moderate | Deaths directly from emergency greater than 1 in 1,000,000 people for the population of interest | Critical injuries with long-term or permanent incapacitation greater than 1 in 1,000,000 people for the population of interest or Serious injuries greater than 1 in 100,000 people for the population of interest |
| Minor | Deaths directly from emergency greater than 1 in 10,000,000 people for the population of interest | Critical injuries with long-term or permanent incapacitation greater than 1 in 10,000,000 people for the population of interest or Serious injuries greater than 1 in 1,000,000 people for the population of interest |
| Insignificant | Not applicable | Serious injuries less than 1 in 1,000,000 people for the population of interest or Minor injuries to any number of people |
| Level | Loss in Economic Activity and/or Asset Value |
|---|---|
| Catastrophic | Decline of economic activity and/or Loss of asset value greater than 4% of gross product produced by the area of interest |
| Major | Decline of economic activity and/or Loss of asset value greater than 0.4% of gross product produced by the area of interest |
| Moderate | Decline of economic activity and/or Loss of asset value greater than 0.04% of gross product produced by the area of interest |
| Minor | Decline of economic activity and/or Loss of asset value greater than 0.004% of gross product produced by the area of interest |
| Insignificant | Decline of economic activity and/or Loss of asset value less than 0.004% of gross product produced by the area of interest |
| Level | State or National Description |
|---|---|
| Catastrophic | Governing bodies and utility providers are unable to deliver their core functions |
| Major | Governing bodies and utility providers encounter severe reduction in the delivery of core functions Governing bodies and utility providers are required to divert a significant amount of available resources to deliver core functions or seek external assistance to deliver the majority of their core functions |
| Moderate | Governing bodies and utility providers encounter significant reduction in the delivery of core functions Governing bodies and utility providers are required to divert some available resources to deliver core functions or seek external assistance to deliver some of their core functions |
| Minor | Governing bodies and utility providers encounter limited reduction in the delivery of core functions |
| Insignificant | Governing bodies’ and utility providers’ delivery of core functions is unaffected or within normal parameters |
| Decision Criterion | Scale | Measure |
|---|---|---|
| Cost effectiveness | Continuous | BCR > 0 |
| Risk reduction | Categorical | Difference between risk categories (after-before mitigation) |
| Social benefits | Categorical | Difference between social benefit categories (after-before mitigation) |
| Level | Scaled Values |
|---|---|
| Insignificant | 0–0.0001 |
| Minor | 0.0001–0.001 |
| Moderate | 0.001–0.01 |
| Major | 0.01–0.1 |
| Catastrophic | 0.1–1 |
| Likelihood | Indicative Frequency | Annual Exceedance Probability (AEP) | Average Recurrence Interval (ARI) |
|---|---|---|---|
| Almost certain | Once or more per year | 63% per year, or more | 1 year or less |
| Likely | Once per 10 years | 10%–63% per year | 1–10 years |
| Unlikely | Once per 100 years | 1%–10% per year | 11–100 years |
| Rare | Once per 1000 years | 0.1%–1% per year | 101–1000 years |
| Very rare | Once per 10,000 years | 0.01%–0.1% per year | 1001–10,000 years |
| Extremely rare | Once per 100,000 years | 0.001%–0.01% per year | More than 10,000 years |
| Level | Scaled Value |
|---|---|
| Insignificant | 0.00005 |
| Minor | 0.00055 |
| Moderate | 0.0055 |
| Major | 0.055 |
| Catastrophic | 0.55 |
| Project | Cost ($m) (C_i) | MCDA "Benefit Score" (0–100) (V_i) | Cost-Effectiveness Ratio (×100) |
|---|---|---|---|
| 1 | 22 | 0.66 | 3.000 |
| 2 | 4 | 0.49 | 12.250 |
| 3 | 15 | 0.45 | 3.000 |
| 4 | 47 | 0.82 | 1.745 |
| 5 | 2 | 0.4 | 20.000 |
| 6 | 6 | 0.34 | 5.667 |
| 7 | 20 | 0.37 | 1.850 |
| 8 | 7 | 0.31 | 4.429 |
| 9 | 10 | 0.64 | 6.400 |
| 133 |
| Project | Cost ($m) (C_i) | MCDA "Benefit Score" (0–100) (V_i) | Cost-Effectiveness Ratio (×100) | Y_i | C_i*Y_i |
|---|---|---|---|---|---|
| 1 | 22 | 0.66 | 3.000 | 0 | 0.00 |
| 2 | 4 | 0.49 | 12.250 | 1 | 4.00 |
| 3 | 15 | 0.45 | 3.000 | 1 | 15.00 |
| 4 | 47 | 0.82 | 1.745 | 0 | 0.00 |
| 5 | 2 | 0.4 | 20.000 | 1 | 2.00 |
| 6 | 6 | 0.34 | 5.667 | 1 | 6.00 |
| 7 | 20 | 0.37 | 1.850 | 0 | 0.00 |
| 8 | 7 | 0.31 | 4.429 | 1 | 7.00 |
| 9 | 10 | 0.64 | 6.400 | 1 | 10.00 |
| 133 | 6 | 44.00 |
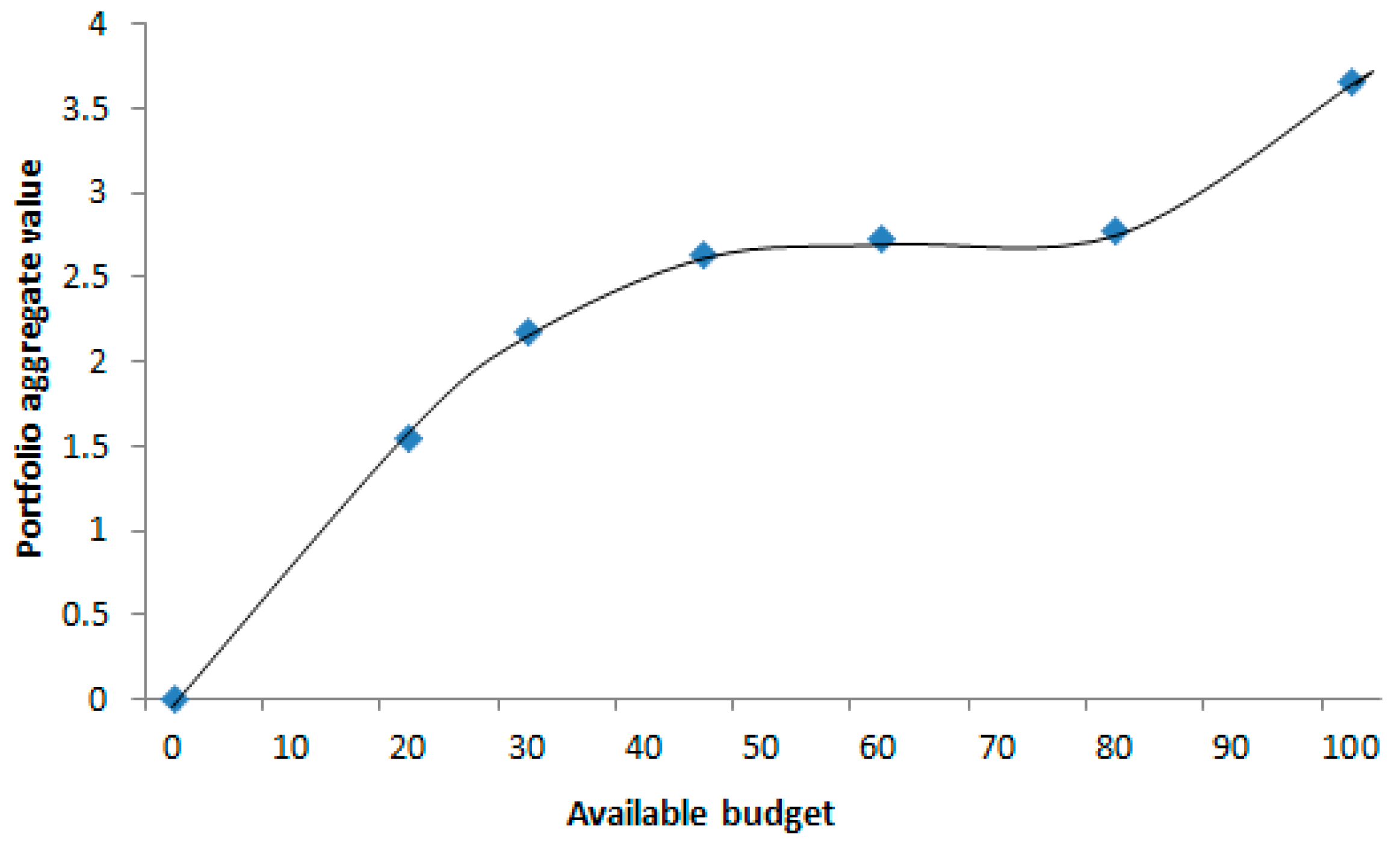
| Budget ($ Million) | ||||||
|---|---|---|---|---|---|---|
| Project | 20 | 30 | 45 | 60 | 80 | 100 |
| 1 | x | x | x | |||
| 2 | x | x | x | x | ||
| 3 | x | x | x | |||
| 4 | ||||||
| 5 | x | x | x | x | x | |
| 6 | x | x | x | x | x | x |
| 7 | x | x | x | |||
| 8 | x | x | x | x | x | x |
| 9 | x | x | x | x | x | |
| Projects included | 4 | 5 | 6 | 6 | 6 | 8 |
| Portfolio aggregate value | 1.54 | 2.18 | 2.63 | 2.72 | 2.77 | 3.66 |
| Unused budget | 1 | 1 | 1 | 0 | 0 | 14 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van den Honert, R.C. Improving Decision Making about Natural Disaster Mitigation Funding in Australia—A Framework. Resources 2016, 5, 28. https://doi.org/10.3390/resources5030028
Van den Honert RC. Improving Decision Making about Natural Disaster Mitigation Funding in Australia—A Framework. Resources. 2016; 5(3):28. https://doi.org/10.3390/resources5030028
Chicago/Turabian StyleVan den Honert, Robin C. 2016. "Improving Decision Making about Natural Disaster Mitigation Funding in Australia—A Framework" Resources 5, no. 3: 28. https://doi.org/10.3390/resources5030028
APA StyleVan den Honert, R. C. (2016). Improving Decision Making about Natural Disaster Mitigation Funding in Australia—A Framework. Resources, 5(3), 28. https://doi.org/10.3390/resources5030028






