1. Systems Theory in a Crisis?
Systems theory has reached something of an impasse. While early work yielded a range of insights about general system behaviour [
1,
2], the field has failed to live up to this early promise. Indeed, the periodic rise and fall of interest in cybernetics, systems, complex systems and, now, complex adaptive systems suggests that the field is hitting a barrier that it is struggling to overcome. Here, I will argue that re-examining the notion of context can help us to progress.
We will start with a consideration of the very notion of a system. What allows us to model some part of the world as a system, separate from its surroundings? This will lead to a discussion of the idea of a measurement that can be performed upon a system. At this point, we shall see that only a very small subset of systems displays objective behaviour upon measurement. This observation allowed entire fields to progress in their attempts to understand reality; however, the systems modelled by fields, such as physics and chemistry, are not all there is to reality; we must be very careful as to how deeply we hold the idea that objective responses to measurement are essential to the very idea of science. Many systems do not display such behaviour, and it is essential that we understand the different ways in which they can violate what might otherwise be regarded as a core tenet of science.
The attempt to understand this violation of objectivity will form the core contribution of this work. We will consider the notion of context and the way in which contextual behaviour leads to the manifestation of behaviour that is often denoted as complex. Contextual behaviour has been witnessed in physics, too, and quantum theory (QT) was the result. QT has developed a whole range of formalisms to describe contextuality, but there is no a priori reason why these cannot be used beyond the domain of physics. Indeed, a new field of research has sprung up from the attempt to create quantum-like formalisms to describe the behaviour of systems exhibiting contextual behaviour.
However, stepping back from this general modelling paradigm, it is possible to realise that QT did not cease with the standard formulation of quantum mechanics. The description of structures appearing and disappearing required a move to quantum field theory (QFT), historically through the mechanism of second quantization, but this is not the only path available, as demonstrated by the functional methods of QFT [
3]. A more direct set of mappings should be sought in any attempt to describe complex emergent systems, and we shall discuss the manner in which this might be achieved within the framework of a contextualised general systems theory (CGST).
We begin with the notion of a system.
1.1. What Is a System?
At its simplest, a system
is a set of entities that are interacting via a set of relationships [
4]. It is something that we can single out from some sort of environment
and is designated as either closed or open, depending on whether it interacts with that environment. Some fields of science have discovered a dynamics (or set of laws) that describe their systems, but other fields have been finding it harder to discover even the requisite underlying kinematics (or general behaviour) of their systems of interest. Here, we shall take the notion of separability to be key to the definition of a system. Such a move is hardly unique; indeed, both the Latin word systēma, and the Greek word ϛúστεμα have this same notion of a set of components that form something distinct from their surrounds. This concept went on to motivate the very notion of reduction, which is central to the basic understanding of science [
5,
6], and yet, many different fields have challenged this fundamental notion of separability. Thus, we see scenarios, such as biological systems, which display phenotypic plasticity, and, so, depend not just upon their genetic sequences, but upon the environment in which they evolve [
7,
8] and the people who give responses to questions about the length of a line, which depend upon the responses that have been given before by a set of conspirators [
9]. Even that bastion of reduction, physics, has shown what might be regarded as a surprising tendency to throw up contradictions when we assume that reductive models of the Universe will prove appropriate, with phenomena like entanglement/non-locality [
10], colour confinement [
11,
12] and collective dynamics [
13], all presenting their challenges to reductive explanations.
Some examples will serve as guiding illustrations for the arguments that we will develop here.
A tennis ball is notably distinct from its environment. If we know the mass of the ball, its initial velocity and the value of gravity, then we can easily map out the trajectory of a system such as this (and a school student is frequently expected to do so). Indeed, the movements of objects like this very much motivated the development of modern physics (and so our conceptualisation of science). However, even an example as simple as this one becomes problematic upon closer examination. Gravity changes in different places; friction becomes important (in the form of air resistance), and even the surface of the ball can affect its trajectory. Of course, these effects are second order, and we only care about them in the case where a highly accurate prediction about where the ball falls becomes necessary. However, a projectile that is moving fast enough requires an entirely new theory, General Relativity, in order to reach the accuracy required in some cases (e.g., when we are trying to estimate where satellites will be for our global GPS infrastructure). Thus, even in the paradigmatically simple case of projectile motion, there is no one model or theory that universally applies.
A steam engine provides a slightly more complex example due to its internal mechanisms, which are dependent upon thermodynamic principles. Measurements can still be performed upon such a system, and depending upon how well it is isolated from the environment, we will see well-defined behaviour emerge. Much of modern statistical mechanics arose from relaxing conditions about how isolated a system is from its environment (with the formalism describing microcanonical, canonical and grand canonical ensembles as the system becomes more open). One particularly new aspect presents upon comparison with our original tennis ball; steam engines can exchange material with their environments and, so, should no longer be regarded as closed. Indeed, as long as a steady supply of combustible material is maintained, the steam engine will enter a steady state, where the energy it produces becomes a constant (despite requiring this constant input).
Biological systems are more difficult to separate from their surrounding environment. An organism, while distinct and following physical laws (such as the same gravitational laws affecting the tennis ball), must interact with its environment in order to survive. It is an open system and is generally considered to be dissipative [
14] (in contrast even to systems described by the grand canonical ensemble, which is assumed to be in equilibrium). This means that biological systems rely in principle upon the environment to ensure their ongoing structural and functional stability, and their models tend to make this openness more explicit than is the case for statistical mechanics. Biological systems are also inherently contextual, with genes, species and even ecosystems capable of exhibiting profoundly different responses to the same stimulus if it occurs within a different context [
15]. These characteristics already make the notion of a system very different in biology compared to those that are commonly considered in physics.
Language arises within a population in a society, and so, it makes almost no sense to talk about the notion of a system and its environment in this case. However, structurally, language is frequently assumed to be separable, at least at the syntactic level. Indeed, a centrally held dogma in linguistics, the principle of compositionality, states that the meanings of higher order expressions, such as sentences, are determined from a combination of the meanings of its constituent parts [
16]. If this principle were true, then it would imply that linguistic systems can be straightforwardly separated from their surrounding environment; however, this is very difficult to justify either theoretically or empirically. The social nature of language implies that the meaning we attribute to words is probabilistically modified not just by other words [
17], but also by our experiences, education, social identity, demographics and our current context. As a result, fields, such as cognitive science, still struggle to produce models of language that incorporate well-known effects.
Societies exhibit a wide range of complex interdependencies. For example, social psychology has developed a highly sophisticated understanding of the complexities inherent in human interactions, with phenomena like cognitive dissonance, attitude change, prejudice, the conceptualisations of self and identity and the formation of ideologies, all subject to intensive investigation [
18]. Most of these studies consistently reveal strong interdependencies between the system under study and the environment. Should we draw our separating line around the people in the society? Should we include their technology and domesticated animals? What of the way in which different societies change their terrain (e.g., by draining swamps, deforestation, the emission of carbon,
etc.). It is difficult to find a clear dividing line between a society and its environment. Social factors also affect the individual. For example, Asch’s line judgement task [
9] shows that the context in which people make judgements even about the length of a line can be profoundly affected by their social context. This makes it highly difficult to draw a clean line around a social system; even the experimentalist can have a strong influence upon a social system, with issues such as framing [
19] showing that how you ask a question can profoundly affect the result that you obtain from a subject.
Of course, many different behaviours can be described by the tools developed in physics, which suggests that the framework of a system plus the environment,
, (this is a general notation, referring to a general system with two components; the ⊕ symbol is meant to be general, and does not refer to a direct sum in any way) is remarkably useful. For example, Albert and Barabási [
20] have combined network theory and statistical mechanics to describe some characteristics of biological, linguistic and social systems. However, the characteristics of the systems described by models such as these are not particularly complex [
21]; are we selecting for those behaviours that we can model using these techniques?
1.2. General Systems
General systems theory (GST) attempts to specify a set of principles that can apply to all types of systems [
1]. Its history traces back to attempts to respond to the challenges posed by non-physical (e.g., biological, cognitive and social) systems to our reductive techniques [
2]. Indeed, von Bertalanffy’s attempt to argue for a ‘middle way’ perspectivism between absolutism and radical relativism [
2] suggests that GST arose from an acceptance that the full set of behaviour and properties pertaining to some objects might be difficult to describe using models that derive purely from physics. Von Bertalanffy argued that biology needed not just empirical “facts”, but hypotheses and eventually laws of some form. However, this raises an important problem: biological systems are inherently contextual (as are many cognitive and social systems), which makes many of the tools of the modern scientific method very difficult to apply. The assumption that these systems can be described as objects, behaving objectively (
i.e., independently of the manner in which we observe them) becomes highly problematic [
15,
21], and so, assumptions routinely used in physics begin to lose their validity. Separability, reduction and independence between components increasingly find themselves questioned, and new notions become important, including emergence, holism and downward causation [
6,
22,
23,
24].
However, formalising these notions has proven to be difficult. Instead of a generalised formal model, we have seen a range of different approaches and methods proposed, especially as GST was gradually replaced by complex systems science (CSS). Network theory, agent-based modelling, statistical models, spin glass models and evolutionary approaches have all been applied to the modelling of systems well beyond the physical [
25,
26]. However, caution is necessary. von Bertalanffy noted the difference between “description” and “explanation”, bemoaning the fact that biology was stuck in a descriptive, or pre-Copernican, period [
2], which could provide an explanation for this wide range of models and approaches. Are we stuck in a descriptive phase? Or do we require multiple models?
1.3. Model Complexity
The complexity required of a model depends not just upon the system to be described. The requirements of the modeller also play a role.
Even for the case of the tennis ball, we saw that varying levels of model complexity were possible. However, in that case, it was possible to choose between them according to the accuracy required of the model. This is because tennis balls exhibit a clear boundary separating the ball from its environment, which means that it is only necessary to consider those factors in the environment that are required for an accurate enough description of its dynamics. This relatively straightforward scenario can be contrasted with other systems that do not display such a clear separation. In particular, it is frequently the case that different levels of description are possible within the one system. Thus, in the case of an ecosystem, we see that:
Depending on the spatiotemporal scale or window through which one is viewing the world, a forest stand may appear (1) as a dynamic entity in its own right, (2) as a constant (i.e., nondynamic) background within which an organism operates, or (3) as inconsequential noise in major geomorphological processes.
(O’Neill
et al. [
27], p. 83)
Of course, this emphasis on levels of description is by no means new. For example, in cognitive science, Marr proposed that three complementary levels of analysis should be used to understand information processing systems: (i) computational; (ii) representational and algorithmic; and (iii) implementational [
28]. These levels can respectively be understood as the function, procedures and physical mechanisms of the cognitive system [
29]. In both Marr’s approach to understanding information and the scenario described by O’Neill
et al. [
27], we see that the scale used to model the forest stand depends upon the requirements of the modeller. Is a botanical, zoological or geological model required for the forest stand? Alternatively, are we seeking a algorithmic, functional or hardware-driven model of cognition? Different modellers are interested in different aspects, or perspectives, of the same system [
29]. Indeed, this form of argument can be traced back to at least Aristotle’s four classifications of cause: material, formal, efficient and final [
24], each describing different causal categories that can be used in the explanation of some general thing (be it object, relation, law,
etc.).
Such levels of description pose a challenge to the more standard definitions of complexity, which often list a series of properties that are displayed by complex systems. For example, Mitchell [
25] suggests that complex systems must exhibit: (i) complex collective behaviour; (ii) signalling and information processing; and (iii) adaptation. While this is by no means a poor definition, it fails to acknowledge the contextuality of the very definition of a system as complex. Returning to the forest stand example above, these characteristics are only exhibited when it is the forest itself that is under study. In a larger scale model (say of an ecosystem, which is usually also regarded as complex by this kind of a definition), the complexity of the forest stand often disappears, to be replaced by a very simple model. Thus, for the system under examination by O’Neill
et al. [
27], the forest stand is modelled as a simple random noise term in comparison to major geomorphological processes and by a constant factor when it is the species living inside the forest under consideration. Neither of these models would be considered complex according to the definition of Mitchell [
25]. If the forest were something that we had never been interested in, then we would never have thought to designate it as complex. Therefore, while more is no doubt different [
30], it seems inappropriate to designate a system as either simple or complex without consideration of the level at which it is to be understood. Indeed:
The way we look determines what we see, or rather it co-determines the latter, in conjunction with what there is.
But this raises an interesting question; how are we to analyse such contextual complexity?
For many systems, the decision as to which level of description should be adopted depends upon the observer, who is required to make an epistemic cut between the system and the environment [
32]. There are very few systems with a natural cut, and historically, most of them were found in physics, which appears to have a very special status in modelling. Thus, many of our approaches to modelling (and our associated assumptions) have been derived from a field in which such separations are generally assumed to be possible (and historically have been). However, even in physics, assumptions of noncontextuality and separability have become problematic. It is often the case that in examining complex systems, we are far more than passive observers. Yet, we have very few theoretical tools that can represent such behaviour.
However, our understanding of the role of the observer suggests that understanding measurement is key to understanding contextuality. For this reason, we shall now turn to a consideration of measurement. In what follows, we shall gradually increase the contextuality of the behaviour revealed by measurement, asking what this tells us about the formalism required to understand and model the resulting behaviour.
2. Measuring General Systems
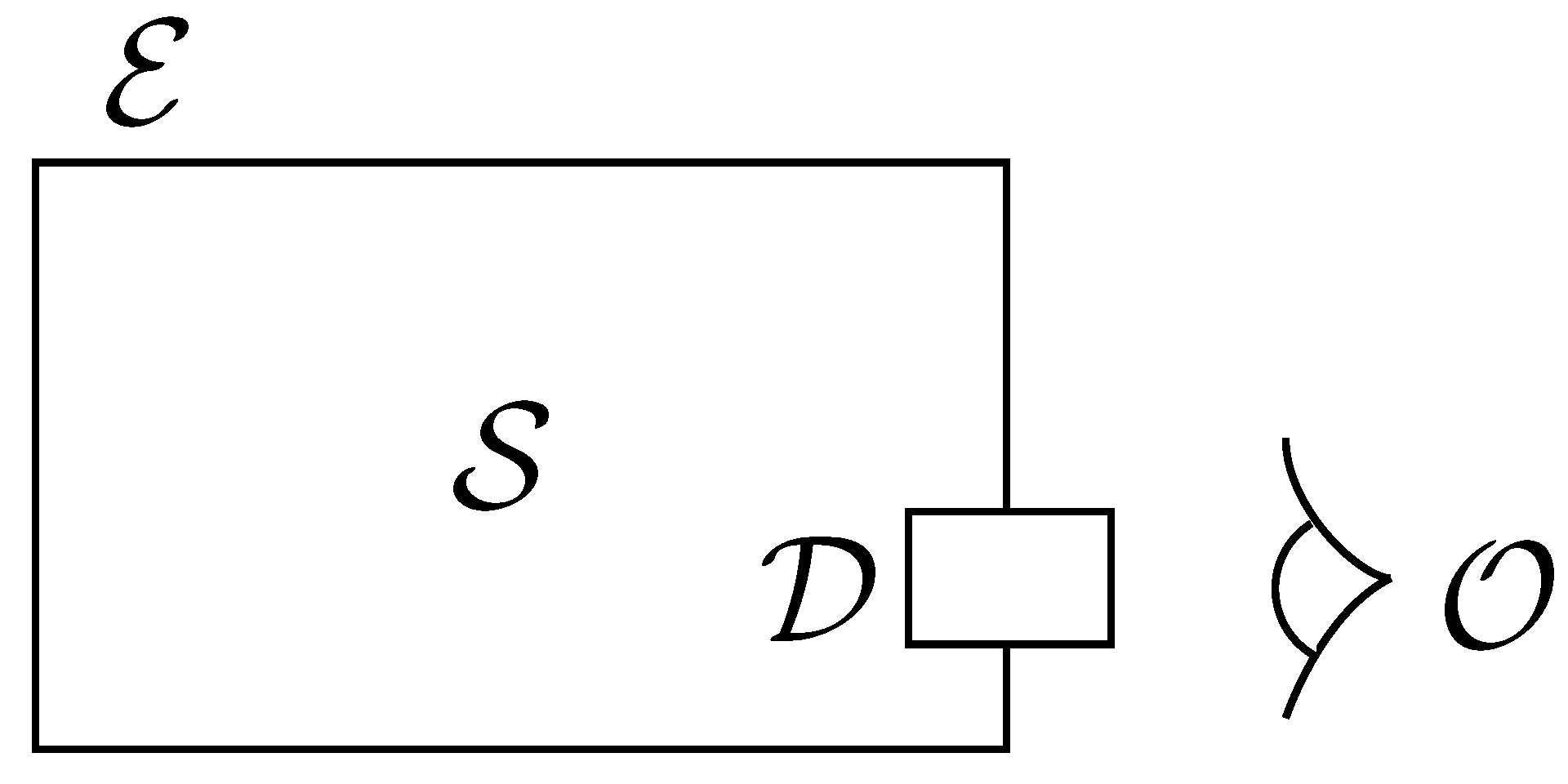
In order to describe measurement, we will have to enlarge our notion of a system. Measurements form a boundary between the system and the environment (in which the observer traditionally resides). Introducing both the observer
and a measuring device
leaves us with the more specific system shown in
Figure 1, one that it is possible to experimentally probe and investigate.
Figure 1.
At its simplest, a system is something that can be considered as distinct from its environment in some manner. Some systems can be measured by a device that discovers information about the state of the system and reports it to an observer , who resides in the environment.
Figure 1.
At its simplest, a system is something that can be considered as distinct from its environment in some manner. Some systems can be measured by a device that discovers information about the state of the system and reports it to an observer , who resides in the environment.
The classical ball, moving according to the laws of Newtonian physics, must hit a device of some form to be measured. This could be a wall, a basketball hoop, a net, a tennis racket, etc., but will inevitably require an interaction between the system and the device. While the ball has a well-defined position before measurement (which could be extracted using visual observation), this does not count as a measurement due to the way in which perceptual stimuli can be easily misjudged in scenarios of bias. Nonetheless, it is possible to straightforwardly assume that the ball has a position before it is measured and that the measurement merely finds out what it was (in an objective manner, as photons reflected from the ball are incident on the eye). Measurement merely records reality; it does not influence what is found during that measurement.
Such assumptions, while sometimes correct, can be markedly dangerous. For example, assuming that a photon can be described in the same way as the tennis ball results in surprise. Consider, for example, the modern quantum version of the Young’s double slit experiment, which reveals interference patterns even when single electrons are sent into the apparatus [
33], unless a measurement is performed at one of the slits to find out which way it went (in which case, a diffusion pattern results).
Further afield, the concept of a ‘gene’ in biology has moved from protein coding sequences to a more modern understanding that genes are comprised of many interdependent elements and that this makes it very difficult to delimit even the boundaries of a gene. Even when classically conceived, it is not clear where the boundary between selective units and their environments lie. A gene is subject to its environment, but this includes not only its cellular and extracellular environment; other genes and regulatory elements, homologues,
etc., are also important. Increasingly, we see the notion of functional genetic units expanding to include network modules, rather than just genes [
34].
Similarly, in psychology and sociology, we find that the way we ask questions inevitably affects the response that we obtain. For example, framing a question in a positive or negative light can result in statistically significant preference changes, even if the same question is being asked [
19].
Systems, such as these, pose problems for any theory that assumes that a system ‘has’ objectively defined properties, without reference to the context in which these occur (which could be a measurement scenario, an environment, another confounding measurement, etc.). Thus, an organism does not have a phenotype without reference to its environment, and a wide range of experimental data shows that it is highly problematic to assume that attitudes, opinions, affect and decisions can be measured objectively (i.e., without reference to the social context in which they occur). This contextuality presents many problems for the modeller. A context cannot be something that is within the system (); rather, it is beyond the thing that was originally designated as interesting. Conversely, a context is somehow interesting in its own right; it is not something that should be relegated to an environment (and, by implication, deemed uninteresting). However, this leaves us in an awkward position: what is a context precisely? This question is not one that has been satisfactorily answered from a systems perspective. The factors that have been termed a ‘context’ are more diverse than the fields that utilise the term. Sometimes, a context is a location (e.g., in mobile technologies); sometimes, it is a set of parameters (e.g., when a context is stored during a task interruption), and a context might indicate how much information is assumed by the members of a culture (in anthropology) or the words that influence the semantic association a subject gives to another word (in linguistics). This list is by no means exhaustive. Context appears to be a grab bag term, used to denote something that is interesting, but not really a part of the originally envisaged system.
This variety of different uses often results in category errors. Much of what we call contextual can be reduced to an extra parameter in a model (e.g., the location of a mobile device). Such data exist out there; we do not know this, but these have a well-defined value. This calls into question the original designation of such a factor as contextual. If this data were relevant to the description of the system of interest, then we have drawn our boundary incorrectly (in this case, around the mobile phone, opting for a model that is primarily influenced by the boundaries of objects, instead of the more abstract model that described the object in a location). Note that the biotic system that is placed in a different environment is not of the same form. It is impossible to be sure what form the phenotype will have as it depends upon an interaction between the system and the environment, and here, we find an important clue. Contextuality must be ontological. That is, it must refer to fundamental uncertainty that is displayed by the system once a level of analysis has been designated.
Very few tools have been developed for the description of contextual behaviour. This problem is compounded when we consider the manner in which this behaviour manifests; it is often the case that our very attempts to measure, model or interact with a contextually-dependent system result in a change to the very results obtained from our measurements of that system (not just its future dynamics). Consider the way in which the assumption that the global financial market was crash-free led to the Black–Scholes model, which itself precipitated the 1987 stock market crash [
35]. Here, we see a situation where the model adopted to describe a system affected its very dynamics,
i.e., in incorrectly assuming that the economy was separate from the scientific process of its analysis and description, the very model created to describe the dynamics of the stock market became responsible for a change in its dynamics.
There appear to be a number of different classes of contextuality that might be displayed by a system of interest. We might initially expect that different effects would result from contextual responses:
- (1)
Between components where the responses of one component will depend upon the input from other components of the system: Consider, for example, the genetic pathways that can be identified in different cellular responses to stimuli [
36]. These depend very heavily upon the prior activation of the different genes involved; the same response will not always be exhibited in response to what appeared to be the same input. In a different context, very different results might occur. As this is a dependency that arises within the traditional boundaries of a system, there are already many techniques that can be utilised to analyse this form of contextuality. Indeed, many complex system approaches, such as network models [
34,
37] and agent-based modelling (ABM) [
38,
39], already provide a useful framework for the investigation of such inter-component dependencies, although more work will obviously be necessary to develop a full understanding of them [
40].
- (2)
Between system and experimental method, where our theories are consistently failing [
21,
41]: As an extreme example, we can consider the problems of framework and subjectivity that often beset social scientists; how they look at social systems often determines the results that they obtain [
42]. However, we might also consider the complexities inherent in scientifically describing economic responses [
35], social interactions [
43], psychological diagnoses and outcomes [
44], as well as our understanding of language, semantics and meaning [
45]. Many complex systems display highly contextual responses to the method used to analyse them, and this has hindered their description by scientific approaches. Indeed, there are very few formalisms capable of describing such experimental contextuality.
- (3)
Between system and environment context can result in profound effects: One classic example is provided by the phenomenon of phenotypic plasticity, where two organisms with identical genotypes can yield phenotypes so different in two different environments that they are identified as different species [
46]. Indeed, theoretical biology could be identified as one of the key areas in which GST developed a wide range of models that sought to understand environmental contextuality (e.g., [
1,
24,
47,
48]).
These different contextual responses may require different modelling methodologies, but it might also be possible to generalise our understanding of context from a proper consideration of their similarities. While contextual dependencies between components are the focus of much current complex systems science (CSS) research, less work looks at contextual dependencies of Types (2) and (3). Given the apparent prevalence of contextually-dependent complex systems in our modern world, one might wonder at the apparent lack of theories capable of modelling such behaviour. One way forward would involve taking contextuality seriously. Intriguingly, one formalism already exists that takes contextuality between a system and experimental method very seriously: quantum theory.
3. Contextuality in Quantum Systems
Context matters in the formalism of quantum theory (QT). From von Neumann’s measurement theory and the Heisenberg uncertainty relations [
49], to the Bell and Kochen–Specker theorems [
49,
50], the context of a quantum system plays a vital role in the results we obtain when we try to measure its properties and behaviour.
This implicit recognition of context in standard quantum measurement theory can be quickly demonstrated. According to the formalism (see below for more details), the probability of some measurement outcome can be extracted by representing the state of the system (
) with respect to some measurement context. Thus, in
Figure 2, we see a simple measurement of a system that answers a basic yes/no question (e.g., did the particle go up or down when we measured its spin). We represent this scenario using a measurement context
c, which consists of a subspace in which the state
can be embedded. We use an orthonormal basis
to model this subspace, where the two vectors
and
are used to represent the measurement of yes or no in the context
c. QT predicts that the probability of recording a yes to our question in context
c is equal to the square of the projection of
onto the
state, and the probability of recording a no is equal to the square of the projection of
onto the
state.
Figure 2.
A state is represented by the quantum formalism within a context. For this simple illustrative example, we see the state represented within a context c, which is drawn in a two-dimensional space, spanned by the basis . This context could represent the probability of a yes () or a no () result being recorded upon the measurement represented by c. Changing the context of the system can be represented by rotating the basis and would lead to different projections of the state onto that new context.
Figure 2.
A state is represented by the quantum formalism within a context. For this simple illustrative example, we see the state represented within a context c, which is drawn in a two-dimensional space, spanned by the basis . This context could represent the probability of a yes () or a no () result being recorded upon the measurement represented by c. Changing the context of the system can be represented by rotating the basis and would lead to different projections of the state onto that new context.
This is a geometrical account of probability, given by a straightforward application of Pythagoras theorem [
49]. The result is a remarkably different understanding of probability when compared to the more standard epistemological approaches, which take probability as arising due to a lack of information (
i.e., knowing too little about what a state of affairs actually is). A geometrical account of probability allows for a particularly natural representation of how a system might respond to a change in context (when a state of affairs becomes ontologically different). Thus, a rotation of the
basis could represent a different context (e.g., rotating the spin measurement apparatus), and different probabilities would result.
This intuition can be formalised, as follows. First,
is written in terms of a set of basis states,
. This representation of
is obtained by expanding it as a linear superposition (
i.e., an appropriately weighted sum) of one set of basis states (commonly obtained in practice through reference to the choice of apparatus and its orientation, state,
etc., and written as an orthonormal basis, although this is by no means essential). We find that
, where the weight terms
represent the contribution of each component (
) of the basis to the actual state. The choice of basis states is governed by the observable to be measured and the quantization procedure that relates each observable,
A, to its quantum counterpart,
[
49,
51]. Perhaps most importantly, the standard interpretation of quantum theory claims that upon measurement, the quantum system is found to ‘collapse’ onto one of the eigenstates associated with the eigenvalue equation
. Hence, upon measurement, a non-linear outcome occurs due to this process of collapse, which is related to both the state of the system and to the context of that system (as it is represented by the observable). Further experiments will then be performed upon this newly collapsed state, and so, later measurements will also be affected. We see that the probabilities of QT arise not from a lack of details (as is the case for standard Kolmogorovian probabilities), but rather from the geometrical representation of a state that is implied by Q’Ts formal recognition of context in the process of measurement [
49].
This simple approach to the modelling of measurement means that the quantum formalism incorporates the experimental context of a system into its description of that system, and this context can profoundly affect the experimental result obtained. Thus, QT can describe the system contextuality of Type (2). This is a highly unusual state of affairs in scientific modelling, which almost by definition assumes that a system of interest can be separated from the models that are used to analyse its behaviour.
The generalisation of QT beyond the physical realm would make it possible to model similar contextual effects in systems not presently well modelled by the scientific method. Indeed, this process has begun already; quantum inspired models have already been used to model a wide range of non-physical systems [
52,
53], including: decision making [
54,
55,
56,
57,
58], attitude change [
59], language and memory [
60,
61,
62,
63], biology [
15,
64,
65,
66], creativity and cultural evolution [
67,
68], vision [
69], economics [
70,
71] and information retrieval [
72,
73,
74], to name just a few examples.
3.1. Non-Separability and Openness in Quantum Models
In addition to this immediate application to the description of contextual measurements, the phenomenon of entanglement [
49,
51,
75] allows us to extend the quantum formalism to the description of systems exhibiting contextual dependency of Type (1). If we consider two components
and
of a system
S, then a contextual dependency between the two implies that it is not possible to consider them separately. The quantum formalism provides a very clear description of this state of affairs. If we denote the states of the two components by
and
, then a separable combined system,
, will be one that can be decomposed using a tensor product:
(Here, and in what follows, we will use a standard formalism where ⊕ is used to denote the combination of two systems via a general operator,
i.e., it is not necessarily an addition operation, whereas ⊗ denotes the specifics of a tensor product, which can be used to model this combination when the system is technically separable). In contrast, a system for which the components cannot be considered independently is represented in the quantum formalism using an entangled state. Thus, if, for example, component
always exhibits response
a when
does and response
b when
does, then we might represent the combined system as
, where
and
take the role of some normalisation factor (
i.e.,
). If such a state is impossible to represent as a tensor product, then it is deemed non-separable and termed entangled. Entangled states are responsible for many of the counter-intuitive results of QT [
75], but most interesting to the current argument, they exhibit contextual responses to measurement [
76,
77], where they play an essential role. According to the standard interpretation of QT, a measuring device must first become entangled with the system of interest before collapse occurs and a result is obtained [
49]. This suggests that systems of Types (1) and (2), in fact, share the same dynamics.
Finally, contextual dependencies of Type (3) can sometimes be modelled using dissipative, or open, quantum models [
78,
79]. These systems are subject to ongoing interaction with their surroundings (which, at a first approximation, can be treated as a measurement), and so, the complexity of their dynamics increases substantially. While some work has been completed that uses this formalism in quantum-like models (e.g., [
58,
66]), this is a new and fast developing field. Open quantum systems are made even more interesting by the way in which they are often related to ontological models of emergence. For example, Vitiello has modelled the contextuality of memory using an open quantum model [
13]. As many complex systems are generally open to environmental influences, this is an area that is likely to become the focus of much future work.
Thus, we see that the three forms of contextuality introduced in
Section 2 can be accommodated within a consistent set of models inspired by the quantum formalism. What more specific tools does QT provide? Could these be used in a contextualised general systems theory?
3.2. Tests for Contextuality
There are a wide range of contextuality effects in QT. In this section, we will start with a class of tests that can be used on systems with one component and then gradually increase the system complexity, by adding more components, and the possibility of interactions between those components. We shall see that QT has provided an entire class of tests that can be used to determine the validity of the assumption that a system is non-contextual. Violations of the Law of Total Probability, Bell’s theorem, the Clauser–Horne–Shimony–Holt theorem, the Kochen–Specker theorem and Fine’s theorems all generate strong restrictions on the possible form that a separable system can have, and their violation frequently entails contextual behaviour. Here, we shall only explore some of the more accessible examples. The interested reader is encouraged to consult the many different references cited here and elsewhere for further details.
3.2.1. Context in Measurement
Quantum measurements are frequently shown to behave in a contextual manner using a violation of the Law of Total Probability as a test [
52].
For example, Busemeyer
et al. [
54] resolve the well-known Linda problem, which arises from applying the standard conjunction rule of probability to human reasoning. This rule tells us that the probability of some event
A occurring in conjunction with a specific event
is smaller than that of the same event occurring in conjunction with a more general event
:
This basic law of probability is frequently violated by humans across a wide range of demographics (including educational ones). Such violations are commonly generated via a story that proceeds something like the following:
Linda is 31 years old, single, outspoken and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice and also participated in anti-nuclear demonstrations. Which is more probable?
A large majority of people (85% in the original case presented by Tversky and Kahneman [
80]) choose the second option, thus making statements that are more specific than necessary (e.g.,
), hence less likely according to standard probability. We see that the preceding story is affecting the way in which people reason probabilistically about Linda. This violation of the conjunction rule is well explained by a quantum model, which uses projections in geometric spaces and interference between different framings of a problem to explain how the context in which human subjects form a model of ‘Linda’ is affected by the context of the preceding story. This model is used to explain a wide range of effects traditionally considered disparate in psychology and cognitive science, including the disjunction fallacy and the hot hand fallacy [
52,
54,
55,
81,
82]. The standard approach followed in these scenarios involves finding a dataset where the Law of Total Probability is violated and then fitting the data with quantum interference terms, which adjust the probabilities in the model to fit the experimental results (see e.g., Busemeyer and Bruza [
52] for a general introduction).
It might be claimed that this form of contextuality is not particularly interesting; the context of a stimulus is affecting a behavioural response (i.e., the decision of a subject about Linda’s status), which would be expected by any researcher in a field such as psychology. However, the quantum formalism offers a methodology that shows promise for describing a wide range of contextual effects within a unified formalism, rather than an ad hoc and incremental set of approaches. More examples as we continue will help to demonstrate this potential.
Another form of contextuality upon measurement is exhibited by systems that display order effects (meaning that the order in which two measurements are performed affects the outcome). Wang and Busemeyer [
83] discuss a number of well-known scenarios, unifying them in an approach based upon quantum probability. For example, Moore [
84] showed that asking subjects about the trustworthiness of Bill Clinton and then Al Gore reduced Gore’s rating (down to 60% from a value of 68%, obtained when Gore was rated first). That is, in the comparative context of Clinton, Gore seems less trustworthy. Clinton was similarly rated as more trustworthy when subjects were asked to rate Gore first (57% from a non-comparative result of 50%). This effect was modelled by Wang and Busemeyer [
83] using projection operators to represent the probability of responding yes to Question A (e.g., “Is Al Gore trustworthy?”) as
(similarly, that of responding no to A as
). Asking one question is seen to project the cognitive state into a subspace, which then changes the probabilities of a subject answering yes to Question B (as was discussed above for the general model). Wang and Busemeyer [
83] use the formalism of QT to define an equality that must be satisfied by any system exhibiting pure quantum behaviour, the q-test:
where
and
, which are two probabilities referring to the probability of having different answers to two questions (A and B) in the orders AB and BA, respectively. They use this test to explain the results reported in Moore [
84], thus unifying the violation of the LTPdiscussed above, with that of order effects in psychology.
A further experiment, discussed by White
et al. [
85] demonstrates that the constructive role of measurement is likely to be causing the change in probabilities that arise in these scenarios. This paper introduces a very simple paradigm, where subjects are exposed to two images in a row, with half of the subjects asked to articulate their impressions about the first image before being shown the second and all subjects asked to articulate their impressions about the second image. This experiment shows that even a slight modification in the instructions given to a subject can have a significant impact upon their response, even keeping all other factors constant (in this case, order and images). Such a modification is most naturally treated as a context if we take the geometric model discussed above. Asking a subject to express their impression about the first image effectively performs a measurement on that subject’s cognitive state, and this, in turn, modifies their state. The next measurement is performed upon a different system.
This section has discussed a number of different types of context, along with a consistent model that can be used to describe them. Furthermore, this model provides natural tests that can be used to determine whether contextuality is being displayed by the system under consideration or not. However, this is only a first step towards what we might call a contextualised generalised systems theory. A second set of models and tests come from the quantum formalism when it is applied to systems that consist of multi-component states. These tests can be used to discover whether the system should be considered using a reductive model or not, and while they are related to the tests and models discussed in this section (as they still involve measurement), they add to the formalism by providing further information about the internal behaviour of the system (i.e., between the components).
3.2.2. Bell-Type Theorems
What happens when we combine two component systems into one joint system? The quantum formalism has a well-developed mechanism for combining systems, using the tensor product and time evolution operations [
49]. However, once two originally separate systems interact, can we still model them as separable systems? QT has provided a highly sophisticated toolkit for considering questions such as these.
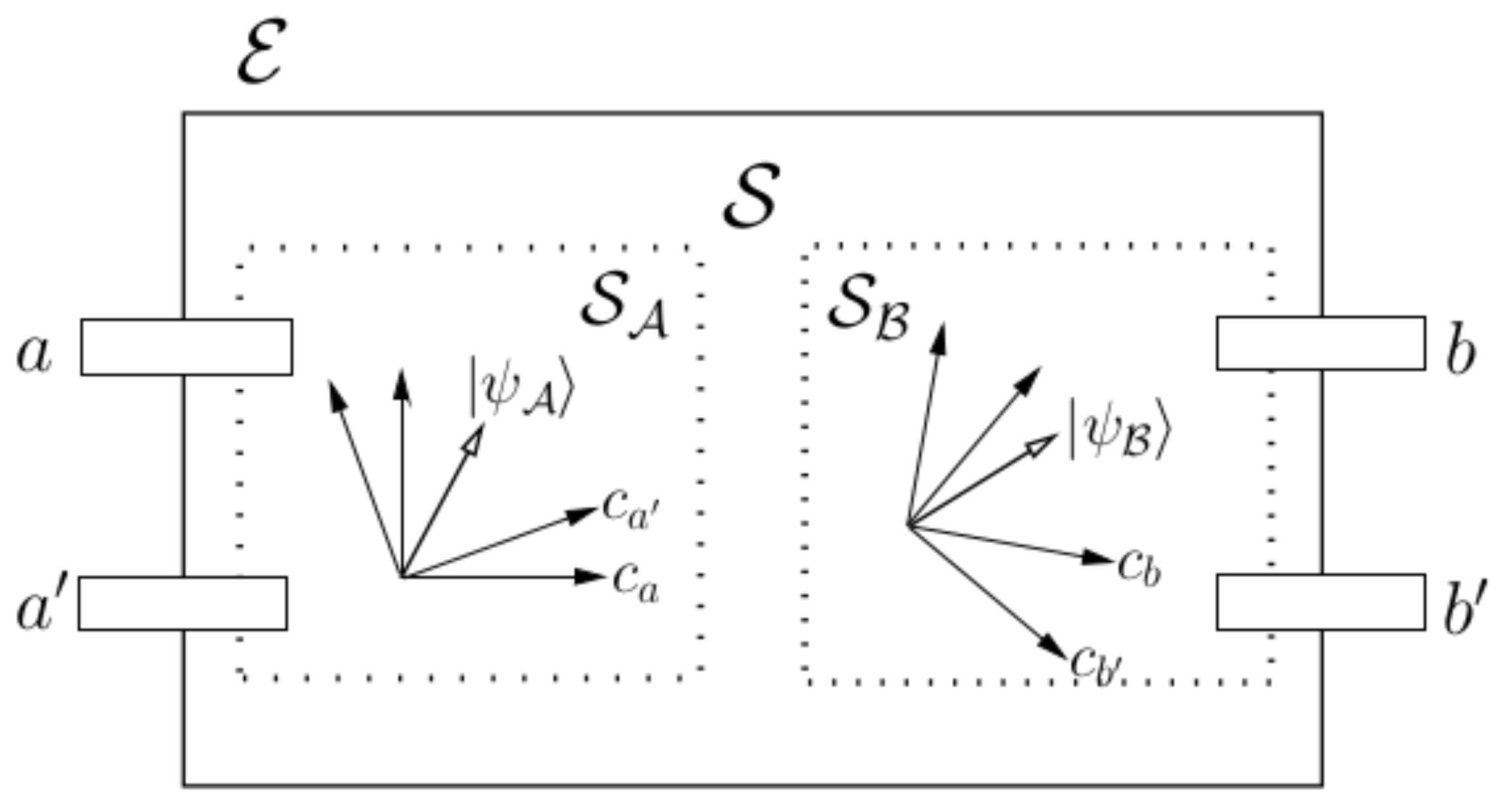
Figure 3 depicts a hypothetical system
, in an environment
, which consists of two components
and
that were originally separate (or that we have perhaps imagined could be separated), but have since interacted. There are many questions that can be asked about this system: can
and
still be regarded as separate or do they somehow influence one another? Would a consideration of the combined system
give the same specification of behaviour as
? What components of this system exhibit causal interdependencies? QT allows us to move such questions from what are largely philosophical discussions into the experimental realm.
While it is generally assumed that systems are by definition separable in a well-defined manner from their environments, a similar separation between and is not something that can be straightforwardly achieved in QT, even when there is no apparent causal connection between the two components.
For example, suppose that two different experiments can be carried out upon each of the presumed subsystems, which will answer a set of ‘questions’ with binary outcomes. We shall represent these questions using four possible measurement settings, consisting of two alternative questions asked of either sub-component. Thus, a choice of two experimental settings a or can be applied to sub-component , and similarly, b or can be applied to sub-component B. Each of these experimental questions lead to a binary outcome (e.g., a detector clicks or it does not), which represents either a ‘yes’ or a ‘no’ answer to the question asked of the system. For the sake of generality, we shall denote these responses as or zero, respectively; they form a set of random variables that we shall label as and . It is now possible to consider the notion of the probability distribution over these outcomes; what characteristics will be possessed by the random variables describing this system?
Figure 3.
A potentially compositional system
, consisting of two assumed sub-components
and
.
can perhaps be understood in terms of a mutually exclusive choice of experiments upon those sub-components. Two alternative experimental settings probe either proposed sub-component, represented by
a or
for sub-component
and
for sub-component
. Each of these experimental settings corresponds to a context
, which is used to represent the sub-system (and sometimes the system, as well) in that context, using the formalism introduced in
Figure 2.
Figure 3.
A potentially compositional system
, consisting of two assumed sub-components
and
.
can perhaps be understood in terms of a mutually exclusive choice of experiments upon those sub-components. Two alternative experimental settings probe either proposed sub-component, represented by
a or
for sub-component
and
for sub-component
. Each of these experimental settings corresponds to a context
, which is used to represent the sub-system (and sometimes the system, as well) in that context, using the formalism introduced in
Figure 2.
As with many systems, the outcomes of our experiments will have a statistical distribution over all available outcomes, and this can be used to determine whether the sub-components can be considered as isolated, influencing one another or in some sense irreducible. Frequently, joint probability distributions, such as
, are used to model the behaviour of systems like that represented in
Figure 3; however, it has been shown that this joint probability does not exist for certain quantum [
75,
86] and psychological systems [
17,
52,
87]. When such behaviour is evident, we have clear reason to suppose that the system under examination is contextual; experiments performed upon sub-system
affect the results of experiments performed upon sub-system
, even though the two sub-systems were presumed independent. Thus, the context of sub-system
, as represented by sub-system
, can have a well-defined influence upon its behaviour, which is not causal in any of the more traditional understandings.
It is possible to derive a number of restrictions on the probability distributions that must be satisfied by a separable system. For example, we could define such a system as one for which experiments performed at
will not affect those performed at
and
vice versa. More specifically, a person committed to reductive modelling would normally assume that the result of running experiments
a or
does not depend upon the experimental settings used on subsystem
(
i.e.,
b or
) and that the results of experimentally interacting with subsystem
do not depend upon the experimental settings applied to
(
i.e.,
a or
). It is possible to construct a joint probability describing this state of affairs and how it might depend upon a set of hidden parameters, or latent variables, denoted
λ, which is assumed to have a normalised probability distribution
. The joint probability for experimental arrangement
becomes:
and a similar set of relationships can be constructed for all experimental arrangements. Simple algebra allows us to form a number of inequalities that result from this assumption. For example, we can derive the Clauser–Horne–Shimony–Holt (CHSH) inequality [
88], which has become somewhat notorious in the field of quantum physics:
This is a very general statement about the possibility of separating a system into objective components that interact only via the proposed variable
λ. If this inequality is violated, then this separation is impossible. It is worth emphasising the generality of this result. While it was originally obtained in the field of quantum theory, the derivation of Equation (
4) makes no assumptions as to the nature of the system that is modelled by the probabilistic framework that it proposes, merely as to the potential separability of
.
This class of tests and their more advanced forms have been applied to both language [
17,
89,
90] and biological systems [
15]. It has also been shown to have a close connection with the notion of selective influences in psychology [
87]. We see that very clear tests can be constructed to determine whether two apparently separate systems can indeed be modelled reductively, or not.
There are a number of extensions of this test. Many of them either use multi-partite systems or describe two-partite systems with a larger number of operators [
50,
75,
91,
92,
93]. Many of these extensions allow for the construction of direct counterfactual scenarios, where if a particular experimental outcome is realised, then a separable model of the system becomes impossible. The Greenberger–Horne–Zeilinger (GHZ) [
92] and Hardy constructions [
94], as well as the Kochen–Specker theorem [
50,
95] would provide very strong additional tests about non-separability if they could be adapted and generalised beyond standard QT. While such tests are yet to be realised in a quantum-like model they provide a potentially fruitful avenue for future work.
3.3. Quantum Models of Emergence
Standard QT (or quantum mechanics) does not describe the emergence of novelty. Indeed, physicists found it necessary to extend the formalism of QT with quantum field theory (QFT) when they started to model situations, such as the creation and annihilation of particles within physics. In contrast to standard QT, which preserves the number of particles in a system and, hence, cannot describe the complex interactions occurring in much of the physical world (such as, for example, the behaviour of atomic nuclei), QFT allows for the description of a number of inequivalent representations of the same physical system [
13]. This means that a QFT can model systems with many different ground states (lowest energy states), a far more natural state of affairs for complex systems, as these often have a range of stable configurations. If a QFT exhibits spontaneous symmetry breaking, meaning that the symmetry of the dynamics of the system is different from that of the ground state, then collective excitations can arise (termed Nambu–Goldstone modes [
79,
96]), corresponding to the number of broken symmetries. These modes are massless and, hence, long range, which means that information can be transmitted very efficiently in such theories. It is also possible to construct dissipative QFTs, which take into account the generally open nature of a complex system and have the added benefit of providing an essentially infinite capacity for the system. Thus, in Vitiello’s QFT brain model [
13], the memory capacity of the brain is practically infinite due to the openness of our interactions with the world; there is an inexhaustible supply of different stable memory states and a way of changing from one to the other in time.
While those approaches that use standard QT are modelling the context of the system in terms of different observations, it seems likely that QFT can provide science with a genuine theory of ontological emergence [
21,
41,
41]. While a general theory is yet to be developed, initially promising results have been found describing the brain [
13], stock market dynamics [
71], conceptual combination [
97] and differentiation [
15,
21].
Stepping back, it is necessary to briefly consider where exactly a quantum field theoretic model of ontological emergence could fit into the larger understanding of emergence and into systems theory as a whole. One overarching understanding is provided by Atmanspacher [
6], who identifies four classes of relations between two levels in a system exhibiting emergent behaviour. Each of these classes lead to very different expectations of emergence, as they arise from a different understanding of how the description of features at one level of a system relate to those at a higher level. Thus: (i) if the description at the low level is necessary and sufficient for a complete understanding at the higher level, then the system is reductive (implying no emergence at all); (ii) if the low level is neither necessary nor sufficient for description at the higher level, then there are no relevant conditions for connecting the two levels (this is termed radical emergence). The two more interesting categories come from dropping one of the two sufficiency criteria: Atmanspacher [
6] claims that: (iii) supervenience results from the dropping of the necessary condition; and (iv) contextual emergence as resultant from dropping the sufficiency condition. Thus, in the description of a contextually emergent system, ontological emergence can occur, but a model that refers only to the lower level will not prove sufficient for describing the dynamics of the system at the higher level. Contextual systems that require an epistemic cut will fall into this class of contextually emergent systems, as they require extra information beyond that of the original system to be incorporated into a model that captures their full behaviour.
This brings us to our final discussion: how do all of the concepts that we have discussed so far fit together into an overarching framework that could drive a new contextualised general systems theory?
4. Towards a General Theory
At the beginning of this discussion, we started by examining the notion of a system. We saw that while a system in an environment is easy to imagine, the reality is not so simple. We quickly found examples of systems that exhibit a variety of contextual responses to measurement and their environment, which makes it markedly difficult to draw a clean line between the system and the environment. Many of these systems are termed complex; however, the designation of a system as complex often depends upon what aspect of it we are interested in modelling; it is necessary to specify the level of description before we can make statements as to a system’s complexity. We then sought to examine the manner in which system contextuality affects measurement results, and the advantage of the quantum formalism became apparent. It is a formalism that recognises the manner in which our interactions with a contextually-dependent system will affect the results of measurements that we perform upon it. The geometric probabilities used in QT link experimental manipulations made by an observer with the behaviour exhibited by the system, which provides an invaluable modelling tool. A number of different proposals have been made as to why QT should be used to model systems that are not traditionally deemed physical (see e.g., [
13,
15,
52,
53,
98,
99]). Here, I have attempted to show that QT provides us with a methodology that can consistently approach the notion of contextuality, between any combination of system components, experiments and environments. QT thus provides a possibility for unifying our understanding of a number of hitherto disparate contextuality effects, across a wide range of fields. Of course, such an understanding requires much more work before it can be considered as complete; an ongoing program of research is required.
One particularly important clarification will require a much more sophisticated understanding of quantum operators for non-physical systems. QT arose in physics only after a notion of classical measurement was defined. This meant that a dynamics had been defined classically, which mapped naturally into QT via Hamiltonians, energy, Pauli matrices, etc. Each one of these concepts have a well-defined meaning in physics, but this is much more difficult to discern in the quantum-like world (i.e., beyond physics). This makes many powerful analytical techniques inaccessible to the field, at least for now. For example, it is very difficult to understand how a quantum-like system will evolve in time without a Hamiltonian. While dynamics can perhaps be reverse engineered (say by performing the same measurement over a series of time steps), the very contextuality of these systems makes it hard to know what is causing changes in experimental results. It seems likely that many quantum-like systems will not be modelled via the standard physical technique of quantization (where a classical system is identified and the operators are then subject to a well-defined procedure that results in a quantum system). Quantum-like systems are being modelled by the quantum formalism precisely because they never exhibited non-contextual behaviour, but this makes it very difficult to develop even a quantum formalism for these systems.
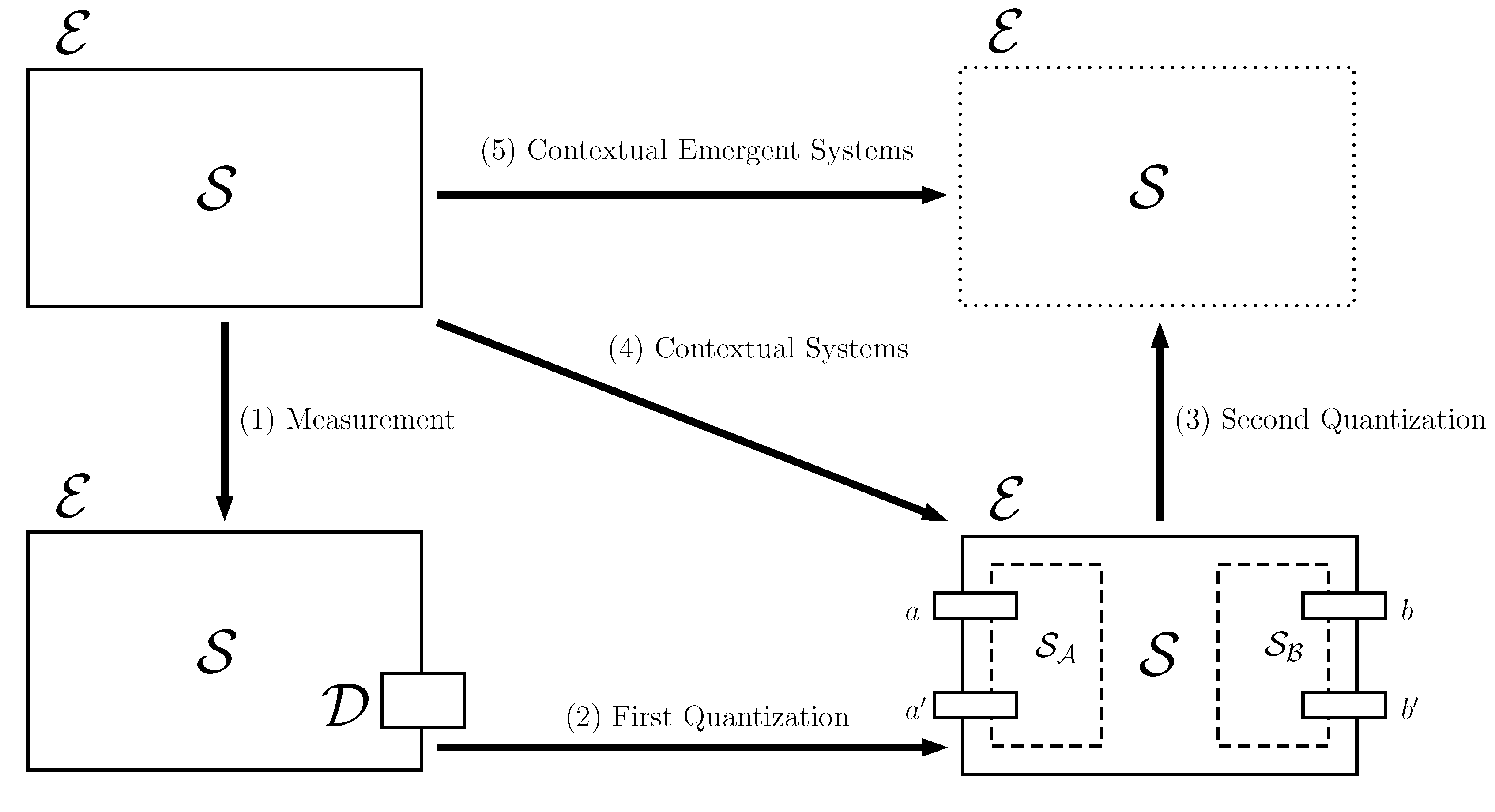
Referring to
Figure 4, this would imply that we need a procedure for following Mapping (4) directly (
i.e., skipping the measurement to first quantization paths). This is a difficult proposition, and it is made more difficult when we consider the manner in which systems of Type (3) are likely to be modelled most productively by following Path (5), which would require moving directly from acknowledging that a system exits to the recognition that it has open boundaries and is exhibiting emergent behaviour. We need new techniques. These would provide a direct map from the identification of a system to follow either:
Path (4): A contextual model of its behaviour that did not require the construction of a classical model that was then subject to quantization (currently only understood via the alternate Paths (1)→(2) route).
Path (5): A contextual model of emergent behaviour that also left out the second quantization option.
If direct paths could be found, then they would allow for models of contextual systems to be constructed without following the standard reductive modelling methodology, where we assume a set of objects and then gradually relax our assumptions about their behaviour (through first and second quantization).
Figure 4.
A contextual general systems theory would explain all of the relationships between the below four types of systems. Importantly, it would provide natural explanations of how Paths (4) and (5) could be followed without assuming a classical (i.e., non-contextual) model at the outset.
Figure 4.
A contextual general systems theory would explain all of the relationships between the below four types of systems. Importantly, it would provide natural explanations of how Paths (4) and (5) could be followed without assuming a classical (i.e., non-contextual) model at the outset.
One extant theory almost follows Path (5). Modern path integral forms of quantum field theory [
96,
100] proceed by identifying a system and then modelling correlations between two points (which can correspond to experimental settings). Thus, modern QFT proceeds directly to the description of contextual emergent systems, from the identification of a classical dynamics. Essential to this move is the identification of a set of groups and symmetries. Similarly, even following Path (4) requires the identification of a group structure for the description of both time evolution and certain associated measurements (e.g., spin in standard QT). However, this is no easy challenge. There is no guarantee that the systems of biology, cognition or society will follow the same symmetries as those of physics. Indeed, it is quite likely that they will prove to be far more complex.
It is worth noting that the schema proposed here is not a hierarchy of theories (such as the one proposed by Marr; see
Section 1.3) or the varying approaches to understanding emergence. Rather,
Figure 4 is a set of relationships between different conceptualisations of a system. Different systems will be most naturally modelled at different positions in this diagram, but the relationships show us what kind of an effort would be involved in ‘scaling up’ the complexity away from the simple
assumption. It also goes some way towards demonstrating what types of behaviours would need to be exhibited by a system at the level of analysis that we had chosen for it before such a move became necessary.