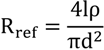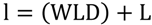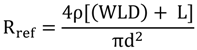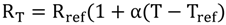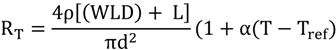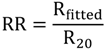1. Introduction
In last few years, within the domain of electronic textiles, rigorous research has been carried out, predominantly in respect of the inclusion of sensing functions into the textile products. Textiles are comfortable to wear and offer a flexible platform for imparting sensing functions. The direct outcome of applying this technology is the advancement of Wearable Health Monitoring Systems (WHMS) intended for round the clock monitoring of the vital signs of the human body over extended periods of time. One of the important components of WHMS is the sensor which receives vital signs information from the wearer and relays it for further processing. This information may be utilized to help generate a general health picture for the diagnosis of various diseases and its management [
1].
Within the domain of WHMS, the focal point of most of the research has been the development of textile integrated Electrocardiography (ECG) and respiration sensors. For the measurement of human body temperature, most researchers have relied on commercially available thermistor and temperature ICs, which are generally attached outwardly to the garment [
2,
3,
4,
5]. The literature also demonstrates that the fabrication of sensing fabric for temperature measurement has only been little explored in a few individual studies [
6,
7]. These studies were preliminary in nature and their products were manufactured by cumbersome manual processes.
Human body temperature is one of the four vital signs which are standard in medical settings in addition to heart rate, blood pressure and respiratory rate. Vital signs information is used for the medical assessment of the state of the health. Human body temperature is an important indicator of the physical condition of human body. It relates to the comfort and performance of human body in heat and cold stresses. The deviation of few degrees, from the normal body temperature,
i.e., 37 °C can cause impairment and fatality to the human body [
8].
This paper presents preliminary research into the design, manufacturing and testing of Temperature Sensing Fabric (TSF), developed by embedding fine metallic wire into the structure of textile material. The operational principle of the TSF is based on the inherent tendency of metal wire to change in its electrical resistance because of the change in its temperature. Samples created on a commercial textile manufacturing machine have been tested in various thermal environments, under laboratory conditions, to study the relationship between the resistance and temperature of the sensing fabric. The temperature-resistance relationship demonstrated a linear trend with a goodness of fit (r2-value) of over 99%.
2. Materials and Methods
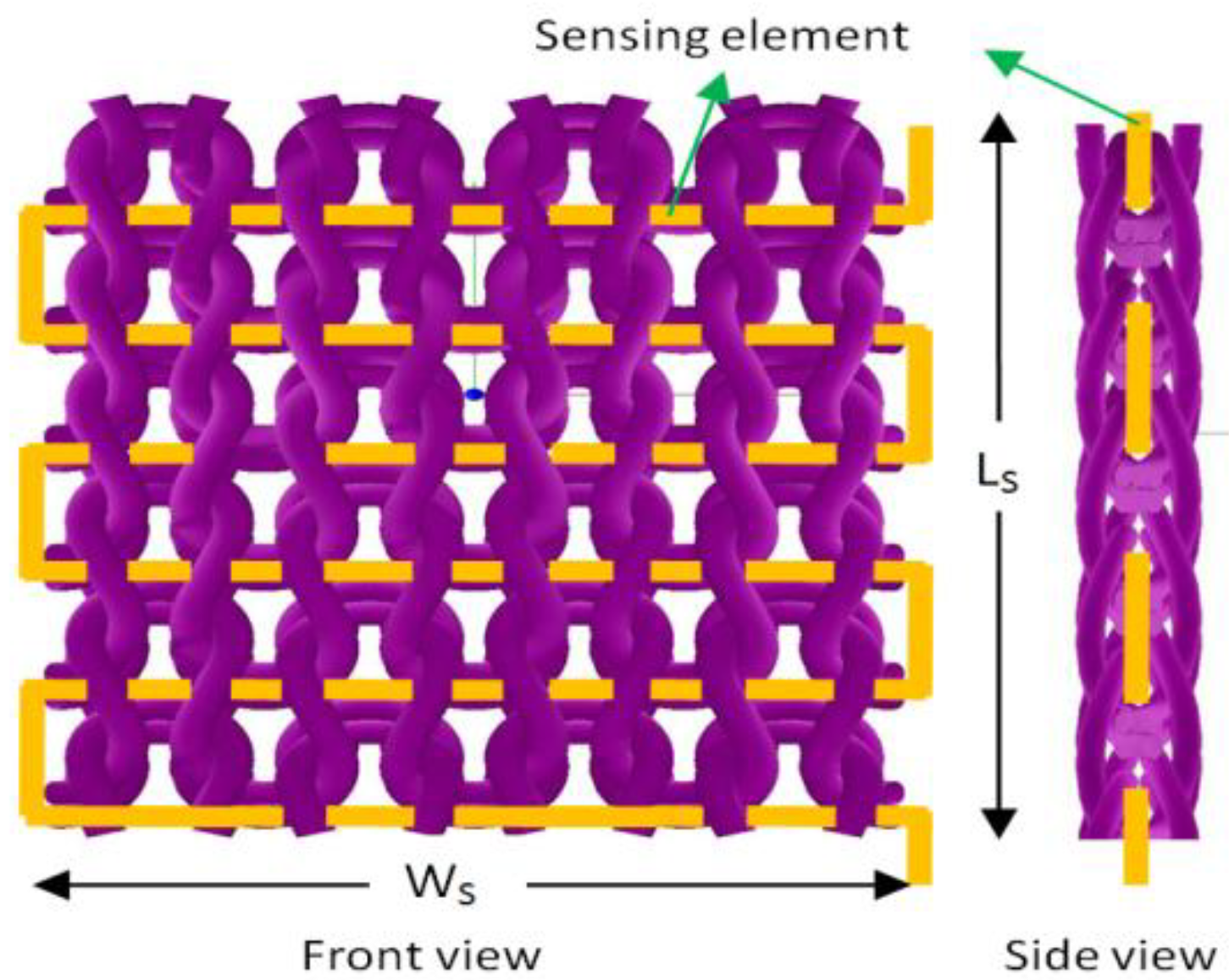
The Temperature Sensing Fabric (TSF) was constructed by laying-in a defined length of a fine metallic wire within the courses of a double layer knitted structure as shown in
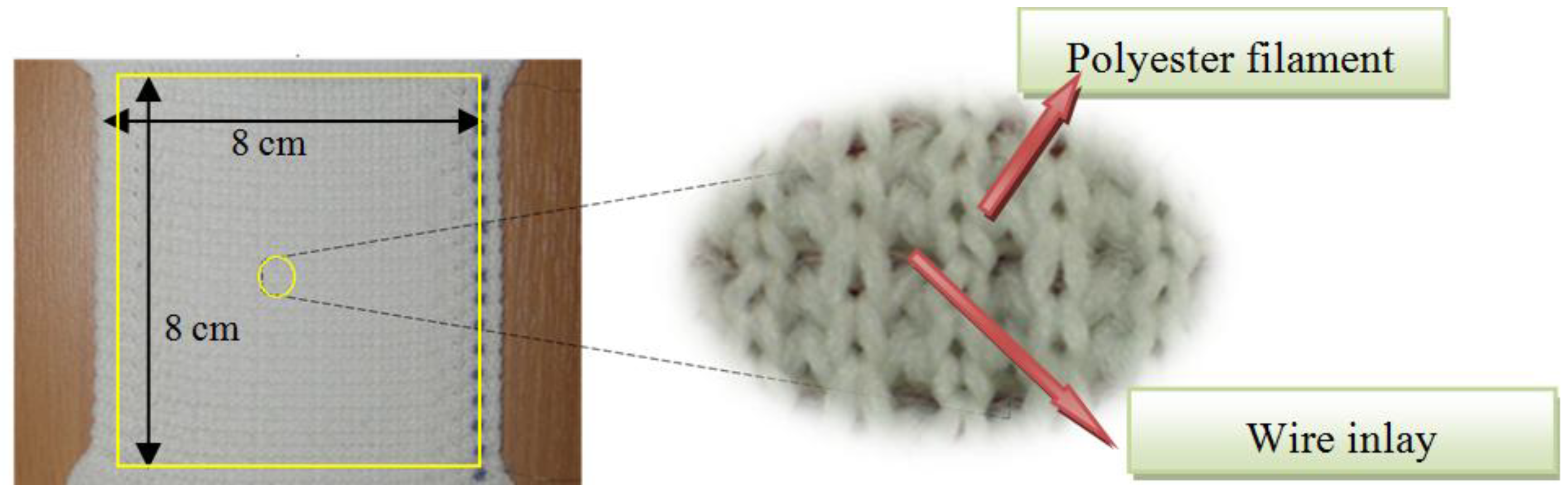
Figure 1. The structure of the TSF fabric was designed in the Shima Seiki Knit Paint environment before being manufactured on a 10 gauge Shima Seiki flat bed knitting machine. Samples were developed with an 8 cm × 8 cm sensing area as shown in
Figure 2.. Each sample comprised of 39 wales; 33 for the inlay area and 6 for the protective edging. In order to achieve high sensitivity from a small-sized TSF, it was desirable to pack a high density of wire inlay into the designated sensing area. Therefore, extra spacer courses were introduced, along with knit courses to prevent the surface of individual lengths of wire from touching adjacent wires. TSF samples were developed with two different wire inlay densities,
i.e., 4.7 and 6.4 inlays/cm. Low inlay Density (LD) samples required more spacer yarn than High inlay Density (HD) to achieve the same compactness as HD samples.
For a base fabric of TSF, knitted structures were preferred over woven structures because of their comfort and ability to conform according to body shape. The metal filament is embedded exactly in the middle of a double layer structure; hence it is barely visible and does not affect the aesthetic properties of the fabric. The double layer structure of the TSF also provides protection of the metal wire from wear and tear.
Figure 1.
Concept of Temperature Sensing Fabric (TSF); sensing wire inlaid in a double layer knitted structure.
Figure 1.
Concept of Temperature Sensing Fabric (TSF); sensing wire inlaid in a double layer knitted structure.
Figure 2.
A TSF sample of sensing area of 8 cm × 8 cm along with its magnified view.
Figure 2.
A TSF sample of sensing area of 8 cm × 8 cm along with its magnified view.
The classic equation representing the relationship of the resistance of metal wire R
ref to its diameter (d), length (1) and resistivity (ρ) is expressed in equation (1) [
9]:
Resistance (R
ref) is expressed at a reference temperature. Resistivity (ρ) is a function of the metal, while diameter (d) & length (1) are the functions of the wire. The length of metal wire can be mathematically related to the dimensions of the TSF as:
Where L and W represents the length and width of the TSF and (D) denotes the packing density of the metal wire. From Equation (2), it can be noticed that a metal wire of one meter (with packing density of 6 cm
−1) can easily be contained in a 4 cm × 4 cm patch of TSF. A modified relationship between resistance of TSF to its dimensional parameters may be obtained by combining Equations (1) and (2):
Once the diameter and resistivity of the wire are known, dimensions of a TSF patch can be optimized in order to meet required reference resistance by making use of Equation (3). By employing sensing element of high resistivity and fine diameter, the target reference resistance may be achieved on a small sensing area. Therefore it is important to lay-in the sensing wire as compactly as possible to accomplish the maximum ratio of the TSF reference resistance to the TSF sensing area. In order to realize highly sensitive TSF, high value of reference resistance is desirable; while small sensing area is desirable for producing highly responsive (thermally) TSF. The relationship between the temperature (T) of the metal wire to its resistance can be expressed as [
10].
Where α is the temperature coefficient of resistance. After merging Equation (3) and Equation (4), the resistance–temperature relationship of the TSF can be expressed in the following form:
Various types of metal wire could be employed as the sensing element of a TSF. Nickel, tungsten and copper wires were selected as experimental sensing elements for TSF samples, because of their high resistivity and temperature coefficient of resistivity, and to take advantage of their linear temperature-resistance relationship between 0 °C and 100 °C. Besides that, they are easily available in the market and relatively inexpensive.
Table 1 presents the classification of developed samples according to inlay density and type of metal wire.
Table 1.
Categories of TSF samples along with parameters for modelling.
Table 1.
Categories of TSF samples along with parameters for modelling.
| Sample Tag | Sensing Wire | Dia. (µm) | Inlay Density (cm−1) | Sensing Area (Length × Width) cm2 | Resistivity (Ωm) at 20 °C | Temp. Resist. Coeff. (/°C) |
|---|
| N100HD | Nickel | 100 | 6.4–High | 8 × 8 | 9.5e-08 | 0.0048 |
| N100LD | 4.7–Low |
| W50HD | Tungsten | 50 | 6.4–High | 8 × 8 | 6.4e-08 | 0.0035 |
| W50LD | 4.7–Low |
| NC125HD | Copper (Nickel Coated) | 125 | 6.4–High | 8 × 8 | 2.2e-08 | 0.0040 |
| NC125LD | 4.7–Low |
TSF samples were calibrated at steady thermal points of 20, 30, 40, 50 and 60 °C in a laboratory oven. An Agilent multimeter 34401 was used to measure resistance at steady temperature points.
3. Results and Discussion
The reference resistance (R
20) of the TSF samples was measured at a reference temperature of 20 °C.
Table 2 presents the comparison between average experimental and modelled reference resistance for each sample category. It can be observed that modelled resistance is slightly higher than the experimental resistance in all instances. This could be due to the non-conformance of the sensing fabric to its designed dimension of 8 cm × 8 cm. Unlike in electronics, where the boundaries of a circuit may be defined with high precision, textile materials exhibit a much higher degree of manufacturing tolerance. It has been observed that experimental resistance of all the samples and their replicates were within 2 percent of their modelled counterparts. This gave a 98% confidence level in respect of Equation (3) prior to the design of sensing fabrics with the required reference resistance.
Table 2.
Comparison of experimental and modelled reference resistance (at 20 °C).
Table 2.
Comparison of experimental and modelled reference resistance (at 20 °C).
| Sample Type | Experimental Resistance (Ω) | Modelled Resistance (Ω) | Difference (Ω) | % change |
|---|
| N100HD | 46.33 | 47.13 | 0.80 | 1.72 |
| N100LD | 35.10 | 35.35 | 0.25 | 0.70 |
| W50HD | 121.81 | 124.16 | 2.35 | 1.93 |
| W50LD | 92.19 | 92.95 | 0.76 | 0.82 |
| NC125HD | 6.64 | 6.74 | 0.10 | 1.56 |
| NC125LD | 5.04 | 5.06 | 0.02 | 0.46 |
Irrespective of the type of sensing element and the wire diameter, the experimental resistance of samples with Low inlay Density (LD) are closer to their modelling counterparts, as compared to samples with High inlay Density (HD). One of the possible reasons could be the sensing wire making unplanned contact with itself at the fabric edges. Since HD samples have high wire density and fewer spacer courses, so the chances of reduced resistance, by wire to wire shorting at the edges of the sample, are higher.
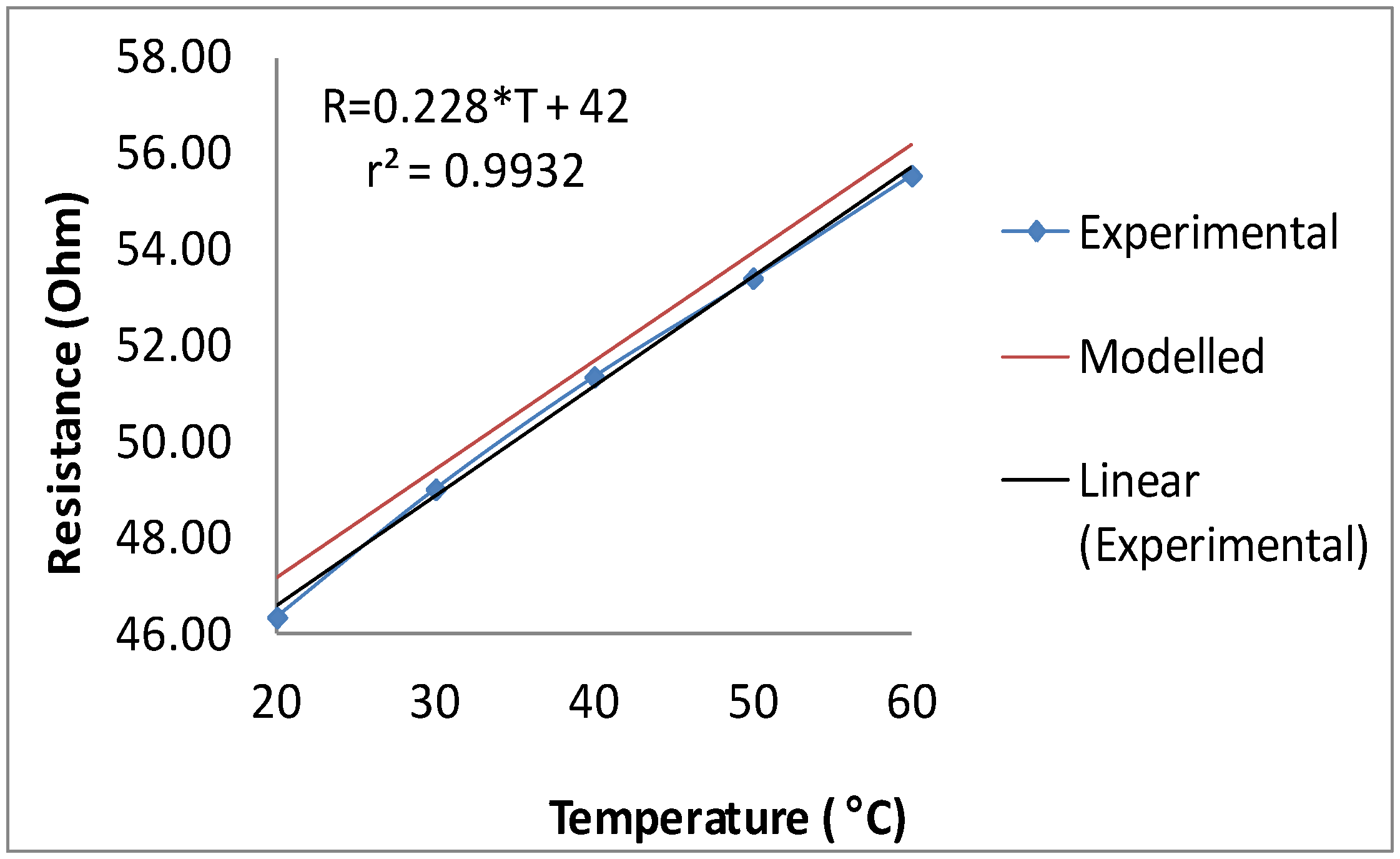
Experimental Resistance-Temperature data shows a linear correlation and follows the same behavior as their modeled counterparts.
Figure 3 presents the one such correlation belongs to the TSF sample N100HD1. Resistance-Temperature data from all the TSF samples has been fitted with straight line polynomials. Variance between RT data points and the fitted polynomial has been calculated and presented in the form of r
2-value (coefficient of determination).
Figure 3.
Comparison of experimental and modelled temperature-resistance relationship of sample N100HD-S1.
Figure 3.
Comparison of experimental and modelled temperature-resistance relationship of sample N100HD-S1.
Table 3 presents the average r
2-value and the reference equation of each sample category. It can be seen from
Table 3 that all samples exhibit a high value of r
2 i.e., over 99%. The r
2-values of HD samples is slightly less than for the LD samples. A possible reason could be wire-to-wire contact at the edges of the samples caused by small changes in the length of the wire by thermal expansion at elevated temperatures.
Table 3.
Coefficient of determination and reference equation of each sample category.
Table 3.
Coefficient of determination and reference equation of each sample category.
| Sample Type | r2-value | Reference Equation |
|---|
| N100HD | 0.992 | R = 0.23*T + 42.05 |
| N100LD | 0.996 | R = 0.17*T + 31.86 |
| W50HD | 0.989 | R = 0.43*T + 113.78 |
| W50LD | 0.999 | R = 0.32*T + 85.76 |
| NC125HD | 0.990 | R = 0.027*T + 6.14 |
| NC125LD | 0.995 | R = 0.020*T + 4.61 |
The Resistance-Temperature curves of the TSF samples can also be defined in terms of Resistance Ratio (RR), which was calculated by taking the ratio of “fitted resistanc (Rfitted) at temperature (T)” to “reference resistance (R20) at a reference temperature of 20 °C.
Defining the TSF resistance-temperature data by normalizing their resistance data with respect to their reference resistance has several advantages [
11]. TSF samples comprised of different inlay density and dimensions but with the same type of sensing element could be readily compared in this way.
The resistance-ratio curves of all the TSF samples are shown in
Figure 4. All TSF samples with the same type of sensing wire exhibited the same trend irrespective of their inlay density. In the same figure, experimental values for the temperature coefficient of resistivity (α) are also shown; these have been calculated using the reference equations presented in
Table 3. As expected, nickel shows the highest alpha values. Usually the copper alpha value is expected to be close to 0.0042; hence the increased value for nickel-coated copper wire almost certainly derives from the nickel coating. As expected, tungsten possesses the lowest alpha values.
Figure 4.
Fitted resistance ratios along with their corresponding alpha values (Temperature coefficient of resistivity).
Figure 4.
Fitted resistance ratios along with their corresponding alpha values (Temperature coefficient of resistivity).
It should, however, be borne in mind that the alpha values cannot on their own be used to judge the sensitivity of the sensing fabric, as the reference resistance of the TSF is equally important. Due to the high reference resistance of the TSF fabric samples made with nickel and tungsten elements, they possess high sensitivities.
Figure 5 shows the average sensitivity of each sample type calculated by considering the change in resistance resulting from a 1 °C change in temperature. Due to the low sensitivity of nickel-coated copper wire, it would be difficult to develop an electronic circuit with a resolution of 0.1 °C.
Figure 5.
Sensitivity analysis; change of resistance (mΩ) for 1 °C change in temperature.
Figure 5.
Sensitivity analysis; change of resistance (mΩ) for 1 °C change in temperature.
It has also been observed that inlaid wire showed constant values of experimental sensitivity over the tested temperature range. These observations suggest that each sample has to be calibrated individually at one temperature point, which would be enough to generate a calibration equation.
It has been previously mentioned that researchers have developed smart garments with integrated textile-based ECG, respiration and activity sensors. This new design of temperature sensing fabric can be used either as a standalone sensing device to measure human body temperature or, in conjunction with other integrated textile-based sensors, as part of a smart shirt to provide a complete health picture. It may also be used to measure the temperature of the environment by embedding it into the outer layer of jackets. A combination of two sensing patches integrated into the inner and outer strata of the garment can also help us to measure the heat flux or loss of heat from the body to the environment [
12].
4. Conclusions
This paper reports preliminary investigation into the design and development of commercially knitted smart fabric for temperature measurement that can be integrated into garments, for the measurement of skin temperatures of the human body. Nickel and tungsten wires proved to be good candidates for the sensing element of the temperature sensitive fabric because of their high reference resistance, sensitivity and availability. A modified mathematical relationship can be used, to design the sensing fabric with optimised dimensions, in order to achieve a targeted reference resistance. It has been observed that experimental reference resistance of all samples were within two percent of their modelled values. Experimental temperature-resistance curves show a linear relationship and follow the same trend as their modelled counterparts. The packing density of the wire within the knitted samples has a small effect on the reference resistance and on the smoothness of the RT curves, as low inlay densities demonstrated better agreement of results with their modelled values. Future work includes the development of a smart shirt with integrated temperature sensing patches and its testing in a realistic environment to specify the baseline characteristics i.e., accuracy, response time, thermal conduction errors, self heating, insulation resistance, etc.