Marching-on-in-Degree Time-Domain Integral Equation Solver for Transient Electromagnetic Analysis of Graphene
Abstract
:1. Introduction
2. Formulation
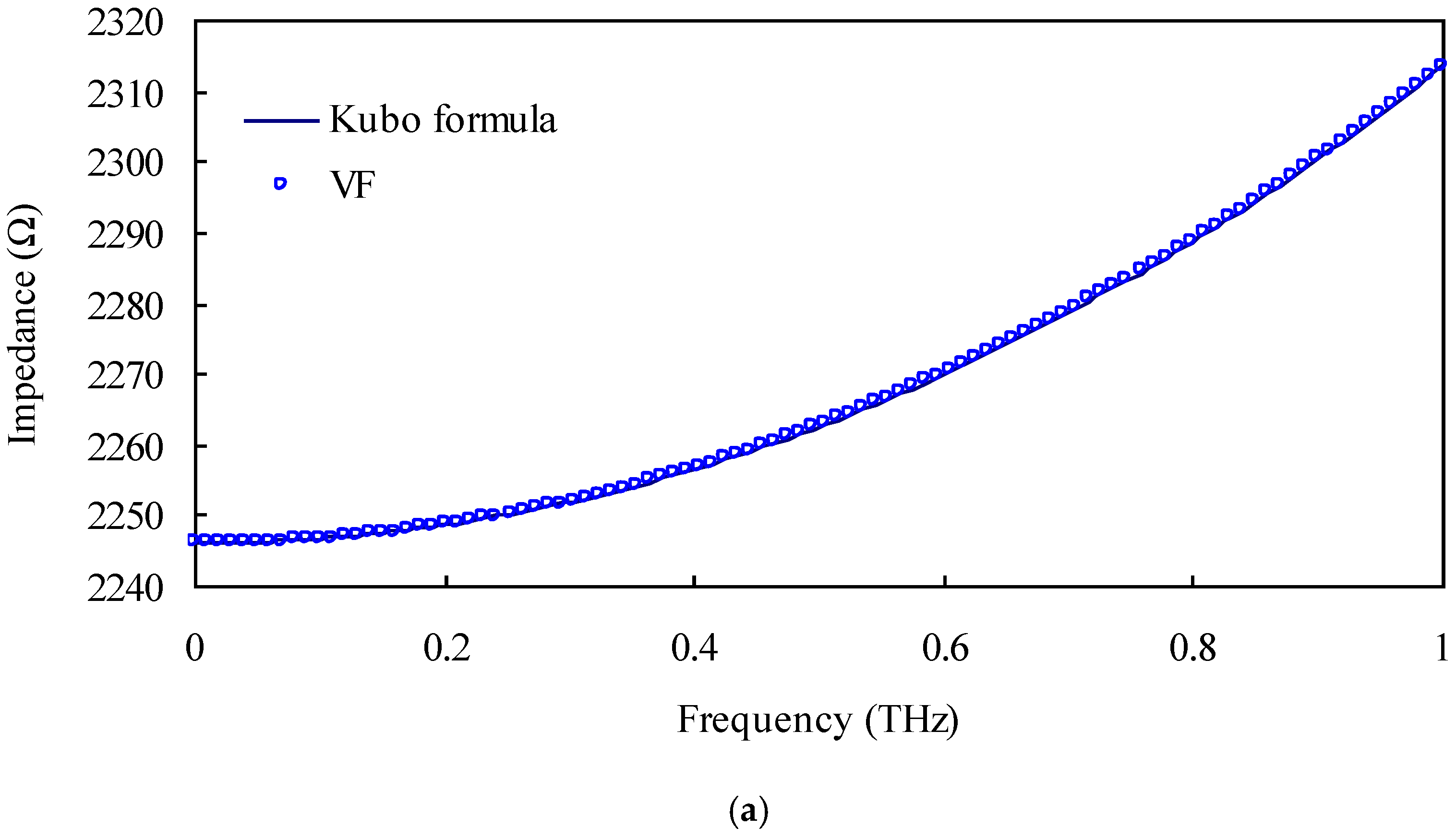
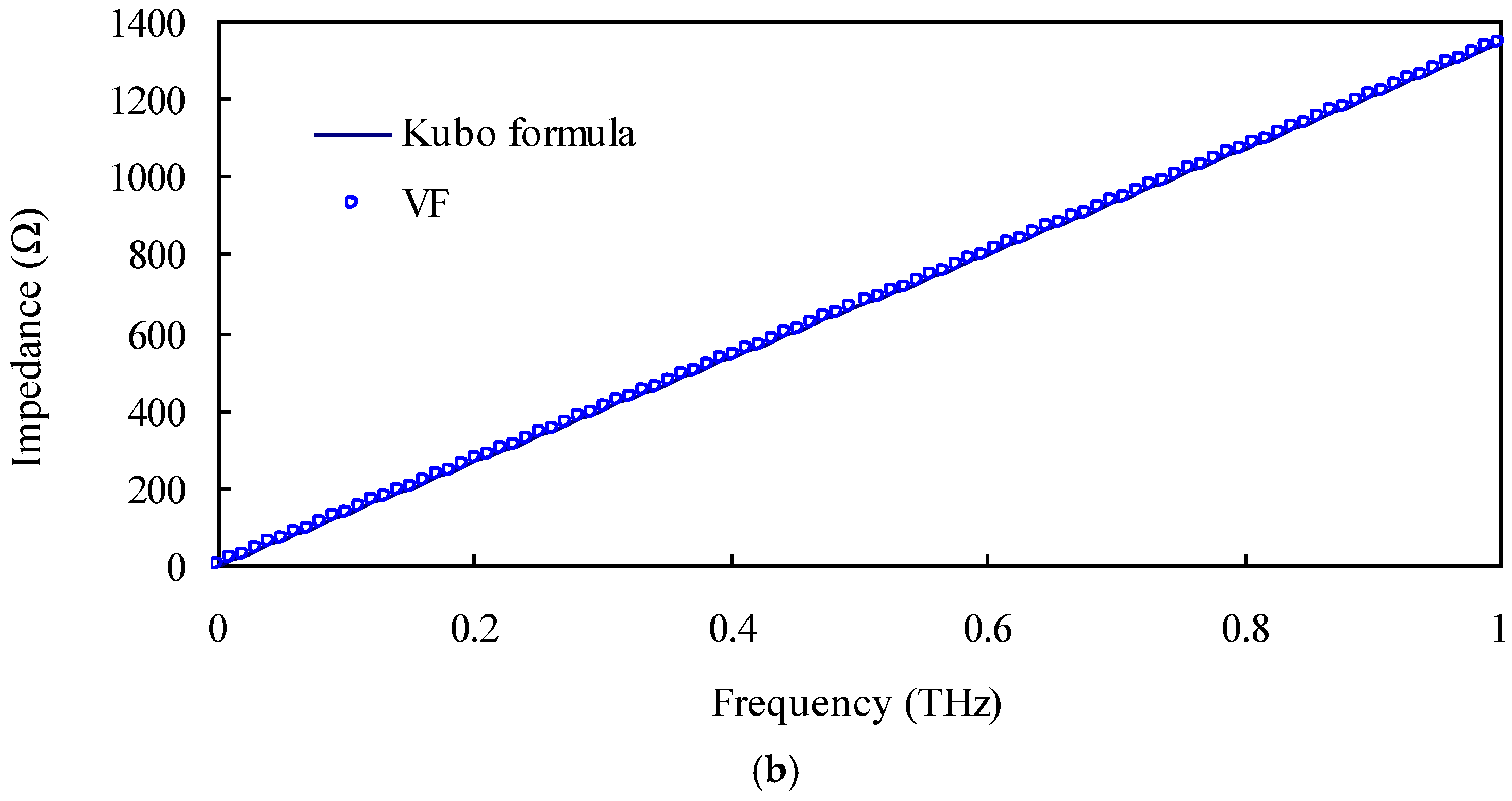
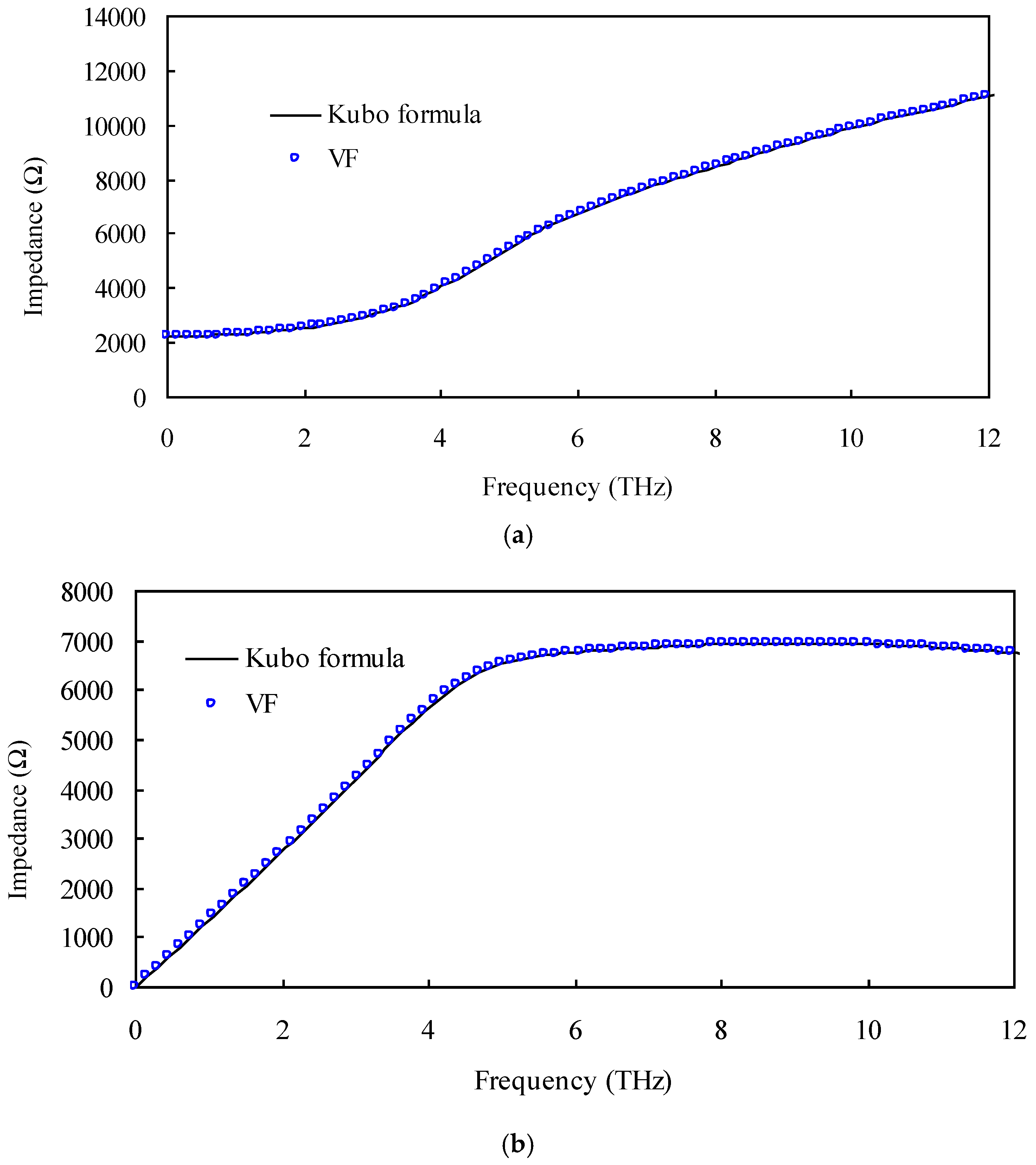
2.1. Modeling of Graphene and VF Method
2.2. TDIE and Temporal Convolution
2.3. MOD Scheme
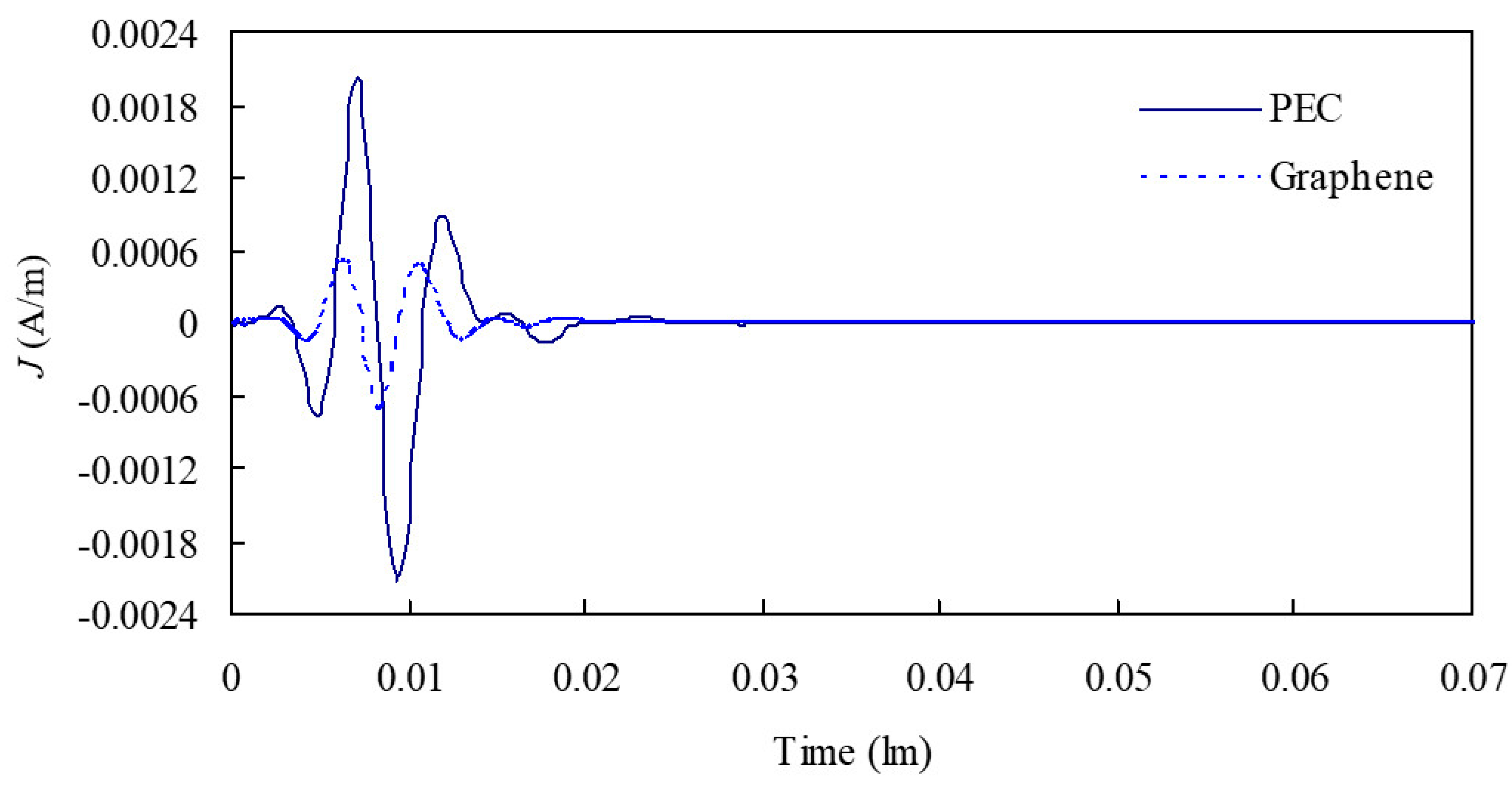
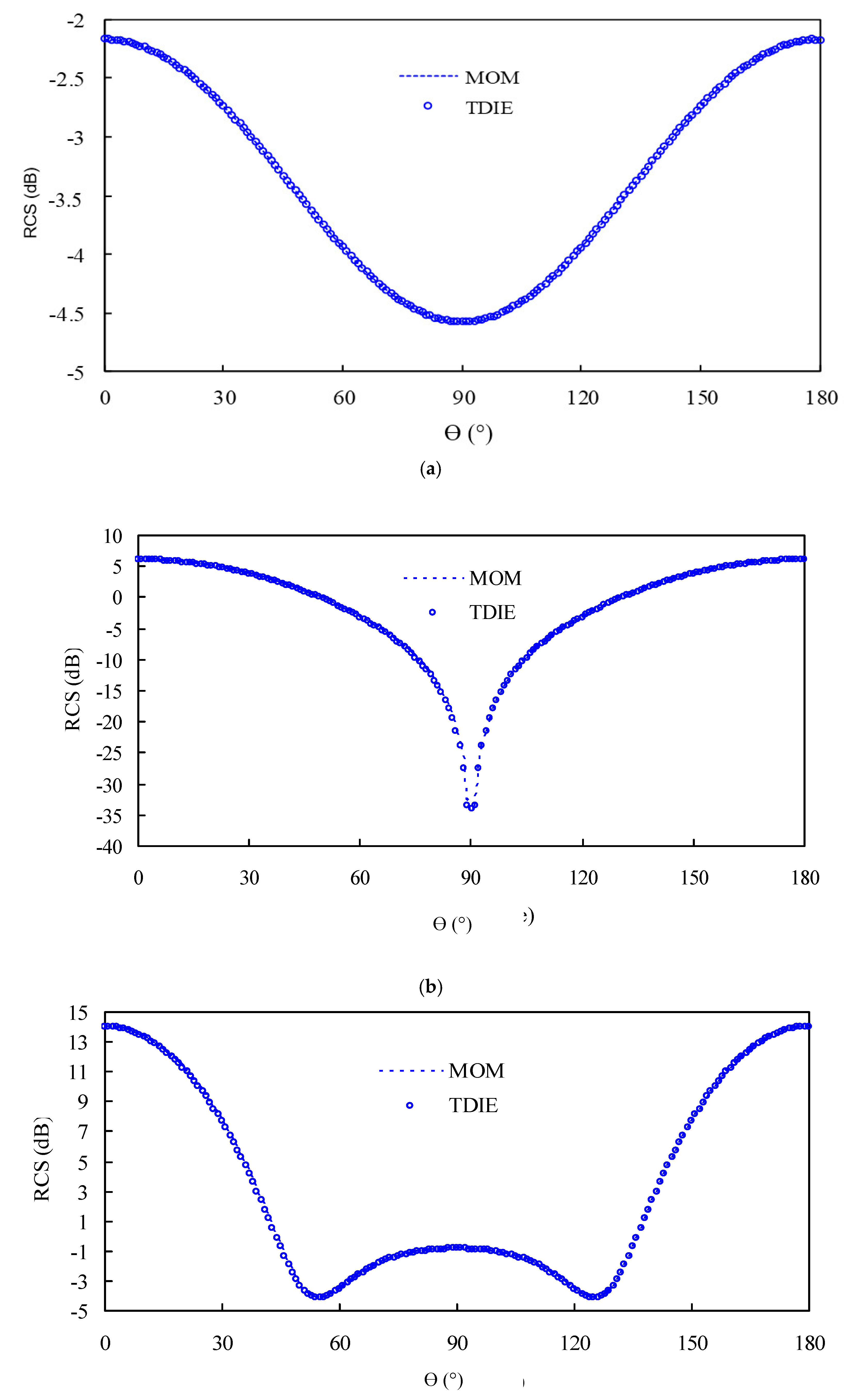
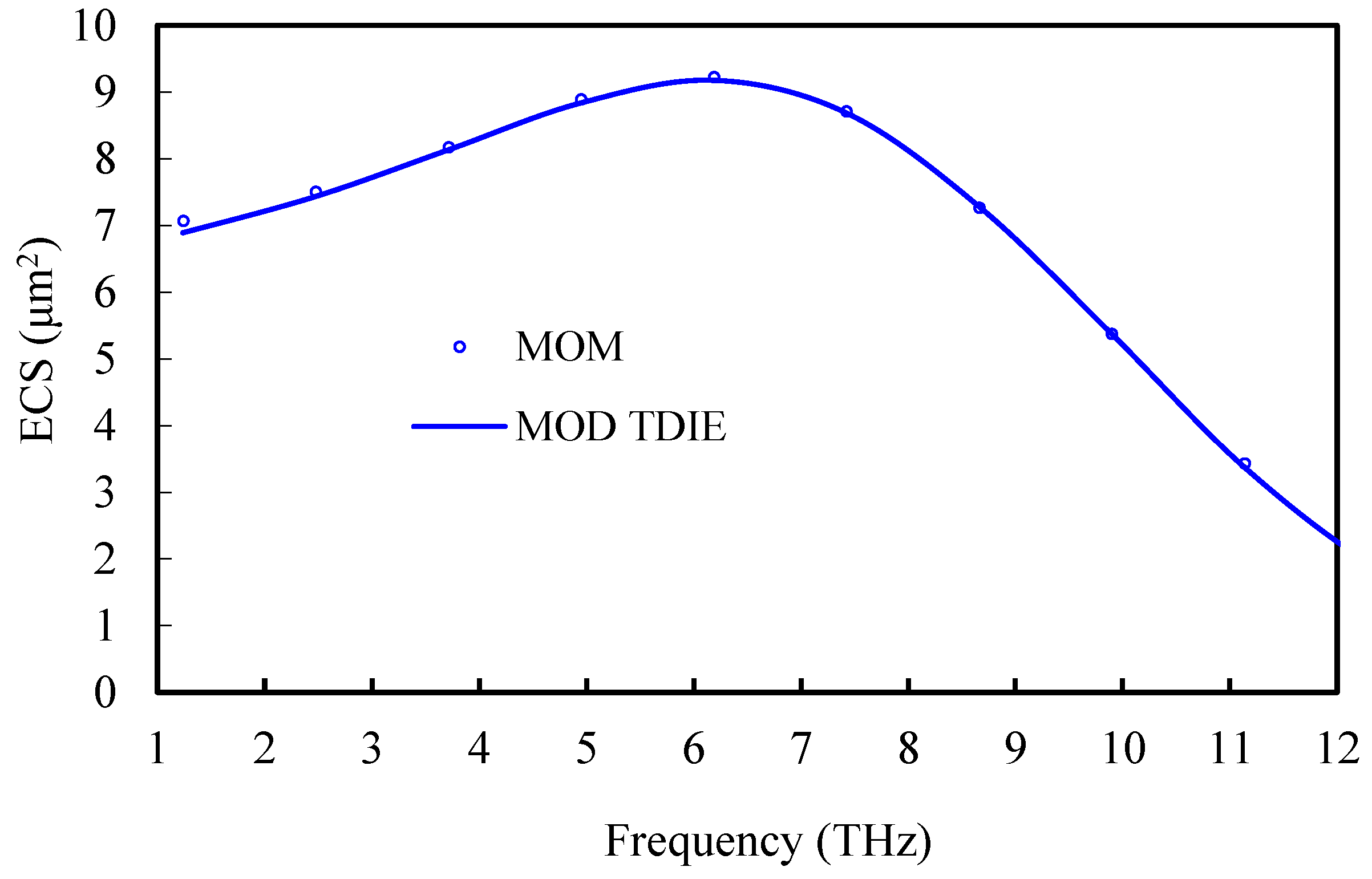
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Warner, J.H.; Schäffel, F.; Rümmeli, M.; Bachmatiuk, A. Graphene: Fundamentals and Emergent Applications, 1st ed.; Elsevier: Oxford, UK, 2012. [Google Scholar]
- Balci, O.; Polat, E.O.; Kakenov, N.; Kocabas, C. Graphene-enabled electrically switchable radar-absorbing surfaces. Nat. Commun. 2015, 6, 6628. [Google Scholar] [CrossRef] [PubMed]
- Wan, T.H.; Chiu, Y.F.; Chen, C.W.; Hsu, C.C.; Cheng, I.C.; Chen, J.Z. Atmospheric-pressure plasma jet processed Pt-decorated reduced graphene oxides for counter-electrodes of dye-sensitized solar cells. Coatings 2016, 6, 44. [Google Scholar] [CrossRef]
- Zheng, G.G.; Zhang, H.J.; Bu, L.B. Narrow-band enhanced absorption of monolayer graphene at near-infrared (NIR) sandwiched by dual gratings. Plasmonics 2017, 12, 271–276. [Google Scholar] [CrossRef]
- Zhu, W.R.; Xiao, F.J.; Kang, M.; Sikdar, D.; Premaratne, M. Tunable terahertz left-handed metamaterial based on multi-layer graphene-dielectric composite. Appl. Phys. Lett. 2014, 104, 051902. [Google Scholar] [CrossRef]
- Thampy, A.S.; Darak, M.S.; Dhamodharan, S.K. Analysis of graphene based optically transparent patch antenna for terahertz communications. Physica E 2015, 66, 67–73. [Google Scholar] [CrossRef]
- Fallahi, A.; Perruisseau-Carrier, J. Design of tunable biperiodic graphene metasurfaces. Phys. Rev. B 2012, 86, 195408. [Google Scholar] [CrossRef]
- Chen, Y.P.; Sha, W.E.I.; Jiang, L.J.; Hu, J. Graphene plasmonics for tuning photon decay rate near metallic split-ring resonator in a multilayered substrate. Opt. Express 2015, 23, 2798–2807. [Google Scholar] [CrossRef] [PubMed]
- Shapoval, O.V.; Gomez-Diaz, J.S.; Perruisseau-Carrier, J.; Mosig, J.R.; Nosich, A.I. Integral equation analysis of plane wave scattering by coplanar graphene-strip gratings in the THz range. IEEE Trans. THz Sci. Technol. 2013, 3, 666–674. [Google Scholar] [CrossRef]
- Balaban, M.V.; Shapoval, O.V.; Nosich, A.I. THz wave scattering by a graphene strip and a disk in the free space: Integral equation analysis and surface plasmon resonances. J. Opt. 2013, 15, 114007. [Google Scholar] [CrossRef]
- Lin, H.; Pantoja, M.F.; Angulo, L.D.; Alvarez, J.; Martin, R.G.; Garcia, S.G. FDTD modeling of graphene devices using complex conjugate dispersion material model. IEEE Microw. Wirel. Compon. Lett. 2012, 22, 612–614. [Google Scholar] [CrossRef]
- Nayyeri, V.; Soleimani, M.; Ramahi, O.M. Wideband modeling of graphene using the finite-difference time-domain method. IEEE Trans. Antennas Propag. 2013, 61, 6107–6114. [Google Scholar] [CrossRef]
- Wang, D.W.; Zhao, W.S.; Gu, X.Q.; Chen, W.C.; Yin, W.Y. Wideband modeling of graphene-based structures at different temperatures using hybrid FDTD method. IEEE Trans. Nanotechnol. 2015, 14, 250–258. [Google Scholar] [CrossRef]
- Li, P.; Jiang, L.J.; Bağci, H. A resistive boundary condition enhanced DGTD scheme for the transient analysis of graphene. IEEE Trans. Antennas Propag. 2015, 63, 3065–3076. [Google Scholar] [CrossRef]
- Li, P.; Jiang, L.J. Modeling of magnetized graphene from microwave to THz range by DGTD with a scalar RBC and an ADE. IEEE Trans. Antennas Propag. 2015, 63, 4458–4467. [Google Scholar] [CrossRef]
- Li, P.; Shi, Y.F.; Jiang, L.J.; Bağci, H. DGTD analysis of electromagnetic scattering from penetrable conductive objects with IBC. IEEE Trans. Antennas Propag. 2015, 63, 5686–5697. [Google Scholar]
- Shi, Y.F.; Uysal, I.E.; Li, P.; Ulku, H.A.; Bağci, H. Analysis of electromagnetic wave interactions on graphene sheets using time domain integral equations. In Proceedings of the International ACES Conference, Williamsburg, VA, USA, 22–26 March 2015. [Google Scholar]
- Shi, Y.F.; Li, P.; Uysal, I.E.; Ulku, H.A.; Bağci, H. An MOT-TDIE solver for analyzing transient fields on graphene-based devices. In Proceedings of the IEEE International Symposium Antennas Propagation (APSURSI), Fajardo, Puerto Rico, 26 June–1 July 2016. [Google Scholar]
- Jung, B.H.; Chung, Y.S.; Sarkar, T.K. Time-domain EFIE, MFIE, and CFIE formulations using Laguerre polynomials as temporal basis functions for the analysis of transient scattering from arbitrary shaped conducting structures. Prog. Electromagn. Res. 2003, 39, 1–45. [Google Scholar] [CrossRef]
- Chung, Y.S.; Lee, Y.J.; So, J.H.; Kim, J.Y.; Cheon, C.Y.; Lee, B.J.; Sarkar, T.K. A stable solution of time domain electric field integral equation using weighted Laguerre polynomials. Microw. Opt. Tech. Lett. 2007, 49, 2789–2793. [Google Scholar] [CrossRef]
- Mei, Z.C.; Zhang, Y.; Sarkar, T.K.; Salazar-Palma, M.; Jung, B.H. Analysis of arbitrary frequency-dependent losses associated with conducting structures in a time-domain electric field integral equation. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 678–681. [Google Scholar]
- Shi, Y.; Jin, J.M. Time-domain augmented EFIE and its marching-on-in-degree solution. Microw. Opt. Technol. Lett. 2011, 53, 1439–1444. [Google Scholar] [CrossRef]
- Shi, Y.; Jin, J.M. A time-domain volume integral equation and its marching-on-in-degree solution for analysis of dispersive dielectric objects. IEEE Trans. Antennas Propag. 2011, 59, 969–978. [Google Scholar] [CrossRef]
- Wang, Q.Q.; Liu, Z.W.; Shi, Y.F.; Zhang, H.H.; Chen, R.S. Efficient generation of aggregative basis functions in the marching-on-in-degree time-domain integral equation solver. Electromagnetics 2013, 33, 370–378. [Google Scholar] [CrossRef]
- He, Z.; Chen, R.S.; Sha, W.E.I. An Efficient marching-on-in-degree solution of transient multiscale EM scattering problems. IEEE Trans. Antennas Propag. 2016, 64, 3039–3046. [Google Scholar] [CrossRef]
- Valdes, F.; Andriulli, F.P.; Bağci, H.; Michielssen, E. Time-domain single-source integral equations for analyzing scattering from homogeneous penetrable objects. IEEE Trans. Antennas Propag. 2013, 61, 1239–1254. [Google Scholar] [CrossRef]
- Shi, Y.F.; Bağci, H.; Lu, M.Y. On the internal resonant modes in marching-on-in-time solution of the time domain electric field integral equation. IEEE Trans. Antennas Propag. 2013, 61, 4389–4392. [Google Scholar] [CrossRef]
- Shi, Y.F.; Bağci, H.; Lu, M.Y. On the static loop modes in the marching-on-in-time solution of the time-domain electric field integral equation. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 317–320. [Google Scholar]
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 1999, 14, 1052–1061. [Google Scholar] [CrossRef]
- Gustavsen, B. Improving the pole relocating properties of vector fitting. IEEE Trans. Power Deliv. 2006, 21, 1587–1592. [Google Scholar] [CrossRef]
- Deschrijver, D.; Mrozowski, M.; Dhaene, T.; de Zutter, D. Macromodeling of multiport systems using a fast implementation of the vector fitting method. IEEE Microw. Wirel. Compon. Lett. 2008, 18, 383–385. [Google Scholar] [CrossRef]
- Romano, D.; Antonini, G. Partial element equivalent circuit-based transient analysis of graphene-based interconnects. IEEE Trans. Electromagn. Compat. 2016, 58, 801–810. [Google Scholar] [CrossRef]
- Zhao, P.; Wu, K.L. Model-based vector-fitting method for circuit model extraction of coupled-resonator diplexers. IEEE Trans. Microw. Theory Tech. 2016, 64, 1787–1797. [Google Scholar] [CrossRef]
- Parvaz, R.; Karami, H. Far-infrared multi-resonant graphene-based metamaterial absorber. Opt. Commun. 2017, 396, 267–274. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
| l | al | cl |
|---|---|---|
| 1 | (–1.4148 + j6.8532) × 1013 | (5.5230 + j0.3378) × 1017 |
| 2 | (–1.4148 – j6.8532) × 1013 | (5.5230 – j0.3378) × 1017 |
| l | al | cl |
|---|---|---|
| 1 | –6.5249 × 1013 | –8.5729 × 1017 |
| 2 | –2.7141 × 1016 | 4.4980 × 1020 |
| 3 | (–1.2248 + j2.6437) × 1013 | (–0.8148 + j1.5576) × 1016 |
| 4 | (–1.2248 – j2.6437) × 1013 | (–0.8148 – j1.5576) × 1016 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Liu, H.; Wang, Y.; Jiang, Z. Marching-on-in-Degree Time-Domain Integral Equation Solver for Transient Electromagnetic Analysis of Graphene. Coatings 2017, 7, 170. https://doi.org/10.3390/coatings7100170
Wang Q, Liu H, Wang Y, Jiang Z. Marching-on-in-Degree Time-Domain Integral Equation Solver for Transient Electromagnetic Analysis of Graphene. Coatings. 2017; 7(10):170. https://doi.org/10.3390/coatings7100170
Chicago/Turabian StyleWang, Quanquan, Huazhong Liu, Yan Wang, and Zhaoneng Jiang. 2017. "Marching-on-in-Degree Time-Domain Integral Equation Solver for Transient Electromagnetic Analysis of Graphene" Coatings 7, no. 10: 170. https://doi.org/10.3390/coatings7100170






