Completely Analytical Tools for the Next Generation of Surface and Coating Optimization
Abstract
:1. Introduction
1.1. Simple First Principle Based Interatomic Potential Description of Mechanical Material Behavior
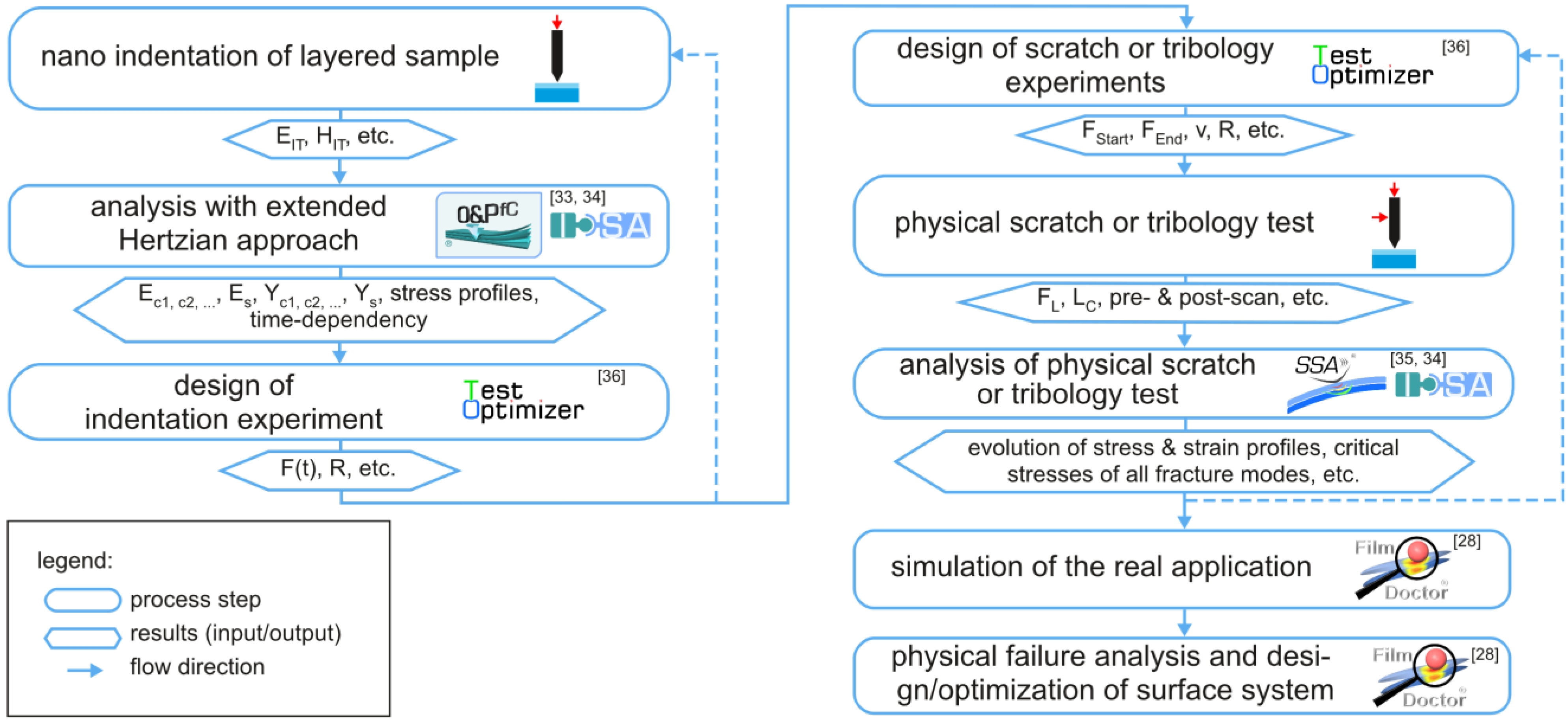
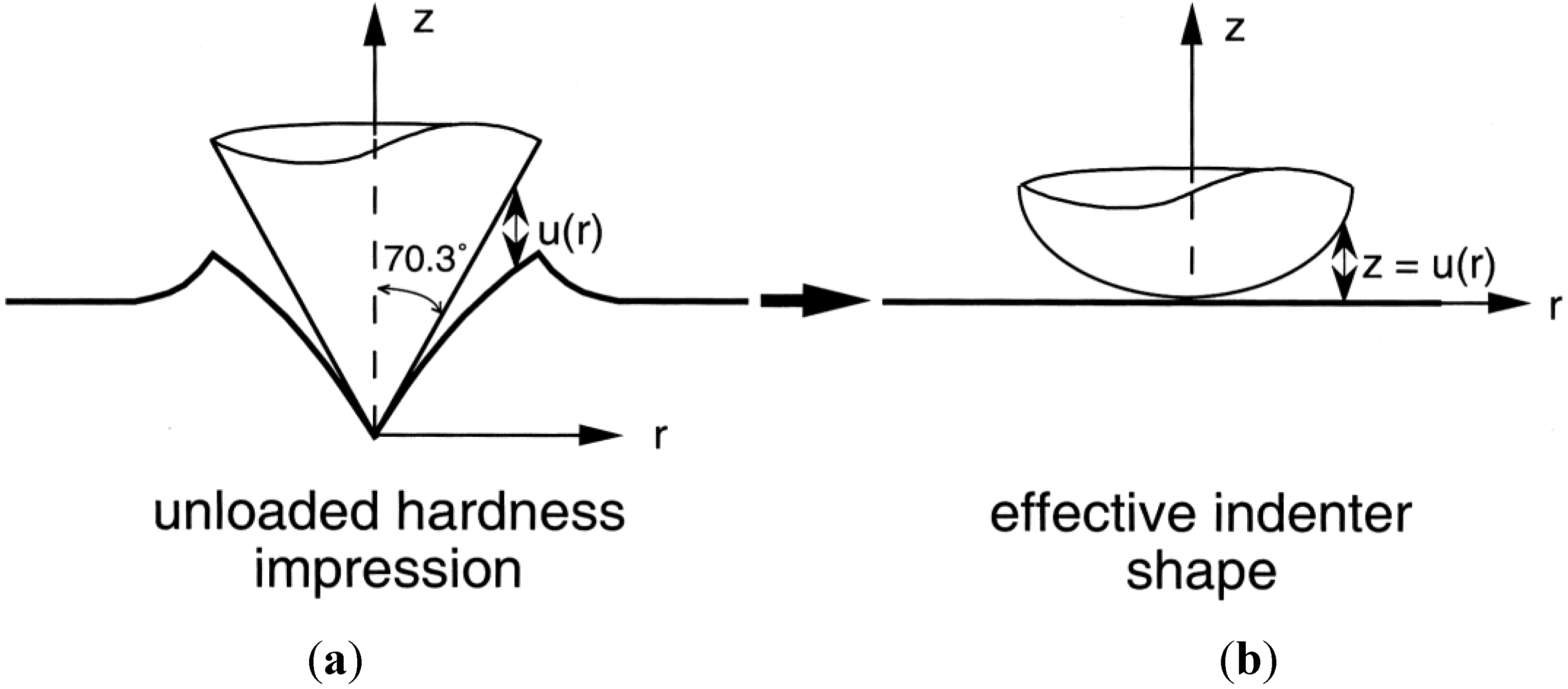
1.2. Brief Story about the “Effective Indenter Concept” and Its Extension to Layered Materials
1.3. About the Extension of the Oliver and Pharr Method to Analyze Nanoindentation Data of Layered Materials and Time Dependent Mechanical Behavior
Making the Classical Oliver and Pharr Method Fit for Time Dependent Mechanical Behavior
1.4. Introduction into the Physical Scratch and/or Tribological Test and Its Analysis
2. Theory Section
2.1. First Principle Based Interatomic Potential Description of Mechanical Material Behavior
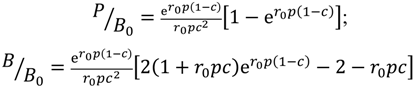
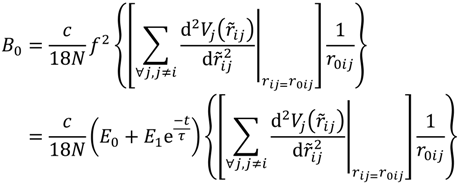
 we have a resulting phenomenological Young’s modulus structure of the form:
we have a resulting phenomenological Young’s modulus structure of the form:
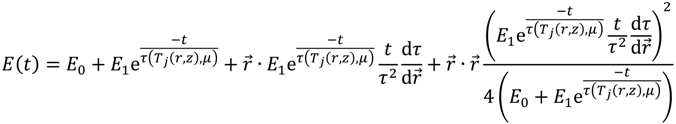
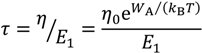
2.2. The Effective Indenter Concept
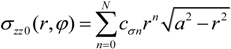
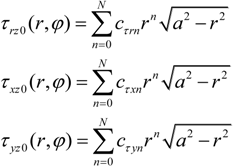
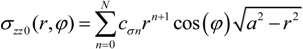
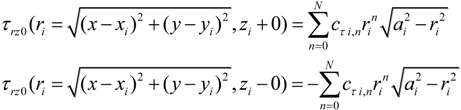
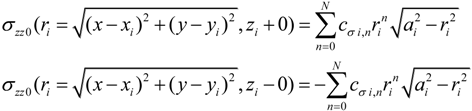
2.3. The Extension of the Oliver and Pharr Method to Analyze Nanoindentation Data to Layered Materials and Time Dependent Mechanical Behavior
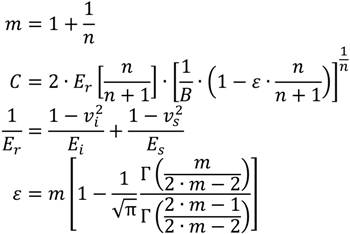
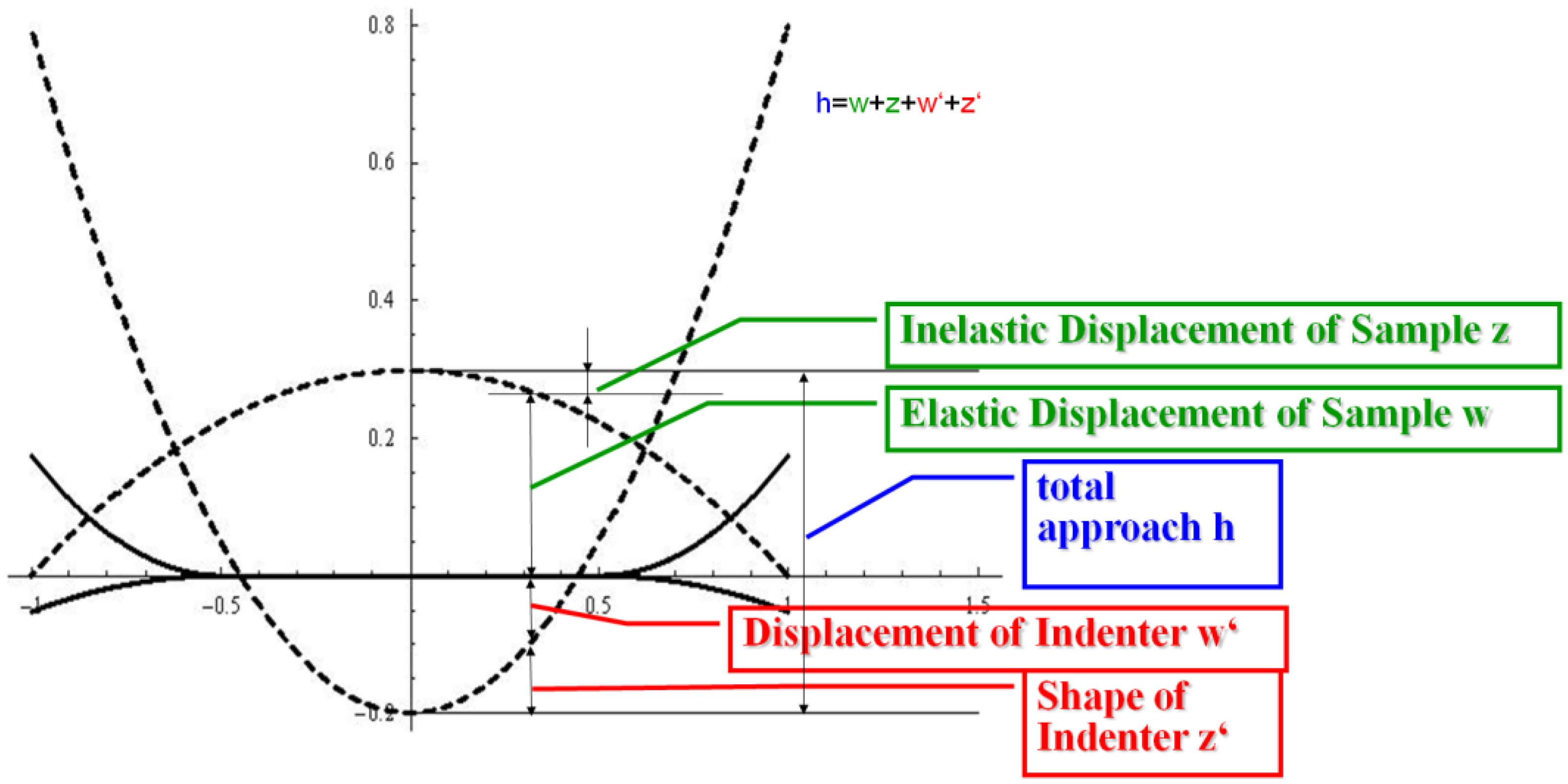
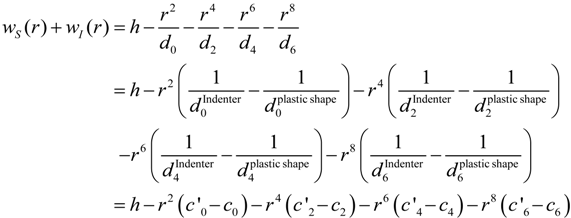
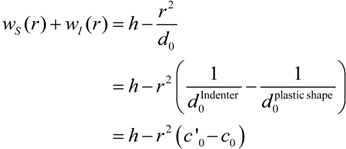
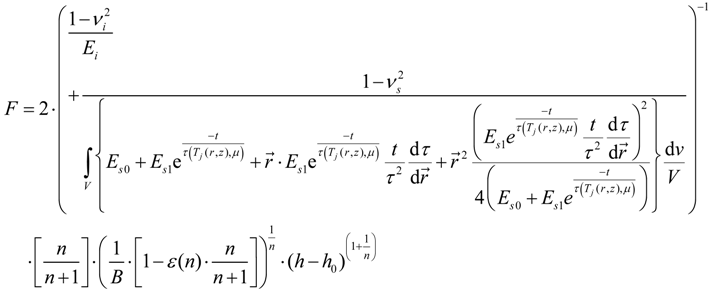
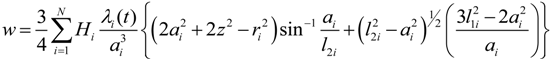
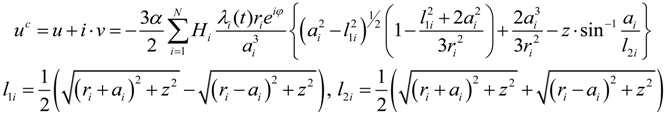
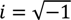 , u displacement in x- and v in y-direction, while w gives the displacement in z-direction). The coordinates ri have to be understood as
, u displacement in x- and v in y-direction, while w gives the displacement in z-direction). The coordinates ri have to be understood as 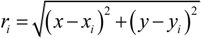 with xi and yi defining the positions of the various load dots. The material functions, respectively, constants Hi and α, are defined through:
with xi and yi defining the positions of the various load dots. The material functions, respectively, constants Hi and α, are defined through:

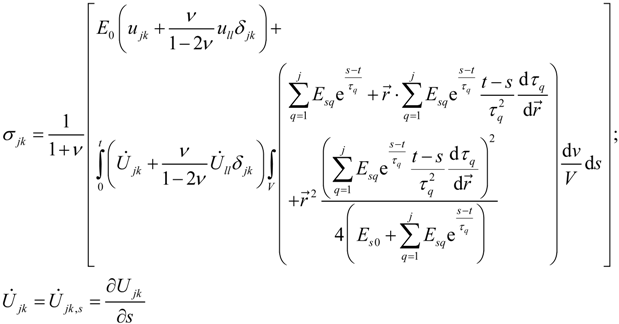
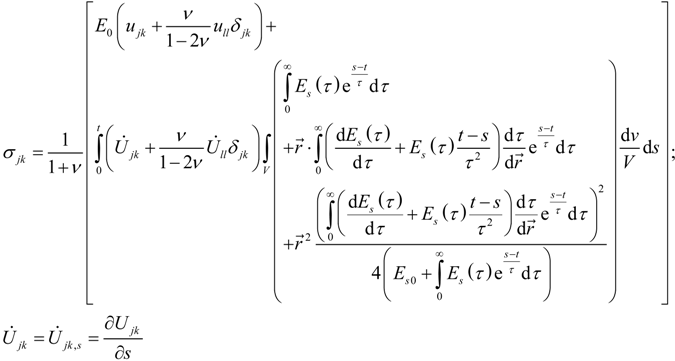
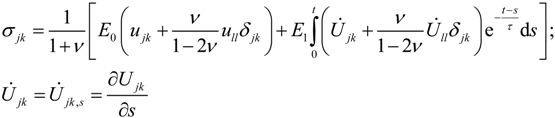
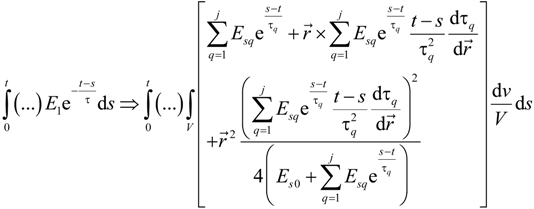
2.4. Theory for the Physical Scratch and/or Tribological Test
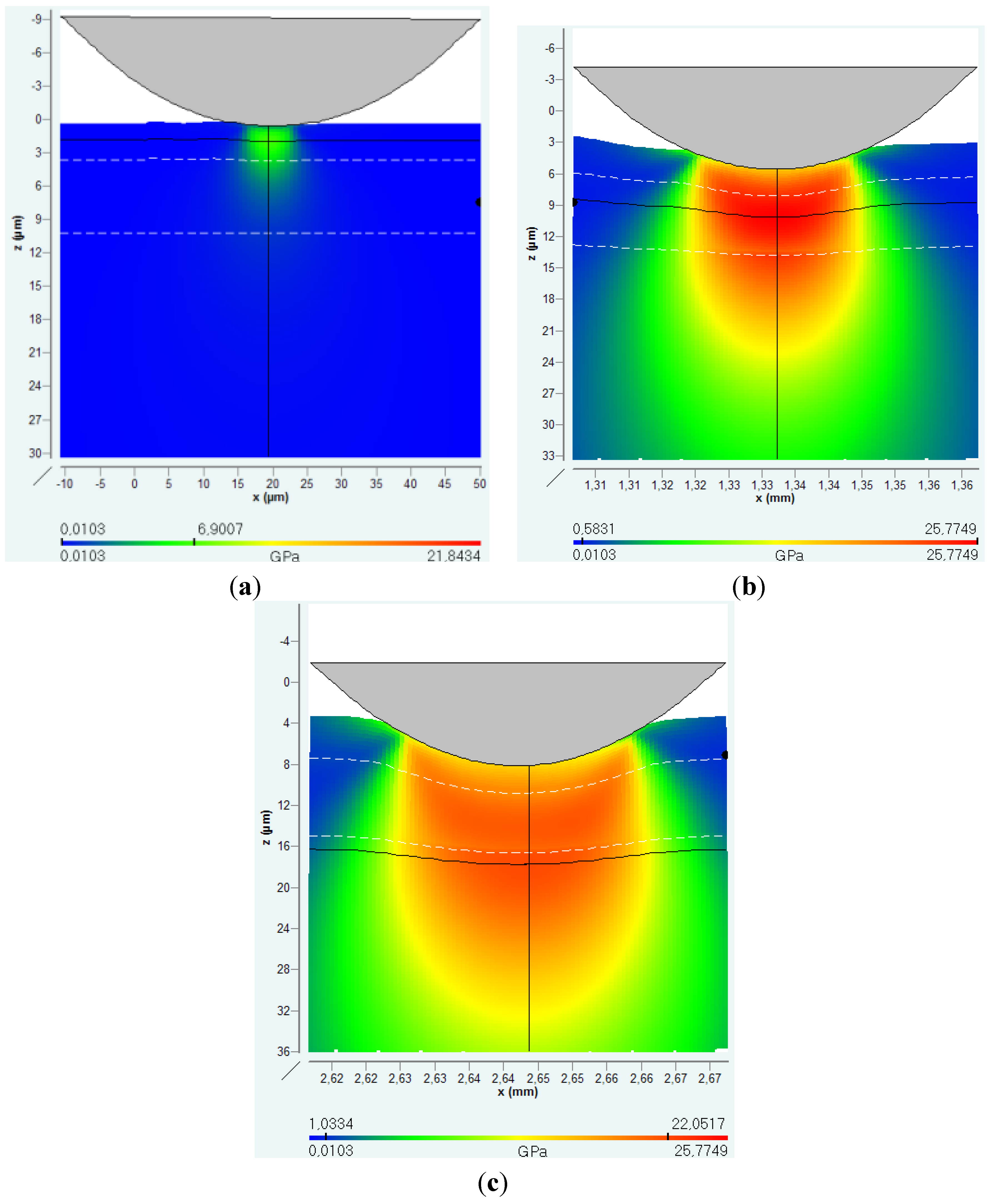
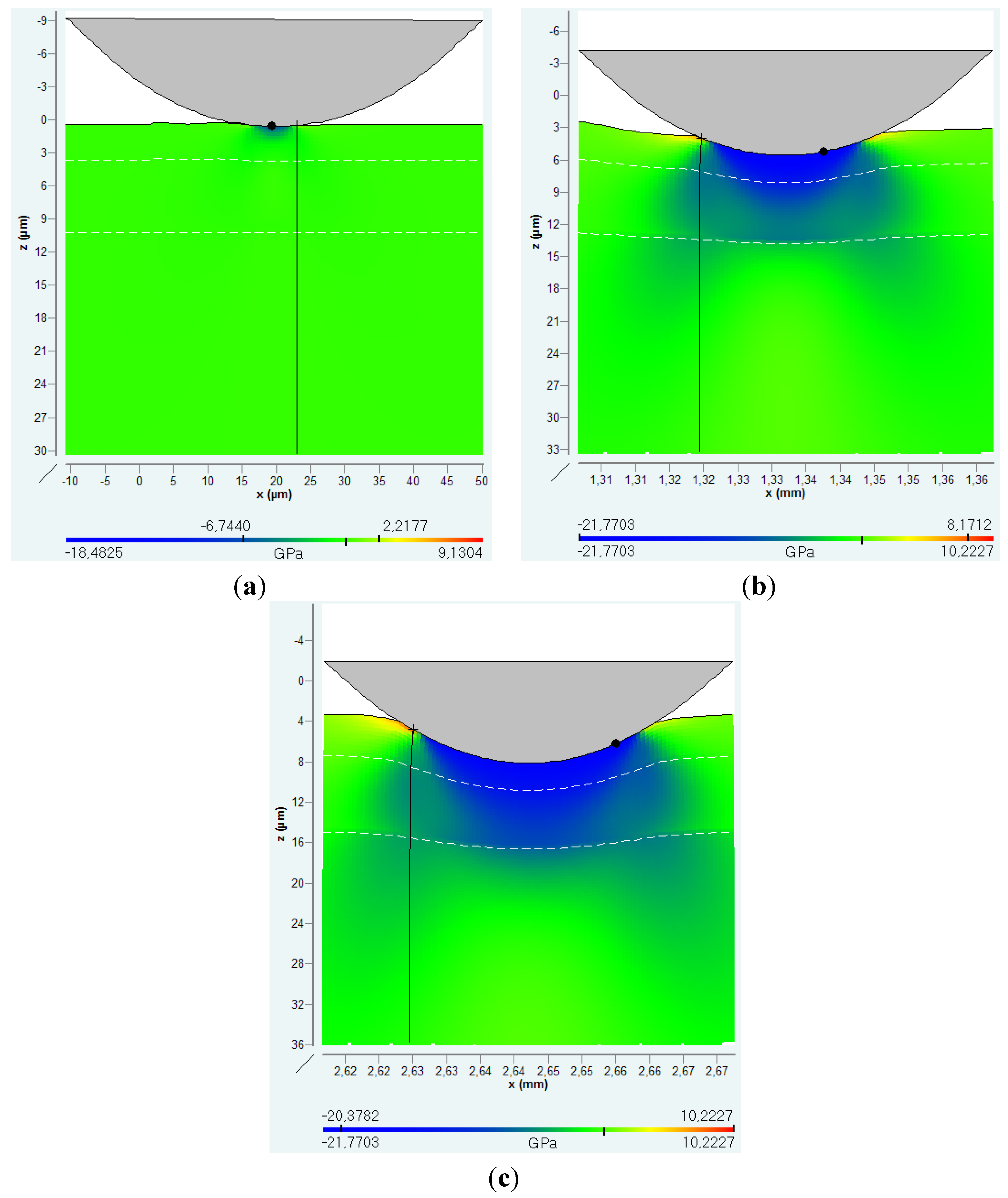
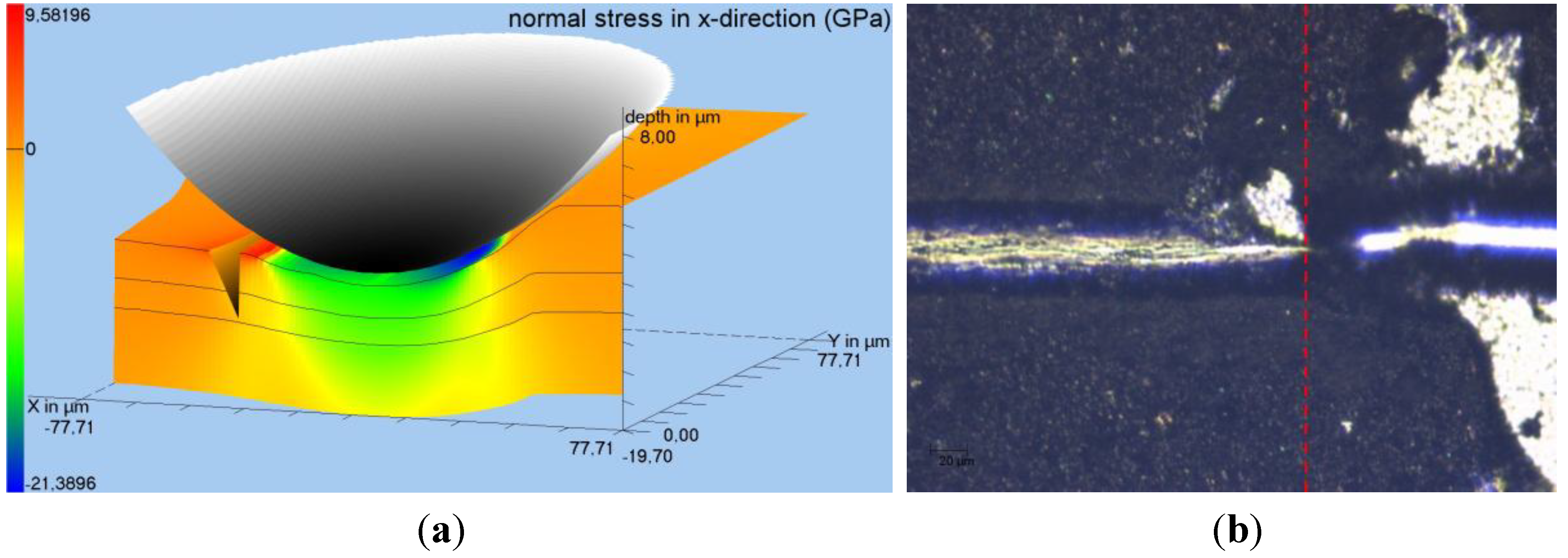
From Quasi-Static Experiments and Parameters to Dynamic Wear, Fretting and Tribological Tests
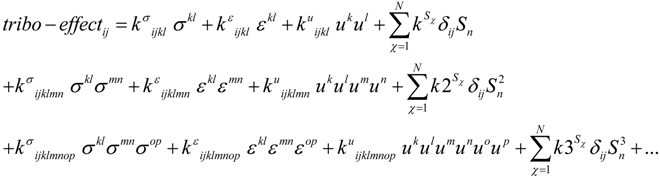
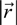 . One could formulate this as:
. One could formulate this as:
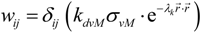
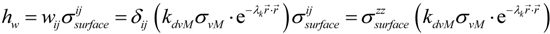
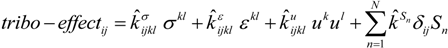
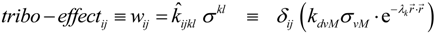
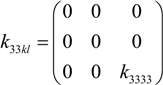
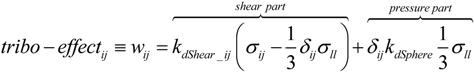
3. Experimental Section
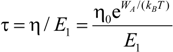
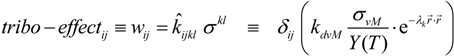
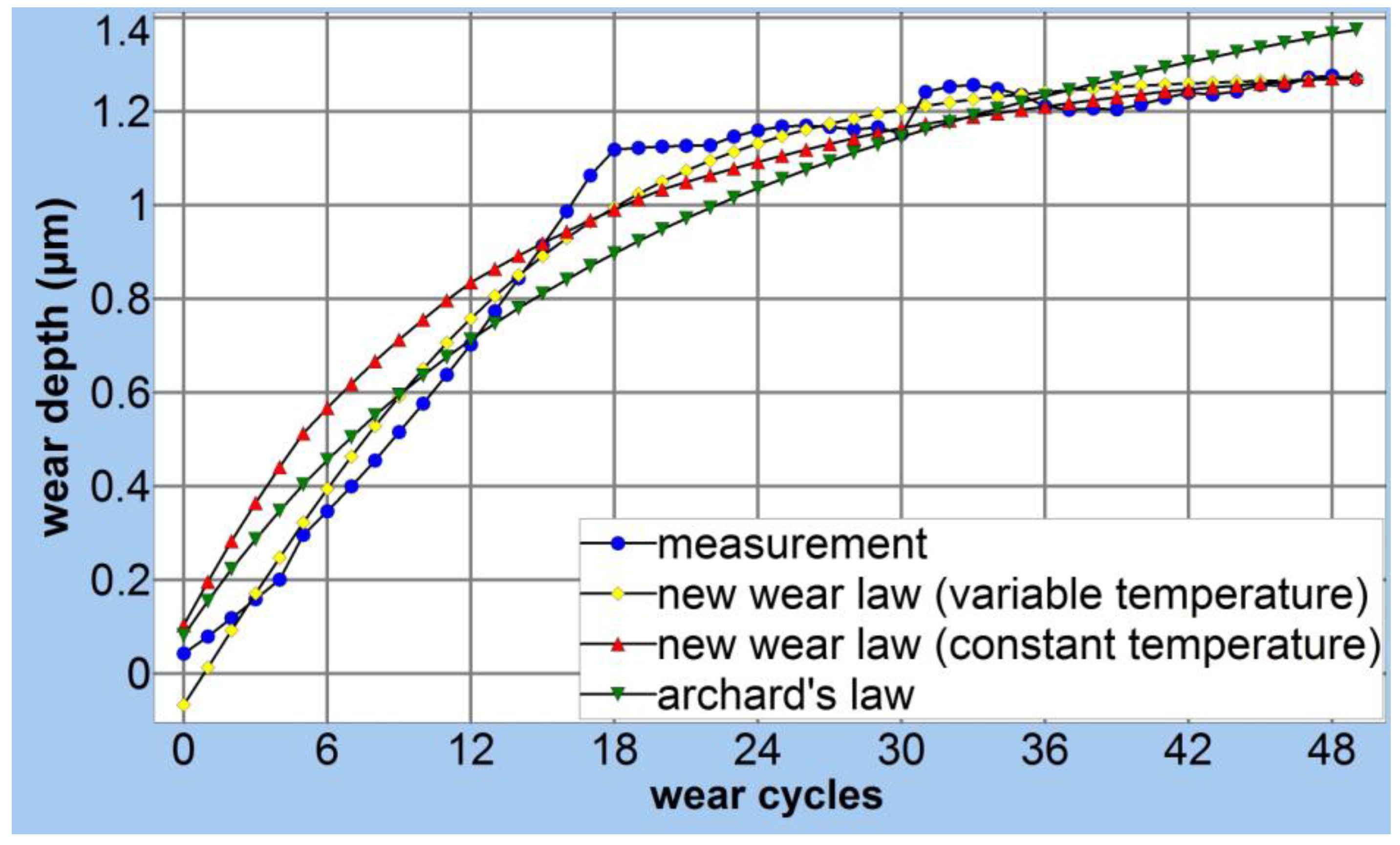
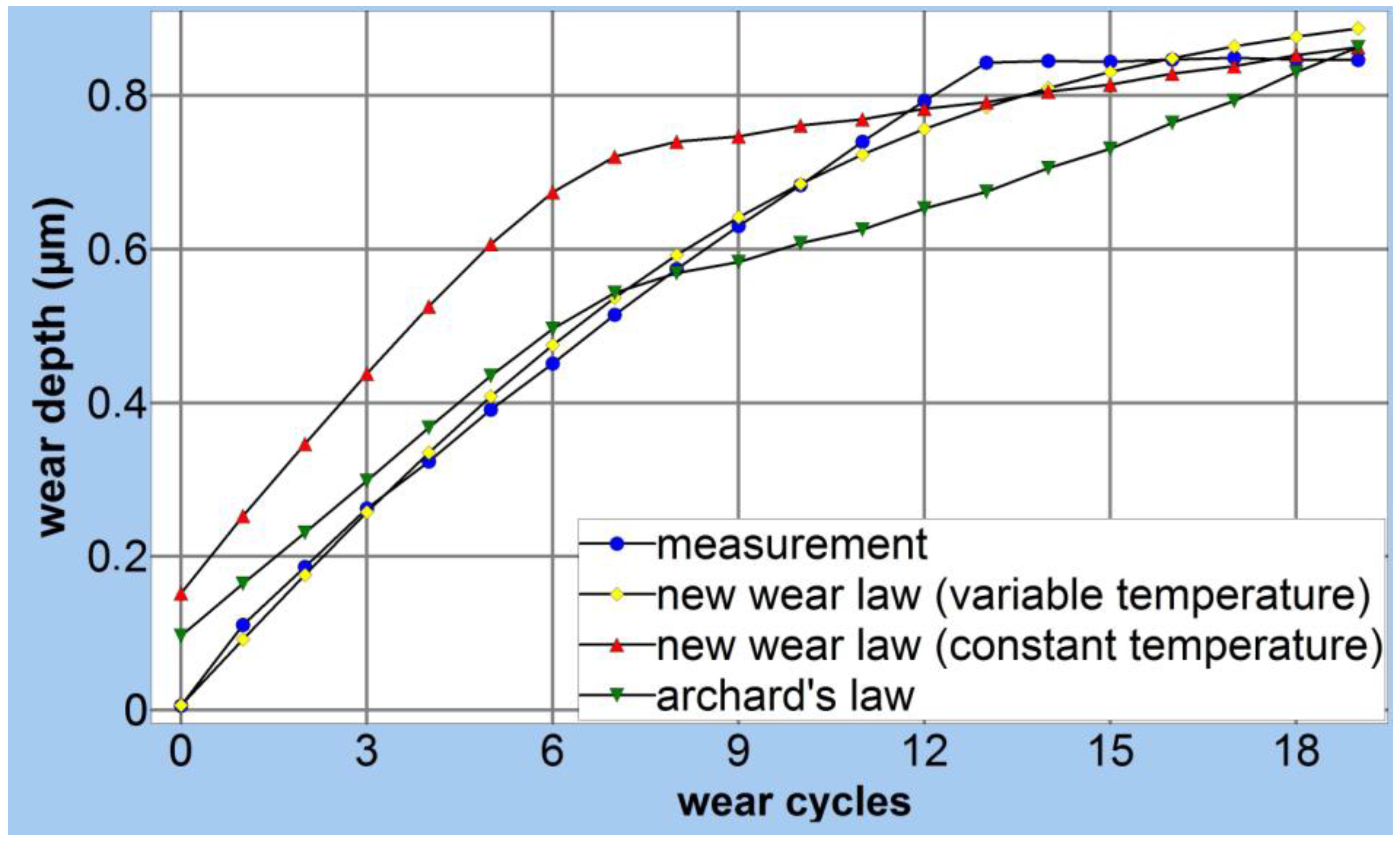
4. Conclusions
Acknowledgements
Appendix
Arbitrary Hertzian Load Dots
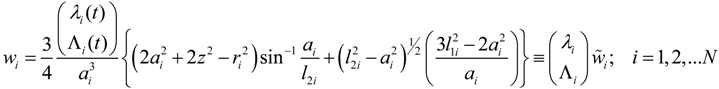
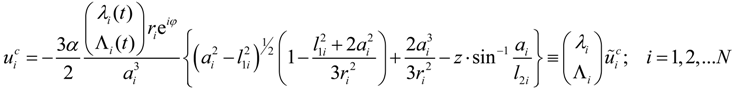
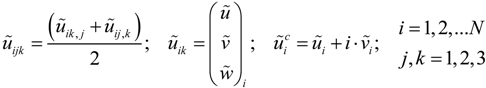
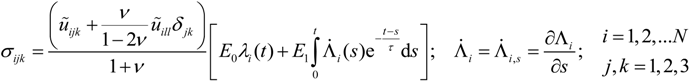
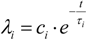 which here only is chosen as an example we obtain the solution:
which here only is chosen as an example we obtain the solution:
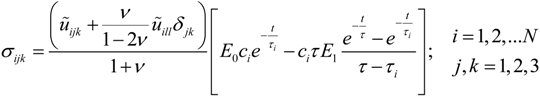
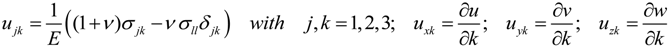
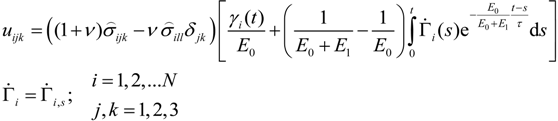
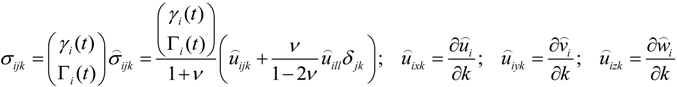
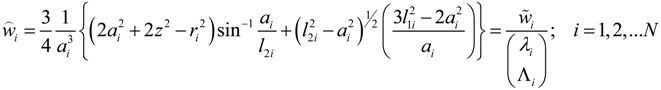
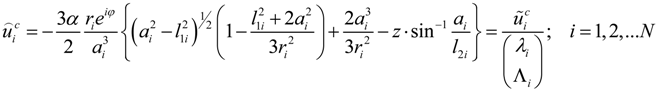
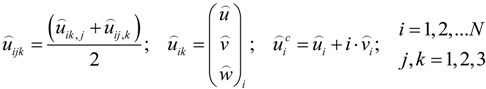
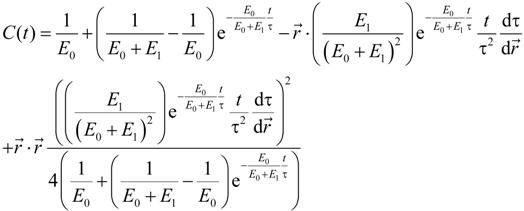
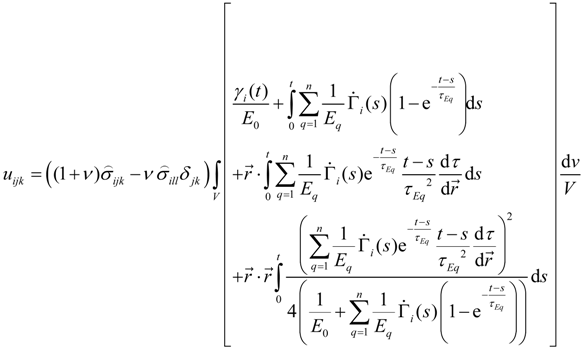
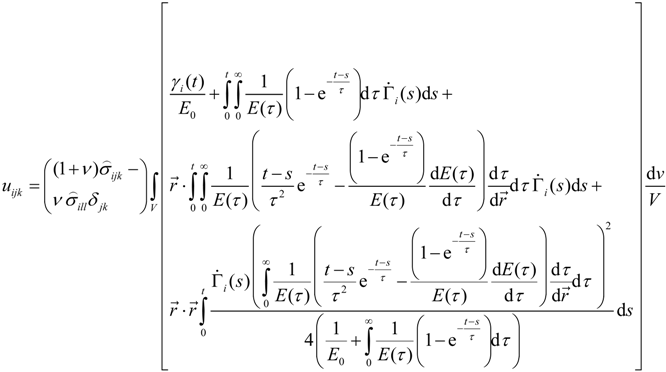
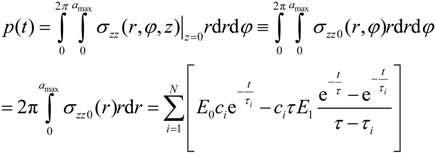
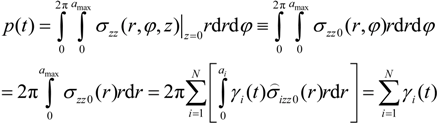
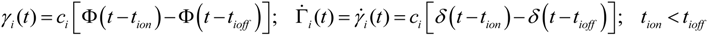

Conflicts of Interest
References
- Schwarzer, N. Short note on the effect of pressure induced increase of Young’s modulus. Philos. Mag. 2012, 92, 1631–1648. [Google Scholar] [CrossRef]
- Schwarzer, N. From interatomic interaction potentials via Einstein field equation techniques to time dependent contact mechanics. Mater. Res. Express 2014, 1. [Google Scholar] [CrossRef]
- Bolshakov, A.; Oliver, W.C.; Pharr, G.M. An Explanation for the Shape of Nanoindentation Unloading Curves based on Finite Element Simulation. MRS Symp. Proc. 1994, 356. [Google Scholar] [CrossRef]
- Pharr, G.M.; Bolshakov, B. Understanding nanoindentation unloading curves. J. Mater. Res. 2002, 17, 2660–2671. [Google Scholar] [CrossRef]
- Schwarzer, N.; Pharr, G.M. On the evaluation of stresses during nanoindentation with sharp indenters. Thin Solid Films 2004, 469–470, 194–200. [Google Scholar] [CrossRef]
- Schwarzer, N. The extended Hertzian theory and its uses in analysing indentation experiments. Philos. Mag. 2006, 86, 5153–5767. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mat. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Schwarzer, N.; Chudoba, T.; Pharr, G.M. On the evaluation of stresses for coated materials during nanoindentation with sharp indenters. Surf. Coat. Technol. 2006, 200, 4220–4226. [Google Scholar] [CrossRef]
- Schwarzer, N.; Chudoba, T.; Richter, F. Investigation of ultra thin coatings using nanoindentation. Surf. Coat. Technol. 2006, 200, 5566–5580. [Google Scholar] [CrossRef]
- Fuchs, M.; Favaro, G. Physical characterization of coated surfaces—Part I: instrumented indentation. Available online: http://www.csm-instruments.com/en/Physical-characterization-of-coated-surfaces-Part-I-%3A-Instrumented-Indentation (accessed on 17 April 2014).
- Fuchs, M.; Favaro, G. Physical characterization of coated surfaces—Part II: scratch test. Available online: www.csm-instruments.com/en/Physical-characterization-of-coated-surfaces-Part-II-%3A-Scratch-Test (accessed on 17 April 2014).
- Schwarzer, N.; Duong, Q.-H.; Bierwisch, N.; Favaro, G.; Fuchs, M.; Kempe, P.; Widrig, B.; Ramm, J. Optimization of the scratch test for specific coating designs. Surf. Coat. Technol. 2011, 206, 1327–1335. [Google Scholar] [CrossRef]
- Gies, A.; Chudoba, T.; Schwarzer, N.; Becker, J. Influence of the coating structure of a-C:H-W coatings on their wear-performance: A theoretical approach and its practical confirmation. In Proceedings of International Conference on Metallurgical Coatings and Thin Films (ICMCTF), San Diego, CA, USA, 29 April–3 May 2013.
- Liskiewicz, T.; Beake, B.; Schwarzer, N.; Davies, M. Short note on improved integration of mechanical testing in predictive wear models. In Proceedings of International Conference on Metallurgical Coatings and Thin Films (ICMCTF), San Diego, CA, USA, 29 April–3 May 2013.
- Schwarzer, N. Is ultra-hardness possible—A brief feasibility study. Available online: http://www.siomec.de/ultra-hard-coatings (accessed on 17 April 2014).
- Lie, M.; Chen, N.X. Möbius inversion transform for diamond-type materials and phonon dispersions. Phys. Rev. B 1995, 52, 997–1003. [Google Scholar] [CrossRef]
- Dick, T.; Cailletaud, G. Fretting modelling with a crystal plasticity model of Ti6Al4V. Comput. Mater. Sci. 2006, 38, 113–125. [Google Scholar]
- Guilemany, J.M.; Dosta, S.; Miguel, J.R. The enhancement of the properties of WC-Co HVOF coatings through the use of nanostructured and microstructured feedstock powders. Surf. Coat. Technol. 2006, 201, 1180–1190. [Google Scholar] [CrossRef]
- Hegadekatte, V.; Huber, N.; Kraft, O. Modeling and simulation of wear in a pin on disc tribometer. Tribol. Lett. 2006, 24, 51–60. [Google Scholar] [CrossRef]
- Holm, R. Electric Contacts; Almqvist and Wiksells Boktryxkeri AB: Uppsala, Sweden, 1946. [Google Scholar]
- Holmberg, K.; Matthews, A. Coatings Tribology, 2nd ed.; Springer: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Schwarzer, N. Arbitrary load distribution on a layered half space. ASME J. Tribol. 2000, 122, 672–681. [Google Scholar] [CrossRef]
- Chudoba, T.; Herrmann, K. Verfahren zur Ermittlung der realen Spitzenform von VICKERS- und BERKOVICH-Eindringkörpern. HTM Härt. Mitt. 2001, 56, 258–264. (In German) [Google Scholar]
- Schwarzer, N. Elastic surface deformation due to indenters with arbitrary symmetry of revolution. J. Phys. D 2004, 37, 2761–2772. [Google Scholar] [CrossRef]
- Schwarzer, N. Analysing nanoindenation unloading curves using Pharr’s concept of the effective indenter shape. Thin Solid Films 2006, 494, 168–172. [Google Scholar] [CrossRef]
- Richter, F.; Herrmann, M.; Molnar, F.; Chudoba, T.; Schwarzer, N.; Keunecke, M.; Bewilogua, K.; Xiang, X.W.; Boyen, H.-G.; Ziemann, P. On the evaluation of stresses in coated materials during nanoindentation with sharp indenters Substrate influence in Young’s modulus determination of thin films by indentation methods: Cubic boron nitride as an example. Surf. Coat. Technol. 2006, 201, 3577–3587. [Google Scholar] [CrossRef]
- Puschmann, R.; Schwarzer, N.; Richter, F.; Frühauf, S.; Schulz, S.E. An applicable concept for the indentation of thin porous films. In Proceedings of the NanoMech 5, Hückelhoven, Germany, 7–9 September 2004; pp. 1–6.
- FilmDoctor; Saxonian Institute of Surface Mechanics: Ummanz, Germany, 2010.
- Fischer-Cripps, A.C. A simple phenomenological approach to nanoindentation creep. Mater. Sci. Eng. A 2004, 385, 74–82. [Google Scholar] [CrossRef]
- François, D.; Pineau, A.; Zaoui, A. Mechanical Behaviour of Materials; Springer, Dordrecht, The Netherlands, 2012. [Google Scholar]
- ISO 20502:2005 Fine Ceramics (Advanced Ceramics, Advanced Technical Ceramics)—Determination of Adhesion of Ceramic Coatings by Scratch Testing; ISO: Geneva, Switzerland, 2005.
- ASTM C1624 Standard Test Method for Adhesion Strength and Mechanical Failure Modes of Ceramic Coatings by Quantitative Single Point SCRATCH Testing; ASTM International: West Conshohocken, PA, USA, 2010.
- O&PfC; Saxonian Institute of Surface Mechanics: Ummanz, Germany, 2010.
- ISA; Saxonian Institute of Surface Mechanics: Ummanz, Germany, 2010.
- SSA; Saxonian Institute of Surface Mechanics: Ummanz, Germany, 2010.
- TestOptimizer; Saxonian Institute of Surface Mechanics: Ummanz, Germany, 2013.
- Ehlert, J.; Batz, W.J. Der Einfluss von Druck und Temperatur auf die effektive Viskosität in geschmierten kontra-formen Kontakten. Rheol. Acta 1976, 15, 356–364. (In German) [Google Scholar] [CrossRef]
- Phillips, R.B. Crystals, Defects and Microstructures; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Schwarzer, N. Some basic equations for the next generation of surface testers solving the problem of pile-up, sink-in and making area-function-calibration obsolete. J. Mater. Res. 2009, 24, 1032–1036. [Google Scholar] [CrossRef]
- Schwarzer, N. Basic equations for the next generation of surface testers for the case of an elastic indenter and a layered samples. Saxionian Institute of Surface Mechanics. Available online: http://www.siomec.de/pub/2008/001 (accessed on 17 April 2014).
- Schwarzer, N. Intrinsic stresses—Their influence on the yield strength and their measurement via nanoindentation. Saxonian Institute of Surface Mechanics. Available online: http://www.siomec.de/pub/2007/001 (accessed on 17 April 2014).
- Schwarzer, N. Modelling of contact problems of rough surfaces. Saxonian Institute of Surface Mechanics. Available online: http://www.siomec.de/pub/2007/007 (accessed on 17 April 2014).
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Schwarzer, N. Analyse und Simulation der mechanischen Eigenschaften beschichteter Polymere unter Berücksichtigung der meist zeitabhängigen Materialparameter. In Proceedings of the V2011 Industrieausstellung & Workshop-Woche, Dresden, Germany, 17–20 October 2011; pp. 96–101. (In German)
- Kohl, J.G.; Randall, N.X.; Schwarzer, N.; Ngo, T.T.; Shockley, J.M.; Nair, R.P. An investigation of scratch testing of silicone elastomer coatings with a thickness gradient. J Appl. Polym. Sci. 2012, 124, 2978–2986. [Google Scholar] [CrossRef]
- Lucas, B.N.; Hay, J.L.; Oliver, W.C. Using multi-dimensional contact mechanics experiments to measure Poisson’s ratio of porous low-k films. J. Mater. Res. 2004, 19, 58–65. [Google Scholar] [CrossRef]
- Molnár, O. Investigations of Nanoindentation Data Obtained by the Combination of Normal and Mixed (Normal and Lateral) Forces. Ph.D. Thesis, Technical University of Chemnitz, Chemnitz, Germany, 2010. [Google Scholar]
- Karniychuk, M. Combination of Lateral and Normal Forces for Investigation of Mechanical Properties and Tribological Behaviour of Bulk and Coated Materials on the Micro-Scale. Ph.D. Thesis, Technical University of Chemnitz, Chemnitz, Germany, 2006. [Google Scholar]
- Chudoba, T.; Linss, V.; Karniychuk, M.; Richter, F. Lateral force–displacement measurements—A new technique for the investigation of mechanical surface properties. Surf. Coat. Technol. 2005, 200, 315–320. [Google Scholar] [CrossRef]
- Gies, A.; Schwarzer, N.; Becker, J.; Rudigier, H. Untersuchung der mechanischen Eigenschaften von DLC-Schichtsystemen mittels Nanoindentation und deren Modellierung; Tagungsband der ThGOT: Jena, Germany, 2010; pp. 104–109. (In German) [Google Scholar]
- Schwarzer, N. Coating design due to analytical modelling of mechanical contact problems on multilayer systems. In Proceedings of the International Conference on Metallurgical Coatings and Thin Films (ICMCTF), San Diego, CA, USA, 10–14 April 2000; pp. 397–402.
- Fabrikant, V.I. Several elliptical punches on an elastic half space. J. Appl. Mech. 1986, 53, 390–394. [Google Scholar] [CrossRef]
- Argatov, I.I. Asymptotic models of contact interaction among elliptic punches on a semiclassical foundation. Int. Appl. Mech. 2006, 42, 67–83. [Google Scholar] [CrossRef]
- Popov, G.I. Axisymmetric contact problem for an elastic inhomogeneous half-space in the presence of cohesion. Prikl. Math. I Mech. 1973, 37, 1109–1116. (In Russian) [Google Scholar]
- Fabrikant, V.I. Application of Potential Theory in Mechanics: A Selection of New Results; Kluver Academic Publishers: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Rostovtsev, N.A. On certain solutions of an integral equation of the theory of a linearly deformable foundation. Prikl. Math. I Mech. 1961, 25, 164–168. (In Russian) [Google Scholar]
- Schwarzer, N. Modelling of the mechanics of thin films using analytical linear elastic approaches. Available online: www.siomec.de/pub/ and http://archiv.tu-chemnitz.de/pub/2004/0077 (accessed on 17 April 2014).
- Schwarzer, N. Effect of lateral displacement on the surface stress distribution for cone and sphere contact. Phil. Mag. 2006, 86, 5231–5237. [Google Scholar] [CrossRef]
- Schwarzer, N.; Richter, F. On the determination of film stress from substrate bending: Stoney’s formula and its limits. Online Archive of the Technical University of Chemnitz, Chemnitz, Germany. Available online: http://archiv.tu-chemnitz.de/pub/2006/0011 (accessed on 17 Arpil 2014).
- Schwarzer, N. Endlessly touchable—the next generation of surface and coating optimization. Saxionian Institute of Surface Mechanics. Available online: http://www.siomec.de/pub/2013/001 (accessed on 17 April 2014).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Schwarzer, N. Completely Analytical Tools for the Next Generation of Surface and Coating Optimization. Coatings 2014, 4, 253-281. https://doi.org/10.3390/coatings4020253
Schwarzer N. Completely Analytical Tools for the Next Generation of Surface and Coating Optimization. Coatings. 2014; 4(2):253-281. https://doi.org/10.3390/coatings4020253
Chicago/Turabian StyleSchwarzer, Norbert. 2014. "Completely Analytical Tools for the Next Generation of Surface and Coating Optimization" Coatings 4, no. 2: 253-281. https://doi.org/10.3390/coatings4020253
APA StyleSchwarzer, N. (2014). Completely Analytical Tools for the Next Generation of Surface and Coating Optimization. Coatings, 4(2), 253-281. https://doi.org/10.3390/coatings4020253