The Electronic Structure and Optical Properties of CdGeAs2 Crystal: A DFT and HSE06 Study
Abstract
:1. Introduction
2. Theoretical Model and Calculation Method
2.1. Theoretical Model
2.2. Calculation Method
3. Results and Discussion
3.1. Geometric Optimization Results
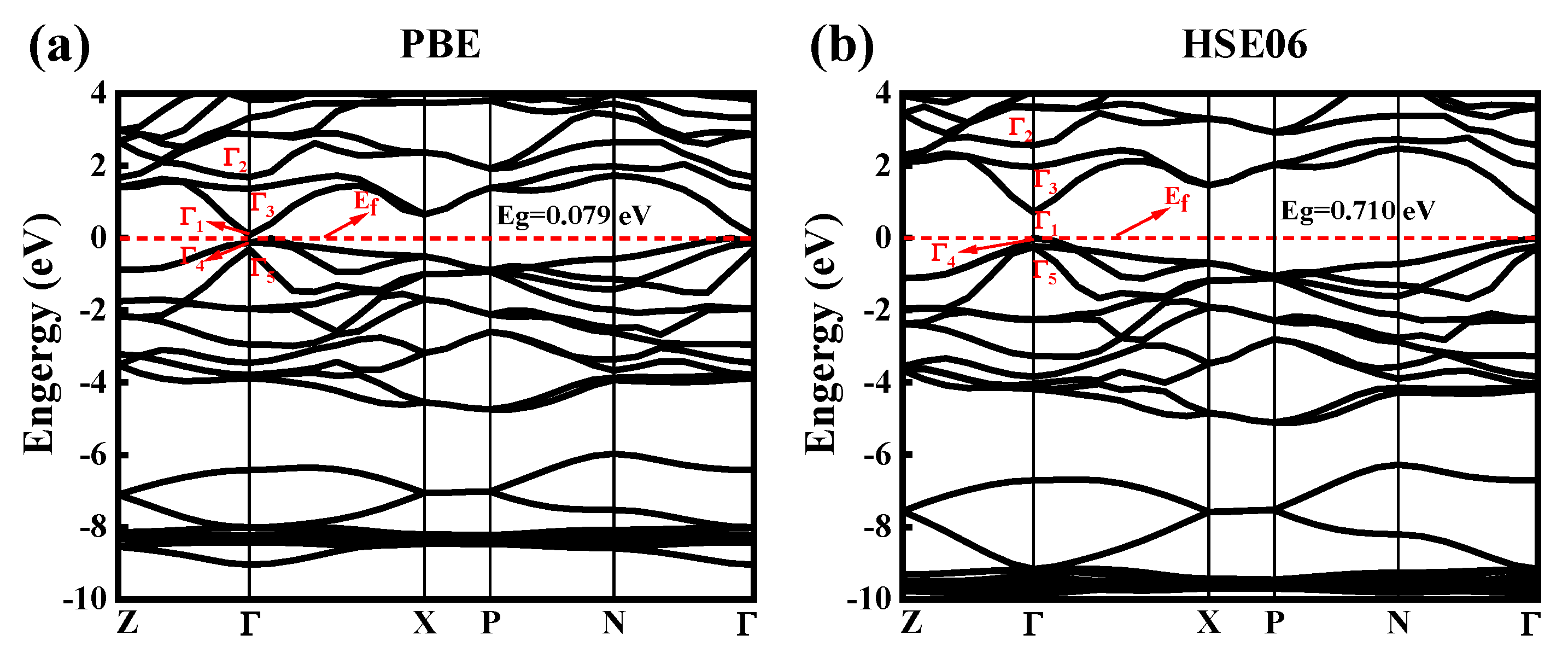
3.2. Electronic Structure
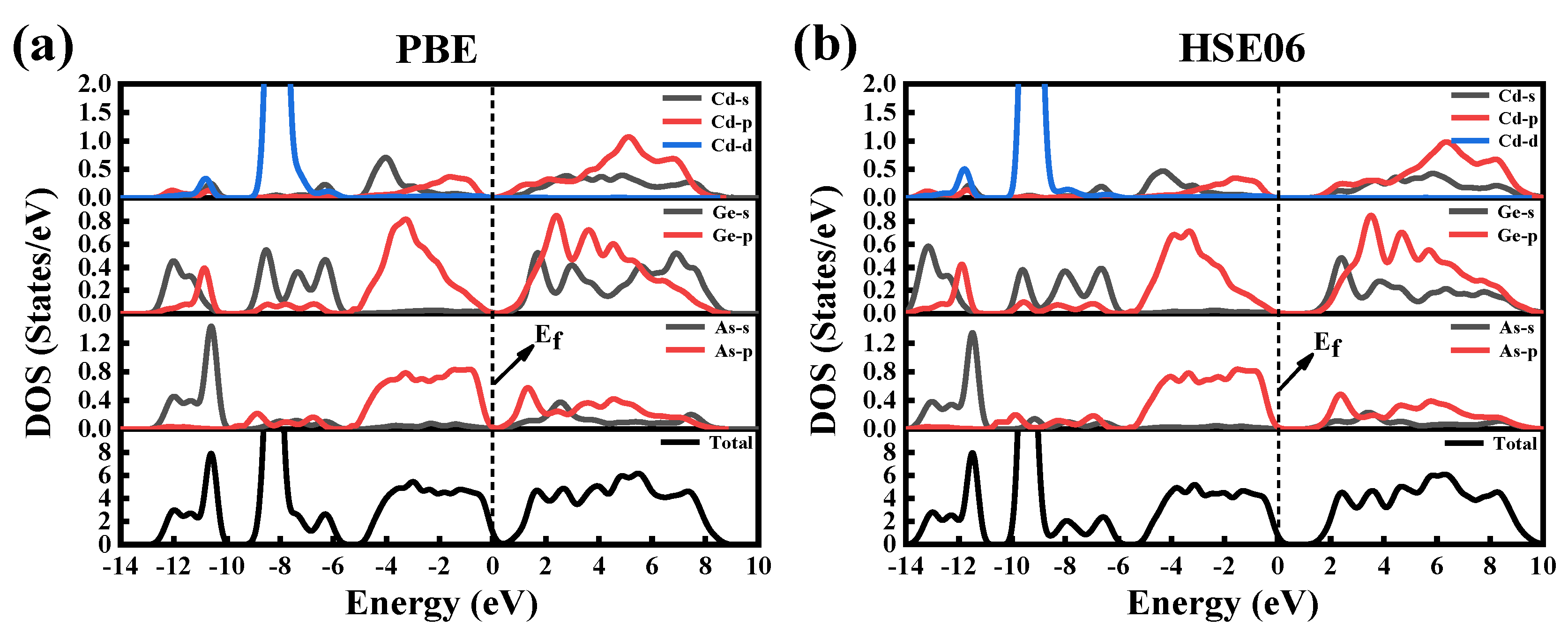
3.3. Mulliken Charge Population Analysis
3.4. The Differential Charge Density
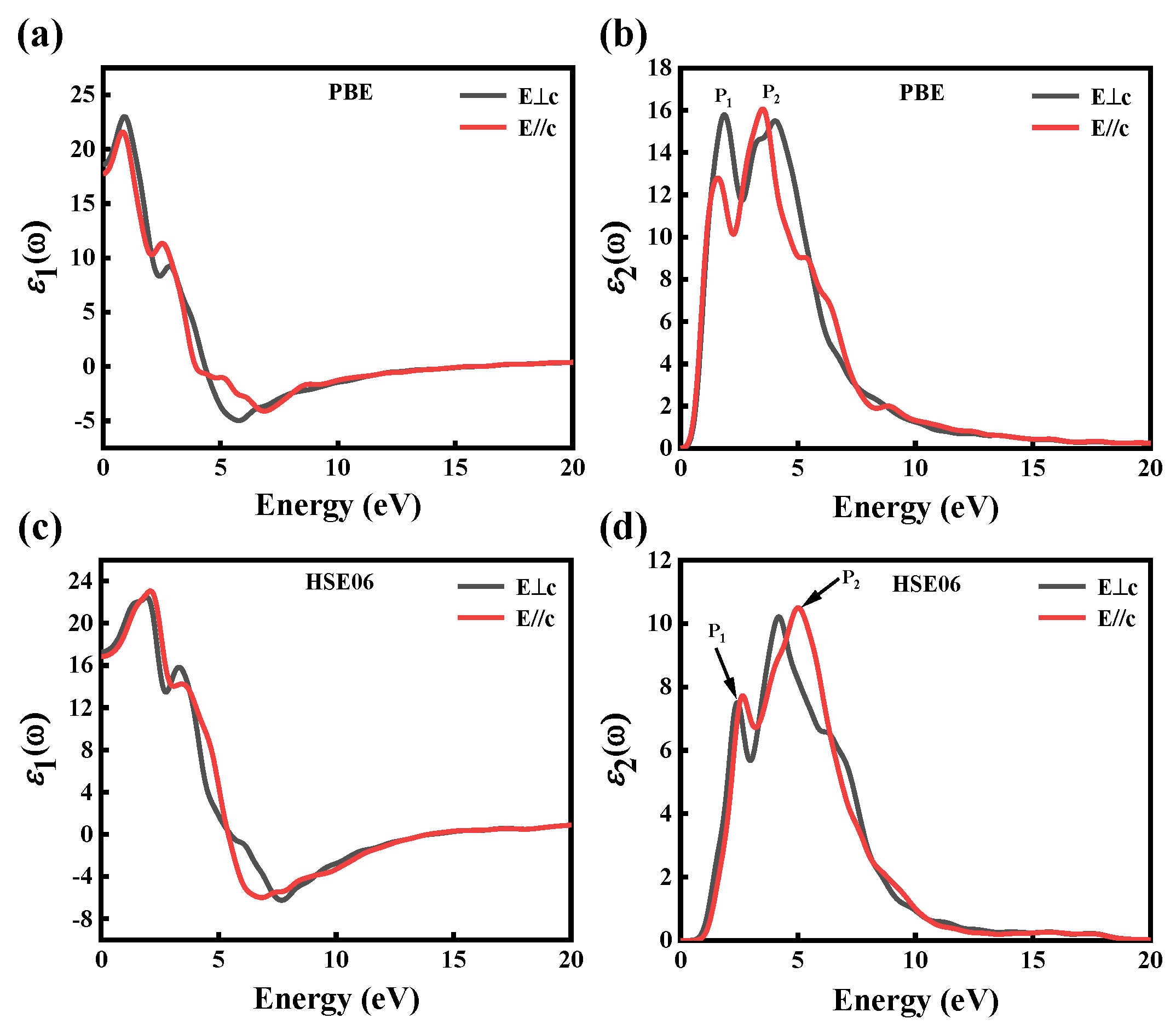
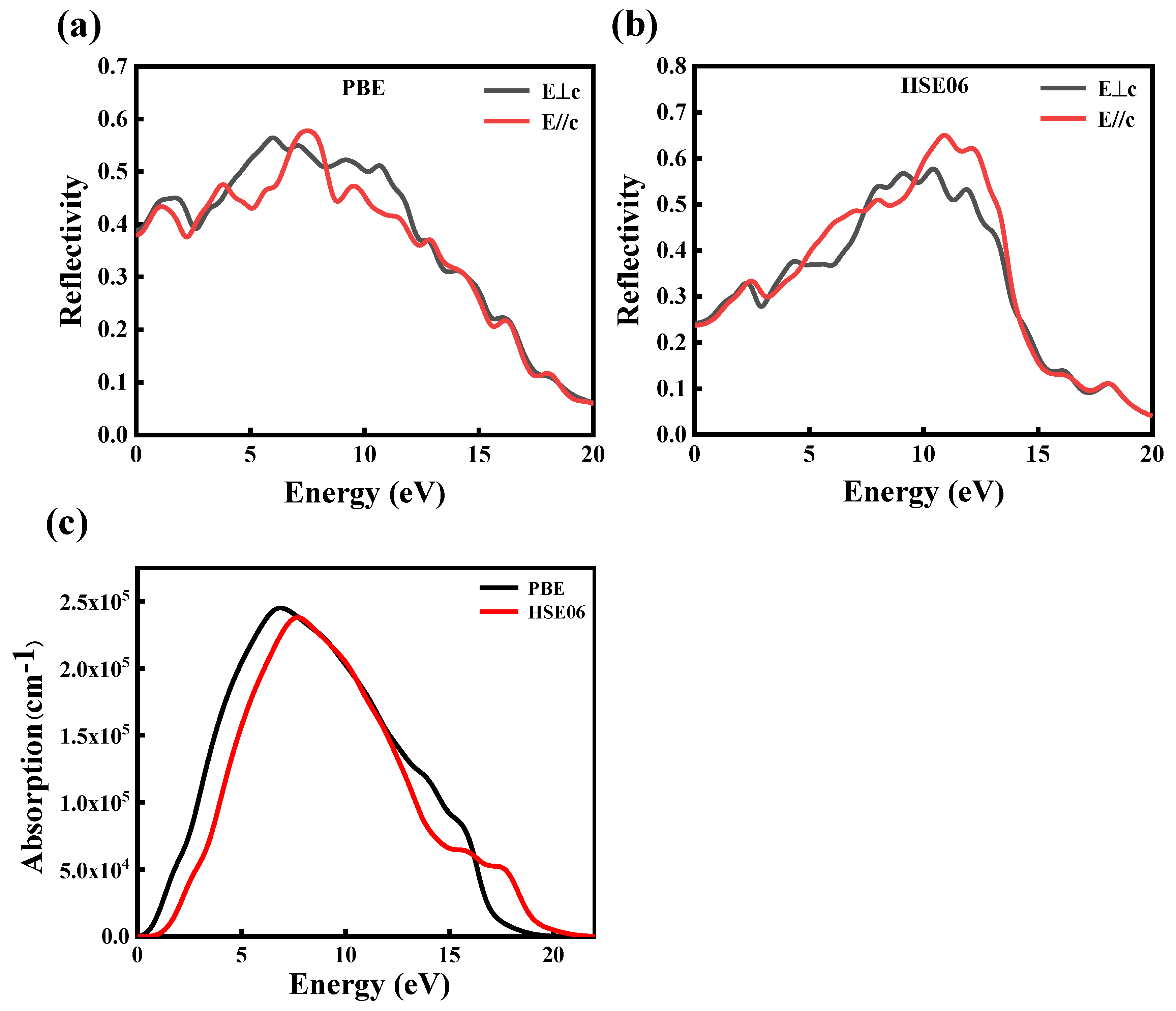
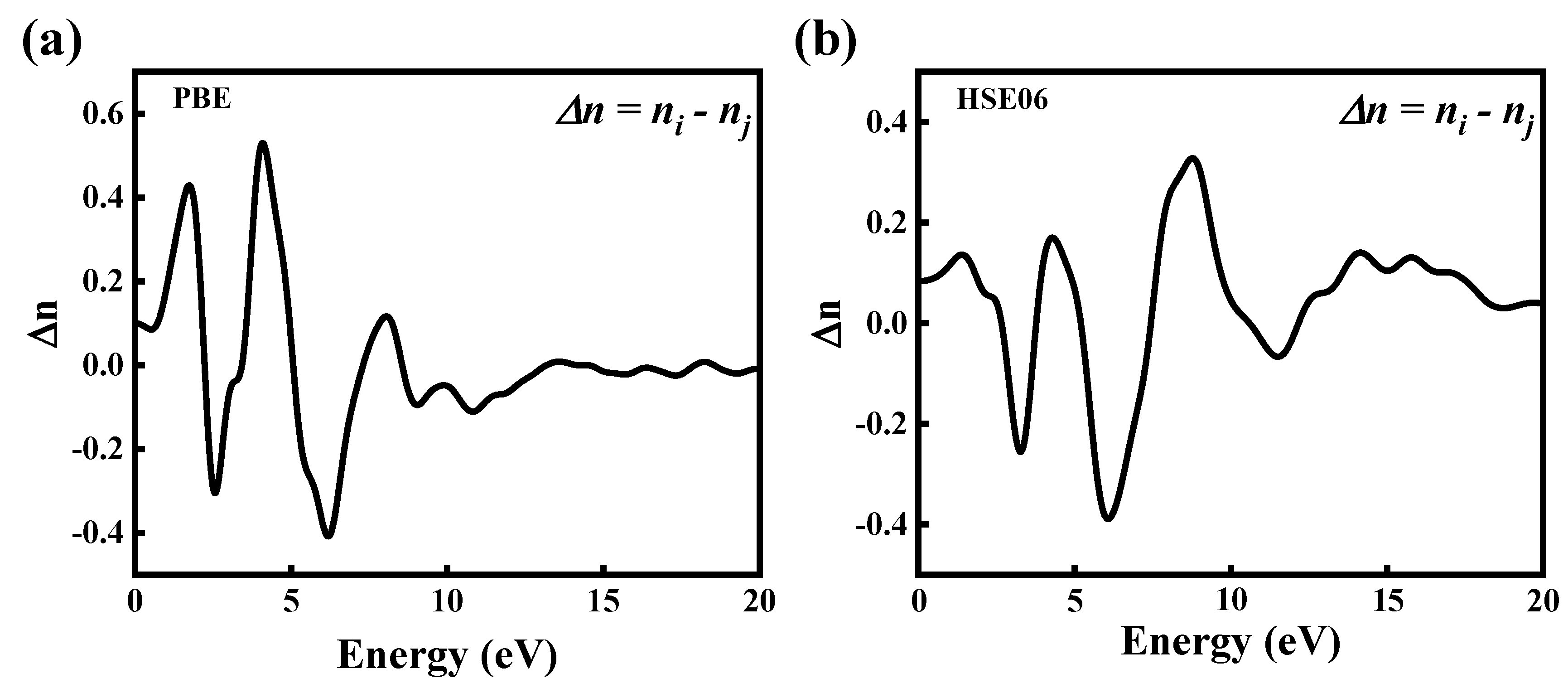
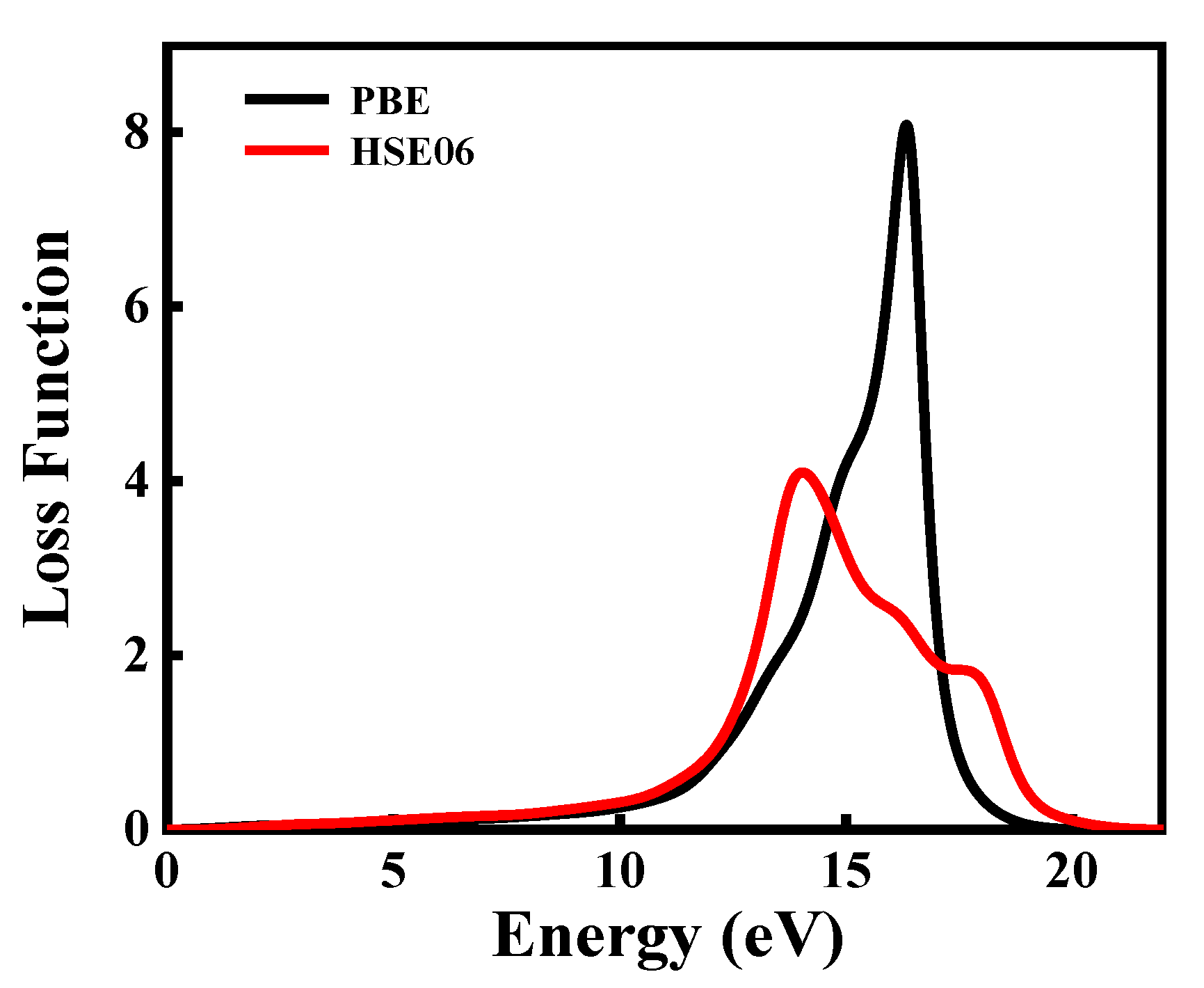
3.5. Optical Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, W.; Zhao, B.; Zhu, S.; He, Z.; Chen, B.; Yu, Y. Vibrational modes of chalcopyrite CdGeAs2 crystal. Mater. Res. Bull. 2016, 81, 107–113. [Google Scholar] [CrossRef]
- Huang, W.; Zhao, B.; Zhu, S.; He, Z.; Chen, B.; Zhen, Z.; Pu, Y. Correlation between dislocation etch pits, carrier concentration and optical absorption in CdGeAs2 grown by modified Vertical Bridgman method. J. Alloys Compd. 2016, 656, 818–824. [Google Scholar] [CrossRef]
- Pu, Y.; Zhu, S.; Zhao, B.; He, Z.; Chen, B.; Huang, W. Growth and characterization of Cr-doped CdGeAs2 crystal. J. Cryst. Growth 2017, 467, 150–154. [Google Scholar] [CrossRef]
- Li, J.; Zhu, S.; Zhao, B.; He, Z.; Chen, B. XPS Analysis and Determination of Surface Damage Layer of CdGeAs2 Single Crystal. Rare Met. Mater. Eng. 2015, 44, 844–847. [Google Scholar]
- Vodopyanova, K.L.; Knippels, G.M.H.; van der Meer, A.F.G.; Maffetonec, J.P.; Zwieback, I. Optical parametric generation in CGA crystal. Opt. Commun. 2002, 202, 205–208. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Zhao, B.; Zhu, S.; Gao, T.; Hou, H. Ab initio vibrational and dielectric properties of chalcopyrite CdGeAs2. Solid State Sci. 2011, 13, 422–426. [Google Scholar] [CrossRef]
- Mei, D.; Jiang, J.; Liang, F.; Zhang, S.; Wu, Y.; Sun, C.; Xue, D.; Lin, Z. Design and Synthesis of Nonlinear Optical Material with Wide Band Gap: From SrB4O7 to BaAl4S7. J. Mater. Chem. C 2018, 6, 2684–2689. [Google Scholar] [CrossRef]
- Lin, Z.; Jiang, X.; Kang, L.; Gong, P.; Luo, S.; Lee, M. First-principles materials applications and design of nonlinear optical crystals. J. Phys. D 2014, 47, 253001. [Google Scholar] [CrossRef] [Green Version]
- Bera, T.K.; Song, J.H.; Freeman, A.J.; Jang, J.I.; Ketterson, J.B.; Kanatzidis, M.G. Soluble Direct-Band-Gap Semiconductors LiAsS2 and NaAsS2: Large Electronic Structure Effects from Weak As···S Interactions and Strong Nonlinear Optical Response. Angew. Chem. Int. Ed. 2008, 47, 7828–7832. [Google Scholar] [CrossRef]
- Lei, Y.; Yu, M.; Li, J.; Wu, J.; Chen, B.; Yu, Y.; Huang, W.; He, Z. Synthesis, growth and mechanical properties of mid-infrared nonlinear optical crystal CdGeAs2. J. Cryst. Growth 2021, 562, 126060. [Google Scholar] [CrossRef]
- Bai, L.; Xu, C.; Nagashio, K.; Yang, C.; Feigelson, R.S.; Schunemann, P.G.; Giles, N.C. Photoluminescence of n-type CdGeAs2. J. Phys. Condens. Matter. 2005, 17, 5687–5696. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Zhao, B.; Zhu, S.; He, Z.; Chen, B.; Li, J.; Yu, Y.; Tang, J.; Liu, W. Effect of thermal annealing on the optical properties of CdGeAs2 wafers. J. Cryst. Growth 2013, 362, 291–295. [Google Scholar] [CrossRef]
- Bai, L.; Poston, J.A.; Schunemann, P.G.; Nagashio, K.; Feigelson, R.S.; Giles, N.C. Luminescence and optical absorption study of p-type CdGeAs2. J. Phys. Condens. Matter. 2004, 16, 1279–1286. [Google Scholar] [CrossRef]
- Blanco, M.A.; Costales, A.; Luaña, V.; Pandey, R. Theoretical study of the group-IV antisite acceptor defects in CdGeAs2. Appl. Phys. Lett. 2004, 85, 4376–4378. [Google Scholar] [CrossRef] [Green Version]
- Garces, N.Y.; Giles, N.C.; Halliburton, L.E.; Nagashio, K.; Feigelson, R.S.; Schunemann, P.G. Electron paramagnetic resonance of Cr2+ and Cr4+ ions in CdGeAs2 crystals. J. Appl. Phys. 2003, 94, 7567–7570. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, B.; Zhu, S.; Gao, T.; Hou, H.; He, Z. Ab initio study of the linear and nonlinear optical properties of chalcopyrite CdGeAs2. J Solid State Chem. 2012, 185, 264–270. [Google Scholar] [CrossRef]
- Ma, C.G.; Krasnenko, V.; Brik, M.G. Effects of composition on the properties of mixed CdSi1-xGexAs2 chalcopyrites as explored by the first-principles calculations. Mater. Des. 2017, 126, 250–258. [Google Scholar] [CrossRef]
- Yu, M.; Xiao, X.; Xiong, Z.; Li, J.; Liu, X.; Huang, W.; Chen, B.; He, Z. Structural, electronic and optical properties of CdGeAs2 with hybrid density functional (HSE06). Mater. Today Commun. 2022, 31, 103276. [Google Scholar] [CrossRef]
- Bai, L.; Schunemann, P.G.; Pollak, T.M.; Giles, N.C. Luminescence study of donors and acceptors in CdGeAs2. Opt. Mater. 2004, 26, 501–505. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef] [Green Version]
- Moussa, J.E.; Schultz, P.A.; Chelikowsky, J.R. Analysis of the Heyd-Scuseria-Ernzerhof density functional parameter space. J. Chem. Phys. 2012, 136, 204117. [Google Scholar] [CrossRef] [PubMed]
- Jaffe, J.E.; Zunger, A. Theory of the band-gap anomaly in ABC2 chalcopyrite semiconductors. Phys. Rev. B 1984, 29, 1882–1906. [Google Scholar] [CrossRef] [Green Version]
- Marenkin, S.F.; Novotortsev, V.M.; Palkina, K.K.; Mikhailov, S.G.; Kalinnikov, V.T. Preparation and structure of CdGeAs2 crystals. Inorg. Mater. 2004, 40, 135–137. [Google Scholar] [CrossRef]
- Hafner, J. Ab-Initio Simulations of Materials Using VASP: Density-Functional Theory and Beyond. J Comput Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
- Tomas, B.; Jurgen, H.; Sebastien, L.; Janos, G.A. Improved Description of the Structure of Molecular and Layered Crystals: Ab Initio DFT Calculations with van der Waals Corrections. J. Phys. Chem. A 2010, 114, 11814–11824. [Google Scholar]
- Abrahams, S.C.; Bernstein, J.L. Piezoelectric nonlinear optic CuGaSe2 and CdGeAs2: Crystal structure, chalcopyrite microhardness, and sublattice distortion. J. Chem. Phys. 1974, 61, 1140–1146. [Google Scholar] [CrossRef]
- Isomura, S.; Takahashi, S.; Masumoto, K. Electrical and optical properties of CdGeAs2. J. Appl. Phys. 1977, 16, 1723. [Google Scholar] [CrossRef]
- Limpijumnong, S.; Lambrecht, W.R.L. Band structure of CdGeAs2 near the fundamental gap. Phys. Rev. B. 2002, 65, 165204. [Google Scholar] [CrossRef]
- El Moctar, C.O.; Kambas, K.; Marsillac, S.; Anagnostopoulos, A.; Bernede, J.C.; Benchouck, K. Optical properties of CuAlX2 (X=Se, Te) thin films obtained by annealing of copper, aluminum and chalcogen layers sequentially deposited. Thin Solid Film. 2000, 371, 195–200. [Google Scholar] [CrossRef]
- Polygalov, Y.I.; Poplavnoi, A.S. Energy band sturcture of CdSnAs2 and CdGeAs2. Russ. Phys. J. 1981, 24, 1139–1142. [Google Scholar]
- Tauc, J. Optical properties and electronic structure of amorphous Ge and Si. Mat. Res. Bull. 1968, 3, 37–46. [Google Scholar] [CrossRef]
- Pandey, R.; Ohmer, M.; Gale, J. A theoretical study of native acceptors in CdGeAs2. J. Phys. Condens. Matter 1998, 10, 5525–5533. [Google Scholar] [CrossRef]
- Kang, L.; Zhou, M.; Yao, J.; Lin, Z.; Wu, Y.; Chen, C. Metal Thiophosphates with Good Mid-Infrared Nonlinear Optical Performances: A First-Principles Prediction and Analysis. J. Am. Chem. Soc. 2015, 137, 13049–13059. [Google Scholar] [CrossRef] [PubMed]
- Boyd, G.; Buehler, E.; Storz, F.; Wernick, J. Linear and nonlinear optical properties of ternary AIIBIVC2V chalcopyrite semiconductors. IEEE J. Quantum Electron. 1972, 8, 419–426. [Google Scholar] [CrossRef]

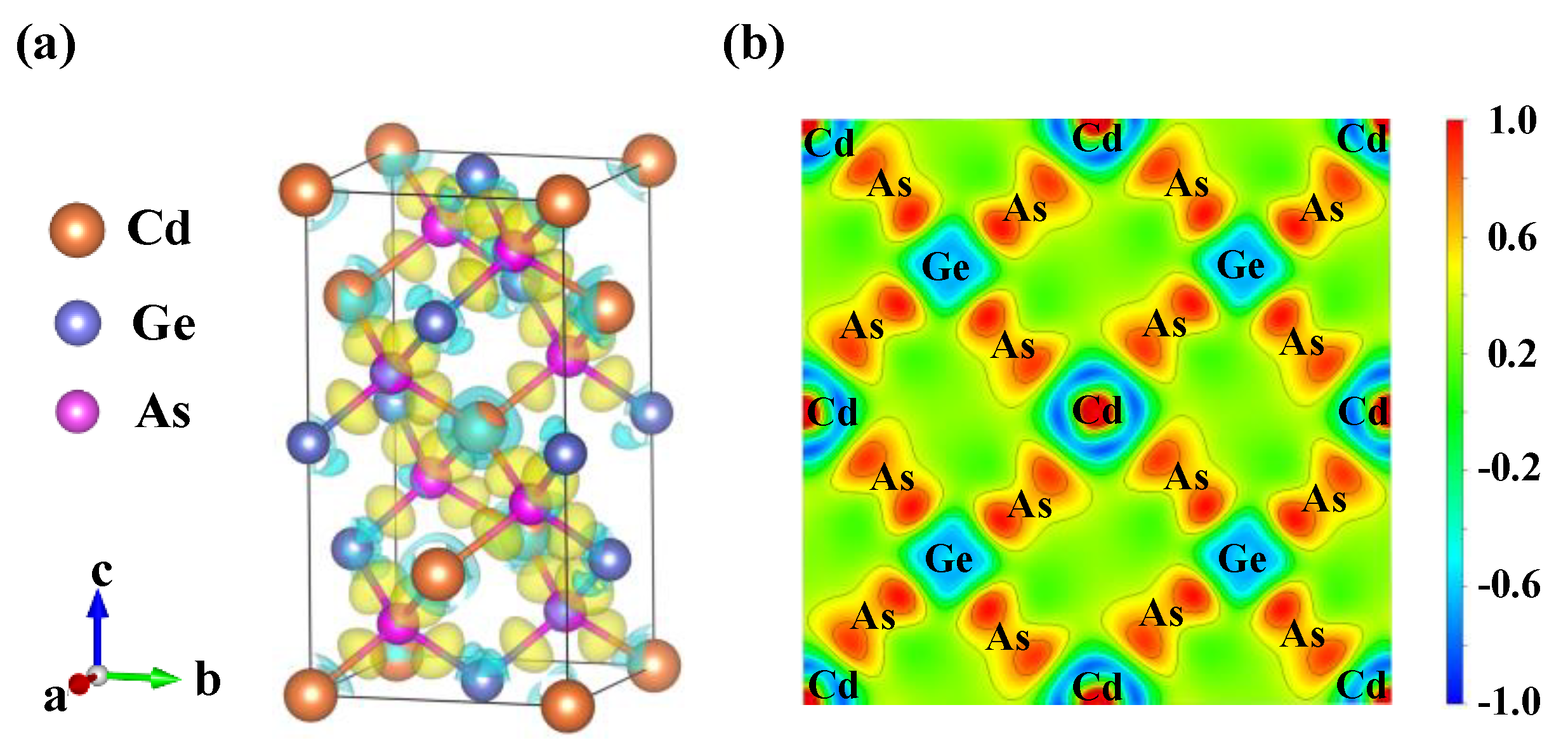

| Parameter | This Work | Experimental Value [26] | Relative Error |
|---|---|---|---|
| a = b/Å | 6.041 | 5.94 | 1.7% |
| c/Å | 11.407 | 11.22 | 1.7% |
| u | 0.278 | 0.279 | 0.4% |
| α = β = γ (°) | 90 | - | - |
| Method | Parameter | Z | Γ | X | P | N |
|---|---|---|---|---|---|---|
| GGA–PBE | EV (eV) | 1.400 | 0.079 | 0.650 | 1.390 | 1.730 |
| EC (eV) | −0.875 | 0 | −0.509 | −0.891 | −0.580 | |
| HSE06 | EV (eV) | 2.120 | 0.710 | 1.450 | 2.040 | 2.480 |
| EC (eV) | −1.110 | 0 | −0.686 | −1.050 | −0.730 |
| Method | This Work (eV) | Experimental Value (eV) [18,27] | Mean Relative Error |
|---|---|---|---|
| PBE | 0.079 | 0.67 or 0.53 | 86.65 % |
| HSE06 | 0.710 | 0.67 or 0.53 | 19.97% |
| Methods | Atom | s | p | d | Total | Charge | Bond | Length (Å) | Population |
|---|---|---|---|---|---|---|---|---|---|
| PBE | Cd | 0.95 | 1.08 | 9.97 | 12.00 | −0.00 | Cd–As | 2.47100 | 0.27 |
| Ge | 1.17 | 2.36 | 0 | 3.53 | 0.47 | Ge–As | 2.67279 | 0.04 | |
| As | 1.67 | 3.56 | 0 | 5.23 | −0.23 | - | - | - | |
| HSE06 | Cd | 0.78 | 1.06 | 9.97 | 11.81 | 0.19 | Cd–As | 2.46677 | 0.67 |
| Ge | 1.53 | 2.34 | 0 | 3.87 | 0.13 | Ge–As | 2.68291 | 0.26 | |
| As | 1.43 | 3.73 | 0 | 5.16 | −0.16 | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, S.; Ning, J.; Zhang, B.; Wu, Q.; Zhang, F.; Zhang, W. The Electronic Structure and Optical Properties of CdGeAs2 Crystal: A DFT and HSE06 Study. Coatings 2022, 12, 1778. https://doi.org/10.3390/coatings12111778
Xue S, Ning J, Zhang B, Wu Q, Zhang F, Zhang W. The Electronic Structure and Optical Properties of CdGeAs2 Crystal: A DFT and HSE06 Study. Coatings. 2022; 12(11):1778. https://doi.org/10.3390/coatings12111778
Chicago/Turabian StyleXue, Suqin, Jing Ning, Bohang Zhang, Qiao Wu, Fuchun Zhang, and Weibin Zhang. 2022. "The Electronic Structure and Optical Properties of CdGeAs2 Crystal: A DFT and HSE06 Study" Coatings 12, no. 11: 1778. https://doi.org/10.3390/coatings12111778






