Complex Dynamics of Photoinduced Mass Transport and Surface Relief Gratings Formation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Polymer Chains Functionalized with Azo-Dyes: Bond Fluctuation Model
2.2. Monte Carlo Simulations of Functionalized BFM Chains
2.3. Characterization of the Displacement of the Chain
3. Results
3.1. Anomalous Dynamics: Bulk
3.2. Anomalous Dynamics: Single Chains
3.2.1. Homogeneous Illumination
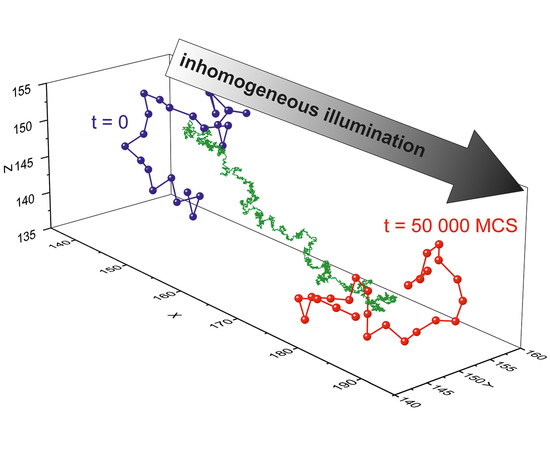
3.2.2. Inhomogeneous Illumination
3.2.3. Role of Chain’s Length
3.3. Continuous Time Random Walk Model for Inscription of Surface Relief Grating
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sekkat, Z.; Knoll, W. (Eds.) Photoreactive Organic Thin Films; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Kim, D.Y.; Tripathy, S.K.; Li, L.; Kumar, J. Laser-induced holographic surface relief gratings on nonlinear optical polymer films. Appl. Phys. Lett. 1995, 66, 1166–1168. [Google Scholar] [CrossRef]
- Rochon, P.; Batalla, E.; Natansohn, A. Optically induced surface gratings on azoaromatic polymer films. Appl. Phys. Lett. 1995, 66, 136–138. [Google Scholar] [CrossRef]
- Lee, S.; Kang, H.S.; Park, J.-K. Directional photofluidization lithography: Micro/ nanostructural evolution by photofluidic motions of azobenzene materials. Adv. Mater. 2012, 24, 2069–2103. [Google Scholar] [CrossRef] [PubMed]
- Mahimwalla, Z.; Yager, K.G.; Mamiya, J.; Shishido, A.; Priimagi, A.; Barrett, C.J. Azobenzene photomechanics: Prospects and potential applications. Polym. Bull. 2012, 69, 967–1006. [Google Scholar] [CrossRef]
- Pedersen, T.G.; Johansen, P.M.; Holme, N.C.R.; Ramanujam, P.S.; Hvilosted, S. Mean-field theory of photoinduced formation of surface reliefs in side-chain azobenzene polymers. Phys. Rev. Lett. 1998, 80, 89–92. [Google Scholar] [CrossRef]
- Barrett, C.J.; Natansohn, A.L.; Rochon, P.L. Mechanism of optically inscribed high-efficiency diffraction gratings in azo polymer films. J. Phys. Chem. 1996, 100, 8836–8842. [Google Scholar] [CrossRef]
- Barrett, C.J.; Rochon, P.L.; Natansohn, A.L. Model of laser-driven mass transport in thin films of dye-functionalized polymers. J. Chem. Phys. 1998, 109, 1505–1516. [Google Scholar] [CrossRef]
- Yager, K.G.; Barrett, C.J. Photomechanical surface patterning in azo-polymer materials. Macromolecules 2006, 39, 9320–9326. [Google Scholar] [CrossRef]
- Henneberg, O.; Geue, T.; Saphiannikova, M.; Pietsch, U.; Rochon, P.; Natansohn, A. Formation and dynamics of polymer surface relief gratings. Appl. Surf. Sci. 2001, 182, 272–279. [Google Scholar] [CrossRef]
- Lefin, P.; Fiorini, C.; Nunzi, J.M. Anisotropy of the photoinduced translation diffusion of azo-dyes. Opt. Mater. 1998, 9, 323–328. [Google Scholar] [CrossRef]
- Kumar, J.; Li, L.; Jiang, X.L.; Kim, D.-Y.; Lee, T.S.; Tripathy, S. Gradient force: The mechanism for surface relief grating formation in azobenzene functionalized polymers. Appl. Phys. Lett. 1998, 72, 2096–2098. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.; Bjorkholm, J.E.; Chu, J.E. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef] [PubMed]
- Sumaru, K.; Yamanaka, T.; Fukuda, T.; Matsuda, H. Photoinduced surface relief gratings on azopolymer films: Analysis by a fluid mechanics model. Appl. Phys. Lett. 1999, 75, 1878–1880. [Google Scholar] [CrossRef] [Green Version]
- Sumaru, K.; Fukuda, T.; Kimura, T.; Matsuda, H.; Yamanaka, T. Photoinduced surface relief formation on azopolymer films: A driving force and formed relief profile. J. Appl. Phys. 2002, 91, 3421–3424. [Google Scholar] [CrossRef]
- Bellini, B.; Ackermann, J.; Klein, H.; Grave, C.; Dumas, P.; Safarov, V. Light-induced molecular motion of azobenzene-containing molecules: A random-walk model. J. Phys. Condens. Matter 2006, 18, 1817–1835. [Google Scholar] [CrossRef]
- Juan, M.L.; Plain, J.; Bachelot, R.; Royer, P.; Gray, S.K.; Wiederrecht, G.P. Multiscale model for photoinduced molecular motion in azo polymers. ACS Nano 2009, 3, 1573–1579. [Google Scholar] [CrossRef] [PubMed]
- Juan, M.L.; Plain, J.; Bachelot, R.; Royer, P.; Gray, S.K.; Wiederrecht, G.P. Stochastic model for photoinduced surface relief grating formation through molecular transport in polymer films. Appl. Phys. Lett. 2008, 93, 153304. [Google Scholar] [CrossRef]
- Plain, J.; Wiederrecht, G.P.; Gray, S.K.; Royer, P.; Bachelot, R. Multiscale optical imaging of complex fields based on the use of azobenzene nanomotors. J. Phys. Chem. Lett. 2013, 4, 2124–2132. [Google Scholar] [CrossRef]
- Karageorgiev, P.; Neher, D.; Schulz, B.; Stiller, B.; Pietsch, U.; Giersig, M.; Brehmer, L. From anisotropic photo-fluidity towards nanomanipulation in the optical near-field. Nat. Mater. 2005, 4, 699–703. [Google Scholar] [CrossRef] [PubMed]
- Mechau, N.; Saphiannikova, M.; Neher, D. Dielectric and mechanical properties of azobenzene polymer layers under visible and ultraviolet irradiation. Macromolecules 2005, 38, 3894–3902. [Google Scholar] [CrossRef]
- Mechau, N.; Saphiannikova, M.; Neher, D. Molecular tracer diffusion in thin azobenzene polymer layers. Appl. Phys. Lett. 2006, 89, 251902. [Google Scholar] [CrossRef]
- Srikhirin, T.; Laschitsch, A.; Neher, D.; Johannsmann, D. Light-induced softening of azobenzene dye-doped polymer films probed with quartz crystal resonators. Appl. Phys. Lett. 2000, 77, 963–965. [Google Scholar] [CrossRef]
- Fang, G.J.; Maclennan, J.E.; Yi, Y.; Glaser, M.A.; Farrow, M.; Korblova, E.; Walba, D.M.; Furtak, T.E.; Clark, N.A. Athermal photofluidization of glasses. Nat. Commun. 2013, 4, 1521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hurduc, N.; Donose, B.C.; Macovei, A.; Paius, C.; Ibanescu, C.; Scutaru, D.; Hamel, M.; Branza-Nichita, N.; Rocha, L. Direct observation of athermal photofluidisation in azopolymer films. Soft Matter 2014, 10, 4640–4647. [Google Scholar] [CrossRef] [PubMed]
- Saphiannikova, M.; Toshchevikov, V. Optical deformations of azobenzene polymers: Orientation approach vs. photofluidization concept. J. Soc. Inf. Disp. 2015, 23, 146–153. [Google Scholar] [CrossRef]
- Toshchevikov, V.; Saphiannikova, M.; Heinrich, G. Microscopic Theory of Light-Induced Deformation in Amorphous Side-Chain Azobenzene Polymers. J. Phys. Chem. B 2009, 113, 5032–5045. [Google Scholar] [CrossRef] [PubMed]
- Toshchevikov, V.; Saphiannikova, M.; Heinrich, G. Light-Induced Deformation of Azobenzene Elastomers: A Regular Cubic Network Model. J. Phys. Chem. B 2012, 116, 913–924. [Google Scholar] [CrossRef] [PubMed]
- Toshchevikov, V.; Saphiannikova, M.; Heinrich, G. Theory of Light-Induced Deformation of Azobenzene Elastomers: Influence of Network Structure. J. Chem. Phys. 2012, 137, 024903. [Google Scholar] [CrossRef] [PubMed]
- Toshchevikov, V.; Saphiannikova, M. Theory of Light-Induced Deformation of Azobenzene Elastomers: Effects of the Liquid- Crystalline Interactions and Biaxiality. J. Phys. Chem. B 2014, 118, 12297–12309. [Google Scholar] [CrossRef] [PubMed]
- Petrova, T.; Toshchevikov, V.; Saphiannikova, M. Light-Induced Deformation of Polymer Networks Containing Azobenzene Chromophores and Liquid Crystalline Mesogens. Soft Matter 2015, 11, 3412–3423. [Google Scholar] [CrossRef] [PubMed]
- Ilnytskyi, J.M.; Neher, D.; Saphiannikova, M. Opposite Photo- Induced Deformations in Azobenzene-Containing Polymers with Different Molecular Architecture: Molecular Dynamics Study. J. Chem. Phys. 2011, 135, 044901. [Google Scholar] [CrossRef] [PubMed]
- Ilnytskyi, J.M.; Saphiannikova, M.; Neher, D.; Allen, M.P. Computer Simulation of Side-Chain Liquid Crystal Polymer Melts and Elastomers. In Liquid Crystalline Polymers; Springer: Cham, Switzerland, 2016; Volume 1, pp. 93–129. [Google Scholar]
- Toshchevikov, V.; Petrova, T.; Saphiannikova, M. Kinetics of light-induced ordering and deformation in LC azobenzene-containing materials. Soft Matter 2017, 13, 2823–2835. [Google Scholar] [CrossRef] [PubMed]
- Yadavalli, N.S.; Linde, F.; Kopyshev, A.; Santer, S. Soft matter beats hard matter: Rupturing of thin metallic films induced by mass transport in photosensitive polymer films. ACS Appl. Mater. Interfaces 2013, 5, 7743–7747. [Google Scholar] [CrossRef] [PubMed]
- Di Florio, G.; Brundermann, E.; Yadavalli, N.S.; Santer, S.; Havenith, M. Graphene multilayer as nanosized optical strain gauge for polymer surface relief gratings. Nano Lett. 2014, 14, 5754–5760. [Google Scholar] [CrossRef] [PubMed]
- Toshchevikov, V.; Ilnytskyi, J.; Saphiannikova, M. Photoisomerization kinetics and mechanical stress in azobenzene-containing materials. J. Phys. Chem. Lett. 2017, 8, 1094–1098. [Google Scholar] [CrossRef] [PubMed]
- Pawlik, G.; Miniewicz, A.; Sobolewska, A.; Mitus, A.C. Generic stochastic Monte Carlo model of the photoinduced mass transport in azo-polymers and fine structure of Surface Relief Gratings. Europhys. Lett. 2014, 105, 26002. [Google Scholar] [CrossRef]
- Deutsch, H.P.; Binder, K. Interdiffusion and self-diffusion in polymer mixtures: A Monte Carlo study. J. Chem. Phys. 1991, 94, 2294–2304. [Google Scholar] [CrossRef]
- Schab-Balcerzak, E.; Siwy, M.; Kawalec, M.; Sobolewska, A.; Chamera, A.; Miniewicz, A. Synthesis, characterization, and study of photoinduced optical anisotropy in polyimides containing side azobenzene units. J. Phys. Chem. A 2009, 113, 8765–8780. [Google Scholar] [CrossRef] [PubMed]
- Fabbri, F.; Garrot, D.; Lahlil, K.; Boilot, J.P.; Lassailly, Y.; Peretti, J. Evidence of two distinct mechanisms driving photoinduced matter motion in thin films containing azobenzene derivatives. J. Phys. Chem. B 2011, 115, 1363–1367. [Google Scholar] [CrossRef] [PubMed]
- Carmesin, I.; Kremer, K. The bond fluctuation method: A new effective algorithm for the dynamics of polymers in all spatial dimensions. Macromolecules 1988, 21, 2819–2823. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Kawakatsu, T. Statistical Physics of Polymers. An Introduction; Springer: Berlin, Germany, 2004. [Google Scholar]
- Paul, W.; Binder, K.; Heermann, D.W.; Kremer, K. Dynamics of polymer solutions and melts. Reptation predictions and scaling of relaxation times. J. Chem. Phys. 1991, 95, 7726–7740. [Google Scholar] [CrossRef]
- Jentzsch, C.; Dockhorn, R.; Sommer, J.-U. A Highly Parallelizable Bond Fluctuation Model on the Body-Centered Cubic Lattice. In Parallel Processing and Applied Mathematics; Springer: Cham, Switzerland, 2016; Volume 9574, pp. 301–311. [Google Scholar]
- Lai, P.Y.; Binder, K. Structure and dynamics of grafted polymer layers: A Monte Carlo simulation. J. Chem. Phys. 1991, 95, 9288–9299. [Google Scholar] [CrossRef]
- Lai, P.Y.; Halperin, A. Polymer brush at high coverage. Macromolecules 1991, 24, 4981–4982. [Google Scholar] [CrossRef]
- Lai, P.Y.; Zhulin, E.Z. Monte Carlo test of the self-consistent field theory of a polymer brush. J. Phys. II 1992, 2, 547–560. [Google Scholar] [CrossRef]
- Wang, J.S.; Binder, K. Wetting transitions in polymer blends: A Monte Carlo lattice simulation. J. Chem. Phys. 1991, 94, 8537–8541. [Google Scholar] [CrossRef]
- Wang, J.S.; Binder, K. Chain linear dimensions in the surface-enriched layer of polymer mixtures. Makromol. Chem. Theory Simul. 1992, 1, 49–53. [Google Scholar] [CrossRef]
- Wang, J.S.; Binder, K. Enrichment of the chain ends in polymer melts at interfaces. J. Phys. I 1991, 1, 1583–1590. [Google Scholar] [CrossRef]
- Wittmann, H.-P.; Kremer, K.; Binder, K. Glass transition of polymer melts: A twodimensional Monte Carlo study in the framework of the bond uctuation method. J. Chem. Phys. 1992, 96, 6291–6306. [Google Scholar] [CrossRef]
- Wittmer, J.P.; Cavallo, A.; Kreer, T.; Baschnagel, J.; Johner, A. A finite excluded volume bond-fluctuation model: Static properties of dense polymer melts revisited. J. Chem. Phys. 2009, 131, 064901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baschnagel, J.; Wittmer, J.P.; Meyer, H. Computational Soft Matter: From Synthetic Polymers to Proteins; Attig, N., Ed.; NIC Series; NIC-Directors: Juelich, Germany, 2004; Volume 23, pp. 83–140. [Google Scholar]
- Mueller, M. Handbook of Materials Modeling; Yip, S., Ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Pawlik, G.; Mitus, A.C.; Mysliwiec, J.; Miniewicz, A.; Grote, J.G. Photochromic dye semi-intercalation into DNA-based polymeric matrix: Computer modeling and experiment. Chem. Phys. Lett. 2010, 484, 321–323. [Google Scholar] [CrossRef]
- Pawlik, G.; Radosz, W.; Mitus, A.C.; Mysliwiec, J.; Miniewicz, A.; Kajzar, F.; Rau, I. Holographic grating inscription in DR1: DNA-CTMA thin films: The puzzle of time scales. Cent. Eur. J. Chem. 2014, 12, 886–892. [Google Scholar] [CrossRef]
- Pawlik, G.; Mitus, A.C.; Miniewicz, A.; Kajzar, F. Monte Carlo simulations of temperature dependence of the kinetics of diffraction gratings formation in a polymer matrix containing azobenzene chromophores. J. Nonlinear Opt. Phys. Mater. 2004, 13, 481–489. [Google Scholar] [CrossRef]
- Pawlik, G.; Mitus, A.C.; Miniewicz, A.; Sobolewska, A.; Kajzar, F. Temperature dependence of the kinetics of diffraction gratings formation in a polymer matrix containing azobenzene chromophores: Monte Carlo simulations and experiment. Mol. Cryst. Liq. Cryst. 2005, 426, 243–252. [Google Scholar] [CrossRef]
- Pawlik, G.; Orlik, R.; Radosz, W.; Mitus, A.C.; Kuzyk, M.G. Towards understanding the photomechanical effect in polymeric fibers: Analysis of free volume in a model polymeric matrix. Proc. SPIE 2012, 8474, 84740A. [Google Scholar]
- Pawlik, G.; Rau, I.; Kajzar, F.; Mitus, A.C. Second-harmonic generation in poled polymers: Pre-poling history paradigm. Opt. Express 2010, 18, 18793–18804. [Google Scholar] [CrossRef] [PubMed]
- Radosz, W.; Pawlik, G.; Mitus, A.C. Complex Dynamics of Photo-Switchable Guest Molecules in All-Optical Poling Close to the Glass Transition: Kinetic Monte Carlo Modeling. J. Phys. Chem. B 2018, 122, 1756–1765. [Google Scholar] [CrossRef] [PubMed]
- Landau, D.P.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Binder, K. (Ed.) Monte Carlo and Molecular Dynamics Simulations in Polymer Science; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Pawlik, G.; Mitus, A.C.; Miniewicz, A.; Kajzar, F. Kinetics of diffraction gratings formation in a polymer matrix containing azobenzene chromophores: Experiments and Monte Carlo simulations. J. Chem. Phys. 2003, 119, 6789–6801. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Fulger, D.; Scalas, E.; Germano, G. Monte Carlo simulation of uncoupled continuous-time random walks yielding a stochastic solution of the space-time fractional diffusion equation. Phys. Rev. E 2008, 77, 021122. [Google Scholar] [CrossRef] [PubMed]
- Abid, J.-P.; Frigoli, M.; Pansu, R.; Szeftel, J.; Zyss, J.; Larpent, C.; Brasselet, S. Light-driven directed motion of azobenzene-coated polymer nanoparticles in an aqueous medium. Langmuir 2011, 27, 7967–7971. [Google Scholar] [CrossRef] [PubMed]
- Wysoczanski, T.; Mitus, A.C.; Radosz, W.; Pawlik, G. Photoinduced (anomalous) dynamics of functionalized polymer chains: Applications for Surface Relief Grating modelling. Proc. SPIE 2017, 10101, 101010W. [Google Scholar]













© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawlik, G.; Wysoczanski, T.; Mitus, A.C. Complex Dynamics of Photoinduced Mass Transport and Surface Relief Gratings Formation. Nanomaterials 2019, 9, 352. https://doi.org/10.3390/nano9030352
Pawlik G, Wysoczanski T, Mitus AC. Complex Dynamics of Photoinduced Mass Transport and Surface Relief Gratings Formation. Nanomaterials. 2019; 9(3):352. https://doi.org/10.3390/nano9030352
Chicago/Turabian StylePawlik, Grzegorz, Tomasz Wysoczanski, and Antoni C. Mitus. 2019. "Complex Dynamics of Photoinduced Mass Transport and Surface Relief Gratings Formation" Nanomaterials 9, no. 3: 352. https://doi.org/10.3390/nano9030352