Vibration and Buckling of Shear Deformable Functionally Graded Nanoporous Metal Foam Nanoshells
Abstract
:1. Introduction
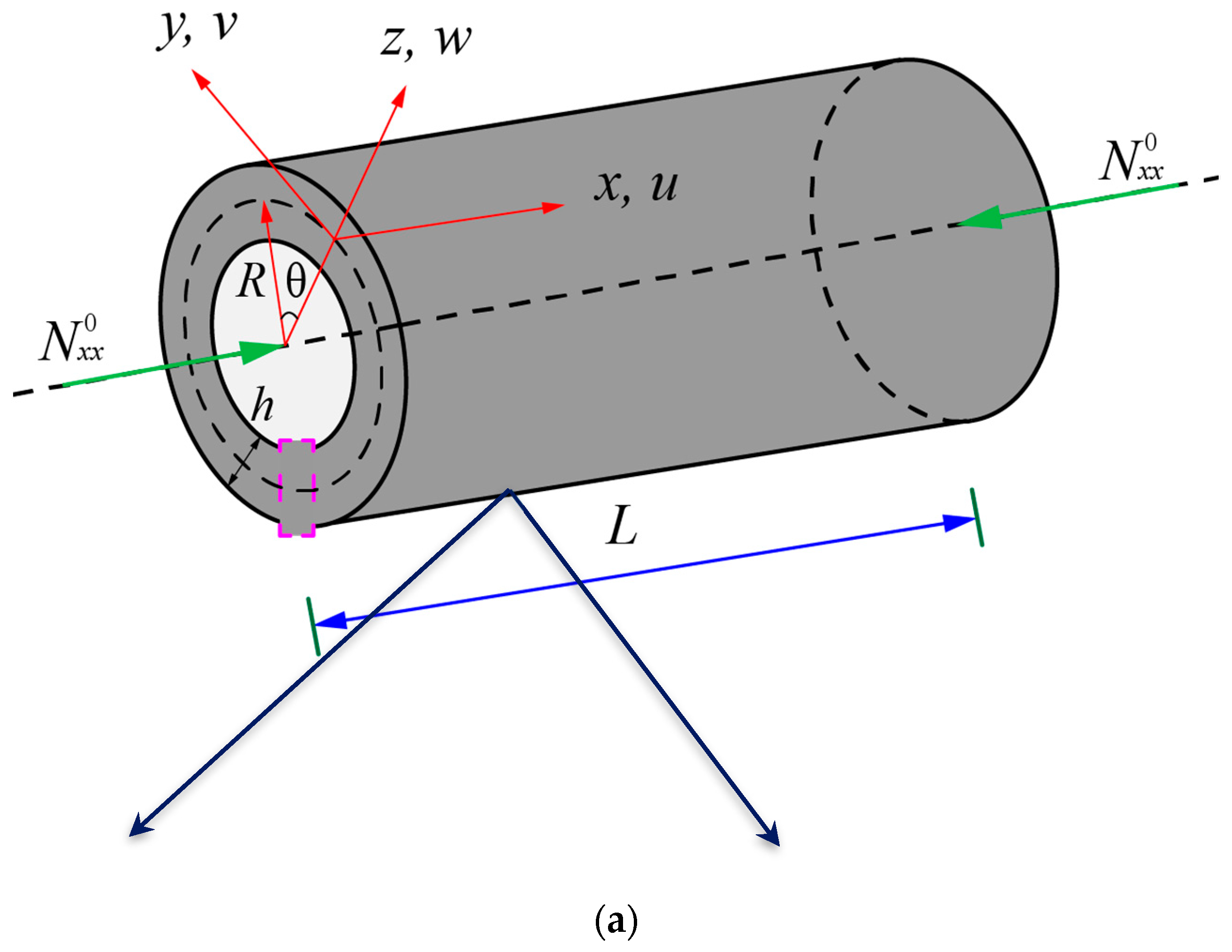
2. FG NPMF Circular Cylindrical Nanoshells
3. Theory and Formulation
3.1. General SGT
3.2. Constitutive Relations and Strain Energy
3.3. Kinetic Energy and External Work
3.4. Variational Formulation
4. Closed-Form Solution
5. Validation
5.1. Example 1: Homogeneous Cylindrical Nanoshell Based on the MSGT
5.2. Example 2: Homogeneous Cylindrical Nanoshells Based on the MCST
5.3. Example 3: FG Cylindrical Shell
6. Results and Discussion
6.1. Free Vibration Analysis
6.2. Buckling Analysis
7. Conclusions
- (1)
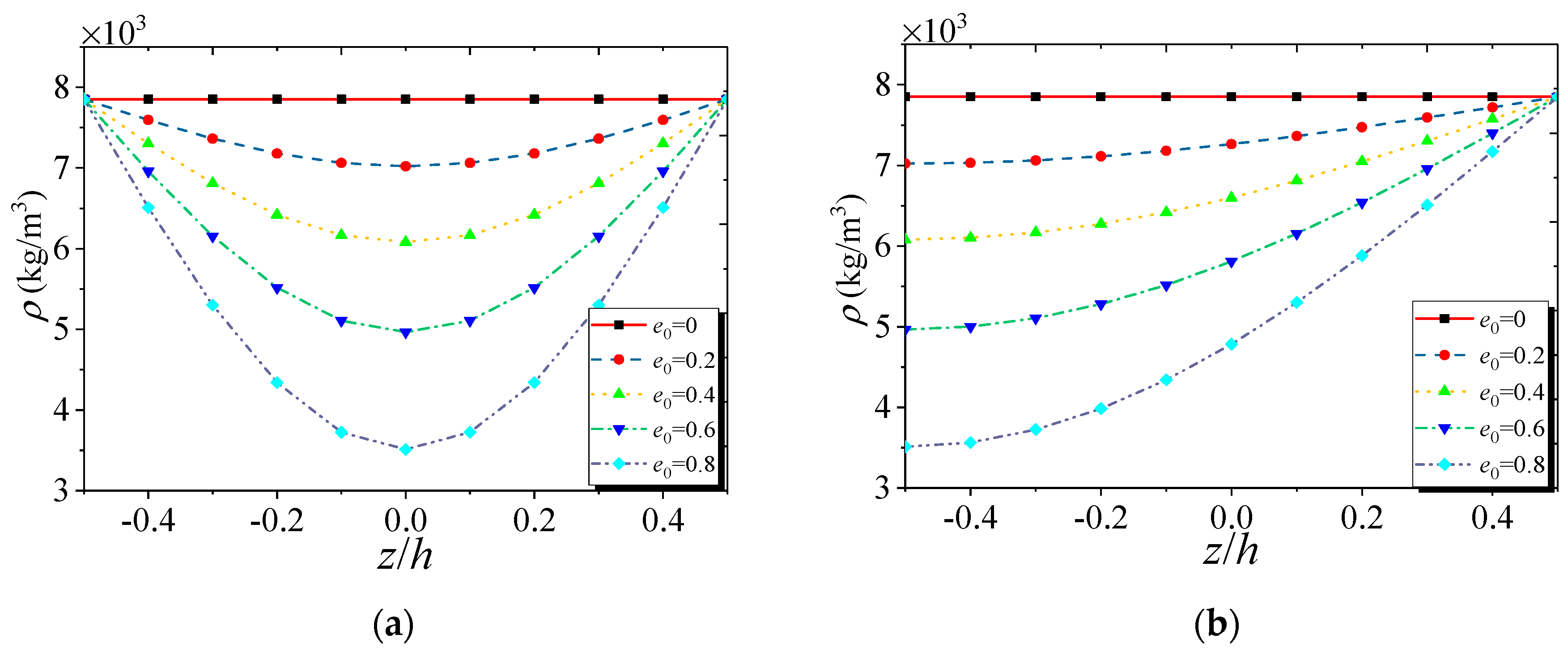
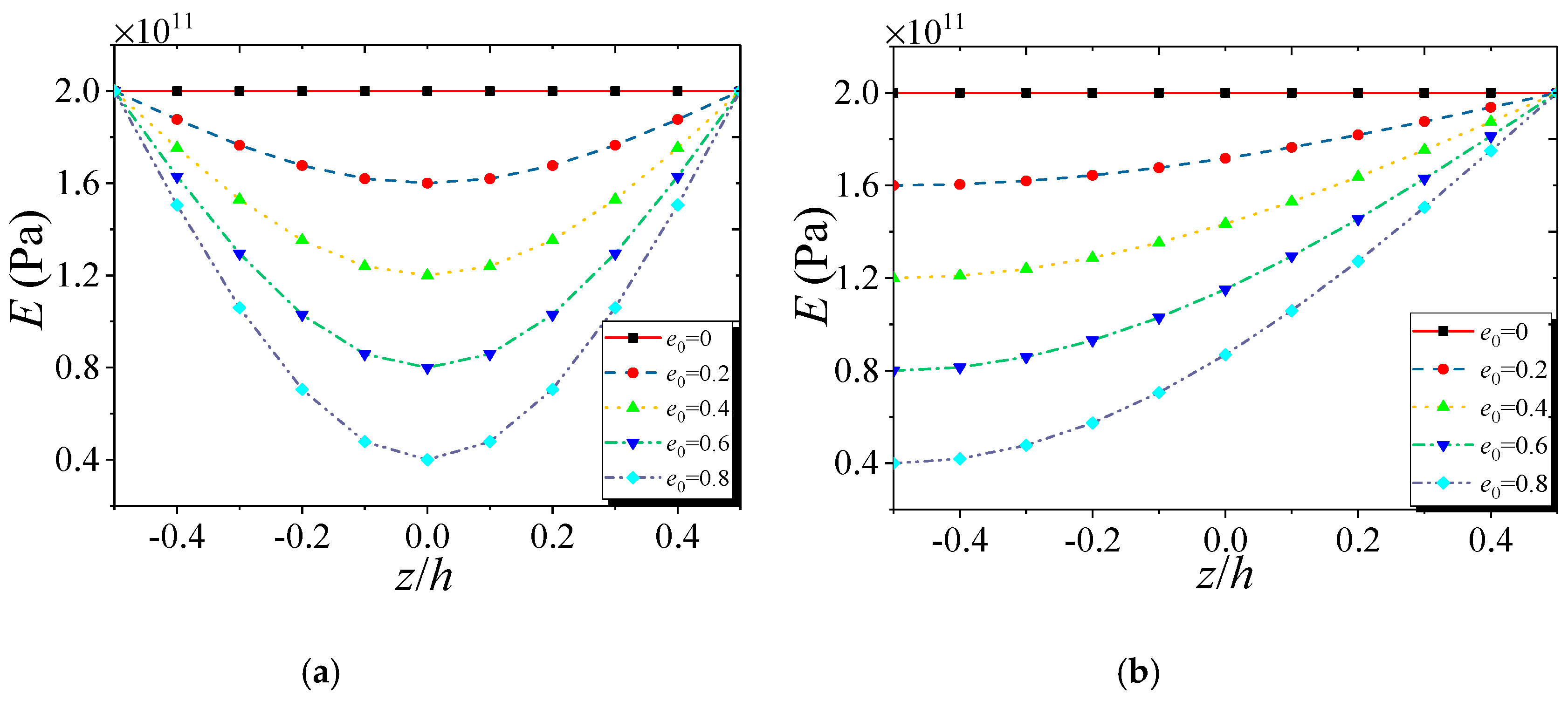
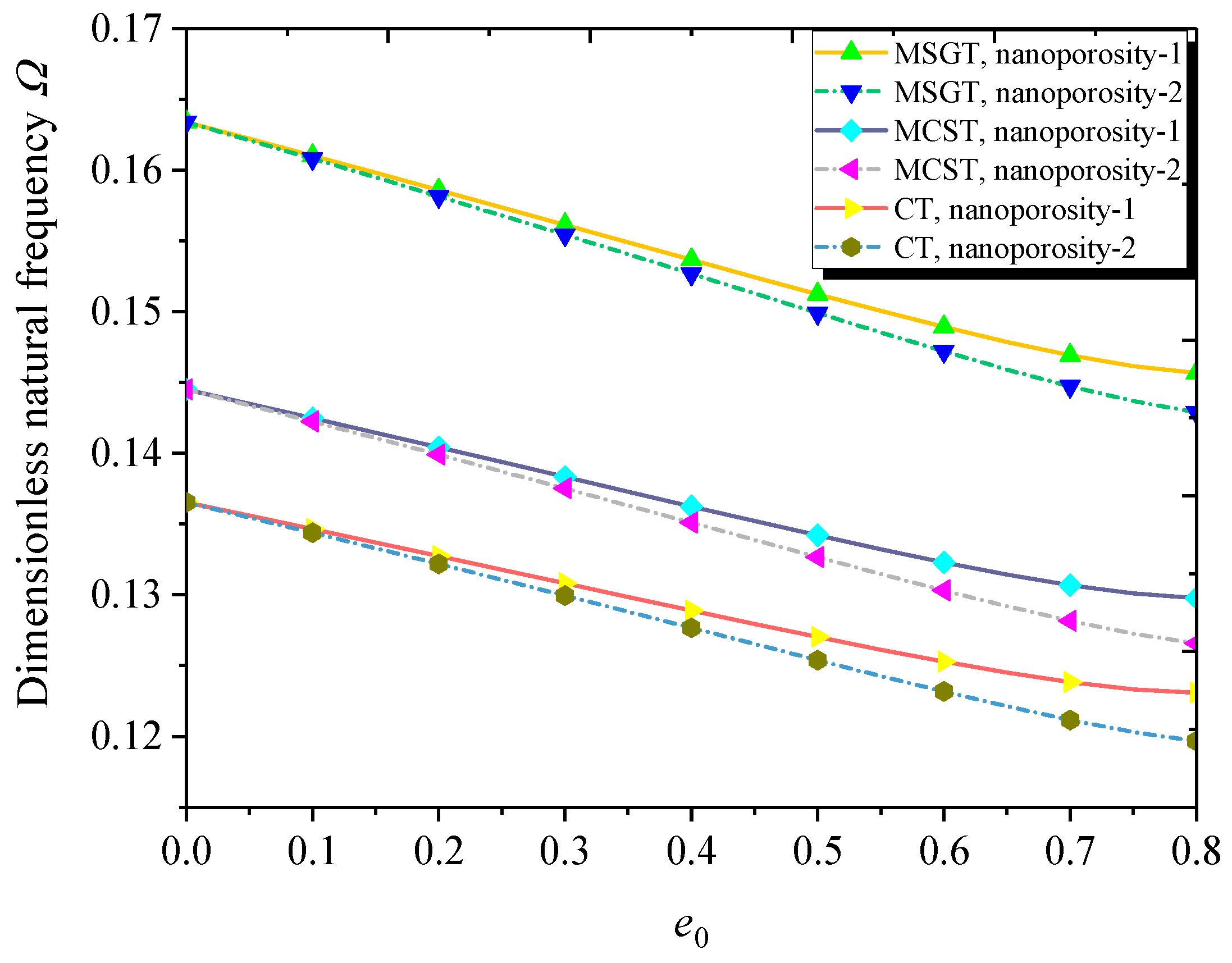
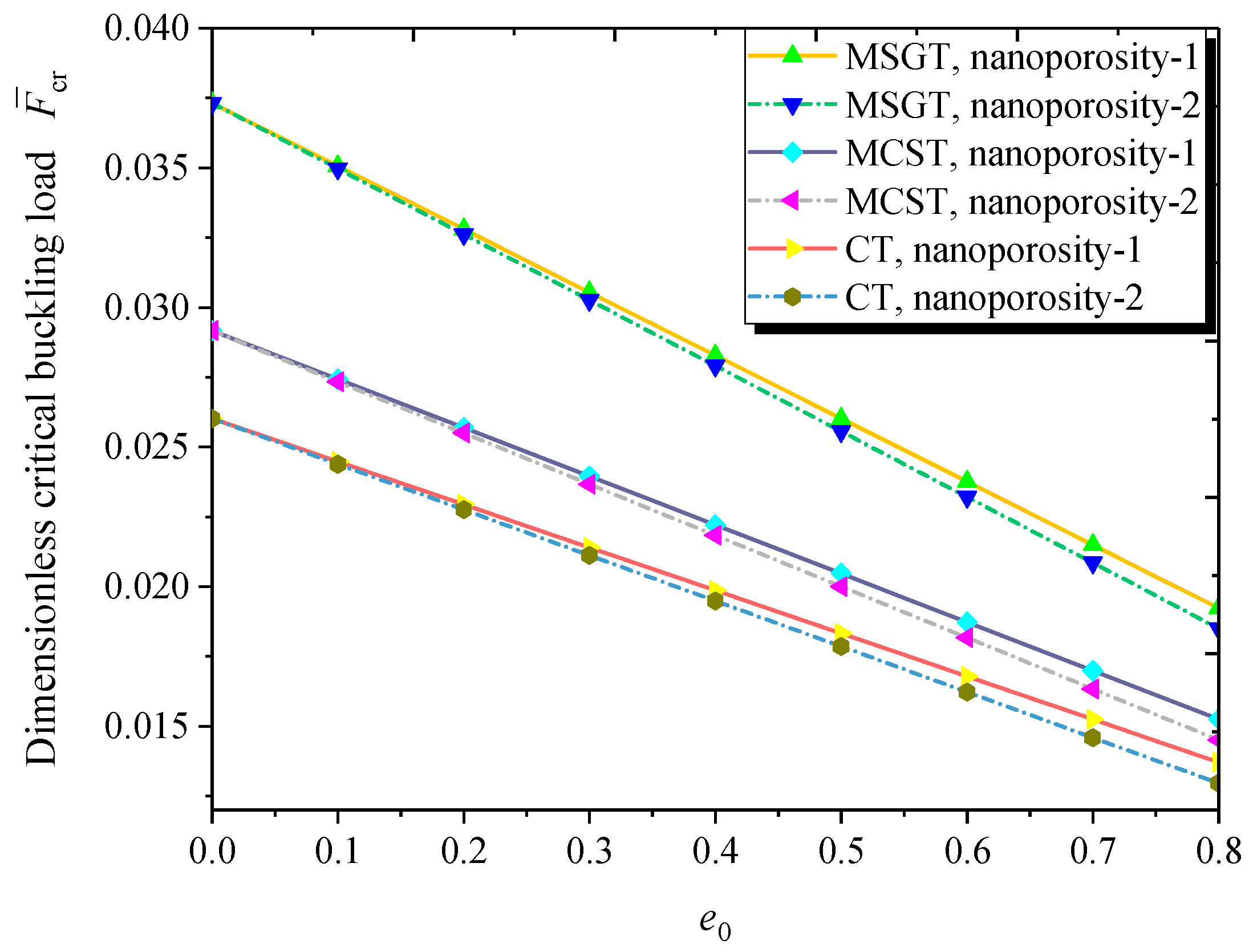
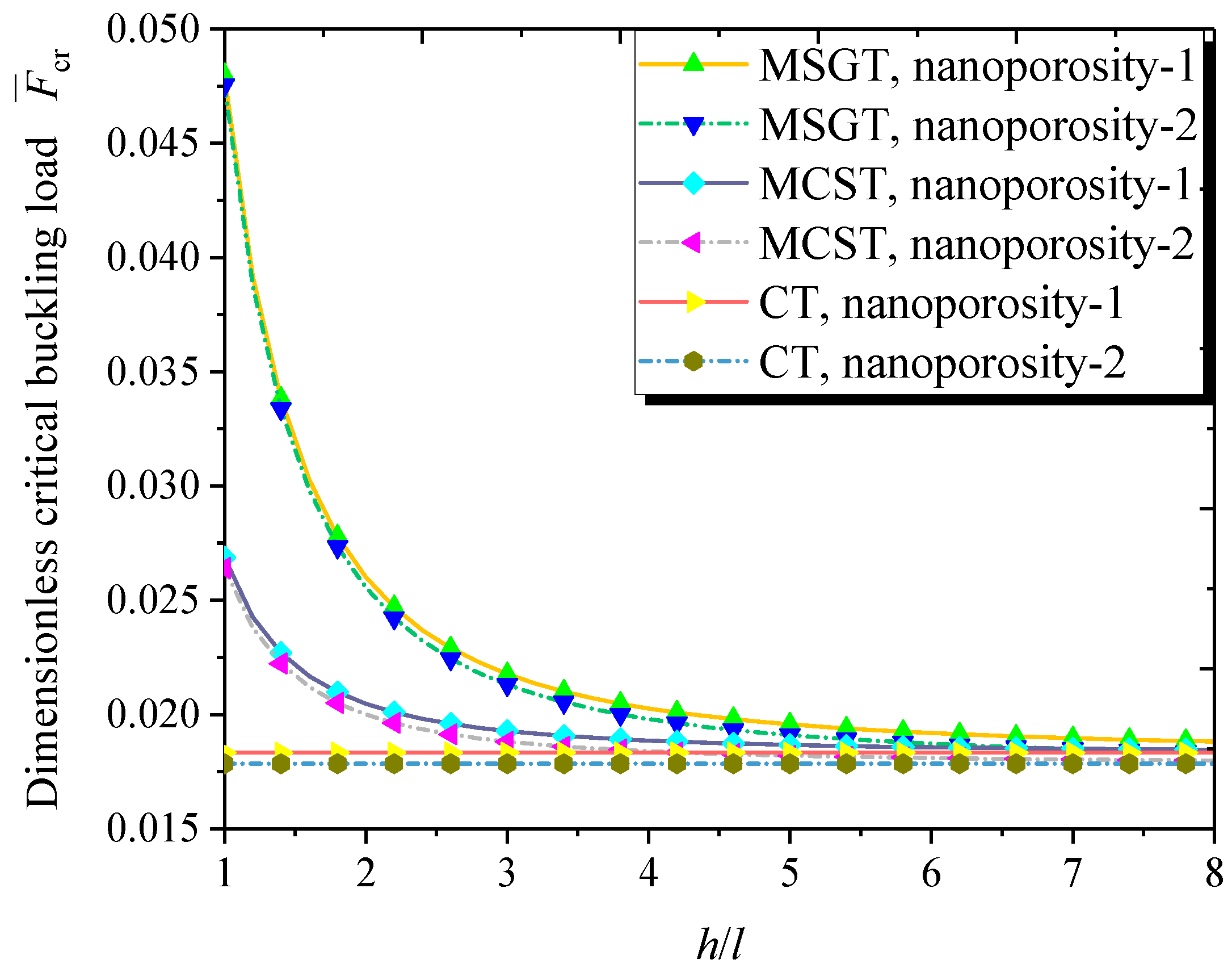
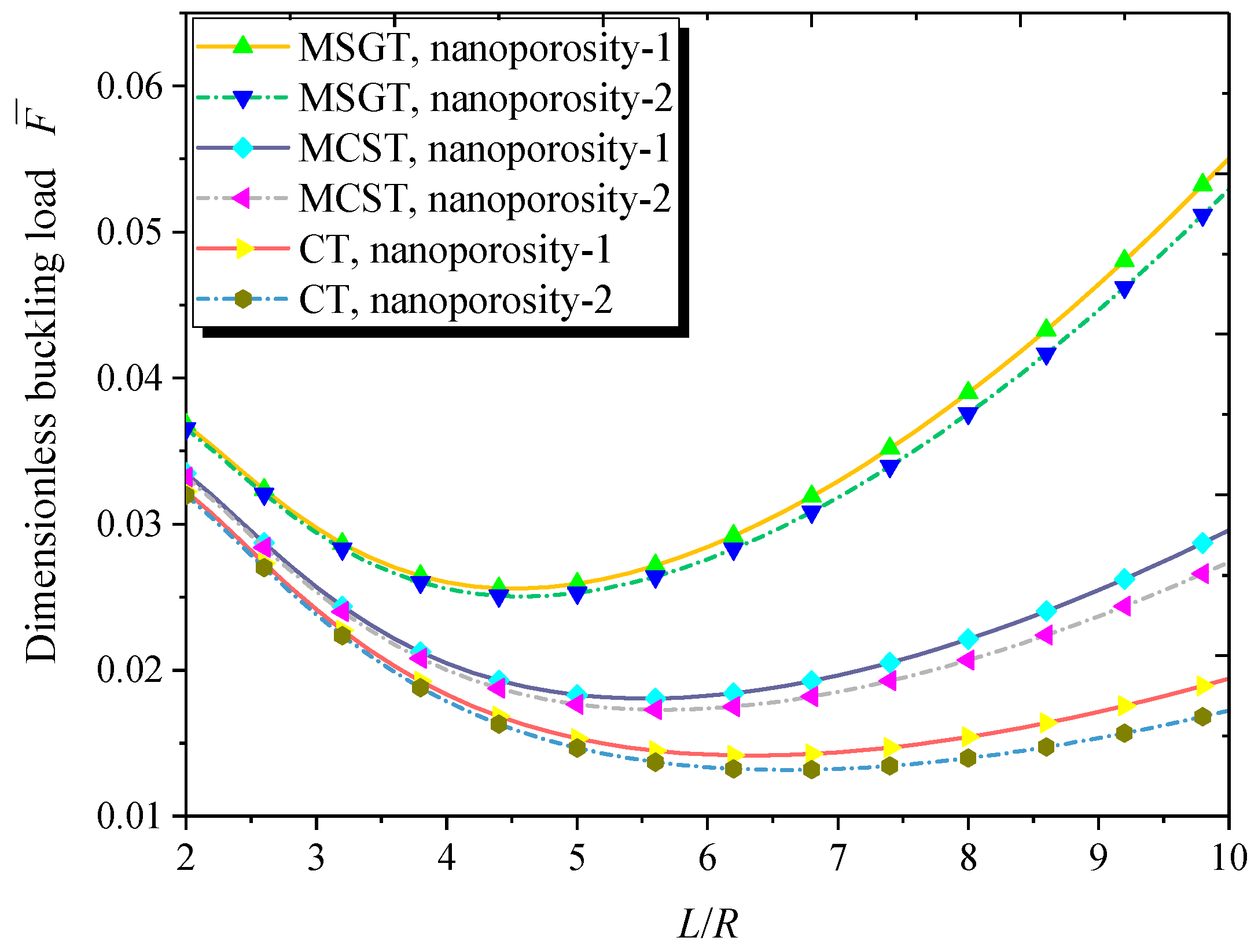
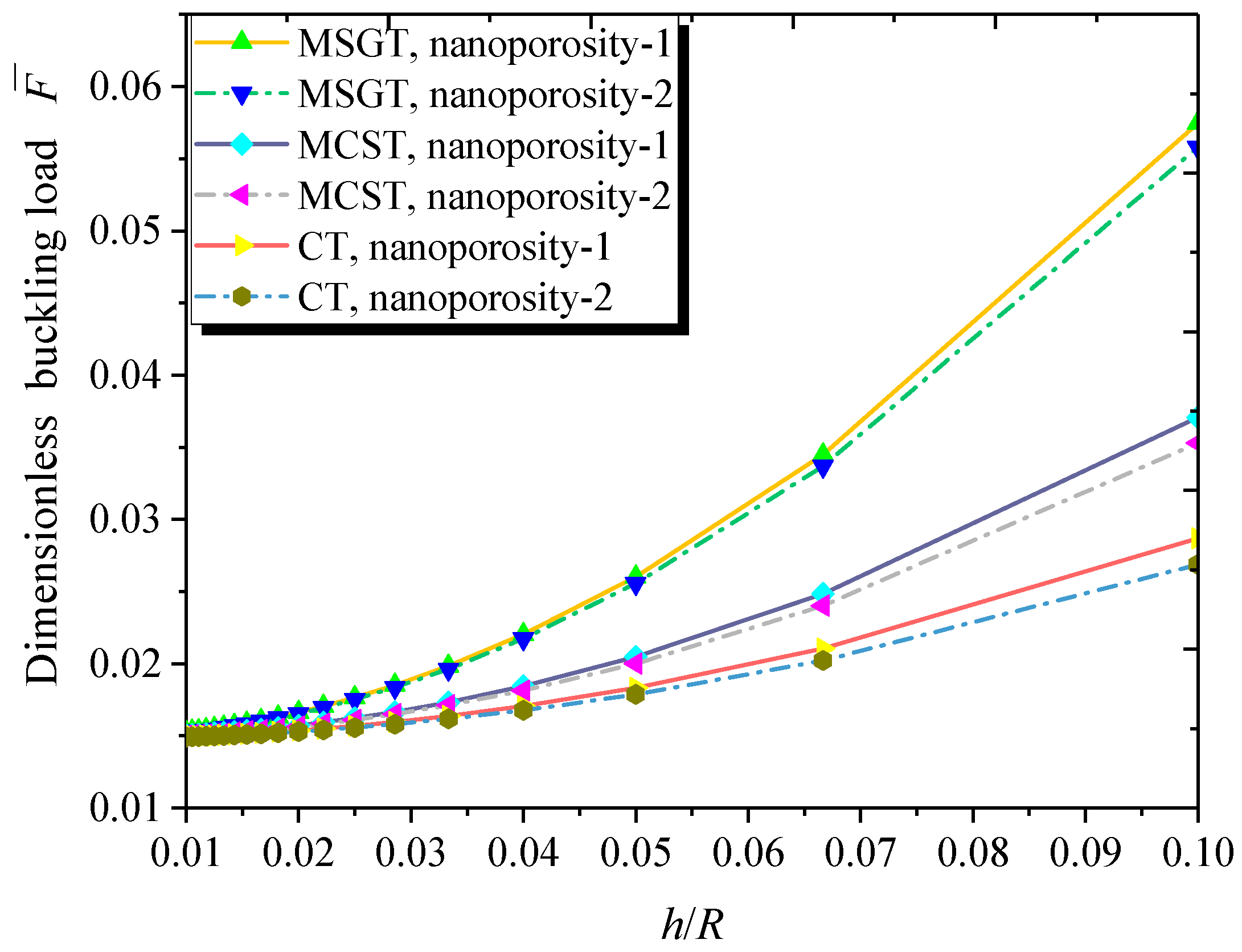
- Nanoporosity distribution has a significant influence on the vibration and buckling characteristics of FG NPMF nanoshells. Natural frequencies and buckling loads of the nanoporosity-2 nanoshell are lower than those of the nanoporosity-1 nanoshell. As the nanoporosity coefficient increases, natural frequencies and buckling loads of the nanoshell decrease.
- (2)
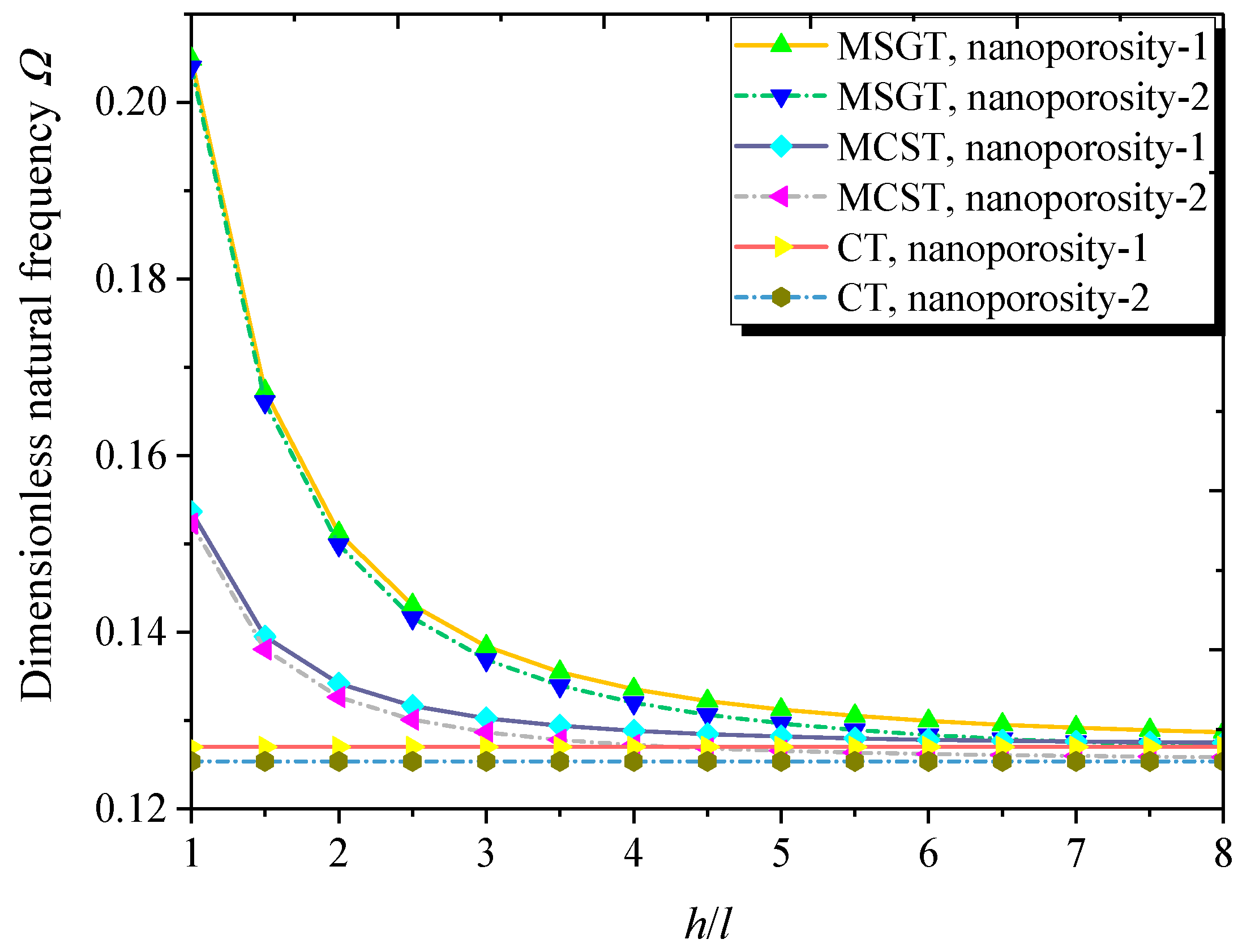
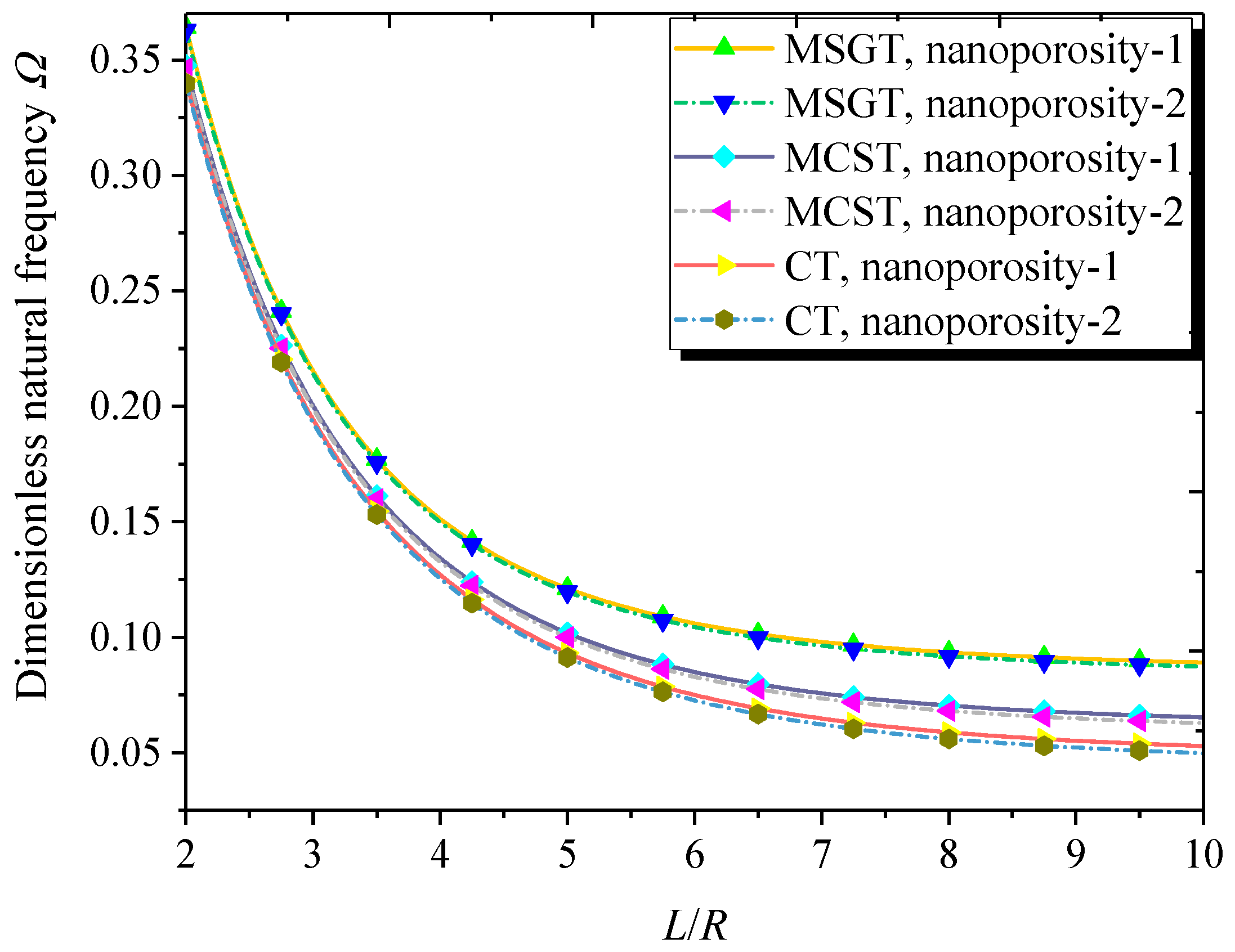
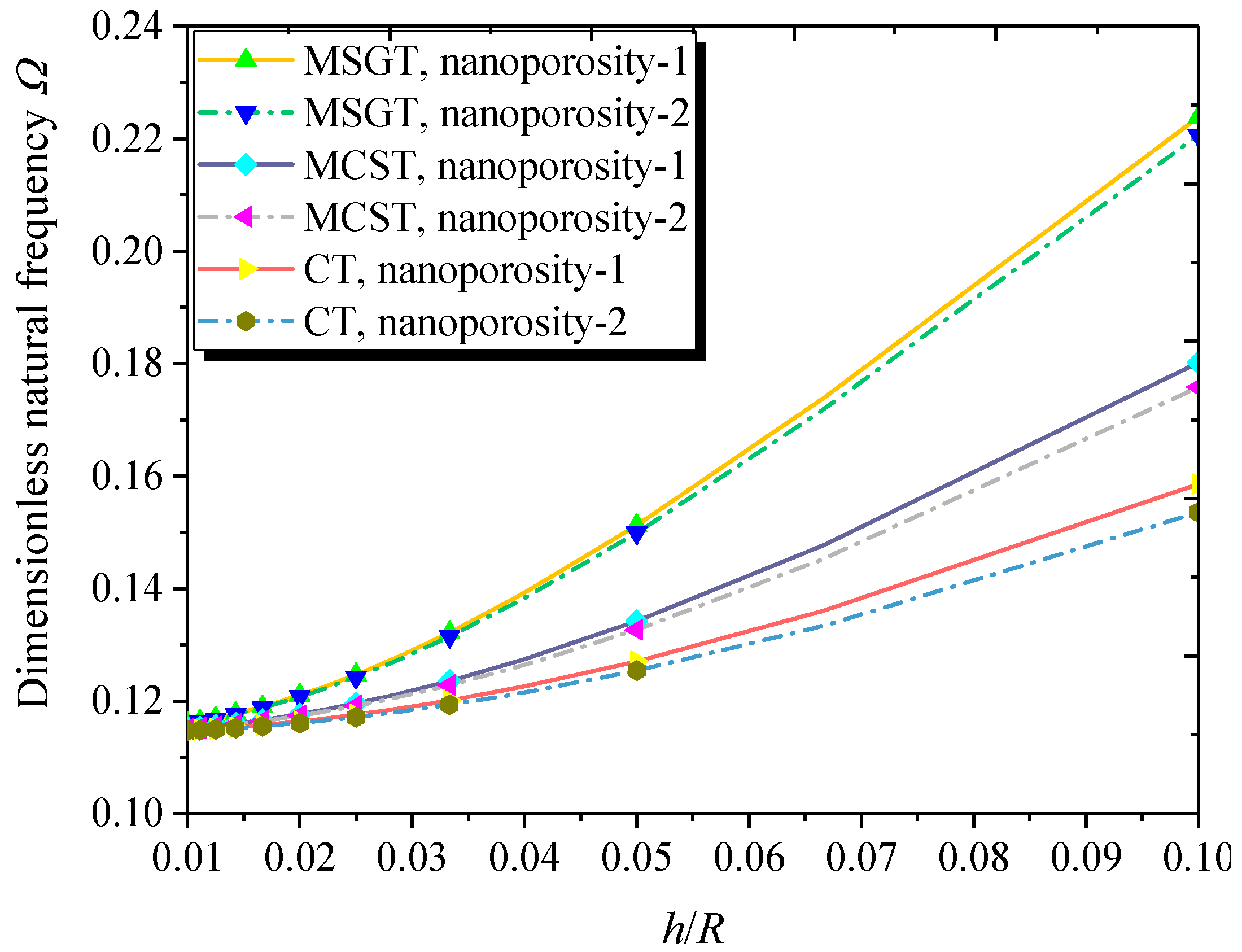
- Natural frequencies of the FG NPMF nanoshells decrease with the increasing length-to-radius ratio. Additionally, the larger thickness-to-radius ratio leads to the higher natural frequency of the FG NPMF nanoshell.
- (3)
- Buckling loads decrease first and then increase with the increase of the length-to-radius ratio. Furthermore, buckling loads increase with the increasing thickness-to-radius ratio of the nanoshell.
- (4)
- When the nanoshell thickness is approximately equal to the length scale parameter, the MSGT is more appropriate than the CT and MCST for free vibration and buckling analysis of FG NPMF nanoshells.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Wang, Y.; Ye, C.; Zu, J. Identifying the temperature effect on the vibrations of functionally graded cylindrical shells with porosities. Appl. Math. Mech. 2018, 39, 1587–1604. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Nonlinear dynamics of a translational FGM plate with strong mode interaction. Int. J. Struct. Stab. Dyn. 2018, 18, 1850031. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Wan, Y.H.; Zhang, Y.F. Vibrations of longitudinally traveling functionally graded material plates with porosities. Eur. J. Mech.-A/Solids 2017, 66, 55–68. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Yang, Z. Nonlinear vibrations of moving functionally graded plates containing porosities and contacting with liquid: Internal resonance. Nonlinear Dyn. 2017, 90, 1461–1480. [Google Scholar] [CrossRef]
- Nejati, M.; Asanjarani, A.; Dimitri, R.; Tornabene, F. Static and free vibration analysis of functionally graded conical shells reinforced by carbon nanotubes. Int. J. Mech. Sci. 2017, 130, 383–398. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Nonlinear dynamic thermoelastic response of rectangular FGM plates with longitudinal velocity. Compos. Part B Eng. 2017, 117, 74–88. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Large-amplitude vibration of sigmoid functionally graded thin plates with porosities. Thin-Walled Struct. 2017, 119, 911–924. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Porosity-dependent nonlinear forced vibration analysis of functionally graded piezoelectric smart material plates. Smart Mater. Struct. 2017, 26, 105014. [Google Scholar] [CrossRef]
- Wang, Y.; Zu, J. Nonlinear oscillations of sigmoid functionally graded material plates moving in longitudinal direction. Appl. Math. Mech. 2017, 38, 1533–1550. [Google Scholar] [CrossRef]
- Trinh, M.-C.; Kim, S.-E. Nonlinear thermomechanical behaviors of thin functionally graded sandwich shells with double curvature. Compos. Struct. 2018, 195, 335–348. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Nonlinear dynamics of functionally graded material plates under dynamic liquid load and with longitudinal speed. Int. J. Appl. Mech. 2017, 9, 1750054. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Speed-dependent nonlinear broadband vibrations of smart functionally graded piezoelectric material plates. J. Intell. Mater. Syst. Struct. 2018, 29, 1764–1776. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Vibration characteristics of moving sigmoid functionally graded plates containing porosities. Int. J. Mech. Mater. Des. 2018, 14, 473–489. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos. Part B Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Wang, Y.; Zu, J.W. Nonlinear dynamic behavior of inhomogeneous functional plates composed of sigmoid graded metal-ceramic materials. Sci. China Technol. Sci. 2018, 61, 1654–1665. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Dimitri, R. Free vibration analysis of arbitrarily shaped Functionally Graded Carbon Nanotube-reinforced plates. Compos. Part B Eng. 2017, 115, 384–408. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, J.; Hao, Y. Chaotic vibrations of an orthotropic FGM rectangular plate based on third-order shear deformation theory. Nonlinear Dyn. 2010, 59, 619–660. [Google Scholar] [CrossRef]
- Hao, Y.; Zhang, W.; Yang, J. Nonlinear dynamics of a FGM plate with two clamped opposite edges and two free edges. Acta Mech. Solida Sin. 2014, 27, 394–406. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Nonlinear steady-state responses of longitudinally traveling functionally graded material plates in contact with liquid. Compos. Struct. 2017, 164, 130–144. [Google Scholar] [CrossRef]
- Zhang, W.; Hao, Y.; Guo, X.; Chen, L. Complicated nonlinear responses of a simply supported FGM rectangular plate under combined parametric and external excitations. Meccanica 2012, 47, 985–1014. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Vibration behaviors of functionally graded rectangular plates with porosities and moving in thermal environment. Aerosp. Sci. Technol. 2017, 69, 550–562. [Google Scholar] [CrossRef]
- Zhang, W.; Hao, Y.; Yang, J. Nonlinear dynamics of FGM circular cylindrical shell with clamped–clamped edges. Compos. Struct. 2012, 94, 1075–1086. [Google Scholar] [CrossRef]
- Wang, Y.Q. Electro-mechanical vibration analysis of functionally graded piezoelectric porous plates in the translation state. Acta Astronaut. 2018, 143, 263–271. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Wan, Y.H.; Zu, J.W. Nonlinear dynamic characteristics of functionally graded sandwich thin nanoshells conveying fluid incorporating surface stress influence. Thin-Walled Struct. 2019, 135, 537–547. [Google Scholar] [CrossRef]
- Hassani, A.; Habibolahzadeh, A.; Bafti, H. Production of graded aluminum foams via powder space holder technique. Mater. Des. 2012, 40, 510–515. [Google Scholar] [CrossRef]
- He, S.Y.; Zhang, Y.; Dai, G.; Jiang, J.Q. Preparation of density-graded aluminum foam. Mater. Sci. Eng. A 2014, 618, 496–499. [Google Scholar] [CrossRef]
- Hangai, Y.; Takahashi, K.; Utsunomiya, T.; Kitahara, S.; Kuwazuru, O.; Yoshikawa, N. Fabrication of functionally graded aluminum foam using aluminum alloy die castings by friction stir processing. Mater. Sci. Eng. A 2012, 534, 716–719. [Google Scholar] [CrossRef]
- Hangai, Y.; Saito, K.; Utsunomiya, T.; Kitahara, S.; Kuwazuru, O.; Yoshikawa, N. Compression properties of Al/Al–Si–Cu alloy functionally graded aluminum foam fabricated by friction stir processing route. Mater. Trans. 2013, 54, 405–408. [Google Scholar] [CrossRef]
- Pia, G.; Delogu, F. On the elastic deformation behavior of nanoporous metal foams. Scr. Mater. 2013, 69, 781–784. [Google Scholar] [CrossRef]
- Park, H.; Ahn, C.; Jo, H.; Choi, M.; Kim, D.S.; Kim, D.K.; Jeon, S.; Choe, H. Large-area metal foams with highly ordered sub-micrometer-scale pores for potential applications in energy areas. Mater. Lett. 2014, 129, 174–177. [Google Scholar] [CrossRef]
- Heydari, H.; Moosavifard, S.E.; Shahraki, M.; Elyasi, S. Facile synthesis of nanoporous CuS nanospheres for high-performance supercapacitor electrodes. J. Energy Chem. 2017, 26, 762–767. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Xiao, T.; Tan, X.; Xiang, P.; Jiang, L.; Deng, C.; Li, W.; Li, M. Controllable preparation of nanoporous Ni3S2 films by sulfuration of nickel foam as promising asymmetric supercapacitor electrodes. Appl. Surf. Sci. 2017, 420, 919–926. [Google Scholar] [CrossRef]
- Fu, Y.; Du, H.; Zhang, S. Functionally graded TiN/TiNi shape memory alloy films. Mater. Lett. 2003, 57, 2995–2999. [Google Scholar] [CrossRef]
- Li, X.; Bhushan, B.; Takashima, K.; Baek, C.-W.; Kim, Y.-K. Mechanical characterization of micro/nanoscale structures for MEMS/NEMS applications using nanoindentation techniques. Ultramicroscopy 2003, 97, 481–494. [Google Scholar] [CrossRef]
- Moser, Y.; Gijs, M.A. Miniaturized flexible temperature sensor. J. Microelectromech. Syst. 2007, 16, 1349–1354. [Google Scholar] [CrossRef]
- Fleck, N.; Muller, G.; Ashby, M.; Hutchinson, J. Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Lam, D.C.; Yang, F.; Chong, A.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Miller, R.E.; Shenoy, V.B. Size-dependent elastic properties of nanosized structural elements. Nanotechnology 2000, 11, 139. [Google Scholar] [CrossRef]
- Xu, F.; Qin, Q.; Mishra, A.; Gu, Y.; Zhu, Y. Mechanical properties of ZnO nanowires under different loading modes. Nano Res. 2010, 3, 271–280. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Eshel, N. On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, J.; Zhou, S. A micro scale Timoshenko beam model based on strain gradient elasticity theory. Eur. J. Mech.-A/Solids 2010, 29, 591–599. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R.; Faghih Shojaei, M.; Mohammadi, V.; Sahmani, S. Size-dependent bending, buckling and free vibration of functionally graded Timoshenko microbeams based on the most general strain gradient theory. Compos. Struct. 2013, 100, 385–397. [Google Scholar] [CrossRef]
- Kong, S.; Zhou, S.; Nie, Z.; Wang, K. Static and dynamic analysis of micro beams based on strain gradient elasticity theory. Int. J. Eng. Sci. 2009, 47, 487–498. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Analysis of micro-sized beams for various boundary conditions based on the strain gradient elasticity theory. Arch. Appl. Mech. 2012, 82, 423–443. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, S.; Zhao, J.; Chen, X. A size-dependent Kirchhoff micro-plate model based on strain gradient elasticity theory. Eur. J. Mech.-A/Solids 2011, 30, 517–524. [Google Scholar] [CrossRef]
- Movassagh, A.A.; Mahmoodi, M. A micro-scale modeling of Kirchhoff plate based on modified strain-gradient elasticity theory. Eur. J. Mech.-A/Solids 2013, 40, 50–59. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. A microstructure-dependent sinusoidal plate model based on the strain gradient elasticity theory. Acta Mech. 2015, 226, 2277–2294. [Google Scholar] [CrossRef]
- Zeighampour, H.; Beni, Y.T. Cylindrical thin-shell model based on modified strain gradient theory. Int. J. Eng. Sci. 2014, 78, 27–47. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R.; Norouzzadeh, A. Size-dependent thermo-mechanical vibration and instability of conveying fluid functionally graded nanoshells based on Mindlin’s strain gradient theory. Thin-Walled Struct. 2016, 105, 172–184. [Google Scholar] [CrossRef]
- Zeighampour, H.; Beni, Y.T.; Karimipour, I. Torsional vibration and static analysis of the cylindrical shell based on strain gradient theory. Arabian J. Sci. Eng. 2016, 41, 1713–1722. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Barati, M.R.; Zenkour, A.M. Investigating post-buckling of geometrically imperfect metal foam nanobeams with symmetric and asymmetric porosity distributions. Compos. Struct. 2017, 182, 91–98. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.M.; Rabczuk, T. Nonlinear bending of functionally graded porous micro/nano-beams reinforced with graphene platelets based upon nonlocal strain gradient theory. Compos. Struct. 2018, 186, 68–78. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zhao, H.L.; Ye, C.; Zu, J.W. A Porous Microbeam Model for Bending and Vibration Analysis Based on the Sinusoidal Beam Theory and Modified Strain Gradient Theory. Int. J. Appl. Mech. 2018, 10, 1850059. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, X.; Chang, H.; Li, H. Nonlinear dynamic response of rotating circular cylindrical shells with precession of vibrating shape—Part I: Numerical solution. Int. J. Mech. Sci. 2010, 52, 1217–1224. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, X.; Chang, H.; Li, H. Nonlinear dynamic response of rotating circular cylindrical shells with precession of vibrating shape—Part II: Approximate analytical solution. Int. J. Mech. Sci. 2010, 52, 1208–1216. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Liang, L.; Guo, X.H. Internal resonance of axially moving laminated circular cylindrical shells. J. Sound Vib. 2013, 332, 6434–6450. [Google Scholar] [CrossRef]
- Wang, Y.Q. Nonlinear vibration of a rotating laminated composite circular cylindrical shell: Traveling wave vibration. Nonlinear Dyn. 2014, 77, 1693–1707. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, X.; Li, Y.; Li, J. Nonlinear traveling wave vibration of a circular cylindrical shell subjected to a moving concentrated harmonic force. J. Sound Vib. 2010, 329, 338–352. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, L.; Guo, X.; Li, J.; Liu, J.; Liu, P. Nonlinear vibration response and bifurcation of circular cylindrical shells under traveling concentrated harmonic excitation. Acta Mech. Solida Sin. 2013, 26, 277–291. [Google Scholar] [CrossRef]
- Nejati, M.; Dimitri, R.; Tornabene, F.; Hossein Yas, M. Thermal buckling of nanocomposite stiffened cylindrical shells reinforced by functionally graded wavy carbon nanotubes with temperature-dependent properties. Appl. Sci. 2017, 7, 1223. [Google Scholar] [CrossRef]
- Baughman, R.H.; Cui, C.; Zakhidov, A.A.; Iqbal, Z.; Barisci, J.N.; Spinks, G.M.; Wallace, G.G.; Mazzoldi, A.; De Rossi, D.; Rinzler, A.G. Carbon nanotube actuators. Science 1999, 284, 1340–1344. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Hu, Y.; Zhao, J.; Lan, T.; Wang, D.; Liu, Y.; Chen, W. Ordered and Active Nanochannel Electrode Design for High-Performance Electrochemical Actuator. Small 2016, 12, 4986–4992. [Google Scholar] [CrossRef] [PubMed]
- Raschke, G.; Brogl, S.; Susha, A.; Rogach, A.; Klar, T.; Feldmann, J.; Fieres, B.; Petkov, N.; Bein, T.; Nichtl, A. Gold nanoshells improve single nanoparticle molecular sensors. Nano Lett. 2004, 4, 1853–1857. [Google Scholar] [CrossRef]
- Hoseinzadeh, M.; Khadem, S. A nonlocal shell theory model for evaluation of thermoelastic damping in the vibration of a double-walled carbon nanotube. Phys. E Low-Dimens. Syst. Nanostruct. 2014, 57, 6–11. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.; Bahrami, M. Nonlinear buckling and postbuckling behavior of cylindrical nanoshells subjected to combined axial and radial compressions incorporating surface stress effects. Compos. Part B Eng. 2015, 79, 676–691. [Google Scholar] [CrossRef]
- Ansari, R.; Rouhi, H.; Sahmani, S. Thermal effect on axial buckling behavior of multi-walled carbon nanotubes based on nonlocal shell model. Phys. E Low-Dimens. Syst. Nanostruct. 2011, 44, 373–378. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Li, H.; Zhang, Y.; Zu, J.W. A nonlinear surface-stress-dependent model for vibration analysis of cylindrical nanoscale shells conveying fluid. Appl. Math. Model. 2018, 64, 55–70. [Google Scholar] [CrossRef]
- Magnucki, K.; Stasiewicz, P. Elastic buckling of a porous beam. J. Theor. Appl. Mech. 2004, 42, 859–868. [Google Scholar]
- Jabbari, M.; Mojahedin, A.; Khorshidvand, A.; Eslami, M. Buckling analysis of a functionally graded thin circular plate made of saturated porous materials. J. Eng. Mech. 2013, 140, 287–295. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Liang, C. Wave propagation characteristics in nanoporous metal foam nanobeams. Results Phys. 2019, 12, 287–297. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Liang, C.; Zu, J.W. Examining wave propagation characteristics in metal foam beams: Euler–Bernoulli and Timoshenko models. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 565. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z. Non-local buckling analysis of functionally graded nanoporous metal foam nanoplates. Coatings 2018, 8, 389. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Ye, C.; Zu, J.W. Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aerosp. Sci. Technol. 2019, 85, 359–370. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Elastic buckling and static bending of shear deformable functionally graded porous beam. Compos. Struct. 2015, 133, 54–61. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Free and forced vibrations of shear deformable functionally graded porous beams. Int. J. Mech. Sci. 2016, 108, 14–22. [Google Scholar] [CrossRef]
- Fleck, N.; Hutchinson, J. Strain gradient plasticity. Adv. Appl. Mech. 1997, 33, 296–361. [Google Scholar]
- Rahim, M.Z.; Ding, S.; Hu, B.; Mo, J. Crater size prediction in electrical discharge grinding (EDG) of polycrystalline diamond (PCD). Nonconv. Technol. Rev./Revista de Tehnologii Neconventionale 2014, 18, 92–97. [Google Scholar]
- Rezaiee-Pajand, M.; Pourhekmat, D.; Arabi, E. Thermo-mechanical stability analysis of functionally graded shells. Eng. Struct. 2019, 178, 1–11. [Google Scholar] [CrossRef]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Leissa, A.W. Vibration of Shells; Scientific and Technical Information Office, National Aeronautics and Space Administration: Washington, DC, USA, 1973.
- Kamarian, S.; Salim, M.; Dimitri, R.; Tornabene, F. Free vibration analysis of conical shells reinforced with agglomerated Carbon Nanotubes. Int. J. Mech. Sci. 2016, 108, 157–165. [Google Scholar] [CrossRef]
- Kiani, Y.; Dimitri, R.; Tornabene, F. Free vibration study of composite conical panels reinforced with FG-CNTs. Polym. Compos. 2018, 172, 472–482. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M.; Fantuzzi, N.; Reddy, J. Multiscale approach for three-phase CNT/polymer/fiber laminated nanocomposite structures. Polym. Compos. 2017. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Christoforou, A.; Swanson, S. Analysis of simply-supported orthotropic cylindrical shells subject to lateral impact loads. J. Appl. Mech. 1990, 57, 376–382. [Google Scholar] [CrossRef]
- Thai, H.-T.; Choi, D.-H. A simple first-order shear deformation theory for the bending and free vibration analysis of functionally graded plates. Compos. Struct. 2013, 101, 332–340. [Google Scholar] [CrossRef]
- Whitney, J.; Pagano, N. Shear deformation in heterogeneous anisotropic plates. J. Appl. Mech. 1970, 37, 1031–1036. [Google Scholar] [CrossRef]
- Kiani, Y.; Shakeri, M.; Eslami, M. Thermoelastic free vibration and dynamic behaviour of an FGM doubly curved panel via the analytical hybrid Laplace–Fourier transformation. Acta Mech. 2012, 223, 1199–1218. [Google Scholar] [CrossRef]
- Ke, L.-L.; Wang, Y.-S.; Yang, J.; Kitipornchai, S. Nonlinear free vibration of size-dependent functionally graded microbeams. Int. J. Eng. Sci. 2012, 50, 256–267. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Huang, X.B.; Li, J. Hydroelastic dynamic analysis of axially moving plates in continuous hot-dip galvanizing process. Int. J. Mech. Sci. 2016, 110, 201–216. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Liu, Y.F.; Zu, J.W. Analytical treatment of nonlocal vibration of multilayer functionally graded piezoelectric nanoscale shells incorporating thermal and electrical effect. Eur. Phys. J. Plus 2019, 134, 54. [Google Scholar] [CrossRef]
- Wang, Y.; Zu, J. Analytical analysis for vibration of longitudinally moving plate submerged in infinite liquid domain. Appl. Math. Mech. 2017, 38, 625–646. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Instability of viscoelastic plates with longitudinally variable speed and immersed in ideal liquid. Int. J. Appl. Mech. 2017, 9, 1750005. [Google Scholar] [CrossRef]
- Wang, Y.; Du, W.; Huang, X.; Xue, S. Study on the dynamic behavior of axially moving rectangular plates partially submersed in fluid. Acta Mech. Solida Sin. 2015, 28, 706–721. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Xue, S.W.; Huang, X.B.; Du, W. Vibrations of axially moving vertical rectangular plates in contact with fluid. Int. J. Struct. Stab. Dyn. 2016, 16, 1450092. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Guo, X.H.; Sun, Z.; Li, J. Stability and dynamics of axially moving unidirectional plates partially immersed in a liquid. Int. J. Struct. Stab. Dyn. 2014, 14, 1450010. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.; Liu, D.; Shen, L.; Lei, J. Free vibration analysis of four-unknown shear deformable functionally graded cylindrical microshells based on the strain gradient elasticity theory. Compos. Struct. 2015, 119, 578–597. [Google Scholar] [CrossRef]
- Ghadiri, M.; SafarPour, H. Free vibration analysis of size-dependent functionally graded porous cylindrical microshells in thermal environment. J. Therm. Stress. 2017, 40, 55–71. [Google Scholar] [CrossRef]
- Loy, C.; Lam, K.; Reddy, J. Vibration of functionally graded cylindrical shells. Int. J. Mech. Sci. 1999, 41, 309–324. [Google Scholar] [CrossRef]
- Sahmani, S.; Ansari, R. On the free vibration response of functionally graded higher-order shear deformable microplates based on the strain gradient elasticity theory. Compos. Struct. 2013, 95, 430–442. [Google Scholar] [CrossRef]

| (m,n) | h/R | l = 0 | l = h | ||||
|---|---|---|---|---|---|---|---|
| Zhang et al. [99] | Present | Error (%) | Zhang et al. [99] | Present | Error (%) | ||
| (1, 1) | 0.02 | 0.19536 | 0.19536 | 0.00 | 0.19595 | 0.19561 | 0.10 |
| 0.05 | 0.19542 | 0.19542 | 0.00 | 0.19908 | 0.19694 | 0.20 | |
| 0.1 | 0.19561 | 0.19564 | 0.01 | 0.20386 | 0.20148 | 1.17 | |
| (2, 2) | 0.02 | 0.25285 | 0.25271 | 0.05 | 0.27108 | 0.27004 | 0.30 |
| 0.05 | 0.25969 | 0.25885 | 0.30 | 0.35606 | 0.34641 | 0.96 | |
| 0.1 | 0.28080 | 0.27931 | 0.50 | 0.50626 | 0.50145 | 0.90 | |
| (3, 3) | 0.02 | 0.27627 | 0.27580 | 0.16 | 0.37783 | 0.37382 | 1.39 |
| 0.05 | 0.31667 | 0.31413 | 0.80 | 0.71543 | 0.69918 | 2.27 | |
| 0.1 | 0.40671 | 0.41916 | 2.97 | 1.08810 | 1.07892 | 0.84 | |
| h/R | (m, n) | l = 0 | l = h | ||||
|---|---|---|---|---|---|---|---|
| Ghadiri et al. [100] | Present | Error (%) | Ghadiri et al. [100] | Present | Error (%) | ||
| 0.02 | m = n = 1 | 0.19536215 | 0.19536215 | 0.00 | 0.19543206 | 0.19548050 | 0.01 |
| m = n = 2 | 0.25271274 | 0.25271274 | 0.00 | 0.25731258 | 0.25785715 | 0.09 | |
| m = n = 3 | 0.27580092 | 0.27580092 | 0.00 | 0.30621690 | 0.30717244 | 0.10 | |
| 0.05 | m = n = 1 | 0.19542305 | 0.19542305 | 0.00 | 0.19585782 | 0.19618570 | 0.16 |
| m = n = 2 | 0.25884786 | 0.25884786 | 0.00 | 0.28543902 | 0.28780026 | 0.80 | |
| m = n = 3 | 0.31407326 | 0.31407326 | 0.00 | 0.45457555 | 0.46000081 | 1.10 | |
| h/R | N | Loy et al. [101] | Present | ||||
|---|---|---|---|---|---|---|---|
| m = 1 | m = 2 | m = 3 | m = 1 | m = 2 | m = 3 | ||
| 0.002 | 0 | 13.548 | 4.5920 | 4.2633 | 13.548 | 4.5920 | 4.2633 |
| 0.5 | 13.321 | 4.5168 | 4.1911 | 13.321 | 4.5168 | 4.1911 | |
| 1 | 13.211 | 4.4800 | 4.1569 | 13.211 | 4.4800 | 4.1569 | |
| 2 | 13.103 | 4.4435 | 4.1235 | 13.103 | 4.4434 | 4.1234 | |
| 5 | 12.998 | 4.4068 | 4.0891 | 12.998 | 4.4068 | 4.0891 | |
| 0.05 | 0 | 13.572 | 33.296 | 93.001 | 13.572 | 33.242 | 92.634 |
| 0.5 | 13.345 | 32.702 | 91.319 | 13.345 | 32.645 | 90.943 | |
| 1 | 13.235 | 32.430 | 90.553 | 13.235 | 32.370 | 90.172 | |
| 2 | 13.127 | 32.170 | 89.828 | 13.127 | 32.111 | 89.451 | |
| 5 | 13.021 | 31.910 | 89.109 | 13.021 | 31.854 | 88.743 | |
| h/l = 1 | h/l = 1.5 | h/l = 2 | h/l = 3 | h/l = 4 | h/l = 5 | h/l = 10 | |
|---|---|---|---|---|---|---|---|
| n = 1 | 0.25824 | 0.25723 | 0.25687 | 0.25662 | 0.25653 | 0.25649 | 0.25643 |
| n = 2 | 0.20493 | 0.16730 | 0.15125 | 0.13840 | 0.13356 | 0.13125 | 0.12809 |
| n = 3 | 0.42938 | 0.31512 | 0.25919 | 0.20833 | 0.18683 | 0.17591 | 0.16009 |
| n = 4 | 0.76650 | 0.56684 | 0.46542 | 0.37079 | 0.32994 | 0.30894 | 0.27818 |
| n = 5 | 1.17537 | 0.88269 | 0.72927 | 0.58336 | 0.51961 | 0.48665 | 0.43816 |
| n = 6 | 1.64107 | 1.25206 | 1.04209 | 0.83851 | 0.74844 | 0.70162 | 0.63245 |
| h/l = 1 | h/l = 1.5 | h/l = 2 | h/l = 3 | h/l = 4 | h/l = 5 | h/l = 10 | |
|---|---|---|---|---|---|---|---|
| n = 1 | 0.12274 | 0.12167 | 0.12129 | 0.12101 | 0.12092 | 0.12087 | 0.12081 |
| n = 2 | 0.04801 | 0.03188 | 0.02603 | 0.02177 | 0.02027 | 0.01957 | 0.01864 |
| n = 3 | 0.18358 | 0.09853 | 0.06657 | 0.04297 | 0.03455 | 0.03062 | 0.02536 |
| n = 4 | 0.55614 | 0.30326 | 0.20422 | 0.12951 | 0.10252 | 0.08987 | 0.07285 |
| n = 5 | 1.27769 | 0.71906 | 0.49043 | 0.31364 | 0.24878 | 0.21820 | 0.17686 |
| n = 6 | 2.45989 | 1.43011 | 0.99029 | 0.64101 | 0.51065 | 0.44875 | 0.36462 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, F. Vibration and Buckling of Shear Deformable Functionally Graded Nanoporous Metal Foam Nanoshells. Nanomaterials 2019, 9, 271. https://doi.org/10.3390/nano9020271
Zhang Y, Zhang F. Vibration and Buckling of Shear Deformable Functionally Graded Nanoporous Metal Foam Nanoshells. Nanomaterials. 2019; 9(2):271. https://doi.org/10.3390/nano9020271
Chicago/Turabian StyleZhang, Yufei, and Fei Zhang. 2019. "Vibration and Buckling of Shear Deformable Functionally Graded Nanoporous Metal Foam Nanoshells" Nanomaterials 9, no. 2: 271. https://doi.org/10.3390/nano9020271





