Vibration Analysis of Vacancy Defected Graphene Sheets by Monte Carlo Based Finite Element Method
Abstract
:1. Introduction
2. Materials and Methods
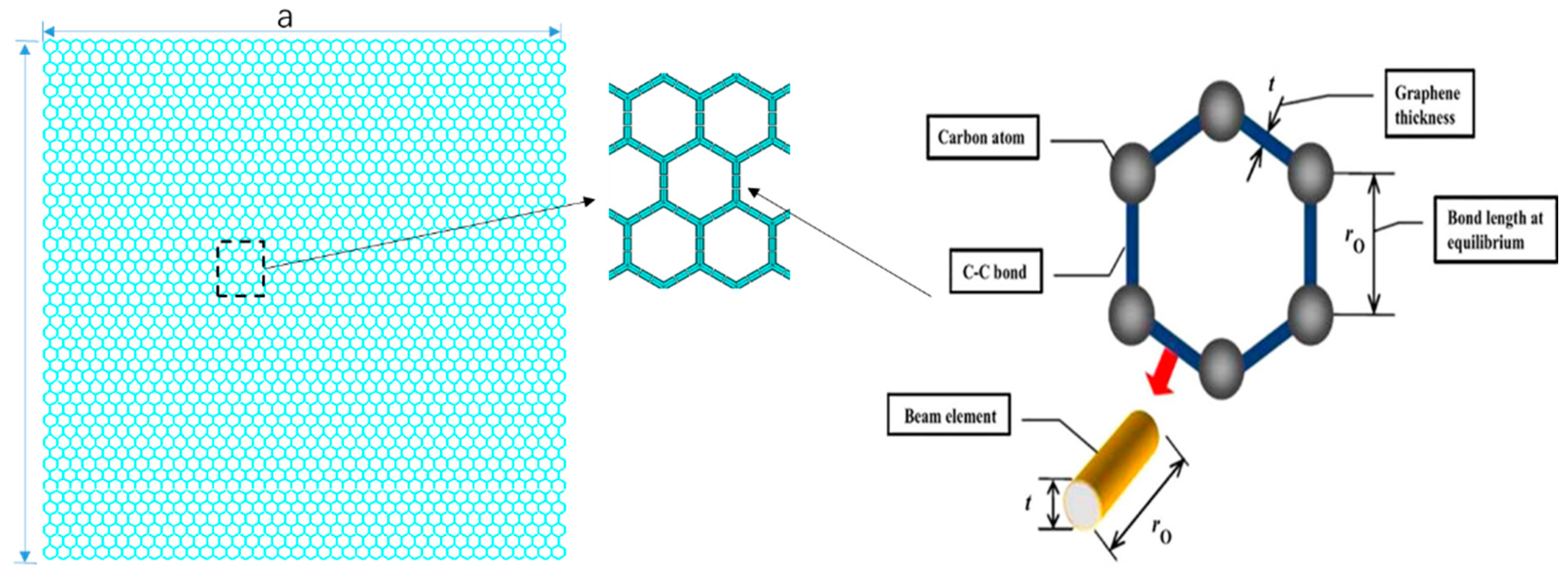
2.1. Graphene Sheets
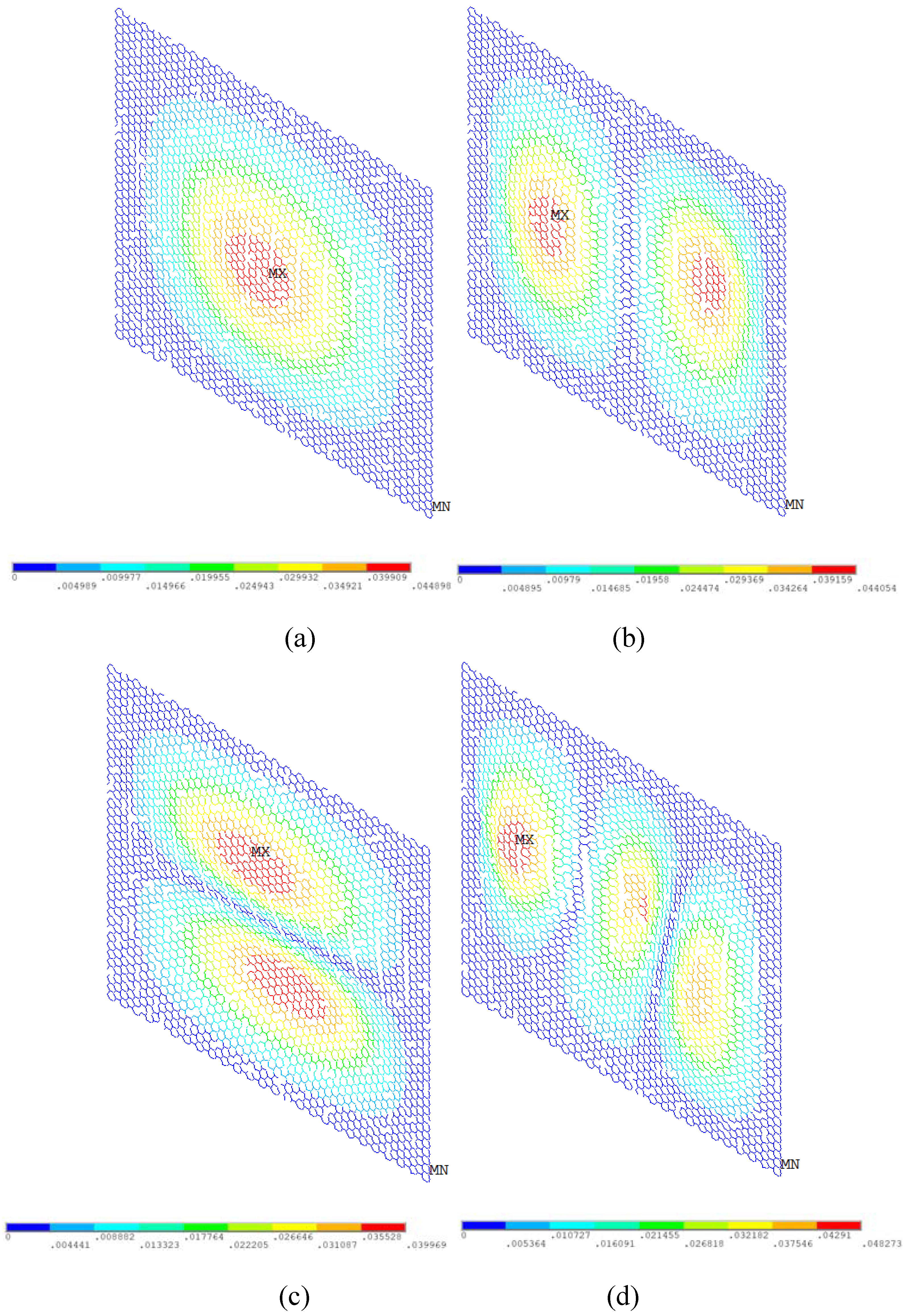
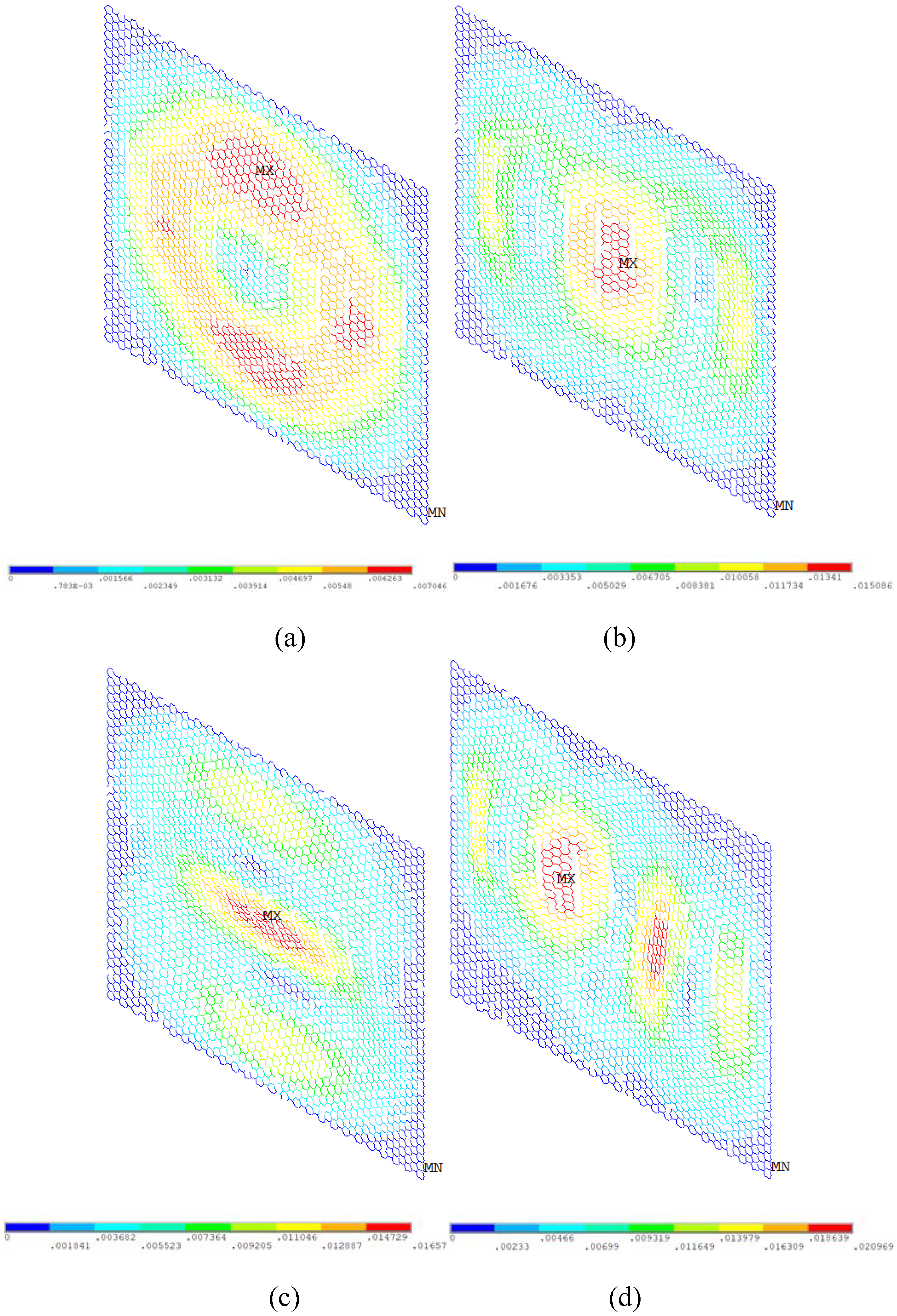
2.2. Finite Element Model in Vibration Analysis
2.3. Monte Carlo Based Finite Element Method
- Step 1:
- Define the initial configuration of graphene sheets, which includes corresponding parameters of bonds’ length, height, and width of a hexagonal 2D lattice, and also thickness or diameter of the section.
- Step 2:
- Fix material property parameters, which consist of the Young’s modulus, Poisson ratio, physical density. The accuracy of the finite element model for graphene sheets heavily depends on exact parameters of material property.
- Step 3:
- Mesh the beam elements and apply the boundary conditions, which is a traditional step of the finite element method.
- Step 4:
- Perform the finite element method and use the Block Lanczos eigenvalue extraction for natural frequencies in each mode vibration of graphene sheets. If the deterministic finite element model is confirmed to be validated, the Monte Carlo simulation will commence, otherwise, return back to the step of initial configuration.
- Step 5:
- Apply the Monte Carlo simulation method to randomly disperse vacancy defects in the graphene sheets in the certain percentage. The corresponding number of chosen bonds is evident and can be used to create the vacancy defects in the graphene.
- Step 6:
- Mesh the beam elements and apply the boundary conditions, and perform the finite element model computation.
- Step 7:
- Capture the natural frequencies of graphene with vacancy defects in the vibration mode and output the results.
3. Validation of the Model
4. Results and Discussion
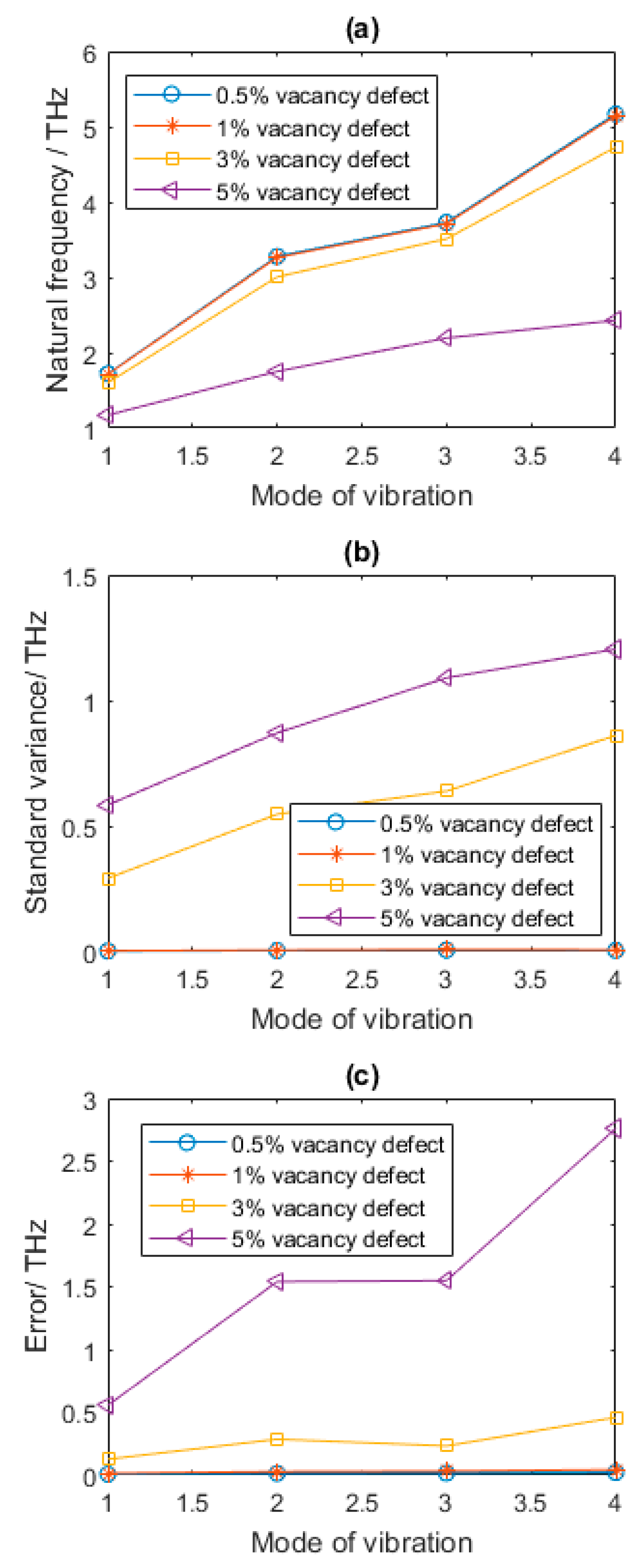
4.1. Amount of Vacancy Defects
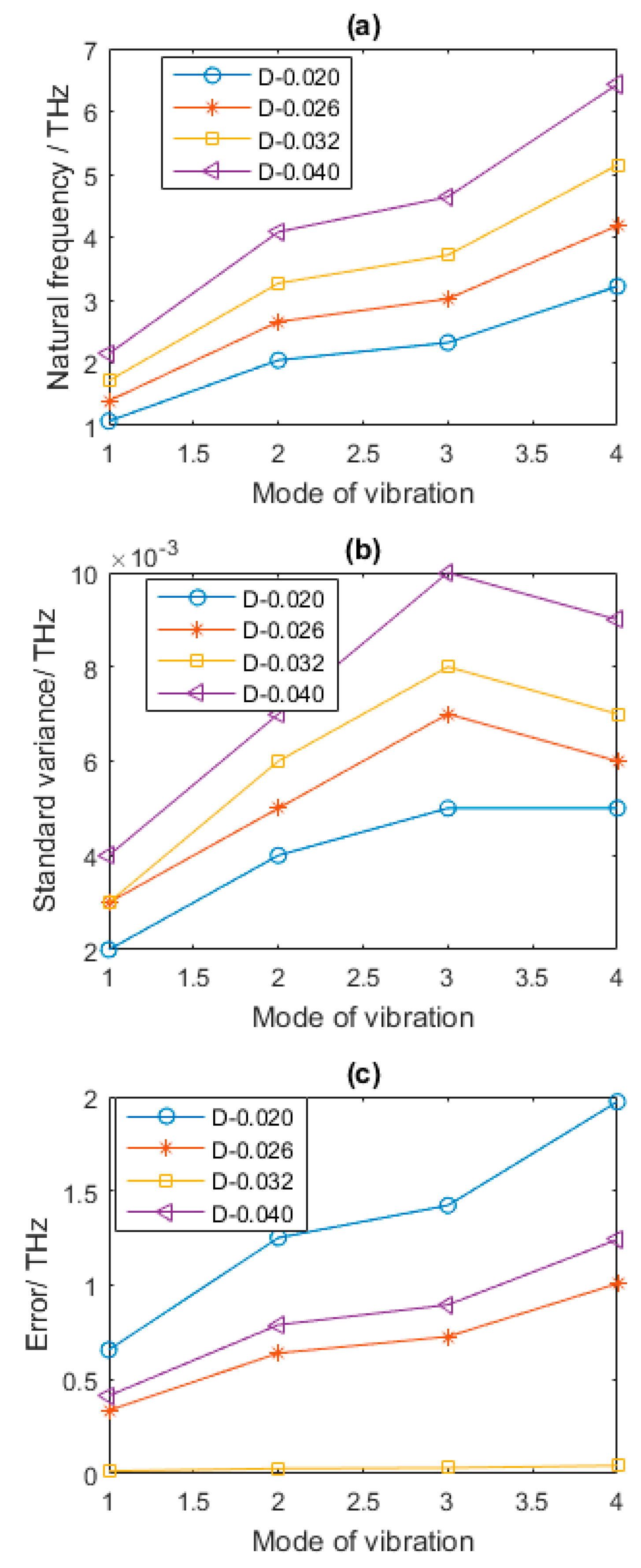
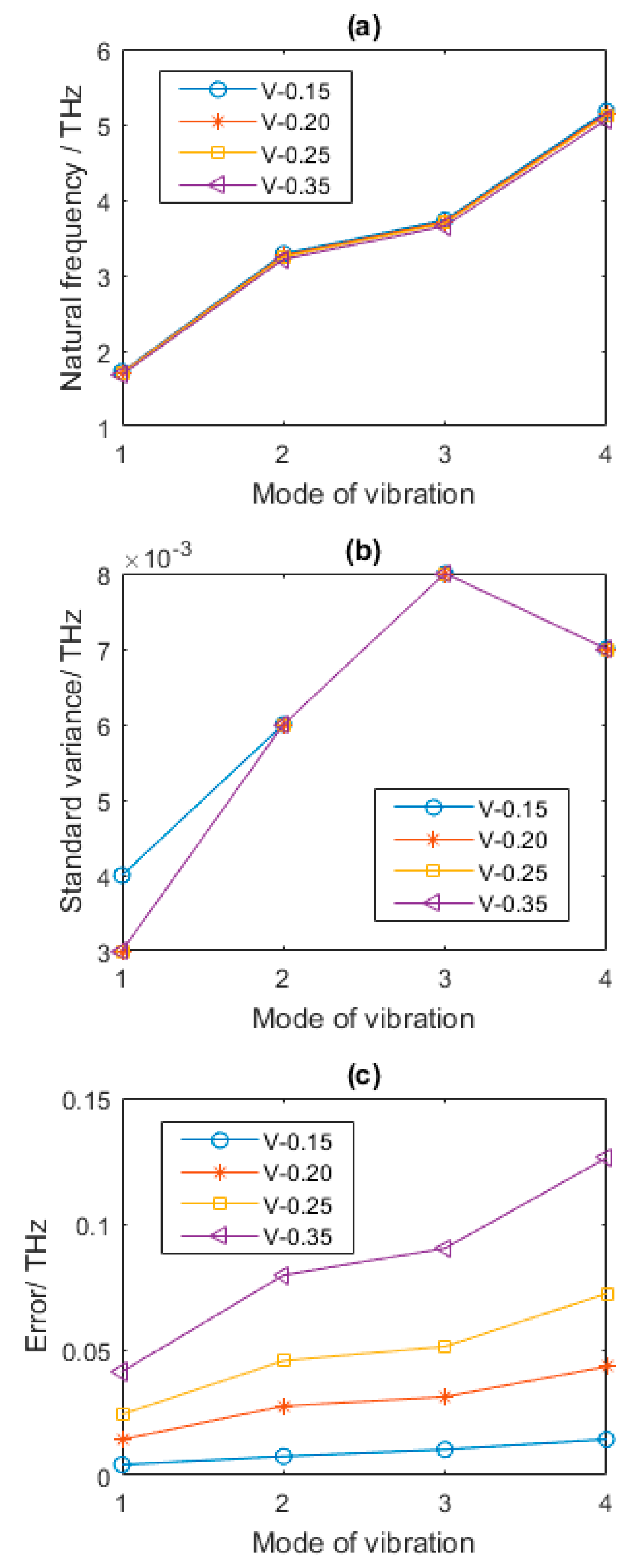
4.2. Geometrical Parameters
4.3. Material Parameters
4.4. Graphene Sheets with Vacancy Defects
5. Conclusions
- The natural frequencies of vibration decrease dramatically with the increase of the vacancy defects when Per is larger than 1%.
- The regular and symmetrical properties of vibration behavior in displacement and rotation are evidently destroyed when Per reaches 5%.
- Furthermore, with the augment of the vacancy defects quantity, the variances caused by randomly dispersion location of vacancy defects become large.
- From the discussion about geometrical and material parameters, it can be concluded that the increment of length of each bond in hexagons of graphene sheets distinctly reduces the first four order natural frequencies.
- For vacancy defected graphene sheets, the amount of hexagons in the long side of the graphene sheet has a similar effect on natural frequencies with length of each bond in hexagon, but it is more complicated.
- With the increase of thickness of the graphene sheets and Young’s modulus, the natural frequencies of vacancy defected graphene become smaller.
Author Contributions
Funding
Conflicts of Interest
References
- Lee, C.; Wei, X.; Kysar, J.W.; James, H. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Mielke, S.L.; Troya, D.; Zhang, S.; Li, L.-L.; Xiao, S.; Car, R.; Ruoff, R.S.; Schatz, G.C.; Belytschko, T. The role of vacancy defects and holes in the fracture of carbon nanotubes. Chem. Phys. Lett. 2004, 390, 413–420. [Google Scholar] [CrossRef]
- Tserpes, K.I.; Vatistas, I. Buckling analysis of pristine and defected graphene. Mech. Res. Commun. 2015, 64, 50–56. [Google Scholar] [CrossRef]
- Banhart, F.; Jani, K.; Arkady, V. Krasheninnikov Structural Defects in Graphene. ACS Nano 2011, 5, 26–41. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Thai, H.-T.; Vo, T.P. A nonlocal sinusoidal shear deformation beam theory with application to bending, buckling, and vibration of nanobeams. Int. J. Eng. Sci. 2012, 54, 58–66. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Reddy, J.N. Analytical solutions for bending, vibration, and buckling of FGM plates using a couple stress-based third-order theory. Compos. Struct. 2013, 103, 86–98. [Google Scholar] [CrossRef]
- Togun, N.; Bağdatli, S.M. Size dependent nonlinear vibration of the tensioned nanobeam based on the modified couple stress theory. Compos. Part B Eng. 2016, 97, 255–262. [Google Scholar] [CrossRef]
- Kambali, P.N.; Nikhil, V.S.; Pandey, A.K. Surface and nonlocal effects on response of linear and nonlinear NEMS devices. Appl. Math. Model. 2016, 43, 252–267. [Google Scholar] [CrossRef]
- Nazemnezhad, R.; Zare, M.; Hosseini-Hashemi, S.; Shokrollahi, H. Molecular dynamics simulation for interlayer interactions of graphene nanoribbons with multiple layers. Superlattices Microstruct. 2016, 98, 228–234. [Google Scholar] [CrossRef]
- Maslov, M.M.; Katin, K.K. High kinetic stability of hypercubane: Tight-binding molecular dynamics study. Chem. Phys. Lett. 2016, 644, 280–283. [Google Scholar] [CrossRef]
- Lee, H.W.; Moon, H.S.; Hur, J.; Kim, I.T.; Park, M.S.; Yun, J.M.; Kim, K.H.; Lee, S.G. Mechanism of sodium adsorption on N-doped graphene nanoribbons for sodium ion battery applications: A density functional theory approach. Carbon 2017, 119, 492–501. [Google Scholar] [CrossRef]
- Kundalwal, S.I.; Meguid, S.A.; Weng, G.J. Strain gradient polarization in graphene. Carbon 2017, 117, 462–472. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Sharifpour, F.; Ilkhani, M.R. On the free vibrations of size-dependent closed micro/nano spherical shell based on the modified couple stress theory. Int. J. Mech. Sci. 2016, 115–116, 501–515. [Google Scholar] [CrossRef]
- Anjomshoa, A.; Shahidi, A.R.; Hassani, B.; Jomehzadeh, E. Finite element buckling analysis of multi-layered graphene sheets on elastic substrate based on nonlocal elasticity theory. Appl. Math. Model. 2014, 38, 5934–5955. [Google Scholar] [CrossRef]
- Jing, N.; Xue, Q.; Ling, C.; Shan, M.; Zhang, T.; Zhou, X.; Jiao, Z. Effect of defects on Young’s modulus of graphene sheets: A molecular dynamics simulation. RSC Adv. 2012, 2, 9124–9129. [Google Scholar] [CrossRef]
- Xiao, J.R.; Staniszewski, J.; Gillespie, J.W., Jr. Tensile behaviors of graphene sheets and carbon nanotubes with multiple Stone–Wales defects. Mater. Sci. Eng. A 2010, 527, 715–723. [Google Scholar] [CrossRef]
- Ansari, R.; Ajori, S.; Motevalli, B. Mechanical properties of defective single-layered graphene sheets via molecular dynamics simulation. Superlattices Microstruct. 2012, 51, 274–289. [Google Scholar] [CrossRef]
- Asbaghian Namin, S.F.; Pilafkan, R. Vibration analysis of defective graphene sheets using nonlocal elasticity theory. Physics E 2017, 93, 257–264. [Google Scholar] [CrossRef]
- Ulybyshev, M.V.; Buividovich, P.V.; Katsnelson, M.I.; Polikarpov, M.I. Monte Carlo study of the semimetal-insulator phase transition in monolayer graphene with a realistic interelectron interaction potential. Phys. Rev. Lett. 2013, 111, 056801. [Google Scholar] [CrossRef] [PubMed]
- Armour, W.; Simon, H.; Strouthos, C. Monte Carlo simulation of the semimetal-insulator phase transition in monolayer graphene. Phys. Rev. B 2010, 81, 125105. [Google Scholar] [CrossRef]
- Feldner, H.; Meng, Z.Y.; Honecker, A.; Cabra, D.; Wessel, S.; Assaad, F.F. Magnetism of finite graphene samples: Mean-field theory compared with exact diagonalization and quantum Monte Carlo simulations. Phys. Rev. B 2010, 81, 115416. [Google Scholar] [CrossRef]
- Whitesides, R.; Frenklach, M. Detailed kinetic Monte Carlo simulations of graphene-edge growth. J. Phys. Chem. A 2009, 114, 689–703. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Cursi, E.S.D.; Hami, A.E.; Eid, M. Application of Latin Hypercube Sampling Based Kriging Surrogate Models in Reliability Assessment. Sci. J. Appl. Math. Stat. 2015, 3, 263–274. [Google Scholar]
- Liu, C.; Cursi, E.S.D.; Hami, A.E.; Eid, M. Reliability Based Optimization with Metaheuristic Algorithms and Latin Hypercube Sampling Based Surrogate Models. Appl. Comput. Math. 2015, 4, 462–468. [Google Scholar]
- Fang, L.; Pingbing, M.; Li, J. Ab initio calculation of ideal strength and phonon instability of graphene under tension. Phys. Rev. B 2007, 76, 064120. [Google Scholar]
- Kudin, K.N.; Scuseria, G.E.; Yakobson, B.I. C2F, BN, and C nanoshell elasticity from ab initio computations. Phys. Rev. B 2001, 64, 235406. [Google Scholar] [CrossRef]
- Gupta, S.; Dharamvir, K.; Jindal, V.K. Elastic moduli of single-walled carbon nanotubes and their ropes. Phys. Rev. B 2005, 72, 165428. [Google Scholar] [CrossRef]
- Lu, Q.; Rui, H. Nonlinear mechanics of single-atomic-layer graphene sheets. Int. J. Appl. Mech. 2009, 1, 443–467. [Google Scholar] [CrossRef]
- Wei, X.; Fragneaud, B.; Marianetti, C.A.; Kysar, J.M. Nonlinear elastic behavior of graphene: Ab initio calculations to continuum description. Phys. Rev. B 2009, 80, 205407. [Google Scholar] [CrossRef]
- Cadelano, E.; Palla, P.L.; Giordano, S.; Colombo, L. Nonlinear elasticity of monolayer graphene. Phys. Rev. Lett. 2009, 102, 235502. [Google Scholar] [CrossRef] [PubMed]
- Reddy, C.D.; Rajendran, S.; Liew, K.M. Equilibrium configuration and continuum elastic properties of finite sized graphene. Nanotechnology 2006, 17, 864. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, Y.; Cao, G. Elastic properties of monolayer graphene with different chiralities. J. Phys. Condens. Matter 2013, 25, 125302. [Google Scholar] [CrossRef] [PubMed]
- Sadeghzadeh, S.; Khatibi, M.M. Modal identification of single layer graphene nano-sheets from ambient responses using frequency domain decomposition. Eur. J. Mech. A/Solids 2017, 65, 70–78. [Google Scholar] [CrossRef]
- Tserpes, K.I.; Papanikos, P. Finite element modeling of single-walled carbon nanotubes. Compos. B Eng. 2005, 36, 468–477. [Google Scholar] [CrossRef]
- Sang, J.L.; Park, K.S. Vibrations of Timoshenko beams with isogeometric approach. Appl. Math. Model. 2013, 37, 9174–9190. [Google Scholar]
- Shang, H.Y. Enriched finite element methods for Timoshenko beam free vibration analysis. Appl. Math. Model. 2016, 40, 7012–7033. [Google Scholar] [CrossRef]
- Rajakumar, C. Lanczos algorithm for the quadratic eigenvalue problem in engineering applications. Comput. Methods Appl. Mech. Eng. 1993, 105, 1–22. [Google Scholar] [CrossRef]
- Cullum, J.; Willoughby, R.A. A survey of Lanczos procedures for very large real ‘symmetric’ eigenvalue problems. J. Comput. Appl. Math. 1985, 12–13, 37–60. [Google Scholar] [CrossRef]
- López-Polín, G.; Gómez-Navarro, C.; Parente, V.; Guinea, F.; Katsnelson, M.I.; Perez-Murano, F.; Gomez-Herrero, J. Increasing the elastic modulus of graphene by controlled defect creation. Nat. Phys. 2014, 11, 26–31. [Google Scholar] [CrossRef]
- Dettori, R.; Cadelano, E.; Colombo, L. Elastic fields and moduli in defected graphene. J. Phys. Condens. Matter 2012, 24, 104020. [Google Scholar] [CrossRef] [PubMed]
- Tserpes, K.I. Strength of graphenes containing randomly dispersed vacancies. Acta Mech. 2012, 223, 669–678. [Google Scholar] [CrossRef]
- Shen, L.; Jackie, L. Transversely isotropic elastic properties of multiwalled carbon nanotubes. Phys. Rev. B 2005, 71, 035412. [Google Scholar] [CrossRef]
- Tserpes, K.I.; Papanikos, P. The effect of Stone–Wales defect on the tensile behavior and fracture of single-walled carbon nanotubes. Compos. Struct. 2007, 74, 581–589. [Google Scholar] [CrossRef]
- Pellegrino, F.M.D.; Angilella, G.G.N.; Pucci, R. Effect of impurities in high-symmetry lattice positions on the local density of states and conductivity of graphene. Phys. Rev. B 2009, 80, 094203. [Google Scholar] [CrossRef]
- Parisi, L.; Angilella, G.G.N.; Deretzis, I.; Renato, P.; Magna, A.L. Role of H Distribution on Coherent Quantum Transport of Electrons in Hydrogenated Graphene. Condens. Matter 2017, 2, 37. [Google Scholar] [CrossRef]

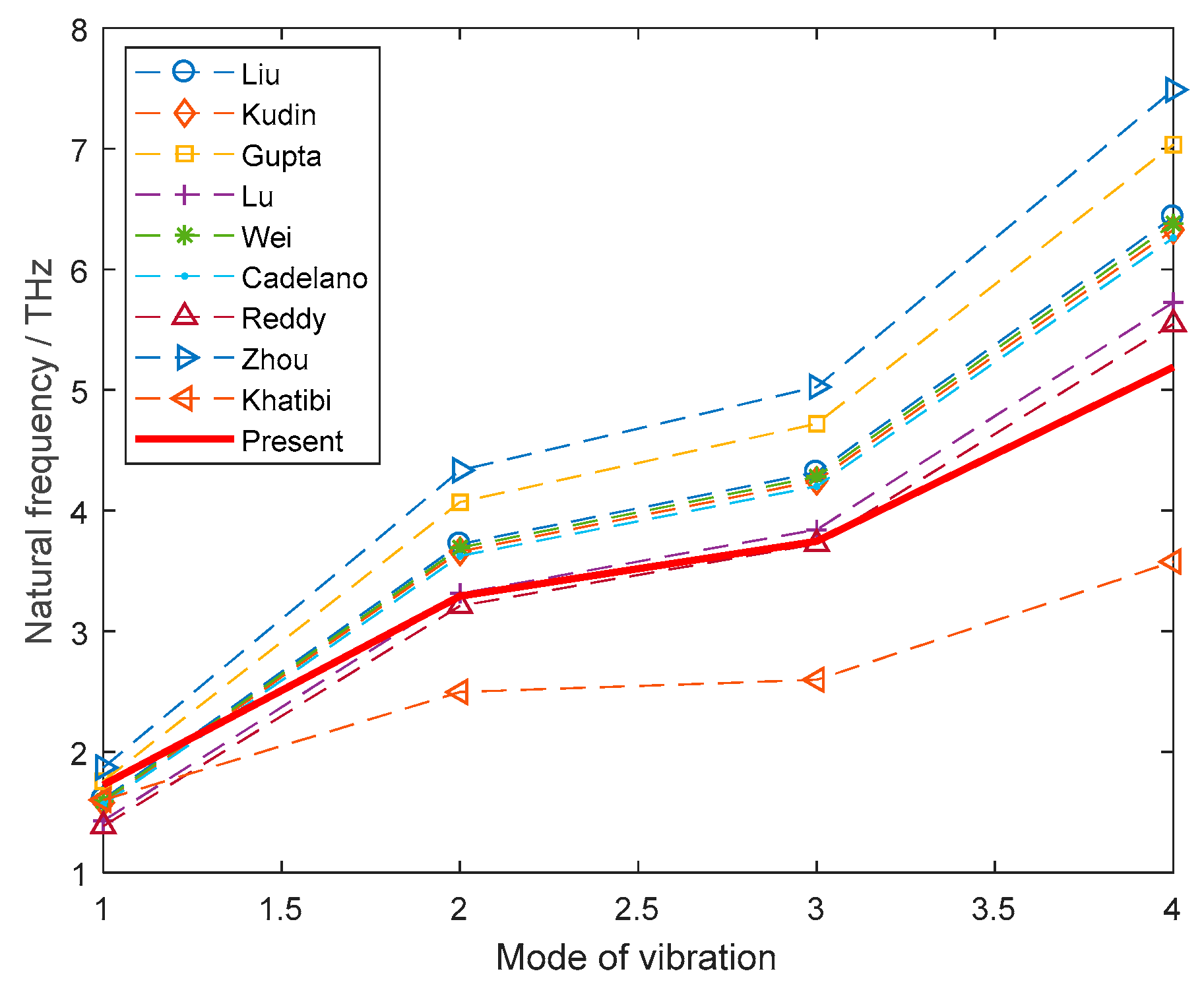




| Reference | Simulation Method | Elastic Modulus (TPa) | Poisson’s Ratio | 1/THz | 2/THz | 3/THz | 4/THz |
|---|---|---|---|---|---|---|---|
| Liu [26] | DFT | 1.050 | 0.186 | 1.6081 | 3.7232 | 4.3172 | 6.4323 |
| Kudin [27] | DFT | 1.029 | 0.149 | 1.5818 | 3.6623 | 4.2466 | 6.3271 |
| Gupta [28] | MD | 1.272 | 0.147 | 1.7581 | 4.0706 | 4.7201 | 7.0325 |
| Lu [29] | MD | 0.725 | 0.398 | 1.4311 | 3.3135 | 3.8422 | 5.7246 |
| Wei [30] | DFT | 1.039 | 0.169 | 1.5946 | 3.6921 | 4.2811 | 6.3786 |
| Cadelano [31] | TB | 0.931 | 0.310 | 1.5649 | 3.6232 | 4.2012 | 6.2595 |
| Reddy [32] | MM | 0.669 | 0.416 | 1.3869 | 3.2111 | 3.7234 | 5.5475 |
| Zhou [33] | MM | 1.167 | 0.456 | 1.8716 | 4.3334 | 5.0248 | 7.4865 |
| Khatibi [34] | MD + FDD | 1.050 | 0.170 | 1.6030 | 2.4970 | 2.5980 | 3.5770 |
| Present | SFEM | 1.200 | 0.200 | 1.7282 | 3.2925 | 3.7442 | 5.1892 |
| Per (%) | Mode | Mean (THz) | Variance^0.5 | Skewness | Kurtosis |
|---|---|---|---|---|---|
| 0.5 | 1 | 1.721 | 0.002 | −0.852 | 5.179 |
| 2 | 3.279 | 0.004 | −0.646 | 3.751 | |
| 3 | 3.729 | 0.006 | −0.536 | 3.935 | |
| 4 | 5.168 | 0.005 | −0.620 | 3.625 | |
| 1 | 1 | 1.714 | 0.003 | −0.446 | 3.144 |
| 2 | 3.265 | 0.006 | −0.559 | 3.558 | |
| 3 | 3.713 | 0.008 | −0.495 | 3.537 | |
| 4 | 5.146 | 0.007 | −0.308 | 2.757 | |
| 3 | 1 | 1.602 | 0.292 | −5.313 | 29.246 |
| 2 | 3.007 | 0.547 | −5.312 | 29.240 | |
| 3 | 3.512 | 0.639 | −5.312 | 29.242 | |
| 4 | 4.730 | 0.861 | −5.312 | 29.243 | |
| 5 | 1 | 1.172 | 0.584 | −1.488 | 3.247 |
| 2 | 1.752 | 0.871 | −1.491 | 3.270 | |
| 3 | 2.196 | 1.090 | −1.501 | 3.300 | |
| 4 | 2.429 | 1.204 | −1.509 | 3.316 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, L.; Shi, J.; Souza de Cursi, E. Vibration Analysis of Vacancy Defected Graphene Sheets by Monte Carlo Based Finite Element Method. Nanomaterials 2018, 8, 489. https://doi.org/10.3390/nano8070489
Chu L, Shi J, Souza de Cursi E. Vibration Analysis of Vacancy Defected Graphene Sheets by Monte Carlo Based Finite Element Method. Nanomaterials. 2018; 8(7):489. https://doi.org/10.3390/nano8070489
Chicago/Turabian StyleChu, Liu, Jiajia Shi, and Eduardo Souza de Cursi. 2018. "Vibration Analysis of Vacancy Defected Graphene Sheets by Monte Carlo Based Finite Element Method" Nanomaterials 8, no. 7: 489. https://doi.org/10.3390/nano8070489






